A Hybrid Deep Reinforcement Learning and Metaheuristic Framework for Heritage Tourism Route Optimization in Warin Chamrap’s Old Town
Abstract
1. Introduction
2. Related Work
2.1. Multi-Objective Metaheuristics for Tourism Route Planning
2.2. Deep Reinforcement Learning for Adaptive and Context-Aware Routing
2.3. Hybridization of Learning and Metaheuristic Strategies
2.4. Digital Twin Environments for Tourism and Mobility Systems
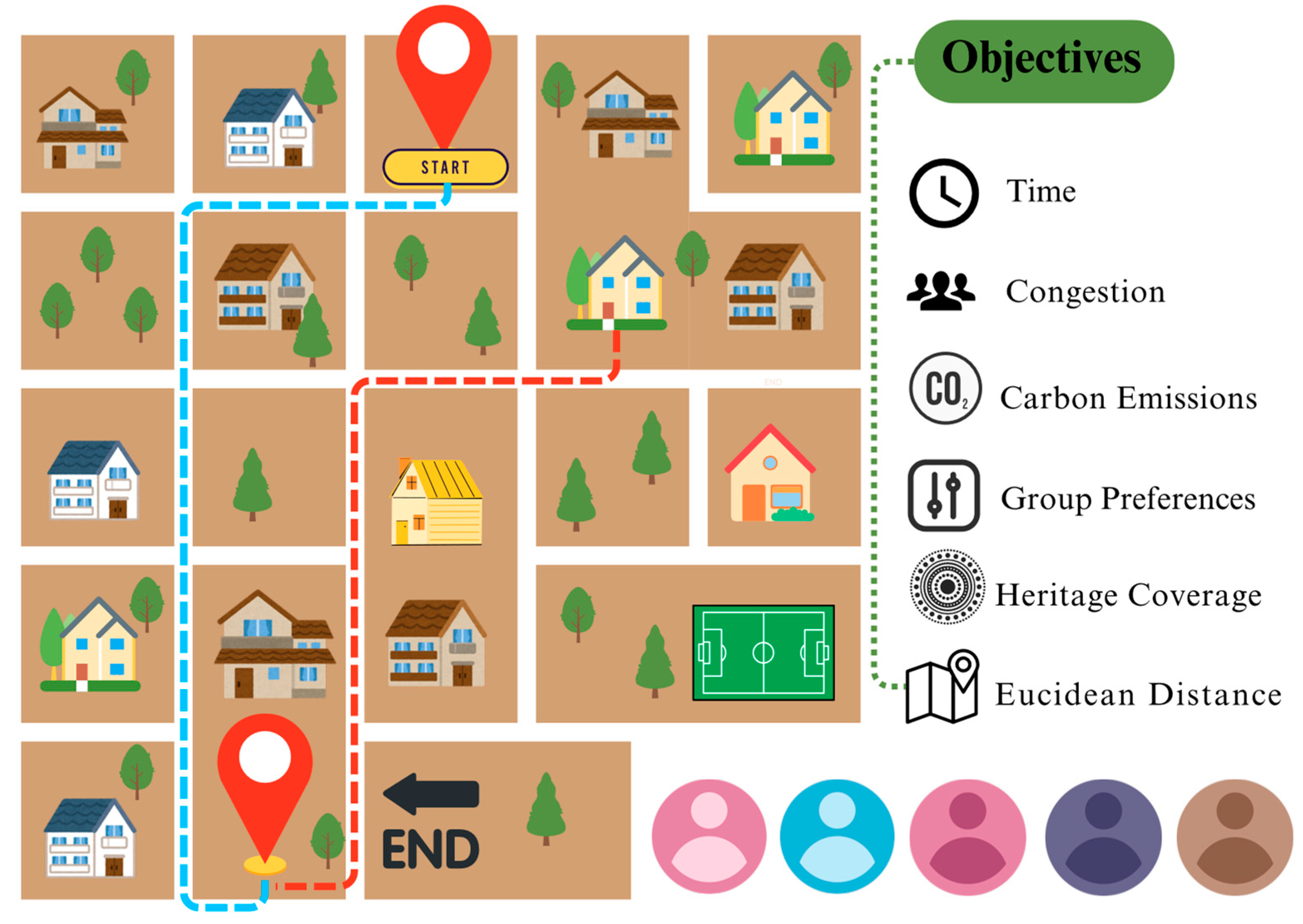
3. Problem Formulation
- Sets and Indices
| Set of all POIs (points of interest), with generic elements | |
| Set of directed pedestrian arcs | |
| POI subsets by category | |
| Designated start and end nodes | |
| set of group members, with generic element |
- Parameters
| Symbol | Domain | Interpretation |
| heritage (coverage) score of POI i | ||
| average dwell time at i | ||
| walking time along arc (i,j) | ||
| Euclidean distance (i,j) | ||
| carbon emissions on (i,j) | ||
| real-time congestion index at i | ||
| heading angle of arc (i,j) | ||
| global route-time budget | ||
| total emissions cap | ||
| cumulative congestion cap | ||
| total walking-distance cap | ||
| minimum visits per category | ||
| maximum POIs in the route | ||
| big-MMM constant for timing constraints | ||
| preference score of member g for POI i | ||
| individual time budget of g | ||
| minimum satisfaction required for g | ||
| weights for scalarised objective |
- Decision Variables
| 1 if arc is traversed | |
| 1 if POI I is visited | |
| Arrival time at POI i | |
| Auxiliary MTZ variable for subtour elimination | |
| 1 if member g is “satisfied” by visiting i |
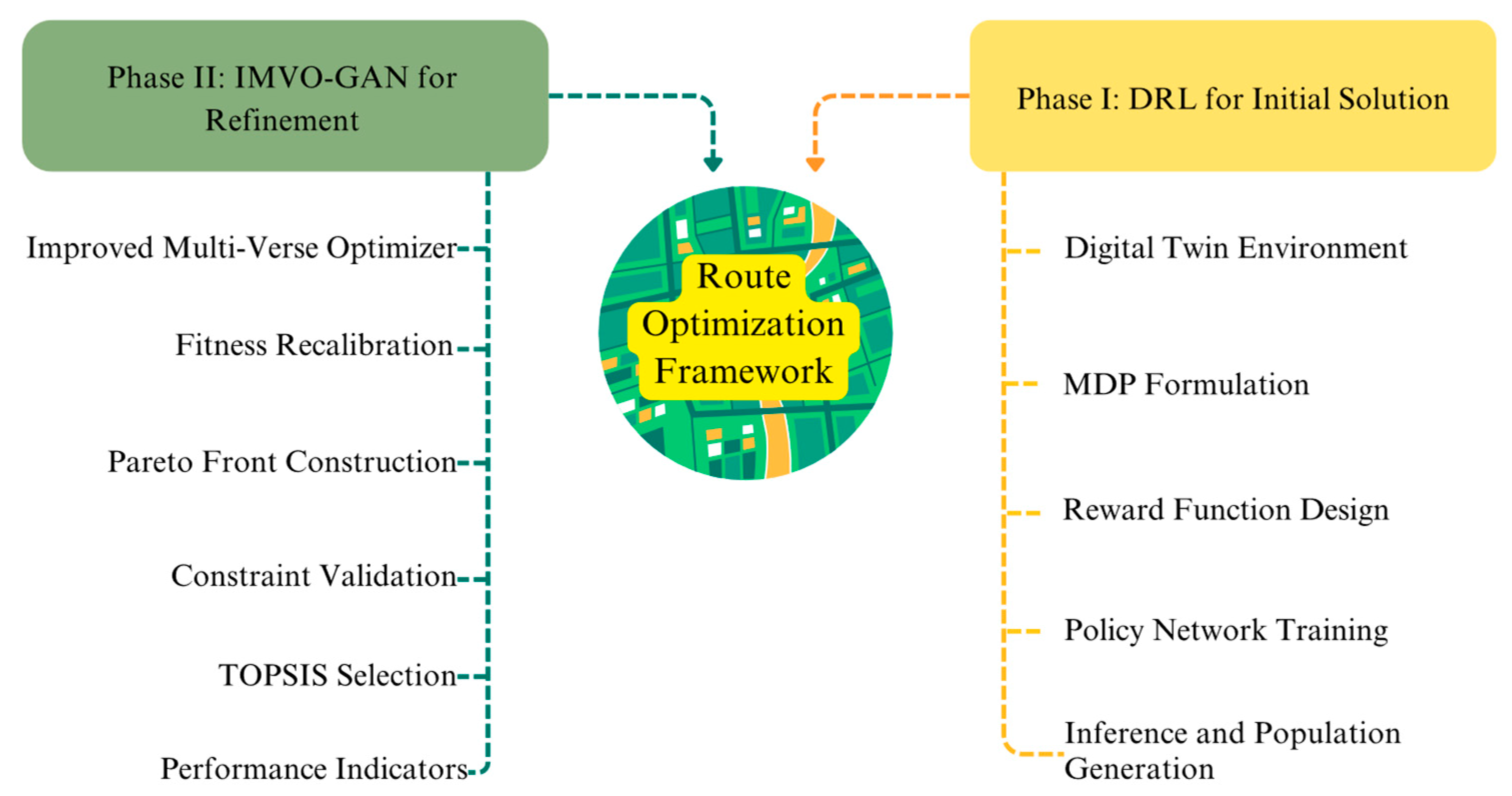
4. Research Methodology
4.1. Case Study: Heritage-Tour Planning in Warin Chamrap’s Old Town
Study Area, POI Inventory, and Infrastructure Modelling
4.2. Phase I: Deep Reinforcement Learning for Solution Construction
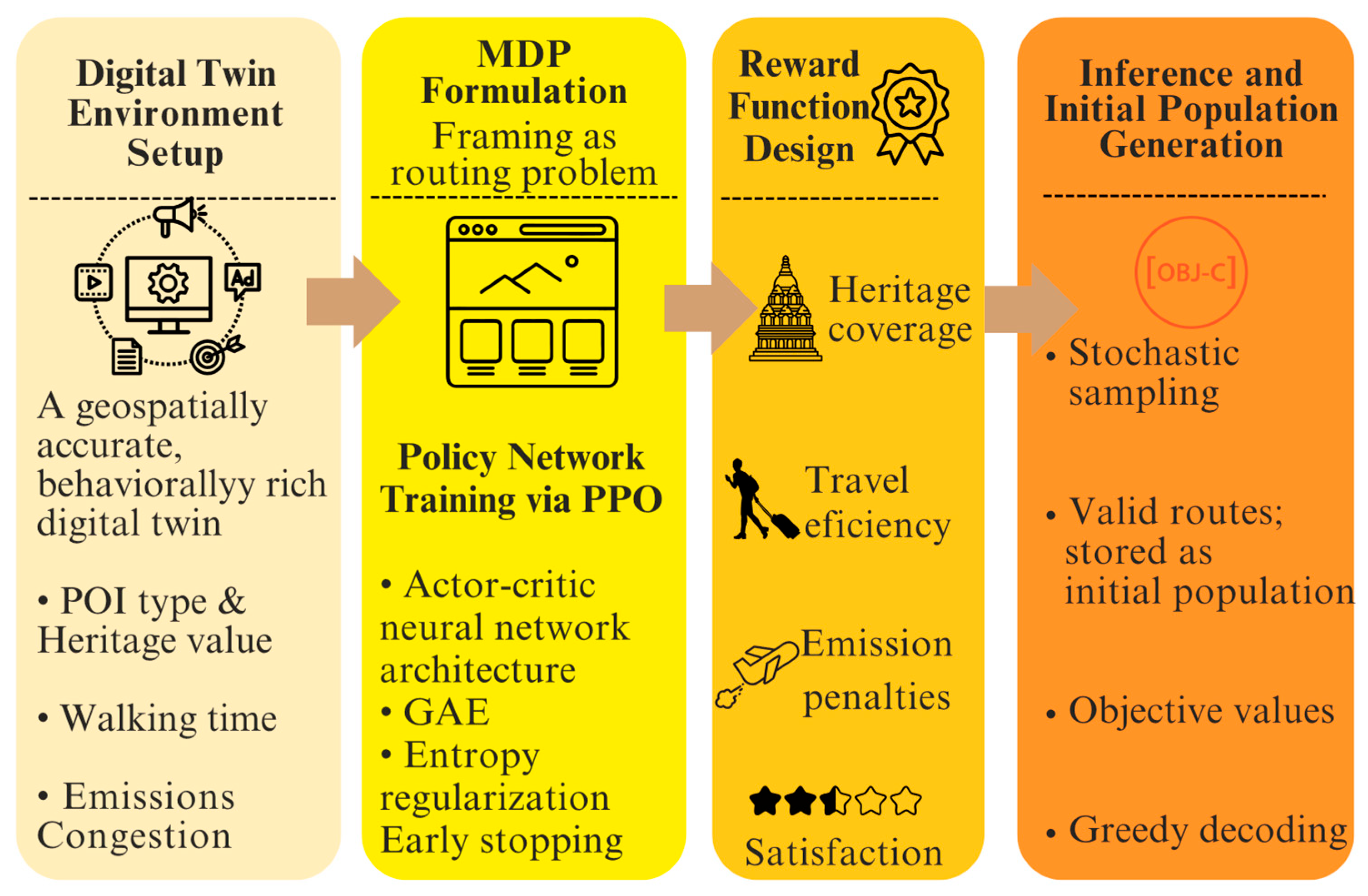
4.2.1. Digital Twin Environment
- Spatial positions and category types of POIs: Each node is mapped using GPS coordinates derived from open-source geospatial databases and verified by municipal land-use records. Each POI is categorized into one of several functional groups, such as historic houses, temples, museums, or food establishments. Metadata for each POI includes average dwell time, operating hours, cultural significance (heritage score), and group relevance (preference weight vectors).
- Arc-based pedestrian infrastructure with travel time and distance matrices: The arcs in set AAA are extracted from high-resolution pedestrian networks using OpenStreetMap and cross-validated with satellite imagery and ground surveys. Each arc is annotated with its Euclidean distance , estimated walking time , and angular direction , for use in route smoothness evaluation. These attributes are stored in sparse matrices and accessed during state transitions in the DRL framework.
- Real-time and historical crowd density heatmaps: A time-indexed congestion index is assigned to each POI using data aggregated from mobile device signals, CCTV analytics, and historical pedestrian surveys. This layer allows the digital twin to dynamically reflect variable foot traffic across different times of day, enabling the routing agent to anticipate and adapt to crowding effects.
- Carbon emission coefficients for walking paths: Each arc is also assigned an emission estimate , based on energy expenditure models for pedestrian locomotion under urban conditions. While walking itself is low-emission, total route emissions are still tracked and constrained to reflect carbon accountability in sustainable tourism systems.
4.2.2. MDP Formulation and Policy Design
- is the set of environment states,
- is the set of admissible actions,
- defines transition dynamics,
- is the reward function,
- is the reward discount factor, and
- is the maximum decision horizon.
State Representation
- is the current POI,
- is a binary visitation vector,
- denote cumulative travel time, emissions, and distance,
- tracks visited POIs by category (house, restaurant, museum),
- is the group preference vector.
Action Space and Feasibility Masking
Transition Dynamics
- incrementing cumulative metrics based on ,
- updating the visitation vector ,
- incrementing the relevant category count in ,
- changing the current location to .
Policy Parameterization
Episode Termination
- The terminal POI is reached (i.e., the end-node constraint is satisfied),
- No further feasible POIs remain in
- Any hard constraint (e.g., time or emission) is violated during an attempted transition.
4.2.3. Reward Function Design
Composite Reward Structure
- 1.
- Heritage Coverage Reward ()
- 2.
- Travel Efficiency Penalty ()
- 3.
- Emission Control Penalty ()
- 4.
- Quota Fulfillment Reward ()
- 5.
- Group Preference Satisfaction Reward ()
- 6.
- Smoothness Reward ()
- 7.
- Infeasibility Penalty ()
Terminal Rewards and Episode Evaluation
- A feasibility bonus is awarded if all constraints (e.g., time, quota, emissions, end node reachability) are satisfied.
- A completeness reward is issued if all five objective dimensions (heritage, travel, emissions, satisfaction, smoothness) exceed predefined performance thresholds.
- A failure penalty is applied if the episode terminates prematurely due to infeasibility or dead ends.
Reward Normalization and Curriculum Scheduling
4.2.4. Policy Network Architecture and Training Procedure
Neural Network Architecture
Input Layer
- Current POI Position: A one-hot encoded vector of size where the index corresponding to the current POI is set to 1, and all others to 0.Example (for and current POI = node 3):
- Cumulative Travel Metrics: Three normalized scalar values representing total time used, total emissions, and total walking distance up to step t.Example:
- POI Visitation History: A binary vector of size ∣N∣ indicating whether each POI has been visited (1) or not (0).Example (nodes 0, 2, and 3 visited):
- Category Quota Progress: A 3-dimensional integer vector tracking how many POIs from each mandatory category (e.g., house, restaurant, museum) have been visited.Example (2 houses, 1 restaurant, 0 museums visited):
- Group Preference Vector: A continuous vector representing the interest level of the tourist group for each POI. This captures personalized bias toward specific nodes.Example (simplified preference weights):
- Normalized Remaining Budgets: A 3-dimensional vector indicating the proportion of remaining time, emissions, and distance budget (all normalized to [0, 1]).Example (70% time left, 90% emissions left, 60% distance left):
- 8 dimensions for current POI position,
- 3 for cumulative metrics,
- 8 for visitation flags,
- 3 for quota progress,
- 8 for preferences,
- and 3 for normalized budgets—totaling 33 dimensions.
- Encoder Backbone: The shared backbone consists of two fully connected layers of size 256 and 128 neurons, respectively, each followed by ReLU activations and dropout layers (rate = 0.2) for regularization. This subnetwork extracts high-level routing context features from the raw state input.
- Actor Head: The actor network outputs a probability distribution over the current admissible action set To ensure constraint compliance, infeasible actions are masked before Softmax normalization (Equation (28)):where is the encoder output, is the feasibility mask, and denotes elementwise multiplication.
- Critic Head: The critic estimates the state-value function using a separate linear layer over the shared encoding (Equation (29)):
Training Configuration
Constraint-Aware Sampling and Masking
Curriculum Learning and Policy Stabilization
- Early stopping based on validation reward trends,
- Reward normalization based on moving average bounds, and
- Periodic reseeding to encourage diversity when learning plateaus.
4.2.5. Initial Solution Set Extraction
DRL-Guided Solution Sampling
- Greedy decoding (maximum likelihood) is employed in 40% of the runs to promote high-reward exploitation.
- Stochastic sampling is used in 60% of the runs to encourage exploratory variation and structure diversity.
Feasibility Enforcement and Route Validation
- The total cumulative travel time does not exceed the global time budget ,
- Emissions and walking distance remain within upper bounds
- Required category quotas are fulfilled,
- All POIs in the route are distinct (no repetition), and the sequence includes the designated end node t,
- All group members achieve their required minimum preference satisfaction
Structure of the Initial Solution Set
- POI sequence:
- Arc decision matrix : binary indicators of arc traversals,
- Arrival time vector
- Quota count vector
- Group satisfaction scores for each ,
- Objective function values: (heritage), (travel time), (emissions), (smoothness), (group satisfaction).
Diversity Maintenance and Quality Screening
- Levenshtein distance between POI sequences,
- Hamming distance between visitation vectors,
- or Pareto-dominance novelty in objective space.
Representative Examples
4.3. Phase II: IMVO-GAN Refinement and Local Search
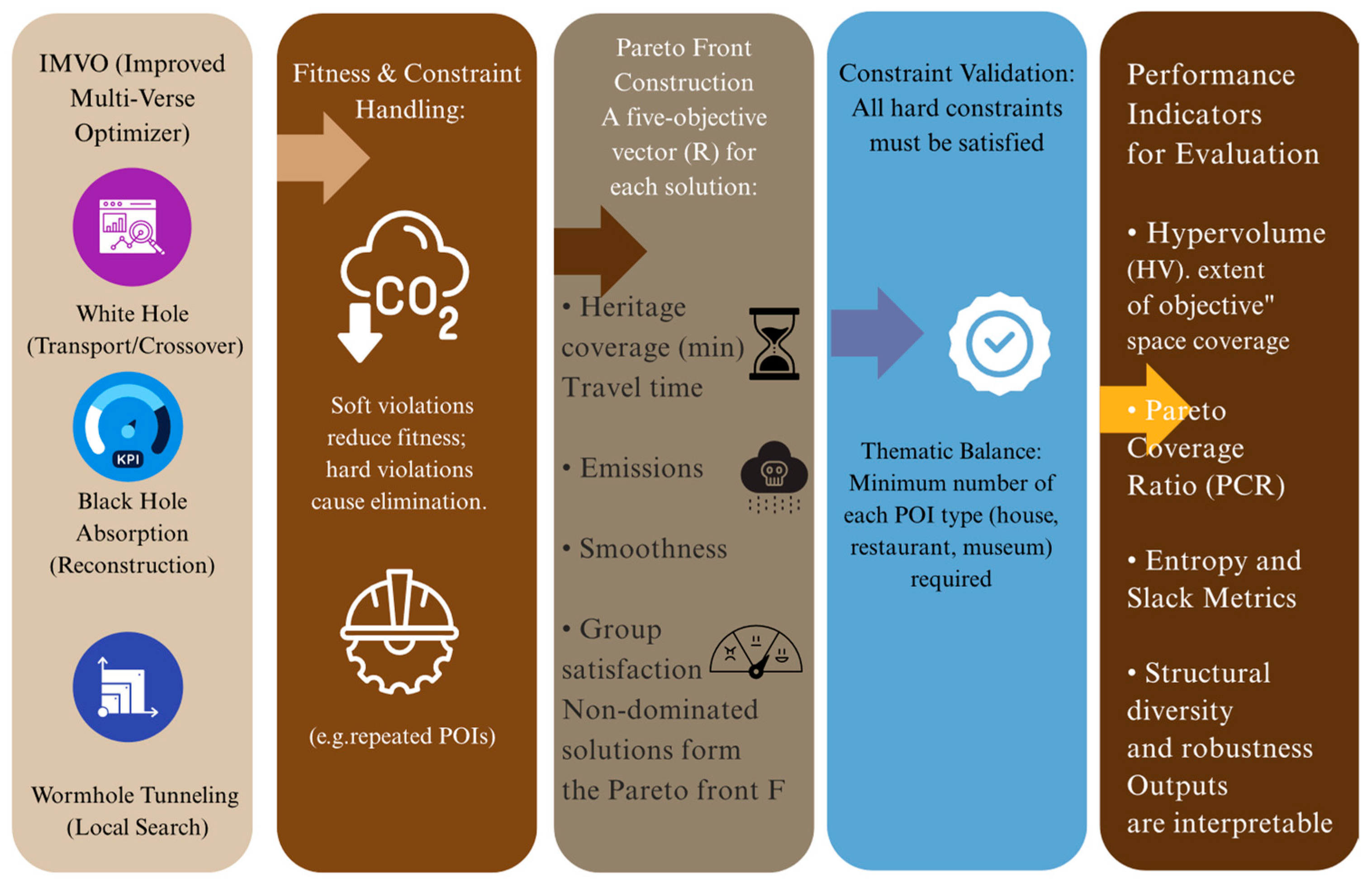
Improved Multi-Verse Optimizer (IMVO) for Constraint-Aware Evolution
Universe Representation and Fitness Scaling
Evolutionary Mechanics and Examples
- White Hole Transport (Crossover)
- Black Hole Absorption (Replacement)
- Wormhole Tunneling (Local Perturbation)
- –
- POI swaps: Exchanging positions of two non-adjacent POIs, such as swapping C and E in , resulting in .
- –
- Segment reversals: Reversing in the same route produces, which may improve angular smoothness.
- –
- Conditional insertions: Inserting a highly preferred POI before the end node if remaining time budget allows, such as:
Constraint-Adaptive Fitness Adjustment
- , , , and represent soft violations in time, emissions, category quotas, and group satisfaction, respectively;
- are empirically tuned penalty coefficients.
Evolution Control and Termination
- Maintains an elitist archive of non-dominated solutions,
- Preserves structural variety via POI visitation entropy and angular transition variance,
- Dynamically adjusts selection pressure based on front dispersion and constraint stress levels.
4.4. Solution Evaluation and Pareto Front Construction
- : heritage coverage adjusted for crowd congestion (maximize),
- : total travel time (minimize),
- : cumulative carbon emissions (minimize),
- : angular deviation representing route smoothness (minimize),
- : group preference satisfaction (maximize).
| Algorithm 1. DRL-based personalized tour construction in digital twin. |
| Algorithm DRL-Based Personalized Tour Construction in Digital Twin Input: Digital Twin Graph G(N, A), preference profiles p_g for group G, constraints B^{time}, B^{CO2}, Q^{category}, terminal node t Output: Initial solution population \mathcal{P}_0 of feasible tour routes 1: Initialize digital twin environment with: a. POI metadata: category, dwell time, heritage score, operating hours b. Arc attributes: distance d_{ij}, time \tau_{ij}, emissions \epsilon_{ij}, angle \phi_{ij} c. Real-time congestion heatmaps \kappa_i(t) d. Group preference vector p_g 2: Define Markov Decision Process M = \langle S, A, P, R, \gamma, T_{max} \rangle a. State s_t = [current POI x_t, visitation vector v_t, cumulative metrics \Delta, quota q_t, preference p_g] b. Action a_t: next POI j in filtered feasible set A(s_t) c. Transition: update state s_{t+1} with cumulative \Delta metrics and POI j d. Reward r_t = weighted combination of 7 sub-rewards (heritage, travel, emission, quota, satisfaction, smoothness, penalty) 3: Design policy network \pi_\theta(a_t|s_t) using actor-critic PPO with: a. Feature vector f_t = concat(x_t, \Delta metrics, v_t, q_t, p_g, normalized budget) b. Actor head: action logits over A(s_t) with softmax masking c. Critic head: state-value V_\psi(s_t) d. Train using PPO: GAE, reward normalization, entropy regularization 4: Curriculum learning: a. Begin with relaxed constraints (B^{time}_{init}, Q^{category}_{init}) b. Tighten every epoch toward real-world thresholds c. Use early stopping when policy stabilizes 5: Inference mode: a. For i = 1 to NP do: i. Sample full episode with \pi_\theta using greedy (40%) or stochastic (60%) decoding ii. Construct candidate route R_k with full POI sequence and trajectory metadata iii. Validate R_k under hard constraints: - Time, Emission, Distance Budget - Category Quotas - Terminal POI match (x_T = t) - Group satisfaction minimum \sum_i p_{ig} \geq R_g, \forall g iv. If R_k is valid and diverse, add to \mathcal{P}_0 b. Until |\mathcal{P}_0| = NP 6: Return \mathcal{P}_0 as initial feasible, diverse, and personalized population |
4.5. Parameter Configuration and Constraint Settings
4.5.1. Simulation Protocol
4.5.2. Evaluation Metrics
4.6. Compared Methods
5. Computational Results and Performance Evaluation
5.1. Comparative Evaluation of Multi-Objective Optimization Performance
5.2. Ablation Study: Evaluating the Effectiveness of Individual Framework Components
5.3. Performance Under Preference-Oriented Weighting Schemes
5.3.1. Equal-Weight Scenario (All Objectives Weighted Equally)
5.3.2. Heritage-Focused Scenario (F1 = 0.6)
5.3.3. Travel Time-Focused Scenario (F2 = 0.6)
5.3.4. Emissions-Focused Scenario (F3 = 0.6)
5.3.5. Smoothness-Focused Scenario (F4 = 0.6)
5.3.6. Group Preference-Focused Scenario (F5 = 0.6)
5.4. Generalization Across User Group Types and Interest Diversity
5.5. Zero/Few-Shot Transfer to Unseen Scenarios
- Zero-Shot: New POIs–introducing 12 new POIs (not seen during training), including mixed-category sites and unbalanced heritage values.
- Zero-Shot: Altered Congestion Patterns–dynamically shifting κᵢ values to simulate peak-hour or festival-period congestion intensities.
- Few-Shot: New Group Profiles–injecting five new simulated tourist profiles with distinct interest distributions and constraints.
- Few-Shot: Reduced Emissions Budget–reducing the available emission allowance (B_CO2) from 1.8 kg to 1.2 kg to test eco-constrained adaptability.
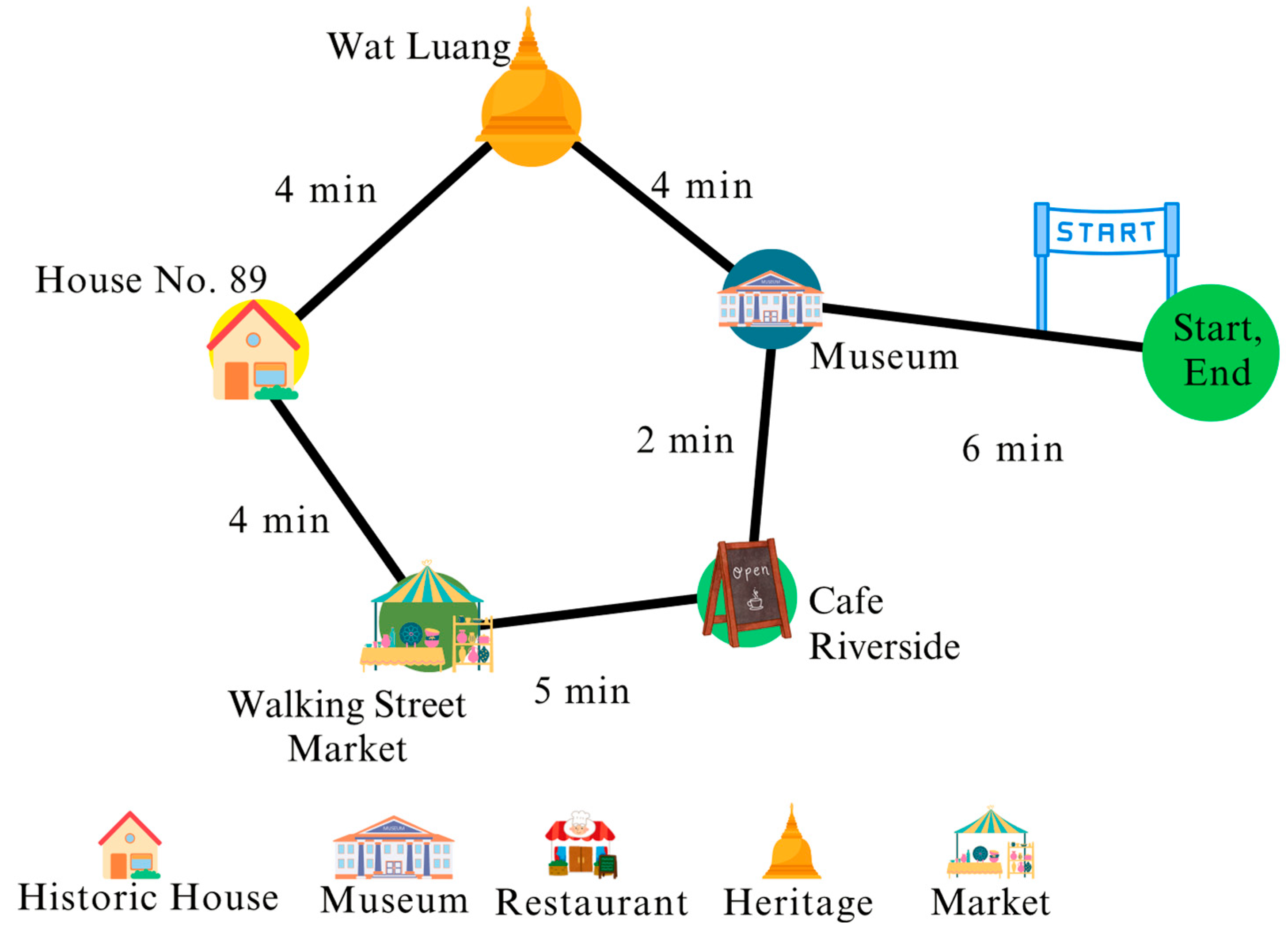
5.6. Route Visualization and Behavioral Interpretation
- The early inclusion of high-heritage POIs with low congestion scores (e.g., Wat Luang) maximizes F1 and F5 in the first half of the tour.
- The mid-route transition to restaurants illustrates balancing F2 (travel time) and F3 (carbon emissions), as these sites were spatially clustered and accessible via short, smooth transitions.
- The route ends with Walking Street, selected for its proximity to the exit node and alignment with both F5 (preference) and F4 (angular smoothness).
5.7. Multi-Objective Convergence Trajectories
6. Discussion
6.1. Performance of the Proposed Method
6.2. Robustness and Adaptability
6.3. Interpretability and Behavioral Coherence
6.4. Practical and Strategic Implications
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, B.; Xiao, X.; Wang, Y.; Kang, Y.; Chen, Y.; Wang, P.; Lin, H. Concept and Framework of Digital Twin Human Geographical Environment. J. Environ. Manag. 2025, 373, 123866. [Google Scholar] [CrossRef]
- Alvi, M.; Dutta, H.; Minerva, R.; Crespi, N.; Raza, S.M.; Herath, M. Global Perspectives on Digital Twin Smart Cities: Innovations, Challenges, And Pathways to A Sustainable Urban Future. Sustain. Cities Soc. 2025, 126, 106356. [Google Scholar] [CrossRef]
- Di Napoli, C.; Paragliola, G.; Ribino, P.; Serino, L. Deep-Reinforcement-Learning-Based Planner for City Tours for Cruise Passengers. Algorithms 2023, 16, 362. [Google Scholar] [CrossRef]
- Orabi, M.; Afyouni, I.; Al Aghbari, Z. TourPIE: Empowering Tourists with Multi-Criteria Event-Driven Personalized Travel Sequences. Inf. Process. Manag. 2025, 62, 103970. [Google Scholar] [CrossRef]
- Pitakaso, R.; Sethanan, K.; Chien, C.-F.; Srichok, T.; Khonjun, S.; Nanthasamroeng, N.; Gonwirat, S. Integrating Reinforcement Learning and Metaheuristics for Safe and Sustainable Health Tourist Trip Design Problem. Appl. Soft Comput. 2024, 161, 111719. [Google Scholar] [CrossRef]
- Song, J.; Chen, Y. Optimizing Cultural Heritage Tourism Routes Using Q-Learning: A Case Study of Macau. Sustain. Communities 2025, 2, 2475794. [Google Scholar] [CrossRef]
- Aliahmadi, S.Z.; Jabbarzadeh, A.; Hof, L.A. A Multi-Objective Optimization Approach for Sustainable and Personalized Trip Planning: A Self-Adaptive Evolutionary Algorithm with Case Study. Expert Syst. Appl. 2025, 261, 125412. [Google Scholar] [CrossRef]
- Pinho, M.; Leal, F. AI-Enhanced Strategies to Ensure New Sustainable Destination Tourism Trends Among the 27 European Union Member States. Sustainability 2024, 16, 9844. [Google Scholar] [CrossRef]
- Suanpang, P.; Pothipassa, P. Integrating Generative AI and IoT for Sustainable Smart Tourism Destinations. Sustainability 2024, 16, 7435. [Google Scholar] [CrossRef]
- Ding, X.; Zheng, M.; Zheng, X. The Constraints of Tourism Development for A Cultural Heritage Destination: The Case of Kampong Ayer (Water Village) in Brunei Darussalam. Land 2021, 10, 526. [Google Scholar] [CrossRef]
- Filho, A.A.; Morabito, R. An Effective Approach for Bi-Objective Multi-Period Touristic Itinerary Planning. Expert Syst. Appl. 2024, 240, 122437. [Google Scholar] [CrossRef]
- Ghobadi, F.; Divsalar, A.; Jandaghi, H.; Nozari, R.B. An Integrated Recommender System for Multi-Day Tourist Itinerary. Appl. Soft Comput. 2023, 149, 110942. [Google Scholar] [CrossRef]
- Pitakaso, R.; Srichok, T.; Khonjun, S.; Gonwirat, S.; Nanthasamroeng, N.; Boonmee, C. Multi-Objective Sustainability Tourist Trip Design: An Innovative Approach for Balancing Tourists’ Preferences with Key Sustainability Considerations. J. Clean. Prod. 2024, 449, 141486. [Google Scholar] [CrossRef]
- Sabar, N.R.; Bhaskar, A.; Chung, E.; Turky, A.; Song, A. A Self-Adaptive Evolutionary Algorithm for Dynamic Vehicle Routing Problems with Traffic Congestion. Swarm Evol. Comput. 2019, 44, 1018–1027. [Google Scholar] [CrossRef]
- Zhang, S.; Lin, J.; Feng, Z.; Wu, Y.; Zhao, Q.; Liu, S.; Ren, Y.; Li, H. Construction of Cultural Heritage Evaluation System and Personalized Cultural Tourism Path Decision Model: An International Historical and Cultural City. J. Urban Manag. 2023, 12, 96–111. [Google Scholar] [CrossRef]
- Lin, X.; Shen, Z.; Teng, X.; Mao, Q. Cultural Routes as Cultural Tourism Products for Heritage Conservation and Regional Development: A Systematic Review. Heritage 2024, 7, 2399–2425. [Google Scholar] [CrossRef]
- Xue, Y.; Bao, G.; Tan, C.; Chen, H.; Liu, J.; He, T.; Qiu, Y.; Zhang, B.; Li, J.; Guan, H. Dynamic Evolutionary Game on Travel Mode Choices Among Buses, Ride-Sharing Vehicles, and Driving Alone in Shared Bus Lane Scenarios. Sustainability 2025, 17, 2101. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, X.; Liu, T. Linear Cultural Heritage Eco-Cultural Spatial System: A Case Study of the Great Tea Route in Shanxi. Front. Archit. Res. 2025, 14, 1063–1075. [Google Scholar] [CrossRef]
- Ahmad, A. The Application of Genetic Algorithm in Land Use Optimization Research: A Review. Tour. Manag. Perspect. 2013, 8, 106–113. [Google Scholar] [CrossRef]
- Kim, H.; Kim, Y.-J.; Kim, W.-T. Deep Reinforcement Learning-Based Adaptive Scheduling for Wireless Time-Sensitive Networking. Sensors 2024, 24, 5281. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Zuo, X.; Chen, G.; Ai, G.; Wan, X. Multi-Agent Deep Reinforcement Learning Based Real-Time Planning Approach for Responsive Customized Bus Routes. Comput. Ind. Eng. 2024, 188, 109840. [Google Scholar] [CrossRef]
- Geng, Y.; Liu, E.; Wang, R.; Liu, Y.; Rao, W.; Feng, S.; Dong, Z.; Fu, Z.; Chen, Y. Deep Reinforcement Learning Based Dynamic Route Planning for Minimizing Travel Time. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Bhadrachalam, K.; Lalitha, B. An Energy Efficient Location Aware Geographic Routing Protocol Based on Anchor Node Path Planning and Optimized Q-Learning Model. Sustain. Comput. Inform. Syst. 2025, 46, 101084. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, G.; Liang, W.; Wang, Y. Multi-Objective Reinforcement Learning Approach for Trip Recommendation. Expert Syst. Appl. 2023, 226, 120145. [Google Scholar] [CrossRef]
- Shafqat, W.; Byun, Y.-C. A Context-Aware Location Recommendation System for Tourists Using Hierarchical LSTM Model. Sustainability 2020, 12, 4107. [Google Scholar] [CrossRef]
- Kapoor, S. Explainable and Context-Aware Graph Neural Networks for Dynamic Electric Vehicle Route Optimization to Optimal Charging Station. Expert Syst. Appl. 2025, 283, 127331. [Google Scholar] [CrossRef]
- Lazaridis, A.; Fachantidis, A.; Vlahavas, I. Deep Reinforcement Learning: A State-of-the-Art Walkthrough. J. Artif. Intell. Res. 2020, 69, 1421–1471. [Google Scholar] [CrossRef]
- Pitakaso, R.; Sethanan, K.; Chamnanlor, C.; Chien, C.-F.; Gonwirat, S.; Worasan, K.; Limg, M.K. Optimizing Sugarcane Bale Logistics Operations: Leveraging Reinforcement Learning and Artificial Multiple Intelligence for Dynamic Multi-Fleet Management and Multi-Period Scheduling under Machine Breakdown Constraints. Comput. Electron. Agric. 2025, 236, 110431. [Google Scholar] [CrossRef]
- Torabi, P.; Hemmati, A.; Oleynik, A.; Alendal, G. A Deep Reinforcement Learning Hyperheuristic for the Covering Tour Problem with Varying Coverage. Comput. Oper. Res. 2025, 174, 106881. [Google Scholar] [CrossRef]
- Sun, X.; Shen, W.; Fan, J.; Vogel-Heuser, B.; Bi, F.; Zhang, C. Deep Reinforcement Learning-Based Multi-Objective Scheduling for Distributed Heterogeneous Hybrid Flow Shops with Blocking Constraints. Engineering 2025, 46, 278–291. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, G.; Zhang, Y.; D’Ariano, A.; Wu, Y. Railcar Itinerary Optimization in Railway Marshalling Yards: A Graph Neural Network Based Deep Reinforcement Learning Method. Transp. Res. Part C Emerg. Technol. 2025, 171, 104970. [Google Scholar] [CrossRef]
- de Araujo-Filho, P.F.; Kaddoum, G.; Naili, M.; Fapi, E.T.; Zhu, Z. Multi-Objective GAN-Based Adversarial Attack Technique for Modulation Classifiers. IEEE Commun. Lett. 2022, 26, 1583–1587. [Google Scholar] [CrossRef]
- Zhao, W.; Mahmoud, Q.H.; Alwidian, S. Evaluation of GAN-Based Model for Adversarial Training. Sensors 2023, 23, 2697. [Google Scholar] [CrossRef]
- Ruiz-Meza, J.; Brito, J.; Montoya-Torres, J.R. A GRASP-VND Algorithm to Solve the Multi-Objective Fuzzy and Sustainable Tourist Trip Design Problem for Groups. Appl. Soft Comput. 2022, 131, 109716. [Google Scholar] [CrossRef]
- Derya, T.; Atalay, K.D.; Dinler, E.; Keçeci, B. Selective Clustered Tourist Trip Design Problem with Time Windows Under Intuitionistic Fuzzy Score and Exponential Travel Times. Expert Syst. Appl. 2024, 255, 124792. [Google Scholar] [CrossRef]
- Gavalas, D.; Pantziou, G.; Konstantopoulos, C.; Vansteenwegen, P. Tourist Trip Planning: Algorithmic Foundations. Appl. Soft Comput. 2024, 166, 112280. [Google Scholar] [CrossRef]
- Florido-Benítez, L. The Use of Digital Twins to Address Smart Tourist Destinations’ Future Challenges. Platforms 2024, 2, 234–254. [Google Scholar] [CrossRef]
- Litavniece, L.; Kodors, S.; Adamoniene, R.; Kijasko, J. Digital Twin: An Approach to Enhancing Tourism Competitiveness. WHATT 2023, 15, 538–548. [Google Scholar] [CrossRef]
- Aghaabbasi, M.; Sabri, S. Potentials of Digital Twin System for Analyzing Travel Behavior Decisions. Travel Behav. Soc. 2025, 38, 100902. [Google Scholar] [CrossRef]
- Torrens, P.M.; Kim, R. Using Immersive Virtual Reality to Study Road-Crossing Sustainability in Fleeting Moments of Space and Time. Sustainability 2024, 16, 1327. [Google Scholar] [CrossRef]
- Reffat, R. An Intelligent Computational Real-Time Virtual Environment Model for Efficient Crowd Management. Int. J. Transp. Sci. Technol. 2012, 1, 365–378. [Google Scholar] [CrossRef]
- Oliveira, R.; Raposo, D.; Luís, M.; Sargento, S. Optimal Action-Selection Optimization of Wireless Networks Based on Virtual Representation. Comput. Netw. 2025, 264, 111258. [Google Scholar] [CrossRef]
- Aslam, A.M.; Chaudhary, R.; Bhardwaj, A.; Kumar, N.; Buyya, R. Digital Twins-Enabled Game Theoretical Models and Techniques for Metaverse Connected and Autonomous Vehicles: A Survey. J. Netw. Comput. Appl. 2025, 238, 104138. [Google Scholar] [CrossRef]
- Parrinello, S.; Picchio, F. Digital Strategies to Enhance Cultural Heritage Routes: From Integrated Survey to Digital Twins of Different European Architectural Scenarios. Drones 2023, 7, 576. [Google Scholar] [CrossRef]
- Hu, Y.; Dong, H.; Liu, J.; Zhuang, C.; Zhang, F. A Learning-Guided Hybrid Genetic Algorithm and Multi-Neighborhood Search for the Integrated Process Planning and Scheduling Problem with Reconfigurable Manufacturing Cells. Robot. Comput.-Integr. Manuf. 2025, 93, 102919. [Google Scholar] [CrossRef]
- Li, Y.-Z.; Liu, W.; Xu, G.-S.; Li, M.-D.; Chen, K.; He, S.-L. Quantum Circuit Mapping Based on Discrete Particle Swarm Optimization and Deep Reinforcement Learning. Swarm Evol. Comput. 2025, 95, 101923. [Google Scholar] [CrossRef]
- Wang, X.; Ning, F.; Lin, Z.; Zhang, Z. Efficient Ship Pipeline Routing with Dual-Strategy Enhanced Ant Colony Optimization: Active Behavior Adjustment and Passive Environmental Adaptability. J. Manuf. Syst. 2025, 80, 673–693. [Google Scholar] [CrossRef]
- Sait, S.M.; Oughali, F.C.; Al-Asli, M. Design Partitioning and Layer Assignment For 3D Integrated Circuits Using Tabu Search and Simulated Annealing. J. Appl. Res. Technol. 2016, 14, 67–76. [Google Scholar] [CrossRef]
- Costa, A.; Fernandez-Viagas, V. A Modified Harmony Search for the T-Single Machine Scheduling Problem with Variable and Flexible Maintenance. Expert Syst. Appl. 2022, 198, 116897. [Google Scholar] [CrossRef]
- Eiter, T.; Geibinger, T.; Ruiz, N.H.; Musliu, N.; Oetsch, J.; Pfliegler, D.; Stepanova, D. Adaptive Large-Neighbourhood Search for Optimisation in Answer-Set Programming. Artif. Intell. 2024, 337, 104230. [Google Scholar] [CrossRef]
- Chen, B.; Ouyang, H.; Li, S.; Ding, W. Dual-Stage Self-Adaptive Differential Evolution with Complementary and Ensemble Mutation Strategies. Swarm Evol. Comput. 2025, 93, 101855. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Discount factor (γ\gammaγ) | 0.99 |
| GAE lambda | 0.95 |
| Clipping coefficient (ϵ\epsilonϵ) | 0.2 |
| Entropy regularization weight | 0.01 |
| Learning rate | 3 × 10−4 |
| Batch size | 128 |
| Update epochs per batch | 4 |
| Optimizer | Adam |
| Route ID | POI Sequence (Abbreviated) | Travel Time (min) | Distance (km) | Emissions (kgCO2) | Congestion Index | Satisfaction Avg. | Smoothness Score | Feasibility |
|---|---|---|---|---|---|---|---|---|
| R1 | Wat Luang → Old Market → Museum → Rest. A → House 2 → City Gate | 78 | 3.2 | 0.52 | 0.21 | 0.82 | 6.2 | ✓ |
| R2 | Heritage Gate → Art Gallery → Candle Museum → Food Court → Post Office | 65 | 2.5 | 0.44 | 0.32 | 0.81 | 5.1 | ✓ |
| R3 | Clock Tower → Workshop → House 3 → Café → Walking Street | 42 | 1.9 | 0.31 | 0.16 | 0.63 | 4.8 | ✓ |
| Symbol | Unit | Values or Range |
|---|---|---|
| score | [1.0–10.0] | |
| minutes | [10–45] | |
| minutes | [1–10] | |
| meters | [50–550] | |
| kgCO2 | [0.05–0.15] | |
| index [0–1] | [0.10–0.85] | |
| degrees | [0°–360°] | |
| minutes | 150 | |
| kgCO2 | 1.8 | |
| index | 6.0 | |
| km | 6.0 | |
| count | 3, 2, 1 | |
| POIs | 12 | |
| constant | 106 | |
| score [0–1] | [0.0–1.0] | |
| minutes | [100–160] | |
| score | [2.0–4.5] |
| Group ID | Group Type | Time Budget (min) | Sustainability Awareness | Heritage Interest | Food Interest | Museum Interest | Min. Satisfaction |
|---|---|---|---|---|---|---|---|
| G1 | Cultural Enthusiasts | 150 | Moderate | High (0.85) | Low (0.25) | High (0.80) | 3.8 |
| G2 | Family with Children | 120 | Low | Moderate (0.60) | High (0.90) | Moderate (0.50) | 3.2 |
| G3 | Green Explorers | 140 | High | Moderate (0.70) | Moderate (0.60) | Low (0.30) | 3.6 |
| G4 | Senior Travelers | 100 | Medium | High (0.75) | Moderate (0.55) | High (0.70) | 3.5 |
| G5 | Casual Walkers | 90 | Low | Low (0.35) | High (0.85) | Low (0.20) | 2.5 |
| POI Name | Category | Heritage Score | Avg. Dwell Time (min) | Est. Congestion | Description |
|---|---|---|---|---|---|
| Wat Luang Old Temple | Historic House | 9.5 | 30 | 0.45 | A centuries-old wooden temple known for its teak carvings and community rituals. |
| Warin Walking Street Market | Restaurant | 4.0 | 25 | 0.65 | A bustling street food zone with regional Isan cuisine and weekend night fairs. |
| Phaya Thian Candle Museum | Museum | 8.8 | 40 | 0.30 | A cultural museum featuring the art of Ubon’s candle-carving traditions. |
| House No. 89 Cultural Home | Historic House | 7.2 | 20 | 0.20 | A private heritage residence showcasing colonial-era architecture and oral history exhibits. |
| Nong Bua Riverside Café | Restaurant | 3.5 | 35 | 0.50 | A scenic coffee shop along the river, favored by families and cyclists. |
| Method | HV | PCR | RSI ↓ | POI Entropy ↑ | Time Slack (min) ↑ | Emission Slack (kgCO2) ↑ | Congestion Slack ↑ | Category Slack ↑ | Satisfaction Slack ↑ |
|---|---|---|---|---|---|---|---|---|---|
| DRL–IMVO–GAN (Proposed) | 0.85 | 0.95 | 4.2 | 0.92 | 12.5 | 0.35 | 1.8 | 1.2 | 0.75 |
| Genetic + MNS | 0.76 | 0.81 | 5.6 | 0.83 | 7.8 | 0.22 | 1.2 | 0.7 | 0.42 |
| PSO + DRL | 0.79 | 0.87 | 5.1 | 0.86 | 9.1 | 0.28 | 1.4 | 0.9 | 0.53 |
| Dual-ACO | 0.72 | 0.76 | 5.9 | 0.79 | 6.3 | 0.19 | 1.0 | 0.5 | 0.36 |
| Tabu-SA | 0.75 | 0.83 | 5.3 | 0.84 | 8.5 | 0.26 | 1.3 | 0.8 | 0.50 |
| Harmony Search | 0.77 | 0.84 | 5.0 | 0.85 | 8.9 | 0.27 | 1.4 | 0.9 | 0.51 |
| ALNS-ASP | 0.78 | 0.85 | 5.2 | 0.88 | 9.0 | 0.29 | 1.5 | 1.0 | 0.54 |
| DE with Ensemble Mutation | 0.74 | 0.80 | 5.4 | 0.82 | 7.2 | 0.23 | 1.1 | 0.6 | 0.45 |
| Method | HV | PCR | RSI ↓ | Entropy ↑ | Time Slack ↑ | Emission Slack ↑ | Satisfaction Slack ↑ |
|---|---|---|---|---|---|---|---|
| Full DRL–IMVO–GAN | 0.85 | 0.95 | 4.2 | 0.92 | 12.5 | 0.35 | 0.75 |
| Baseline B (DRL + IMVO) | 0.82 | 0.91 | 4.5 | 0.89 | 11.2 | 0.31 | 0.68 |
| Baseline C (IMVO + GAN) | 0.80 | 0.88 | 4.6 | 0.87 | 10.4 | 0.28 | 0.64 |
| Baseline A (IMVO only) | 0.76 | 0.82 | 5.1 | 0.83 | 8.9 | 0.24 | 0.56 |
| PSO + DRL | 0.79 | 0.87 | 5.1 | 0.86 | 9.1 | 0.28 | 0.53 |
| ALNS-ASP | 0.78 | 0.85 | 5.2 | 0.88 | 9.0 | 0.29 | 0.54 |
| Method | F1: Heritage ↑ | F2: Travel Time ↓ | F3: Emissions ↓ | F4: Smoothness ↓ | F5: Preference ↑ |
|---|---|---|---|---|---|
| DRL–IMVO–GAN (Proposed) | 74.2 | 21.3 | 0.65 | 208.5 | 17.5 |
| Genetic + MNS | 68.5 | 25.8 | 0.92 | 245.7 | 15.2 |
| PSO + DRL | 67.9 | 26.4 | 0.97 | 251.3 | 14.9 |
| Dual-ACO | 66.4 | 27.1 | 1.01 | 258.2 | 14.3 |
| Tabu-SA | 65.8 | 28.0 | 1.05 | 262.9 | 14.0 |
| Harmony Search | 64.2 | 28.7 | 1.08 | 268.5 | 13.6 |
| ALNS-ASP | 63.4 | 29.5 | 1.12 | 275.0 | 13.1 |
| DE with Ensemble Mutation | 62.7 | 30.1 | 1.18 | 280.6 | 12.8 |
| Method | F1: Heritage ↑ | F2: Travel Time ↓ | F3: Emissions ↓ | F4: Smoothness ↓ | F5: Preference ↑ |
|---|---|---|---|---|---|
| DRL–IMVO–GAN (Proposed) | 74.8 | 21.9 | 0.67 | 212.3 | 17.3 |
| Genetic + MNS | 70.4 | 26.0 | 0.91 | 248.0 | 15.0 |
| PSO + DRL | 69.1 | 26.5 | 0.95 | 253.8 | 14.8 |
| Dual-ACO | 68.7 | 27.3 | 0.99 | 260.6 | 14.2 |
| Tabu-SA | 67.2 | 28.1 | 1.02 | 265.1 | 13.9 |
| Harmony Search | 66.0 | 29.0 | 1.06 | 270.8 | 13.4 |
| ALNS-ASP | 65.1 | 30.0 | 1.09 | 276.2 | 12.9 |
| DE with Ensemble Mutation | 64.6 | 30.7 | 1.13 | 281.5 | 12.6 |
| Method | F1: Heritage ↑ | F2: Travel Time ↓ | F3: Emissions ↓ | F4: Smoothness ↓ | F5: Preference ↑ |
|---|---|---|---|---|---|
| DRL–IMVO–GAN (Proposed) | 73.1 | 20.5 | 0.63 | 207.4 | 17.2 |
| Genetic + MNS | 67.9 | 23.1 | 0.87 | 243.6 | 15.0 |
| PSO + DRL | 66.5 | 23.6 | 0.91 | 250.1 | 14.7 |
| Dual-ACO | 65.4 | 24.2 | 0.95 | 256.3 | 14.0 |
| Tabu-SA | 64.7 | 25.0 | 0.99 | 261.7 | 13.8 |
| Harmony Search | 63.8 | 25.7 | 1.03 | 267.2 | 13.3 |
| ALNS-ASP | 62.9 | 26.5 | 1.07 | 272.4 | 12.9 |
| DE with Ensemble Mutation | 62.3 | 27.0 | 1.12 | 278.6 | 12.5 |
| Method | F1: Heritage ↑ | F2: Travel Time ↓ | F3: Emissions ↓ | F4: Smoothness ↓ | F5: Preference ↑ |
|---|---|---|---|---|---|
| DRL–IMVO–GAN (Proposed) | 72.6 | 21.0 | 0.59 | 210.2 | 17.0 |
| Genetic + MNS | 67.5 | 24.8 | 0.79 | 245.2 | 14.9 |
| PSO + DRL | 66.3 | 25.4 | 0.83 | 251.9 | 14.6 |
| Dual-ACO | 65.0 | 26.0 | 0.86 | 258.7 | 14.1 |
| Tabu-SA | 64.5 | 26.9 | 0.89 | 263.3 | 13.7 |
| Harmony Search | 63.3 | 27.4 | 0.92 | 269.6 | 13.2 |
| ALNS-ASP | 62.8 | 28.2 | 0.95 | 274.9 | 12.8 |
| DE with Ensemble Mutation | 62.1 | 28.9 | 0.98 | 280.1 | 12.3 |
| Method | F1: Heritage ↑ | F2: Travel Time ↓ | F3: Emissions ↓ | F4: Smoothness ↓ | F5: Preference ↑ |
|---|---|---|---|---|---|
| DRL–IMVO–GAN (Proposed) | 73.5 | 21.5 | 0.64 | 205.7 | 17.4 |
| Genetic + MNS | 68.1 | 25.3 | 0.88 | 239.5 | 15.1 |
| PSO + DRL | 66.8 | 25.9 | 0.92 | 246.7 | 14.8 |
| Dual-ACO | 65.6 | 26.5 | 0.95 | 252.3 | 14.3 |
| Tabu-SA | 64.9 | 27.4 | 0.99 | 258.0 | 13.9 |
| Harmony Search | 63.7 | 28.0 | 1.03 | 264.4 | 13.4 |
| ALNS-ASP | 62.9 | 28.7 | 1.06 | 270.8 | 12.9 |
| DE with Ensemble Mutation | 62.2 | 29.3 | 1.10 | 276.5 | 12.4 |
| Method | F1: Heritage ↑ | F2: Travel Time ↓ | F3: Emissions ↓ | F4: Smoothness ↓ | F5: Preference ↑ |
|---|---|---|---|---|---|
| DRL–IMVO–GAN (Proposed) | 74.0 | 21.2 | 0.62 | 209.3 | 17.8 |
| Genetic + MNS | 68.8 | 25.6 | 0.89 | 246.5 | 15.3 |
| PSO + DRL | 67.4 | 26.1 | 0.93 | 252.8 | 15.0 |
| Dual-ACO | 66.2 | 26.7 | 0.97 | 259.1 | 14.5 |
| Tabu-SA | 65.6 | 27.5 | 1.01 | 264.9 | 14.1 |
| Harmony Search | 64.4 | 28.3 | 1.04 | 270.6 | 13.6 |
| ALNS-ASP | 63.7 | 29.0 | 1.08 | 275.8 | 13.2 |
| DE with Ensemble Mutation | 63.0 | 29.8 | 1.11 | 280.4 | 12.7 |
| Group Profile | F1: Heritage ↑ | F2: Travel Time ↓ | F3: Emissions ↓ | F4: Smoothness ↓ | F5: Preference ↑ |
|---|---|---|---|---|---|
| G1: Cultural Enthusiasts | 74.9 | 21.5 | 0.64 | 210.8 | 17.9 |
| G2: Family with Children | 72.1 | 22.3 | 0.68 | 214.6 | 17.1 |
| G3: Green Explorers | 70.8 | 21.8 | 0.58 | 209.2 | 17.4 |
| G4: Senior Travelers | 71.5 | 22.0 | 0.62 | 211.1 | 17.2 |
| G5: Casual Walkers | 69.7 | 21.6 | 0.66 | 212.5 | 17.0 |
| Scenario | Hypervolume (HV) | POI Entropy ↑ | Satisfaction Score ↑ |
|---|---|---|---|
| Original Scenario (Validation Set) | 0.85 | 0.92 | 17.5 |
| Zero-Shot: New POIs | 0.82 | 0.89 | 16.8 |
| Zero-Shot: Altered Congestion Patterns | 0.81 | 0.87 | 16.6 |
| Few-Shot: New Group Profiles (5 examples) | 0.84 | 0.91 | 17.2 |
| Few-Shot: Reduced Emission Budget (B(CO2) = 1.2) | 0.83 | 0.90 | 17.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pitakaso, R.; Srichok, T.; Khonjun, S.; Nanthasamroeng, N.; Sawettham, A.; Khampukka, P.; Dinkoksung, S.; Jungvimut, K.; Jirasirilerd, G.; Supasarn, C.; et al. A Hybrid Deep Reinforcement Learning and Metaheuristic Framework for Heritage Tourism Route Optimization in Warin Chamrap’s Old Town. Heritage 2025, 8, 301. https://doi.org/10.3390/heritage8080301
Pitakaso R, Srichok T, Khonjun S, Nanthasamroeng N, Sawettham A, Khampukka P, Dinkoksung S, Jungvimut K, Jirasirilerd G, Supasarn C, et al. A Hybrid Deep Reinforcement Learning and Metaheuristic Framework for Heritage Tourism Route Optimization in Warin Chamrap’s Old Town. Heritage. 2025; 8(8):301. https://doi.org/10.3390/heritage8080301
Chicago/Turabian StylePitakaso, Rapeepan, Thanatkij Srichok, Surajet Khonjun, Natthapong Nanthasamroeng, Arunrat Sawettham, Paweena Khampukka, Sairoong Dinkoksung, Kanya Jungvimut, Ganokgarn Jirasirilerd, Chawapot Supasarn, and et al. 2025. "A Hybrid Deep Reinforcement Learning and Metaheuristic Framework for Heritage Tourism Route Optimization in Warin Chamrap’s Old Town" Heritage 8, no. 8: 301. https://doi.org/10.3390/heritage8080301
APA StylePitakaso, R., Srichok, T., Khonjun, S., Nanthasamroeng, N., Sawettham, A., Khampukka, P., Dinkoksung, S., Jungvimut, K., Jirasirilerd, G., Supasarn, C., Mongkhonngam, P., & Boonarree, Y. (2025). A Hybrid Deep Reinforcement Learning and Metaheuristic Framework for Heritage Tourism Route Optimization in Warin Chamrap’s Old Town. Heritage, 8(8), 301. https://doi.org/10.3390/heritage8080301













