Fuzzy Frequencies: Finding Tonal Structures in Audio Recordings of Renaissance Polyphony

Abstract

Understanding tonal structures in Renaissance music has been a long-standing musicological problem. Computational analysis on a large scale could shed new light on this. Encoded scores provide easy access to pitch content, but the availability of such data is low. This paper addresses this shortage of data by exploring the potential of audio recordings. Analysing audio, however, is challenging due to the presence of harmonics, reverb and noise, which may obscure the pitch content. We test several multiple pitch estimation models on audio recordings, using encoded scores from the Josquin Research Project (JRP) as a benchmark for evaluation. We present a dataset of multiple pitch estimations from 611 compositions in the JRP. We use the pitch estimations to create pitch profiles and pitch class profiles, and to estimate the lowest final pitch of each recording. Our findings indicate that the Multif0 model yields pitch profiles, pitch class profiles and finals most closely aligned with symbolic encodings. Furthermore, we found no effect of year of recording, number of voices and ensemble composition on the accuracy of pitch estimations. Finally, we demonstrate how these models can be applied to gain insight into tonal structures in early polyphony.

1. Introduction

To a distant listener, the sound of Renaissance music is fairly similar to that of later music. But on a closer look, we observe different patterns in the way pitch is organised, and such tonal structures [1] show an evolution over time. Understanding this evolution poses a major challenge in historical musicology. A quantitative approach would be to analyse machine-readable encodings of a large sample from the repertoire using music analysis software. However, encoding sources is a slow and complicated process that has resulted so far in relatively small corpora [2]. Audio recordings are available in a much larger amount. Therefore, this paper explores the potential of audio recordings in the large-scale analysis of tonal structures. In this exploratory phase, we focus on three simple characteristics of tonal structures, namely, the final pitch, pitch class profile and pitch profile.

1.1. Analysing Tonal Structures

In the analysis of tonal structures, there are roughly two approaches: the traditional musicological qualitative approach investigates a limited number of compositions in depth, while the computational approach with its quantitative methods can survey large numbers of compositions. Peter Urquhart’s study on accidentals in the Franco-Flemish Renaissance [3] takes a middle course by manually analysing 1047 motets on melodic patterns in cadences. A search on the Motet Online Database [4] reveals more than 33.000 Renaissance motets found in sources from all over Europe. Urquhart’s study covers 3% of these motets and with the manual approach, this is about the upper limit of the number of compositions that can reasonably be analysed.

Pitch class profiles and pitch profiles are an important means to study tonal structures in music information computing. They have been applied to music from the seventeenth to twentieth century [5,6,7] as well as to medieval plainchant [8]. In this study, we define a pitch profile as the relative presence of each pitch in a musical work, recorded or notated (see Section 3.4.2 for the exact calculations). By convention, sharps and flats are not distinguished and ’sharp’ labels are used.

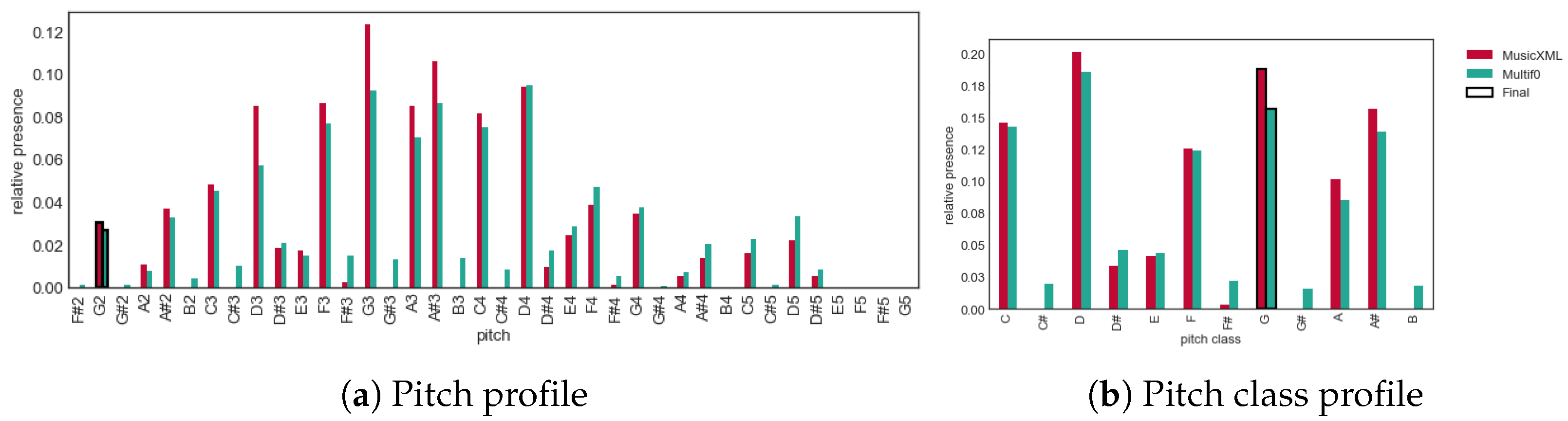
A pitch class profile is similar to a pitch profile, but with all the pitches folded into the space of one octave. Figure 1 shows a comparison between pitch and pitch class profiles extracted from an encoded score—henceforth, symbolic encoding1—and from audio for a specific composition.

We will use these profiles to study the modes in Section 5. Modes describe the scales used in Renaissance music; these scales resemble but are not identical to the modern major and minor keys.

1.2. Data Availability

For almost any period in music history, there are more recordings available than encodings, and certainly for the period we are interested in. The Dutch national CD library, Muziekweb [10], has more than 35.000 albums containing at least one composition by a composer whose life touched the period 1500–1700. A conservative estimate translates this into 350.000 tracks. A rough estimate of the number of symbolic encodings in this period is 20.000 to 40.000 according to [2]. Please note that both estimates are counts of instances, not of unique compositions.

Compared to symbolic encodings, audio recordings have properties that obscure the pitch content, such as harmonics, reverb, vibrato, instrumental characteristics—like the fast decay of lute tones, and extraneous noise in the recording—like birdsong. In addition, the handling of audio requires more computing power than processing encodings, since a WAV file is about 500 times as large as a MusicXML encoding of the same composition and because pitch extraction is computationally expensive.

While symbolic encodings come in many types that are not fully compatible with each other (for example, **kern, MusicXML, Lilypond, MIDI), audio files are available as WAV or another easily convertible format. Therefore, while audio analysis presents us with the challenge of pitch extraction, we can avoid problems of compatibility and conversion of formats.

1.3. Research Questions

Before we can attempt a study of tonal structures using pitch content extracted from audio as main data source, we must assess the quality of the pitch extraction models. The main research question therefore is:

Is the output of extraction models accurate enough for music historical research, specifically, when studying tonal structures in the 16th and 17th centuries?

In this paper, we will answer that question and give a preview of the possibilities that such a model will enable. More specifically, we will investigate the following subquestions:

• What are suitable state-of-the-art audio pitch extraction models?
• What is the pitch extraction model that results in pitch (class) profiles most similar to those extracted from symbolic encodings?
• What is the effect of year of recording, number of voices and the ensemble composition on the quality of pitch (class) profiles?
• How can we study tonal structures using pitch content extracted from audio?

In Section 2, we will outline three lightweight pitch extraction models and three state-of-the-art multiple pitch extraction models, trained with (deep) neural networks. The methods to find the best pitch extraction model and the effect of characteristics in the performance will be addressed in Section 3 and Section 4. As an example of how the multiple pitch extractions can be used to study tonal structures in Renaissance music, a modal cycle by Palestrina and Gesualdo’s Sixth book of madrigals will be analysed in Section 5. In Section 6, we will discuss the limitations of our work and make some observations on the extraction models. We will finish with a conclusion on the research questions and with suggestions for future work.

2. Background

In this section, we will provide background on the modes and corpus studies. We will also give a brief overview of current pitch extraction models and select those that we will evaluate.

2.1. Modes

Modes, originally describing the pitch organisation in Gregorian plainchant melodies, were widely applied to polyphony from the 15th century onwards. They are an example of intangible intellectual and cognitive heritage: music theorists describe the modes, composers applied them in creating new works and listeners developed mental models of the modes that helped to process the music they heard. Modes make use of the diatonic scale2. In the traditional 8-mode system, the notes D, E, F and G can act as the final pitch of two modes: an authentic and a plagal mode. Melodies in the four authentic modes have a high range with respect to the final (usually extending to the octave above the final); while those in the four plagal modes have a lower range, often from the lower fourth to the upper fifth. Other important properties of a mode are its reciting tone, see also

Table 1. The 12 untransposed modes with their final, range and reciting tone (undefined for modes 9–12). In polyphony, modes are regularly transposed to the lower 5th or upper 4th and notated with a signature of one flat. Other transpositions are rare.

Mode	Final	Range	Reciting Tone
1	D	high (authentic)	A
2	D	low (plagal)	F
3	E	high (authentic)	C
4	E	low (plagal)	A
5	F	high (authentic)	C
6	F	low (plagal)	A
7	G	high (authentic)	D
8	G	low (plagal)	C
9	A	high (authentic)	-
10	A	low (plagal)	-
11	C	high (authentic)	-
12	C	low (plagal)	-

, and the tones on which intermediate closures can be made. Because of these properties, each mode has a distinctive pitch profile or pitch class profile [8].

Due to the transfer of the modal system to polyphony, controversies arose in the 16th century about some of its characteristics. The most conspicuous was the much-debated extension to 12 modes proposed by Glarean (1547) [11], adding A and C as regular modal finals. Also, composers often did not adhere closely to the theoretical models. Much practical evidence about composing in the modes can be gained from studying modal cycles; such sets of compositions through all the modes were created by many of the major Renaissance composers. However, from the end of the 16th century onwards, polyphonic modality went through a phase of transition and was ultimately replaced by modern tonality that emphasises harmony.

2.2. Music Corpus Studies

The aim of corpus studies is to discover patterns in larger music datasets that preferably are selected for and tailored to the research question at hand.

Table 2. Corpus studies that include music composed before 1700.

Study	Data Type	Items	Dataset
Rose et al. (2015) [12]	Metadata	2,000,000	British Library of printed music, Hughes’s catalogue of manuscript music in the British Museum, RISM A/II
Broze & Huron (2013) [14]	Audio	880,906	Naxos track samples and some smaller subsets
Park et al. (2015) [13]	Metadata	63,679	ArkivMusic and All Music Guide
Harasim et al. (2021) [7]	Encoding	13,402	Classical Archives, Lost Voices, ELVIS, CRIM
Yust (2019) [15]	Encodings	4544	YCAC
Upham & Cumming (2020) [16]	Encodings	2016	JRP, RenCOmp7
Moss (2019) [17]	Encodings	2012	ABC, CCARH, CDPL, DCML, Koẑeluh
Moss et al. (2024) [18]	Encodings	2012	TP3C
Weiß et al. (2018) [19]	Audio	2000	Cross-Era Dataset
Geelen et al. (2021) [20]	Encodings	1248	JRP
Arthur (2021) [21]	Encodings	707	Palestrina Masses

lists the corpus studies that include more than 500 records, and that contain 16th and 17th century compositions. Large numbers of items are found in corpus studies that use metadata as their source. Rose et al. [12] studied almost 2,000,000 metadata records to explore the potential of metadata for historical musicology, and Park [13] studied metadata of 63,679 CDs to investigate composer networks.

To our knowledge, there are only two studies that use audio as their source—the 2019 study by Weiß et al. [19] on style evolution, and the 2013 study by Broze and Huron [14] on the relation between pitch and tempo. The remaining studies focus on symbolic encodings with relatively small datasets. A general observation on these datasets is that, while the 18th and 19th centuries are well represented, the proportion of early music is fairly small. For example, in the TP3C corpus [22], 66% of the works are 18th or 19th century compositions, whereas the 14th to 17th century are represented by only 25%.

None of the datasets listed in Table 2 were created as a representative sample of the repertoire at which the studies are aimed; rather, they seem to be convenience selections from the available materials. This is especially true for the encodings—their distribution over time is irregular and usually only the big composer names are represented.

Amending this problem by creating more encodings would require a huge investment. On the other hand, musical audio is available in much higher quantities already now, which potentially allows us to select a more carefully composed corpus for research. As an initial step, we demonstrate this by an audio corpus that parallels the Josquin Research Project (JRP) corpus [23].

2.3. Multiple Pitch Estimation

In the past decades, various approaches [24,25] have been developed for multiple pitch estimation (MPE) and music transcription. Many works focus on the transcription of piano music, where annotations can be obtained using Disklavier pianos that record the performance of each note in real time in MIDI-format [26]. Other studies, such as Mel-RoFormer [27] and MT3 [28], focus on stream-level transcription, mainly in popular music3. Other studies propose models trained partially or fully on vocal classical music, including Deep Salience [29], Multif0 [9], Multipitch [30] and NoteTranscription [31]. Since these models are computationally expensive, there are attempts to create faster models without loss of performance: Basicpitch [32] is a low-resource neural network-based model.

For this study, we are interested in models specifically trained on vocal music that demonstrate state-of-the-art performance: Multif0, Multipitch, and NoteTranscription. However, at the time of submission, the training weights for NoteTranscription were unavailable. Therefore, of these models, we will compare Multif0 and Multipitch. To complement these computationally demanding models, we also include Basicpitch as a fast reference model.

Since this study focusses only on pitch profiles and pitch class profiles as features, we will compare the MPE models with two fast, spectral models, the Harmonic Pitch Class Profile [33], henceforth HPCP, and the Constant-Q transform (CQT) [34]. In Section 2.4, we will discuss the models evaluated in this study in more detail.

2.4. Models in This Study

Among lightweight models, HPCP is particularly interesting for analysing tonal content, as it is specifically designed for analysis of harmonics and pitch estimation. The process involves extracting spectral peaks (from the Short-Time Fourier Transform), filtering the peaks within the expected melodic range, assigning them to pitch-class bins, and then applying spectral whitening to equalize the energy distribution across frequencies. This prevents low frequencies—which naturally have higher energy—from dominating the representation. Since HPCP emphasises harmonic content, HPCP is often favoured over the CQT, which covers the full frequency range (including less relevant frequencies for pitch analysis) and does not suppress non-harmonic content.

In the conventional Fourier transformation, all pitch bins have the same size, resulting in too low a resolution for the low pitches and too high a resolution for the high pitches, because of the logarithmic relation between frequency and pitch. To approach musical pitch perception, CQT transforms a signal into the time-frequency domain with geometrically spaced frequency bins, doubling in frequency for each octave [35].

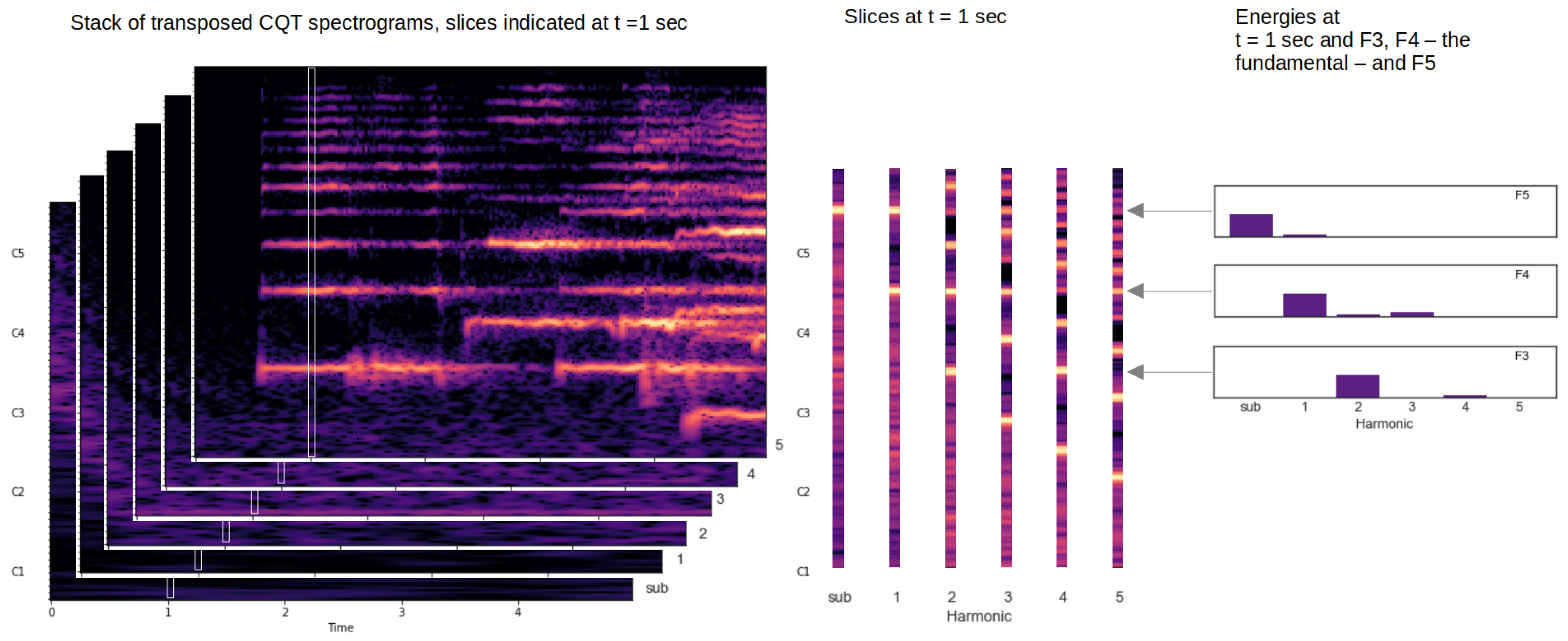
Multif0, Basicpitch and Multipitch use a modified version of CQT as the main input. This modification entails the transformation of the CQT to a set of harmonics and subharmonics as explained in Figure 2. This transformation is called Harmonic ConstantQ transform (HCQT) [29] and it supports a neural network in finding the harmonic content more easily. Although all three models use HCQT as input, they differ in several aspects, as listed in

Table 3. Specifics of the multiple pitch estimation models.

	Multif0 [9]	Multipitch [30]	Basicpitch [32]
Model input	HCQT + phase differentials	HCQT	HCQT
HCQT harmonics	1, 2, 3, 4, 5	0.5, 1, 2, 3, 4, 5	0.5, 1, 2, 3, 4, 5, 6, 7
Input bin size in cents	20	33	33
Output bin size in cents	20	100	100
Tracks in training	69	744	4127
Instrumentation in training	a capella	opera, chamber music, symphonic, a capella	vocal guitar, piano, synthesizers, orchestra
Genre	classical	classical	classical and pop
Polyphonic/monophonic	polyphonic	polyphonic	monophonic and polyphonic
Annotation	f0 annotation per voice	mixed: aligned scores, multitrack, midi-guided performance	unspecified
Architecture	Late/Deep CNN	Deep Residual CNN	CNN
Loudness in output	yes	no	no

.

Multif0 preprocesses the audio by binning the pitches into five bins per semitone, and the output is also in 20 cent bins. Multipitch and Basicpitch use three bins per semitone in the preprocessing, and the binning into semitones is performed as an integral part of the CNN. The training data show a notable difference in size; while Multif0 is trained with only 69 tracks of a capella music—data augmentation not counted—Multipitch is trained by diverse sets of 744 tracks in total, and Basicpitch even with 4127 tracks.

Having answered research question 1 on suitable audio pitch-extraction models, we can now move on to the evaluation of the selected models.

3. Methods

In this section, we describe the steps to answer research question 2, namely, which pitch extraction model results in pitch (class) profiles most similar to those extracted from symbolic encodings. We have chosen the features pitch profiles and pitch class profiles because these are important and simple features in the musicological study of tonal structures.

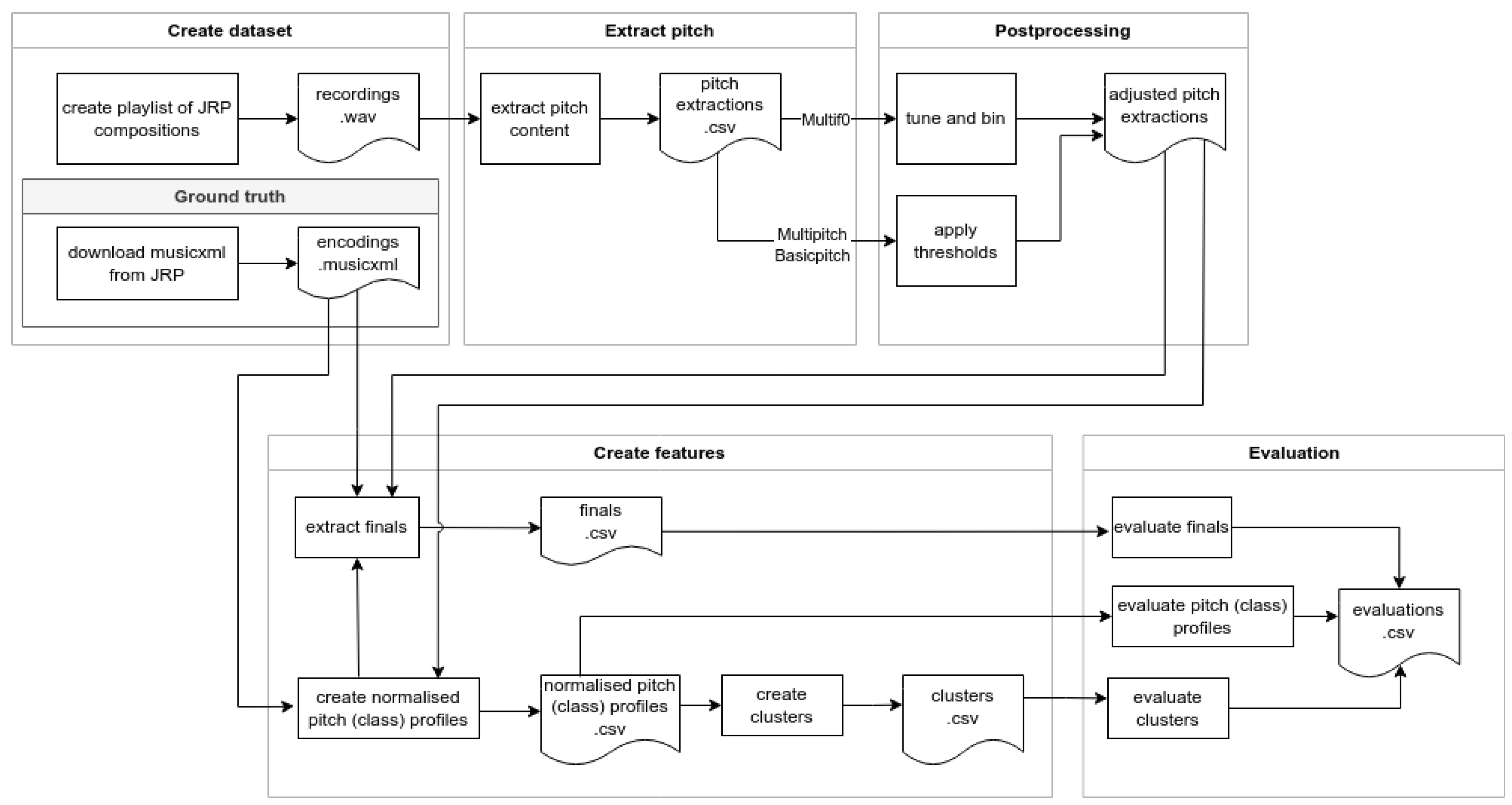
The workflow of this study consists of five phases: creating the dataset, extracting the pitches with various models, postprocessing the data, extracting the features, and evaluating the features relative to the ground truth, as laid out in Figure 3. Each phase is discussed in detail below. Finally, in Section 3.6, we describe how research question 3 will be answered, namely, what is the effect of the recording characteristics on the quality of the profiles?

3.1. Create Dataset

For this study, the data of the Josquin Research Project (JRP) [23] are used. The JRP originally aimed to secure attribution of compositions to Josquin des Prez (c. 1450–1455 to 1521) and now contains more than 900 symbolic high-quality representations of compositions by Josquin, his predecessors and contemporaries. To create an accompanying audio corpus, we collected recordings, preferably a capella, by professionally schooled performers adhering to historically informed performance practice. Some performances do not meet all criteria; these are incorporated nevertheless for the sake of completeness. Each recording has been checked by ear to ensure it is in line with the encoding; repetitions and instrumentation type are described in the metadata. The Sanctus movements in the masses are a special case—in the encodings, the order of the Sanctus parts is Sanctus-Hosanna-Benedictus, in the recording, the order is Sanctus-Hosanna-Benedictus-Hosanna. This impacts the final of the symbolic encodings (Benedictus final is taken instead of Hosanna final) and the pitch (class) profile. This is annotated in the metadata.

3.2. Extract Pitch

For each recording in the dataset, pitch is extracted using the selected models, resulting in CSV files. Multif0 returns extracted fundamental frequencies (rounded to the closest 20 cents frequency bin) with a sample rate of 86 slices per second, and frequencies ordered from low to high. Multipitch returns the relative energy for each MIDI tone in the range 24–96 with a sample rate of 434. The output of Basicpitch is similar to the MIDI representation: note events with a start and end time, a MIDI tone, the velocity (loudness) and a list of pitch bends (microtonal pitch deviations). As voice leading is a yet unsolved problem in the field of music information computing, none of the models assign the extracted pitches to separate voices, other than an ordering of the extracted pitches by height.

3.3. Postprocessing Pitch Extractions

To extract finals and profiles properly, we need to overcome two challenges that are inherent in recordings: concert pitch and transposition. Concert pitch is the microtonal deviation of the performance from the standard tuning of 440 Hz, while transposition is the deviation in semitones from the written notation. The concert pitch chosen may severely disturb the attribution of pitches to pitch bins or midi tones, whereas an uncorrected transposition makes a comparison between a recording and a symbolic encoding impossible. In our workflow, adjusting for the concert pitch is the first step. We calculate the pitch deviation in MIDI tones, and add this deviation to each individual pitch in the pitch extraction.

3.3.1. Concert Pitch

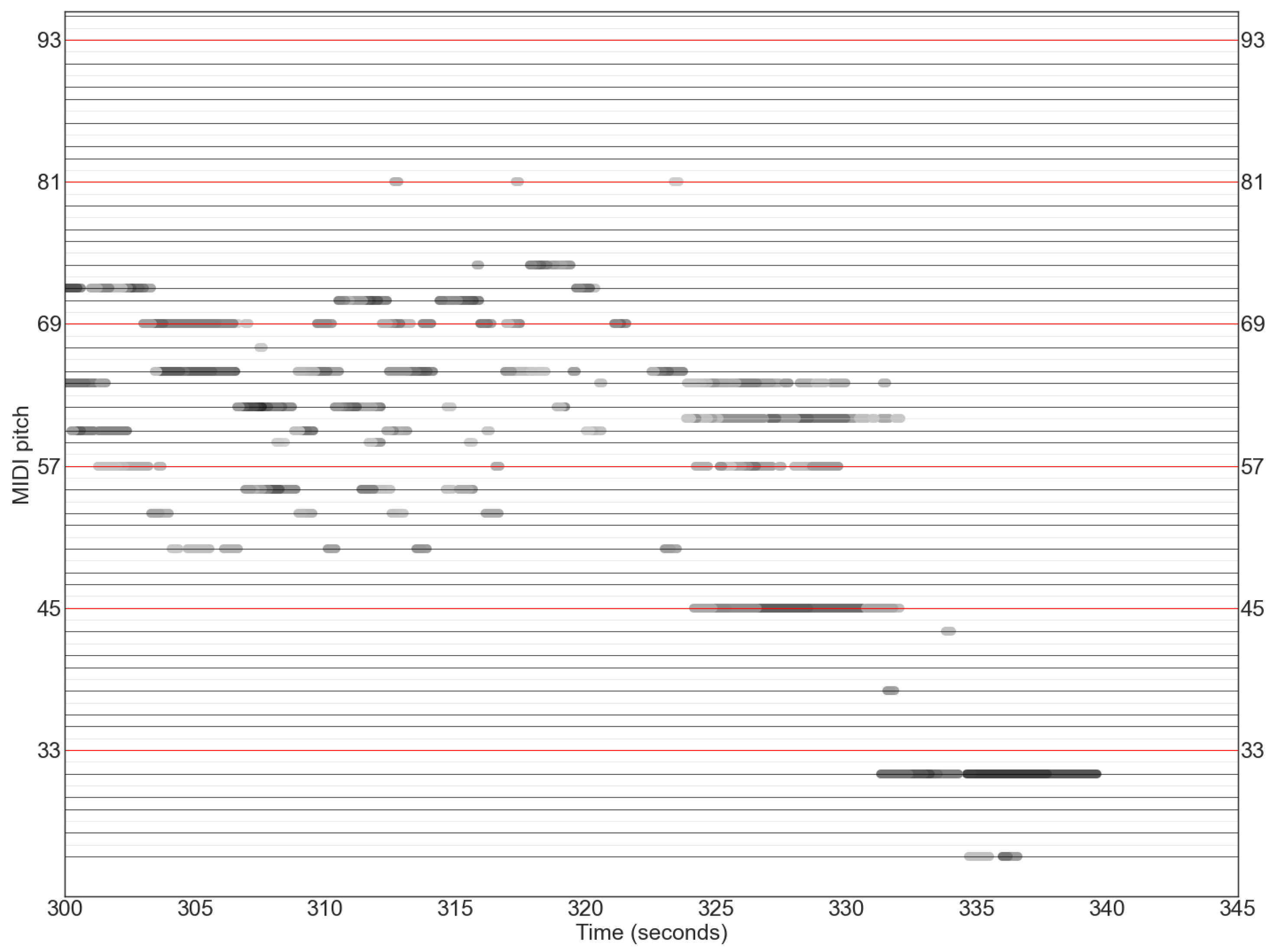
In the piano roll in Figure 4, we see many simultaneously sounding semitones. This is an artifact caused by the performance pitch not being identical to the concert pitch. The pitches are around the pitch bin edges and consequently they are assigned to two neighbouring bins.

In Multif0, with its five bins per semitone, we can compensate for this as it allows us to measure the deviation of a recording from the standard tuning of 440 Hz.

We do this as follows. In an ideal situation, we expect one in five bins to be the most prominent because they correspond to the intended pitch. We can use this intuition to determine the distance of the prominent bin to the standard 440 Hz tuning.

The concert pitch is measured by selecting the most frequent pitch bin $B_n$ in the Multif0 output and its four neighbouring bins $B_{n-2}$, $B_{n-1}$, $B_{n+1}$ and $B_{n+2}$. We then calculate the weighted average $\overline{B}$ of the five bins $B_{n-2}$, …, $B_{n+2}$ weighted by their relative presence $w_n$:

$$\overline{B}={\displaystyle \frac{{\displaystyle \sum _{i=n-2}^{n+2}}{w}_i·B_i}{{\displaystyle \sum _{i=n-2}^{n+2}}{w}_i}}$$

(1)

We define the deviation from 440 Hz in MIDI tones as follows:

$$\delta =\overline{B}-\mathrm{round}\left(\overline{B}\right)$$

(2)

This deviation $\delta$ is used to adjust the pitch binning, enabling precise extraction of the finals and construction of the pitch class profiles.

3.3.2. Pitch Binning

Pitch binning is an inseparable part of the Basicpitch and Multipitch models. For Multipitch, this leads to problems in cases where there is some pitch instability within a recording. In Figure 4, the frequencies of each pitch are just in between two bins and are alternately assigned to two adjacent pitch bins.

For Multif0, pitch binning is a separate step in our workflow as the Multif0 output has five bins per semitone. In this step, we merge these bins into new bins of the size of one MIDI tone, where the boundaries between the bins are decided by the concert pitch as measured by the method in Section 3.3.1.

3.3.3. Loudness Thresholding

Multif0 applies loudness thresholding as part of the neural network, whereas Multipitch and Basicpitch extractions include the loudness (or velocity in MIDI terms) of each pitch for each time slice. For Multipitch, we apply a global loudness threshold, whereas a dynamic loudness threshold is used for Basicpitch. These thresholds are applied in creating the profiles from the raw pitch extractions.

3.4. Create Features

3.4.1. Finals

We define the final as the lowest note in the last chord of a composition. The final of an encoding or recording is an important prerequisite for two reasons: first, to enable the alignment of the encoding and (transposed) recording; secondly, to be able to connect profiles to modes. Each extraction model needs its own custom settings to detect the final. We optimised the final detection in the Multipitch and Basicpitch extractions by means of several thresholds: minimum loudness, window size (where in the extraction to look for the final) and the minimum duration of the final, the values of which can be found in the code5 The extraction of the final from the audio pitch extraction is not trivial and needs a custom thresholding method for each extraction type. After establishing a ground truth for all recordings in the JRP dataset, we optimise the final detectors for each model using thresholds for loudness, the minimum length of a final, and the window in which a final has to be sought. In addition, the pitch candidates for a final are filtered by the pitch class profile; only pitches belonging to pitch classes in the top seven of the pitch class profile are candidates for the final. Basicpitch and Multipitch are sensitive for noise and reverb in the recording. Low noise appears to be particularly problematic, as this results in the wrong final. By allowing only pitches that have more than 1% representation in the pitch profile, we filter out low noise at the end of a recording. This approach does not solve all problems. The piano roll representation of a Basicpitch extraction in Figure 5 suggests that midi tone 31 is the final, while in reality, the final is midi tone 53. Midi tone 31 has a frequency of 49 Hz, which is near the European power grid frequency of 50 Hz. We chose not to develop a final detector for HPCP and CQT; these algorithms borrow their final from the ground truth.

3.4.2. Pitch Profiles and Pitch Class Profiles

To create the pitch profiles, we compute the relative presence of each MIDI tone, weighted for duration. To create the pitch class profiles, we fold the pitch profiles into the space of one octave. Each extraction model returns a different format, which impacts the exact calculation of the presence of each tone. For Multipitch and Multif0, we use the number of timestamps on which the pitch occurs; for Basicpitch and for the encodings, we sum the durations of the tones.

3.4.3. Distance Between Profiles

We calculate the Euclidean distance between the pitch (class) profiles of the recording and the symbolic encoding. Given two pitch (class) profiles $p=(p_1,p_2,\dots ,p_n)$ and $q=(q_1,q_2,\dots ,q_n)$, the Euclidean distance D between them is computed as follows:

$$D=\sqrt{{\displaystyle \sum _{i=1}^n}{(p_i-q_i)}^2}$$

(3)

In performance, it is not uncommon for the bass part to sing or play the final an octave lower than is notated. This practice has no effect on the pitch class profile, but it has on the pitch profile—every pitch is one octave off. Conversely, the Multif0 extractor sometimes misses the lowest sounding final because of instrumentation6 or dynamics. For this reason, we calculate the distance between the audio and encoded pitch profile three times, with the audio extraction at pitch, and transposed an octave up and down. Then, we take the minimum of these three distances.

3.5. Evaluation

The performance of the models is evaluated at two abstraction levels: similarity of pitch (class) profiles and similarity of clustering. At the first level, for each composition, we compare the profiles from the encoding to the audio extractions by calculating the Euclidean distance D. Then, for each model, we take the mean $\mu$ of these distances:

$$\mu ={\displaystyle \frac{{\sum }_{j=1}^J\left(D_j\right)}{J}}$$

(4)

where J is the number of compositions in the JRP dataset.

We consider the model with the lowest mean distance between the symbolic and the audio extraction to be the best. Ideally, this model would also show a low standard deviation.

Given that the data are not normally distributed, the extraction models are independent of one another, and we are comparing three or more groups, a Kruskal–Wallis test is employed to determine if there are statistically significant differences among the mean distances of the various models. Following this, a Dunn test is utilised to identify which specific pairs of models show significant differences.

At the second level, we examine the clustering of the profiles to assess whether clustering audio profiles yields results comparable to clustering symbolic profiles. Initially, we identify the optimal number of clusters using K-means clustering [36] and evaluate the clustering quality with a silhouette score [37]. Subsequently, we apply t-SNE [38] with standard parameters to reduce dimensionality, facilitating visualisation. We then assess which extraction model produces the most similar clustering outcomes using the Adjusted Rand Index (ARI) [39] and the Adjusted Mutual Information (AMI) score [40].

The ARI provides a similarity measure between two clusterings by considering all pairs of samples and counting those assigned to the same or different clusters in both the predicted and true clusterings. The AMI adjusts the Mutual Information (MI, the amount of information that is shared between two clusterings) score to account for chance, addressing the tendency of MI to yield higher values for clusterings with a larger number of clusters, regardless of the actual shared information.

Finally, in Section 5, we investigate two musicological cases in detail.

3.6. Exploring the Effect of Performance and Recording on Pitch Extractions of the Best Extraction Model

To answer research question 3, we conduct a multiple regression analysis for the independent variables year of recording, number of voices and ensemble composition on the accuracy of the pitch (class) profiles extracted with the best performing pitch extraction model resulting from Section 3.5. We test the hypotheses:

• Recent recordings yield more accurate pitch (class) profiles.
• A lower number of voices yields more more accurate pitch (class) profiles.
• The ensemble composition on which the model is trained yields the most accurate pitch (class) profiles.

4. Results

In this section, we first present the CANTO-JRP dataset, then we answer research questions 2 and 3.

4.1. The CANTO-JRP Dataset

The CANTO-JRP dataset is based on the dataset in the Josquin Research Project (JRP), a project dedicated to the composer Josquin des Prez (c.1450–1521). Aiming to support studies on composer attribution, the JRP contains 902 works by Josquin, 21 of his contemporaries, and anonymous works. The dataset contains:

• Metadata: composer, composition title, number of voices, instrumentation category, recording decade, performer(s), final pitch, the extent to which the audio is similar to the encoding. Figure 6 provides some characteristics of the dataset, and shows that the dataset mainly consists of recent a cappella recordings for four voices.
• Recordings: for 611 out of the 902 works on the JRP website, usable recordings have been found on Spotify; these are collected in a playlist 7 For convenient reference, the order of the playlist has been maintained in the metadata.
• Pitch estimations: on each of these recordings Multif0, Basicpitch and Multipitch (both 195f and 214c) have been applied. The extractions are made available in the dataset.
• Encodings: the encodings of the 611 works in the dataset have been copied from the JRP website.

4.2. Finals

The final of a recording is the reference to make the pitch (class) profiles of multiple recordings comparable. In Section 3.4.1, we established a ground truth;

Table 4. Percentage of correct finals for each model within the range of one semitone. The finals of HPCP and CQT are not generated and for the remainder of this study are provided by the ground truth. Best scores are in bold.

Extraction Model	Correct Pitch of Finals	Correct Pitch Class of Finals
Multif0	95.4%	99.0%
Mp 195f	90.3%	94.6%
Mp 214c	93.1%	95.3%
Basicpitch	72.8%	84.0%

shows a comparison between the different extraction models.

Since differences of one semitone can occur as a consequence of concert pitch adjustment, we allow a deviation of one semitone.

4.3. Distance Between Extractions and Encoding

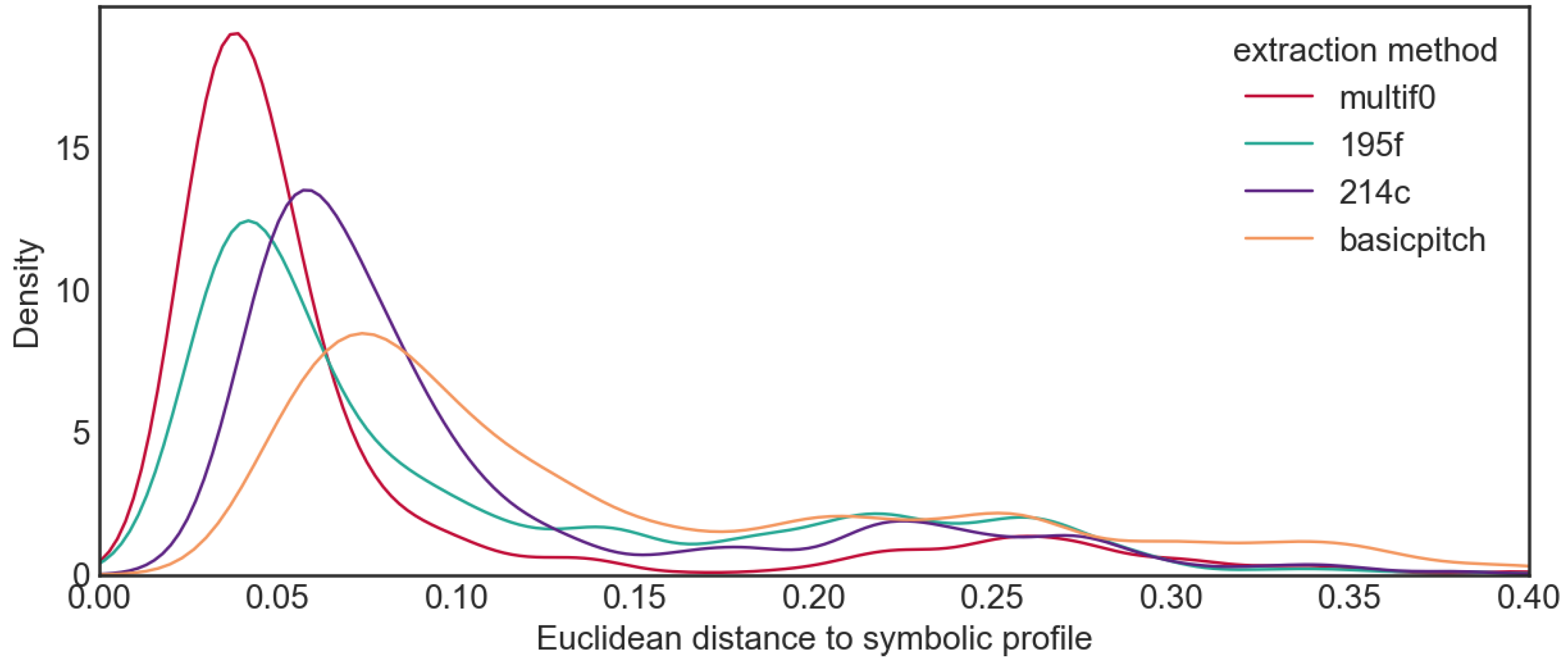
For each recording in the dataset, we compared the Euclidean distance between the pitch (class) profiles created from the different pitch extractions and from the symbolic encoding. The distribution of the distances for each extraction model is visualised in Figure 7 for the pitch class profiles and Figure 8 for the pitch profiles.

The figures suggest that Multif0 performs better than the other models for both the pitch profiles and the pitch class profiles. The statistics support this supposition (see

Table 5. Euclidean distances between profiles of the six tested models and the ground truth of the symbolic encodings. Best scores are in bold.

Extraction Model	Pitch Class Profiles			Pitch Profiles
	Mean	Median	Stdev	Mean	Median	Stdev
Multif0 [9]	0.0481	0.0400	0.0414	0.0741	0.0442	0.0770
Mp 195f [30]	0.0954	0.0506	0.0911	0.1028	0.0611	0.0838
Mp 214c [30]	0.0932	0.0609	0.0819	0.1047	0.0727	0.0766
Basicpitch [32]	0.1143	0.0705	0.1018	0.1464	0.1073	0.0948
CQT [34]	0.2036	0.2007	0.0380
HPCP [33]	0.1495	0.1383	0.0502

). A Kruskal–Wallis test was conducted to examine the effect of the extraction model on the distance between the pitch class profile of the extraction and the pitch profile of the encoding. This revealed a significant effect of the pitch extraction model: ${\chi }^2(5,N=611)=1580$, $p<0.001$, with a large effect size (${\eta }^2=0.43$), indicating that 43% of the variance in the pitch class profile distance can be attributed to differences in the extraction models.

A Kruskal–Wallis test was conducted to examine the effect of the extraction model on the distance between the pitch profile of the extraction and the pitch profile of the encoding. This revealed a significant effect of the pitch extraction model: ${\chi }^2(3,N=611)=467$, $p<0.001$, with a large effect size (${\eta }^2=0.19$), indicating that 19% of the variance in the pitch profile distance can be attributed to differences in the extraction models.

A Dunn’s test was conducted to evaluate the pairwise differences between the extraction models. For the pitch class profiles, all differences were significant ($p<0.01$), except between 195f and 214c ($p=0.25$), which are two versions of the same model and show similar results, as reported in

Table 6. Pairwise Dunn’s test results for pitch class profiles. Lower p-values indicate statistically more significant differences.

	Mp 195f	Mp 214c	Basicpitch	CQT	HPCP
Multif0	$5.2\times {10}^{-23}$	$3.0\times {10}^{-28}$	$2.3\times {10}^{-54}$	$6.3\times {10}^{-273}$	$5.5\times {10}^{-149}$
Mp 195f		$2.5\times {10}^{-1}$	$1.6\times {10}^{-8}$	$1.5\times {10}^{-142}$	$1.9\times {10}^{-58}$
Mp 214c			$6.7\times {10}^{-6}$	$3.5\times {10}^{-130}$	$1.1\times {10}^{-50}$
Basicpitch				$5.2\times {10}^{-87}$	$1.2\times {10}^{-25}$
CQT					$1.4\times {10}^{-20}$

. For the pitch profiles, all models show significant differences ($p<0.01$), as presented in

Table 7. Pairwise Dunn’s test results for pitch profiles. Lower p-values indicate statistically more significant differences.

	Mp 195f	Mp 214c	Basicpitch
Multif0	$1.1\times {10}^{-18}$	$7.6\times {10}^{-39}$	$1.3\times {10}^{-99}$
Mp 195f		$2.5\times {10}^{-05}$	$4.0\times {10}^{-35}$
Mp 214c			$3.6\times {10}^{-16}$

.

Multif0 is the pitch extraction model that results in the pitch (class) profiles most similar to those extracted from the symbolic encodings.

4.4. Clustering Profiles with Various Extraction Models

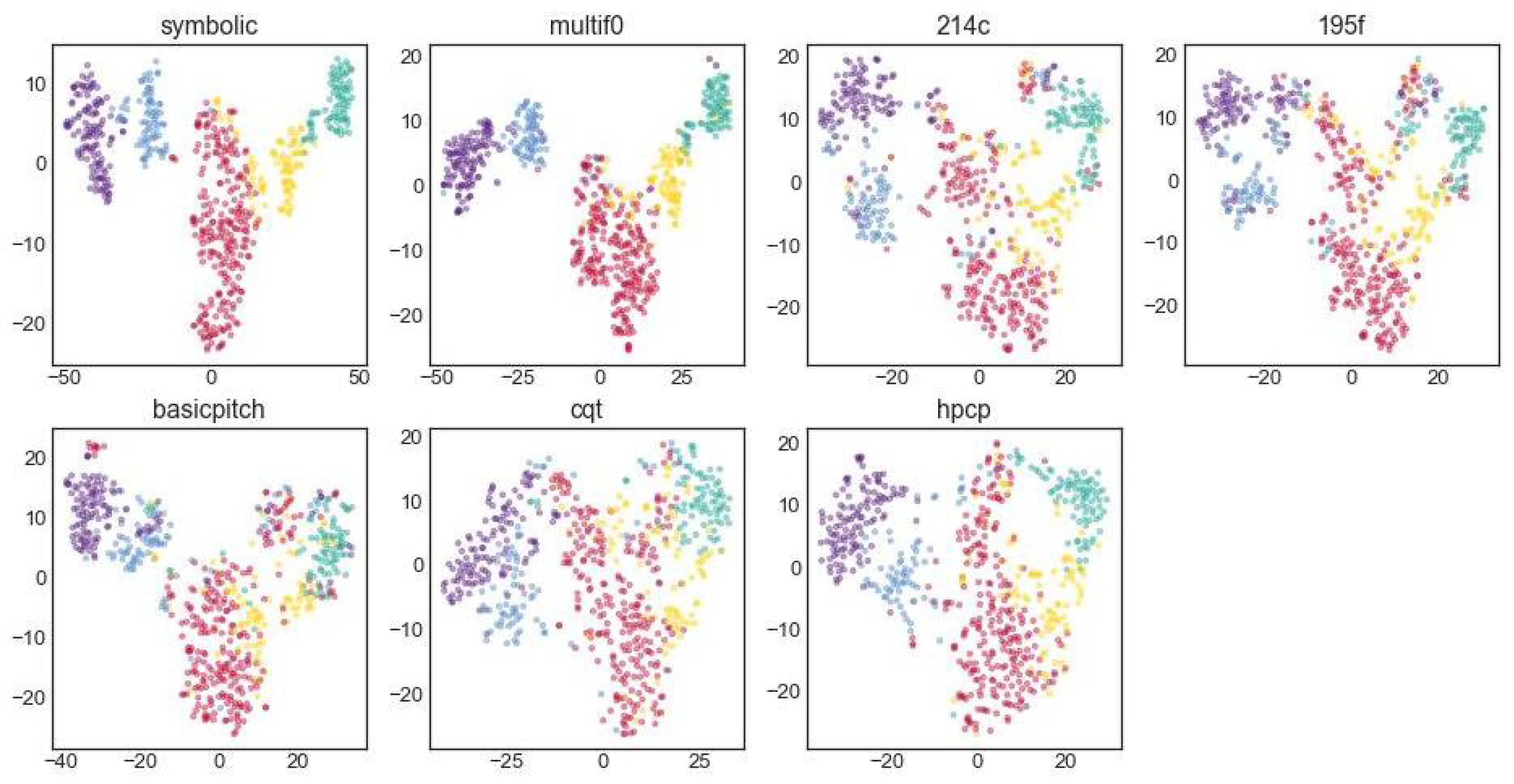
To assess whether the pitch (class) profiles obtained from the audio pitch extractions are of practical use, we clustered the pitch (class) profiles based on encoded scores and all the pitch extraction models. We then evaluated how similar the clusters based on the pitch extractions are to the clusters based on the encodings, both visually and quantitatively.

Using K-means and the silhouette score, we found five to be the optimal number of clusters in the encoded data. We then applied t-SNE with five clusters on the profiles. In Figure 9, the five clusters for the symbolic pitch class profiles are clearly discernible. Multif0 shows a very similar pattern, while the similarity decreases for Multipitch (195f and 214c), Basicpitch, HPCP and CQT. This is confirmed by the ARI and AMI scores in

Table 8. ARI and AMI scores for the clustering of pitch (class) profiles using the pitch extraction in this study. Best scores are in bold.

Extraction Model	Pitch Class Profiles		Pitch Profiles
	ARI	AMI	ARI	AMI
Multif0 [9]	0.84	0.79	0.58	0.61
Mp 195f [30]	0.45	0.47	0.32	0.36
Mp 214c [30]	0.52	0.53	0.35	0.40
Basicpitch [32]	0.44	0.42	0.34	0.34
CQT [34]	0.34	0.42
HPCP [33]	0.50	0.56

, which show the same order as one would infer from the images.

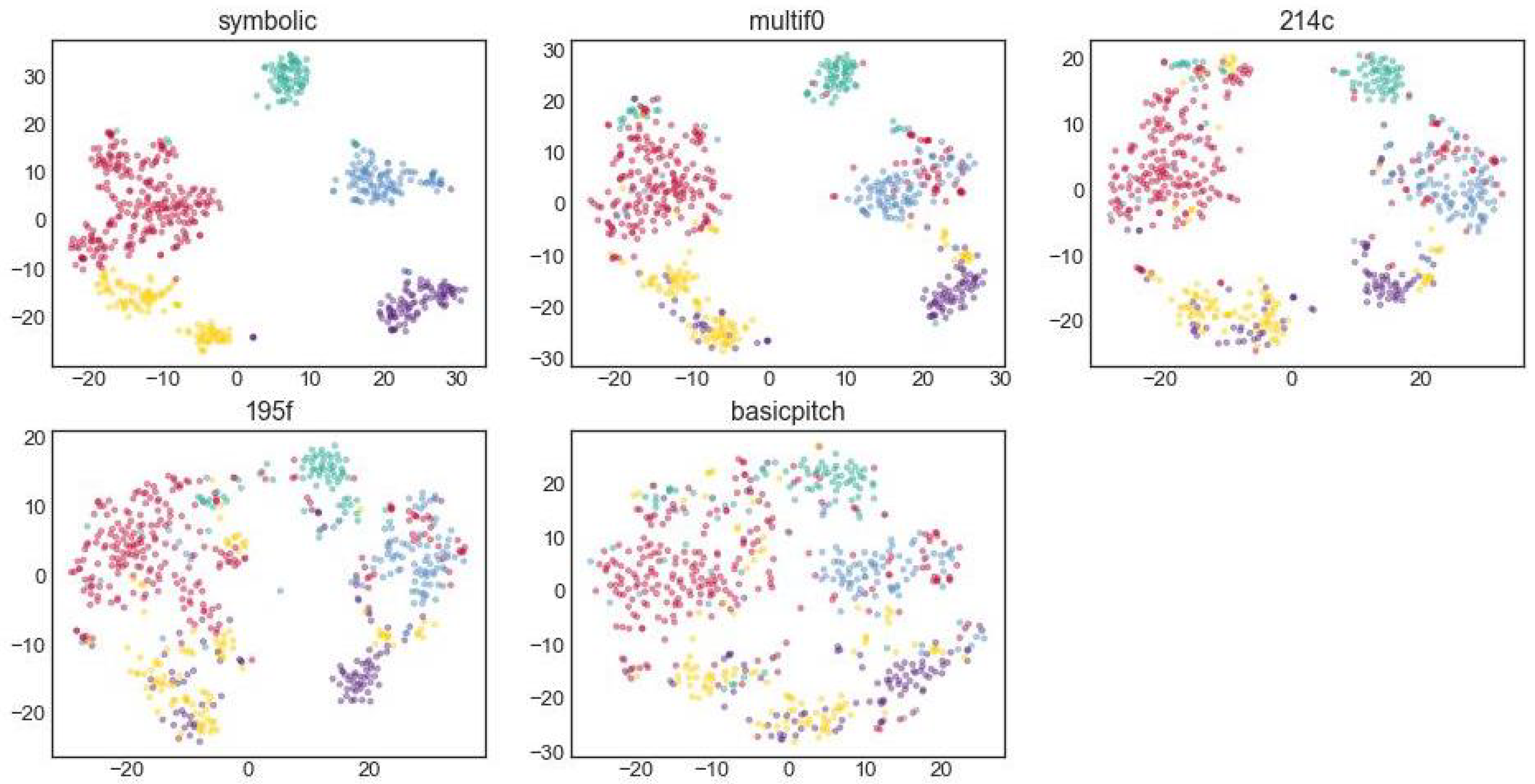
The clustering of the pitch profiles show a similar trend in Figure 10, but these clusters appear to be more scattered than the pitch class profiles. The main reason for this could be that the pitch class profiles are octave-invariant, whereas the pitch profiles are sensitive to the octave of the final—if the bass sounds in another octave than notated, the distance is larger than musical intuition would suggest. The ARI and AMI scores of the pitch profiles are also lower than those of the pitch class profiles.

The main takeaway from the clustering experiments is that the clusters of encodings and audio are very similar under the condition that the right pitch estimation model is applied. Since the clustering is unsupervised, these clusters are not necessarily in line with musicological models of tonality. However, the pitch class profiles within the same cluster seem to be based mainly on the (untransposed) modal scales of Table 1: cluster 1 contains works ending on finals F and C, cluster 2 works ending on G, cluster 3 works ending on E, cluster 4 works ending on E, and cluster 5 works ending on D.

4.5. The Effect of Performance and Recording on Pitch Class Profiles

We tested the effect of year of recording, number of voices and the ensemble composition (vocal, instrumental, mixed; as recorded in the metadata file) on the accuracy of the pitch class profiles and the pitch profiles generated from Multif0 pitch extractions. The multiple regression analysis yielded an R-squared value of 0.071 for the pitch class profiles and 0.086 for the pitch profiles. This suggests that the three independent variables contribute only about 7% to 9% of the variance in the pitch (class) profiles. Please note that there are only two recordings before 1980 in the dataset; the effect of earlier recordings is not investigated in this study.

5. Case Studies in Polyphonic Modality

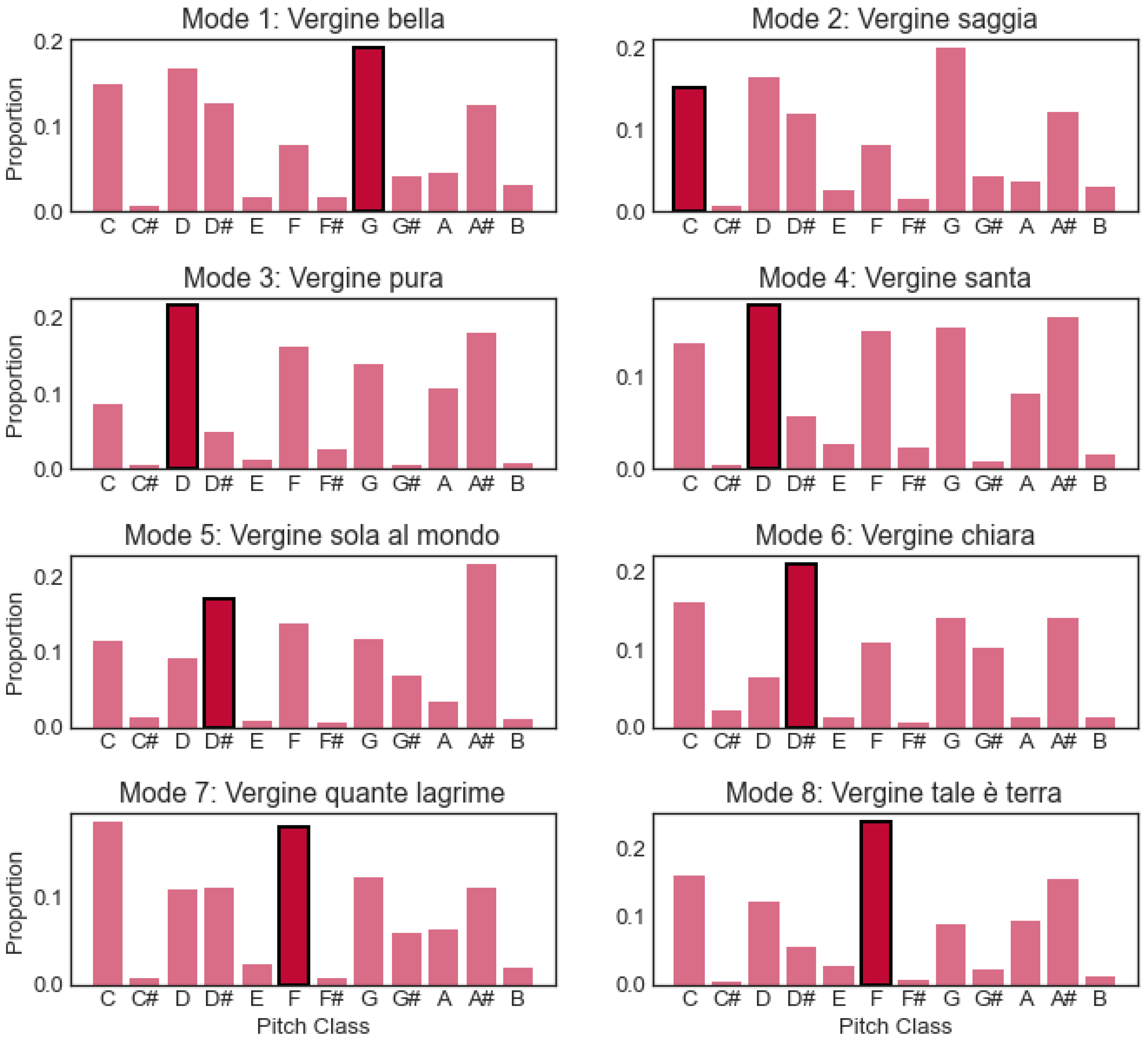
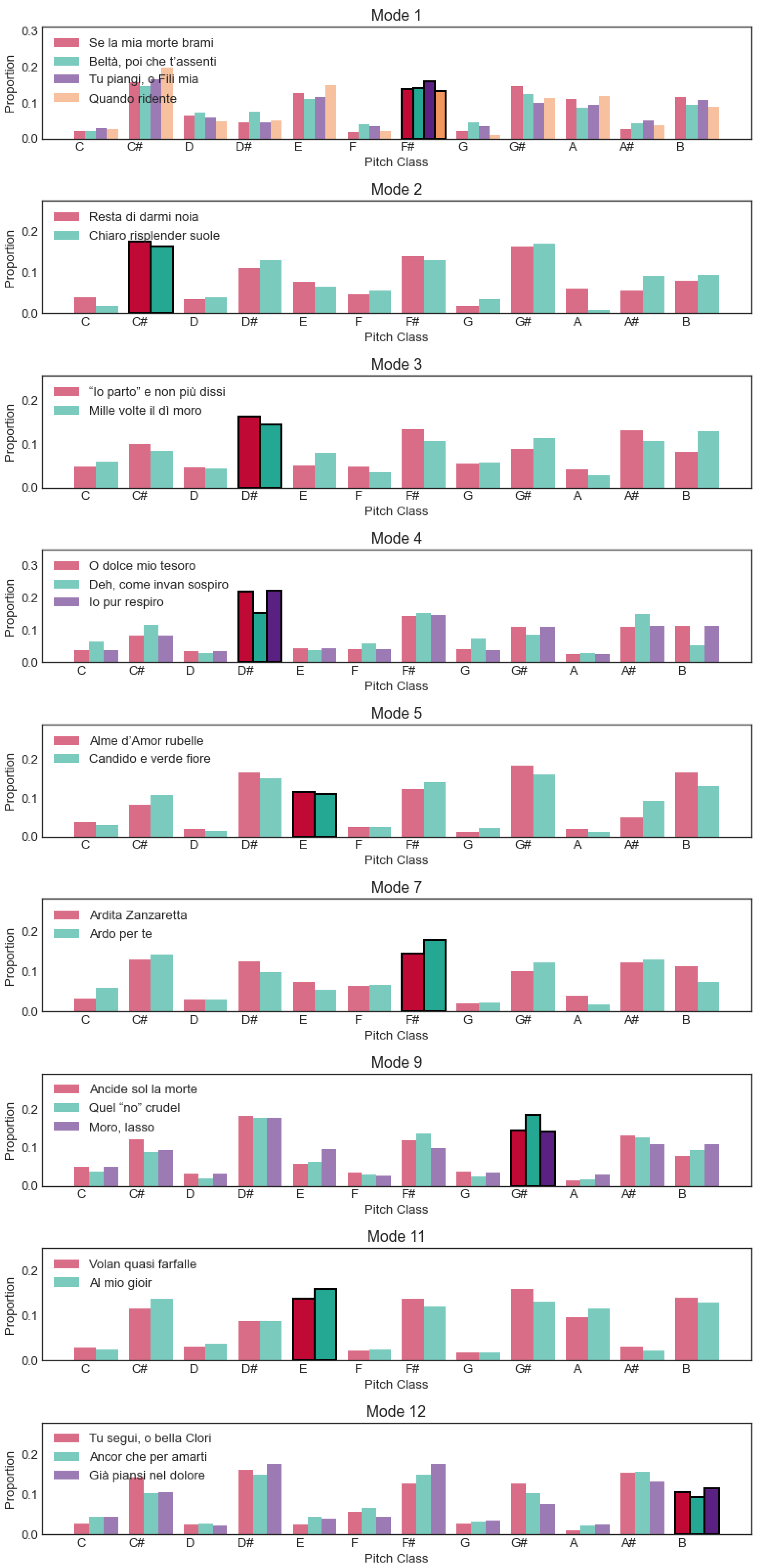
As a preliminary answer to research question 4, we present two short case studies that illustrate how the pitch class profiles extracted from recordings by Multif0 may be interpreted from a musicological point of view. The first case is Palestrina’s Vergine cycle (published in 1581). This modal cycle consists of eight madrigals, one for each of the eight modes. The profiles of each modal pair (1–2, 3–4 etc.) show a comparable though slightly different distribution of pitch classes in Figure 11. The profiles of mode 1 and 2 are very similar except the final. In fact, the piece in mode 1 seems to end not on the final but on the fifth above it. This peculiar feature is found in multiple compositions by Giovanni Pierluigi da Palestrina and seems to be his personal solution to differentiate the two modes [41]. The repeated observation in the musicological literature [42,43,44,45] that similar compositions in mode 1 strongly resemble his mode 2 works is now confirmed (for this cycle) by their virtually identical pitch class profiles. In comparison to mode 3, the final of mode 4 is only weakly differentiated from other prominent pitches, with a quite strong presence of C, the major second below the final, in mode 4. In authentic modes 5 and 7, the fifths above the final (A# and C, respectively) have a much stronger presence than in plagal modes 6 and 8. Powers’ insight [42] that Palestrina’s modes 5–8 follow a conventional pattern while modes 1–4 use a more peculiar approach is thus already reflected in the pitch class profiles.

Modes evolved over time, and often chromaticism (the use of pitches foreign to the modal scales) is identified as one of the catalysts for this development. Therefore, we analysed all 23 works from the Madrigali libro sesto by Carlo Gesualdo (published in 1611), using the mode attributions from [46]. The pitch class profiles in Figure 12 show that, even though the pitch class profiles are flatter than those in Figure 11 (because of the increase in chromatic pitches), they remain recognisable and there are no dramatic differences between pieces in the same mode. The profiles of modes 1 and 2 differ mainly in the minor third above and major second below the final. Those of modes 3 and 4 are quite similar, with maybe a stronger presence of the very characteristic minor second above the final in mode 3. Modes 11 and 12 differ most strikingly in the ratio between the final and the semitone below. Overall, the modes seem to keep their characteristics despite the increase in chromatic pitches.

These brief case studies indicate that the pitch class profiles are robust enough to serve as evidence in the study of the modes, complementing qualitative approaches. Realising their potential goes in two directions: systematically extracting pitch information from modal cycles and designing more sophisticated features than the simple pitch and pitch class profiles.

6. Discussion and Perspectives for Music History Research

6.1. Limitations of This Study

This study is aimed towards the usability of audio pitch extractions for the analysis of pitch (class) profiles and finals of complete audio tracks. We did not test the performance of pitch extraction models for shorter segments within tracks, which would allow us to draw conclusions on a more granular level than complete tracks. Although there is some variation in the audio of the CANTO-JRP dataset regarding timbre, ensemble composition and year of recording, the selection highly favours recent recordings of professional performances that adhere to the current historically informed performance practice. Therefore, the dataset mainly contains recordings after 1980, and we can not draw conclusions about the accuracy of pitch extractions from recordings earlier than 1980. The instruments in the recordings in this study are mainly voice, lute, recorder, viol, Renaissance brass and organ; harpsichord has not been tested. Please note that only a subset of the Renaissance repertoire has been tested; we cannot guarantee if these conclusions hold for other expressions of early music.

6.2. Observations on Multiple Pitch Estimation Models

The models evaluated in this study show a good performance, even though they are trained with different data than used in this study, as presented in Table 3. Heterogenous timbres within a single frame, and ’wilder data’, such as choirs with lots of vibrato, pitch instability and extraneous noise, may negatively impact performance of the models.

Multipitch and Basicpitch are more sensitive to this than Multif0. An example of a recurrent problem is the combination of lute and voice: the pitch extractions from solo voice or solo lute are accurate, but when combined, the thresholding of Multif0 leads to non-detection of the lute in the decay phase. To improve robustness, training multiple pitch estimation models on a diverse range of complex musical textures and recording conditions would be beneficial.

Another factor influencing model flexibility is the size of the output pitch bins. Models that use 100-cent bins offer limited opportunities to correct or study intonation and tuning deviations, whereas the 20-cent bins of Multif0 allow for more detailed performance practice studies, as well as for study of microtonal repertoires from various musical cultures.

A trade-off exists between loudness thresholding and sensitivity to noise. Multif0 returns frequencies without loudness information, whereas Multipitch and Basicpitch provide both loudness and pitch estimates. However, analysing results from the latter two models requires custom thresholding to filter out noise, a problem that Multif0 solves by incorporating loudness thresholding directly into its neural network.

Additionally, computational demands must be considered. The best-performing algorithms require GPU power to handle large datasets, such as the CANTO-JRP dataset. Processing times are often longer than the duration of the audio tracks.

Given these findings, future work on multiple pitch estimation should prioritize training models on recordings with diverse timbres, loudness variations and decay characteristics. Following the approach of Multif0, incorporating loudness thresholding within the neural network while providing both thresholded and non-thresholded outputs would accommodate different user needs. Furthermore, maintaining a small output pitch bin size would prevent unnecessary data loss, as pitch binning can be easily performed as a post-processing step.

7. Conclusions and Future Work

For this study, we selected five state-of-the-art pitch extraction models: the basic chroma-based models CQT and HPCP, and the (deep) neural network models Multif0, Multipitch and Basicpitch (RQ1). Although computationally expensive, the trained models have a strong performance compared to HPCP and CQT. From these models, Multif0 shows the best performance on detection of the final, pitch profiles and pitch class profiles.

We tested the quality of the clustering of audio pitch extractions and found that the clusters of pitch (class) profiles created by means of Multif0 yield a clustering closest to the clustering based on symbolic encodings (RQ2). Although we expected effects of the year of recording, number of voices and ensemble composition on the accuracy of the pitch (class) profiles, we could not find any significant effect (RQ3). The case studies show how the extractions can provide useful information for the analysis of tonal structures of 16th and 17th century music (RQ4). In conclusion, the results strongly suggest that Multif0 extractions can be used meaningfully for the same quantitative research into tonal patterns in early music as symbolic data (main research question).

In addition, we deliver the new CANTO-JRP dataset of pitch extractions by the neural network models, accompanied by metadata. For proprietary reasons, the audio cannot be shared. Although the CANTO-JRP dataset is intended first of all as a test set for the evaluation of multiple pitch estimation models, it can be used for a variety of MIR studies with methods closely related to the methods used to study symbolic encodings as well as for performance research. Finally, we provide a codebase containing a workflow for evaluating other multiple pitch estimation models.

We have demonstrated the potential of multiple pitch estimation for feature extraction in recordings of early music, using simple features such as the pitch (class) profiles and final pitch. More advanced features that are similar to the features used in study of encoded music, for example features related to dissonance, could also be designed. Such features would enable the study of audio recordings using techniques developed for encoded music, such as detection of modes and keys, cadence analysis and exploration of tonal structures in general.

As stated in Section 2.2, symbolic early music corpora for early music are limited in size and representativeness. Since our results indicate good performance on recordings of early music, a next step would be creating large corpora of extractions of pre-1700 music, such as modal cycles (of which there are hundreds) or a balanced corpus that is fit for a longitudinal study. These large corpora could then be used to study the evolution of tonal structures using the proposed features.

This article has demonstrated the usability of current audio analysis methods for musicological purposes. As multiple pitch estimation models advance, future research can further bridge the gap between encoded and recorded music, especially in cases where symbolic datasets are scarce.