Three-Dimensional Analysis for the Documentation of the Restoration of an Earthquake-Damaged Triptych
Abstract
1. Introduction
2. Materials and Methods
2.1. Case Study
2.2. Close-Range Photogrammetry
Metrics
2.3. Structured-Light Projection
2.4. Laser Scanning Micro-Profilometry
3. Results
3.1. Three-Dimensional Data-Quality Evaluation
3.2. Study of the Artist’s Technique through Profilometric Data Processing
3.3. Multi-Scale and Multi-Resolution Fusion of 3D Data
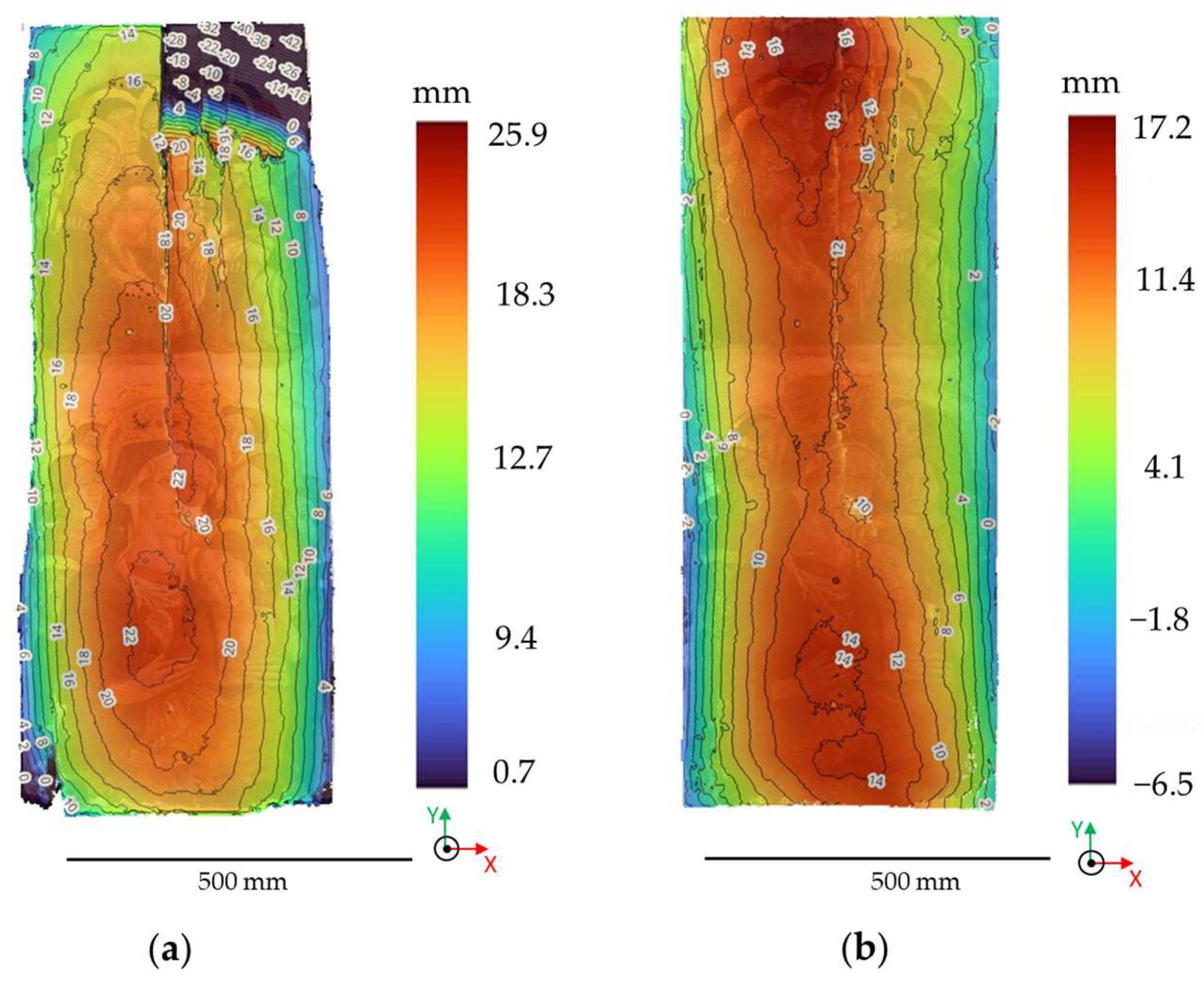
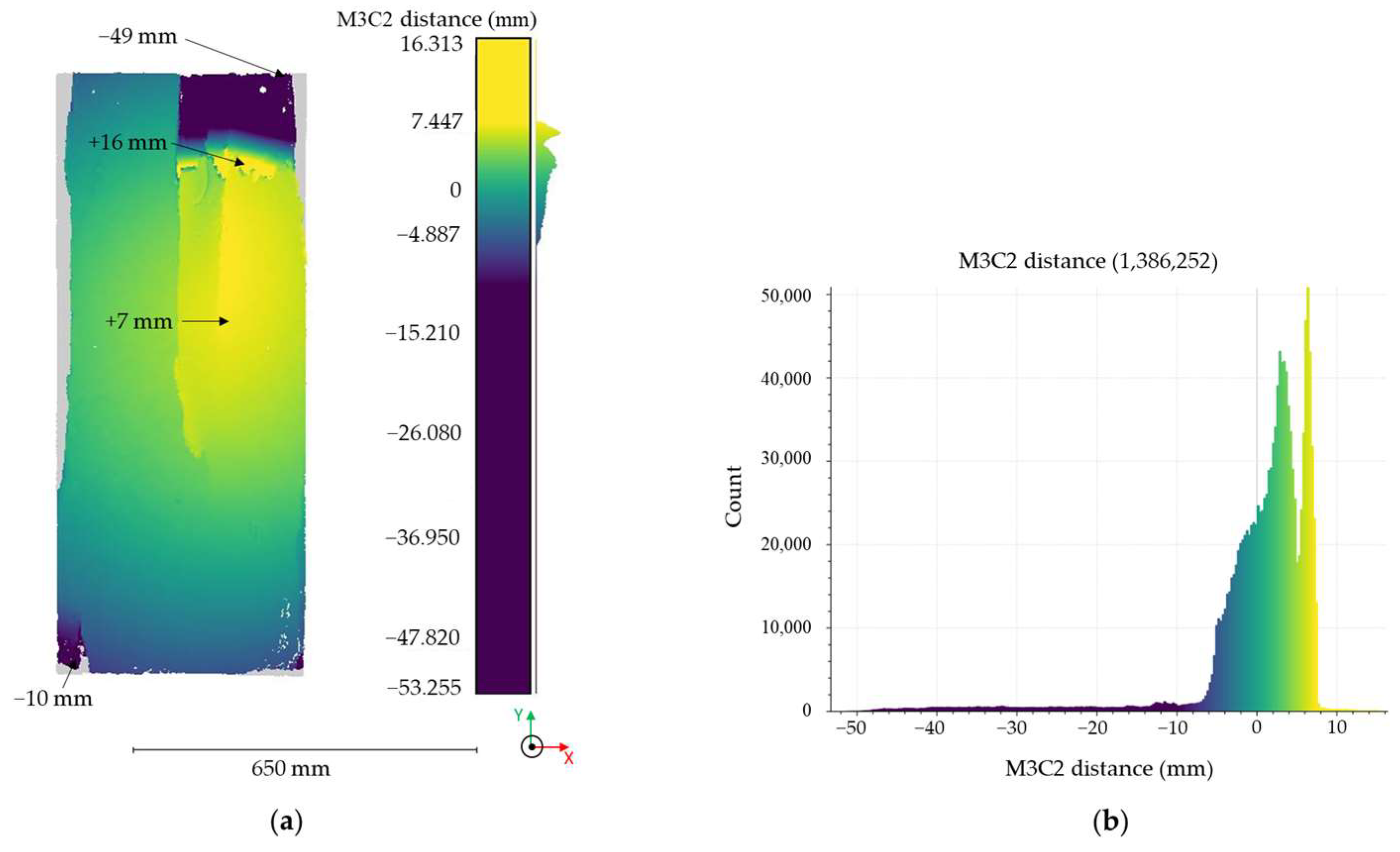
3.4. Three-Dimensional Data for Restoration Monitoring
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arbace, L.; Sonnino, E.; Callieri, M.; Dellepiane, M.; Fabbri, M.; Idelson, A.I.; Scopigno, R. Innovative Uses of 3D Digital Technologies to Assist the Restoration of a Fragmented Terracotta Statue. J. Cult. Heritage 2013, 14, 332–345. [Google Scholar] [CrossRef]
- Pieraccini, M.; Guidi, G.; Atzeni, C. 3D Digitizing of Cultural Heritage. J. Cult. Heritage 2001, 2, 63–70. [Google Scholar] [CrossRef]
- Gabellone, F. Digital Twin: A New Perspective for Cultural Heritage Management and Fruition. Acta IMEKO 2022, 11, 7. [Google Scholar] [CrossRef]
- Apollonio, F.I.; Basilissi, V.; Callieri, M.; Dellepiane, M.; Gaiani, M.; Ponchio, F.; Rizzo, F.; Rubino, A.R.; Scopigno, R.; Sobra’, G. A 3D-Centered Information System for the Documentation of a Complex Restoration Intervention. J. Cult. Heritage 2018, 29, 89–99. [Google Scholar] [CrossRef]
- Robson, S.; Bucklow, S.; Woodhouse, N.; Papadaki, H. Periodic Photogrammetric Monitoring and Surface Reconstruction of a Historical Wood Panel Painting for Restoration Purposes. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 395–400. [Google Scholar]
- Bratasz, L.; Jakiela, S.; Kozlowski, R. Allowable Thresholds in Dynamic Changes of Microclimate for Wooden Cultural Objects: Monitoring in Situ and Modelling. In Proceedings of the ICOM Committee for Conservation, 14th Triennial Meeting, The Hague, The Netherlands, 12–16 September 2005; pp. 582–589. [Google Scholar]
- Guidi, G.; Beraldin, J.-A.; Atzeni, C. Wood artworks dimensional monitoring through high-resolution 3D cameras. Proc. SPIE 2007, 6491, 64910T. [Google Scholar] [CrossRef]
- Hess, M.; Korenberg, C.; Ward, C.; Robson, S.; Entwistle, C. Use of 3D Laser Scanning for Monitoring the Dimensional Stability of a Byzantine Ivory Panel. Stud. Conserv. 2015, 60, S126–S133. [Google Scholar] [CrossRef][Green Version]
- Palma, G.; Pingi, P.; Siotto, E.; Bellucci, R.; Guidi, G.; Scopigno, R. Deformation Analysis of Leonardo da Vinci’s “Adorazione dei Magi” through Temporal Unrelated 3D Digitization. J. Cult. Heritage 2019, 38, 174–185. [Google Scholar] [CrossRef]
- Guidi, G.; Atzeni, C.; Seracini, M.; Lazzari, S. Painting Survey by 3D Optical Scanning: The Case of “Adoration of the Magi” by Leonardo Da Vinci. Stud. Conserv. 2004, 49, 1–12. [Google Scholar] [CrossRef]
- Baribeau, R.; Rioux, M.; Godin, G. Recent Advances in the Use of a Laser Scanner in the Examination of Paintings. In Proceedings of the Restoration ’92 Conference, Amsterdam, The Netherlands, 20–22 October 1992. [Google Scholar]
- Bertani, D.; Cetica, M.; Melozzi, M.; Pezzati, L. High-Resolution Optical Topography Applied to Ancient Painting Diagnostics. Opt. Eng. 1995, 34, 1219–1225. [Google Scholar] [CrossRef]
- Brewer, A.; Forno, C. Moiré Fringe Analysis of Cradled Panel Paintings. Stud. Conserv. 1997, 42, 211–230. [Google Scholar] [CrossRef]
- Abate, D.; Menna, F.; Remondino, F.; Gattari, M. 3D Painting Documentation: Evaluation of Conservation Conditions with 3D Imaging and Ranging Techniques. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2014, XL-5, 1–8. [Google Scholar] [CrossRef]
- Targowski, P.; Iwanicka, M. Optical Coherence Tomography: Its Role in the Non-Invasive Structural Examination and Conservation of Cultural Heritage Objects—A Review. Appl. Phys. A 2012, 106, 265–277. [Google Scholar] [CrossRef]
- Daffara, C.; Mazzocato, S. Surface Metrology Based on Scanning Conoscopic Holography for In Situ and In-Process Monitoring of Microtexture in Paintings. Sensors 2022, 22, 6637. [Google Scholar] [CrossRef]
- Ramos, M.M.; Remondino, F. Data fusion in Cultural Heritage—A Review. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2015, XL-5/W7, 359–363. [Google Scholar] [CrossRef]
- Gašparović, M.; Malarić, I. Increase of readability and accuracy of 3D models using fusion of close range photogrammetry and laser scanning. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2012, XXXIX–B5, 93–98. [Google Scholar] [CrossRef]
- Fontana, R.; Gambino, M.C.; Greco, M.; Marras, L.; Materazzi, M.; Pampaloni, E.; Pezzati, L.; Poggi, P. Integrating 2D and 3D Data for Diagnostics of Panel Paintings. Proc. SPIE 2003, 5146, 88–98. [Google Scholar] [CrossRef]
- Grifoni, E.; Legnaioli, S.; Nieri, P.; Campanella, B.; Lorenzetti, G.; Pagnotta, S.; Poggialini, F.; Palleschi, V. Construction and Comparison of 3D Multi-Source Multi-Band Models for Cultural Heritage Applications. J. Cult. Heritage 2018, 34, 261–267. [Google Scholar] [CrossRef]
- Chane, C.S.; Mansouri, A.; Marzani, F.S.; Boochs, F. Integration of 3D and Multispectral Data for Cultural Heritage Applications: Survey and Perspectives. Image Vis. Comput. 2013, 31, 91–102. [Google Scholar] [CrossRef]
- Fontana, R.; Gambino, M.C.; Greco, M.; Marras, L.; Materazzi, M.; Pampaloni, E.; Pelagotti, A.; Pezzati, L.; Poggi, P.; Sanapo, C. 2D and 3D Optical Diagnostic Techniques Applied to Madonna Dei Fusi by Leonardo Da Vinci. Proc. SPIE 2005, 5857, 166–176. [Google Scholar] [CrossRef]
- Guarnieri, A.; Remondino, F.; Vettore, A. Digital Photogrammetry and TLS Data Fusion Applied to Cultural Heritage 3D Modeling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 1–6. [Google Scholar]
- Bastonero, P.; Donadio, E.; Chiabrando, F.; Spanò, A. Fusion of 3D Models Derived from TLS and Image-Based Techniques for CH Enhanced Documentation. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2014, II–5, 73–80. [Google Scholar] [CrossRef]
- AA. VV. Restauri nelle Marche. Testimonianze Acquisti e Recuperi; Arti Grafiche Editoriali: Urbino, Italia, 1973. [Google Scholar]
- Barucca, G. Galleria Degli Uffizi Facciamo Presto! Marche 2016–2017: Tesori Salvati, Tesori Da Salvare; Prima Edizione; Giunti Firenze Musei: Firenze, Italy, 2017; ISBN 978-88-09-85696-7. [Google Scholar]
- Campbell, J.B.; Wynne, R.H.; Thomas, V.A. Introduction to Remote Sensing, 6th ed.; The Guilford Press: New York, NY, USA, 2023; ISBN 978-1-4625-4940-5. [Google Scholar]
- Linder, W. Digital Photogrammetry: Theory and Applications; Springer: Berlin/Heidelberg, 2013; ISBN 978-3-662-06725-3. [Google Scholar]
- Grifoni, E.; Vannini, E.; Lunghi, I.; Faraioli, P.; Ginanni, M.; Santacesarea, A.; Fontana, R. 3D Multi-Modal Point Clouds data Fusion for Metrological Analysis and Restoration Assessment of a Panel Painting. J. Cult. Heritage 2024, 66, 356–366. [Google Scholar] [CrossRef]
- Lehoczky, M.; Abdurakhmonov, Z. Present Software of Photogrammetric Processing of Digital Images. E3S Web Conf. 2021, 227, 04001. [Google Scholar] [CrossRef]
- Remondino, F.; Nocerino, E.; Toschi, I.; Menna, F. A Critical review of automated photogrammetric processing of large datasets. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII–2/W5, 591–599. [Google Scholar] [CrossRef]
- Lavecchia, F.; Guerra, M.G.; Galantucci, L.M. Performance Verification of a Photogrammetric Scanning System for Micro-Parts Using a Three-Dimensional Artifact: Adjustment and Calibration. Int. J. Adv. Manuf. Technol. 2018, 96, 4267–4279. [Google Scholar] [CrossRef]
- Luhmann, T.; Robson, S.; Kyle, S. Close-Range Photogrammetry: Principles, Methods and Applications; Whittles: Dunbeath, UK, 2006; ISBN 978-1-870325-50-9. [Google Scholar]
- Bertin, S.; Friedrich, H.; Delmas, P.; Chan, E.; Gimel’farb, G. Digital Stereo Photogrammetry for Grain-Scale Monitoring of Fluvial Surfaces: Error Evaluation and Workflow Optimisation. ISPRS J. Photogramm. Remote. Sens. 2015, 101, 193–208. [Google Scholar] [CrossRef]
- Remondino, F.; El-Hakim, S. Image-based 3D Modelling: A Review. Photogramm. Rec. 2006, 21, 269–291. [Google Scholar] [CrossRef]
- Remondino, F.; Rizzi, A.; Barazzetti, L.; Scaioni, M.; Fassi, F.; Brumana, R.; Pelagotti, A. Review of Geometric and Radiometric Analyses of Paintings. Photogramm. Rec. 2011, 26, 439–461. [Google Scholar] [CrossRef]
- Brutto, M.L.; Garraffa, A.; Pellegrino, L.; Di Natale, B. 3D Mosaic Documentation Using Close Range Photogrammetry. In Proceedings of the 1st International Conference on Metrology for Archaeology, Benevento, Italy, 21–23 October 2015; pp. 22–23. [Google Scholar]
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging; De Gruyter: Berlin, Germany, 2019; ISBN 978-3-11-060725-3. [Google Scholar]
- Bell, T.; Li, B.; Zhang, S. Structured Light Techniques and Applications. In Wiley Encyclopedia of Electrical and Electronics Engineering; Webster, J.G., Ed.; Wiley: Hoboken, NJ, USA, 2016; pp. 1–24. ISBN 978-0-471-34608-1. [Google Scholar]
- Akca, D.; Remondino, F.; Novák, D.; Hanusch, T.; Schrotter, G.; Gruen, A. Performance evaluation of a coded structured light system for cultural heritage applications. Proc. SPIE 2007, 6491, 64910V. [Google Scholar] [CrossRef]
- Fontana, R.; Gambino, M.C.; Mazzotta, C.; Greco, M.; Pampaloni, E.; Pezzati, L. High-Resolution 3D Survey of Artworks. Proc. SPIE 2004, 5457, 719–726. [Google Scholar] [CrossRef]
- Carcagni, P.; Daffara, C.; Fontana, R.; Gambino, M.C.; Mastroianni, M.; Mazzotta, C.; Pampaloni, E.; Pezzati, L. Optical Micro-Profilometry for Archaeology. Proc. SPIE 2005, 5857, 58570F. [Google Scholar] [CrossRef]
- Daffara, C.; Mazzocato, S.; Marchioro, G. Multiscale Roughness Analysis by Microprofilometry Based on Conoscopic Holography: A New Tool for Treatment Monitoring in Highly Reflective Metal Artworks. Eur. Phys. J. Plus 2022, 137, 430. [Google Scholar] [CrossRef]
- Mazzocato, S.; Cimino, D.; Daffara, C. Integrated Microprofilometry and Multispectral Imaging for Full-Field Analysis of Ancient Manuscripts. J. Cult. Heritage 2024, 66, 110–116. [Google Scholar] [CrossRef]
- Fovo, A.D.; Striova, J.; Pampaloni, E.; Fontana, R. Unveiling the Invisible in Uffizi Gallery’s Drawing 8P by Leonardo with Non-Invasive Optical Techniques. Appl. Sci. 2021, 11, 7995. [Google Scholar] [CrossRef]
- Pamart, A.; Abergel, V.; de Luca, L.; Veron, P. Toward a Data Fusion Index for the Assessment and Enhancement of 3D Multimodal Reconstruction of Built Cultural Heritage. Remote. Sens. 2023, 15, 2408. [Google Scholar] [CrossRef]
- Moyano, J.; Nieto-Julián, J.E.; Bienvenido-Huertas, D.; Marín-García, D. Validation of Close-Range Photogrammetry for Architectural and Archaeological Heritage: Analysis of Point Density and 3D Mesh Geometry. Remote Sens. 2020, 12, 3571. [Google Scholar] [CrossRef]
- Kodors, S. Point Distribution as True Quality of LiDAR Point Cloud. Balt. J. Mod. Comput. 2017, 5, 362–378. [Google Scholar] [CrossRef]
- Burgio, L.; Clark, R.J. Library of FT-Raman Spectra of Pigments, Minerals, Pigment Media and Varnishes, and Supplement to Existing Library of Raman Spectra of Pigments with Visible Excitation. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2001, 57, 1491–1521. [Google Scholar] [CrossRef] [PubMed]
- Riminesi, C.; Del Fà, R.M.; Brizzi, S.; Rocco, A.; Fontana, R.; Bertasa, M.; Grifoni, E.; Impallaria, A.; Leucci, G.; De Giorgi, L.; et al. Architectural Assessment of Wall Paintings Using a Multimodal and Multi-Resolution Diagnostic Approach: The Test Site of the Brancacci Chapel in Firenze. J. Cult. Heritage 2024, 66, 99–109. [Google Scholar] [CrossRef]
- Cocchi, L.; Bertrand, M.; Mazzanti, P.; Uzielli, L.; Castelli, C.; Santacesaria, A. Verfica Del Funzionamento Di Una Traversatura Elastica Applicata Su Un Dipinto Su Tavola: La Deposizione Dalla Croce Di Anonimo Abruzzese, XVI Secolo. OPD Restauro 2014, 26, 83–94. Available online: https://www.jstor.org/stable/24398164 (accessed on 13 January 2024).
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D Comparison of Complex Topography with Terrestrial Laser Scanner: Application to the Rangitikei Canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Rose, W.; Bedford, J.; Howe, E.; Tringham, S. Trialling an Accessible Non-Contact Photogrammetric Monitoring Technique to Detect 3D Change on Wall Paintings. Stud. Conserv. 2022, 67, 545–555. [Google Scholar] [CrossRef]
- La Rocca, A.; Lingua, A.M.; Grigillio, D. A photogrammetry application to rockfall monitoring: The Belca, Slovenia case study. GEAM 2020, 1208, 16–33. [Google Scholar] [CrossRef]
- Nourbakhshbeidokhti, S.; Kinoshita, A.M.; Chin, A.; Florsheim, J.L. A Workflow to Estimate Topographic and Volumetric Changes and Errors in Channel Sedimentation after Disturbance. Remote. Sens. 2019, 11, 586. [Google Scholar] [CrossRef]



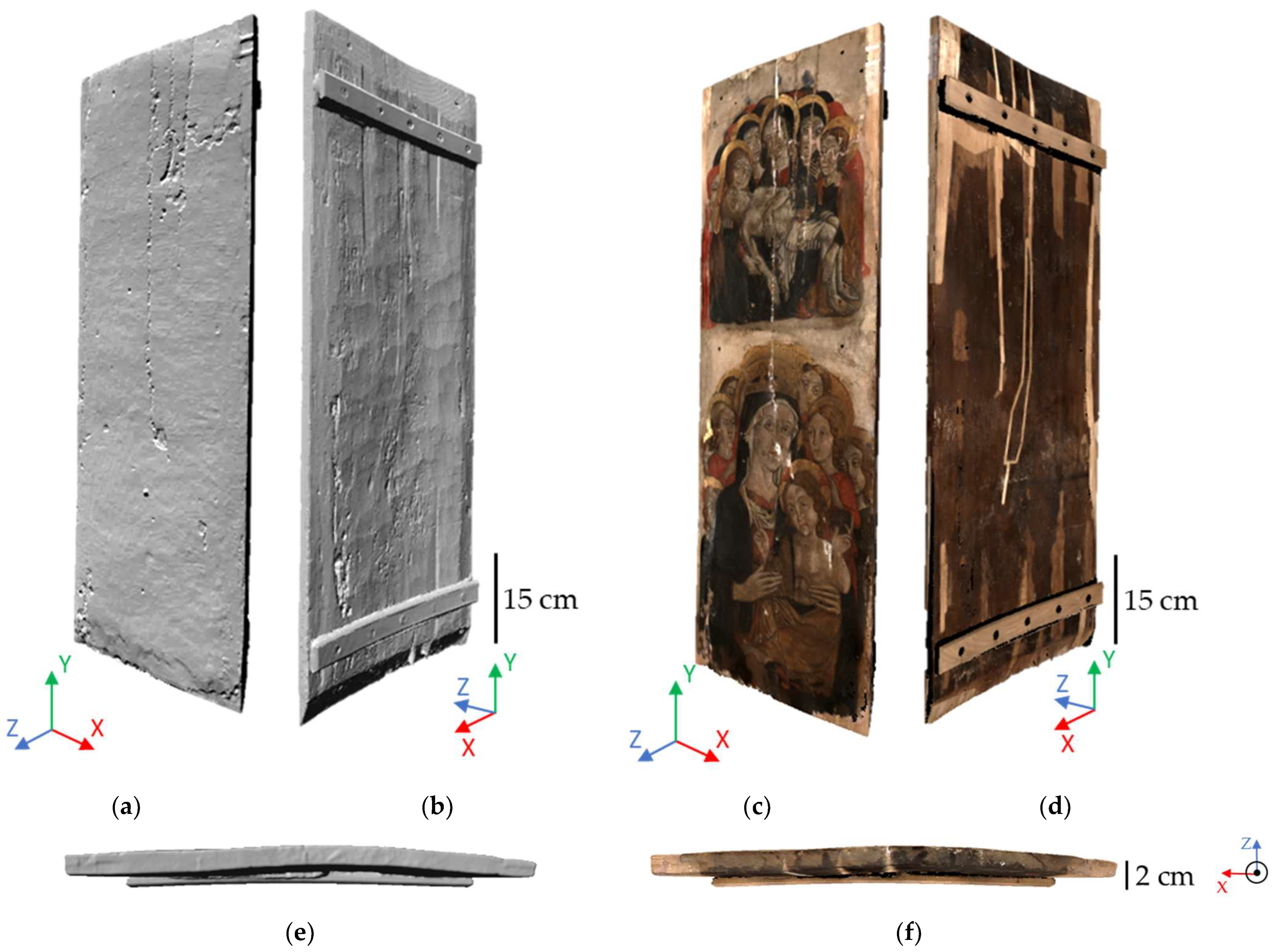

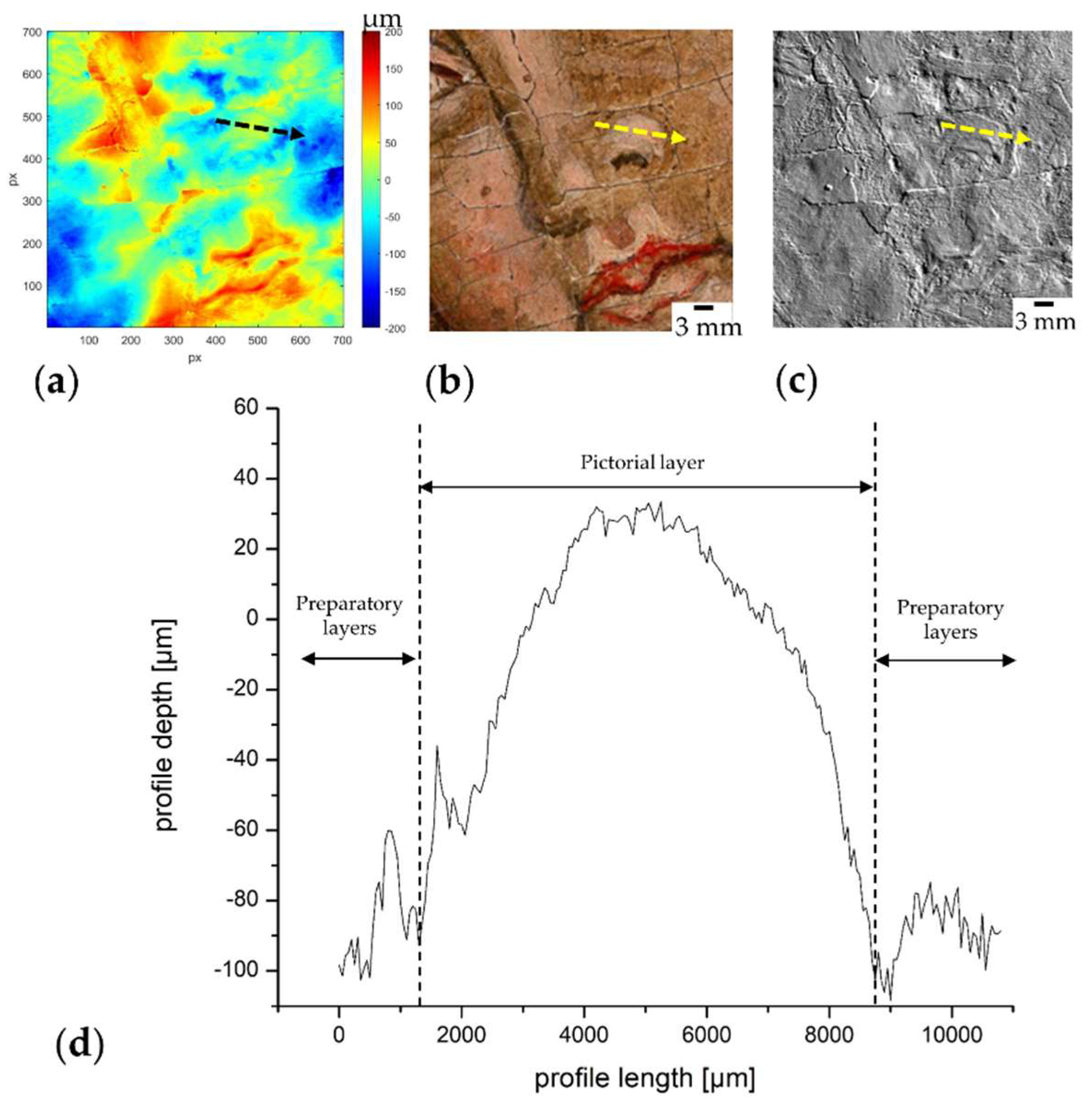
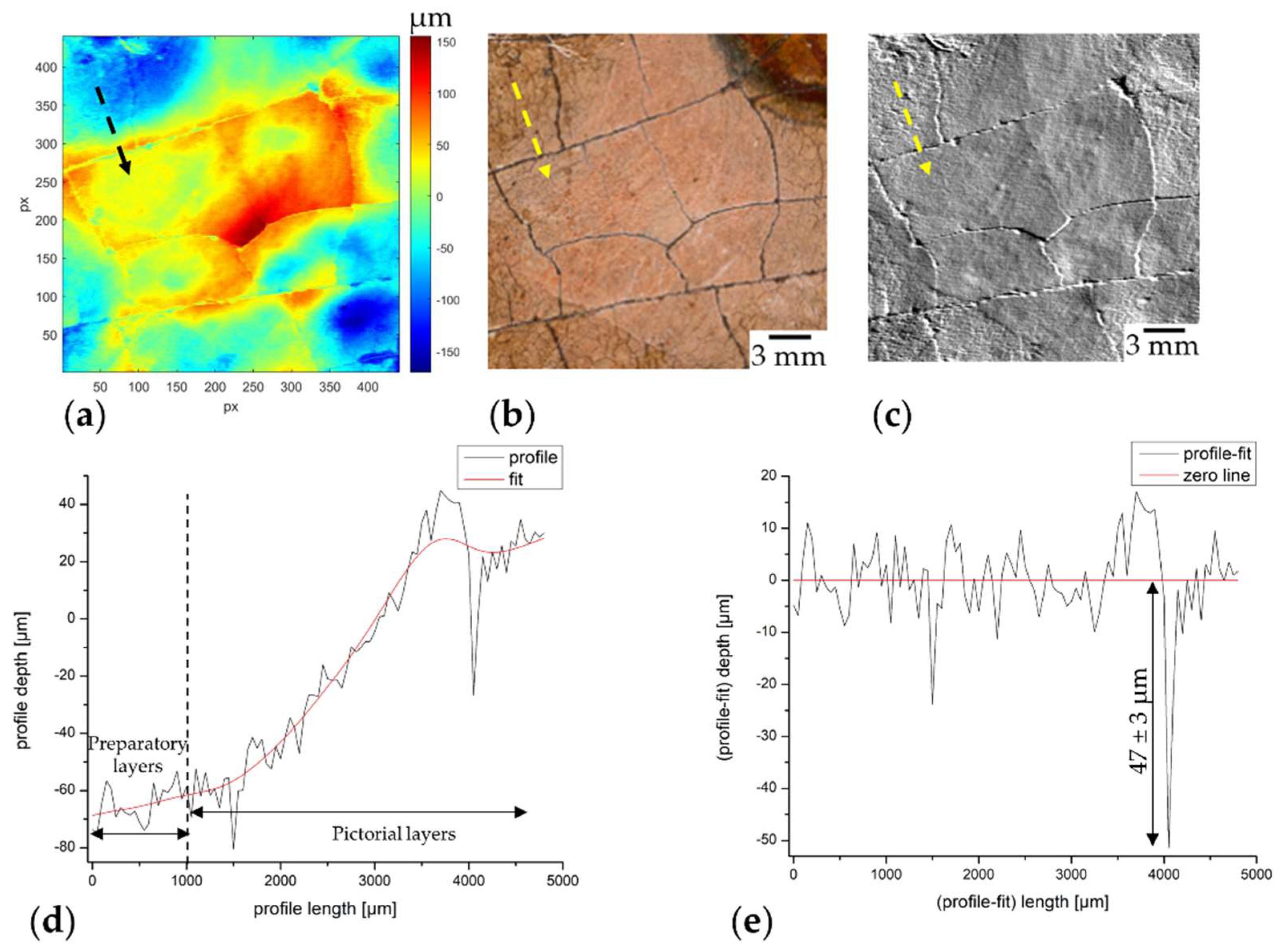

| GSD Ground Sampling Distance [µm] | dz Depth Resolution [µm] | Accuracy in Image Space [µm] | In-Plane Theoretical Precision [µm] | Axial Theoretical Precision [µm] | Overall Precision [µm] |
|---|---|---|---|---|---|
| 83.4 | 463 | 2.175 | 41.2 | 232 | 239 |
| Techniques | Sampled Area [cm2] | Number of Points | Number of Vertices | Number of Faces | Point Density with R = 0.5 mm [pp/mm2] | |
|---|---|---|---|---|---|---|
| Pre-restoration (front) | Photogrammetry | 45 120 | 6,380,304 | 80,762 | 160,369 | 12 ± 1 |
| Post-restoration (front) | Structured-light topography | 45 120 | 35,634,635 | 6,013,775 | 12,007,973 | 74 ± 29 |
| Child’s face | Micro-profilometry | 9 10.5 | 3,609,905 | 3,609,905 | 7,176,312 | 384 ± 29 |
| Mean Value ± St. Dev. [μm] | |||
|---|---|---|---|
| Post-Restoration Model with the Sections Where the Arrows Were Calculated Highlighted in Pink | Number of Section | Pre-Restoration Point Cloud | Post-Restoration Point Cloud |
 | 1 | 18.3 ± 0.4 | 16.4 ± 0.4 |
| 2 | 19.2 ± 0.1 | 16.7 ± 0.3 | |
| 3 | 18.7 ± 0.1 | 17.0 ± 0.3 | |
| 4 | 19.0 ± 0.1 | 16.6 ± 0.1 | |
| 5 | 18.5 ± 0.1 | 15.3 ± 0.5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vannini, E.; Lunghi, I.; Grifoni, E.; Farioli, P.; Ginanni, M.; Santacesaria, A.; Fontana, R. Three-Dimensional Analysis for the Documentation of the Restoration of an Earthquake-Damaged Triptych. Heritage 2024, 7, 2176-2194. https://doi.org/10.3390/heritage7040103
Vannini E, Lunghi I, Grifoni E, Farioli P, Ginanni M, Santacesaria A, Fontana R. Three-Dimensional Analysis for the Documentation of the Restoration of an Earthquake-Damaged Triptych. Heritage. 2024; 7(4):2176-2194. https://doi.org/10.3390/heritage7040103
Chicago/Turabian StyleVannini, Emma, Irene Lunghi, Emanuela Grifoni, Petra Farioli, Marina Ginanni, Andrea Santacesaria, and Raffaella Fontana. 2024. "Three-Dimensional Analysis for the Documentation of the Restoration of an Earthquake-Damaged Triptych" Heritage 7, no. 4: 2176-2194. https://doi.org/10.3390/heritage7040103
APA StyleVannini, E., Lunghi, I., Grifoni, E., Farioli, P., Ginanni, M., Santacesaria, A., & Fontana, R. (2024). Three-Dimensional Analysis for the Documentation of the Restoration of an Earthquake-Damaged Triptych. Heritage, 7(4), 2176-2194. https://doi.org/10.3390/heritage7040103









