An Overview of Geophysical Techniques and Their Potential Suitability for Archaeological Studies
Abstract
1. Introduction
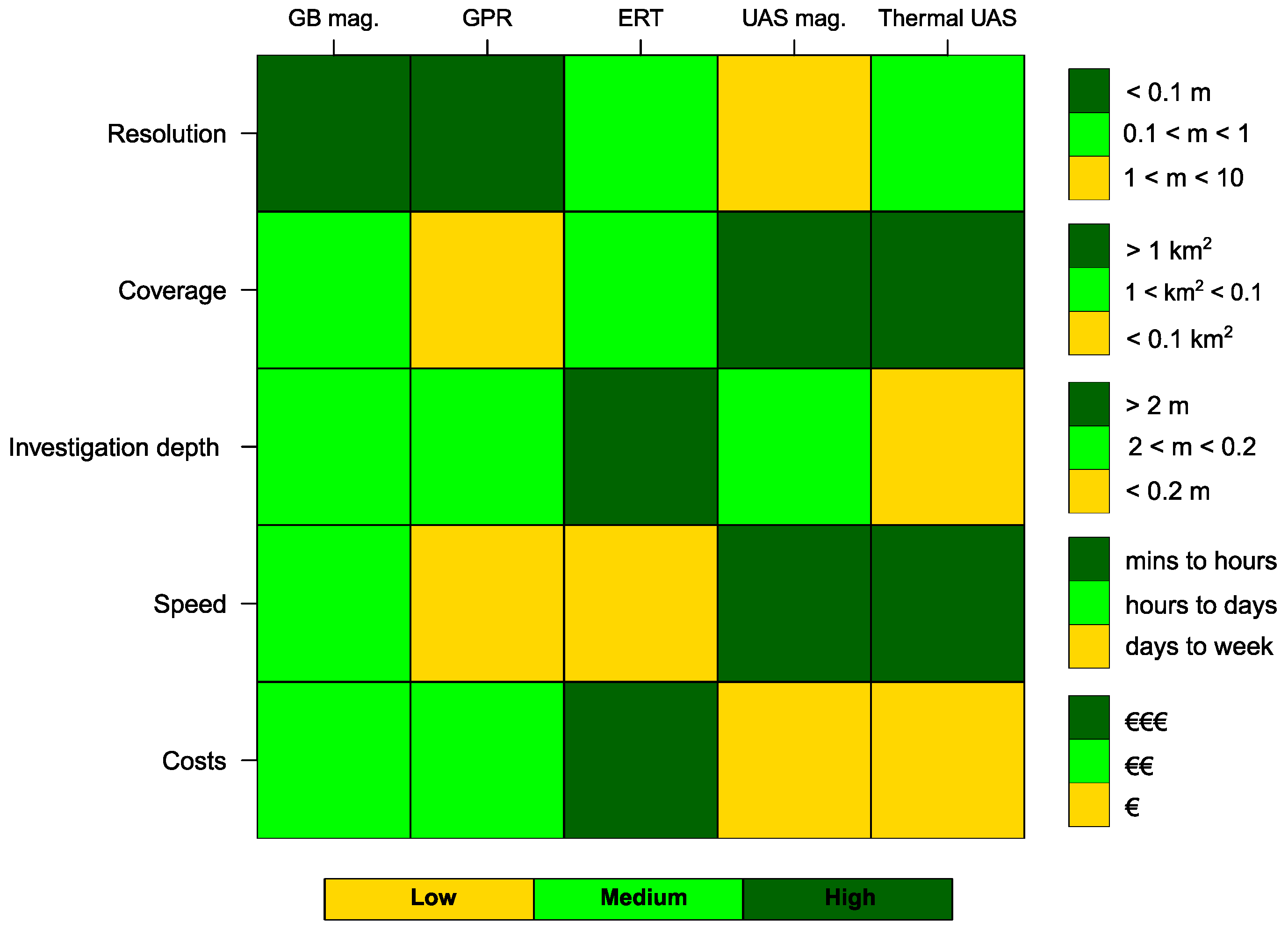
2. Magnetometry
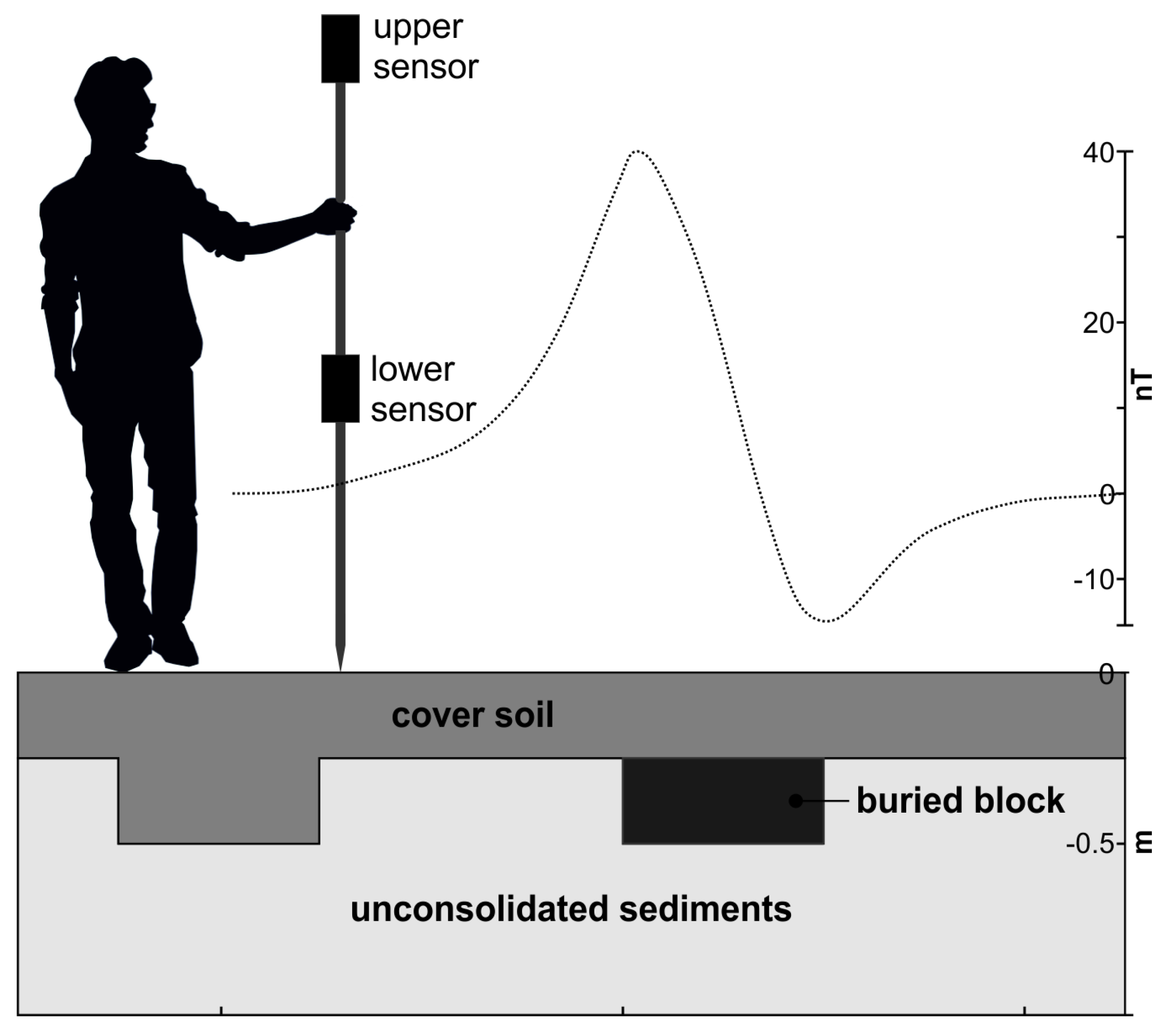
2.1. Basic Principles of the Magnetic Method
2.2. Magnetic Method: Acquisition and Instrumentation
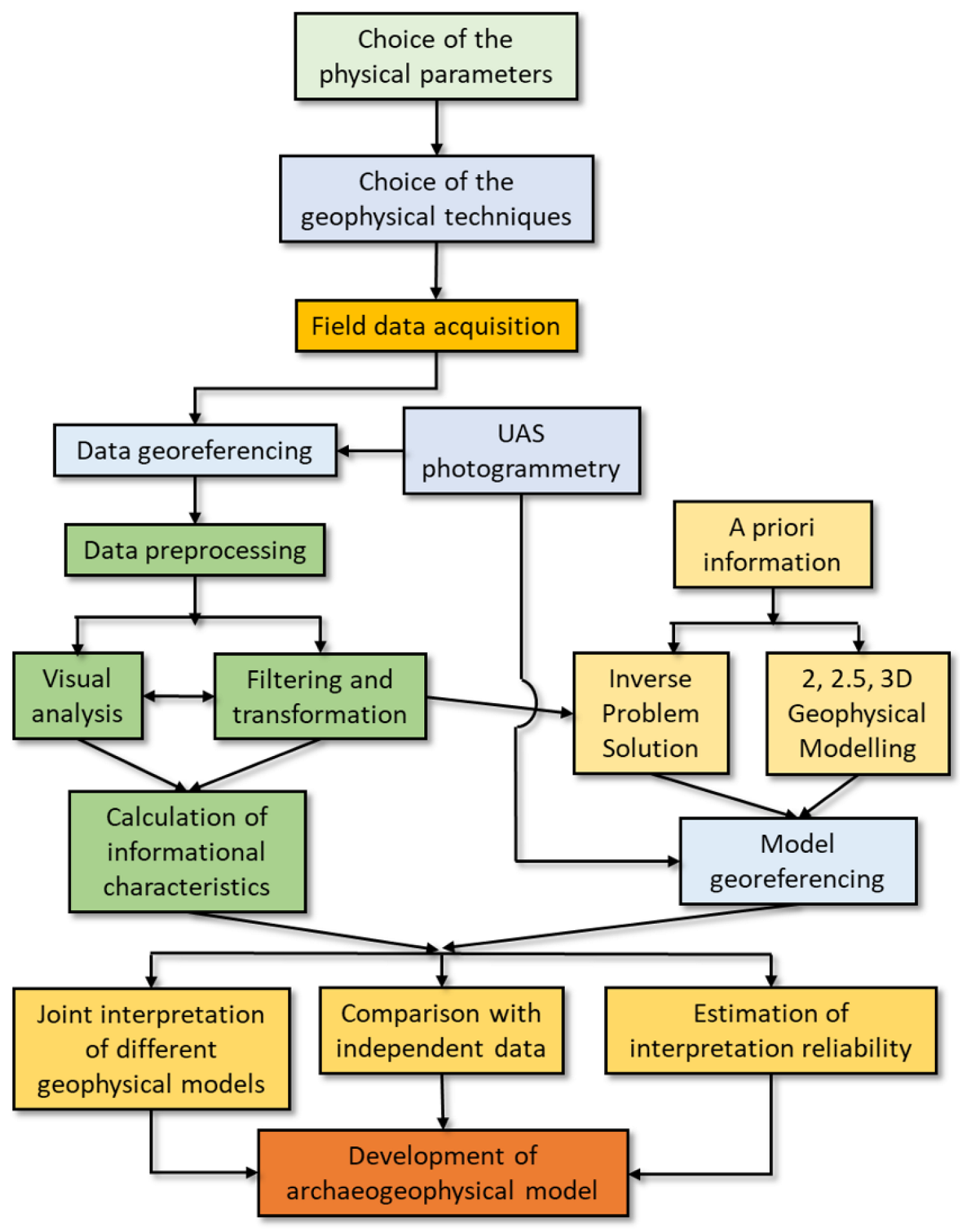
2.3. Data Correction, Processing, and Interpretation
2.4. Magnetic Modelling: Forward and Inverse Problems
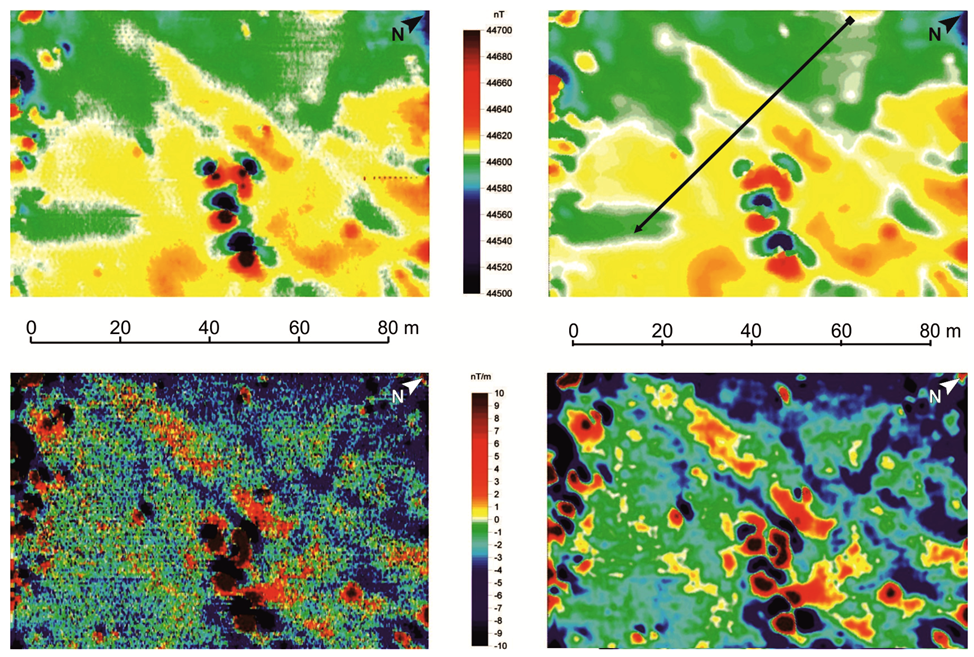
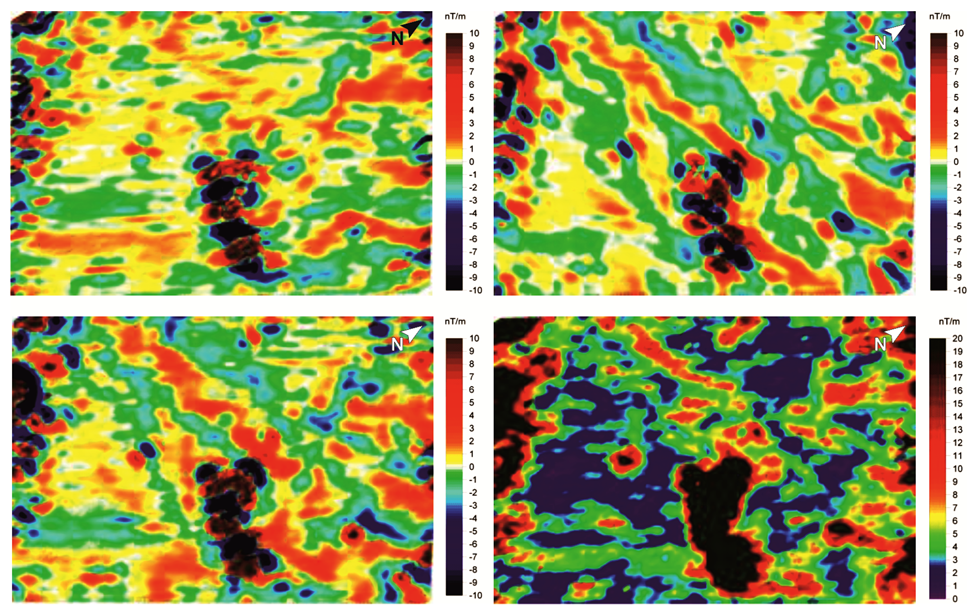
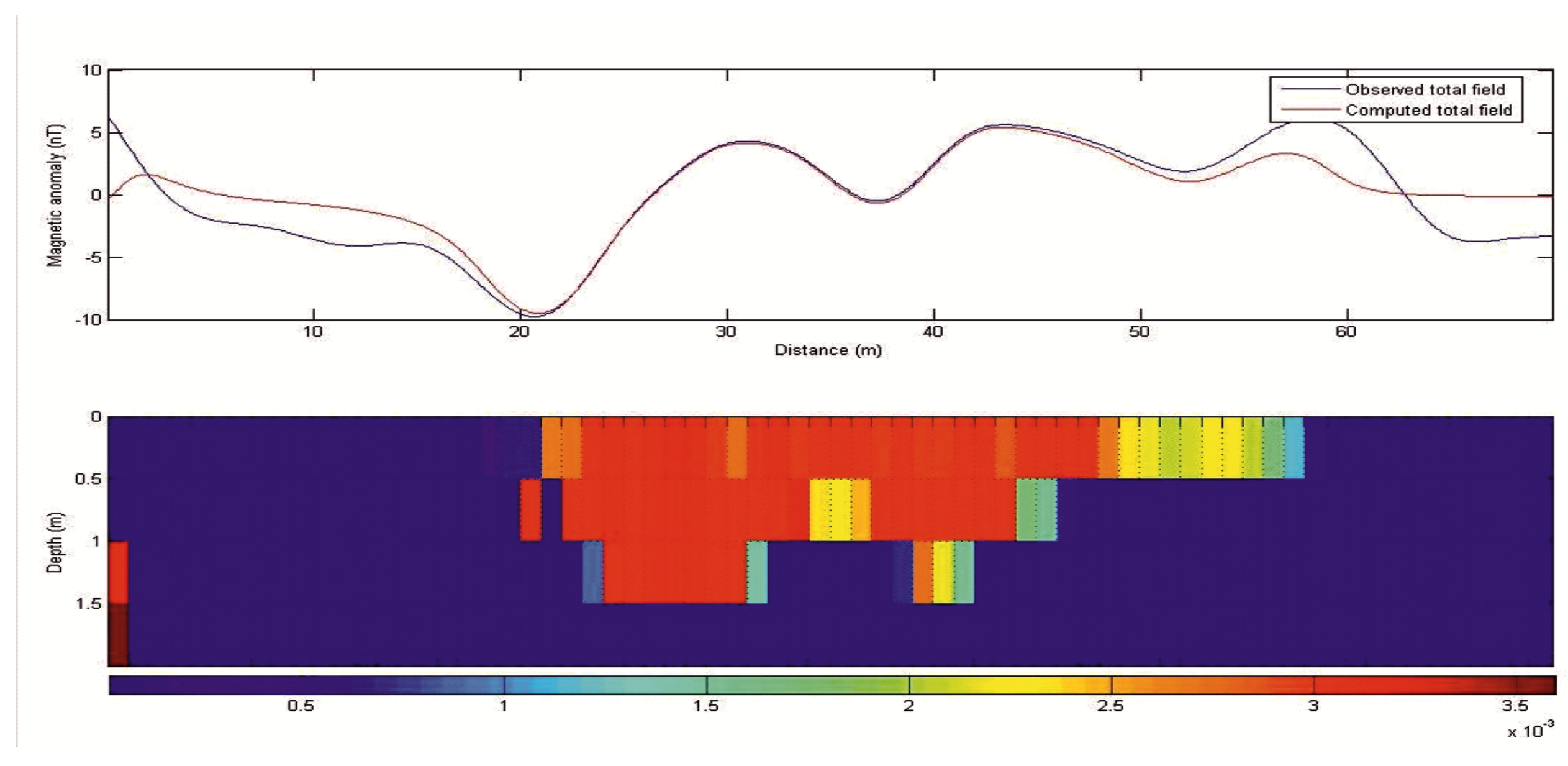
2.5. A Field Application: The “Capo Lilibeo” Archaeological Site (Italy)
2.6. Remarks
3. Ground Penetrating Radar
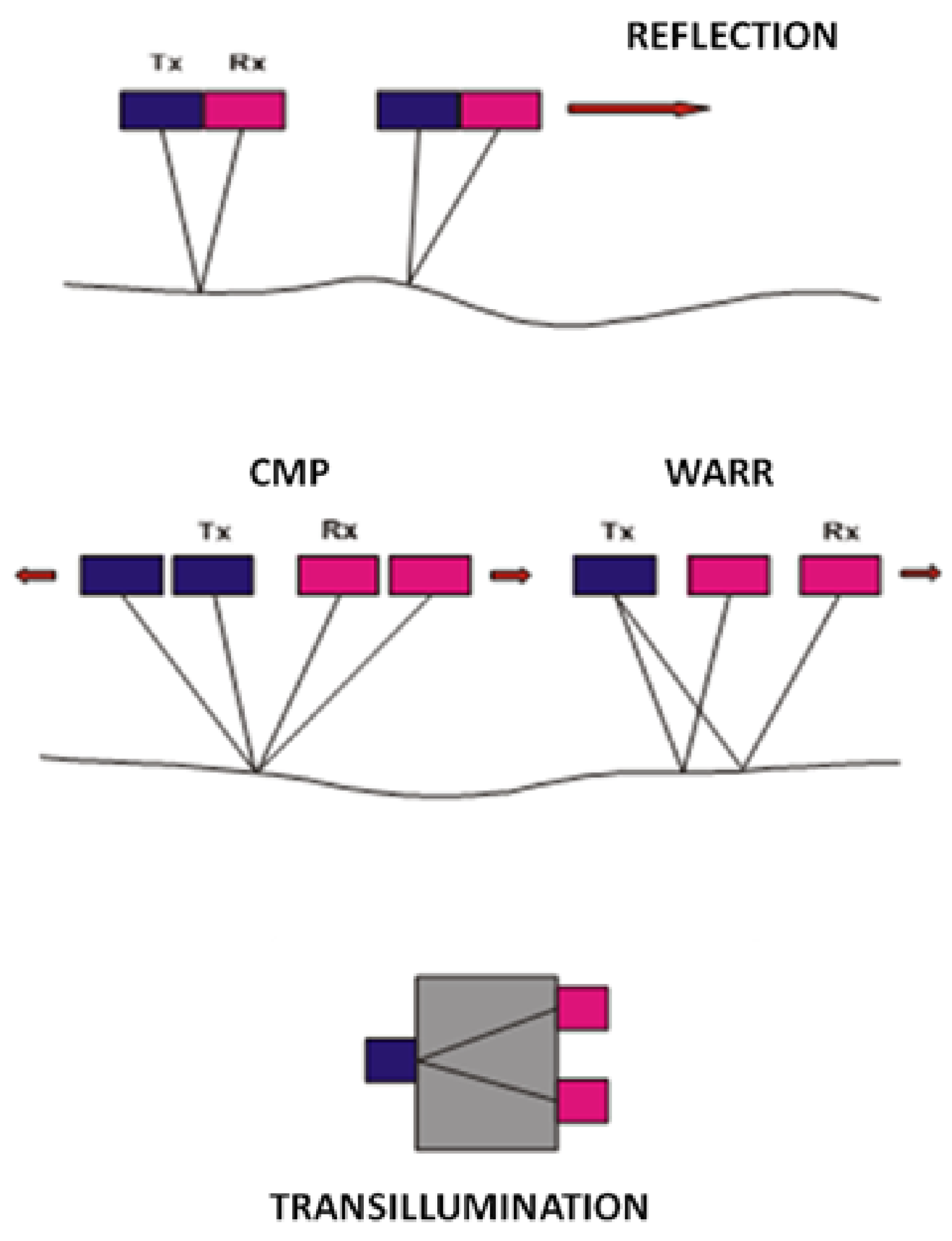
3.1. Basic Principles of the GPR Method
- 1.
- The reflection technique, in which antennas are kept in a fixed configuration and move over the ground. This results in a section being displayed showing the time to the radar reflectors along the vertical axis and the antenna position along the horizontal axis.
- 2.
- The CMP (Common Mid-Point) technique, which requires that the antennas be moved symmetrically to a fixed point.
- 3.
- The WARR (Wide Angle Reflection Radar) technique, which uses a fixed transmitting antenna and a mobile receiver (or vice versa), which moves along a profile.
- 4.
- The technique of transillumination, which is carried out by lowering the antennas in wells parallel to each other or making them move on the opposite walls of a building, e.g., walls, pillars, etc.
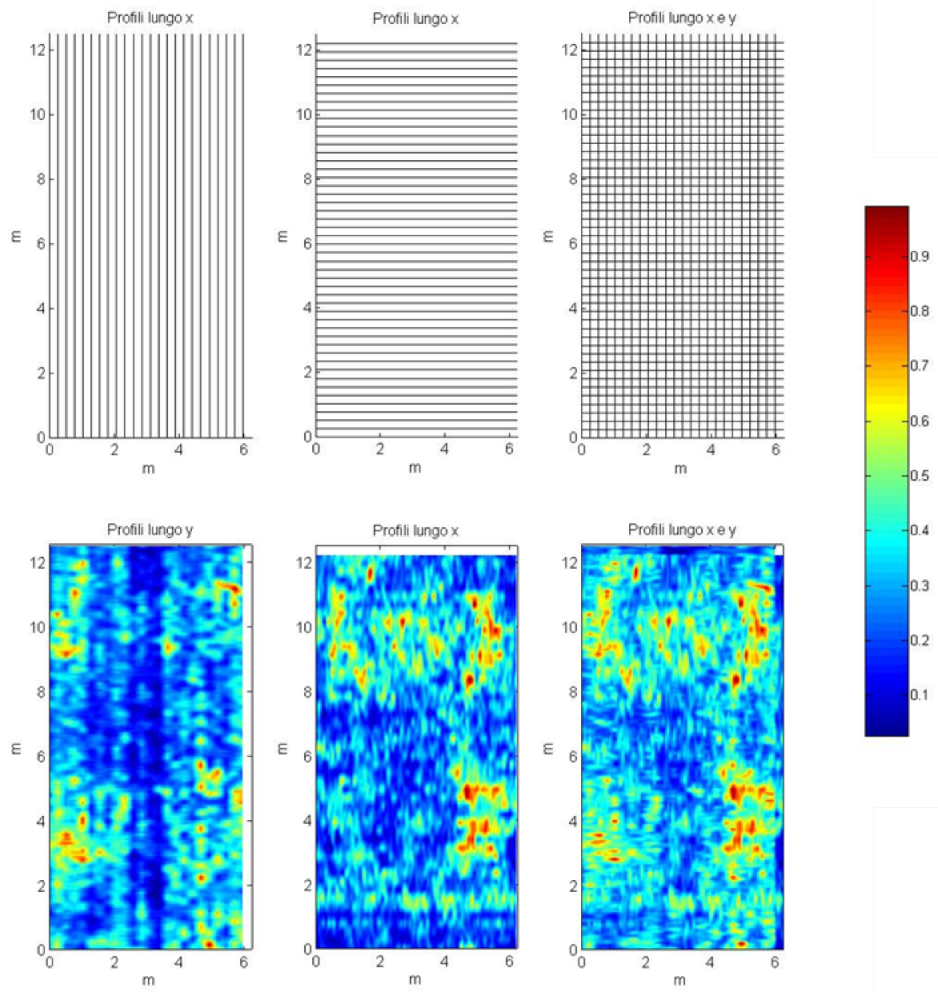
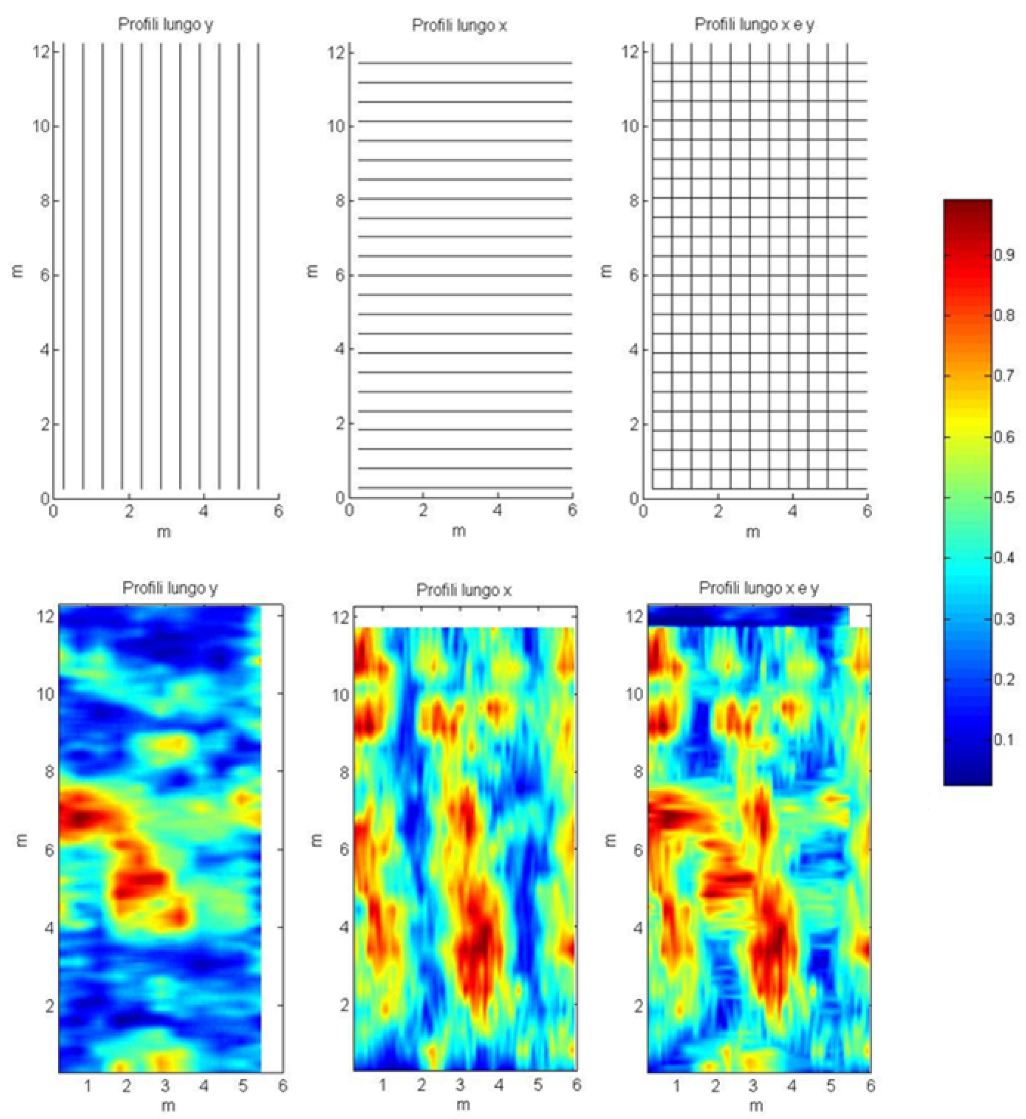
3.2. Processing and Timeslice Technique
- 1.
- Static correction, which performs correction on each trace in the time direction; it is applied to eliminate time delays related to trigger errors.
- 2.
- Frequency filtering, which eliminates electromagnetic noise (characterized by frequencies other than those of the transmitted signal).
- 3.
- Energy decay, which is useful for highlighting low ranges of amplitudes of the acquired signal against the highest ones.
- 4.
- Background removal, a 2D filter that allows temporally consistent noise to be eliminated and is useful for making certain signal portions covered by noise more visible.
- 5.
- Kirchoff migration, which is a velocity-weighted summation computed for each point of the profile based on the hyperbolas of reflection within a preset bandwidth.
3.3. Issues and Proposals for Archaeology and Cultural Heritage
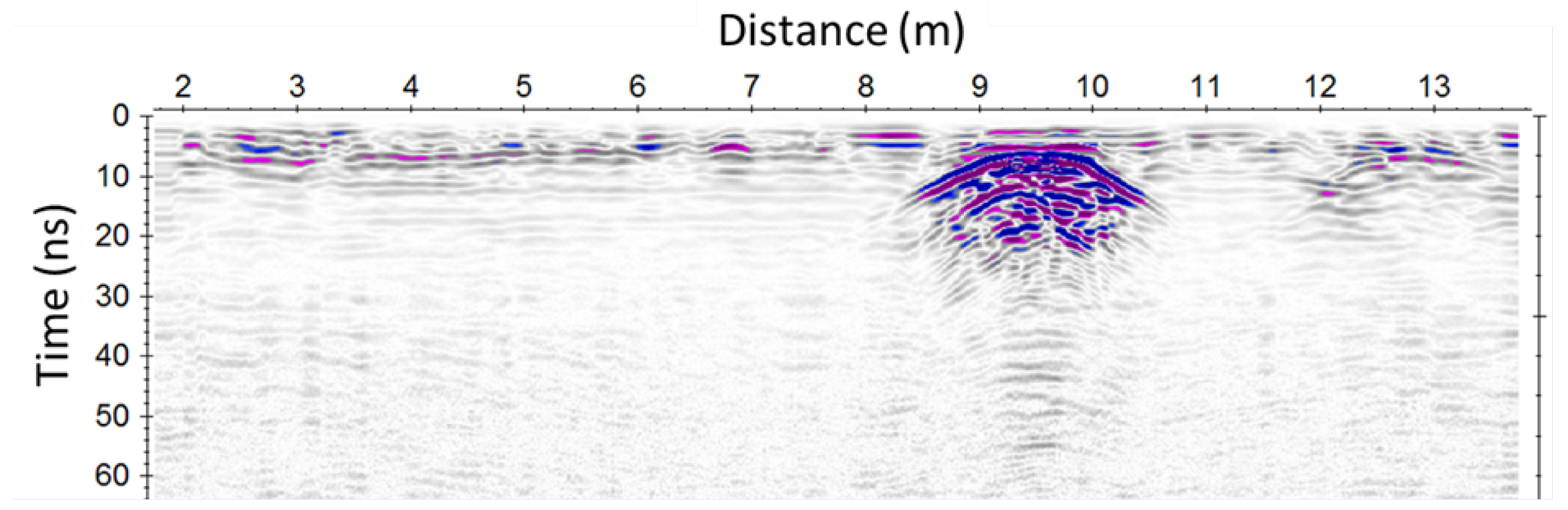
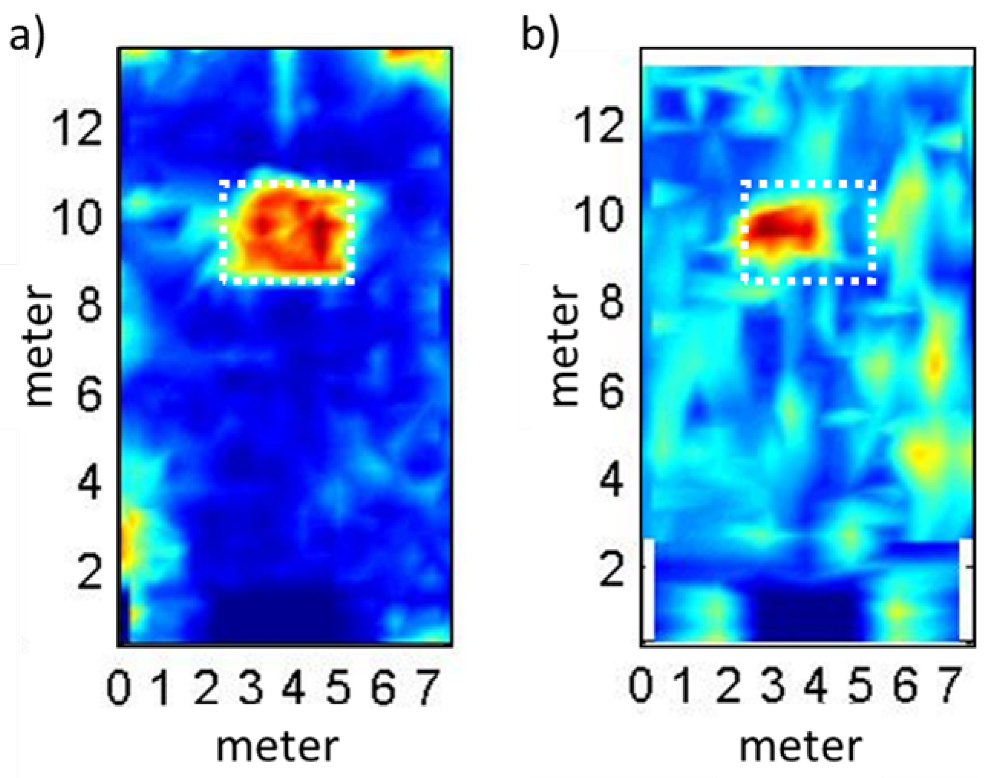
3.4. A Field Application: The Ex-Oratory of Santo Stefano Protomartire in Palermo
4. Electrical Resistivity Tomography
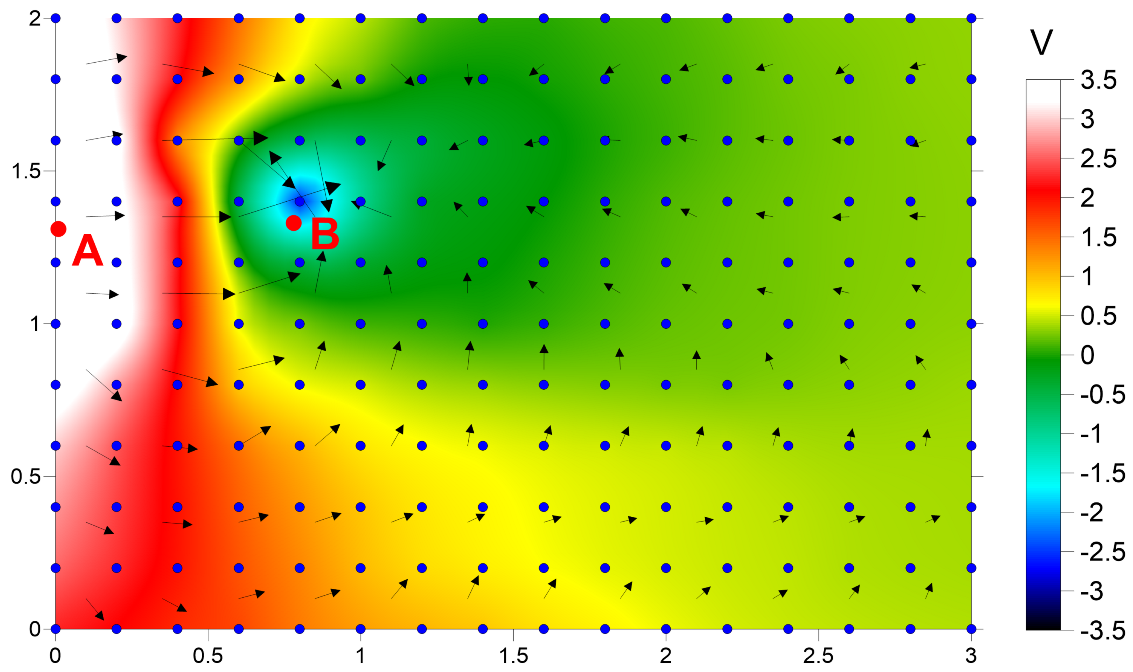
4.1. Basic Principles of the Resistivity Method
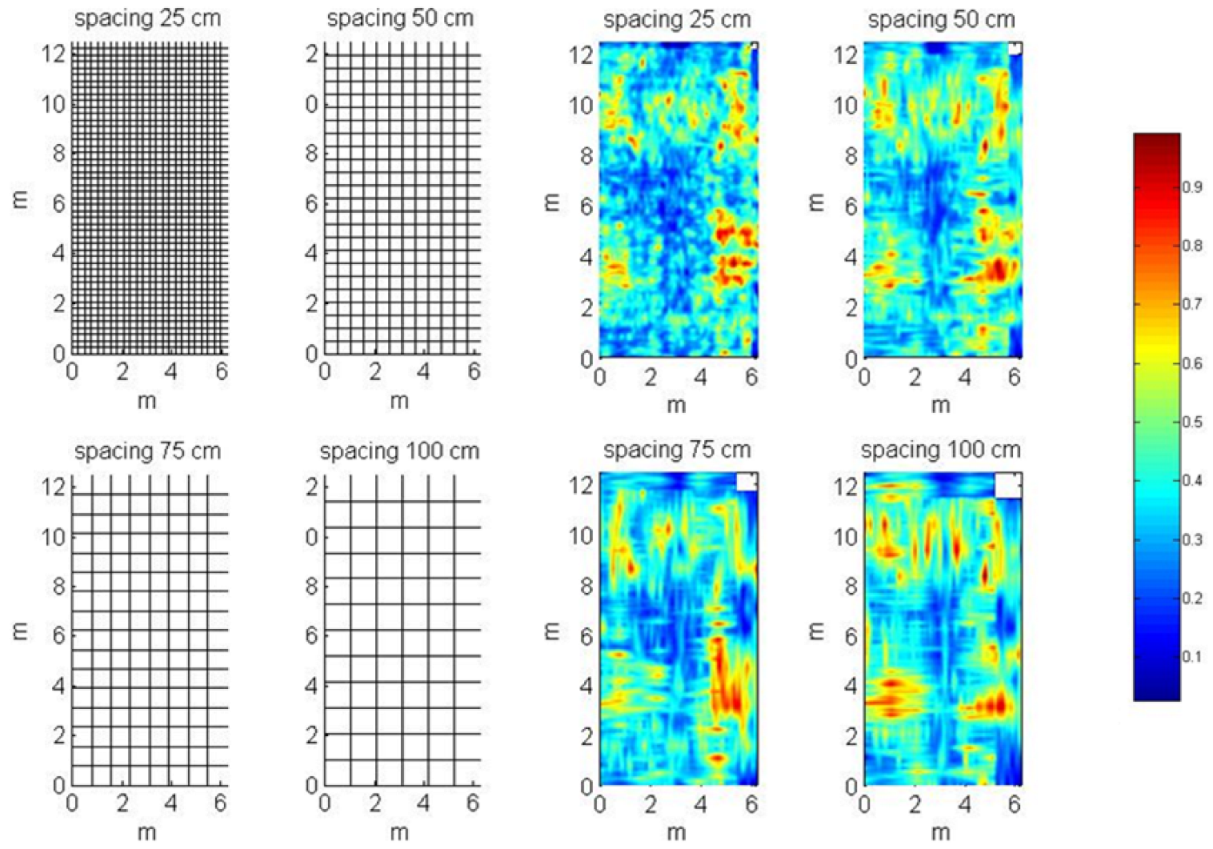
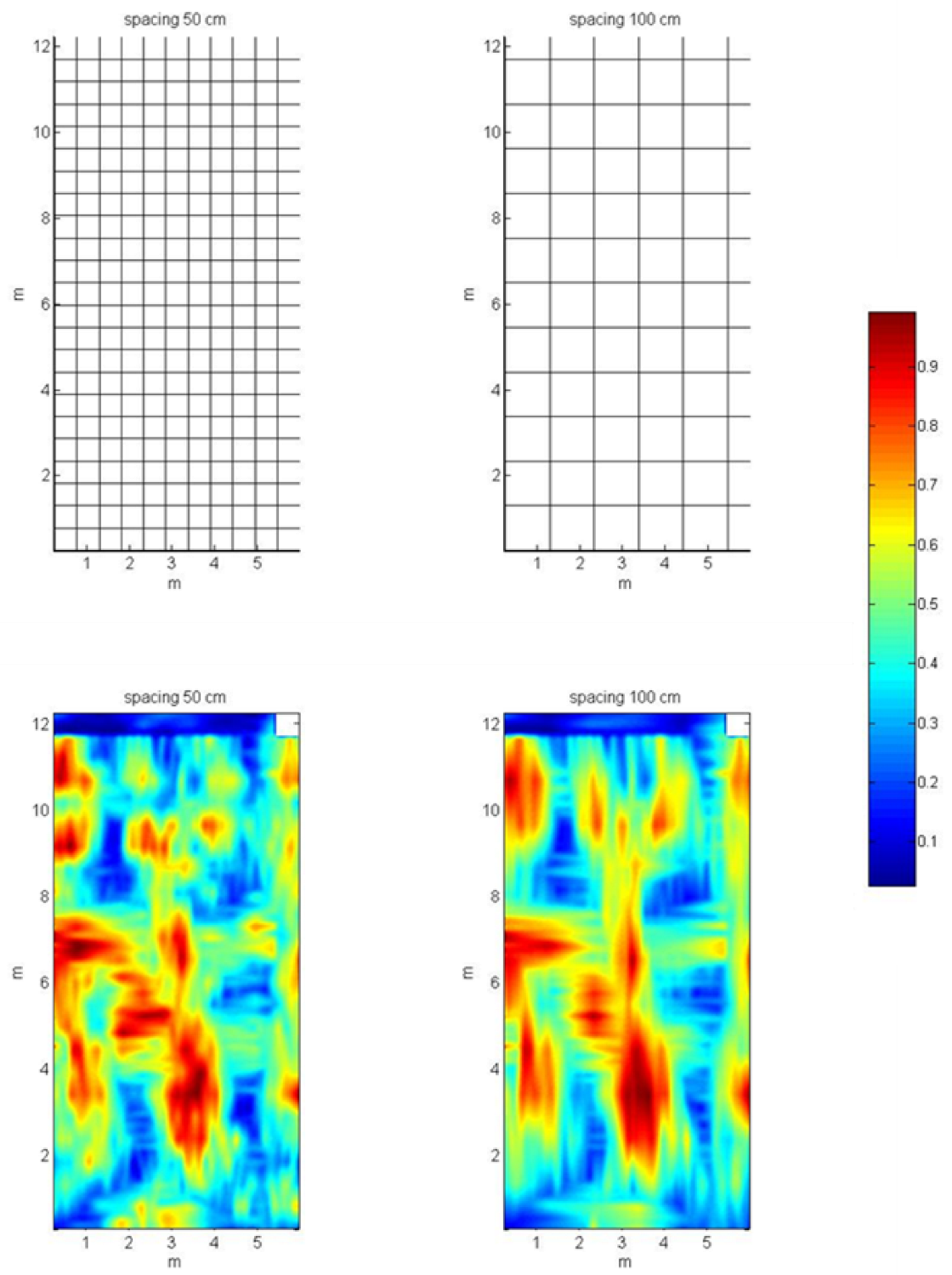
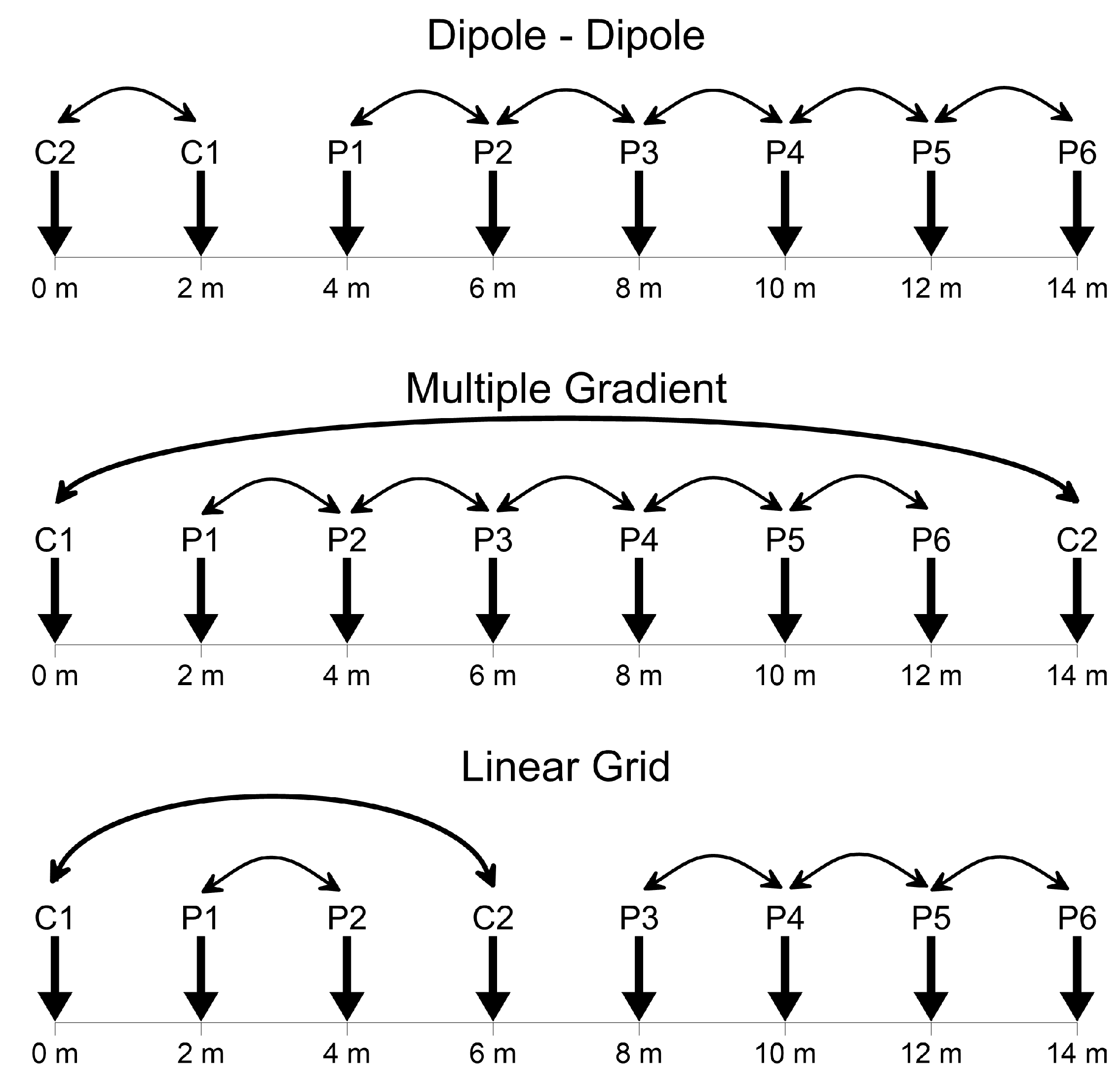
4.2. Acquisition with Multi-Electrode Systems
4.3. Issues and Proposals for Archaeology and Cultural Heritage
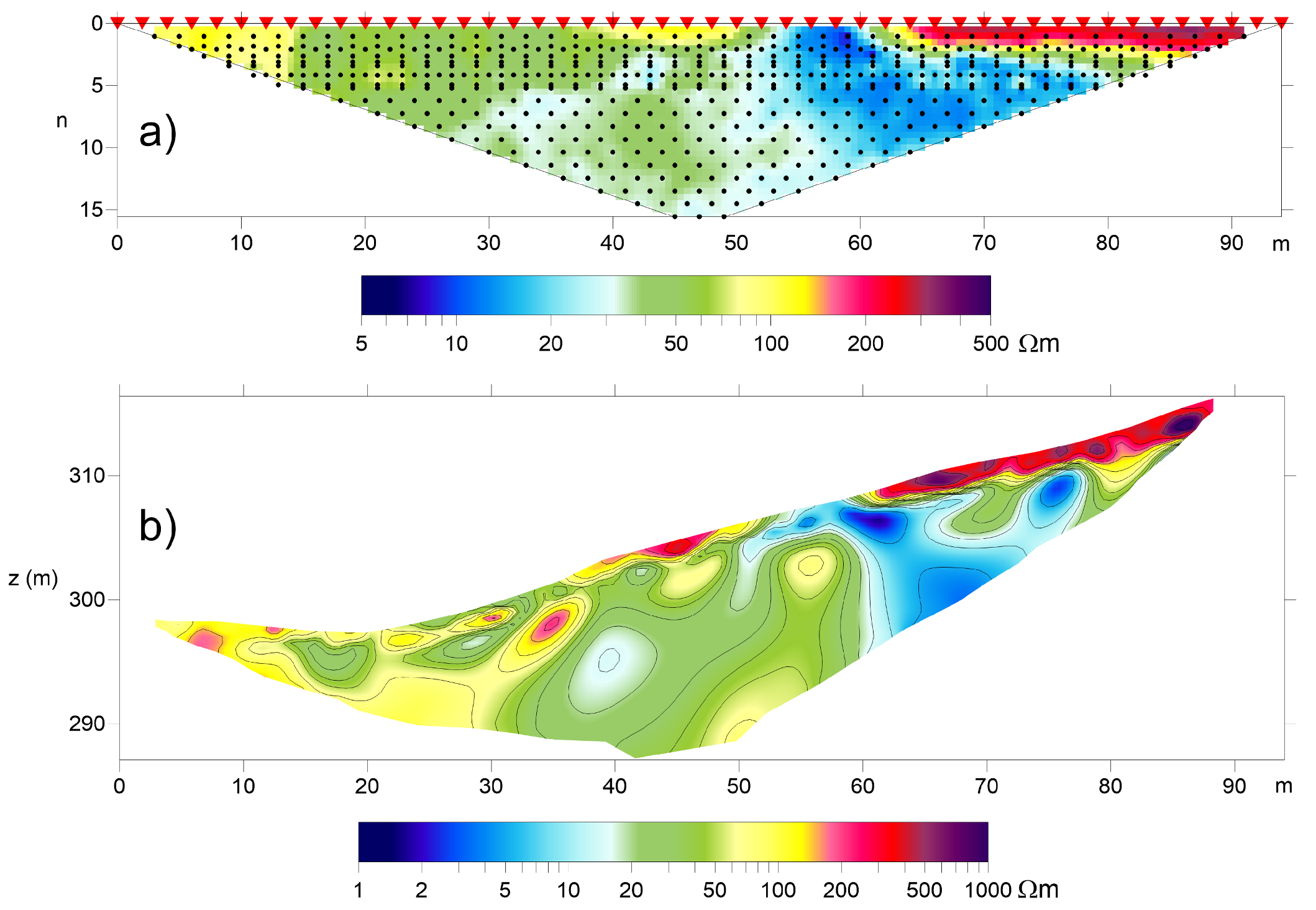
4.4. A Field Application: The “Fountain Room” of the Zisa Palace (Palermo, Italy)
5. Aerial Archaeology
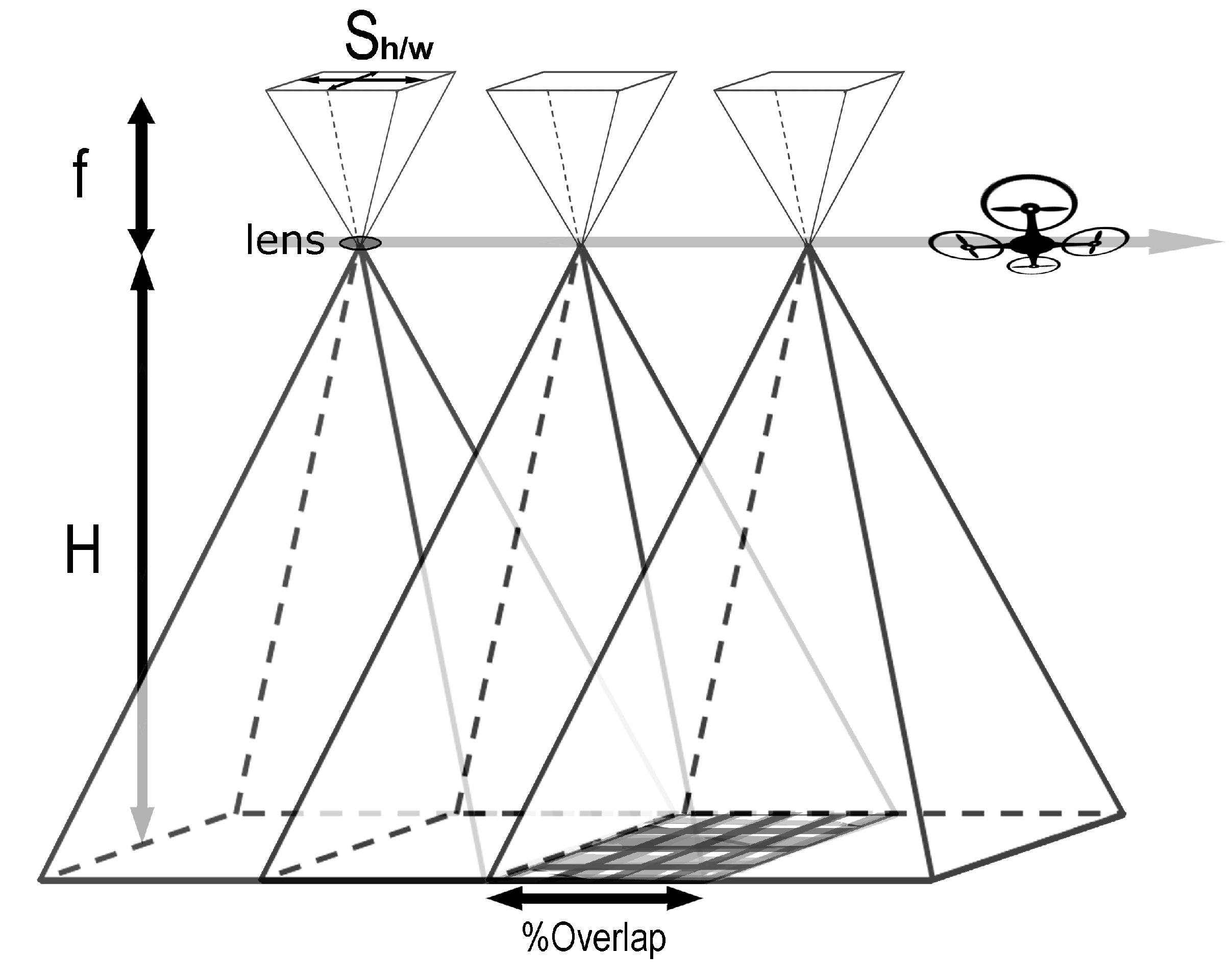
5.1. UAS Photogrammetry
5.2. Aerial Triangulation
5.3. Photogrammetric Aerial Survey
5.4. Aerial Infrared Thermography
5.5. Thermal Infrared Aerial Survey
5.6. Magnetic Aerial Survey
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Batayneh, A.T. Archaeogeophysics–archaeological prospection—A mini review. J. King Saud-Univ. Sci. 2011, 23, 83–89. [Google Scholar] [CrossRef]
- Deiana, R.; Leucci, G.; Martorana, R. New perspectives on geophysics for archaeology: A special issue. Surv. Geophys. 2018, 39, 1035–1038. [Google Scholar] [CrossRef]
- Barone, P.M.; Ruffell, A.; Tsokas, G.N.; Rizzo, E. Geophysical Surveys for Archaeology and Cultural Heritage Preservation. Heritage 2019, 2, 2814–2817. [Google Scholar] [CrossRef]
- Cozzolino, M.; Di Giovanni, E.; Mauriello, P.; Piro, S.; Zamuner, D. Geophysical Methods for Cultural Heritage Management; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- El-Qady, G.; Metwaly, M. Archaeogeophysics: State of the Art and Case Studies; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Brizzolari, E.; Ermolli, F.; Orlando, L.; Piro, S.; Versino, L. Integrated geophysical methods in archaeological surveys. J. Appl. Geophys. 1992, 29, 47–55. [Google Scholar] [CrossRef]
- Urbini, S.; Cafarella, L.; Marchetti, M.; Chiarucci, P.; Bonini, D. Fast geophysical prospecting applied to archaeology: Results at «Villa ai Cavallacci»(Albano Laziale, Rome) site. Ann. Geophys. 2007, 50, 291–299. [Google Scholar] [CrossRef]
- Scudero, S.; Martorana, R.; Capizzi, P.; Pisciotta, A.; D’Alessandro, A.; Bottari, C.; Di Stefano, G. Integrated Geophysical Investigations at the Greek Kamarina Site (Southern Sicily, Italy). Surv. Geophys. 2018, 39, 1181–1200. [Google Scholar] [CrossRef]
- Martinho, E.; Dionísio, A. Main geophysical techniques used for non-destructive evaluation in cultural built heritage: A review. J. Geophys. Eng. 2014, 11, 053001. [Google Scholar] [CrossRef]
- Ekinci, Y.L.; Özyalın, Ş.; Sındırgı, P.; Balkaya, Ç.; Göktürkler, G. Amplitude inversion of the 2D analytic signal of magnetic anomalies through the differential evolution algorithm. J. Geophys. Eng. 2017, 14, 1492–1508. [Google Scholar] [CrossRef]
- Doll, W.E.; Miller, R.D.; Bradford, J. The emergence and future of near-surface geophysics. Lead. Edge 2012, 31, 684–692. [Google Scholar] [CrossRef]
- Maher, B.A.; Taylor, R.M. Formation of ultrafine-grained magnetite in soils. Nature 1988, 336, 368–370. [Google Scholar] [CrossRef]
- Magiera, T.; Strzyszcz, Z.; Kapicka, A.; Petrovsky, E.; MAGPROX TEAM. Discrimination of lithogenic and anthropogenic influences on topsoil magnetic susceptibility in Central Europe. Geoderma 2006, 130, 299–311. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Cosentino, P.; Capizzi, P.; Fiandaca, G.; Martorana, R.; Messina, P. Advances in microgeophysics for engineering and cultural heritage. J. Earth Sci. 2009, 20, 626–639. [Google Scholar] [CrossRef]
- Cosentino, P.; Capizzi, P.; Martorana, R.; Messina, P.; Schiavone, S. From geophysics to microgeophysics for engineering and cultural heritage. Int. J. Geophys. 2011. Available online: https://www.hindawi.com/journals/ijge/2011/428412/ (accessed on 10 December 2022). [CrossRef]
- Masini, N.; Soldovieri, F. Integrated non-invasive sensing techniques and geophysical methods for the study and conservation of architectural, archaeological and artistic heritage. J. Geophys. Eng. 2011, 8, E01. [Google Scholar] [CrossRef]
- Sala, J.; Linford, N. Processing stepped frequency continuous wave GPR systems to obtain maximum value from archaeological data sets. Near Surf. Geophys. 2012, 10, 3–10. [Google Scholar] [CrossRef]
- Bottari, C.; Capizzi, P.; Martorana, R.; Azzaro, R.; Branca, S.; Civico, R.; Fucile, M.; Pecora, E. Diagnostic Multidisciplinary Investigations for Cultural Heritage at Etna Volcano: A Case Study from the 1669 Eruption in the Mother Church at the Old Settlement of Misterbianco. Remote Sens. 2022, 14, 2388. [Google Scholar] [CrossRef]
- Capizzi, P.; Martorana, R.; Messina, P.; Cosentino, P. Geophysical and geotechnical investigations to support the restoration project of the Roman ‘Villa del Casale’, Piazza Armerina, Sicily, Italy. Near Surf. Geophys. 2012, 10, 145–160. [Google Scholar] [CrossRef]
- Casas, A.; Cosentino, P.L.; Fiandaca, G.; Himi, M.; Macias, J.M.; Martorana, R.; Muñoz, A.; Rivero, L.; Sala, R.; Teixell, I. Non-invasive geophysical surveys in search of the Roman Temple of Augustus under the Cathedral of Tarragona (Catalonia, Spain): A case study. Surv. Geophys. 2018, 39, 1107–1124. [Google Scholar] [CrossRef]
- Capozzoli, L.; Mutino, S.; Liseno, M.G.; De Martino, G. Searching for the History of the Ancient Basilicata: Archaeogeophysics Applied to the Roman Site of Forentum. Heritage 2019, 2, 1097–1116. [Google Scholar] [CrossRef]
- Martorana, R.; Capizzi, P. Seismic and non-invasive geophysical surveys for the renovation project of Branciforte Palace in Palermo. Archaeol. Prospect. 2020. Available online: https://onlinelibrary.wiley.com/doi/10.1002/arp.1781 (accessed on 10 December 2022). [CrossRef]
- Costanzo, A.; Pisciotta, A.; Pannaccione Apa, M.I.; Bongiovanni, S.; Capizzi, P.; D’Alessandro, A.; Falcone, S.; La Piana, C.; Martorana, R. Integrated use of unmanned aerial vehicle photogrammetry and terrestrial laser scanning to support archaeological analysis: The Acropolis of Selinunte case (Sicily, Italy). Archaeol. Prospect. 2021, 28, 153–165. [Google Scholar] [CrossRef]
- Caldeira, B.; Oliveira, R.J.; Teixidó, T.; Borges, J.F.; Henriques, R.; Carneiro, A.; Peña, J.A. Studying the construction of floor mosaics in the Roman Villa of Pisões (Portugal) using noninvasive methods: High-resolution 3D GPR and photogrammetry. Remote Sens. 2019, 11, 1882. [Google Scholar] [CrossRef]
- Biscarini, C.; Catapano, I.; Cavalagli, N.; Ludeno, G.; Pepe, F.; Ubertini, F. UAV photogrammetry, infrared thermography and GPR for enhancing structural and material degradation evaluation of the Roman masonry bridge of Ponte Lucano in Italy. NDT E Int. 2020, 115, 102287. [Google Scholar] [CrossRef]
- Masini, N.; Sogliani, F.; Sileo, M.; Abate, N.; Danese, M.; Vitale, V.; Lasaponara, R.; Piro, S. Fusion and integration of heterogeneous close range remote sensing and geophysical data. The case of Grumentum. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; Volume 2204, p. 012018. [Google Scholar]
- Zhao, Y.; Ling, C.; Zhang, K.; Gao, Y.; Sun, B.; Wang, X. Detection of hidden mining-induced ground fissures via unmanned aerial vehicle infrared system and ground-penetrating radar. Int. J. Rock Mech. Min. Sci. 2022, 160, 105254. [Google Scholar] [CrossRef]
- Nabighian, M.N.; Grauch, V.; Hansen, R.; LaFehr, T.; Li, Y.; Peirce, J.W.; Phillips, J.D.; Ruder, M. The historical development of the magnetic method in exploration. Geophysics 2005, 70, 33ND–61ND. [Google Scholar] [CrossRef]
- Kvamme, K.L. Magnetometry: Nature’s gift to archaeology. In Remote Sensing in Archaeology: An Explicitly North American Perspective; The University of Alabama Press: Tuscaloosa, Alabama, 2006; pp. 205–233. [Google Scholar]
- Gaffney, C. Detecting trends in the prediction of the buried past: A review of geophysical techniques in archaeology. Archaeometry 2008, 50, 313–336. [Google Scholar] [CrossRef]
- Fassbinder, J.W. Seeing beneath the farmland, steppe and desert soil: Magnetic prospecting and soil magnetism. J. Archaeol. Sci. 2015, 56, 85–95. [Google Scholar] [CrossRef]
- Garrison, E.G. Techniques in Archaeological Geology; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Fedi, M.; Cella, F.; Florio, G.; Manna, M.L.; Paoletti, V. Geomagnetometry for archaeology. In Sensing the Past; Springer: Berlin/Heidelberg, Germany, 2017; pp. 203–230. [Google Scholar]
- Campbell, W.H. Introduction to Geomagnetic Fields; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Love, J.J. Magnetic monitoring of Earth and space. Phys. Today 2008, 61, 31. [Google Scholar] [CrossRef]
- Hinze, W.J.; Von Frese, R.R.; Von Frese, R.; Saad, A.H. Gravity and Magnetic Exploration: Principles, Practices, and Applications; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Becker, H. From nanotesla to picotesla—A new window for magnetic prospecting in archaeology. Archaeol. Prospect. 1995, 2, 217–228. [Google Scholar] [CrossRef]
- Smekalova, T.N.; Smekalov, S.L.; Voss, O.; Bevan, B.W. Magnetic Surveying in Archaeology: More than 10 Years of Using the Overhauser GSM-19 Gradiometer; Wormianum: Højbjerg, Denmark, 2008. [Google Scholar]
- Ciminale, M.; Loddo, M. Aspects of magnetic data processing. Archaeol. Prospect. 2001, 8, 239–246. [Google Scholar] [CrossRef]
- Bruniaux, G.; Mathé, V.; Lévêque, F.; Camus, A.; Ard, V. Data processing chain for high spatial resolution magnetic survey: Application on the Neolithic site of le Pontet (Charente-maritime, France). Archaeol. Prospect. 2018, 25, 3–16. [Google Scholar] [CrossRef]
- Chianese, D.; D’Emilio, M.; Di Salvia, S.; Lapenna, V.; Ragosta, M.; Rizzo, E. Magnetic mapping, ground penetrating radar surveys and magnetic susceptibility measurements for the study of the archaeological site of Serra di Vaglio (southern Italy). J. Archaeol. Sci. 2004, 31, 633–643. [Google Scholar] [CrossRef]
- Scollar, I.; Tabbagh, A.; Hesse, A.; Herzog, I. Archaeological Prospecting and Remote Sensing; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Noviello, M.; Ciminale, M.; Del Gaudio, V.; Amoruso, L. Advances in reconstructing archaeological magnetic signals; An algorithm for filtering noise due to the ploughing effect. Archaeol. Prospect. 2017, 24, 87–99. [Google Scholar] [CrossRef]
- Roest, W.R.; Verhoef, J.; Pilkington, M. Magnetic interpretation using the 3-D analytic signal. Geophysics 1992, 57, 116–125. [Google Scholar] [CrossRef]
- Sheriff, S.D.; Macdonald, D.; Dick, D. Decorrugation, edge detection, and modelling of total field magnetic observations from a historic town site, Yellowstone National Park, USA. Archaeol. Prospect. 2010, 17, 49–60. [Google Scholar] [CrossRef]
- Cooper, G.R.; Cowan, D.R. Edge enhancement of potential-field data using normalized statistics. Geophysics 2008, 73, H1–H4. [Google Scholar] [CrossRef]
- Lee, M.; Morris, W.; Harris, J.; Leblanc, G. An automatic network-extraction algorithm applied to magnetic survey data for the identification and extraction of geologic lineaments. Lead. Edge 2012, 31, 26–31. [Google Scholar] [CrossRef]
- Stampolidis, A.; Tsokas, G.N. Use of edge delineating methods in interpreting magnetic archaeological prospection data. Archaeol. Prospect. 2012, 19, 123–140. [Google Scholar] [CrossRef]
- Ferreira, F.J.; de Souza, J.; de Barros e Silva Bongiolo, A.; de Castro, L.G. Enhancement of the total horizontal gradient of magnetic anomalies using the tilt angle. Geophysics 2013, 78, J33–J41. [Google Scholar] [CrossRef]
- Du, W.; Wu, Y.; Guan, Y.; Hao, M. Edge detection in potential filed using the correlation coefficients between the average and standard deviation of vertical derivatives. J. Appl. Geophys. 2017, 143, 231–238. [Google Scholar] [CrossRef]
- Zuo, B.; Hu, X.; Liu, S.; Geng, M. Delineation of overlapping magnetic field source boundaries with a 3-D multi-layer convolution model. J. Appl. Geophys. 2018, 150, 74–83. [Google Scholar] [CrossRef]
- Cooper, G. Forward modelling of magnetic data. Comput. Geosci. 1997, 23, 1125–1129. [Google Scholar] [CrossRef]
- Quesnel, Y.; Langlais, B.; Sotin, C.; Galdéano, A. Modelling and inversion of local magnetic anomalies. J. Geophys. Eng. 2008, 5, 387–400. [Google Scholar] [CrossRef]
- Bott, M. Two methods applicable to computers for evaluating magnetic anomalies due to finite three dimensional bodies. Geophys. Prospect. 1963, 11, 292–299. [Google Scholar] [CrossRef]
- Talwani, M. Computation with the help of a digital computer of magnetic anomalies caused by bodies of arbitrary shape. Geophysics 1965, 30, 797–817. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Herwanger, J.; Maurer, H.; Green, A.G.; Leckebusch, J. 3-D inversions of magnetic gradiometer data in archeological prospecting: Possibilities and limitations. Geophysics 2000, 65, 849–860. [Google Scholar] [CrossRef]
- Cheyney, S.; Fishwick, S.; Hill, I.; Linford, N. Successful adaptation of three-dimensional inversion methodologies for archaeological-scale, total-field magnetic data sets. Geophys. J. Int. 2015, 202, 1271–1288. [Google Scholar] [CrossRef]
- Cosentino, P.; Fiandaca, G.; Godio, A.; Luzio, D.; Martorana, R.; Messina, N.; Stocco, S. Indagini integrate (magnetometriche e georadar nell’area archeologica di Capo Lilibeo (Marsala, Sicilia Occidentale). In Proceedings of the 25° Convegno Nazionale GNGTS. GNGTS-CNR, Roma, Italy, 28–30 November 2006; pp. 437–440. [Google Scholar]
- Godio, A.; Piro, S. Integrated data processing for archeological magnetic surveys. Lead. Edge 2005, 24, 1138–1144. [Google Scholar] [CrossRef]
- Domínguez, R.E.G.; Bandy, W.L.; Gutiérrez, C.A.M.; Ramírez, J.O. Geophysical-Archaeological Survey in Lake Tequesquitengo, Morelos, Mexico. GeofíSica Int. 2013, 52, 261–275. [Google Scholar] [CrossRef]
- Ekinci, Y.L.; Balkaya, Ç.; Şeren, A.; Kaya, M.A.; Lightfoot, C.S. Geomagnetic and geoelectrical prospection for buried archaeological remains on the Upper City of Amorium, a Byzantine city in midwestern Turkey. J. Geophys. Eng. 2014, 11, 015012. [Google Scholar] [CrossRef]
- Cella, F.; Fedi, M. High-resolution geophysical 3D imaging for archaeology by magnetic and EM data: The case of the iron age settlement of Torre Galli, Southern Italy. Surv. Geophys. 2015, 36, 831–850. [Google Scholar] [CrossRef]
- Leucci, G.; Masini, N.; Rizzo, E.; Capozzoli, L.; De Martino, G.; De Giorgi, L.; Marzo, C.; Roubis, D.; Sogliani, F. Integrated archaeogeophysical approach for the study of a medieval monastic settlement in Basilicata. Open Archaeol. 2015, 1. [Google Scholar] [CrossRef]
- Khouas, A.; Hamoudi, M.; Khaldaoui, F.; Mihoubi, H.; Hadji, Y.R. Subsurface geophysics applied to archaeological investigation of Thabudeos Roman fortress (Biskra, Algeria). Arab. J. Geosci. 2017, 10, 1–15. [Google Scholar] [CrossRef]
- Welc, F.; Mieszkowski, R.; Lipovac-Vrkljan, G.; Konestra, A. An attempt to integration of different geophysical methods (magnetic, GPR and ERT); a case study from the late Roman settlement on the Island of Rab in Croatia. Stud. Quat. 2017, 34, 47–59. [Google Scholar] [CrossRef]
- Bottari, C.; Albano, M.; Capizzi, P.; D’Alessandro, A.; Doumaz, F.; Martorana, R.; Moro, M.; Saroli, M. Recognition of earthquake-induced damage in the Abakainon necropolis (NE Sicily): Results from geomorphological, geophysical and numerical analyses. Pure Appl. Geophys. 2018, 175, 133–148. [Google Scholar] [CrossRef]
- Masini, N.; Capozzoli, L.; Romano, G.; Sieczkowska, D.; Sileo, M.; Bastante, J.; Astete Victoria, F.; Ziolkowski, M.; Lasaponara, R. Archaeogeophysical-based approach for inca archaeology: Overview and one operational application. Surv. Geophys. 2018, 39, 1239–1262. [Google Scholar] [CrossRef]
- Rizzo, E.; Santoriello, A.; Capozzoli, L.; De Martino, G.; De Vita, C.B.; Musmeci, D.; Perciante, F. Geophysical survey and archaeological data at Masseria Grasso (Benevento, Italy). Surv. Geophys. 2018, 39, 1201–1217. [Google Scholar] [CrossRef]
- Jol, H.M. Ground Penetrating Radar Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Persico, R. Introduction to Ground Penetrating Radar: Inverse Scattering and Data Processing; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Conyers, L.B. Ground-penetrating radar for archaeological mapping. In Remote Sensing in Archaeology; Springer: Berlin/Heidelberg, Germany, 2006; pp. 329–344. [Google Scholar]
- Goodman, D.; Piro, S. GPR Remote Sensing in Archaeology; Springer: Berlin/Heidelberg, Germany, 2013; Volume 9. [Google Scholar]
- Fontul, S.; Solla, M.; Cruz, H.; Machado, J.; Pajewski, L. Ground Penetrating Radar Investigations in the Noble Hall of São Carlos Theater in Lisbon, Portugal. Surv. Geophys. 2018, 39, 1125–1147. [Google Scholar] [CrossRef]
- Gizzi, F.T.; Leucci, G. Global research patterns on ground penetrating radar (GPR). Surv. Geophys. 2018, 39, 1039–1068. [Google Scholar] [CrossRef]
- Trinks, I.; Johansson, B.; Gustafsson, J.; Emilsson, J.; Friborg, J.; Gustafsson, C.; Nissen, J.; Hinterleitner, A. Efficient, large-scale archaeological prospection using a true three-dimensional ground-penetrating radar array system. Archaeol. Prospect. 2010, 17, 175–186. [Google Scholar] [CrossRef]
- Leucci, G.; De Giorgi, L.; Di Giacomo, G.; Ditaranto, I.; Miccoli, I.; Scardozzi, G. 3D GPR survey for the archaeological characterization of the ancient Messapian necropolis in Lecce, South Italy. J. Archaeol. Sci. Rep. 2016, 7, 290–302. [Google Scholar] [CrossRef]
- Deiana, R.; Bonetto, J.; Mazzariol, A. Integrated electrical resistivity tomography and ground penetrating radar measurements applied to tomb detection. Surv. Geophys. 2018, 39, 1081–1105. [Google Scholar] [CrossRef]
- Lazzari, M.; De Giorgi, L.; Ceraudo, G.; Persico, R. Geoprospecting survey in the archaeological site of Aquinum (Lazio, central Italy). Surv. Geophys. 2018, 39, 1167–1180. [Google Scholar] [CrossRef]
- Ranalli, D.; Scozzafava, M.; Tallini, M. Ground penetrating radar investigations for the restoration of historic buildings: The case study of the Collemaggio Basilica (L’Aquila, Italy). J. Cult. Herit. 2004, 5, 91–99. [Google Scholar] [CrossRef]
- Santos-Assunçao, S.; Perez-Gracia, V.; Caselles, O.; Clapes, J.; Salinas, V. Assessment of complex masonry structures with GPR compared to other non-destructive testing studies. Remote Sens. 2014, 6, 8220–8237. [Google Scholar] [CrossRef]
- Barone, P.; Di Matteo, A.; Graziano, F.; Mattei, E.; Pettinelli, E. GPR application to the structural control of historical buildings: Two case studies in Rome, Italy. Near Surf. Geophys. 2010, 8, 407–413. [Google Scholar] [CrossRef]
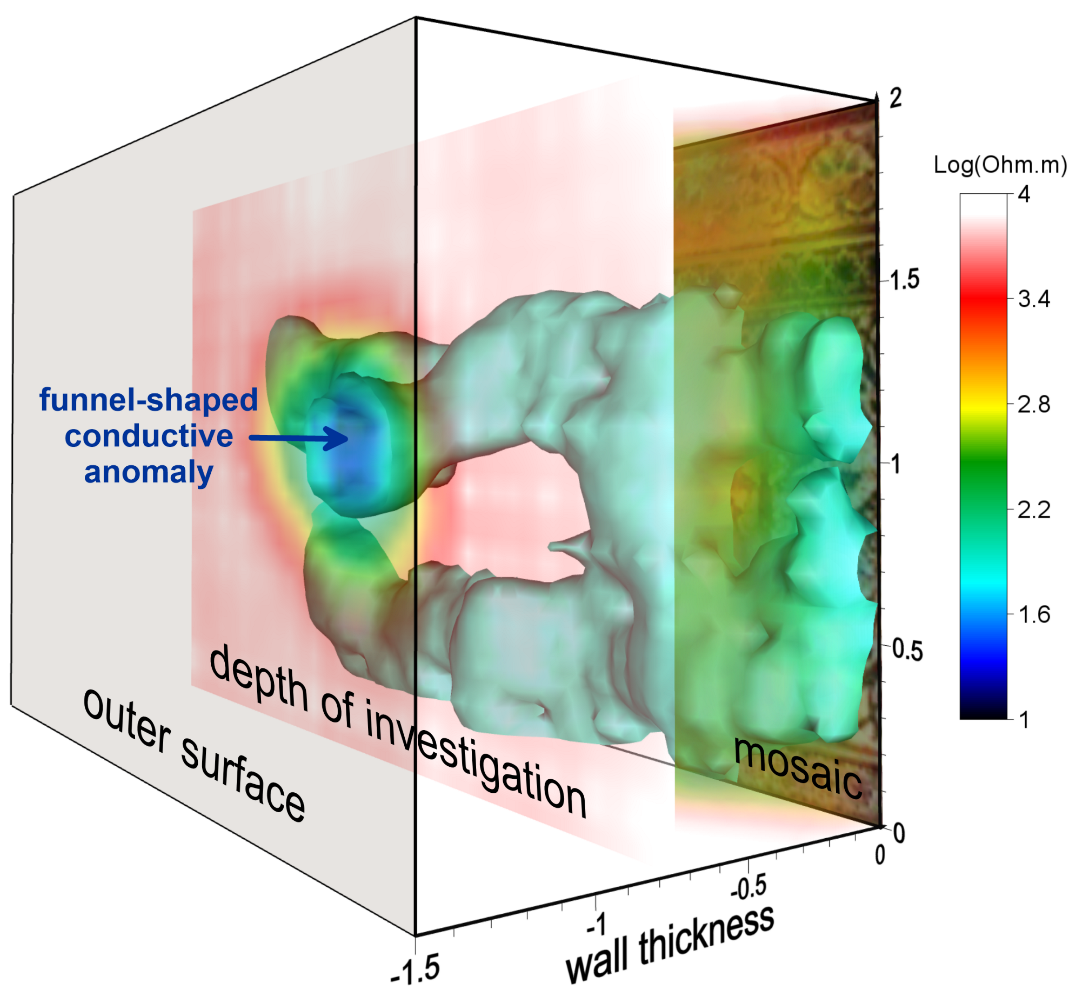
- Martorana, R.; Capizzi, P. Joint Investigation with Ground Penetrating Radar and Infrared Thermography as a Diagnostic Support for the Restoration of Two Wall Mosaics in the Church of St. Mary of the Admiral in Palermo, Italy. Heritage 2022, 5, 2298–2314. [Google Scholar] [CrossRef]
- Annan, A. Electromagnetic principles of ground penetrating radar. Ground Penetr. Radar Theory Appl. 2009, 1, 1–37. [Google Scholar]
- Cassidy, N.J.; Jol, H. Electrical and Magnetic Properties of Rocks, Soils and Fluids; 2009. Volume 2. Available online: https://www.sciencedirect.com/science/article/pii/B9780444533487000028 (accessed on 10 December 2022).
- Koppenjan, S. Ground penetrating radar systems and design. Ground Penetr. Radar Theory Appl. 2009, 1. [Google Scholar]
- Daniels, D.J. Ground Penetrating Radar; IET: Lodon, UK, 2004; Volume 1. [Google Scholar]
- Capizzi, P.; Cosentino, P.; Fiandaca, G.; Martorana, R.; Messina, P.; Vassallo, S. Geophysical investigations at the Himera archaeological site, northern Sicily. Near Surf. Geophys. 2007, 5, 417–426. [Google Scholar] [CrossRef]
- Conyers, L.B. Discovery, mapping and interpretation of buried cultural resources non-invasively with ground-penetrating radar. J. Geophys. Eng. 2011, 8, S13–S22. [Google Scholar] [CrossRef]
- Piro, S.; Ceraudo, G.; Zamuner, D. Integrated geophysical and archaeological investigations of Aquinum in Frosinone, Italy. Archaeol. Prospect. 2011, 18, 127–138. [Google Scholar] [CrossRef]
- Trinks, I.; Neubauer, W.; Hinterleitner, A. First high-resolution GPR and magnetic archaeological prospection at the Viking Age settlement of Birka in Sweden. Archaeol. Prospect. 2014, 21, 185–199. [Google Scholar] [CrossRef]
- Rizzo, E.; Masini, N.; Lasaponara, R.; Orefici, G. Archaeo-geophysical methods in the Templo del Escalonado, Cahuachi, Nasca (Peru). Near Surf. Geophys. 2010, 8, 433–439. [Google Scholar] [CrossRef]
- Masini, N.; Capozzoli, L.; Chen, P.; Chen, F.; Romano, G.; Lu, P.; Tang, P.; Sileo, M.; Ge, Q.; Lasaponara, R. Towards an operational use of geophysics for archaeology in Henan (China): Methodological approach and results in Kaifeng. Remote. Sens. 2017, 9, 809. [Google Scholar] [CrossRef]
- Griffiths, D.; Barker, R. Electrical imaging in archaeology. J. Archaeol. Sci. 1994, 21, 153–158. [Google Scholar] [CrossRef]
- Tsokas, G.; Tsourlos, P.; Vargemezis, G.; Novack, M. Non-destructive electrical resistivity tomography for indoor investigation: The case of Kapnikarea Church in Athens. Archaeol. Prospect. 2008, 15, 47–61. [Google Scholar] [CrossRef]
- Linderholm, P.; Marescot, L.; Loke, M.H.; Renaud, P. Cell culture imaging using microimpedance tomography. IEEE Trans. Biomed. Eng. 2007, 55, 138–146. [Google Scholar] [CrossRef] [PubMed]
- Storz, H.; Storz, W.; Jacobs, F. Electrical resistivity tomography to investigate geological structures of the earth’s upper crust. Geophys. Prospect. 2000, 48, 455–472. [Google Scholar] [CrossRef]
- Loke, M.; Chambers, J.; Rucker, D.; Kuras, O.; Wilkinson, P. Recent developments in the direct-current geoelectrical imaging method. J. Appl. Geophys. 2013, 95, 135–156. [Google Scholar] [CrossRef]
- Koefoed, O. Resistivity Sounding measurements, Elsevier Scientific Publishing Company. Geosounding Princ. 1979, 1, 19–27. [Google Scholar]
- Dey, A.; Morrison, H. Resistivity modelling for arbitrarily shaped two-dimensional structures. Geophys. Prospect. 1979, 27, 106–136. [Google Scholar] [CrossRef]
- Dey, A.; Morrison, H.F. Resistivity modeling for arbitrarily shaped three-dimensional structures. Geophysics 1979, 44, 753–780. [Google Scholar] [CrossRef]
- Pidlisecky, A.; Haber, E.; Knight, R. RESINVM3D: A 3D resistivity inversion package. Geophysics 2007, 72, H1–H10. [Google Scholar] [CrossRef]
- Coggon, J. Electromagnetic and electrical modeling by the finite element method. Geophysics 1971, 36, 132–155. [Google Scholar] [CrossRef]
- Inman, J.R. Resistivity inversion with ridge regression. Geophysics 1975, 40, 798–817. [Google Scholar] [CrossRef]
- deGroot Hedlin, C.; Constable, S. Occam’s inversion to generate smooth, two-dimensional models from magnetotelluric data. Geophysics 1990, 55, 1613–1624. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Oldenburg, D.W. Non-linear inversion using general measures of data misfit and model structure. Geophys. J. Int. 1998, 134, 213–227. [Google Scholar] [CrossRef]
- Loke, M.H.; Acworth, I.; Dahlin, T. A comparison of smooth and blocky inversion methods in 2D electrical imaging surveys. Explor. Geophys. 2003, 34, 182–187. [Google Scholar] [CrossRef]
- Loke, M.; Barker, R. Practical techniques for 3D resistivity surveys and data inversion1. Geophys. Prospect. 1996, 44, 499–523. [Google Scholar] [CrossRef]
- Dahlin, T.; Zhou, B. A numerical comparison of 2D resistivity imaging with 10 electrode arrays. Geophys. Prospect. 2004, 52, 379–398. [Google Scholar] [CrossRef]
- Szalai, S.; Szarka, L. On the classification of surface geoelectric arrays. Geophys. Prospect. 2008, 56, 159–175. [Google Scholar] [CrossRef]
- Martorana, R.; Fiandaca, G.; Ponsati, A.C.; Cosentino, P. Comparative tests on different multi-electrode arrays using models in near-surface geophysics. J. Geophys. Eng. 2008, 6, 1. [Google Scholar] [CrossRef]
- Loke, M.; Wilkinson, P.; Chambers, J.; Uhlemann, S.; Sorensen, J. Optimized arrays for 2-D resistivity survey lines with a large number of electrodes. J. Appl. Geophys. 2015, 112, 136–146. [Google Scholar] [CrossRef]
- Martorana, R.; Capizzi, P.; D’Alessandro, A.; Luzio, D. Comparison of different sets of array configurations for multichannel 2D ERT acquisition. J. Appl. Geophys. 2017, 137, 34–48. [Google Scholar] [CrossRef]
- Dahlin, T.; Zhou, B. Multiple-gradient array measurements for multichannel 2D resistivity imaging. Near Surf. Geophys. 2006, 4, 113–123. [Google Scholar] [CrossRef]
- Martorana, R.; Capizzi, P.; D’ALESSANDRO, A.; Luzio, D. Electrical resistivity and induced polarization tomographies to test the efficiency and safety of the new landfill of Bellolampo (Palermo, Italy). Boll. Geofis. Teor. Appl. 2016, 57. [Google Scholar]
- Wilkinson, P.B.; Meldrum, P.I.; Chambers, J.E.; Kuras, O.; Ogilvy, R.D. Improved strategies for the automatic selection of optimized sets of electrical resistivity tomography measurement configurations. Geophys. J. Int. 2006, 167, 1119–1126. [Google Scholar] [CrossRef]
- Abdullah, F.M.; Loke, M.; Nawawi, M.; Abdullah, K. Assessing the reliability and performance of optimized and conventional resistivity arrays for shallow subsurface investigations. J. Appl. Geophys. 2018, 155, 237–245. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. Approximate inverse mappings in DC resistivity problems. Geophys. J. Int. 1992, 109, 343–362. [Google Scholar] [CrossRef]
- Hung, Y.C.; Lin, C.P.; Lee, C.T.; Weng, K.W. 3D and boundary effects on 2D electrical resistivity tomography. Appl. Sci. 2019, 9, 2963. [Google Scholar] [CrossRef]
- Martorana, R.; Capizzi, P. Evaluation of Artifacts and Misinterpretation in 2D Electrical Resistivity Tomography Caused by Three-Dimensional Resistive Structures of Regular or Irregular Shapes. Appl. Sci. 2023, 13, 2015. [Google Scholar] [CrossRef]
- Chambers, J.E.; Kuras, O.; Meldrum, P.I.; Ogilvy, R.D.; Hollands, J. Electrical resistivity tomography applied to geologic, hydrogeologic, and engineering investigations at a former waste-disposal site. Geophysics 2006, 71, B231–B239. [Google Scholar] [CrossRef]
- Aizebeokhai, A.; Olayinka, A. Anomaly effects of arrays for 3d geoelectrical resistivity imaging using orthogonal or parallel 2d profiles. Afr. J. Environ. Sci. Technol. 2010, 4, 446–454. [Google Scholar]
- Jones, G.; Zielinski, M.; Sentenac, P. Mapping desiccation fissures using 3-D electrical resistivity tomography. J. Appl. Geophys. 2012, 84, 39–51. [Google Scholar] [CrossRef]
- Johnson, T.C.; Versteeg, R.J.; Ward, A.; Day-Lewis, F.D.; Revil, A. Improved hydrogeophysical characterization and monitoring through parallel modeling and inversion of time-domain resistivity andinduced-polarization data. Geophysics 2010, 75, WA27–WA41. [Google Scholar] [CrossRef]
- Fiandaca, G.; Martorana, R.; Messina, P.; Cosentino, P. The MYG methodology to carry out 3D electrical resistivity tomography on media covered by vulnerable surfaces of artistic value. Il Nuovo C. B 2010, 125, 711–718. [Google Scholar]
- Gharibi, M.; Bentley, L.R. Resolution of 3-D electrical resistivity images from inversions of 2-D orthogonal lines. J. Environ. Eng. Geophys. 2005, 10, 339–349. [Google Scholar] [CrossRef]
- Rucker, D.F.; Levitt, M.T.; Greenwood, W.J. Three-dimensional electrical resistivity model of a nuclear waste disposal site. J. Appl. Geophys. 2009, 69, 150–164. [Google Scholar] [CrossRef]
- Aizebeokhai, A.; Olayinka, A.; Singh, V.; Uhuegbu, C. Effectiveness of 3D geoelectrical resistivity imaging using parallel 2D profiles. Curr. Sci. 2011, 101, 1036–1052. [Google Scholar]
- Inoue, K.; Nakazato, H.; Takeuchi, M.; Sugimoto, Y.; Kim, H.J.; Yoshisako, H.; Konno, M.; Shoda, D. Investigation of the line arrangement of 2D resistivity surveys for 3D inversion. Explor. Geophys. 2018, 49, 231–241. [Google Scholar] [CrossRef]
- Bellanova, J.; Calamita, G.; Catapano, I.; Ciucci, A.; Cornacchia, C.; Gennarelli, G.; Giocoli, A.; Fisangher, F.; Ludeno, G.; Morelli, G.; et al. GPR and ERT investigations in urban areas: The case-study of Matera (southern Italy). Remote Sens. 2020, 12, 1879. [Google Scholar] [CrossRef]
- Chávez, G.; Tejero, A.; Alcantara, M.; Chavez, R. The ‘L-Array’, a tool to characterize a fracture pattern in an urban zone: Extended Abstracts of the 2011 Near Surface Geophysics meeting. In Proceedings of the European Section Meeting, Leicester, UK, 12–14 September 2011. [Google Scholar]
- Tejero-Andrade, A.; Cifuentes, G.; Chávez, R.E.; López-González, A.E.; Delgado-Solórzano, C. L-and CORNER-arrays for 3D electric resistivity tomography: An alternative for geophysical surveys in urban zones. Near Surf. Geophys. 2015, 13, 355–368. [Google Scholar] [CrossRef]
- Noel, M.; Xu, B. Archaeological investigation by electrical resistivity tomography: A preliminary study. Geophys. J. Int. 1991, 107, 95–102. [Google Scholar] [CrossRef]
- Wake, T.A.; Mojica, A.O.; Davis, M.H.; Campbell, C.J.; Mendizabal, T. Electrical resistivity surveying and pseudo-three-dimensional tomographic imaging at Sitio Drago, Bocas del Toro, Panama. Archaeol. Prospect. 2012, 19, 49–58. [Google Scholar] [CrossRef]
- Hegyi, A.; Diaconescu, D.; Urdea, P.; Sarris, A.; Pisz, M.; Onaca, A. Using Geophysics to Characterize a Prehistoric Burial Mound in Romania. Remote Sens. 2021, 13, 842. [Google Scholar] [CrossRef]
- Berge, M.A.; Drahor, M.G. Electrical resistivity tomography investigations of multilayered archaeological settlements: Part I–modelling. Archaeol. Prospect. 2011, 18, 159–171. [Google Scholar] [CrossRef]
- Berge, M.A.; Drahor, M.G. Electrical resistivity tomography investigations of multilayered archaeological settlements: Part II—A case from old Smyrna Hoyuk, Turkey. Archaeol. Prospect. 2011, 18, 291–302. [Google Scholar] [CrossRef]
- Deiana, R.; Vicenzutto, D.; Deidda, G.P.; Boaga, J.; Cupitò, M. Remote sensing, archaeological, and geophysical data to study the Terramare settlements: The case study of Fondo Paviani (northern Italy). Remote Sens. 2020, 12, 2617. [Google Scholar] [CrossRef]
- Vacilotto, A.; Deiana, R.; Mozzi, P. Understanding ancient landscapes in the venetian plain through an integrated Geoarchaeological and geophysical approach. Remote Sens. 2020, 12, 2973. [Google Scholar] [CrossRef]
- Leucci, G.; Greco, F.; De Giorgi, L.; Mauceri, R. Three-dimensional image of seismic refraction tomography and electrical resistivity tomography survey in the castle of Occhiola (Sicily, Italy). J. Archaeol. Sci. 2007, 34, 233–242. [Google Scholar] [CrossRef]
- Tsokas, G.; Tsourlos, P.; Vargemezis, G.; Pazaras, N.T. Using surface and cross-hole resistivity tomography in an urban environment: An example of imaging the foundations of the ancient wall in Thessaloniki, North Greece. Phys. Chem. Earth Parts A/B/C 2011, 36, 1310–1317. [Google Scholar] [CrossRef]
- Tsourlos, P.; Tsokas, G. Non-destructive electrical resistivity tomography survey at the south walls of the Acropolis of Athens. Archaeol. Prospect. 2011, 18, 173–186. [Google Scholar] [CrossRef]
- Cozzolino, M.; Caliò, L.M.; Gentile, V.; Mauriello, P.; Di Meo, A. The discovery of the theater of Akragas (Valley of Temples, Agrigento, Italy): An archaeological confirmation of the supposed buried structures from a geophysical survey. Geosciences 2020, 10, 161. [Google Scholar] [CrossRef]
- Elwaseif, M.; Slater, L. Quantifying tomb geometries in resistivity images using watershed algorithms. J. Archaeol. Sci. 2010, 37, 1424–1436. [Google Scholar] [CrossRef]
- Berezowski, V.; Mallett, X.; Ellis, J.; Moffat, I. Using ground penetrating radar and resistivity methods to locate unmarked graves: A review. Remote Sens. 2021, 13, 2880. [Google Scholar] [CrossRef]
- Bottari, C.; Aringoli, D.; Carluccio, R.; Castellano, C.; Caracciolo, F.; Gasperini, M.; Materazzi, M.; Nicolosi, I.; Pambianchi, G.; Pieruccini, P.; et al. Geomorphological and geophysical investigations for the characterization of the Roman Carsulae site (Tiber basin, Central Italy). J. Appl. Geophys. 2017, 143, 74–85. [Google Scholar] [CrossRef]
- Bottari, C.; Martorana, R.; Scudero, S.; Capizzi, P.; Cavallaro, D.; Pisciotta, A.; D’Alessandro, A.; Coltelli, M.; Lodato, L. Coseismic damage at an archaeological site in sicily, italy: Evidence of roman age earthquake surface faulting. Surv. Geophys. 2018, 39, 1263–1284. [Google Scholar] [CrossRef]
- Ercoli, M.; Pauselli, C.; Forte, E.; Di Matteo, L.; Mazzocca, M.; Frigeri, A.; Federico, C. A multidisciplinary geological and geophysical approach to define structural and hydrogeological implications of the Molinaccio spring (Spello, Italy). J. Appl. Geophys. 2012, 77, 72–82. [Google Scholar] [CrossRef]
- Capizzi, P.; Martorana, R. Integration of constrained electrical and seismic tomographies to study the landslide affecting the cathedral of Agrigento. J. Geophys. Eng. 2014, 11, 045009. [Google Scholar] [CrossRef]
- Porcelli, F.; Sambuelli, L.; Comina, C.; Spanò, A.; Lingua, A.; Calantropio, A.; Catanzariti, G.; Chiabrando, F.; Fischanger, F.; Maschio, P.; et al. Integrated geophysics and geomatics surveys in the valley of the kings. Sensors 2020, 20, 1552. [Google Scholar] [CrossRef] [PubMed]
- Mol, L.; Preston, P. The writing’s in the wall: A review of new preliminary applications of electrical resistivity tomography within archaeology. Archaeometry 2010, 52, 1079–1095. [Google Scholar] [CrossRef]
- Di Maio, R.; Meola, C.; Grimaldi, M.; Pappalardo, U. New insights for conservation of Villa Imperiale (Pompeii, Italy) through nondestructive exploration. Int. J. Archit. Herit. 2012, 6, 562–578. [Google Scholar] [CrossRef]
- Cafiso, F.; Canzoneri, A.; Capizzi, P.; Carollo, A.; Martorana, R.; Romano, F. Joint interpretation of electrical and seismic data aimed at modelling the foundation soils of the Maredolce monumental complex in Palermo (Italy). Archaeol. Prospect. 2020. [Google Scholar] [CrossRef]
- Xu, S.; Wang, X.; Zhu, R.; Wang, D. Uncertainty Analysis of Inverse Problem of Resistivity Model in Internal Defects Detection of Buildings. Buildings 2022, 12, 622. [Google Scholar] [CrossRef]
- Ward, S.H. The resistivity and induced polarization methods. In Proceedings of the 1st EEGS Symposium on the Application of Geophysics to Engineering and Environmental Problems; European Association of Geoscientists & Engineers: Golden, CO, USA, 1990; p. cp-214-00002. [Google Scholar]
- Athanasiou, E.; Tsourlos, P.; Vargemezis, G.; Papazachos, C.; Tsokas, G. Non-destructive DC resistivity surveying using flat-base electrodes. Near Surf. Geophys. 2007, 5, 263–272. [Google Scholar] [CrossRef]
- Cracknell, A.P. Introduction to Remote Sensing; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- De Ferrières, M. Eléments de Technologie pour Comprendre la Photographie; Editions VM: Paris, France, 2004. [Google Scholar]
- Kraus, K.; Photogrammetry, I. Fundamentals and standard processes. Dümmlers 1993, 1, 397. [Google Scholar]
- Agisoft, L. Agisoft Photoscan Pro. St. Petersburg, Russia. 2014. Available online: http://www.agisoft.com (accessed on 15 November 2022).
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the world from internet photo collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Périsset, M.C.; Tabbagh, A. Interpretation of thermal prospection on bare soils. Archaeometry 1981, 23, 169–187. [Google Scholar] [CrossRef]
- Giardino, M.; Haley, B.S. Airborne remote sensing and geospatial analysis. Remote Sensing in Archaeology: An Explicitly North American Perspective; University of Alabama Press: Tuscaloosa, AL, USA, 2006; pp. 47–77. [Google Scholar]
- Lu, Y.; Horton, R.; Zhang, X.; Ren, T. Accounting for soil porosity improves a thermal inertia model for estimating surface soil water content. Remote Sens. Environ. 2018, 212, 79–89. [Google Scholar] [CrossRef]
- Minacapilli, M.; Cammalleri, C.; Ciraolo, G.; D’Asaro, F.; Iovino, M.; Maltese, A. Thermal inertia modeling for soil surface water content estimation: A laboratory experiment. Soil Sci. Soc. Am. J. 2012, 76, 92–100. [Google Scholar] [CrossRef]
- Côté, J.; Konrad, J.M. A generalized thermal conductivity model for soils and construction materials. Can. Geotech. J. 2005, 42, 443–458. [Google Scholar] [CrossRef]
- Bristow, K.L. Measurement of thermal properties and water content of unsaturated sandy soil using dual-probe heat-pulse probes. Agric. For. Meteorol. 1998, 89, 75–84. [Google Scholar] [CrossRef]
- Stanjek, H.; Fassbinder, J. Soil aspects affecting archaeological details in aerial photographs. Archaeol. Prospect. 1995, 2, 91–101. [Google Scholar] [CrossRef]
- Stoll, J.; Moritz, D. Unmanned aircraft systems for rapid near surface geophysical measurements. In Proceedings of the 75th EAGE Conference & Exhibition-Workshops, London, UK, 10–13 June 2013; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 1988. Available online: https://www.earthdoc.org/content/papers/10.3997/2214-4609.20131212 (accessed on 10 December 2022).
- Macharet, D.G.; Perez-Imaz, H.I.; Rezeck, P.A.; Potje, G.A.; Benyosef, L.C.; Wiermann, A.; Freitas, G.M.; Garcia, L.G.; Campos, M.F. Autonomous aeromagnetic surveys using a fluxgate magnetometer. Sensors 2016, 16, 2169. [Google Scholar] [CrossRef]
- Gavazzi, B.; Le Maire, P.; de Lépinay, J.M.; Calou, P.; Munschy, M. Fluxgate three-component magnetometers for cost-effective ground, UAV and airborne magnetic surveys for industrial and academic geoscience applications and comparison with current industrial standards through case studies. Geomech. Energy Environ. 2019, 20, 100117. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Greco, L.; Scudero, S.; Vitale, G.; Bottari, C.; Capizzi, P.; Croce, F.; Martorana, R.; Pisciotta, A. Low-cost Remotely Operated Underwater and Unmanned Aerial vehicles: New technologies for archaeo-geophysics. In Proceedings of the IMEKO International Conference on Metrology for Archaeology and Cultural Heritage, MetroArchaeo, Lecce, Italy, 23–25 October 2017; pp. 384–386. [Google Scholar]
- Jackisch, R.; Madriz, Y.; Zimmermann, R.; Pirttijärvi, M.; Saartenoja, A.; Heincke, B.H.; Salmirinne, H.; Kujasalo, J.P.; Andreani, L.; Gloaguen, R. Drone-borne hyperspectral and magnetic data integration: Otanmäki Fe-Ti-V deposit in Finland. Remote Sens. 2019, 11, 2084. [Google Scholar] [CrossRef]
- Maire, P.; Bertrand, L.; Munschy, M.; Diraison, M.; Géraud, Y. Aerial magnetic mapping with a UAV and a fluxgate magnetometer: A new method for rapid mapping and upscaling from the field to regional scale. Geophys. Prospect. 2020, 68, 2307–2319. [Google Scholar] [CrossRef]
- Schmidt, V.; Becken, M.; Schmalzl, J. A UAV-borne magnetic survey for archaeological prospection of a Celtic burial site. First Break 2020, 38, 61–66. [Google Scholar] [CrossRef]
- Pisciotta, A.; Vitale, G.; Scudero, S.; Martorana, R.; Capizzi, P.; D’Alessandro, A. A lightweight prototype of a magnetometric system for unmanned aerial vehicles. Sensors 2021, 21, 4691. [Google Scholar] [CrossRef]
- Kulüke, C.; Virgil, C.; Stoll, J.; Hördt, A. A new system to measure the gradient vector of the magnetic field on unmanned aerial vehicles (UAV)-data processing and field experiment. RAS Tech. Instrum. 2022, 1, 65–80. [Google Scholar] [CrossRef]
- Phelps, G.; Bracken, R.; Spritzer, J.; White, D. Achieving sub-nanoTesla precision in multirotor UAV aeromagnetic surveys. J. Appl. Geophys. 2022, 206, 104779. [Google Scholar] [CrossRef]
- Noriega, G. UAV-based magnetometry—Practical considerations, performance measures, and application to magnetic anomaly detection. Lead. Edge 2022, 41, 472–480. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Xing, K.; Zhang, X. Unmanned aerial vehicles for magnetic surveys: A review on platform selection and interference suppression. Drones 2021, 5, 93. [Google Scholar] [CrossRef]
- Vassallo, S. Himera-città Greca: Guida alla Storia e ai Monumenti; Regione Siciliana, Assesorato dei Beni Culturali, Ambientali e della Pubblica Istruzione: Palermo, Italy, 2005. [Google Scholar]
- Cosentino, P.; Luzio, D.; Rotigliano, E. Geoelectrical study of archaeological structures in the Himera plane (North-western Sicily). Ann. Di Geofis. 1996, 39, 109–121. [Google Scholar] [CrossRef]







| Fluxgate | Proton Precession | Cesium Vapor | |
|---|---|---|---|
| Sensitivity | from 1 nT to 0.1 nT | from 0.1 nT to 0.01 nT | <0.01 nT |
| Pros | Rugged and lightweight | Free orientation, rugged, simple, no heading error | Great versatility and high precision |
| Cons | Must be oriented | More precise models are bulky, heavy, and have high power consumption | Fragile, heading errors |
| Applications | Versatile; mainly airborne and gradiometry | Marine, airborne, and ground survey | Ground survey, airborne, gradiometry, labs, etc. |
| Suitability for archaeology/cultural heritage | Preferable for UAS-based surveys | Preferable for ground-based surveys | Suitable but not recommended |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martorana, R.; Capizzi, P.; Pisciotta, A.; Scudero, S.; Bottari, C. An Overview of Geophysical Techniques and Their Potential Suitability for Archaeological Studies. Heritage 2023, 6, 2886-2927. https://doi.org/10.3390/heritage6030154
Martorana R, Capizzi P, Pisciotta A, Scudero S, Bottari C. An Overview of Geophysical Techniques and Their Potential Suitability for Archaeological Studies. Heritage. 2023; 6(3):2886-2927. https://doi.org/10.3390/heritage6030154
Chicago/Turabian StyleMartorana, Raffaele, Patrizia Capizzi, Antonino Pisciotta, Salvatore Scudero, and Carla Bottari. 2023. "An Overview of Geophysical Techniques and Their Potential Suitability for Archaeological Studies" Heritage 6, no. 3: 2886-2927. https://doi.org/10.3390/heritage6030154
APA StyleMartorana, R., Capizzi, P., Pisciotta, A., Scudero, S., & Bottari, C. (2023). An Overview of Geophysical Techniques and Their Potential Suitability for Archaeological Studies. Heritage, 6(3), 2886-2927. https://doi.org/10.3390/heritage6030154









