Abstract
The visual method for assessment of the structural behaviour of historic masonry walls, known by the acronym MQI (Masonry Quality Index) was introduced in 2002 by a team of researchers from the University of Perugia, Italy. This is based on a visual survey of the faces and the cross section of a wall panel, and it aims at verifying if a wall complies with the “rules of the art”. Based on this analysis, it is possible to calculate a numerical index: numerous tests, carried out on site by the authors to validate the method, have demonstrated that the index is able to provide useful information about the mechanical characteristics and structural response, in general, of the analysed wall panel. The failure mode of a wall panel under the action of an earthquake is a critical aspect. In general, the failure modes can be categorized in two classes: masonry disaggregation and the development of a local or global mechanism of wall elements (macroelements). Several theoretical models and numerical simulations only consider the latter. In this paper, application of the MQI method is further investigated, with particular emphasis to those masonry typologies which are more prone to collapse by disaggregation during a seismic event. Under the action of an earthquake, some types of masonry are typically unable to deform and to split in macroelements, and another type of failure occurs: this is the so-called “masonry disaggregation” or “masonry crumbling”. This type of failure anticipates the ones resulting from macroelement methods or stress analysis. As a conclusion, these latter methods become completely inappropriate and potentially hazardous, as they overestimate the seismic capacity of the building under investigation. The MQI method has been adapted to assess the structural response of different types of masonry under the action of an earthquake. In detail, the aim was to verify when the phenomenon of masonry disaggregation is likely to occur.
1. Introduction
Historic masonry buildings in Italy and in many other territories represent a heritage of paramount importance, but earthquakes often threaten this masonry heritage. Structural engineers are primarily concerned with assessment of the building’s structural vulnerabilities and the design of retrofit or repair interventions [1,2,3].
A large amount of research has been published to provide recommendations for the evaluation and rehabilitation of unreinforced masonry buildings [4,5,6]. However academic researchers often suggest using sophisticated and complex numerical methods that result in theoretical models, which are out of touch with the reality of the structural behaviour of masonry buildings. Because of the complexity of these methods, it is often difficult to make a critical analysis of the results obtained. Furthermore, the final result is repeatedly an unacceptable and inappropriate retrofitting intervention.
To compound the situation, it should be noted that conservation agencies and governmental heritage bodies diminish the importance of structural problems, whereas their most urgent concern is for “conservation”, to be read in a narrow and limited sense. Clear needs for structural repairs or interventions have been sometimes ignored, where ordinary common sense and standard methods of assessment of the buildings might have suggested the importance of these needs: the collapse of several historic masonry churches during the 2016 Central Italy earthquake is a painful, not isolated example of this approach to conservation. In many situations, structural problems were well-known and evident, but these were ignored by the heritage bodies.
The situation we face is complex and multifaceted: the approach used by technicians for the assessment of existing masonry buildings varies from the use of very sophisticated numerical simulations to the simple refusal to apply any structural analysis. In this gap, we believe there is space to use simplified methods, based on the basic concepts of the mechanics of structures: these methods could be particularly useful to quickly and effectively highlight structural problems and vulnerabilities [7,8,9,10,11,12,13].
The MQI (Masonry Quality Index) method follows this idea: by using it, it is possible to obtain critical information about the mechanical properties of the masonry under investigation. This visual method is particularly interesting when the masonry building is listed or of heritage value: in this situation, it is not typically possible to carry out structural testing for the damage caused to the building itself [14,15,16,17].
In this paper, this approach has been used to verify if a masonry wall is able to exhibit a structural behaviour consistent with the one adopted in the numerical simulations or in the analytical procedures. These methods often assume that the masonry will behave like a chain of rigid elements (the so-called “macroelements method”), with the failure of single wall elements (“local” collapse mechanisms) or of the entire building (“global” collapse mechanism).
Under the action of an earthquake, some types of masonry are typically unable to deform and to split in macroelements, and another type of failure occurs: this is the so-called “masonry disaggregation” or “masonry crumbling”. This type of failure anticipates the ones resulting from macroelement methods or stress analysis. As a conclusion, these latter methods become completely inappropriate and potentially hazardous, as they overestimate the seismic capacity of the building under investigation.
The MQI method has been proposed by the authors in 2002, and it has been summarized in Appendix A. The revised MQI method, described in this paper, allows to evaluate the phenomenon of masonry disintegration, thus highlighting those real cases where greater attention is required towards this issue. The main aim of this ongoing project is to provide an effective, quick, and easy to use tool for professionals working in conservation engineering for the challenges resulting from structural assessment of existing building stock. The MQI can provide useful information about critical mechanical properties of historic masonry and the most likely failure mode under the action of an earthquake.
2. Knowledge Acquired Through Experience (Past Earthquakes)
Recent seismic events in central Italy have demonstrated the importance of mechanical properties of historic masonry when assessing the overall structural behaviour of a historic building. In the so-called “masonry quality”, we can may include all typological and constructive characteristics (constituent materials; masonry arrangement or texture, form, and structure of the wall cross-section; etc.) having a direct influence on the structural response of the masonry building under investigation.
It is worth noting that the structural behaviour of historic buildings struck by a quake varied depending on the masonry quality: in the areas nearby the earthquake’s epicentre, buildings made of rubble or irregular stone masonry totally or partially collapsed. The prevalent failure mode was due to masonry crumbling (i.e., the walls disintegrated), while conversely, those wall panels complying with the “rules of the art” performed well during an earthquake [18].
Religious buildings were particularly exposed to the destructive effects of a quake: in Norcia, Italy, and nearby areas, numerous churches came down or were seriously damaged. These were made of rubble stone masonry, neither complying with the rules nor fully or properly retrofitted, due to restrictions imposed by conservation authorities.
Unfortunately, the situation we face is more complex: it is difficult to be placed inside well-defined relationships and we cannot say that the only reason for these collapses was the masonry low quality. For example, in addition to the low masonry quality, ineffective wall-to-wall connections, presence of horizontal out-of-plane static forces (for example, due to arched or vaulted structures), and other seismic vulnerabilities were often noted in collapsed buildings. However, a statistical analysis based on a large number of buildings and using the reports of the damage suffered by masonry buildings after the 2016 central Italy earthquake clearly demonstrated that the influence of the masonry quality is critical (Figure 1).
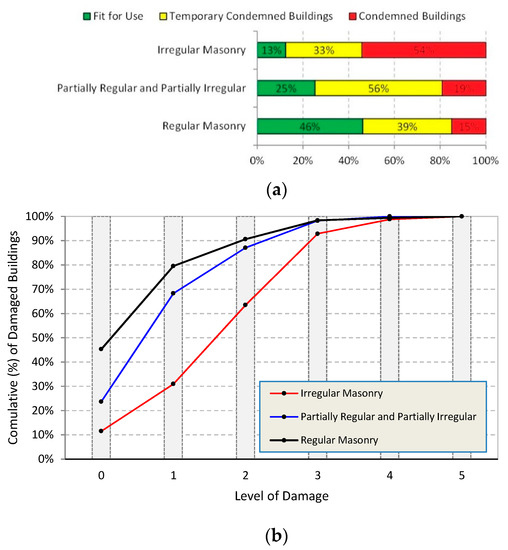
Figure 1.
Results of the post-earthquake assessment of the existing building stock of Norcia, Italy (city centre): (a) classification in terms of masonry typology and (b) cumulative percentage of damaged/collapsed buildings in terms of level of damage (0 = no damage; 5 = building collapse).
The masonry quality often governs the structural response of historic masonry buildings, and the use of the MQI visual method is particularly interesting for the evaluation of the structural safety or for the design of retrofitting interventions of buildings located in areas at high seismic hazard.
3. The Concept of the “Hierarchy of Mechanisms”
It is well accepted that traditional masonry, used for construction of most parts of existing buildings in Italy, is not a material in the modern sense of the word, i.e., the result of an industrial fabrication process, under quality and standardized controls. On the contrary, it is a handmade product that may be differently made from place to place, based on the period of construction, intended use of the building, skills of the masons used for construction, etc.
The assemblage of stone blocks with mortar, more or less rational and orderly, results in a peculiar non-tensile resistant, non-homogenous, and non-isotropic product, with a nonlinear stress–strain relationship in compression. The used mortar was typically lime-based, often with low mechanical properties, the role of which is not to bond the blocks, but primarily to smooth the surfaces between them.
The great variability of constituent materials (i.e., the type of blocks and mortars), constructive details, and onsite practical solutions resulted in a very large number of “masonry declinations”, with different “dialects”, various and diversified through the historic ages and geographical areas.
For each one of these masonry typologies, different mechanical characteristics can be found with a dissimilar structural behaviour. Along with the level of wall-to-wall bond and connections between all structural members, these characteristics may have a critical influence on the overall structural response of a building.
The assessment of these two parameters (masonry quality and connections) is paramount for analysis of the seismic behaviour of a building. Using a simplified and schematic approach, also based on numerous post-quake analyses of the damage, we can assume three different structural responses.
3.1. Type 0 (“Masonry Disaggregation”)
This is the case of a stone masonry wall made of powdery, inconsistent mortar, irregular small stones or peddles, and non-connected wall leaves. When struck by the dynamic action of an earthquake, this type of masonry disaggregates and crumbles. A wall made of this type of masonry is not able to deform or to resist high seismic forces. The wall disaggregation makes the stones fall from gravity, almost like an implosion. The final result is that the ground seems to be randomly covered in small debris (Figure 2a). This paper is aimed at studying this particular type of stone masonry. The objective is to define a parameter able to provide useful preventive indications when the masonry under investigation falls into this category.

Figure 2.
(a) Example of masonry disaggregation of a low-quality masonry in Campi Basso (Perugia, Italy), Italy, after the 2016 Central Italy earthquake and (b) an out-of-plane mechanism of a wall panel of a building in Norcia (Perugia, Italy), Italy (2016 Central Italy Earthquake).
3.2. Type 1 (“Local Collapse Mechanisms”)
If the quality of the masonry is good enough to resist the seismic action without crumbling or disaggregating, it is therefore possible to observe the formation of different collapse mechanisms. The seismic action induces partitioning in so-called “masonry macroelements”. The collapse of these macroelements occurs when a mechanism can develop. This can usually be studied using the more classic method of kinematic chains. The way the macroelements form depends on the geometry of the building and the presence of weakening elements, like openings in the walls, sections where the walls are narrow, and cracks caused by previous earthquakes. In particular, collapse mechanisms may develop from weak areas in the masonry (openings, preexisting cracks, recesses of walls, grafts of floors, etc.) (Figure 2b).
3.3. Type 2 (“Global Collapse Mechanisms”)
This type of structural response under the action of an earthquake includes the same kind of masonry previously described (Type 1). In addition to that, the connections between structural members of the buildings are effective (connections between face-loaded walls and return walls, connections between horizontal diagrams and underlying walls, etc.). In this situation, a “global mechanism” of the building can be expected. The building behaves like a single structure, and all its walls absorb a portion of the seismic forces and transfer them to the other structural members and finally to the foundations. When a single structural element fails (a wall panel or a wall lintel), the seismic forces previously absorbed by this element migrate to the other structural elements, sharing the total seismic load acting on the building on the basis of the stiffness of each structural member (walls, horizontal diaphragms, etc.).
It was against this background that it was possible to develop a strategy for the analysis and design of retrofitting interventions of historic masonry buildings. In analogy to the method used for the analysis of Reinforced Concrete (RC) structures, we have dubbed this strategy the “hierarchy of mechanisms” of masonry constructions. Table 1 summarizes this: it consists of a set of checks and consequent actions. Each check addresses a structural issue, and the total number of checks and actions to be undertaken are prioritized depending on their relevance. By doing this, it is possible to effectively improve the structural response of the building.

Table 1.
The proposed method of analysis (hierarchy of mechanisms).
Every step is an anticipation of the next: this means that the effectiveness of a structural intervention carried out on the building could be undermined if the previous issue has not been addressed adequately. Once the building is selected, the initiating stage should be its survey and analysis. This should primarily include assessment of the quality of the masonry material. If the quality of the masonry is very low, the use of methods of analysis based on mechanical models is useless: the structure is not able to deform under the action of the loads, any expected structural response of the building is anticipated by disaggregation/crumbling of the masonry.
The guidelines for repair of the buildings damaged by the 2016 Central Italy quake defines well this concept: “it is initially required to assess if the masonry construction is able to deform under the action of the seismic forces, by considering the quality of the masonry material. When the type of masonry does not allow such structural response, because of its attitude to crumble under the action of the dynamic loading, the improvement of any structural intervention is nullified. In this situation, it is preliminary essential to prevent the disaggregation of the masonry with appropriate actions. For this type of masonry, the stress and strain analyses suggested by the Building Codes and relevant guidelines are irrelevant”.
The method of analysis suggested by the new Italian Seismic Code [19] and the corresponding Guidelines [20] is another move in the same direction: “modelling of a masonry structure using rigid macroelements is reliable only if phenomena of masonry crumbling under the action of an earthquake can be excluded”. The method of the hierarchy of mechanisms should not be not considered a strict one. This should be intended as a conceptual framework where structural issues of a masonry building (with particular emphasis to analysis of the masonry quality and the connection between structural members) are associated to the effects of high-magnitude earthquake.
4. The Masonry Quality Index (MQI) Applied to Disaggregating Masonry
The MQI method consists in the calculation of a numerical value representative of the masonry quality: this analysis is made by considering a series of critical parameters affecting the structural behaviour of the masonry. The parameters used for the analysis are the so-called “rules of the art”: a series of building rules to abide for an appropriate construction of a wall. If the masonry under investigation fulfils these rules, a numerical value is assigned: the higher the numerical value assigned, the higher the “degree of fulfilment” of the corresponding building rule.
Appendix A reports how to use the MQI method. In this section, we aim to study the phenomenon of masonry disaggregation, using the MQI method: we refer to the type of masonry that is prone to crumbling and disaggregating when struck by a seismic force. We recall that, by using the MQI method, it is possible to achieve an estimation of the mechanical properties of the masonry. The MQI is a visual method that is easy and fast to use. The estimation of several masonry mechanical properties can be made using this method without performing mechanical testing on it. This is particularly interesting for listed historic buildings, where structural engineers are not allowed to conduct any operation, including small localized tests on the masonry materials, that could damage the listed building.
The structural response of a load-bearing, historic, wall panel is different depending on the direction of the acting load (V = vertical compressive loading, I = horizontal in-plane, and O = horizontal out-of-plane loading). As a consequence, we can calculate 3 different values of the MQI index (MQIV, MQII, and MQIO).
The MQI method, as proposed and described in Borri and De Maria [21], is based on the visual analysis of 7 parameters (identified by the acronyms SM, SD, SS, WC, HJ, VJ, and MM (see Appendix A and Table 2)). Analysis of the 7 parameters requires an in-depth knowledge of historical construction methods due to the demands placed upon the engineer to categorize each parameter under three possible outcomes: Fulfilled—F, Partially Fulfilled—PF, and Not Fulfilled—NF. The analysis of each parameter leads to a numerical value (for a total of 7 numerical results) based on its fulfilment category. The combination of the 7 numerical values gives the value of MQI.

Table 2.
The parameters to consider in the visual analysis of the Masonry Quality Index (MQI) method.
The numerical value MQI resulting can range from 0 to 10 (0 for very poor masonry and 10 for very good-quality masonry). MQI may finally provide important information about the structural behaviour of the masonry. Three categories, depending on the value of MQI (A, B, and C, respectively) have been defined. For high values of the MQI index, the category is A (good structural response), while it is C for low values of the MQI index. Category C is clearly related to an unsatisfactory structural response of the masonry. Category B is in between the two other categories (medium or satisfactory structural response of the masonry).
The MQI index has been calibrated against the mechanical properties of the masonry resulting from on-site testing. By using appropriate correlation plots, it is easily possible to obtain an estimation of the strength and deformation characteristics of a masonry typology. More details of these correlations are given in Appendix A. In this section, we want to study the problem of disaggregating masonry based on the use of the MQI method. Because masonry can typically disaggregate and crumble after initial activation of a local rocking (out-of-plane) collapse mechanism, the most important MQI index to consider is MQIO.
When we use the MQI method to study if a building, under the action of an earthquake, will crumble, it is important to remember that its structural response will depend on many factors and the assessment of the quality of the masonry material is only one. We could mention here the magnitude of the quake, its direction and duration, the building’s natural modes of vibration, etc.
However, several considerations could justify this choice: it should be initially said that an assessment method able to provide “true” results does not exist. All methods, including the complex ones, only consider a limited number of parameters affecting the structural response of a building under seismic action. This is the case of historic buildings. In the Italian Seismic Code [19,20], it is clearly reported: “the mechanical properties of the masonry and level of constraint between structural members are affected by a high number of uncertainties. Historic buildings were not designed using the methods of the structural analysis and strength of materials, but using an approach based on observation and intuition. The conditions of equilibrium of rigid bodies and past experience were the only methods used for design of these historic constructions”.
It should be highlighted that peculiar problems of a single building, common in historic constructions, could highly complicate the work of engineers and architects. In these situations, the assessment methods can turn ineffective and be unable to provide useful information about the structural state of the building under investigation. It is evident that the results of these analyses should be intended as more qualitative than quantitative and considered with a critical approach. In such context, past experience from observation and analysis of other similar buildings could be very useful.
Based on the above considerations, we propose here to use the MQI method to study phenomena of disaggregating masonry under the effect of a quake, underlying its probabilistic characteristic. Based on this, when we say that “a masonry wall can crumble if its MQI index is smaller than…”, we only want to say that, using past experience from previous seismic events, similar masonry typologies with comparable features very often collapsed by crumbling and that it is therefore logical to expect an analogous structural response of the wall under investigation when struck by a similar quake.
However, it is true that the numerical results given in this paper are based on a very large number of real cases. The effects of the most serious Italian seismic events in the last 2–3 decades have been studied, both considering collapsed and non-collapsed masonry buildings. In these situations, we have calculated the corresponding MQIO values and we could finally define a “limit” value of the MQIO: when the MQIO is lower than this limit value, we believe that disaggregation of the masonry wall is the most likely collapse mechanism under the effect of a quake.
This is clearly a heuristic method in need of verifications and deepening. While we would prefer to adopt methods able to provide more specific and punctual results, actually unavailable, the MQI method could be useful to obtain critical information on the expected structural and seismic behaviour of the masonry, often subject to disaggregation under the effect of a quake.
This approach is consistent with the instructions given by the new Italian Seismic Code, where the concept of Expected Structural Response is introduced: “For pre-existing masonry buildings, very different structural situations can be found and it is therefore impossible to use specific or predefined methods for all cases. As a consequence, the method to assess the structural safety of a building must be chosen and justified by the engineer, using the concept of expected structural response”.
5. The Masonry Collapse Mechanism by Disaggregation
We previously mentioned that a very low-quality masonry wall (typically made of inconsistent, dusty mortar, small irregular stones or pebbles and double-leaf walls made of unconnected masonry leaves) under the effect of a high-magnitude seismic action is unable to “hold together” its stone elements. Progressive instability of the stones causes disaggregation and crumbling of the entire wall.
This collapse mechanism is mainly governed by the horizontal component of seismic acceleration. However, the vulnerability of the wall will considerably worsen if the earthquake is characterized by high vertical seismic acceleration [9,10]. This mechanism is well-known in the scientific community. This was studied by Giuffrè [22], Lagomarsino and Podestà [23], Lourenço et al. [24], and Borri et al. [25,26]. It is worth to cite here the conclusion drawn by Rondelet [27]: “overall stability is more important that acting forces for the analysis of the integrity of the buildings”. Rondelet states that the equilibrium of the wall panels of “all types of buildings” depends on their slenderness: “a wall panel will be highly stable if its thickness s is 1/8 of its height”, “the wall will exhibit a medium stability if its thickness if 1/10 of the height”, and “it will be almost unstable (lowest stability) if the wall thickness is 1/12 of its height” (Figure 3).
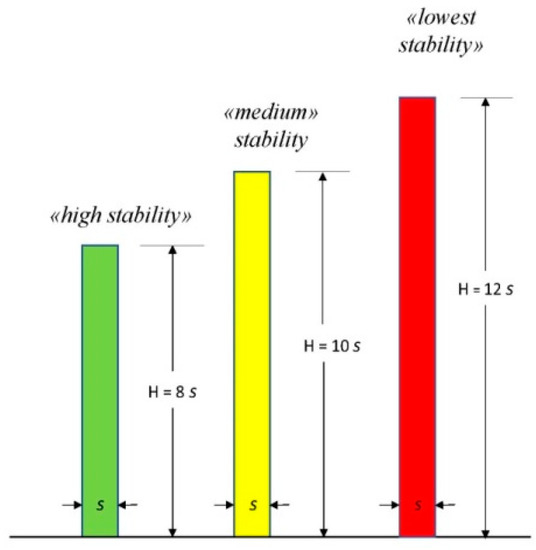
Figure 3.
Stability of wall panels, according to Rondelet [27].
It is also interesting to mention Rondelet’s comment [27] “it seems that time (i.e., seismic and wind action) reduced the walls’ height to make it possible to support themselves”. We can interpret this by saying that the parts of a wall exceeding 12 times its thickness will tend with time to crumble under the predominant action of horizontal loading. Rondelet wrote these conclusions from the observation and analysis of buildings located in Florence, Rome and Naples. These cities are located in areas with a low to medium seismic hazard: the proposed limit values of the wall thicknesses should be “reformulated” for the territories at high seismic hazard.
Giuffrè adapts Rondelet’s conclusions to buildings in seismic prone areas by adding the concept of “masonry quality”. We believe that this is the path to follow to use the MQI method for disaggregating masonry under the action of an earthquake. The main conclusion drawn by Giuffrè is that the failure of a wall panel under the effect of horizontal (i.e., seismic) action is the consequence of its loss of monoliticity and integrity, resulting in a loss of equilibrium. The masonry arrangement and the noncompliance with the “rules of the art” of wall construction methods play a crucial role in this regard. Giuffrè studied the rocking (i.e., out-of-plane) collapse mechanism of three wall panels with identical dimensions (thickness and height), type of applied loads, and constituent materials (Figure 4). The three walls only differed in the arrangement of the blocks: Figure 4a shows a wall where the “rules of the art” are fulfilled (particularly a good connection between adjacent wall leaves), while these are progressively removed for the two walls in Figure 4b,c. The magnitude of the uniformly distributed load needed to activate the wall’s out-of-plane rocking (Figure 5) is significantly smaller for the wall in Figure 4c compared to the one in Figure 4a.

Figure 4.
Rocking of a wall panel: the out-of-plane capacity of the wall depends on the arrangement of the blocks. The horizontal load-capacity of wall in (a) is higher than in (b), that, in turn, is higher than the wall in (c), [22].
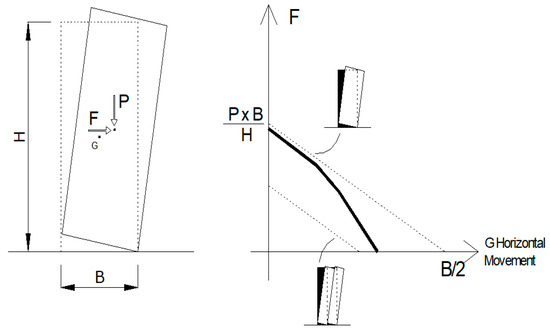
Figure 5.
The rocking behaviour of a wall panel: the bold curve in the graph represents the horizontal load F vs. horizontal movement relationship for a wall panel not fulfilling the “rules of the art”. The two dashed lines are the corresponding relationships for a “rigid” single-leaf and a double-leaf wall panel with unconnected wall leaves, [22].
When the rules of the art are not fulfilled, Figure 5 also shows that the displacement capacity (in terms of horizontal movement at the top) of the wall reduces. The way Giuffrè describes this is illuminating: “when the effectiveness of the headers reduces (to note that the length of the headers is smaller in Figure 4b compared to the thickness of the wall) or their number decreases (to note a smaller number of headers for the wall in Figure 4c), this causes a reduction of the horizontal load producing the rocking mechanism. This load reduction becomes greater as the masonry arrangement differ from the one in Figure 4a. The wall panel will disaggregate due to a loss of equilibrium in a part of it, before the acting load can reach the magnitude corresponding to the rigid and monolithic rocking of the entire wall panel. With this regard, headers will guarantee the monolithic behaviour of the wall under the action of the horizontal load only if they are positioned according to the rules of the art. A decrement (in their number or dimensions) will result in a reduced load-capacity.”
What Giuffrè [22] wants to stress is that only a portion of the wall panel will disaggregate due to a loss of equilibrium. By doing this, he notes that the horizontal load-capacity of a wall depends not only on its geometry and the mechanical properties of the constituent materials but also on the quality and arrangement of the masonry. The monolithic displacement capacity of the wall clearly depends on the masonry quality, and, when the rules of the art are not fulfilled, there is a loss of wall monolithicity.
Therefore, the deformation capacity not only is a problem related to dimensions and geometry of the wall but also depends on the masonry quality, and the design formulations available in the literature, typically based on the ratio B/H (B = wall thickness; H = wall height), only provide an upper load limit. This can be used for design purposes only if the masonry quality is medium or good. Oppositely, for low-quality masonry, the use of these formulations can lead to overestimation of the horizontal load capacity of the wall panels. The corresponding seismic acceleration producing the collapse of a low-quality masonry wall could be significantly smaller.
As an example, Figure 6 shows 4 slides of a video of the collapse of a masonry building located near Foligno, Italy, during the 1997 earthquake. Initially, it can be noted (Figure 6a) that the façade cracked and several wall macroelements formed. This is typically a collapse mechanism according to the theory of kinematic chains (Figure 6b). The rotation of the wall (on the left) appears to suggest a rocking (out-of-plane) mechanism of this wall (Figure 6c). However, the very low quality of the masonry does not allow this mechanism to develop further, and several masonry portions of the building become unstable and collapse. It is the façade wall of the first floor on the front that fails first. Subsequently, the wall on the left and the entire building collapse (Figure 6d).


Figure 6.
Photograms of the collapse mechanism of a building located in Foligno, Italy during the 1997 earthquake: (a) masonry starts cracking; (b) wall macro-elements develops; (c) rocking (out-of-plane) mechanism of wall façade (on the left); (d) masonry disaggregation
It is evident that the structural response of the building under the action of the earthquake highly differs from the theory of macroelements with well-defined collapse mechanisms. These mechanisms cannot further develop because of disaggregation of the masonry.
6. Masonry Disaggregation and Corresponding Limit Value of the MQIO Index
To assess the monolithic behaviour of a wall, Giuffrè [22] believes that the presence and density of headers in a wall is a critical parameter. This parameter governs the failure mode (i.e., disaggregation or out-of-plane rocking). However, this is not the only parameter to consider. The “rules of the art” are the other parameters used for assessment of the seismic behaviour of a wall panel: mechanical characteristics of the mortars, including the presence of pinnings, the shape and dimensions of the blocks, horizontality of the bed joints, staggering of vertical mortar joints, and mechanical properties of the blocks (stones, bricks, etc.). These rules, when used in construction, may effectively prevent premature failure modes.
We remember that the MQI method suggests to use these parameters for analysis. In detail, the MQIO value is the most important index to assess the monolithic response of a wall under the action of an earthquake. To find the limit value of MQIO able to indicate a possible failure mode by disaggregation, we have considered the masonry typologies suggested by the Italian Seismic Code. Looking at the failure mode or the damage suffered by a large number of historic buildings during recent earthquakes in Italy, we categorized each building depending on the failure mode (i.e., masonry disaggregation or development of a mechanism of wall macroelements) and the masonry typology.
It is evident that there are important limitations in this task, given the complexity and dimensions of the problem. It is effectively impossible to consider all masonry typologies used in this territory, but the masonry typologies suggested by the Italian Seismic Code are sufficiently numerous to include a large number of real situations. If the method we are going to use on these typologies is able to provide reliable results, we believe that it will be not difficult to extend its use to other masonry typologies not included in the Code.
The investigated buildings are mainly 2- or 3-story ordinary residences, located in Umbria, Marche, Abruzzi, Latium, and Emilia-Romagna (hence the consequent limitations of the method). These are the five Italian regions struck by a destructive earthquake in the last 23 years: 1997 (Umbria and Marche), 2009 (Abruzzo), 2012 (Emilia-Romagna), and 2016 (Umbria, Marche, Lazio), where the authors could conduct direct on-site post-earthquake buildings surveys. Indirect analyses, based on photographic surveys and technical reports, have been used to calibrate the method for buildings located in Friuli (1976 earthquake) and Irpinia (1980 earthquake). Special buildings (i.e., churches, towers, etc.) or buildings in areas of lower seismicity need to be differently threated, and modifications are required.
Moreover, other parameters not directly related to the masonry quality should be highlighted. These factors may cause the failure mode by disaggregation. All these parameters are analysed in detail as explained below. Firstly, it should be noted that masonry disaggregation only rarely involves the entire building: in most cases, masonry disaggregation only occurs in a portion of the building. Initially, under the action of an earthquake, masonry macroelements develop from the walls of the building. Disaggregation typically occurs for those macroelements subject to out-of-plane actions, where the rocking mechanism initiated.
It was common to study buildings still standing after the earthquake, where the damage was the consequence of the development of an in-plane or out-of-plane mechanism. The analysis of these buildings demonstrated that masonry disaggregation occurred in very limited portions. This was usually the effect of local seismic vulnerabilities (areas of a building with a low level of connection between face-loaded and return walls, walls subject to horizontal thrust, regions with low-thickness walls, areas of adherence between adjacent buildings, etc.). An important structural “flaw”, often the main cause of an out-of-plane mechanism at the upper floors of the building, is an excessive slenderness of the load-bearing walls. It is common in historic buildings that the wall thickness tampers in height, while the heights often remain the same for all floors.
The axial compressive loading, mainly resulting from dead loads and acting on these walls, has an influence. It is well recognized that axial loading has a positive effect in delaying cracking of walls subjected to horizontal actions. A wall panel, where the magnitude of the axial load is small, cannot activate the resisting mechanism induced by friction and mechanical interlocking between constituent materials (blocks and mortar). These panels are more likely to fail by disaggregation. Again, the more vulnerable walls are the ones located at the upper floors of the building.
Finally, we also note that the seismic forces are not uniformly distributed along the height of the building. These are typically greater at the upper floors, as a consequence of the phenomena of dynamic amplification. In addition to the masonry quality, the above parameters had an influence on explaining the causes for the failures of the studied buildings. However, in many situations, the poor masonry quality seems to be an important factor in explaining the collapse or damage of a building struck by an earthquake.
6.1. Masonry Typologies Suggested by the Italian Seismic Code
The Italian Seismic Code considers a limited number of basic masonry typologies. These are reported in Table 3, alongside their main mechanical properties. We could assign most of the existing masonry arrangements into these basic typologies. This table was added by the norm setter to provide the designers with the mechanical properties of historic masonry materials to be used in numerical simulations, structural analyses, and assessment of the structural safety of a masonry building.

Table 3.
Italian Seismic Code [19,20]: basic masonry typologies considered.
This Code reports 8 basic masonry typologies (Table 3). However, the mechanical properties of the masonry material of each basic masonry typology is given upon the assumption of a set of characteristics (the wall bonding patterns fulfil the “rules of the art”; for double-leaf walls, the wall leaves are unconnected; the mortar is of low quality; for stone masonry walls, there are no bricks courses; and walls were not previously retrofitted). If a wall does not fulfil these characteristics, the Code suggests using different multiplication factors of the given mechanical properties. These multiplication factors are shown in another table in the Code.
Multiplication factors can be used in all 8 basic masonry typologies. These factors are typically applied when a wall characteristic differs from the ones assumed. These variations include: 1. good-quality mortar; 2. stone walls layered with bricks courses; 3. walls with a high density of headers; 4. very low-quality mortar; and 5. for brickwork walls, high-thickness mortar joints.
Using the 8 basic masonry typologies suggested by the Italian Code and combining them with the above variations, we can obtain a much larger database of masonry typologies. We have calculated the MQIO index corresponding to each masonry typology and analysed several case studies of particular interest.
It is also important to stress again that the used method of analysis is statistical, based on the post-earthquake observations of a large number of damaged or collapsed buildings. After all, the aim of this research is to provide useful indications on the masonry typologies where failure by disaggregation was detected during a destructive earthquake.
We anticipate that the MQIO upper limit value of 4 was found. Masonry buildings or single masonry structural members with a MQI index varying between 0 and 4 are likely to exhibit the phenomenon of masonry disaggregation when struck by seismic action. In this regard, the main governing factors were the presence of a very-low quality mortar and unconnected multi-leaf walls. When both of these two factors characterized the masonry of the building under investigation, we frequently noted the phenomenon of masonry disaggregation. When only one factor was detected, the overall structural response of the buildings also depended on other factors, for example, the horizontality of the mortar bed joints.
The masonry typologies, where disaggregation was more frequently noted, were irregular, i.e., made of pebbles or erratic hard stones. Masonry disaggregation was also observed in softstone walls, made of barely cut or rubble blocks. Disaggregation was less frequent when the bed joints were sufficiently horizontal, walls were made of good-quality mortar and the wall leaves were mutually connected (i.e., walls with headers). Roughly cut (hard) stone masonry walls; barely cut (hard), properly dressed, stone walls; and squared soft-stone walls did not usually fail by disaggregation. This was more evident when the quality of the mortar was good and there were headers in the walls.
Finally, squared hardstone masonry, and hollow-bricks and cement-mortar masonry walls did not exhibit phenomena of disaggregation when struck by an earthquake. The structural response of lime-mortar brickwork walls was typically satisfactory, with the exception of those cases where the mortar was very weak and there was no transversal connection.
Figure 7 shows the MQIO values of the masonry typologies considered in the Italian Seismic Code. In addition to the MQIO, the figure specifies the quality of the mortar, the masonry arrangement (regular or irregular), and the level of connection between the wall leaves (for multi-leaf walls). A red line for a value of 4 of the MQIO divides the graph in two regions. It can be noted that the masonry typologies characterized by a very weak mortar, unconnected wall leaves, and an irregular arrangement are usually below this line. For these masonry typologies, we believe that it is likely to fail by disaggregation under the action of an earthquake. Oppositely, the MQIO values of masonry typologies, both regular and irregular, and characterized by a non-weak mortar and connected wall leaves is typically higher than 4 (Figure 7).
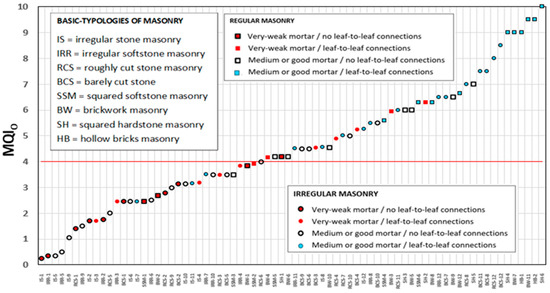
In the following, the basic masonry typologies suggested by the Italian Seismic Code and the derived typologies resulting from the use of the multiplication factors will be examined. All the resulting masonry typologies have been analysed in the following using the MQI method. The MQIO index has been also calculated, and their peculiarities have been described also using representative real examples. By doing this, it will be possible to assess the influence of the different parameters (i.e., the rules of the art) on the overall structural response of a masonry wall subjected to a seismic action.
6.1.1. Irregular Stone Masonry (Pebbles, and Erratic and Irregular Stones)
This is the basic masonry typology where disaggregation is more frequent. Based on our database, it is rare that entire buildings or wall members made of this basic masonry typology can crack when subjected to the seismic action without disaggregating. This happened only when the quality of the mortar was not too weak and there were horizontal mortar bed joints and headers (combination No. 8 in Table 4) or when the mortar was good and there were some headers (combination No. 11 and 12 in Table 4). Table 4 shows the combination of 3 different critical parameters (quality of the mortar (possible outcomes: very weak, medium, and good), horizontality of the bed joints (yes or no), and level of connection between wall leaves (yes or no)), resulting in 12 masonry types. Figure 8 and Figure 9 show two different masonry typologies where masonry disaggregation was noted (Figure 8) and did not occur (Figure 9) during recent seismic events in Italy.

Table 4.
MQIO values for irregular stone masonry (pebbles, and erratic and irregular stones): in bold is the values of MQIO higher than the threshold value of 4.

Figure 8.
A collapsed building in Campi Basso, Norcia, Italy: The masonry (combination No. 1 of Table 4) of this building disaggregated during the earthquake.

Figure 9.
Stonework building in Onna, near L’Aquila in Italy: the arrangement of the stonework is uniform, and the masonry texture is well-organized (homogeneity of the stones and random presence of bricks to improve the overall wall’s stability) (combination No. 12, Table 4). It can be noted that this wall was consolidated using a deep repointing the mortar joints. The medium dimensions of some stones suggest a good connection between wall leaves. The masonry material of this building did not disaggregate during the 2009 Aquila earthquake. It should be also highlighted here that most historic masonry buildings of Onna, typically made of a masonry of lower quality, disaggregated during the 2009 earthquake [28].
6.1.2. Roughly Cut Stone Masonry, with Non-Homogenous Wall Leaves
This basic masonry typology (made of roughly cut stones, conci sbozzati in Italian) is very common in Italy, and a large number of slightly different types of masonry can be categorized here (Figure 10). Under the action of an earthquake, the failure modes can be both by disaggregation or in-plane cracking. The most important parameter, governing the failure mode, is the quality of the mortar. Masonry made with very-low quality mortar typically failed by disaggregation, with the only exception of walls with horizontal bed joints and headers (Table 5).

Figure 10.
A building in Accumoli, near Rieti, in Italy: a large number of large cut stones was used here. This highly increased the level of connection between the wall leaves (combination No. 7, Table 5: cut stone masonry, medium-quality mortar, and effective connection between wall’s leaves). For the upper part of this building, the quality of the masonry is lower and the wall leaves seem unconnected (combination No. 5, Table 5: cut stone masonry, medium-quality mortar, and non-effective connection between wall’s leaves). The masonry of the upper part of this building disaggregated during the 2016 Central Italy earthquake.

Table 5.
MQIO values for roughly cut stone masonry: in bold is the values of MQIO higher than the threshold value of 4.
When the quality of the mortar was better, the presence of headers was critical for the analysis. Oppositely, when the mortar was good, disaggregation was rare and limited to masonry walls with no headers and no horizontal bed joints.
6.1.3. Barely Cut Stone Masonry, Properly Dressed
It is worth noting that “barely cut stones” (pietre a spacco in Italian) are mechanically worked stones (Figure 11). These stone blocks are more regular than roughly cut stones (described in Section 6.1.2). Walls made with barely cut stones exhibited a satisfactory structural response when struck by seismic action. Only when the used mortar was very weak and there were no headers in the walls was masonry disaggregation noted (Table 6).

Figure 11.
Pescara del Tronto, near Ascoli Piceno, in Italy. This is an example of cut-stone masonry, very weak mortar, unconnected wall’s leaves (Combination No.2, Table 6). The building failed due to masonry disaggregation.

Table 6.
MQIO values for barely cut stone masonry, properly dressed: in bold is the values of MQIO higher than the threshold value of 4.
6.1.4. Irregular Softstone Masonry
Because the softstone blocks are irregular, this basic masonry typology exhibits a structural response not very different from the one described in Section 6.1.1. This type of masonry (Figure 12) often disaggregates under the action of an earthquake. Table 7 shows the values of MQIO for this type of masonry for different combinations of the three main parameters (quality of the mortar, horizontality of the bed joints, and level of connection between wall leaves): it can be noted that the MQIO is very often smaller than the limit of 4.

Figure 12.
Tuff stone building in Tuscania, Italy, after the 1971 earthquake: the masonry typology can be classified in combination No. 1 of Table 7: irregular stones, non-horizontal bed joints, unconnected wall leaves, and very weak mortar. The failure mode is by disaggregation.

Table 7.
MQIO values for irregular softstone masonry: in bold is the values of MQIO higher than the threshold value of 4.
6.1.5. Squared Softstone Masonry
This basic typology is common in several parts of Italy. Walls are typically made of a single leaf (Figure 13 and Figure 14). Table 8 shows the different combinations of the three main parameters. It should be highlighted here that, according to the Italian Seismic Code, single-leaf wall panels are equivalent to double-leaf wall panels when there is a high level of connection between wall leaves. Combinations No. 2, 4, and 6 of Table 8 refer to both single-leaf and double-leaf walls with effective connection.

Figure 13.
Tuff block masonry of a building in Norcia, Italy: the quality of the mortar is good (combination No. 6, Table 8). The 2016 earthquake caused the shown failure mode: it can be noted that cracks diffusively opened in the tuff blocks, while this is very rare if the mortar quality is weak. Masonry disaggregation usually does not occur for this masonry typology.

Figure 14.
A tuff masonry building in San Pellegrino (Norcia, Italy): the masonry was made of squared tuff blocks and a very weak mortar (combination No. 2, Table 8). Cracking mainly occurred in the bed joints. The 2016 Central Italy earthquake caused a failure mode by horizontal sliding of the upper part of the building, likely activated by significant vertical component of the seismic action. The phenomenon of masonry disaggregation can be noted at the corner.

Table 8.
MQIO values for squared softstone masonry: in bold is the values of MQIO higher than the threshold value of 4.
Because of the shape (perfectly cut or squared) of the softstone blocks, bed joints are always horizontal. As a consequence, this parameter has been removed and the number of masonry combinations has been reduced to 6. Furthermore, it should be mentioned here, that, based on the experience of the authors, unconnected leaves in double-leaf softstone walls were never found.
6.1.6. Squared Hardstone Masonry
Most historic buildings made of squared hardstone blocks did not fail by masonry disaggregation during recent seismic events in Italy. The value of the MQIO is always bigger than 4 for the six possible combinations (Table 9).

Table 9.
MQIO values for squared hardstone masonry: in bold is the values of MQIO higher than the threshold value of 4.
6.1.7. Brickwork (Lime-Based Mortar)
This basic typology is common in a large number of buildings struck by the 2012 Emilia earthquake (Figure 15). Solid brickwork masonry is also easy to find in Central Italy (Umbria, Marche, and Abruzzi), and several buildings were damaged in recent earthquakes. The mortar used here must be made of lime and sand. This type of masonry does not typically fail by disaggregation, with the exception of some particular situations where brickwork masonry was used to build double-leaf walls using a very-weak lime mortar. This has been noted in several buildings damaged by the 2012 Emilia earthquake. Table 10 shows the MQIO values for the masonry resulting from the combination of three parameters (quality of the mortar, thickness of bed joints, and level of connection between leaves in multi-leaf walls). The Italian Seismic Code defines a “thick joint” if its thickness is larger than 13 mm.

Figure 15.
Brickwork building damaged by the 2012 Emilia earthquake: load-bearing walls were made of two unconnected leaves and a very-weak mortar (combination No.2, Table 10). The disaggregation of masonry is evident.

Table 10.
MQIO values for brickwork masonry (lime-based mortar): in bold is the values of MQIO higher than the threshold value of 4.
6.1.8. Hollow Bricks Masonry (Cement Mortar)
Masonry disaggregation of buildings made of hollow bricks has not been noted in case studies investigated by the authors.
6.2. Special Cases
Particular situations are not rare, and these are not considered by the Italian Seismic Code. As an example, Figure 16 shows a building in Onna, Italy, where the load-bearing walls were made of two different types of masonry: some walls were made of irregular stone masonry (pebbles, and erratic and irregular stones) (combination No. 1, Table 4). For other walls of the same building, solid concrete blocks were used. During the 2009 Aquila earthquake, the irregular stone walls disaggregated while the concrete block wall diffusively cracked, without falling apart. The MQIO index of the stone walls is very low (0.35), while it reaches the value of 9 for the concrete block ones.

Figure 16.
A building made of concrete block and irregular stones in Onna, Italy.
Another interesting case study is shown in Figure 17. Again, the masonry typology cannot be assigned to one of the types suggested by the Italian Seismic Code. This is a brickwork building located in San Possidonio, in Emilia Romagna. The mortar is made of cement, and the type of bond is heading bonding pattern. The 2012 earthquake caused in-plane shear cracking without masonry disaggregation phenomena. The MQIO is 8.5.

Figure 17.
Failure mode of a building made of bricks and cement mortar (San Possidonio, Italy).
7. Conclusions
Based on the experience of the authors, a brief summary of the failure modes of historic masonry buildings was presented, detailing the observations that were made on the performance and the deficiencies that contributed to the damage of unreinforced stone (peddle, barely cut, rubble, and perfectly cut) and solid clay brick masonry buildings, in the Italian regions of Umbria, Marche, Abruzzo, Latium, and Emilia, following recent seismic events.
It was concluded that, when subjected to the higher forces generated by an earthquake, old unreinforced masonry building stock sustained much greater and more widespread damage: this damage was typically caused by phenomena of masonry disaggregation (crumbling) or development of a mechanism of masonry macroelements. While this latter failure mode has been extensively studied in the scientific literature, with considerable attention aimed at defining numerical reliable procedures to be used in design and verification methods, the causes of disaggregation phenomenon have been underestimated or neglected by researchers and professionals. This could negatively affect the assessment of the structural safety of existing masonry buildings: structural engineers and architects dealing with the assessment of the structural safety of existing buildings should be aware that the phenomenon of masonry disaggregation can be initiated by lower seismic forces than the forces needed to activate a macroelement mechanism.
In this paper, the phenomenon of disaggregation of masonry walls under the action of an earthquake has been linked to the so-called “masonry quality”, demonstrating its critical contribution in the definition of the most likely failure mode of a masonry wall.
In detail, this paper addressed the problem of disaggregation of masonry under the action of an earthquake using the MQI visual method. This method, induced by the authors in 2002 and progressively refined, allows to estimate several critical mechanical parameters of a masonry wall and is the most likely failure mode under the action of an earthquake. By considering the so-called rules of the art, i.e., a set of important factors necessary to assess the structural quality of a wall: constituting materials (dimensions, shape, and mechanical characteristics of the blocks, i.e., bricks and stones), wall section dimension, masonry regularity (bed and head joint layout and arrangement), type of wall (single-, double-, or triple-leaf), level of connection between wall leaves, type, state, and mechanical characteristics of the mortar used for walling. The authors have calibrated the MQI method using a very large number of historic buildings, by conducting both pre- and post-earthquake surveys, experimental on-site and laboratory tests, and numerical calculations.
Moving from the masonry typologies suggested by the Italian Seismic Code and using the experience acquired by the authors in assessing the damage of a large number of buildings, it was concluded that masonry disaggregation is likely to occur in ordinary buildings when the MQI index is smaller than or equal to 4.
Future developments will include using a wider number of case-study buildings to calibrate the method and its extension to special buildings (i.e., religious buildings, etc.). Although the MQI method is based on the masonry typologies suggested by the Italian building code, its practicability and validity could be surely extended to a much larger territory. The Italian masonry typologies are not substantially different from the ones of many European and Middle East countries. An effort will be necessary to calibrate the MQI method for other masonry typologies around the world, but the basic concept of the method is clearly nondependent from national buildings codes or the masonry typologies under investigation.
Author Contributions
Conceptualization, A.B. and A.D.M.; formal analysis, M.C. and A.B.; writing—original draft preparation, M.C. and A.D.M.; writing—review and editing, M.C. and A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Italian Ministry for Research and Education, through the project ReLUIS 2019-2021.
Acknowledgments
The authors would like to acknowledge the staff of Structures Laboratory, University of Perugia, Alessio Molinari and Emanuele Bombardieri.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The Quality Masonry Index (MQI) has been proposed by the authors in 2002 and recently refined to account for different masonry typologies [21,25,26,29]. It consists in the observation of masonry and calculation of a numerical value representative of the masonry quality: this analysis is made by considering a series of critical parameters affecting the structural behaviour of the masonry. The parameters used for the analysis are the so-called “rules of the art”: a series of building rules to abide by for appropriate construction of a wall. If the masonry under investigation fulfils these rules, a numerical value is assigned (from 0 to 10): the higher the numerical value assigned, the higher the “degree of fulfilment” of the corresponding building rule.
The new Italian Seismic Code [19] and the 2019 Guidelines [20] suggest the use of assessment methods consistent with the MQI approach. In Section C8.5.3.1 of the Guidelines, it can be read “Existing masonry is the result of the assemblage of different materials, and its structural response is governed by the construction method, installation procedures, mechanical properties of constituent materials and their conservation state”. This statement is at the beginning of the Guidelines’ Section addressing the analysis of preexisting buildings. It is particularly interesting because it confirms that the structural response of preexisting buildings (also including the strength and deformation characteristics of the masonry material) depends on the typological and constructive features of the walls.
It is also important to highlight that the Italian Seismic Code states that the structural behaviour of a wall or of an existing building depends not only on the mechanical properties of their constituent materials (mortar and blocks) but also on construction method and installation procedures, i.e., the method of arrangement of the blocks, their shape, and the wall texture.
In the same Section C.8.5.3.1 of the Guidelines [20], the analysis of the masonry quality using visual methods is again promoted: “Masonry members subjected to on-site testing should be assessed to verify their degree of representability on the building, both in terms of masonry typology and corresponding mechanical properties. To facilitate this task, it could be useful to use visual methods of analysis of the wall leaves and the cross section. The masonry quality should be assessed using visual methods with a proven reliability.”
It is evident that visual methods, such as MQI and others “with a proven reliability”, have the critical function to assess the credibility of on-site testing. Because of the peculiar characteristics of historic masonry, it is important to interpret the results of on-site testing with a critical approach. This regulatory provision is likely based on the assumption that it is impossible to carry out on-site testing on all structural members of a preexisting building, and as a consequence of this, it could be “useful” to estimate the mechanical characteristics of non-tested masonry members by using the MQI method.
We believe that the MQI method has a proven reliability: numerous experimental on-site investigations have confirmed its reliability, and the scientific community, involved in the seismic assessment of preexisting buildings, has had the opportunity to study and consider it.
Appendix A.1. The “Rules of the Art”
Visual analysis of a historic wall is based on 7 seven parameters (identified by the acronyms SM, SD, SS, WC, HJ, VJ, and MM). The analysis of each parameter leads to a numerical value (for a total of 7 numerical results) based on its fulfilment category. Because a single wall panel could be subjected to varying loading conditions which directly affect the masonry quality, the values assigned to the 7 parameters depend on the loading condition acting on the wall under consideration. Three loading conditions were considered: V (vertical static loads), O (out-of-plane static and dynamic loads), and I (in-plane dynamic loads).
Consequently, three different MQI values (MQIV, MQIO, and MQII), can be calculated. The approach is to attribute different weights to the above parameters (between 0 and 3) based on the evidence that they affect the quality of the masonry with different degrees depending on the loading condition. In case of fulfilment of all parameters of quality, the MQI index is 10 irrespective of the loading condition.
Furthermore, according to the MQI values, the masonry is classified in three categories:
- category A, good masonry behaviour
- category B, average masonry behaviour
- category C, inadequate masonry behaviour (i.e., disaggregation of the masonry material under the action of an earthquake).
In consideration of a given masonry structure, integrity of the wall can be assessed by considering several quality factors and constructive solutions. In detail, the integrity of a wall is defined in construction manuals, dating back from Roman to premodern times and it is based on well-documented construction techniques and observation of damage suffered by the buildings during severe loading conditions (both static and dynamic actions). As a consequence of this, a set of rules was introduced since ancient times and, even now, these are unanimously considered by the scientific community as a base for a correct assemblage of a wall. These rules were used here to define the seven parameters needed to calculate the MQI value. The estimation requires in-depth knowledge of historical construction methods due to the demands placed upon the engineer to categorise each parameter under three possible outcomes: Fulfilled—F, Partially Fulfilled—PF, and Not Fulfilled—NF (Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7 and Table A8).
Appendix A.1.1. Quality of the Mortar/Contact between Masonry Units/Pinnings (MM Parameter)
In order to facilitate transfer of the stresses between the masonry units (stones and bricks) and ultimately to the foundations of the building without areas of stress concentration, the units are required to be flat and smooth or to use a mortar interposed between them. The use of pinnings (i.e., a variety of small stones to make the larger stones secure in the wall) may be of help for this, and it is encouraged in many manuals, especially when barely cut stones are used for walling. The quality of the mortar is also important, as this can also confine the stones and facilitate distribution of the loads (Table A1). Mortar used in historical buildings is usually based on lime (aerial or hydraulic). However, variation in the volumetric ratio of the binder, the quality, and type of the lime have a considerable effect on the final mechanical properties of the mortar.

Table A1.
Criteria for analysis of mortar properties (MM).
Table A1.
Criteria for analysis of mortar properties (MM).
| Very weak mortar and dusty mortar with no cohesion No mortar (dry rubble or pebble stonework) Thick bed joints made of weak mortar (thickness comparable to stone/brick thickness) Porous stones/bricks with weak bond to mortar | NF |
| Medium quality mortar, with bed joints not largely notched Masonry made of irregular (rubble) stones and weak mortar, and pinning stones | PF |
| Good-quality and non-degraded mortar, regular bed joints, or thick bed joints made of very good-quality mortar Masonry made of large perfectly cut stones with no mortar (dry) or very thin bed mortar joints | F |
Appendix A.1.2. Level of Connection between Adjacent Wall Leaves/Headers (WC Parameter)
Connection between adjacent wall leaves has a considerable effect on the global structural behaviour of a multi-leaf wall. The level of connection between wall leaves may present remarkable varying degrees. Headers (diatoni in Italian, i.e., masonry units or bricks placed transversally to the wall’s surface) are typically used to connect each multi-leaf wall. Length of the headers can be equal to the wall thickness (through headers) or not (partially through headers). For multi-leaf stonework walls, single- or double-course bricks placed at fixed intervals are used to connect the wall leaves.
For the analysis of wall leaf connections (WC), both the compressive and the out-of-plane behaviours are significantly affected by the presence of headers. Headers facilitate distribution of the vertical static loads along the full cross section of a multi-leaf wall.
Qualitative analysis is used when the wall section is not accessible: the outcome NF is assumed if there are no headers or less than 2/m2. For double-leaf stone walls, the outcome PF is assumed when the wall thickness is larger than the stone larger dimension and when there is a limited number of headers (2–5/m2). The outcome is F when there are many headers (>4–5/m2) and when the length of wall thickness is similar to the stone/brick larger dimension (Table A2).

Table A2.
Criteria for analysis of wall leaf connections (WC) (qualitative analysis for non-accessible vertical cross section of the wall).
Table A2.
Criteria for analysis of wall leaf connections (WC) (qualitative analysis for non-accessible vertical cross section of the wall).
| Small stones No headers | NF |
| For double-leaf walls: Limited number of stone headers Wall thickness larger than stone larger dimension | PF |
| Wall thickness similar to stone larger dimension | F |
All criteria are based on a qualitative analysis [29]. However, for WC, a quantitative criterion, based on the length of some broken lines that can be drawn on a wall section, has been proposed. If the wall section is accessible and visible (quantitative analysis), the “minimum length” Ml between two points can be used. This nondimensional value is the ratio between the minimum distance passing through two points (red line in Figure A1) only through mortar joints and the straight distance between the two points. The straight distance is usually assumed to be equal to 1 m, but smaller values up to 50 cm can be used. Ml values smaller than 1.40 indicate a weak connection between masonry leaves (NF outcome). When this value is bigger than 1.6, the assumed outcome is F (Table A3).
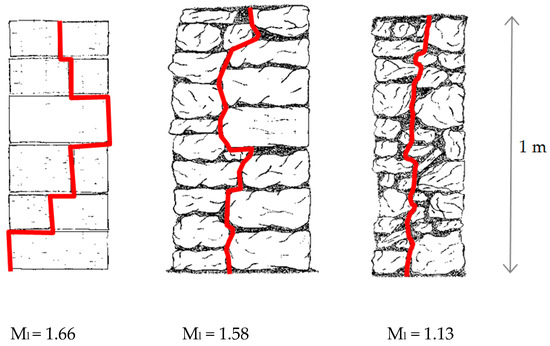
Figure A1.
Calculation method of Ml.

Table A3.
Criteria for analysis of wall leaf connections (WC) (quantitative analysis when the vertical wall section is accessible).
Table A3.
Criteria for analysis of wall leaf connections (WC) (quantitative analysis when the vertical wall section is accessible).
| Single-leaf wall: Ml < 1.4. | NF |
| Double-leaf wall: Ml < 1.4 (on a wall leaf) | |
| and Ml < 1.6 (on the other leaf) | |
| Header bonding (brickwork masonry) | |
| Walls made of small stones | |
| Unconnected wall leaves | |
| Single-leaf wall: 1.4 < Ml < 1.6. | PF |
| Double-leaf wall: | |
| (a) both wall leaves with 1.4 < Ml < 1.6. | |
| (b) Ml > 1.6 for only one wall leaf, Ml < 1.4 for the other | |
| (c) Ml > 1.6 for only one wall leaf, 1.4 < Ml < 1.6 for the other | |
| Single-leaf wall: Ml > 1.6 | F |
| Double-leaf wall: Ml > 1.6 for both wall leaves |
Appendix A.1.3. Shape of the Masonry Units (SS Parameter)
Typically, a stone masonry wall can be made of pebbles, or roughly cut or perfectly cut masonry units. When perfectly cut units are used for walling, the existence of the two horizontal contact surfaces between the block itself and the mortar facilitates activation of a frictional reaction. This reaction is critical for the capacity of a wall to resist horizontal in-plane actions. However, the frictional reaction, which is generated by the static compressive loads acting on the wall, is maximum when the contact surface is horizontal and perpendicular to the direction of the vertical loads (i.e., horizontal contact surfaces) (Table A4).
Appendix A.1.4. Dimensions of the Masonry Units (SD Parameter)
The dimensions of the masonry units, i.e., the ratio between the longest dimension of the block and the wall thickness, is another important factor to consider to assess the quality of a masonry wall. Similar to the effect of headers, a wall made of large masonry units has better seismic and static responses. Large-stone walls are typically more monolithic (disaggregation or crumbling of these walls is more difficult during earthquakes) (Table A5). Furthermore, the high weight of large stones causes a mutual confinement effect between adjacent stones in a wall. These walls also facilitate the distribution of both static (vertical) and dynamic (horizontal) actions along a larger portion of masonry.

Table A4.
Criteria for analysis of stone/brick shape (SS).
Table A4.
Criteria for analysis of stone/brick shape (SS).
| Rubble, or rounded or pebble stonework (predominant) | NF |
| on both masonry leaves | |
| Copresence of rubble, or rounded or pebble stonework; | PF |
| barely/perfectly cut stones; and bricks on both masonry leaves | |
| For double-leaf walls: squared blocks or bricks for one leaf and | |
| pebbles or irregular masonry for the adjacent wall leaf | |
| Masonry made of irregular (rubble, rounded, and pebble) stones, | |
| with pinning stones | |
| Barely cut stones or perfectly cut stones | F |
| on both masonry leaves (predominant) | |
| Brickwork masonry |

Table A5.
Criteria for analysis of stone/brick dimensions (SD).
Table A5.
Criteria for analysis of stone/brick dimensions (SD).
| Predominance of blocks with larger dimension < 20 cm | NF |
| Header bond (no stretchers) | |
| Predominance of blocks with larger dimension of 20–40 cm | PF |
| Copresence of elements of different dimensions | |
| Predominance of blocks with larger dimension ˃ 40 cm | F |
Appendix A.1.5. Staggering of Vertical Mortar Joints (VJ Parameter)
The head joint of a masonry wall could be well staggered, partially staggered, or not staggered at all. This characteristic of the head mortar joint has several positive effects: when vertical joints are properly staggered, the failure surface along the mortar joints (mortar typically is weaker compared to the material of the masonry units, and failure occurs within the mortar) is larger, increasing the frictional reaction during horizontal loading and thus providing the masonry material with limited tensile strength. Mechanical interlocking along a crack is another positive effect of properly joint-staggered walls (Table A6).

Table A6.
Criteria for analysis of stagger properties of vertical (head) joints (VJ) (qualitative analysis).
Table A6.
Criteria for analysis of stagger properties of vertical (head) joints (VJ) (qualitative analysis).
| Vertically aligned head joints Vertically aligned head joints for at least 2 large stones Header bond (no stretchers) No mechanical interlocking between the stones | NF |
| Partially staggered head joints (head joints in successive courses are not offset by one-half the unit length) | PF |
| Properly staggered head joints (head joints in successive courses are offset by one-half the unit length) | F |
For the assessment of stagger properties of head joints (VJ), the authors also proposed a quantitative analysis [26], based on the calculation of “minimum length” Ml between two points. This can be calculated using a wall panel with dimensions of 1 m2 (Table A7, Figure A2).
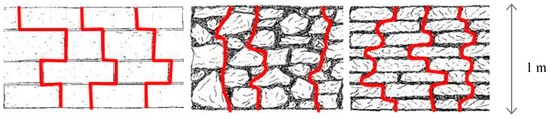
Figure A2.
Calculation method of Ml.

Table A7.
Criteria for analysis of stagger properties of vertical (head) joints (VJ) (quantitative analysis).
Table A7.
Criteria for analysis of stagger properties of vertical (head) joints (VJ) (quantitative analysis).
| Single-leaf wall: Ml < 1.4 | NF |
| Double-leaf wall: Ml > 1.4 for a wall leaf, Ml < 1.6 for the other | |
| Header boding pattern (brickwork masonry) | |
| Walls made of peddles or small stones | |
| No mechanical interlocking between the stones | |
| Single-leaf wall: 1.4 < Ml < 1.6 | PF |
| Double-leaf wall: | |
| (a) both wall leaves 1.4 < Ml < 1.6 (b) Ml > 1.6 for a wall leaf, Ml < 1.4 for the other (c) Ml > 1.6 for a wall leaf, 1.4 < Ml < 1.6 for the other | |
| Single-leaf wall: Ml > 1.6 | F |
| Double-leaf wall: Ml > 1.6 for both wall leaves |

Table A8.
Criteria for analysis of horizontality of mortar bed joints (HJ).
Table A8.
Criteria for analysis of horizontality of mortar bed joints (HJ).
| Bed joints not continuous | NF |
| Bed joints partially continuous | PF |
| For double-leaf wall: only one leaf with continuous bed joints | |
| Bed joints continuous | F |
| Stone masonry wall with bricks courses | |
| (distance between courses < 60 cm) |
Appendix A.1.6. Horizontality of Mortar Bed Joints (HJ Parameter)
Horizontal layers of mortar (bed joints), on which masonry units are laid, are typically used for walling. Depending on the type of masonry and construction technique, mortar layers are sometimes noncontinuous. This may highly affect the lateral and compressive strength of a masonry wall panel. Horizontal and continuous bed joints facilitate a uniform distribution of the vertical loads on the horizontal cross section of the wall. During earthquakes, the continuity and horizontality of bed joints allow the formation of cylindrical hinges, reducing damage from crumbling. A similar effect can be induced by courses of bricks placed at fixed interval in stonework walls. Finally, the horizontality of the bed joints maximizes the frictional reaction (at the contact surface between the block and the mortar), generated by vertical static loads (Table A8).
Appendix A.1.7. Mechanical Characteristics and Quality of Masonry Units (SM Parameter)
The SM parameter takes into account the conservation state and the mechanical properties of the bricks or stones. For unfired and mud bricks, the compressive strength is very low and the outcome is generally NF, while, for softstone masonry (tuff and sandstone), the outcome is typically PF.
The outcome is also NF for hollow bricks (less than 30% solid) or highly degraded stones. Pollution, water, radiation, inappropriate humidity, and temperature may reduce mechanical properties and cause material erosion. Parameter SM takes into account these problems including the common phenomenon of erosion of porous stones (sandstone, tuff, etc.). Table A9 gives the criteria for the identification of the outcome (NF, PF, or F) for stone, and solid and hollow brickwork masonry.

Table A9.
Criteria for analysis of stone/brick mechanical properties and conservation state (SM).
Table A9.
Criteria for analysis of stone/brick mechanical properties and conservation state (SM).
| Degraded/damaged elements (˃50% of total number of elements) | NF |
| Hollow-core bricks (solid < 30%) | |
| Mud bricks | |
| Unfired bricks | |
| Degraded/damaged elements (≥10%; ≤50%) | PF |
| Hollow bricks (55% ≥ solid ≥ 30%) | |
| Sandstone or tuff elements | |
| Undamaged elements or degraded/damaged elements < 10% | F |
| Solid fired bricks | |
| Hollow bricks (55% < solid) | |
| Concrete units | |
| Hardstones |
Appendix A.2. Brick and Stonework Walls
Some differentiations need to be used for the assessment and analysis of brickwork and stonework masonry. The structural response of brickwork and, in general, block masonry (i.e., squared stone masonry) is highly governed by the quality of the mortar. In detail, tangential and compressive strengths are affected by the characteristics of the used mortar. This has been also demonstrated in numerical simulations, and it is based on the following considerations:
- The bonding pattern used in brickwork masonry is very different from the one typically used in ashlar stone masonry. Brickwork masonry can fail without activating phenomena of mechanical interlocking between the bricks;
- The used mortar, although it can be good, is typically of lower mechanical properties compared to the bricks. Furthermore, the brick-to-mortar bonding is often weak. As a consequence, cracking principally occurs only in mortar joints or at the interface of mortar-to-bricks.
Similar phenomena do not occur in stone block (squared) masonry. For this type of masonry, the role of the mortar is to smooth the surface between two adjacent stone blocks. As a consequence, bed joints are typically very thin, and mechanical interlocking is normally activated under loading.
The analysis and formulation in the following sections will consider this differentiation in structural behaviour. A multiplication factor r (rV, rO, and rI, depending on the loading condition) is therefore used to reduce the MQI index. Clearly, this factor needs to be used only for brickwork masonry.
Appendix A.3. Calculation of the MQI Value
The weights given in Table A10 for each parameter have to be used in Equations (A1)–(A6). By doing this, it will be possible to find the value of the MQI index. To take into account the modifications recently introduced in the Italian Guidelines, Equations (A1)–(A6) have been revised and two new multiplication factors have been added:
- a multiplication factor m was added to take into account very-weak mortar quality; this should be applied, when needed, in Equations (A1)–(A6);
- another multiplication factor g was considered for thick bed joints in brickwork masonry or block masonry.
As a consequence, the following formulations should be used for the calculation of the MQI index:
For non-brickwork masonry and non-squared block masonry:
As it can be noted from Equations (A1)–(A3), the m and SM parameters are factored by the summation of the values assigned to the remaining six parameters to produce the value of the final index representing the quality of the masonry, MQI. The factor m was introduced in the original formulation of the MQI in order to take into account the quality of the mortar (for very-weak mortar (compressive strength fm < 0.7 MPa) m = 0.7, otherwise m = 1).

Table A10.
Numerical values of the 7 parameters for the calculation of the MQI.
Table A10.
Numerical values of the 7 parameters for the calculation of the MQI.
| Vertical Loading (V) | Horizontal in-Plane Loading (I) | Horizontal Out-of-Plane Loading (O) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NF | PF | F | NF | PF | F | NF | PF | F | |
| HJ | 0 | 1 | 2 | 0 | 0.5 | 1 | 0 | 1 | 2 |
| WC | 0 | 1 | 1 | 0 | 1 | 2 | 0 | 1.5 | 3 |
| SS | 0 | 1.5 | 3 | 0 | 1 | 2 | 0 | 1 | 2 |
| VJ | 0 | 0.5 | 1 | 0 | 1 | 2 | 0 | 0.5 | 1 |
| SD | 0 | 0.5 | 1 | 0 | 0.5 | 1 | 0 | 0.5 | 1 |
| MM | 0 | 0.5 | 2 | 0 | 1 | 2 | 0 | 0.5 | 1 |
| SM | 0.3 | 0.7 | 1 | 0.3 | 0.7 | 1 | 0.5 | 0.7 | 1 |
The mortar with outcome NF in the parameter MM will be considered “very weak” if the characteristics shown in Table A1 are very accentuated or are widespread on almost all walls.
For solid brickwork masonry and squared block masonry:
The multiplication factors rV, rO, and rI depend on the quality of the mortar and the loading condition. Table A11 reports the values these factors.

Table A11.
Multiplication factors rV, rO, and rI.
Table A11.
Multiplication factors rV, rO, and rI.
| Parameter MM | rV | rO | rI |
|---|---|---|---|
| NF | 0.2 | 1 | 0.1 |
| PF | 0.6 | 1 | 0.85 |
| F | 1 | 1 | 1 |
For thick bed joints (>13 mm), the factor is g = 0.7; otherwise, it is m = 1. It should be highlighted that the highest possible value of the MQI index, resulting from Equations (A1)–(A6), is 10, depending on the loading condition and masonry typology.
Appendix A.4. Determination of the Masonry Category
Once the MQI indexes are calculated and using Table A12, it is possible to find the masonry category for an investigated masonry. This also depends on the loading condition. By assigning the masonry category to an investigated masonry, it is possible to clearly define the most likely structural response of that masonry under the effect of different loading conditions.
In the following, we will consider the expected masonry structural response of a masonry classified in each masonry category. It was assumed that the acting loads are of a magnitude consistent with the expected ones for the investigated building and its site and location (i.e., standard service loading and design seismic action).

Table A12.
Range values of MQI in each masonry category.
Table A12.
Range values of MQI in each masonry category.
| Masonry Category | |||
|---|---|---|---|
| A | B | C | |
| Vertical Loads (V) | 5 ≤ MQIV ≤ 10 | 2.5 ≤ MQIV < 5 | 0 ≤ MQIV< 2.5 |
| Out-of-plane (O) | 7 ≤ MQIO ≤ 10 | 4 < MQIO < 7 | 0 ≤ MQIO ≤ 4 |
| In-plane (I) | 5 < MQII ≤ 10 | 3 < MQII ≤ 5 | 0 ≤ MQII ≤ 3 |
Appendix A.4.1. Vertical Loading
- A masonry wall in category A very unlikely will fail;
- A masonry wall in category B may crack, but its collapse is rare;
- A masonry wall in category C will likely crack under the effect of vertical loading.
Phenomena of out-of-plane rocking are possible as well for high vertical loads, failures, and collapses.
Appendix A.4.2. Out-of-Plane Loading
- A masonry wall in category A is able to exhibit a rigid deformation behaviour under the action of out-of-plane horizontal actions. If its wall leaves are properly mutually connected and the connection between the walls and the horizontal diaphragms (i.e., floors) are effective, the chances to crack or to fail are very limited. Seismic analyses using the macroelement method can be made by assuming a rigid structural response of the walls.
- A masonry wall in category B cannot deform rigidly, and it is likely that cracking and debonding of masonry wall leaves will occur. However, if wall-to-floor and wall-to-wall connections are effective, it is unlikely this will fail. Seismic analyses using the method of kinematic chains of wall macroelements can be used, but it is suggested to assume an ineffective connection between wall leaves (unconnected wall leaves) in the calculations.
- A masonry wall in category C will very likely disaggregate under the action of a quake; failure is common, and given the low masonry quality, the assessment of the level of connection between wall leaves and with the floors is not critical. The use of the analysis method of kinematic chains of wall macroelements is not able to simulate the actual behaviour of a wall in category C under the effect of a seismic action.
Appendix A.4.3. In-Plane Loading
- A masonry wall in category A will unlikely crack.
- Under the action of an earthquake, a masonry wall in category B will likely crack, especially when the shear walls are thin or their surface falls short of the dimensions of the building. However, these cracks will be unlikely serious.
- For a masonry wall in category C, cracking is very likely. Shear cracks will be often serious and thick.
Appendix A.4.4. Relationship between MQI Index and Masonry Mechanical Properties
To calculate the relationships between the MQI values and the most important mechanical parameters of the masonry, the masonry typologies suggested by the Italian Guidelines [20], given in Table C8.5.I, have been considered. Using the multiplication factors provided by the Guidelines at Table C8.5.II and considering the different combinations between the masonry typologies and the possible variations given by the multiplication factors, we could ideally construct 74 virtual walls.
For each virtual wall, the Italian Guidelines provide 5 mechanical parameters (f (compressive strength), τ0 (shear strength, failure mode I, according to Turnšek and Čačovič [30]), fV0 (shear strength, failure mode II—stepped (zig-zag) failure mode) G (shear modulus), and E (Young’s modulus)). For each mechanical parameter, the Italian guidelines report a maximum and minimum value.
The following relationships were calculated and calibrated: MQIV vs. f, MQII vs. τ0, MQII vs. fV0, MQII vs. G, and MQIV vs. E. Figure A3, Figure A4, Figure A5, Figure A6 and Figure A7 show the plots: it can be noted that relationship curves are exponential or parabolic. For each plot, 3 trend curves have been calculated using the minimum, mean, and maximum values of f, τ0, fV0, G, and E. Figure A3, Figure A4, Figure A5, Figure A6 and Figure A7 show the mean trend lines of the 5 mechanical parameters vs. MQI value.
The trend curves are given below together with the values of the coefficients of determination R2. The equations of the trend curves are the following:
For the estimation of the masonry shear strength τ0, failure mode I [30]:
τ0 min = 0.0004 (MQII)2 + 0.0055 (MQII) + 0.0173 R² = 0.825
τ0 mean = 0.0006 (MQII)2 + 0.0075 (MQII) + 0.0224 R² = 0.913
τ0 max = 0.0008 (MQII)2 + 0.0094 (MQII) + 0.0275 R² = 0.843
For the estimation of the masonry Young’s modulus E:
E min = 608 e0.154 (MQIV) R² = 0.709
E mean = 742.1 e0.153 (MQIV) R² = 0.720
E max = 876 e0.151 (MQIV) R² = 0.724
For the estimation of the masonry compressive strength f:
f min = 1.055 e 0.193 (MQIV) R² = 0.803
f mean = 1.444 e 0.182 (MQIV) R² = 0.824
f max = 1.892 e 0.175 (MQIV) R² = 0.828
For the estimation of the masonry shear modulus G:
G min = 201.4 e 0.142 (MQII) R² = 0.652
G mean = 254.6 e 0.141 ((MQII) R² = 0.680
G max = 298.7 e 0.141 (MQII) R² = 0.695
For the estimation of shear strength fV0, failure mode II (stepped or zig-zag failure mode):
fV0 min = 0.03 MQII0.909 R² = 0.893
fV0 mean = 0.0475 MQII0.854 R² = 0.928
fV0 max = 0.0654 MQII0.822 R² = 0.918
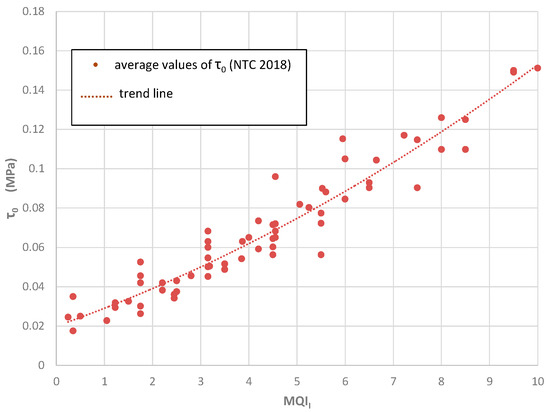
Figure A3.
Masonry shear strength τ0 vs. MQII (NTC 2018, Italian Seismic Code, 2018).
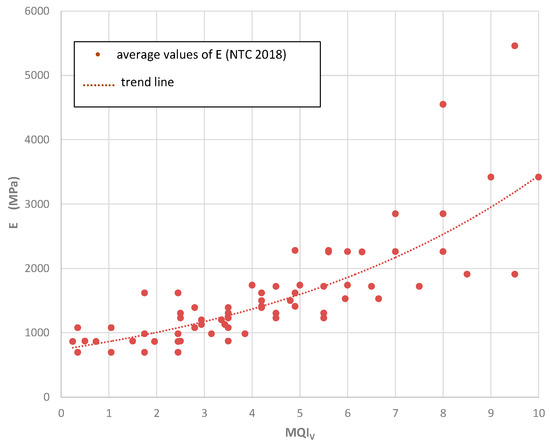
Figure A4.
Masonry Young’s modulus E vs. MQIV.
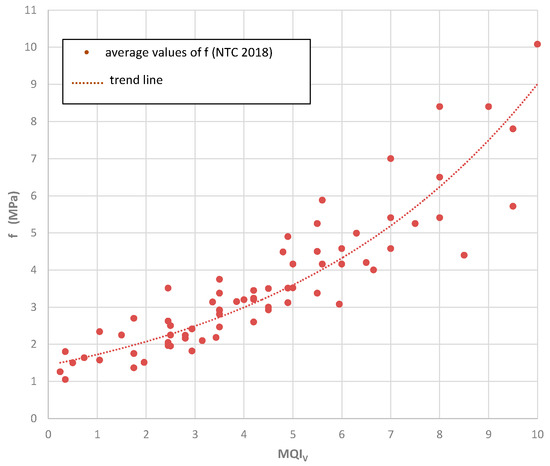
Figure A5.
Masonry compressive strength f vs. MQIV.
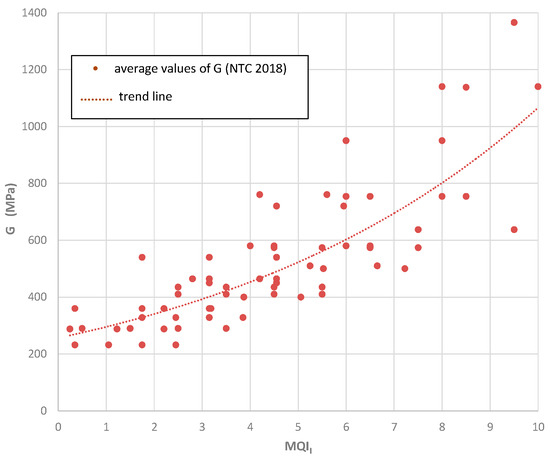
Figure A6.
Masonry shear modulus G vs. MQII.
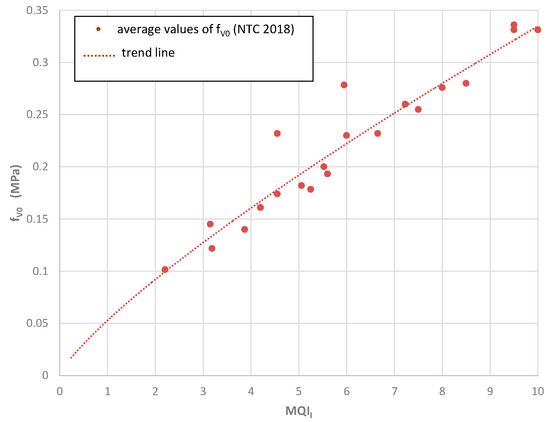
Figure A7.
Masonry shear strength fV0 vs. MQII.
Appendix A.5. Experimental Calibration of the MQI Method
To calibrate the proposed visual method, available experimental evidence has been used. In detail, particular emphasis was devoted to the relationship between the MQII and the available test results in terms of masonry shear strength τ0. This mechanical parameter is fundamental to assess the seismic behaviour of existing masonry buildings (pushover analysis).
Sixty experimental results of diagonal tension tests have been used for calibration purposes. These tests (55 conducted on-site and 5 in the laboratory) have been carried out on full-scale wall panels (1.2 × 1.2 m). Tests used for calibration were carried out at the University of Perugia, Florence and Trieste. On-site testing was performed in buildings located in Italy (Umbria, Abruzzi, Emilia Romagna, and Tuscany regions). In Figure A8, shear strength values τ0 from on-site testing [31,32] are correlated with MQII values. It can be noted that the MQI method is able to provide an adequate estimation of the masonry shear strength: most experimental results fall in between the two upper and lower bound curves of the suggested τ0 vs. MQII relationship.
Finally, to improve reading comprehension and the methodological approach, Figure A9 shows a flow chart of the MQI method for the three different loading conditions (vertical, in-plane, and out-of-plane loading). The analysis begins with the visual analysis of a wall panel and ends with the identification of masonry categories (A, B, or C, Table A12) and the corresponding estimation of the mechanical properties.
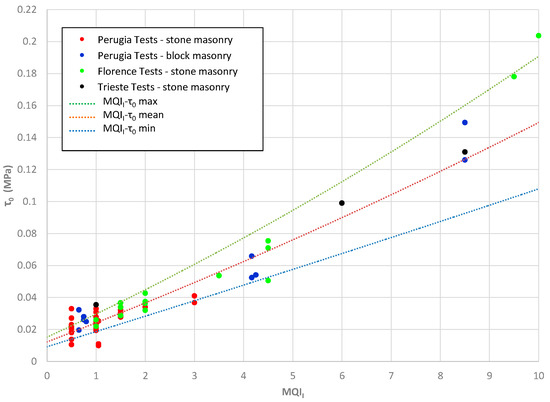
Figure A8.
MQII vs. shear strength τ0: experimental results are compared with suggested relationships.
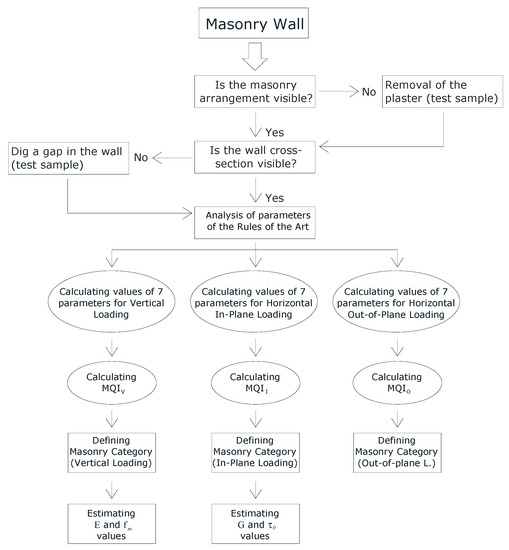
Figure A9.
Scheme of the MQI methodology.
References
- Rovero, L.; Fratini, F. The Medina of Chefchaouen (Morocco): A survey on morphological and mechanical features of the masonries. Constr. Build. Mater. 2013, 47, 465–479. [Google Scholar] [CrossRef]
- Rota, M.; Penna, A.; Magenes, G. A framework for the seismic assessment of existing masonry buildings accounting for different sources of uncertainty. Earthq. Eng. Struct. Dyn. 2014, 43, 1045–1066. [Google Scholar] [CrossRef]
- Penna, A.; Calderini, C.; Sorrentino, L.; Carocci, C.F.; Cescatti, E.; Sisti, R.; Borri, A.; Modena, C.; Prota, A. Damage to churches in the 2016 central Italy earthquakes. Bull. Earthq. Eng. 2019, 17, 5763–5790. [Google Scholar] [CrossRef]
- Schuller, M.P.; Atkinson, R.H.; Noland, J.L. Structural evaluation of historic masonry buildings. APT Bull. 1995, 26, 51–61. [Google Scholar] [CrossRef]
- Valluzzi, M.R.; Da Porto, F.; Modena, C. Behavior and modeling of strengthened three-leaf stone masonry walls. Mater. Struct. 2004, 37, 184–192. [Google Scholar] [CrossRef]
- Pagnini, L.C.; Vicente, R.; Lagomarsino, S.; Varum, H. A mechanical model for the seismic vulnerability assessment of old masonry buildings. Earthq. Struct. 2011, 2, 25–42. [Google Scholar] [CrossRef]
- Chiostrini, S.; Vignoli, A. In-situ determination of the strength properties of masonry walls by destructive shear and compression tests. Mason. Int. 1993, 7, 87–96. [Google Scholar]
- Binda, L.; Saisi, A.; Tiraboschi, C. Investigation procedures for the diagnosis of historic masonries. Constr. Build. Mater. 2000, 14, 199–233. [Google Scholar] [CrossRef]
- Borri, A.; Castori, G.; Corradi, M.; Speranzini, E. Shear behavior of unreinforced and reinforced masonry panels subjected to in-situ diagonal compression tests. Constr. Build. Mater. 2011, 25, 4403–4414. [Google Scholar] [CrossRef]
- Mariani, M.; Pugi, F.; Francioso, A. Sisma Verticale: Modellazione e Analisi in Ambito Professionale Sugli Edifici Esistenti in Muratura. Available online: https://www.ingenio-web.it/22185-sisma-verticale-modellazione-e-analisi-in-ambito-professionale-sugli-edifici-esistenti-in-muratura (accessed on 13 September 2020).
- Borri, A.; Castori, G.; Corradi, M. Determination of shear strength of masonry panels through different tests. Int. J. Archit. Herit. 2015, 9, 913–927. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Castori, G.; Sisti, R.; De Maria, A. Analysis of the collapse mechanisms of medieval churches struck by the 2016 Umbrian earthquake. Int. J. Archit. Herit. 2019, 13, 215–228. [Google Scholar] [CrossRef]
- ReLUIS WP1_1-1_2015UNlPG; Report of the University of Perugia; University of Perugia: Perugia, Italy, 2015.
- D’Ayala, D.F.; Paganoni, S. Assessment and analysis of damage in L’Aquila historic city centre after 6th April 2009. Bull. Earthq. Eng. 2011, 9, 81–104. [Google Scholar] [CrossRef]
- Corradi, M.; Borri, A.; Vignoli, A. Experimental study on the determination of strength of masonry walls. Constr. Build. Mater. 2003, 17, 325–337. [Google Scholar] [CrossRef]
- Corradi, M.; Osofero, A.I.; Coventry, K.; Richardson, A.E.; Udeaja, C.; Vo, T. Analysis and classification of historic construction within the north-east of England. In Proceedings of the 15th International Conference Structural Faults & Repair, London, UK, 8–10 July 2014. [Google Scholar]
- Fonti, R. On the reading of the structural behavior of old masonry: The issue of the seismic assessment of archeological ruins. In Proceedings of the International Conference of Computational Methods in Sciences and Engineering (ICCMSE) 2016, Athens, Greece, 17–20 March 2016; AIP Publishing LLC: Melville, NY, USA, 2016. [Google Scholar]
- Sisti, R.; Di Ludovico, M.; Borri, A.; Prota, A. Damage assessment and the effectiveness of prevention: The response of ordinary unreinforced masonry buildings in Norcia during the Central Italy 2016–2017 seismic sequence. Bull. Earthq. Eng. 2019, 17, 5609–5629. [Google Scholar] [CrossRef]
- Italian Seimic Code 2018, Act (D.M.) 17.01.2018, Aggiornamento delle Norme Tecniche per le Costruzioni. G.U. n. 42, 20 February 2018. Available online: file:///C:/Users/ALEXAN~1/AppData/Local/Temp/20180220_042_SO_008.pdf (accessed on 22 October 2020).
- Italian Seimic Code, Guidelines, 21 Jan. 2019, n. 7 CSLL. Istruzioni per L’applicazione dell’ Aggiornamento delle “Norme Tecniche per le Costruzioni”. Available online: http://www.cngeologi.it/wp-content/uploads/2019/02/Circolare-21-gennaio-2019-n.-7.pdf (accessed on 22 October 2020).
- Borri, A.; De Maria, A. Scheda di Valutazione dell’IQM (Indice di Qualità Muraria); Rete dei Laboratori Universitari di Ingegneria Sismica (RELUIS): Naples, Italy, 2009. [Google Scholar]
- Giuffrè, A. Lettura Sulla Meccanica delle Murature Storiche; Kappa: Rome, Italy, 1991. [Google Scholar]
- Lagomarsino, S.; Podestà, S. Seismic vulnerability of ancient churches: II. Statistical analysis of surveyed data and methods for risk analysis. Earthq. Spectra 2004, 20, 395–412. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Mendesa, N.; Ramosa, L.F.; Oliveira, D.V. Analysis of masonry structures without box behavior. Int. J. Archit. Herit. 2011, 5, 369–382. [Google Scholar] [CrossRef]
- Borri, A.; De Maria, A.; Marino, M.; Neri, F. Experimental data of friction coefficient for some types of masonry and its correlation with an index of quality masonry (IQM). In Proceedings of the 2nd European Conference of Earthquake Engineering and Seismology, Istanbul, Turkey, 25–19 August 2014. [Google Scholar]
- Borri, A.; Castori, G.; Corradi, M.; De Maria, A. A method for the analysis and classification of historic masonry. Bull. Earthq. Eng. 2015, 13, 2647–2665. [Google Scholar] [CrossRef]
- Rondelet, J.B. Traité Théorique et Pratique de Lart de Batir; A Rondelet Fils: Paris, France, 1831. [Google Scholar]
- Aisa, E.; Bernardini, F.; Cittadini, M.; Daniele, L.; De Maria, A.; De Sortis, A.; Fagotti, G.; Nasini, U.; Tanci, M.; Santantoni, M.; et al. Onna prima e dopo il terremoto del 6 aprile 2009—Parte I: Analisi del danno; Provincia di Perugia: Perugia, Italy.
- Borri, A.; Corradi, M.; Sisti, R.; De Maria, A. Calibration of a visual method for the analysis of the mechanical properties of historic masonry. Int. J. Struct. Integr. 2018, 11, 418–427. [Google Scholar] [CrossRef]
- Turnšek, V.; Čačovič, F. Some experimental results on the strength of brick masonry walls. In Proceedings of the 2nd International Brick Masonry Conference, Stoke on Trent, UK, 12–15 April 1970; pp. 149–156. [Google Scholar]
- Standard Test Method for Diagonal Tension (Shear) in Masonry Assemblages; ASTM E519; ASTM International: West Conshohocken, PA, USA, 2010.
- RILEM TC 76-LUM: General recommendations for methods of testing load-bearing masonry. Mater. Struct. 1991, 21, 227–231.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).