Aesthetical Issues of Leonardo Da Vinci’s and Pablo Picasso’s Paintings with Stochastic Evaluation
Abstract
1. Introduction
2. Methodology
2.1. Stochastic Analysis in 2D
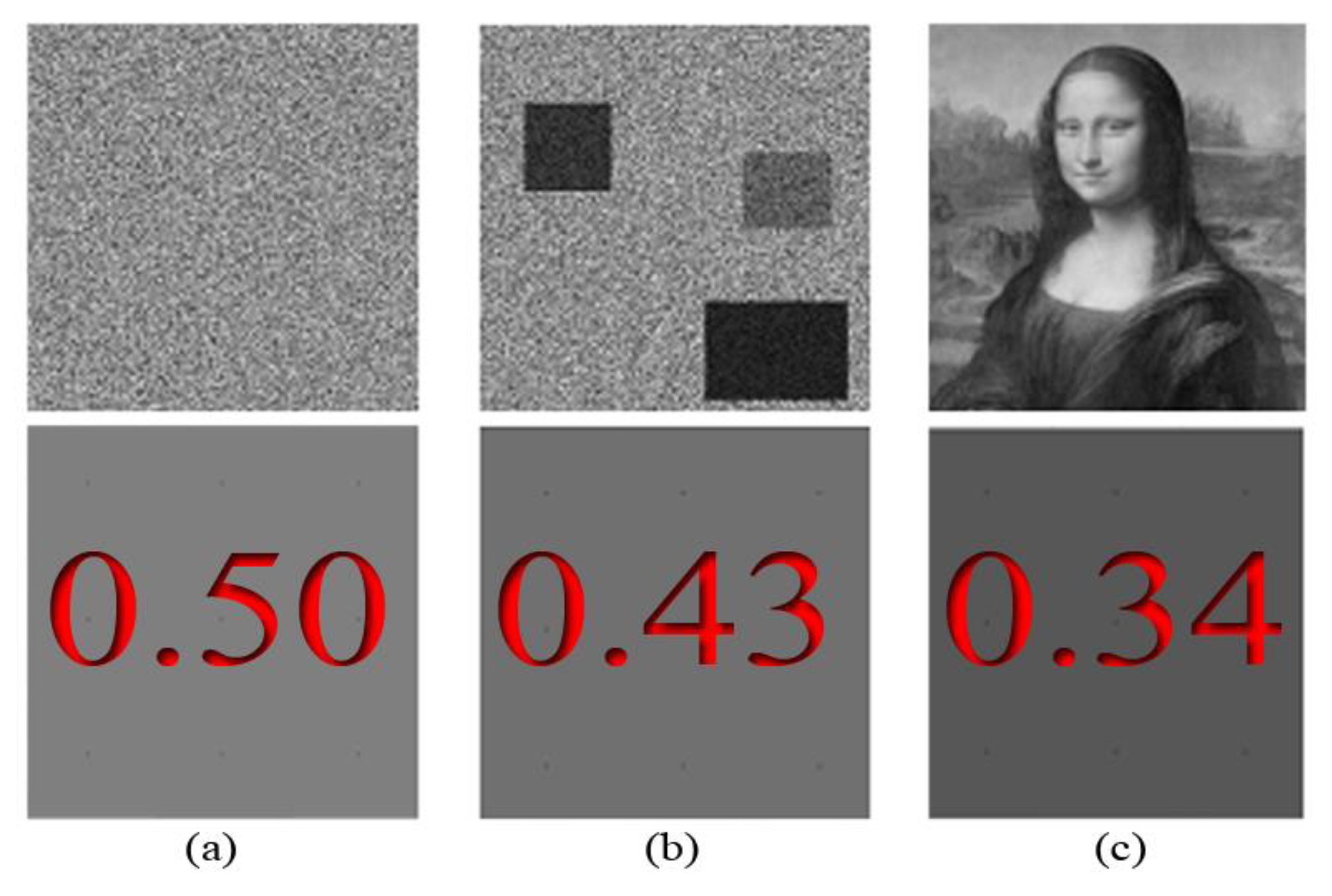
2.2. Illustration of Stochastic Analysis in 2D
3. Stochastic Analysis of the Art Paintings
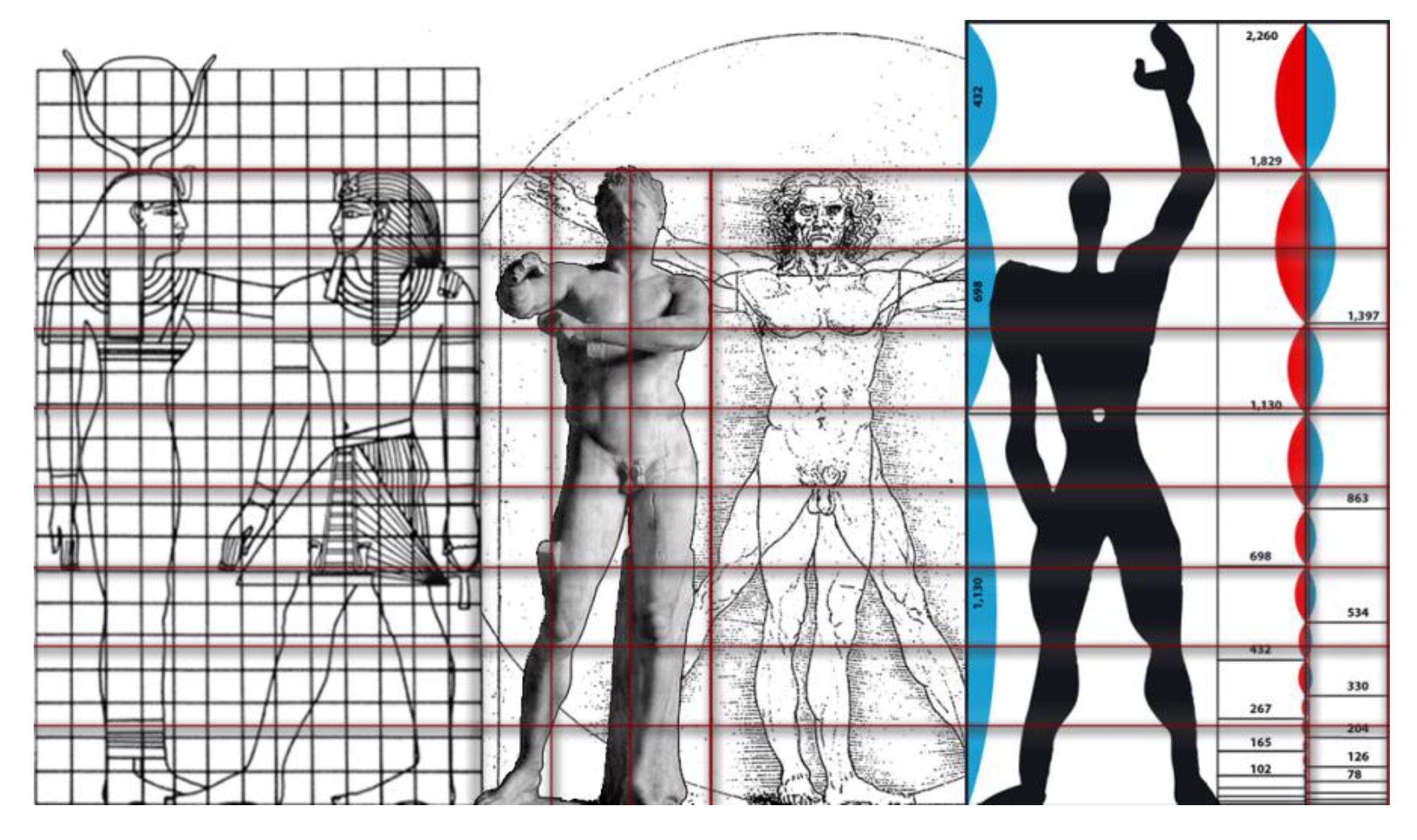
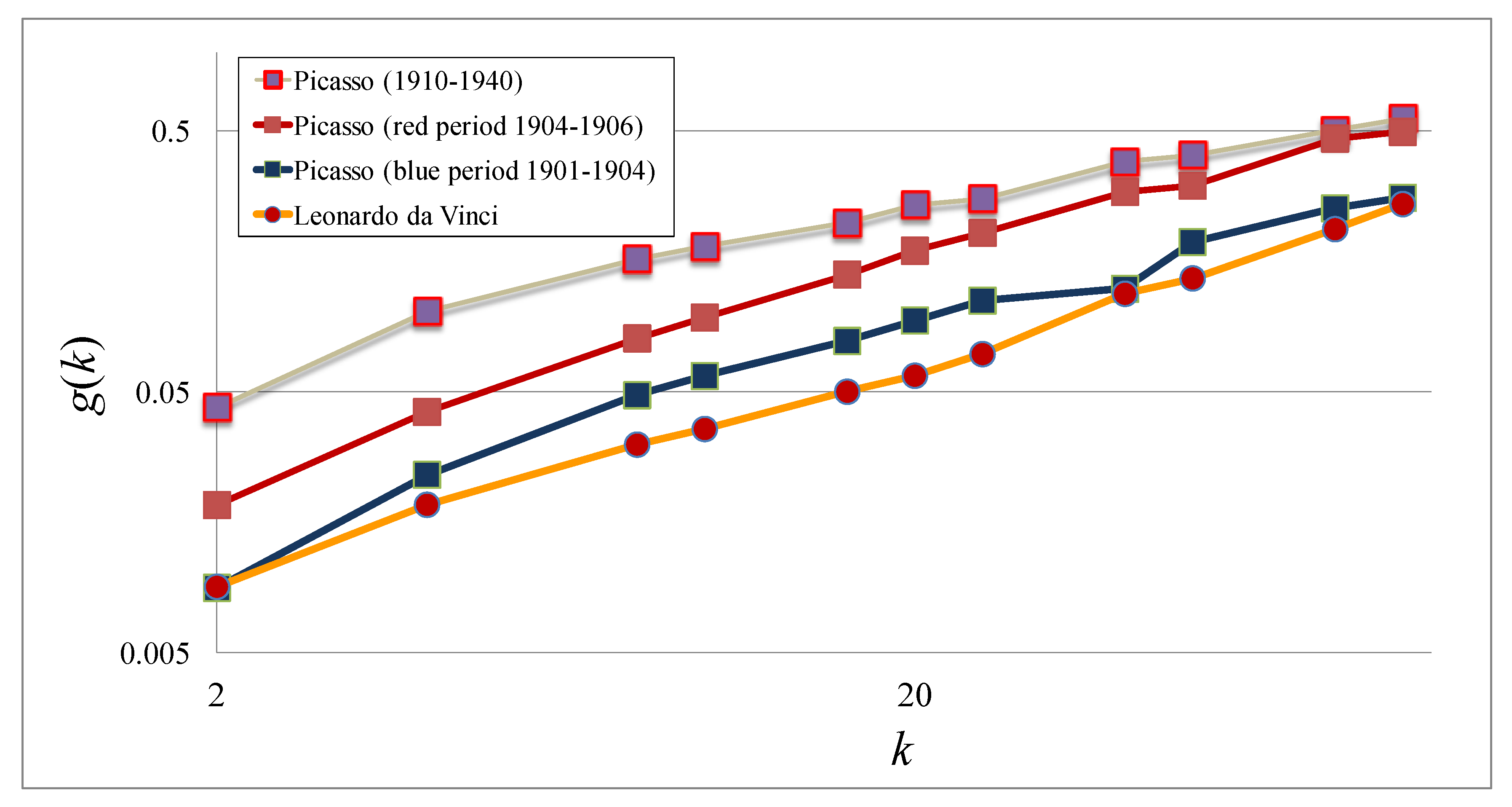
3.1. Stochastic Analysis of the Art Paintings of Leonardo da Vinci (1452–1519) and Pablo Picasso (1881–1973)
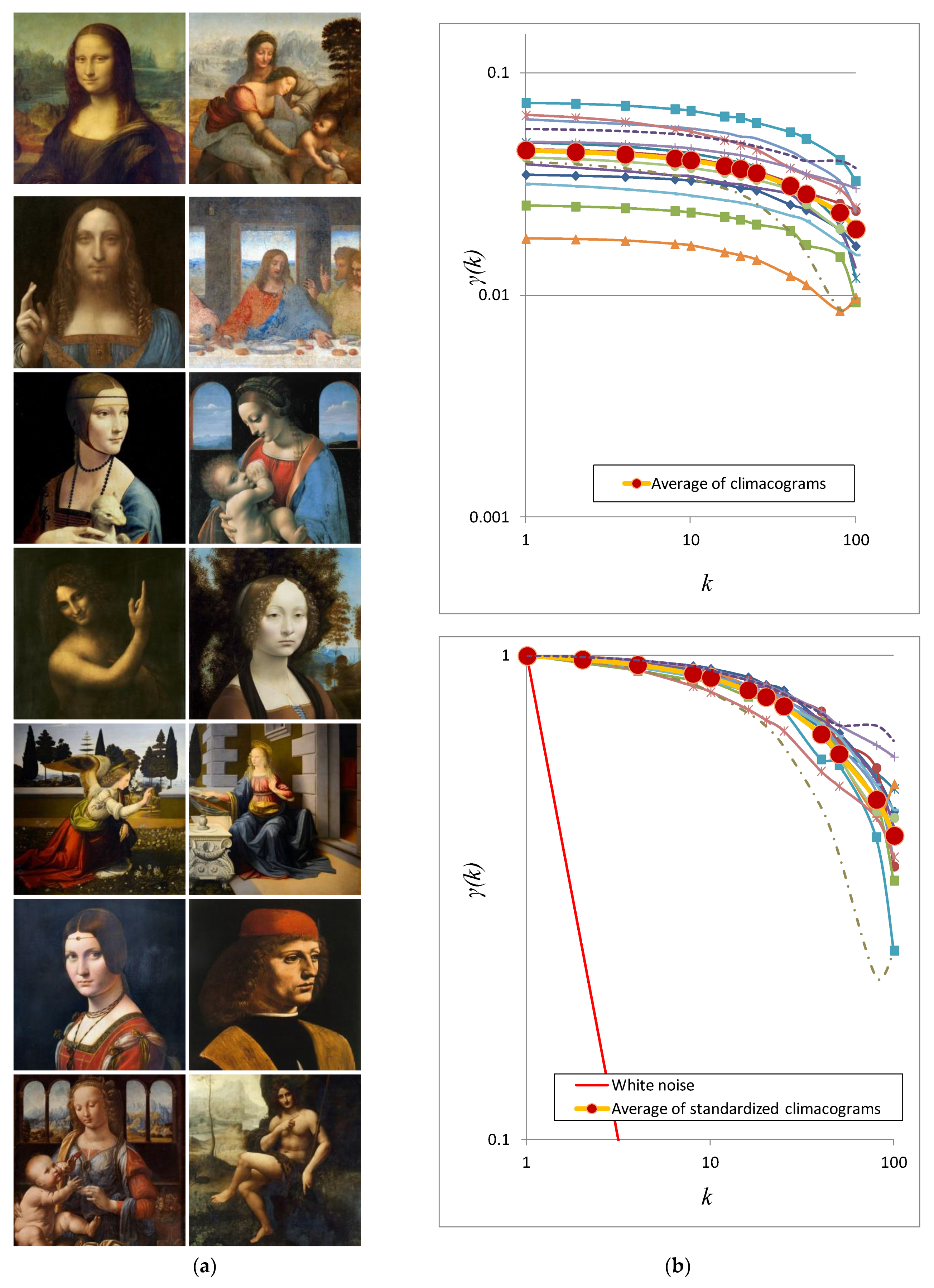
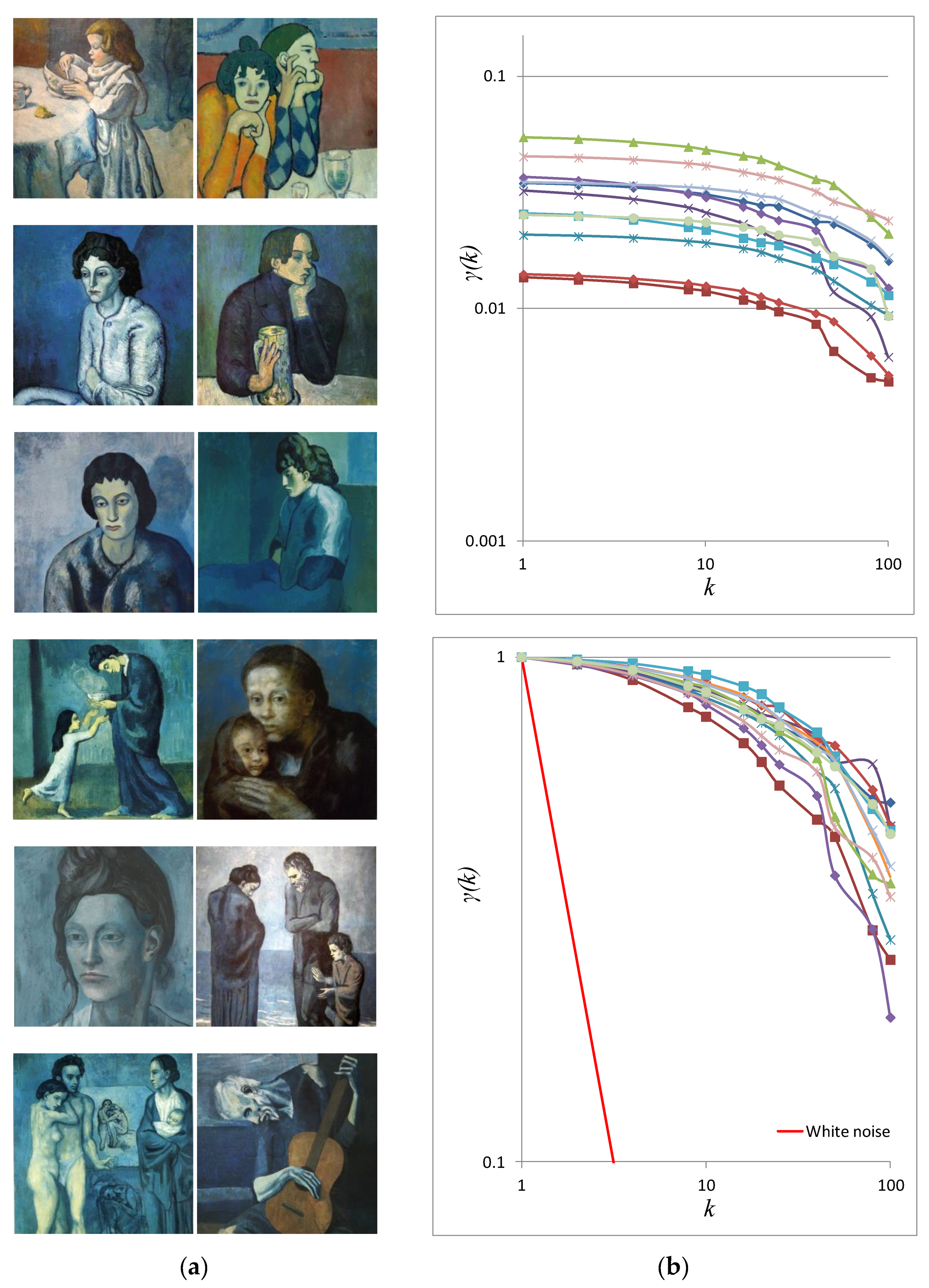
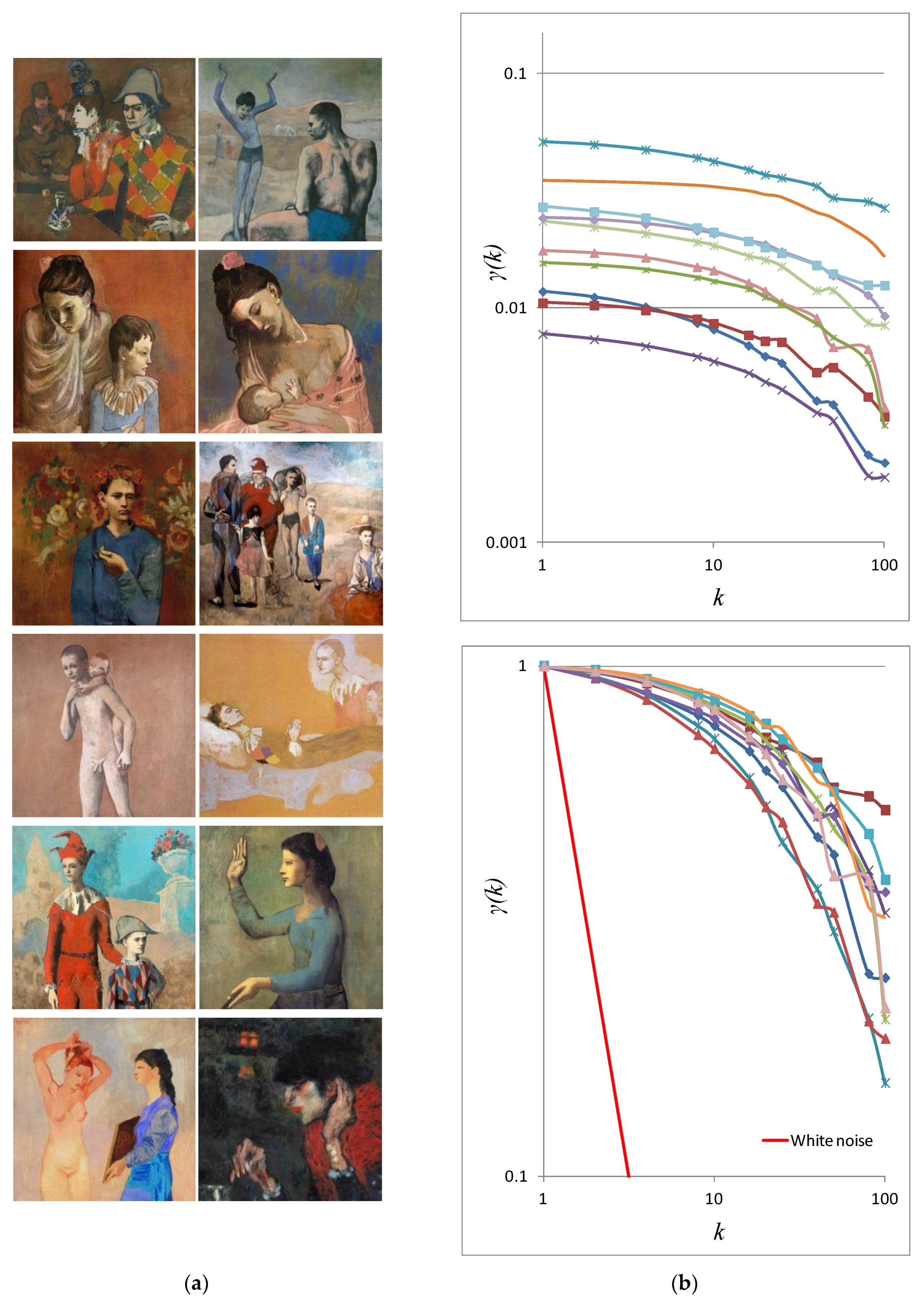
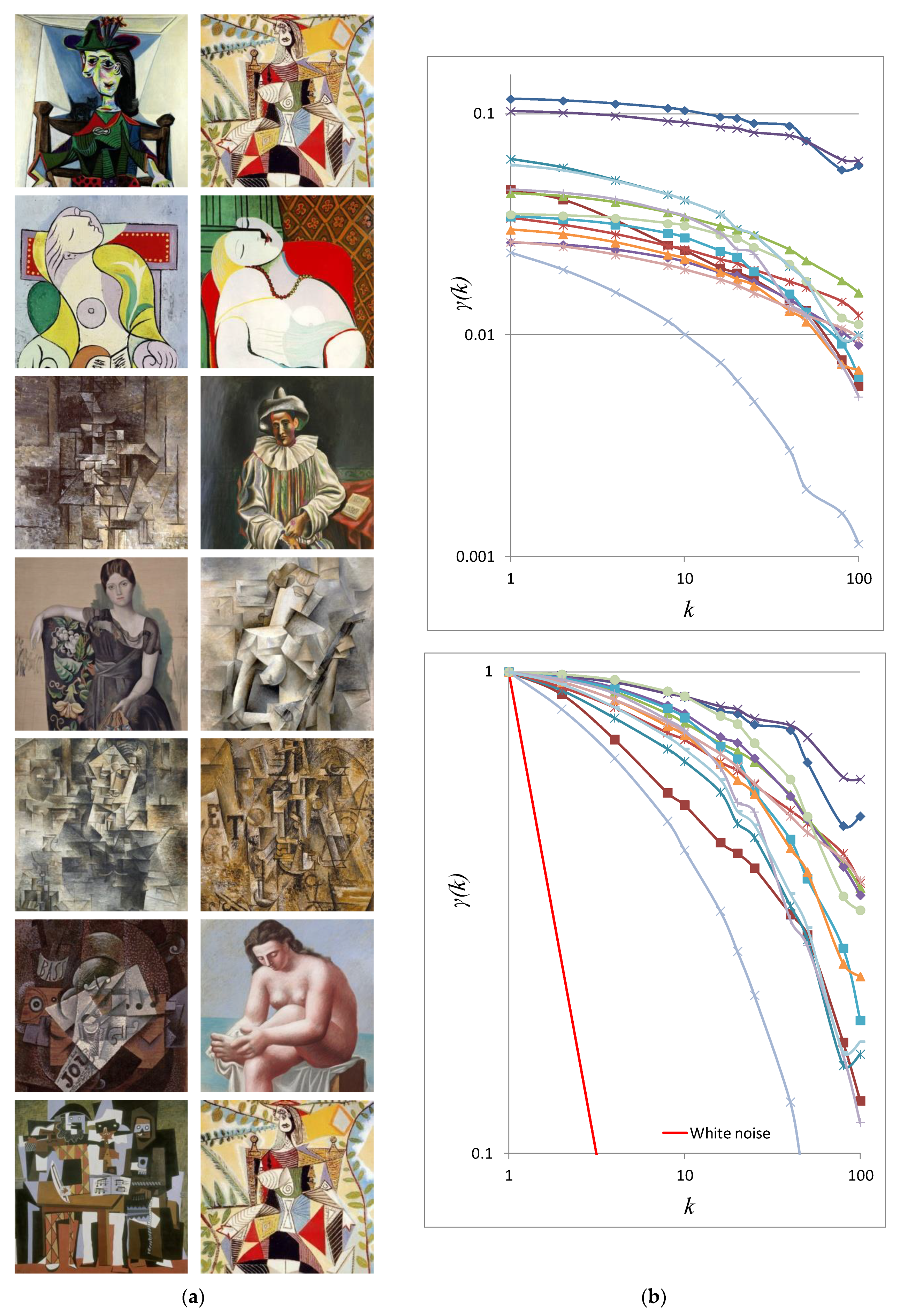
3.2. Stochastic Analysis of of Da Vinci’s Last Supper (1495)
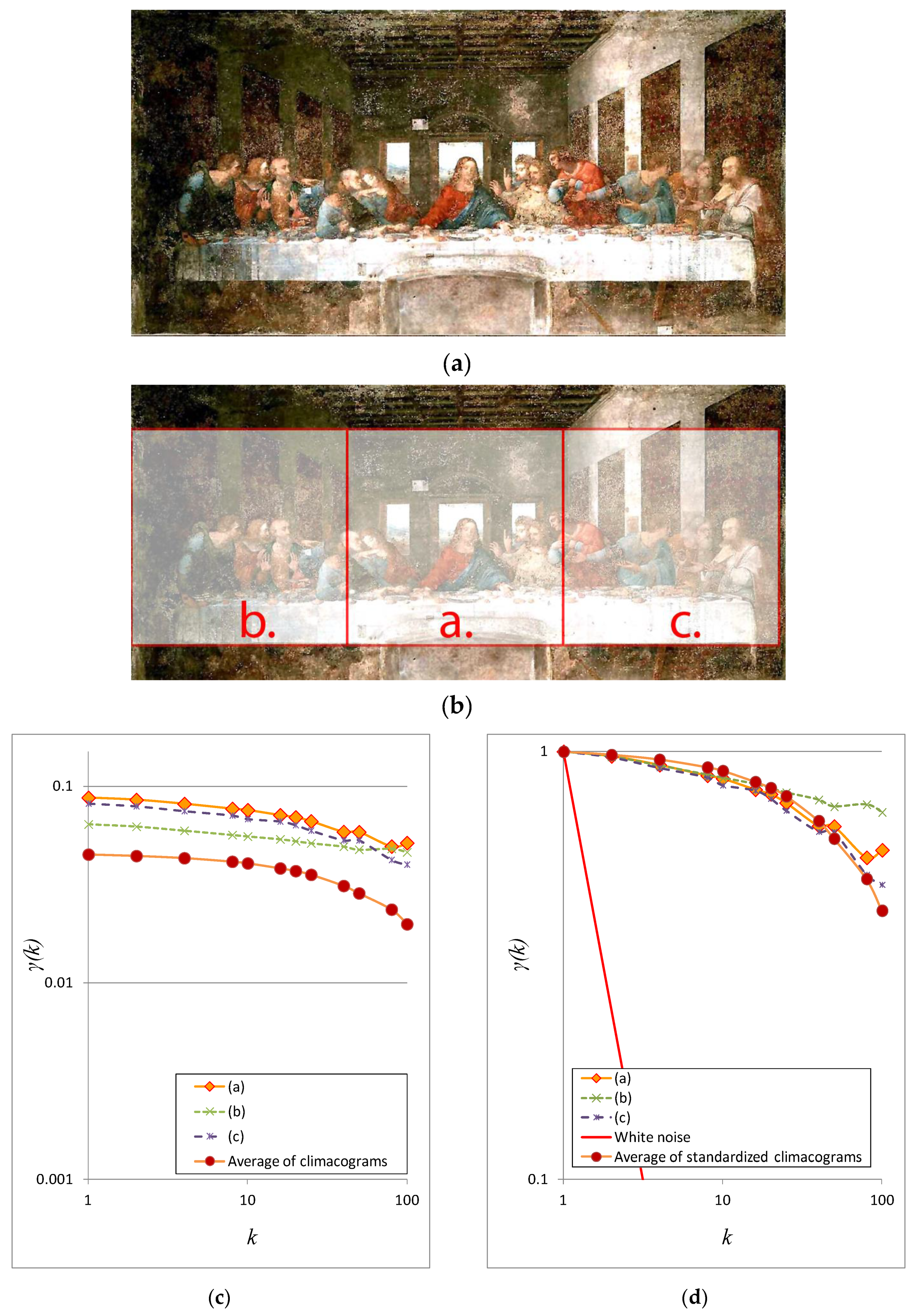
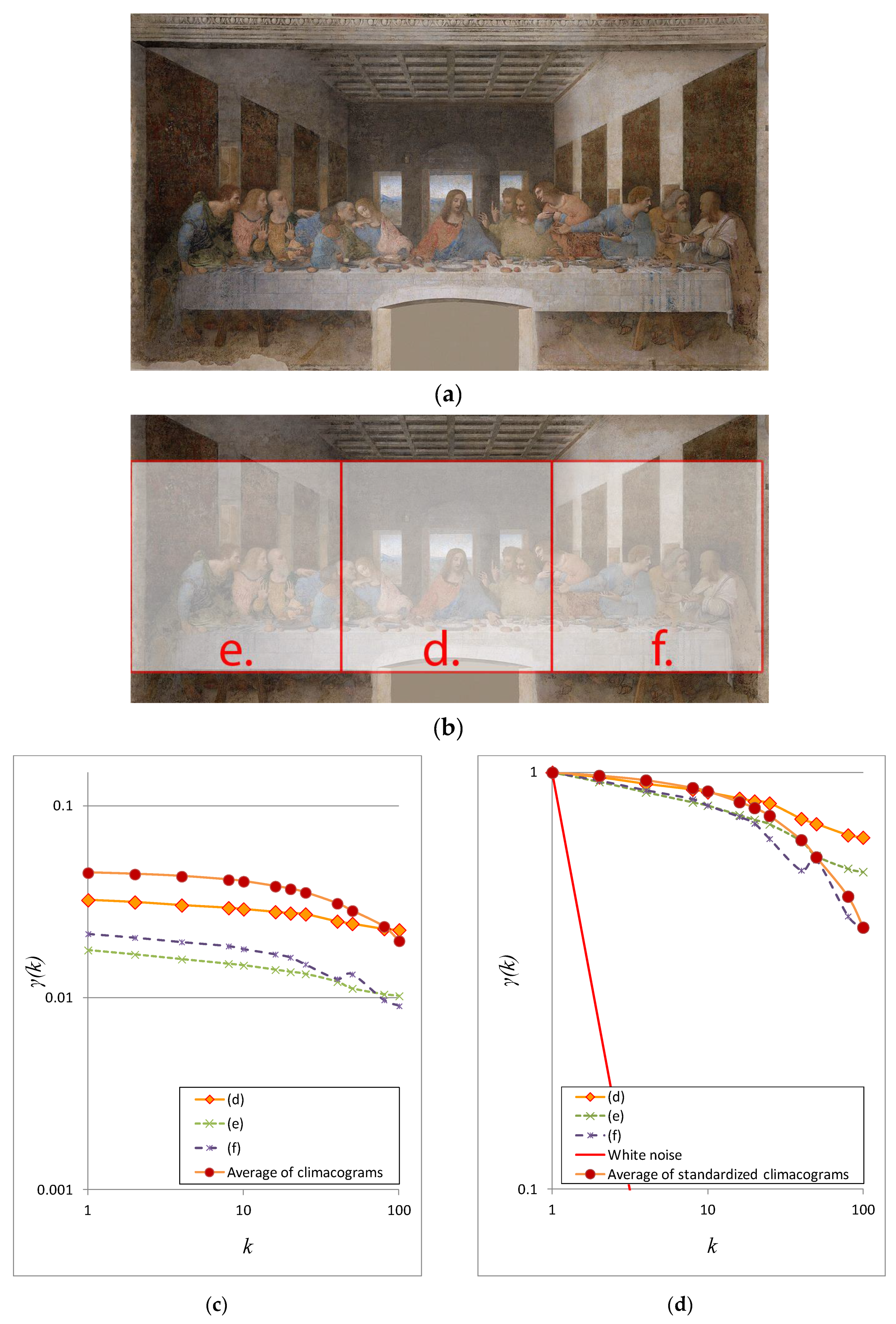
3.3. Stochastic Analysis of Da Vinci’s Annunciation (1472–1475)

3.4. Stochastic Analysis of Da Vinci’s Virgin of the Rocks (1483–1486 and before 1508)



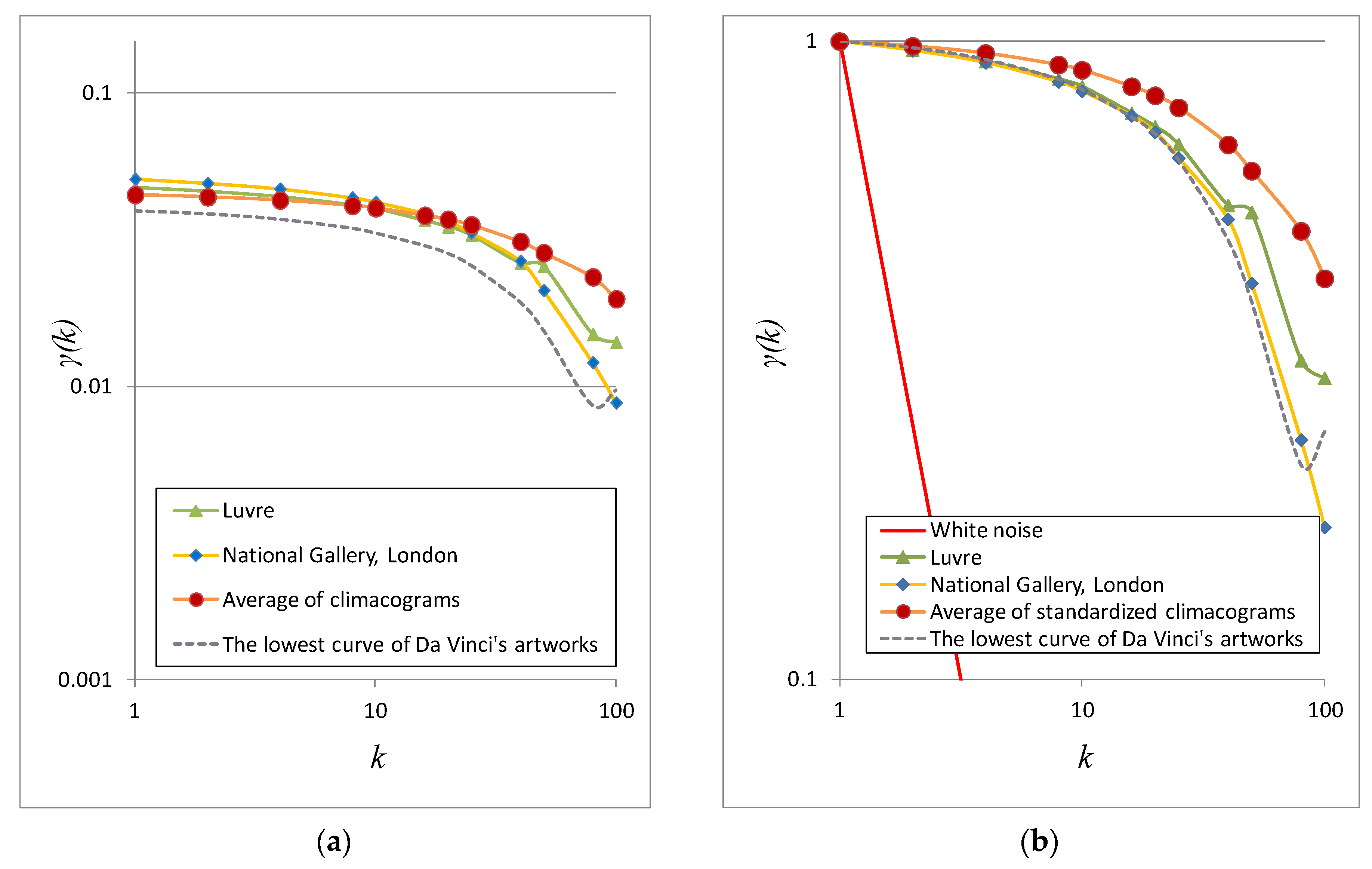
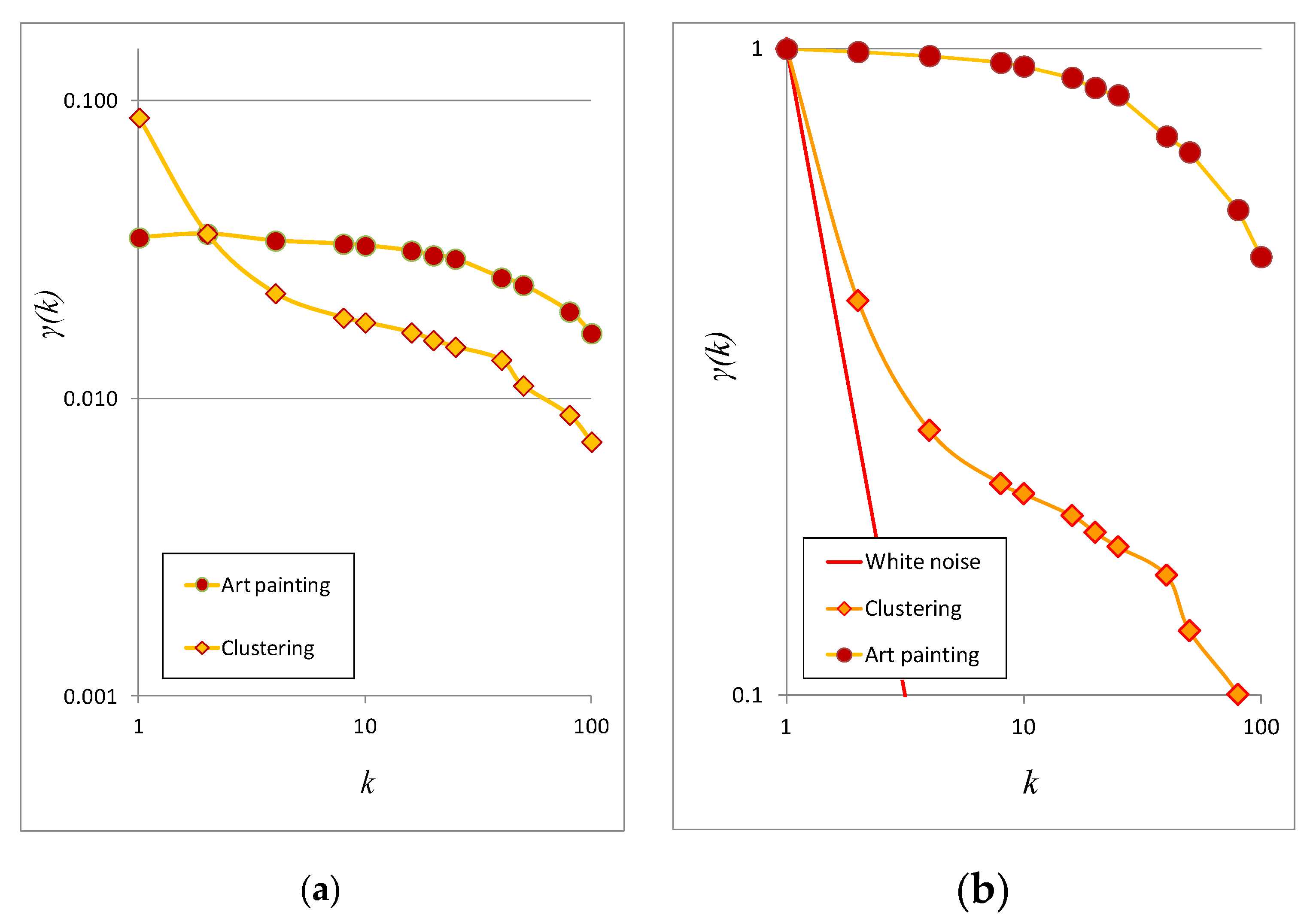
4. Discussion of Stochastic Evaluation
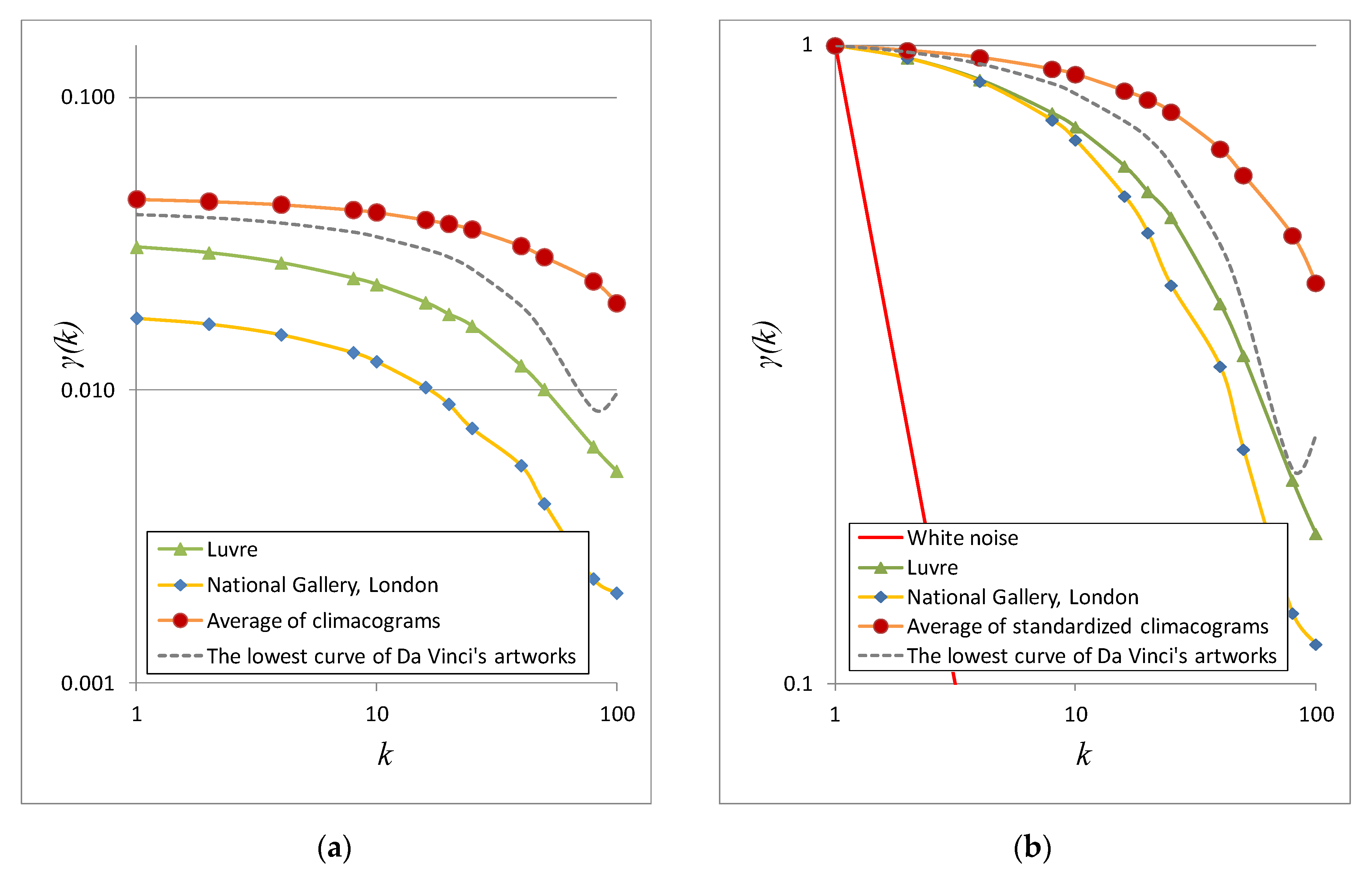
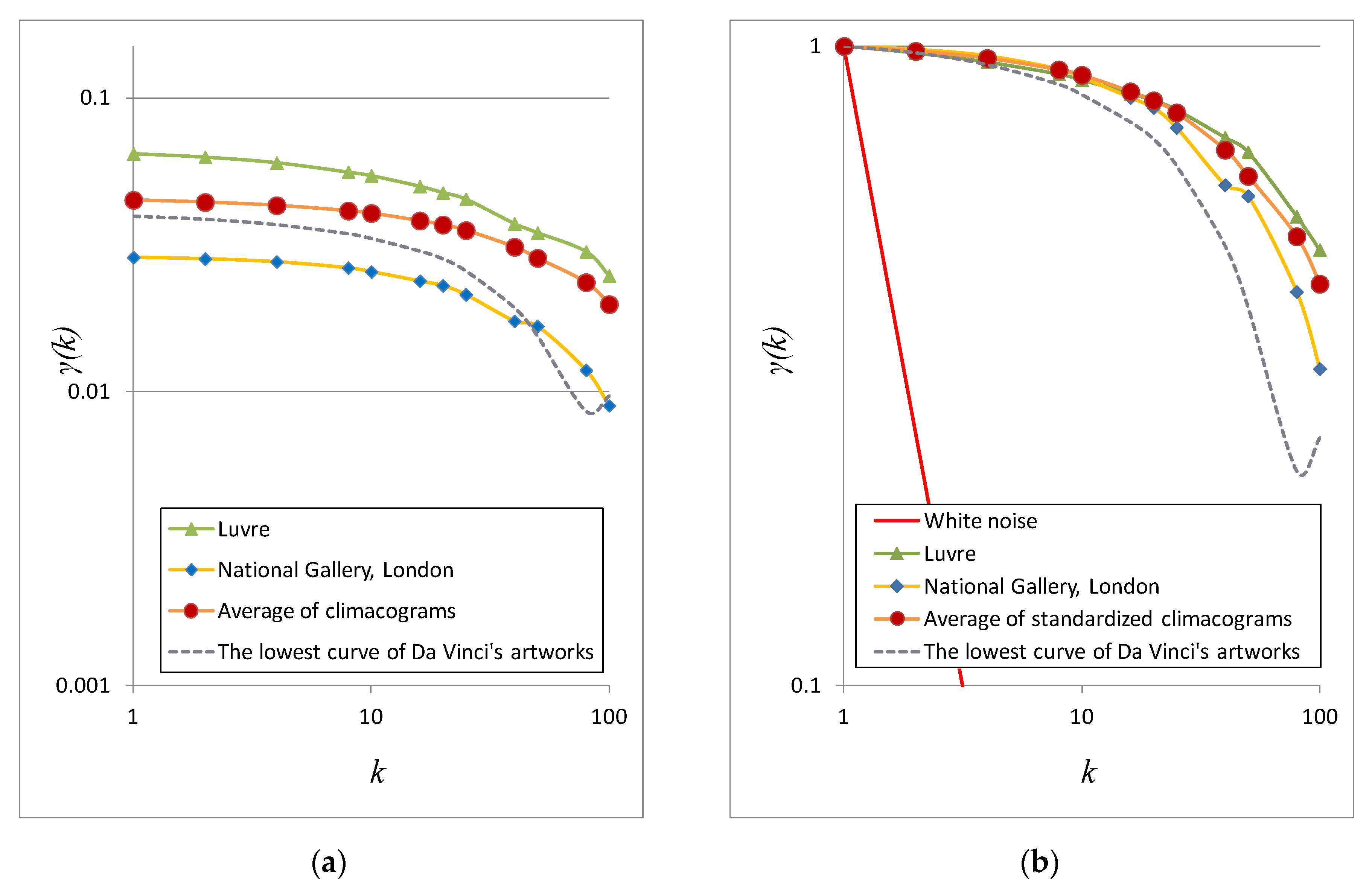
4.1. Stochastic Evaluation of Da Vinci’s and Picasso’s Art Paintings
4.2. Stochastic Evaluation of the Restoration of Da Vinci’s Last Supper
4.3. Stochastic Evaluation of Da Vinci’s Annunciation
4.4. Stochastic Evaluation of Da Vinci’s Virgin of the Rocks
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bullot, N.J.; Seeley, W.P.; Davies, S. Art and Science: A Philosophical Sketch of Their Historical Complexity and Codependence. J. Aesthet. Art Crit. 2017, 75, 453–463. [Google Scholar] [CrossRef]
- Robins, G. Proportion and Style in Ancient Egyptian Art; University of Texas Press: Austin, TX, USA, 1994. [Google Scholar]
- The Sculptor’s Funeral. Available online: www.thesculptorsfuneral.com/episode-05-canons-of-proportion/ (accessed on 21 April 2020).
- Canons of Proportion and the Laws of Nature: Observations on a Permanent and Unresolved Conflict. Arch. Hist. 2014, 2, 19. [CrossRef]
- Riedel, T. Encyclopedia of Aesthetics. Art Doc. J. Art Libr. Soc. N. Am. 1999, 18, 48. [Google Scholar] [CrossRef]
- Thapa, G.B.; Thapa, R. The Relation of Golden Ratio, Mathematics and Aesthetics. J. Inst. Eng. 2018, 14, 188–199. [Google Scholar] [CrossRef]
- Schreiber, P. A Supplement to J. Shallit’s Paper “Origins of the Analysis of the Euclidean Algorithm”. Hist. Math. 1995, 22, 422–424. [Google Scholar] [CrossRef]
- Kennick, W.E.; Beardsley, M.C. Aesthetics from Classical Greece to the Present: A Short History. Philos. Rev. 1969, 78, 270. [Google Scholar] [CrossRef]
- Bulent, A. Math and the Mona Lisa: The Art and Science of Leonardo da Vinci; Simthsonian Institution: London, UK, 2014. [Google Scholar]
- Akhtaruzzaman Shafie, A.A. Geometrical Substantiation of Phi, the Golden Ratio and the Baroque of Nature, Architecture, Design and Engineering. Int. J. Arts 2012, 1, 1–22. [Google Scholar] [CrossRef]
- Omotehinwa, T.O.; Ramon, S.O. Fibonacci Numbers and Golden Ratio in Mathematics and Science. Int. J. Comput. Inf. Technol. 2013, 630–638. [Google Scholar]
- Liu, C.-H.; Ting, C.-K. Polyphonic accompaniment using genetic algorithm with music theory. In Proceedings of the IEEE Congress on Evolutionary Computation, Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Liu, C.-H.; Ting, C.-K. Evolutionary composition using music theory and charts. In Proceedings of the IEEE Symposium on Computational Intelligence for Creativity and Affective Computing (CICAC), Singapore, 16–19 April 2013; pp. 63–70. [Google Scholar] [CrossRef]
- McIntyre, R.A. Bach in a box: The evolution of four part Baroque harmony using the genetic algorithm. In Proceedings of the First IEEE Conference on Evolutionary Computation. IEEE World Congress on Computational Intelligence, Orlando, FL, USA, 27–29 June 2002; Volume 2, pp. 852–857. [Google Scholar]
- Pazos, A.; Del Riego, A.S.; Dorado, J.; Caldalda, J.R. Genetic music compositor. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 2003; Volume 2, pp. 885–890. [Google Scholar] [CrossRef]
- Fogel, D. Imagining machines with imagination. Proc. IEEE 2000, 88, 284–288. [Google Scholar] [CrossRef]
- Feng, S.-Y.; Ting, C.-K. Painting Using Genetic Algorithm with Aesthetic Evaluation of Visual Quality. In Computer Vision; Springer Science and Business Media LLC: Berlin, Germany, 2014; Volume 8916, pp. 124–135. [Google Scholar]
- Berlyne, D.E. (Ed.) Studies in the New Experimental Aesthetics: Steps Toward an Objective Psychology of Aesthetic Appreciation; Hemisphere: New York, NY, USA, 1974. [Google Scholar]
- Fayn, K.; Silvia, P.J.; Erbas, Y.; Tiliopoulos, N.; Kuppens, P. Nuanced aesthetic emotions: Emotion differentiation is related to knowledge of the arts and curiosity. Cogn. Emot. 2017, 32, 593–599. [Google Scholar] [CrossRef] [PubMed]
- Mulkay, M.; Chaplin, E. Aesthetics and the Artistic Career: A Study of Anomie in Fine-Art Painting. Sociol. Q. 1982, 23, 117–138. [Google Scholar] [CrossRef]
- Gordon, D.A. Methodology in the Study of Art Evaluation. J. Aesthet. Art Crit. 1952, 10, 338. [Google Scholar] [CrossRef]
- Bourgeon, D. Evaluating Consumer Behaviour in the Field of Arts and Culture Marketing. Int. J. Arts Manag. 2000, 3, 4–18. [Google Scholar]
- Lombardi, T.E. The Classification of Style in Fine-Art Painting, School of Computer Science and Information Systems; Pace University: New York, NY, USA, 2005. [Google Scholar]
- Thomasson, A.L. The Ontology of Art and Knowledge in Aesthetics. J. Aesthet. Art Crit. 2005, 63, 221–229. [Google Scholar] [CrossRef]
- Swami, V. Context matters: Investigating the impact of contextual information on aesthetic appreciation of paintings by Max Ernst and Pablo Picasso. Psychol. Aesthet. Creat. Arts 2013, 7, 285–295. [Google Scholar] [CrossRef]
- Winston, A.S.; Gerald, C.C. The Evaluation of High Art and Popular Art by Naive and Experienced Viewers. Vis. Arts Res. 1992, 18, 1–14. [Google Scholar]
- De Caro, L.; Matricciani, E.; Fanti, G. Imaging Analysis and Digital Restoration of the Holy Face of Manoppello—Part II. Heritage 2018, 1, 349–364. [Google Scholar] [CrossRef]
- Augello, A.; Infantino, I.; Maniscalco, U.; Pilato, G.; Rizzo, R.; Vella, F. Robotic intelligence and computational creativity. Encycl. Semant. Comput. Robot. Intell. 2018, 2, 1850011. [Google Scholar] [CrossRef]
- Carbonneau, M.-A.; Cheplygina, V.; Granger, E.; Gagnon, G. Multiple instance learning: A survey of problem characteristics and applications. Pattern Recognit. 2018, 77, 329–353. [Google Scholar] [CrossRef]
- Carballal, A.; Santos, A.; Romero, J.; Machado, F.J.P.M.; Correia, J.; Castro, L. Distinguishing paintings from photographs by complexity estimates. Neural Comput. Appl. 2016, 30, 1957–1969. [Google Scholar] [CrossRef]
- Castellano, G.; Vessio, G. Towards a Tool for Visual Link Retrieval and Knowledge Discovery in Painting Datasets. In Communications in Computer and Information Science; Springer Science and Business Media LLC: Berlin, Germany, 2020; Volume 1177, pp. 105–110. [Google Scholar]
- Collomosse, J.; Bui, T.; Wilber, M.; Fang, C.; Jin, H. Sketching with Style: Visual Search with Sketches and Aesthetic Context. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2679–2687. [Google Scholar]
- Leonov, S.C.; Vasilyev, A.; Makovetskii, A.; Diaz-Escobar, J. An algorithm of face recognition based on generative adversarial networks. Appl. Digit. Image Process. Xli 2018, 10752, 107522L. [Google Scholar] [CrossRef]
- Jboor, N.H.; Belhi, A.; Al-Ali, A.K.; Bouras, A.; Jaoua, A. Towards an Inpainting Framework for Visual Cultural Heritage. In Proceedings of the 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 9–11 April 2019; pp. 602–607. [Google Scholar]
- Correia, J.; Machado, P.; Romero, J.; Martins, P.; Cardoso, A.F. Breaking the Mould An Evolutionary Quest for Innovation Through Style Change. In Concept Invention; Springer Science and Business Media LLC: Berlin, Germany, 2019; pp. 353–398. [Google Scholar]
- Neumann, A.; Alexander, B.; Neumann, F. Evolutionary Image Transition and Painting Using Random Walks. Evol. Comput. 2020, 28, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Shen, J. Stochastic modeling western paintings for effective classification. Pattern Recognit. 2009, 42, 293–301. [Google Scholar] [CrossRef]
- Florea, C.; Gieseke, F. Artistic movement recognition by consensus of boosted SVM based experts. J. Vis. Commun. Image Represent. 2018, 56, 220–233. [Google Scholar] [CrossRef]
- Tan, W.R.; Chan, C.S.; Aguirre, H.; Tanaka, K. Ceci n’est pas une pipe: A deep convolutional network for fine-art paintings classification. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 3703–3707. [Google Scholar]
- Van Noord, N.; Postma, E. Learning scale-variant and scale-invariant features for deep image classification. Pattern Recognit. 2017, 61, 583–592. [Google Scholar] [CrossRef]
- Tan, W.R.; Chan, C.S.; Aguirre, H.; Tanaka, K. ArtGAN: Artwork synthesis with conditional categorical GANs. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3760–3764. [Google Scholar]
- Fuchs, R.; Hauser, H. Visualization of Multi-Variate Scientific Data. Comput. Graph. Forum 2009, 28, 1670–1690. [Google Scholar] [CrossRef]
- Trends in Information Visualization, An Overview of Current Trends, Development and Research in Information Visualization; Technical Report LMU-MI-2010-1; University of Munich, Department of Computer Science Media Informatics Group: Munich, Germany, 2010; Available online: http://141.84.8.93/pubdb/publications/pub/baur2010infovisHS/baur2010infovisHS.pdf#page=16 (accessed on 21 April 2020).
- Lecoutre, A.; Negrevergne, B.; Yger, F. Recognizing Art Style Automatically in Painting with Deep Learning. JMLR Workshop Conf. Proc. 2017, 80, 1–17. Available online: https://www.lamsade.dauphine.fr/~bnegrevergne/webpage/documents/2017_rasta.pdf (accessed on 21 April 2020).
- Cetinic, E.; Lipic, T.; Grgic, S. Fine-tuning Convolutional Neural Networks for fine art classification. Expert Syst. Appl. 2018, 114, 107–118. [Google Scholar] [CrossRef]
- Cetinic, E.; Lipic, T.; Grgic, S. Learning the Principles of Art History with convolutional neural networks. Pattern Recognit. Lett. 2020, 129, 56–62. [Google Scholar] [CrossRef]
- Babak, S.; Elgammal, A. Large-Scale Classification of Fine-Art Paintings: Learning the Right Metric on the Right Feature. Int. J. Digit. Art Hist. 2016, 2, 70–93. [Google Scholar]
- Sandoval, C.; Pirogova, E.; Lech, M. Two-Stage Deep Learning Approach to the Classification of Fine-Art Paintings. IEEE Access 2019, 7, 41770–41781. [Google Scholar] [CrossRef]
- Wang, Z.; Lian, J.; Song, C.; Zhang, Z.; Zheng, W.; Yue, S.; Ji, S. SAS: Painting Detection and Recognition via Smart Art System with Mobile Devices. IEEE Access 2019, 7, 135563–135572. [Google Scholar] [CrossRef]
- Cetinic, E.; Lipic, T.; Grgic, S. A Deep Learning Perspective on Beauty, Sentiment, and Remembrance of Art. IEEE Access 2019, 7, 73694–73710. [Google Scholar] [CrossRef]
- Hayn-Leichsenring, G.U.; Lehmann, T.; Redies, C. Subjective Ratings of Beauty and Aesthetics: Correlations with Statistical Image Properties in Western Oil Paintings. i-Perception 2017. [Google Scholar] [CrossRef] [PubMed]
- Sigaki, H.Y.D.; Perc, M.; Ribeiro, H.V. History of art paintings through the lens of entropy and complexity. Proc. Natl. Acad. Sci. USA 2018, 115, E8585–E8594. [Google Scholar] [CrossRef] [PubMed]
- Oomen, E. Classification of Painting Style with Transfer Learning. Master’s Thesis, School of Humanities and Digital Science, Tilburg University, Tilburg, The Netherlands, 2018. [Google Scholar]
- Sabatelli, M.; Kestemont, M.; Daelemans, W.; Geurts, P. Deep Transfer Learning for Art Classification Problems; Springer Science and Business Media LLC: Berlin, Germany, 2019; pp. 631–646. [Google Scholar]
- Carneiro, G.; Da Silva, N.P.; Del Bue, A.; Costeira, J.P. Artistic Image Classification: An Analysis on the PRINTART Database. In Lecture Notes in Computer Science; Springer Science and Business Media LLC: Berlin, Germany, 2012; Volume 7575, pp. 143–157. [Google Scholar]
- Crowley, E.C. Visual Recognition in Art using Machine Learning. Ph.D. Thesis, University of Oxford, Oxford, UK, 2016. [Google Scholar]
- Jafarpour, S.; Polatkan, G.; Brevdo, E.; Hughes, S.; Brasoveanu, A.; Daubechies, I. Stylistic analysis of paintings usingwavelets and machine learning. In Proceedings of the 17th European Signal Processing Conference, Glasgow, UK, 24–28 August 2009; pp. 1220–1224. [Google Scholar]
- Johnson, C.; Hendriks, E.; Berezhnoy, I.; Brevdo, E.; Hughes, S.; Daubechies, I.; Li, J.; Postma, E.O.; Wang, J.Z. Image processing for artist identification. IEEE Signal. Process. Mag. 2008, 25, 37–48. [Google Scholar] [CrossRef]
- Hong, Y.; Jongweon, K. Art Painting Identification using Convolutional Neural Network. Int. J. Appl. Eng. Res. 2017, 12, 532–539. [Google Scholar]
- Li, C.; Chen, T. Aesthetic Visual Quality Assessment of Paintings. IEEE J. Sel. Top. Signal. Process. 2009, 3, 236–252. [Google Scholar] [CrossRef]
- Puthenputhussery, A.; Liu, Q.; Liu, C. Color multi-fusion fisher vector feature for fine art painting categorization and influence analysis. In Proceedings of the 2016 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Placid, NY, USA, 7–10 March 2016; pp. 1–9. [Google Scholar]
- Galanter, P. Computational Aesthetic Evaluation: Past and Future. In Computers and Creativity; Springer Science and Business Media LLC: Berlin, Germany, 2012; pp. 255–293. [Google Scholar]
- Koutsoyiannis, D. HESS Opinions “A random walk on water”. Hydrol. Earth Syst. Sci. 2010, 14, 585–601. [Google Scholar] [CrossRef]
- Dimitriadis, P. Hurst-Kolmogorov Dynamics in Hydrometeorological Processes and in the Microscale of Turbulence. Ph.D. Thesis, Department of Water Resources and Environmental Engineering, National Technical University of Athens, Athens, Greece, 2017. [Google Scholar]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Nikos, M.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Dimitriadis, P.; Ioannidis, R.; Iliopoulou, T.; Koutsoyiannis, D. Stochastic Evaluation of Landscapes Transformed by Renewable Energy Installations and Civil Works. Energies 2019, 12, 2817. [Google Scholar] [CrossRef]
- Zhang, H.; Fritts, J.E.; Goldman, S.A. An entropy-based objective evaluation method for image segmentation. Electron. Imaging 2004 2003, 5307, 38–49. [Google Scholar] [CrossRef]
- Martín, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2002; Volume 2, pp. 416–423. [Google Scholar]
- Kohonen, T.; Somervuo, P. How to make large self-organizing maps for nonvectorial data. Neural Netw. 2002, 15, 945–952. [Google Scholar] [CrossRef]
- Abdou, I.; Pratt, W. Quantitative design and evaluation of enhancement/thresholding edge detectors. Proc. IEEE 1979, 67, 753–763. [Google Scholar] [CrossRef]
- Yasnoff, W.A.; Mui, J.K.; Bacus, J.W. Error measures for scene segmentation. Pattern Recognit. 1977, 9, 217–231. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Soltani, S.; Wong, A.K.C.; Chen, Y.C. Survey: A survey of thresholding techniques. Comput. Vis. Graph. Image Process. 1988, 41, 233–260. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. ManCybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Levine, M.D.; Nazif, A.M. Dynamic Measurement of Computer Generated Image Segmentations. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 7, 155–164. [Google Scholar] [CrossRef]
- Pal, N.R.; Pal, S.K. A review on image segmentation techniques. Pattern Recognit. 1993, 26, 1277–1294. [Google Scholar] [CrossRef]
- Weszka, J.S.; Rosenfeld, A. Threshold Evaluation Techniques. IEEE Trans. Syst. ManCybern. 1978, 8, 622–629. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Encolpion of Stochastics: Fundamentals of Stochastic Processes; Department of Water Resources and Environmental Engineering, National Technical University of Athens: Athens, Greece, 2013. [Google Scholar]
- Koutsoyiannis, D. Climacogram-based pseudospectrum: A simple tool to assess scaling properties. In Proceedings of the European Geosciences Union General Assembly 2013, Vienna, Austria, 7–12 April 2012; Volume 15. EGU2013-4209. [Google Scholar]
- Dimitriadis, P.; Koutsoyiannis, D. Climacogram versus autocovariance and power spectrum in stochastic modelling for Markovian and Hurst–Kolmogorov processes. Stoch. Environ. Res. Risk Assess. 2015, 29, 1649–1669. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; van Ness, J.W. Fractional Brownian Motions, Fractional Noises and Applications. Siam Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Dimitriadis, P.; Iliopoulou, T.; Ioannidis, R.; Koutsoyiannis, D. Stochastic investigation of the Hurst-Kolmogorov behaviour in arts. In Proceedings of the European Geosciences Union General Assembly 2018, Vienna, Austria, 8–13 April 2018; Volume 20. EGU2018-17082. [Google Scholar]
- Dimitriadis, P.; Tzouka, K.; Koutsoyiannis, D.; Tyralis, H.; Kalamioti, A.; Lerias, E.; Voudouris, P. Stochastic investigation of long-term persistence in two-dimensional images of rocks. Spat. Stat. 2019, 29, 177–191. [Google Scholar] [CrossRef]
- Wikipedia, Conservation-Restoration of Leonardo da Vinci’s The Last Supper. Available online: https://en.wikipedia.org/wiki/Conservation-restoration_of_Leonardo_da_Vinci%27s_The_Last_Supper (accessed on 21 April 2020).
- Wallace, R. The World of Leonardo: 1452–1519; Time-Life Books: New York, NY, USA, 1966; p. 30. [Google Scholar]
- Froud, S. Leonardo da Vinci; Routlege Great Minds: London, UK, 2014. [Google Scholar]
- Fitzerald, M.C. Making Modernism, Picasso and the Creation of the Market for Twentieth-Century Art; University of California Press: Los Angeles, CA, USA, 1996. [Google Scholar]
- The Last Supper—by Leonardo Da Vinci. Available online: https://leonardodavinci.net/the-last-supper.jsp (accessed on 21 April 2020).
- Seven Things You Probably Never Knew About The Last Supper Painting. Available online: https://www.godupdates.com/9-things-never-knew-the-last-supper/?fbclid=IwAR1bL0CmrKrCmxrAna-MFkw0fnQRw0OOwNr6DGG2qh9LBulHTNFcMXFSQ8w (accessed on 21 April 2020).
- Before and After Photos of Jesus and John in da Vinci’s “Last Supper”. Available online: https://fisheaters.com/xdavincilastsupperphotos.html (accessed on 21 April 2020).
- The Guardian, Hands off. As the Row Over How to Clean Michelangelo’s Statue of David Rages on, Jonathan Jones Asks Whether Restoration Does More Harm Than Good. Available online: https://www.theguardian.com/artanddesign/2003/jul/17/artsfeatures?fbclid=IwAR1RHYLpum5O28olvxVxrYzvf0pgTpzak64pehj9CN8iM8M_FArEtVlyFUY (accessed on 21 April 2020).
- The Perpetual Restoration of Leonardo’s ‘Last Supper’—Part 1: The Law of Diminishing Returns. Available online: http://artwatch.org.uk/the-perpetual-restoration-of-leonardos-last-supper-part-1-the-law-of-diminishing-returns/ (accessed on 21 April 2020).
- The Perpetual Restoration of Leonardo’s Last Supper, Part 2: A Traumatic Production of “a different Leonardo”. Available online: http://artwatch.org.uk/the-perpetual-restoration-of-leonardos-last-supper-part-2-a-traumatic-production-of-a-different-leonardo-3/?fbclid=IwAR0Y57gMG7ublajYtDFAkHG3Eo3TUfuC_ee3dfMLdj1UzzpdrjJTqiQ9ku8 (accessed on 21 April 2020).
- Cheney, L.D.G. eonardo da Vinci’s theory of vision and creativity: The Uffizi Annunciation. In Renaissance Theories of Vision; Routlege: London, UK, 2016; Chapter 7. [Google Scholar] [CrossRef]
- Joost-Gaugier, C.L.; Brown, D.A. Leonardo da Vinci: Origins of a Genius. Sixt. Century J. 1999, 30, 1175. [Google Scholar] [CrossRef]
- Wikipedia. Virgin of the Rocks. Available online: https://en.wikipedia.org/wiki/Virgin_of_the_Rocks (accessed on 21 April 2020).
- Harris, J.C. The Virgin of the Rocks. Arch. Gen. Psychiatry 2009, 66, 1286. [Google Scholar] [CrossRef] [PubMed]
- The Daffodil Code: Doubts Revived Over Leonardo’s Virgin of the Rocks in London. Dalya Alberge, The Guardian, 9 December 2014. Available online: https://www.theguardian.com/artanddesign/2014/dec/09/leonardo-da-vinci-virgin-rocks-louvre-national-gallery (accessed on 21 April 2020).
- Hurst, H. Long Term Storage Capacity of Reservoirs. In Transactions of the American Society of Civil Engineers; ASCE: Reston, VA, USA, 1951. [Google Scholar]
- Cohn, T.A.; Lins, H. Nature’s style: Naturally trendy. Geophys. Res. Lett. 2005, 32, 1–5. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Yao, H.; Georgakakos, A. Medium-range flow prediction for the Nile: A comparison of stochastic and deterministic methods/Prévision du débit du Nil à moyen terme: Une comparaison de méthodes stochastiques et déterministes. Hydrol. Sci. J. 2008, 53, 142–164. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sargentis, G.-F.; Dimitriadis, P.; Koutsoyiannis, D. Aesthetical Issues of Leonardo Da Vinci’s and Pablo Picasso’s Paintings with Stochastic Evaluation. Heritage 2020, 3, 283-305. https://doi.org/10.3390/heritage3020017
Sargentis G-F, Dimitriadis P, Koutsoyiannis D. Aesthetical Issues of Leonardo Da Vinci’s and Pablo Picasso’s Paintings with Stochastic Evaluation. Heritage. 2020; 3(2):283-305. https://doi.org/10.3390/heritage3020017
Chicago/Turabian StyleSargentis, G.-Fivos, Panayiotis Dimitriadis, and Demetris Koutsoyiannis. 2020. "Aesthetical Issues of Leonardo Da Vinci’s and Pablo Picasso’s Paintings with Stochastic Evaluation" Heritage 3, no. 2: 283-305. https://doi.org/10.3390/heritage3020017
APA StyleSargentis, G.-F., Dimitriadis, P., & Koutsoyiannis, D. (2020). Aesthetical Issues of Leonardo Da Vinci’s and Pablo Picasso’s Paintings with Stochastic Evaluation. Heritage, 3(2), 283-305. https://doi.org/10.3390/heritage3020017






