Enhancing Policy Insights: Machine Learning-Based Forecasting of Euro Area Inflation HICP and Subcomponents

Abstract

Accurate inflation forecasting is of central importance for monetary authorities, governments, and businesses, as it shapes economic decisions and policy responses. While most studies focus on headline inflation, this paper analyses the Harmonised Index of Consumer Prices (HICP) and its 12 subcomponents in the euro area over the period 2000–2023, covering episodes of financial crisis, economic stability, and recent inflationary shocks. We apply a broad set of machine learning and deep learning models, systematically optimized through grid search, and evaluate their performance using the Normalized Mean Absolute Error (NMAE). To complement traditional accuracy measures, we introduce the Forecastability Index (FI) and the Interquartile Range (IQR), which jointly capture both the difficulty and robustness of forecasts. Our results show that RNN and LSTM architectures consistently outperform traditional approaches such as SVR and RFR, particularly in volatile environments. Subcomponents such as Health and Education proved easier to forecast, while Recreation and culture and Restaurants and hotels were among the most challenging. The findings demonstrate that macroeconomic stability enhances forecasting accuracy, whereas crises amplify errors and inter-model dispersion. By highlighting the heterogeneous predictability of inflation subcomponents, this study provides novel insights with strong policy relevance, showing which categories can be forecast with greater confidence and where uncertainty requires more cautious intervention.

1. Introduction

Inflation, the persistent rise in the price of goods and services, is a critical economic phenomenon that affects the financial stability and decision-making processes of businesses, governments and individuals. Inflation forecasts play a key role in addressing these economic challenges by providing insights into future price movements and thereby enabling informed financial planning (BIS, 2021) [1]. Governments rely on inflation forecasts when designing monetary and fiscal policies to stabilize the economy and achieve price stability. Inflation expectations, which reflect the expected rate of future price increases, play a crucial role in shaping actual inflation outcomes. These expectations influence the consumption and investment decisions of households and firms, as well as wage negotiations and pricing strategies (Binder & Kamdar, 2022) [2]. Forecasting inflation involves a variety of methods, ranging from statistical models to simpler survey-based approaches. Inflation forecasts are essential for understanding the complex processes of economic decision-making. By providing insights into future price movements, these forecasts allow economic agents to make informed decisions to mitigate risks and take advantage of opportunities (ECB, 2017) [3] and (ECB, 2021) [4].

In our study, we use the Harmonised Index of Consumer Prices (HICP) and its components used by Eurostat to track price changes. The HICP index is calculated as the weighted average of the price changes of a basket of goods and services consumed by households. Accurate inflation forecasting is important from the perspective of monetary authorities, as it allows them to prepare for intervention in a forward-looking manner. Timely and appropriate intervention reduces the costs of disinflation and does not unnecessarily restrain economic growth. According to modern economic thinking, maintaining price stability is the task of the central bank, but government economic policy also has a strong impact on price changes. Governments not only influence the general level of prices through fiscal stimulus but can also intervene in the development of certain components of inflation through price regulation and support systems. We therefore consider it important to forecast individual inflation components accurately in order to provide a clearer picture of the future for any fiscal interventions. Governments may find it urgent to quickly halt or temporarily slow down price increases in certain product groups, as price increases in certain product groups have an immediate and strong impact on the social situation and well-being of households. The most accurate possible forecasting of inflation and its individual components plays an important role in the planning of interventions.

In our research, we used the data of subcomponent (Food and non-alcoholic beverages; Alcoholic beverages and tobacco; Clothing and footwear; Housing, water, electricity, gas and other fuels; Furnishings, household equipment and routine house maintenance; Health; Transport; Communication; Recreation and culture; Education; Restaurants and hotels; Miscellaneous goods and services) of monthly HICP for the period January 2000 (base period) to December 2023. Inflation data were collected from Eurostat. This period was chosen because it includes the period of calm/control (2016), subprime crisis (2008) and the Russian–Ukrainian conflict (2022). Our aim is to examine which method can better forecast the components of HICP. There were crises with different starting points over the whole period under study. We assess whether the patterns learned for the forecasting models during the earlier crisis period can be used to produce accurate forecasts in the later period. In doing so, we help to refine the modelling of inflation forecasts. We highlight the importance of focusing on specific components of inflation.

Our study is an attempt to determine whether inflation trends can be predicted using “technical” forecasting methods. We do not wish to reflect on the various assumptions of economic thinking as to which economic phenomena are fundamentally linked to inflation trends. We assume that machine learning and deep learning methods are capable of extracting information about the future from inflation data series. From this perspective, we adopt the approach of technical analysts in financial markets, according to which the data series studied themselves concentrate the information content of the factors that shape the data.

1.1. Novelty and Significance of the Study

The novelty of this study lies primarily in its focus not only on the aggregate HICP index but also on its subcomponents. This approach makes it possible to uncover the heterogeneous inflation dynamics across different consumption categories and to highlight substantial differences in their forecastability. While most previous research has concentrated on headline inflation, much less attention has been paid to the heterogeneity of subcomponents and their varying sensitivity to macroeconomic shocks. Another innovative aspect is that the analysis spans three distinct economic periods (2009—post-financial crisis, 2016—stable period, and 2023—pandemic and geopolitical tensions), allowing us to test the temporal robustness of forecasting models. Methodologically, we combine classical machine learning algorithms with deep learning architectures, placing particular emphasis on the role of activation functions. Furthermore, we introduce the use of the Forecastability Index (FI) and the Interquartile Range (IQR) metric, which enable us to assess not only accuracy but also the stability of predictions across models. Together, these measures allow us to rank the forecastability of HICP subcomponents, a perspective that has so far received limited attention in the literature. Our findings therefore contribute to the macroeconomic policy debate by identifying which consumption sectors can be forecast more reliably and where greater uncertainty persists.

1.2. Interpretation of HICP and Subcategories

The HICP has been published since 1997. Several changes have been made to the measurement methodology. The current regulation has been in force since 2016. Regulation on the HICP—Regulation (EU) 2016/792 [5] of the European Parliament and of the Council clarified the rules for the production of the HICP. The HICP is a measure of price changes for goods and services. Goods and services are those that fall within the scope of household final monetary expenditure (EUROSTAT, 2024) [6].

Prices of goods and services are measured according to the Classification of Individual Consumption by Purpose (COICOP). COICOP currently consists of 14 main categories (major groups). The first twelve categories include total individual consumption expenditure of households, while the last two categories include social transfers in kind provided by non-profit institutions serving households and general government. In our study, we interpret this level of aggregation as a subcategory.

1.3. HICP Prediction and the Use of Machine Learning Models in the Literature

The use of a number of methods to predict HICP can be found in the literature, some examples of which are given below. Over the past few years, various methodologies have been applied in the field of inflation forecasting, ranging from traditional approaches (e.g., ARIMA, VAR) to machine learning solutions (e.g., random forest, XGBoost). Combining different models, such as employing performance-based weighting (Hubrich and Skudelny, 2017) [7], can offer advantages in times of crisis by integrating the strengths of multiple techniques. Meanwhile, simpler methods like ARIMA handle short-term fluctuations effectively, and structural VAR models capture macroeconomic relationships more accurately. The European Central Bank (ECB, 2016) [8] emphasizes that core inflation (i.e., excluding energy and food) tends to be less volatile yet exhibits a delayed response to inflation trends.

A study by Stakėnas (2018) [9] on Lithuanian HICP components points out that forecasting sub-indices (e.g., food, energy) individually and then aggregating them can improve accuracy, although this disaggregated approach limits the ability to model interactions among components. Earlier work by Stock and Watson (1996) [10] also suggests that modelling each price category separately can reduce overall forecast errors; however, the ECB (2016) [8] cautions that individual component errors may align simultaneously, thereby diminishing the benefits of disaggregation.

Neural networks have increasingly come to the fore in inflation forecasting. Yang and Guo (2021) [11] used a GRU-RNN architecture on CPI indicators in China, finding that the model effectively captures nonlinear relationships and processes complex long-term time series data, outperforming traditional frameworks in forecast accuracy. Similarly, Astrakhantseva et al. (2021) [12], examining regional inflation in Russia, showed that recurrent networks are adept at modelling nonlinear dynamics and support localized forecasting efforts. Sengupta et al. (2024) [13] proposed the Filtered Ensemble Wavelet Neural Network (FEWNet) to forecast CPI in BRIC countries (Brazil, Russia, India, and China), integrating Economic Policy Uncertainty (EPU) and Geopolitical Risk (GPR). Their wavelet-based model significantly outperformed standard methods, including ARIMA and XGBoost.

Aras and Lisboa (2022) [14] investigated both core and headline inflation in Turkey using tree-based machine learning algorithms, observing that random forest consistently yielded the best results. These authors highlight the importance of variable selection in enhancing performance. In turn, Rodríguez-Vargas (2020) [15], studying inflation forecasts for Costa Rica, found that LSTM models offered the most stable outcomes over multiple forecast horizons, and also concluded that multivariate methods systematically outperformed univariate ones.

Joseph et al. (2024) [16], who employed a bottom-up approach to forecast UK inflation, compared traditional autoregressive (AR) models with methods such as Ridge regression, LASSO, and Elastic Net. They noted that AR models are often difficult to surpass, although shrinkage techniques can prevail when inflation trends shift. Adding macroeconomic variables did not result in markedly improved accuracy, whereas disaggregating CPI data led to better forecasts. Similarly, Paranhos (2021) [17] demonstrated that LSTM networks outperform both autoregressive and UC-SV models over longer forecast horizons in U.S. data, with the ability to incorporate long-term dependencies being particularly valuable during periods of heightened economic uncertainty (e.g., the Great Recession).

Further evidence for the effectiveness of machine learning in inflation forecasting can be found in Naghi et al. (2024) [18], who tested Random Forest, Gradient Boosting, and neural networks using OECD and Eurostat data enriched with various macroeconomic indicators. These approaches outperformed classical structural models, especially in volatile contexts. Stoneman and Duca (2024) [19] applied LSTM and CNN architectures to U.S. inflation amid the COVID–19 environment, concluding that deep learning outperforms traditional (S)ARIMA by better capturing nonlinearities and rapidly shifting inflation patterns. Barkan et al. (2023) [20] introduced a hierarchical RNN structure for disaggregated U.S. CPI components, achieving significant performance gains by leveraging information across higher-level indices.

In a hybrid context, Theoharidis et al. (2023) [21] combined ConvLSTM networks with variational autoencoders (VAEs) to refine U.S. inflation forecasts, reporting noteworthy accuracy enhancements over benchmark models. Marcellino (2008) [22], McAdam and McNelis (2005) [23] explored “thick” models for inflation aggregating linear and neural network-based forecasts to show that these can match or even exceed the best linear approaches in certain conditions. Šestanović (2019) [24], using Jordan Neural Networks, illustrated that Eurozone inflation could be accurately predicted over a two-year horizon, aligning with the Survey of Professional Forecasters. Meanwhile, Li et al. (2023) [25] tested a genetically optimized XGBoost model for Taiwan’s inflation, outperforming not only conventional machine learning but also deep learning models. Similar patterns emerge in Araujo et al. (2023) [26] for Brazil and in Mirza et al. (2024) [27] for Pakistan, where random forest and gradient boosting excelled under high-volatility scenarios. Additionally, Alomani et al. (2025) [28] compared ARIMA to a gradient boosting regressor (GBR) on World Bank data, highlighting GBR’s superior short-term performance, even though ARIMA remained more reliable over extended timeframes.

Overall, these studies collectively indicate that neural network approaches (especially GRU and Jordan Neural Networks) are promising for predicting HICP and other inflation indicators, thanks to their capacity to handle nonlinearities and long-term temporal patterns. Yet the extent to which they decisively outperform traditional statistical and econometric methods is not uniform across all situations, pointing to the need for continued methodological refinements and careful variable selection. By doing so, researchers can improve the accuracy of inflation forecasts, be it at an aggregate level or broken down into specific subcomponents.

2. Materials and Methods

2.1. Applied Methods

2.1.1. Simple Recurrent Neural Network (RNN)

An RNN is a neural network designed to process serial data, such as temporal or sequential information. Unlike traditional feedforward networks, RNN uses feedback connections so that the hidden state of the previous time step is taken into account when calculating the next step. This enables RNN to recognize and learn certain temporal relationships. The hidden states are updated using a nonlinear activation function (e.g., tanh or ReLU), and the resulting states are passed on to the next time step. RNN is useful in tasks such as speech recognition, language model building, or time series analysis. However, the network also has serious drawbacks, notably the problem of vanishing gradients, which makes it difficult to learn long-term relationships. This happens because the gradient values become too small over time, so the network cannot efficiently update information from previous steps. Another problem is an exploding gradient, in which the gradient values become too large, which can make learning unstable. Because of these problems, simple RNNs are rarely used for long sequences, and more advanced architectures such as LSTM or GRU are used instead (Bai et al. 2021) [29]. The following equations can represent the basic structure of an RNN:

$$S_t=\left(U{x}_t+W{S}_{t-1}+b_h\right)$$

(1)

$$y_t=f(V{S}_t+b_0)$$

(2)

where x_t represents the inputs at time t, S_t the outputs of the hidden layer, y_t the information of the output layer, f() the activation function, and b_h and b_o the bias vectors of the hidden and output layers, respectively. The weights are defined as W, which is the weight of the hidden layer; U, which is the weight of the inputs at the current time; and V, which is the weight of the outputs.

2.1.2. Gated Recurrent Unit (GRU)

The GRU is a simplified version of the LSTM, which is also designed to deal with the problem of gradient descent. The GRU structure contains fewer gates than the LSTM, so it is faster and requires fewer computational resources. In contrast to the three gates of the LSTM, the GRU uses only two gates: the update gate and the reset gate. The update gate determines how much information from the previous state is to be retained and how much is to be replaced based on the new input. And the reset gate controls how much information from the old state is forgotten, allowing the network to adapt flexibly to sequences of different lengths. GRU performance can be similar or even better than LSTM, especially for smaller data sets. In addition, it learns faster due to fewer parameters and can therefore be more efficient in environments where computational capacity is limited. For example, GRU is a popular choice for machine learning-based chatbots, machine translation, speech recognition and time-series analysis. Because it has a simpler structure, it can be a preferable alternative to LSTM in many cases, although for some problems LSTM may be more accurate (Xiao et al., 2022) [30]. The following equations govern the GRU:

$$z_t= \sigma (W_z{h}_{t-1}+ U_z{x}_t)$$

(3)

$$r_t=\sigma (W_r{h}_{t-1}+U_r{x}_t)$$

(4)

$${\tilde{h}}_t=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}(W_0\left(h_{t-1} \odot r\right)+U_0{x}_t)$$

(5)

$$h_t=z_t\odot {\tilde{h}}_t+\left(1-z_t\right) \odot h_{t-1}$$

(6)

In this case, $h_{t-1}$ represents the hidden state of the neuron at the previous time step, and σ() denotes the logistic sigmoid function, defined as $\sigma \left(x\right)=1/1+e^{-x}.$ The weight matrices for the update gate are $W_z$ and $U_z$, and for the reset gate, they are $W_r$ and $U_r$. The weight matrices for the intermediate output are represented by $W_0$ and $U_0$. The input value at time t is denoted by $x_t$, while the hidden layer output and the temporary unit state at time t are represented by $\widetilde{h_t}$ and $h_t$, respectively.

2.1.3. Long Short-Term Memory (LSTM)

LSTM is a more advanced version of RNN, developed specifically for learning long-term relationships. LSTM solves the gradient descent problem in simple RNNs by using a special memory cell. This memory cell helps to store and retrieve longer-term information. The LSTM contains three main gates: the input gate, the forget gate and the output gate. The forget gate controls what previous information the cell forgets or retains. The input gate decides what new information is put into the memory cell. The output gate determines what information is passed from the cell to the next time step. The LSTM is therefore able to store important information for a longer period of time while filtering out less important data. For this reason, it is well suited for tasks such as text and speech processing, machine translation or time series prediction. However, LSTM is more computationally intensive than simple RNN because it uses more gates and memory cells and therefore requires more processing power. Nevertheless, it remains one of the most popular solutions among recurrent networks for handling long-term correlations. (Barkan et al., 2023) [20]. The following equations describe the LSTM model:

$$I_t= \sigma (X_t{W}_{xi}+ H_{t-1}{W}_{hi}+b_i)$$

(7)

$$F_t=\sigma (X_t{W}_{xf}+H_{t-1}{W}_{hf}+b_f)$$

(8)

$${\tilde{C}}_t=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}(X_t{W}_{xc}+H_{t-1}{W}_{hc}+b_c)$$

(9)

$$C_t=F_t\odot C_{t-1}+I_t\odot {\tilde{C}}_t$$

(10)

$$O_t=\sigma (X_t{W}_{xo}+H_{t-1}{W}_{ho}+b_o)$$

(11)

The matrices $W_{xc}$ and $W_{hc}$ represent the weight matrices of the gated unit, and $b_c$ is the bias term for this unit. $C_t$ is the current cell state, while $C_{t-1}$ refers to the cell state at the previous time step. Similarly, $W_{xo}$ and $W_{ho}$ are the weight matrices of the output gate, and $b_o$ is the corresponding bias term. Here, $X_t$ denotes the input batch at time t, and $H_{t-1}$ is the hidden state from the previous time step. The weight matrices for the input gate are $W_{xi}$ and $W_{hi}$, with $b_i$ as the bias term, and the sigmoid function σ is used in this equation to control the activation. The weight matrices of the forget gate are $W_{xf}$ and $W_{hf}$, and the bias term is $b_f$. The candidate memory cells are denoted by $C_t$. As mentioned earlier, the weight matrices for the gated unit are $W_{xc}$ and $W_{hc}$, with $b_c$ as the bias term. The current cell state $C_t$ differs from the previous cell state $C_{t-1}$ at this time step, while the output gate’s weight matrices remain $W_{xo}$ and $W_{ho}$, and the bias term remains $b_o$ (Dai et al. 2022) [31].

2.1.4. Support Vector Machine (SVM) Regression

SVM regression (SVR—Support Vector Regression) is a machine learning method based on the principle of the support vector machine (SVM), which aims to find an optimal hyper-plane between the input variables and the target variable. One of the main advantages of SVR is that it is flexible and robust, as it can model not only linear but also nonlinear relationships using kernel truncations (e.g., polynomial or RBF kernels). The SVR introduces an ε-insensitive zone, which means that only data points that fall outside the given error bound are considered by the model. This helps to reduce the sensitivity of the model to noisy data and avoid overfitting. SVR can be mathematically described as an optimization problem, which aims to minimize the error and find the best-fitting plane to the data. The advantages of SVR include good performance on small to medium-sized data sets, and it works well in high-dimensional space. Its disadvantage is that its computational cost can be high on large data sets, as optimization requires quadratic programming. SVR is particularly well suited for financial forecasting, weather forecasting, and bioinformatics problems (Ülke et al., 2018) [32]. The decision boundary is defined in Equation (4), where SVMs can map the input vectors $x_i \in R^d$ into a high-dimensional feature space $\Phi \left(x_i\right)\in H$ and $\Phi$ is mapped by the kernel function $K\left(x_i,x_j\right)$.

$$f\left(x\right)=sgn(\sum _{i=1}^n{\alpha }_i{y}_i\ast K\left(x, x_i\right)+b)$$

(12)

SVMs convert non-separable classes into separable ones with linear, nonlinear, sigmoid, radial basis, and polynomial kernel functions. The formula of the kernel functions is shown in Equations (5)–(7), where γ is the constant of the radial basis function, and d is the degree of the polynomial function. The two adjustable parameters in the sigmoid function are the slope α and the intercepted constant c.

$$\mathrm{R}\mathrm{B}\mathrm{F}:K\left(x_i{x}_j\right)=\mathrm{e}\mathrm{x}\mathrm{p}(-\mathsf{\gamma }{‖x_i-x_j‖}^2)$$

(13)

$$\mathrm{P}\mathrm{o}\mathrm{l}\mathrm{y}\mathrm{n}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{a}\mathrm{l}:K\left(x_i{x}_j\right)={\left(x_i\ast x_j+1\right)}^d$$

(14)

$$\mathrm{S}\mathrm{i}\mathrm{g}\mathrm{m}\mathrm{o}\mathrm{i}\mathrm{d}:K\left(x_i{x}_j\right)=\tanh \left(\alpha x_i^{T}y+c\right)$$

(15)

2.1.5. Random Forest Regression (RFR)

Random Forest regression is an ensemble learning method that combines multiple decision trees to increase the accuracy of the prediction. The method involves building multiple trees on a randomly selected data set, and the final prediction is the averaged or majority voting result of the trees. One of the key techniques is Bootstrap Aggregation (Bagging), where trees learn on different random samples, thus reducing overfitting and improving generalization ability. One of the big advantages of Random Forest is that it is extremely robust, less sensitive to noisy data, and does not require much prior data transformation. It can also handle missing data and nonlinear relationships. A disadvantage is that, although it scales well, it can be more computationally intensive on larger data sets, as it requires the computation of many trees together. Random Forest is excellent for financial forecasting, medical diagnostics, and other predictive modelling problems where large amounts of data are available (Park et al., 2022) [33].

Two important fine-tuning parameters are used in the modelling of RF: one is the number of branches in the cluster (p), and the other is the number of input vectors to be sampled in each split (k). Each decision tree in RF is learned from a random sample of the data set (Ismail et al., 2020) [34].

To build the RF model, three parameters must be defined beforehand: the number of trees (n), the number of variables (K), and the maximum depth of the decision trees (J). Learning sets (D_i, i = 1, …., n) and variable sets (V_i, i = 1, …., n) of decision trees are created by random sampling with replacement, which is called bootstrapping. Each decision tree of depth J generates a weak learner ${\tau }_i$ from each set of learners and variables. Then, these weak learners are used to predict the test data, and then an ensemble of n trees ${\left\{\tau i\right\}}_{i=1}^n$ is generated. For a new sample, the RF can be defined as follows (Park et al. 2022) [33]:

$$\widehat{R}\left(x\right)= {\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\widehat{r}}_i\left(x\right)$$

(16)

where ${\widehat{r}}_i\left(x\right)$ is the predicted value of ${\tau }_i$.

For modelling, the Python programming language version 3.9 was used. Both the Scikit-Learn and Tensorflow libraries, developed for machine learning methods, were helpful in the modelling process.

2.2. Performance Evaluation

The most commonly used metrics in the literature for evaluating the predictive models and assessing their accuracy are root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) (Nti et al., 2020) [35].

2.2.1. Mean Absolute Error (MAE)

Mean Absolute Error (MAE): This indicator measures the average magnitude of the error in a set of predictions.

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|{y_i-\widehat{y}}_i\right|$$

(17)

where ${ \widehat{y}}_i$ is the estimated value produced by the model, $y_i$ is the actual value, and n is the number of observations.

2.2.2. Normalized Mean Absolute Error (NMAE)

However, the database used also contains zero values, so the traditional MAPE indicator could not be used because of the zero denominator. To compare the periods and the different inflation components, the Normalized Mean Absolute Error (NMAE) was used.

$$NMAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|{\displaystyle \frac{{y_i-\widehat{y}}_i}{y_{max}-y_{min}}}\right|$$

(18)

where $y_{max}$ is the maximum value of the data range, and $y_{min}$ is the minimum.

Forecasts have greater accuracy and dependability when the indicator has a lower value. Because the NMAE is not influenced by the price’s nominal magnitude, it can also be used to compare different models and instruments (Terven et al. 2023) [36].

2.2.3. Forecastability Index (FI)

To quantify the predictability of both the inflation subcomponents and the aggregated HICP, we introduced the Forecastability Index (FI). For each category, the index measures the relative magnitude of model errors (NMAE) compared to the best-performing model:

$${FI}_j= {\displaystyle \frac{1}{M}}\sum _{m=1}^M{\displaystyle \frac{{NMAE}_{j.m}}{\underset{k}{\min }{NMAE}_{j.k}}}$$

(19)

where j denotes either an inflation subcomponent or the overall HICP, m refers to a given model, and M is the number of models considered. The term $\underset{k}{\min }{NMAE}_{j.k}$ captures the smallest forecasting error for category j. By construction, an FI_j value close to 1 indicates that the category is relatively easy to predict, whereas higher values reflect greater forecasting difficulty.

2.2.4. Interquartile Range (IQR)

To assess the dispersion of forecasting errors across models, we also computed the interquartile range (IQR). For each category, the IQR is defined as the difference between the 75th and 25th percentiles of the error distribution:

$${IQR}_j= {Q3}_j- {Q1}_j$$

(20)

where Q1_j and Q3_j denote the 25th and 75th percentiles, respectively, of the model errors for category j. A low IQR suggests that forecasting performance is stable and largely independent of model choice, while a high IQR indicates that forecastability is more sensitive to the specific model used, implying reduced robustness.

Taken together, the FI allows us to rank both the subcomponents and the HICP in terms of forecasting difficulty, while the IQR provides complementary insights into the robustness of predictions across different models.

2.3. Hyperparameters

Table 1. Hyperparameters.

Model	Parameters	Value
RNN LSTM GRU	Hidden Layers	2
	Hidden layer neuron count	50, 100, 150
	Batch size	16, 32
	Epochs	40, 60, 80, 100, 120
	Activation	ELU, Tanh, Linear
	Learning rate	0.1; 0.01; 0.001
	Optimizer	Adam
SVR	Kernel	RBF, Polynomial, Sigmoid
	C	10, 100, 1000
	Gamma	0.01; 0.1; 0.5; 0.9
RFR	Max Depth	5, 10, 15
	Random state	42
	Number of trees	100, 150, 200

Source: own research.

reports the set of hyperparameters employed across the models. For each examined period (2009, 2016, and 2023), all models were optimized separately using the full time series of the respective regime, considering both the individual inflation subcomponents and the aggregate HICP index. A 12-month rolling window approach was applied, allowing each forecast to be based on the most recent historical information while mitigating the risk of overfitting. A time-based 90–10% train–test split was used, explicitly avoiding random sampling to preserve the temporal structure of the data. Hyperparameter tuning was performed using a grid search framework combined with time series split cross-validation, ensuring that each validation fold relied strictly on past observations. This setup effectively eliminated any risk of information leakage between the training and testing phases.

For the deep learning models, an early stopping mechanism was implemented based on the validation loss (Mean Absolute Error, MAE), which helped prevent overfitting by halting training once no further improvement was observed. The model weights from the best-performing epoch were retained, improving both the stability and generalization of forecasts. Models were re-optimized for each period and inflation subcategory to ensure that hyperparameters adapted appropriately to the specific macroeconomic environment.

In the case of the neural network architectures, particular emphasis was placed on the specification of the activation functions, given their pivotal role in shaping both the convergence properties and the predictive accuracy of the models. To further underscore their relevance, the results associated with different activation functions are presented and discussed separately, highlighting their influence on the forecastability of the inflation subcomponents. (Apicella et al., 2021; Szandała, 2021; Dubey et al., 2022; Singh et al., 2023; Vancsura et al., 2024) [37,38,39,40,41].

All analyses were conducted in Python 3.11, using the TensorFlow and Keras libraries for deep learning implementation (including tensorflow, keras, numpy, pandas, scikit-learn), while classical machine learning models such as Support Vector Regression (SVR) and Random Forest Regressor (RFR) were implemented using the scikit-learn package (SVR, RandomForestRegressor, GridSearchCV, and TimeSeriesSplit).

2.4. Data

In our research, we used the data of subcomponent (Food and non-alcoholic beverages; Alcoholic beverages and tobacco; Clothing and footwear; Housing, water, electricity, gas and other fuels; Furnishings, household equipment and routine house maintenance; Health; Transport; Communication; Recreation and culture; Education; Restaurants and hotels; Miscellaneous goods and services) of monthly HICP for the period January 2000 (base period) to December 2023. Inflation data were collected from Eurostat. This period was chosen because it includes the period of calm/control (2016), Subprime crisis (2008), and the Russian–Ukrainian conflict (2022).

In our study, we have divided this time period into three sub-samples, the first of which relates to the subprime crisis. In this case, we made forecasts for the 12 months of 2009. The full database covered the period from 1 January 2000 to 31 December 2009. The second sub-sample was defined as a control period. Here, we simulated forecasts for the year 2016, for which the period from 1 January 2007 to 31 December 2016 provided the inflation subtype data. The third sub-sample targeted the period of the Russian–Ukrainian conflict and provided the results of the predictions for the year 2023. The full database covered the interval between 1 January 2014 and 31 December 2023. Indeed, the two crisis periods have been important factors in the analysis for the robustness test of the models. The forecasting targets were defined as the year-on-year (y/y) percentage changes of the HICP and its 12 inflation subcomponents. Accordingly, the input data consisted of monthly aggregated y/y inflation rates, which inherently remove most seasonal patterns; therefore, additional seasonal adjustment was not required. No explicit detrending was applied, as the primary goal was to allow the models to learn the long-term patterns and structural dynamics of inflation directly from the data.

Given the exceptional price shocks and energy market volatility observed in 2022–2023, the data set was examined for potential outliers. Extreme values were retained, as they represent genuine economic phenomena and carry essential information about inflationary dynamics. No missing observations were present in the data set; therefore, no imputation procedures were required.

All data were scaled using a MinMaxScaler fitted exclusively on the training subset and subsequently applied to the validation and test data to prevent information leakage. This scaling approach contributed to stable model convergence, particularly for RNN-based architectures, where linear activation functions can be sensitive to input magnitude. Overall, these preprocessing steps ensured the robustness of model training and the reliability of the resulting forecasts.

For the modelling, the learning and testing datasets were split in a ratio of 90–10%. For each of the forecast periods (2008, 2016, 2023), the forecast period was between 1 January and 31 December. Simulations were carried out using univariate methods.

Before implementing the forecasting models, the time-series properties of the HICP and its twelve subcomponents were examined to ensure the statistical adequacy of the data.

Table 2. Results of Unit Root, Structural Break, and Stationarity Tests for HICP and Its Subcomponents.

Variable	ADF Stat	ADF p-Value	KPSS Stat	KPSS p-Value	PP Stat	PP p-Value	DF-GLS Stat	DF-GLS p-Value	ZA Stat	ZA p-Value	Structural Breaks (Pelt)
Food and non-alcoholic beverages	−1.6069	0.4801	0.3668	0.0915 *	−2.6836	0.0769 *	−0.6996	0.4262	−2.5490	0.9817	April 2011, October 2013, February 2022
Alcoholic beverages, tobacco	−2.6979	0.0744 *	0.2489	0.1000 *	−2.8767	0.0481 **	−1.8992	0.0571 *	−3.5907	0.6203	February 2002, November 2005, August 2014, December 2017, December 2022
Clothing and footwear	−2.9152	0.0436 **	0.2792	0.1000 *	−11.4686	0.0000 ***	−2.7631	0.0059 ***	−3.7399	0.5199	June 2020
Housing, water, electricity, gas, and other fuels	−1.3078	0.6256	0.1335	0.1000 *	−3.1884	0.0207 **	−1.3336	0.1747	−2.7956	0.9554	May 2013, April 2021
Furnishings, household equipment, and routine house maintenance	−0.7170	0.8423	0.3551	0.0965 *	−2.3795	0.1476	−0.4947	0.5248	−0.9916	0.9990	October 2013, September 2021
Health	−2.2030	0.2052	0.6710	0.0162 **	−3.1223	0.0249 **	−2.2165	0.0267 **	−3.8105	0.4718	December 2012, December 2022
Transport	−3.1899	0.0206 **	0.1190	0.1000 *	−3.4197	0.0103 **	−2.3098	0.0210 **	−4.0867	0.2996	May 2013, September 2016
Communication	−4.0646	0.0011 ***	0.5485	0.0307 **	−2.7629	0.0638 *	−3.2045	0.0014 ***	−4.8388	0.0468 **	September 2001, March 2004, March 2009, February 2012, January 2015
Recreation and culture	−1.1338	0.7014	0.8986	0.0100 ***	−4.6128	0.0001 ***	−0.4450	0.5229	−2.6066	0.9774	December 2002, April 2011, September 2021
Education	−2.2991	0.1723	1.0199	0.0100 ***	−2.9600	0.0388 **	−2.1729	0.0298 **	−3.9563	0.3782	February 2007, October 2008, July 2017, July 2022
Restaurants and hotels	−3.4964	0.0081 ***	0.2859	0.1000 *	−2.0876	0.2495	−3.5002	0.0005 ***	−4.5626	0.1011	March 2009, June 2020, September 2021
Miscellaneous goods and services	−1.4434	0.5613	0.3973	0.0783 *	−1.2342	0.6587	−1.4235	0.1493	−2.0356	0.9964	October 2003, October 2013, May 2018, July 2022
HICP	−1.8524	0.3548	0.2733	0.1000 *	−2.7036	0.0734 *	−1.8487	0.0638 *	−3.6012	0.6133	October 2013, September 2016, September 2021

*** p ≤ 0.01; ** p ≤ 0.05; * p ≤ 0.1. Source: own research.

presents the results of the unit root, structural break, and stationarity tests conducted for each category. Specifically, the Augmented Dickey–Fuller (ADF), Phillips–Perron (PP), Kwiatkowski–Phillips–Schmidt–Shin (KPSS), and Elliott–Rothenberg–Stock Dickey–Fuller Generalized Least Squares (DF–GLS) tests were applied to assess the presence of unit roots and mean reversion, while the Zivot–Andrews (ZA) test and the Pelt algorithm were employed to detect structural breaks in the series. The results reveal that inflation subcomponents exhibit heterogeneous stationarity properties, reflecting their differing market and policy structures. In general, categories such as Communication, Transport, and Restaurants and Hotels display stronger evidence of stationarity, with statistically significant ADF and DF-GLS statistics (p < 0.05) and stable KPSS outcomes. For instance, Communication shows robust stationarity (ADF stat = −4.06, p = 0.0011; DFGLS stat = −3.20, p = 0.0014), suggesting a mean-reverting price process, likely driven by regulated tariffs and slower price adjustments. Conversely, subcomponents like Furnishings, Miscellaneous goods and services, and Food and non-alcoholic beverages exhibit weaker evidence of stationarity, as indicated by high ADF p-values (>0.4) and borderline KPSS significance. These series appear to follow near-random-walk dynamics, consistent with persistent or trend-inflation patterns in consumer goods.

The Zivot–Andrews and Pelt tests highlight several structural breaks across nearly all categories, typically clustered around major macroeconomic disruptions such as the 2008 financial crisis, the 2012–2014 euro-area stagnation, and the 2021–2023 inflationary shock. For example, breaks in Housing, water, electricity, gas, and other fuels occur near observations May 2013 and April 2021, corresponding roughly to the 2013 and 2021 periods, associated with energy price shocks and the pandemic onset. The Alcoholic beverages and tobacco and Education series also exhibit multiple structural breaks, possibly reflecting fiscal policy changes and regulated pricing interventions. The existence of these breaks supports the interpretation that inflation dynamics are regime-dependent and shaped by exogenous shocks.

Despite the presence of several non-stationary or near-integrated series and identified structural shifts, the models employed (RNN, LSTM, GRU) are well suited to handle such time-series complexities. Unlike traditional linear econometric methods that assume strict stationarity and homoscedastic residuals, deep learning frameworks can capture nonlinear, non-stationary, and regime-dependent patterns through dynamic weight adaptation and memory mechanisms. Consequently, while some inflation components deviate from classical stationarity assumptions, the applied methodologies remain robust and capable of extracting meaningful temporal dependencies, yielding reliable forecasts under varying macroeconomic regimes.

3. Results

Table 3. Descriptive statistics for the period 1 January 2000 to 31 December 2009.

Inflation Subcomponents	Average	Median	Std	Min	Max	Range	N
Alcoholic beverages, tobacco	4.10	3.65	1.71	1.60	8.60	6.00	120
Clothing and footwear	0.72	0.75	0.85	−3.20	2.80	9.00	120
Communication	−2.46	−1.95	2.17	−9.10	−0.10	8.50	120
Education	3.57	3.30	2.12	0.50	9.60	3.10	120
Food and non-alcoholic beverages	2.33	2.00	1.97	−1.50	6.70	7.00	120
Furnishings, household equipment, and routine house maintenance	1.37	1.30	0.47	0.60	2.20	8.20	120
Health	2.40	1.80	1.92	0.90	8.50	1.60	120
Housing, water, electricity, gas, and other fuels	3.05	3.10	1.79	−1.80	6.70	9.10	120
Miscellaneous goods and services	2.40	2.30	0.39	1.60	3.40	12.70	120
Recreation and culture	0.35	0.20	0.65	−1.00	2.10	1.80	120
Restaurants and hotels	3.04	3.00	0.73	1.20	4.80	3.60	120
Transport	2.53	3.10	2.76	−5.50	7.20	7.60	120
HICP	2.10	2.10	0.80	−0.60	4.10	4.70	120

Source: own research.

presents descriptive statistics for the main subcomponents of inflation over the period from 1 January 2000 to 31 December 2009. The average monthly inflation rates vary considerably across categories, with alcoholic beverages and tobacco (4.10%) and education (3.57%) exhibiting the highest average price increases, while communication experienced a deflationary trend with an average of −2.46%. Notably, the volatility of inflation, as measured by the standard deviation, is particularly high in transport (2.76%) and communication (2.17%), indicating substantial fluctuations in these sectors. In contrast, categories such as miscellaneous goods and services (0.39%) and furnishings (0.47%) show much more stable price developments. The range of values highlights the dispersion in inflationary dynamics, with communication and clothing displaying the widest intervals. The HICP, representing the overall inflation rate, recorded a relatively stable mean of 2.10% with limited variability (standard deviation of 0.80%). These findings underscore the heterogeneity of inflationary pressures across different sectors and emphasize the importance of disaggregated analysis in inflation research.

Table 4. NMAE indicators for the period 1 January 2009 to 31 December 2009.

NMAE	RNN (ELU)	LSTM (ELU)	GRU (ELU)	RNN (tanh)	LSTM (tanh)	GRU (tanh)	RNN (lin)	LSTM (lin)	GRU (lin)	SVR	RFR	Avg.
Alcoholic beverages, tobacco	0.0400	0.0416	0.0393	0.0584	0.0368	0.0409	0.0396	0.0425	0.0390	0.0402	0.0469	0.0423
Clothing and footwear	0.0643	0.0518	0.0707	0.0615	0.0495	0.0685	0.0625	0.0428	0.0680	0.0595	0.0273	0.0569
Communication	0.0561	0.0312	0.0285	0.0376	0.0277	0.0292	0.0365	0.0428	0.0283	0.0438	0.0427	0.0368
Education	0.0867	0.0448	0.0329	0.1077	0.0577	0.0300	0.0830	0.0364	0.0446	0.1847	0.1547	0.0785
Food and non-alcoholic beverages	0.0720	0.0520	0.0442	0.0355	0.0418	0.0343	0.0213	0.0439	0.0360	0.0680	0.1062	0.0505
Furnishings, household equipment, and routine house maintenance	0.0919	0.0818	0.1195	0.0979	0.0707	0.0738	0.0909	0.0702	0.0713	0.0758	0.0926	0.0851
Health	0.0431	0.0292	0.0178	0.0419	0.0194	0.0210	0.0341	0.0248	0.0363	0.0355	0.0231	0.0296
Housing, water, electricity, gas and other fuels	0.0633	0.0532	0.0608	0.0836	0.0553	0.0653	0.0476	0.0726	0.0639	0.0908	0.2006	0.0779
Miscellaneous goods and services	0.0605	0.0473	0.0497	0.0719	0.0466	0.0468	0.0437	0.0484	0.0476	0.0476	0.0418	0.0502
Recreation and culture	0.1263	0.1028	0.1475	0.1417	0.0973	0.1511	0.0968	0.1010	0.1410	0.1536	0.1161	0.1250
Restaurants and hotels	0.2175	0.1314	0.1111	0.0961	0.1207	0.1045	0.0786	0.1204	0.1036	0.2390	0.2292	0.1411
Transport	0.2010	0.0872	0.1024	0.2097	0.1146	0.0944	0.0988	0.1121	0.1146	0.2278	0.2372	0.1454
Average	0.0936	0.0629	0.0687	0.0870	0.0615	0.0633	0.0611	0.0632	0.0662	0.1055	0.1099

Lower NMAE values indicate better forecasting accuracy. To enhance interpretability, the results are displayed using a color scale ranging from dark green (best performance) to dark red (worst performance), allowing for a quick visual comparison across models and categories. Source: own research.

shows the NMAE estimates for the year 2009. In the Alcoholic beverages and tobacco subgroup, the NMAE values were in a narrower range. The best performance was obtained with LSTM (tanh) with a value of 0.0368, while the worst estimation accuracy was obtained with RNN (tanh) with a value of 0.0584. For the Clothing and footwear subcomponent, the RFR model was the most accurate (0.0273), while the GRU (ELU) was the least accurate with a value of 0.0707. For the Communication predictions, the LSTM (tanh) also performed best (0.0277), while the RNN (ELU) algorithm produced the worst prediction (0.0561). For the Education component, the best (0.0300) and worst (0.1847) model performances were in a much wider range. The former was produced by GRU (tanh) and the latter by SVR, which is a rather poor result. For Food and non-alcoholic beverages, a model with a linear activation function, RNN, was the most accurate with an NMAE of 0.0213, while RFR was the least accurate (0.1062). For Furnishings, household equipment, and routine house maintenance, the LSTM (linear) showed the best performance with 0.0702, while the GRU (ELU) had the worst estimation performance (0.1195). It is important to note that in this case, a significant shift in the minimum value of the NMAE values was already observed compared to the previous categories. For the Health subtype, we observed the smallest difference between model performances. GRU (ELU) achieved the most optimal result (0.0178), while RNN (ELU) performed the worst (0.0431). Considering the NMAE values, this category is considered the most predictable of all for the 2009 forecast horizon. When examining the Housing, water, electricity, gas, and other fuels subcomponent, a much more nuanced picture emerges, as there is a significant difference between the most accurate (RNN-linear, 0.0476) and least accurate (RFR, 0.2006) models. On the other hand, for the Miscellaneous goods and services type, the best performance was achieved by the RFR (0.0418), while the least useful algorithm was the RNN (tanh) (0.0719). For both the Recreation and culture and Restaurants and hotels categories, the RNN (linear) model performed best (0.0968 and 0.0786), while the SVR performed worst (0.1536 and 0.2390). For the Transport subtype, the LSTM (ELU) was the most useful with 0.0872, while the RFR was underperforming (0.2372). The latter three categories thus posed significant challenges for the methodologies used. The best result over the period was achieved in the Health category, while the worst was achieved in the Restaurants and hotels category.

Examining the average model performance per subtype, we find that RNN (linear) and LSTM (tanh) performed outstandingly and very similarly. However, the traditional machine learning models scored rather poorly on average.

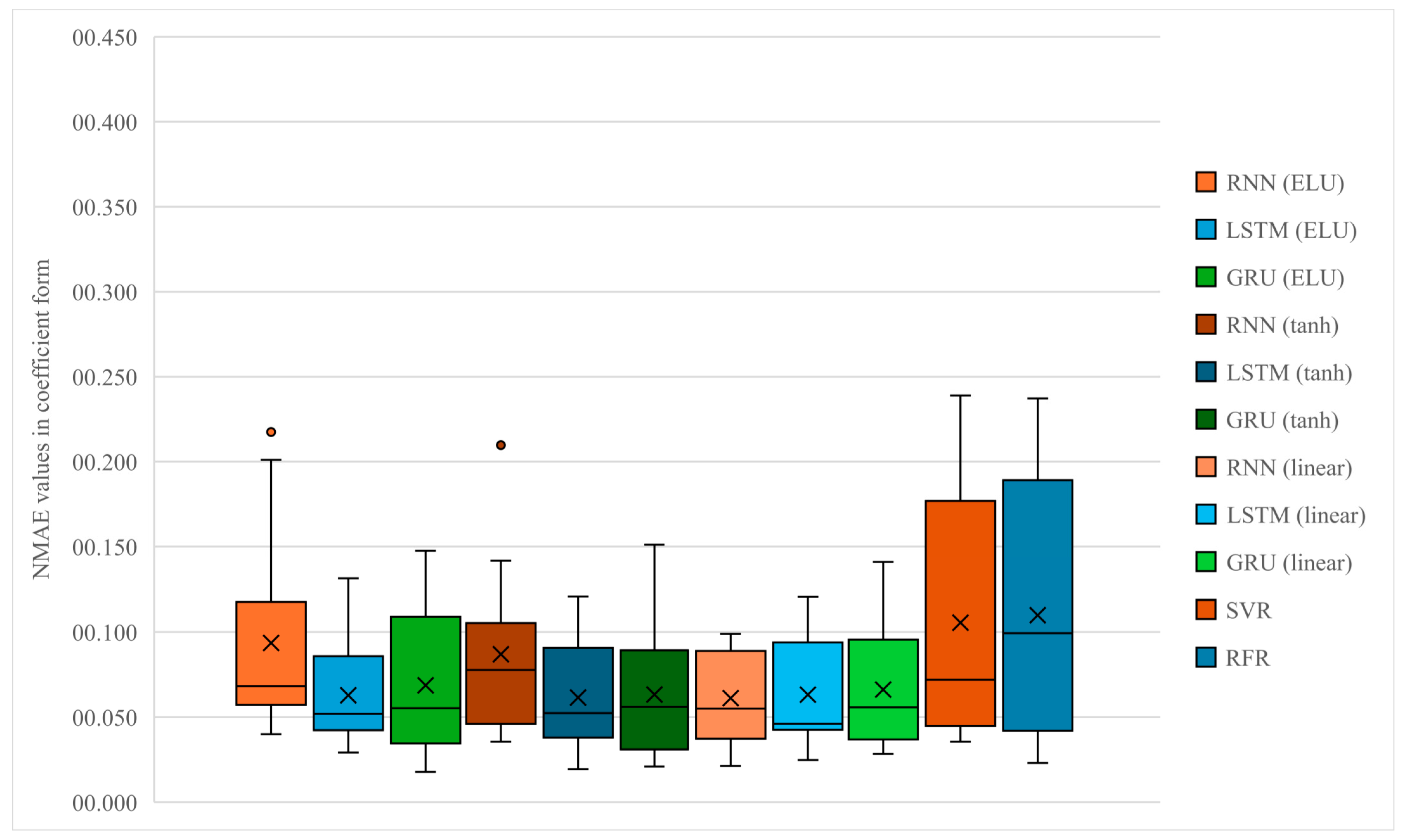
Figure 1 presents the distribution of Normalized Mean Absolute Error (NMAE) values for all forecasting models for the year 2009, which reflects the post-financial crisis environment. The results clearly indicate that deep learning architectures (RNN, LSTM, and GRU) with various activation functions (ELU, tanh, and linear) generally outperform traditional machine learning models such as SVR and RFR. The median NMAE values of neural network-based models are notably lower, accompanied by narrower interquartile ranges, suggesting more stable and consistent forecasting performance. Models using nonlinear activation functions, particularly ELU and tanh, exhibit superior accuracy, implying that these functions are better suited to capture the nonlinear and dynamic nature of inflation series. In contrast, models employing linear activation functions show wider variability and slightly higher median errors, reflecting limitations in representing complex time dependencies. Among the classical algorithms, SVR shows moderate errors, while RFR performs the weakest, with both higher median values and greater dispersion. The RNN (ELU) and LSTM (tanh) models demonstrate the most robust and balanced performance, as evidenced by their compact error distributions and the absence of major outliers. Outlier values were limited to a few inflation subcomponents, with “Restaurants and hotels” and “Transport” showing exceptionally high NMAE scores under the RNN-based models. These deviations suggest that price dynamics in these categories were particularly volatile or less predictable during this period, reducing the models’ forecasting accuracy. Overall, the analysis confirms that deep learning models, particularly those leveraging nonlinear activations, consistently deliver more reliable and accurate inflation forecasts across heterogeneous subcomponents.

Table 5. Descriptive statistics for the period 1 January 2007 to 31 December 2016.

Inflation Subcomponents	Average	Median	Std	Min	Max	Range	N
Alcoholic beverages, tobacco	3.25	3.40	0.90	1.40	4.90	6.00	120
Clothing and footwear	0.59	0.60	0.92	−2.90	3.10	5.10	120
Communication	−1.81	−1.75	1.30	−5.00	0.10	8.50	120
Education	2.34	1.60	2.54	0.30	9.60	4.90	120
Food and non-alcoholic beverages	1.76	1.55	1.87	−1.50	6.70	3.50	120
Furnishings, household equipment, and routine house maintenance	1.01	1.00	0.66	0.00	2.20	8.20	120
Health	1.23	1.10	0.71	−0.60	2.80	2.20	120
Housing, water, electricity, gas, and other fuels	2.03	2.05	2.28	−1.80	6.70	9.30	120
Miscellaneous goods and services	1.78	2.00	0.67	0.70	2.80	12.70	120
Recreation and culture	0.56	0.35	0.89	−1.00	3.90	2.10	120
Restaurants and hotels	2.06	1.80	0.74	1.00	3.60	2.60	120
Transport	1.50	1.30	3.33	−5.50	7.20	3.40	120
HICP	1.47	1.60	1.18	−0.60	4.10	4.70	120

Source: own research.

reports descriptive statistics for the disaggregated components of inflation from 1 January 2007 to 31 December 2016. During this period, the highest average inflation rates were observed in alcoholic beverages and tobacco (3.25%) and education (2.34%), whereas communication remained deflationary with an average rate of −1.81%. Transport exhibited the highest volatility among all subcomponents (standard deviation of 3.33%), reflecting its sensitivity to external shocks such as oil price fluctuations. Conversely, alcoholic beverages and tobacco showed relatively stable price dynamics with the lowest standard deviation (0.90%). The inflation rates for furnishings, health, and miscellaneous goods and services remained moderate and stable, indicating limited variation, recorded an average of 1.47% with moderate dispersion (standard deviation of 1.18%), suggesting stability. The HICP reflects overall inflation; generally, there was a low-inflation environment throughout the decade. These results confirm the continued heterogeneity of inflation behaviour across sectors and highlight the necessity of component-level analysis for better understanding inflationary trends and policy implications.

Table 6. NMAE indicators for the period 1 January 2016 to 31 December 2016.

NMAE	RNN (ELU)	LSTM (ELU)	GRU (ELU)	RNN (tanh)	LSTM (tanh)	GRU (tanh)	RNN (lin)	LSTM (lin)	GRU (lin)	SVR	RFR	Avg.
Alcoholic beverages, tobacco	0.0591	0.0747	0.0434	0.0811	0.0871	0.0446	0.0488	0.0619	0.0548	0.0869	0.1289	0.0701
Clothing and footwear	0.0837	0.0697	0.0858	0.0728	0.0468	0.0755	0.0476	0.0448	0.0472	0.0579	0.0640	0.0632
Communication	0.0359	0.0182	0.0339	0.0501	0.0159	0.0409	0.0186	0.0287	0.0202	0.0711	0.1192	0.0412
Education	0.0277	0.0229	0.0371	0.0236	0.0266	0.0171	0.0237	0.0453	0.0155	0.0274	0.0312	0.0271
Food and non-alcoholic beverages	0.0406	0.0370	0.0532	0.0539	0.0412	0.0393	0.0448	0.0404	0.0430	0.0405	0.0450	0.0435
Furnishings, household equipment, and routine house maintenance	0.0590	0.0495	0.0347	0.0863	0.0477	0.0407	0.0643	0.0445	0.0396	0.0431	0.0301	0.0491
Health	0.0574	0.0363	0.0322	0.0894	0.0241	0.0492	0.0292	0.0272	0.0341	0.0415	0.0364	0.0415
Housing, water, electricity, gas, and other fuels	0.0427	0.0679	0.0395	0.0364	0.0572	0.0360	0.0442	0.0748	0.0734	0.0437	0.0580	0.0522
Miscellaneous goods and services	0.0441	0.0740	0.0401	0.0440	0.0749	0.0403	0.0548	0.0694	0.0518	0.0824	0.0676	0.0585
Recreation and culture	0.4279	0.1684	0.1962	0.1975	0.2692	0.1252	0.1509	0.4129	0.1835	0.1802	0.0977	0.2191
Restaurants and hotels	0.0360	0.0382	0.0427	0.0677	0.0403	0.0448	0.0279	0.0363	0.0407	0.0445	0.0751	0.0449
Transport	0.1453	0.0640	0.0581	0.1041	0.0650	0.0646	0.0677	0.0626	0.0553	0.0729	0.0615	0.0747
Average	0.0883	0.0601	0.0581	0.0756	0.0663	0.0515	0.0519	0.0791	0.0549	0.0660	0.0679

Lower NMAE values indicate better forecasting accuracy. To enhance interpretability, the results are displayed using a color scale ranging from dark green (best performance) to dark red (worst performance), allowing for a quick visual comparison across models and categories. Source: own research.

shows the NMAE estimates for the year 2016. In the Alcoholic beverages and tobacco subgroup, the best performance was achieved with the GRU (ELU) method with a value of 0.0434, while the worst estimation accuracy was shown by the RFR with a value of 0.1289. For the Clothing and footwear subcomponent, the LSTM (linear) model was the most accurate (0.0448), while the GRU (ELU) was the least accurate, with a difference of 0.0858. For the Communication forecast, the LSTM (tanh) performed best (0.0159), while the RFR algorithm produced the weakest forecast (0.1192). For the Education component, the best (0.0155) and worst (0.0453) model performances were in a much narrower range than in 2009. The former was produced by GRU (linear) and the latter by LSTM (linear). For Food and non-alcoholic beverages, the model with an ELU activation function, LSTM, was the most accurate with an NMAE of 0.0370, while the least accurate was RNN (tanh) (0.0539). For Furnishings, household equipment, and routine house maintenance, RFR showed the best performance with 0.0301, while RNN (tanh) had the worst estimation performance (0.0863). For the Health subcomponent, LSTM (tanh) achieved the best result (0.0241), while RNN (tanh) performed the worst (0.0894). For the Housing, water, electricity, gas and other fuels subcomponent, GRU (tanh) was the most accurate with 0.0360, while LSTM (linear) was the least accurate with an NMAE of 0.0748. For the Miscellaneous goods and services type, GRU (ELU) achieved the best performance with 0.0401, while SVR was considered the least accurate algorithm (0.0824). The Recreation and culture category presented the greatest challenge to the models in 2016. This is where the largest gap between the performance of the best (RFR, 0.0977) and worst (RNN-ELU, 0.4279) models is observed. For the Restaurants and hotels sub-type, we obtained much more consolidated results than in the previous period. The best performing model was RNN (linear) (0.0279), while the worst was RFR (0.0751). For the Transport subtype, the GRU (linear) was the most useful with 0.0553, while the RNN (ELU) was considered the worst (0.1453). The best result for the period was obtained for Education, while the worst was obtained for Recreation and culture.

Looking at the average model performance by subtype, we find that GRU (tanh) and RNN (linear) performed outstandingly with minimal variation from each other. The RNN (ELU) model achieved the weakest average rating.

Figure 2 displays the distribution of Normalized Mean Absolute Error (NMAE) values across all forecasting models for the 2016 period, representing a phase of relative macroeconomic stability. Compared with the preceding period, the dispersion of the NMAE values appears generally narrower, suggesting improved model convergence and reduced volatility in forecast errors. The deep learning models (RNN, LSTM, GRU) again outperform the traditional approaches (SVR and RFR), as evidenced by their lower medians and tighter interquartile ranges. Among them, the GRU (ELU) and LSTM (tanh) models exhibit the lowest median errors, reflecting their strong capacity to capture temporal dependencies and nonlinear dynamics in the inflation data. The use of nonlinear activation functions such as ELU and tanh leads to more compact error distributions and fewer extreme outliers, confirming their stabilizing effect on model performance. In contrast, the linear activation variants display slightly higher median NMAE values and larger spreads, indicating lower flexibility when modelling complex price movements. Classical machine learning models, particularly RFR, show higher variability and median errors, reaffirming their weaker adaptability to macroeconomic shocks and structural changes. Nearly all models exhibited outlier values associated with the “Recreation and culture” category, indicating a systemic forecasting challenge rather than a model-specific limitation. This pattern suggests that structural or irregular shocks within this subcomponent may have been difficult to capture even for the more complex learning architectures. Overall, the distribution patterns suggest that nonlinear deep learning models provide not only higher accuracy but also greater robustness, maintaining consistent performance even in a stable inflationary environment.

Table 7. Descriptive statistics for the period 1 January 2014 to 31 December 2023.

Inflation Subcomponents	Average	Median	Std	Min	Max	Range	N
Alcoholic beverages, tobacco	3.21	2.80	1.54	1.40	7.70	9.60	120
Clothing and footwear	0.89	0.50	1.54	−3.30	6.30	4.30	120
Communication	−1.11	−1.00	1.00	−3.30	1.00	29.30	120
Education	0.63	0.50	1.76	−3.60	4.60	8.00	120
Food and non-alcoholic beverages	3.19	1.40	4.53	−1.10	17.50	6.30	120
Furnishings, household equipment and routine house maintenance	1.62	0.40	2.57	−0.10	9.10	18.60	120
Health	1.04	0.90	0.66	0.00	3.00	9.20	120
Housing, water, electricity, gas and other fuels	2.83	1.30	5.65	−6.10	23.20	8.20	120
Miscellaneous goods and services	1.78	1.40	1.32	0.50	5.60	19.10	120
Recreation and culture	1.61	1.00	1.93	−1.40	6.60	5.10	120
Restaurants and hotels	2.84	1.90	2.37	0.20	8.80	8.60	120
Transport	2.19	1.35	4.48	−4.50	14.60	3.00	120
HICP	2.20	1.30	2.74	−0.60	10.60	11.20	120

Source: own research.

summarizes the descriptive statistics of inflation subcomponents between 1 January 2014 to 31 December 2023, a period marked by heightened global economic volatility. Food and non-alcoholic beverages (3.19%) and alcoholic beverages and tobacco (3.21%) registered the highest average inflation rates, while communication once again exhibited a deflationary trend with a mean of −1.11%. Housing-related costs displayed the greatest volatility (standard deviation of 5.65%), with values ranging from −6.10% to 23.20%, underscoring the impact of energy price shocks and regulatory shifts. Transport and food also showed substantial variability, with standard deviations of 4.48% and 4.53%, respectively. In contrast, health (0.66%) and communication (1.00%) remained relatively stable in terms of price fluctuations. Interestingly, while the HICP averaged 2.20%, its standard deviation of 2.74% reflects increased inflation dispersion during this decade, especially in the post-pandemic years. Overall, the data highlight significant heterogeneity and rising volatility in inflation dynamics, necessitating careful monitoring of disaggregated components for accurate inflation forecasting and policy formulation.

Table 8. NMAE indicators for the period 1 January 2023 to 31 December 2023.

NMAE	RNN (ELU)	LSTM (ELU)	GRU (ELU)	RNN (tanh)	LSTM (tanh)	GRU (tanh)	RNN (lin)	LSTM (lin)	GRU (lin)	SVR	RFR	Avg.
Alcoholic beverages, tobacco	0.1338	0.2291	0.2115	0.1809	0.2392	0.2023	0.0575	0.2320	0.1996	0.3622	0.3963	0.2222
Clothing and footwear	0.1682	0.2186	0.1649	0.0728	0.1172	0.3111	0.1599	0.4045	0.4088	0.4967	0.1502	0.2430
Communication	0.0767	0.0702	0.0742	0.0782	0.0748	0.0760	0.0613	0.0774	0.0743	0.0904	0.0669	0.0746
Education	0.3242	0.1254	0.0597	0.1672	0.1110	0.0449	0.0781	0.0867	0.0706	0.5109	0.1484	0.1570
Food and non-alcoholic beverages	0.3822	0.1661	0.2537	0.0982	0.2554	0.2338	0.0849	0.1721	0.2194	0.0907	0.2203	0.1979
Furnishings, household equipment and routine house maintenance	0.2587	0.2702	0.3061	0.0988	0.2684	0.2718	0.2004	0.1784	0.2863	0.1622	0.2710	0.2338
Health	0.1431	0.9958	0.1240	0.0804	0.3936	0.1761	0.0887	0.7170	0.2108	0.3153	0.3552	0.3273
Housing, water, electricity, gas and other fuels	0.0955	0.1096	0.2984	0.1063	0.1676	0.3288	0.1721	0.2676	0.2887	0.2583	0.3039	0.2179
Miscellaneous goods and services	0.4318	1.1947	0.2984	0.1348	0.9374	0.3295	0.2308	1.7279	0.3532	0.1386	0.2054	0.5439
Recreation and culture	0.1024	0.1232	0.1430	0.0865	0.2493	0.1209	0.0845	0.1545	0.2331	0.1140	0.1036	0.1377
Restaurants and hotels	0.1184	0.1084	0.1385	0.0445	0.0833	0.1234	0.1625	0.1240	0.0672	0.0930	0.1104	0.1067
Transport	0.1339	0.1178	0.1243	0.1204	0.1492	0.1004	0.0965	0.1200	0.0946	0.0868	0.1035	0.1134
Average	0.1974	0.3108	0.1831	0.1058	0.2539	0.1933	0.1231	0.3552	0.2089	0.2266	0.2029

Lower NMAE values indicate better forecasting accuracy. To enhance interpretability, the results are displayed using a color scale ranging from dark green (best performance) to dark red (worst performance), allowing for a quick visual comparison across models and categories. Source: own research.

shows the NMAE estimates for the year 2023. The recent global economic problems (COVID, Russian–Ukrainian conflict) have caused a significant rise in inflation globally, with the impact even more pronounced in the European Union. This period is considered to be the most extreme for the tests, which also underpins our performance expectations for the models. In the Alcoholic beverages and tobacco subgroup, the best performance was achieved with the RNN (linear) method with a value of 0.0575, while the worst estimation accuracy was shown by the RFR with a value of 0.3963. For the Clothing and footwear subcomponent, the RNN (tanh) model was the most accurate (0.0728), while the SVR was the least accurate with 0.4967. For the Communication predictions, the RNN (linear) also performed the best (0.0613), while the SVR algorithm produced the weakest prediction result (0.0904). For the Education component, the best (0.0449) and worst (0.5109) model performances were in a much wider range. The former was produced by GRU (tanh) and the latter by SVR, which is a rather poor result. For Food and non-alcoholic beverages, a model with a linear activation function, RNN was the most accurate with an NMAE value of 0.0849, while RNN (ELU) was the least accurate (0.3822). For Furnishings, household equipment, and routine house maintenance, RNN (tanh) showed the best performance with 0.0988, while GRU (ELU) had the worst estimation performance (0.3061). For the Health subtype, we observed one of the largest differences in model performance. The most optimal result was achieved by RNN (tanh) (0.0804), while LSTM (ELU) performed the worst (0.9958). When examining the Housing, water, electricity, gas, and other fuels subcomponent, RNN (ELU) performed the best (0.0955), while GRU (tanh) performed the worst (0.3288). For the Miscellaneous goods and services type, the best performance was achieved by RNN (tanh) with 0.1348, while the least useful algorithm was LSTM (linear) (1.7279), which performed extremely poorly. Considering the NMAE values, this category is considered the most unpredictable of all for the 2023 forecast horizon. For the Recreation and culture category, the highest estimation accuracy was achieved by RNN (linear) (0.0845), while the least performing model was LSTM (tanh) (0.2493). For the Restaurants and hotels subcategory, the best performing algorithm was RNN (tanh) (0.0445), while the worst performing algorithm was RNN (linear) (0.1625). For the Transport subtype, the SVR was able to achieve the lowest result with 0.0868, while the LSTM (tanh) was considered the least useful (0.1492). The best result over time was achieved for Restaurants and hotels, while the worst result was achieved for Miscellaneous goods and services.

As expected, the most challenging period was 2023, which is reflected in the average performance of the models. In this comparison, the best performance is attributed to the RNN (tanh) algorithm, while the worst average performance, with a significant gap, is obtained by the LSTM (linear) model, with a prominent role of the exceptionally poor performance for the Miscellaneous goods and services subtype.

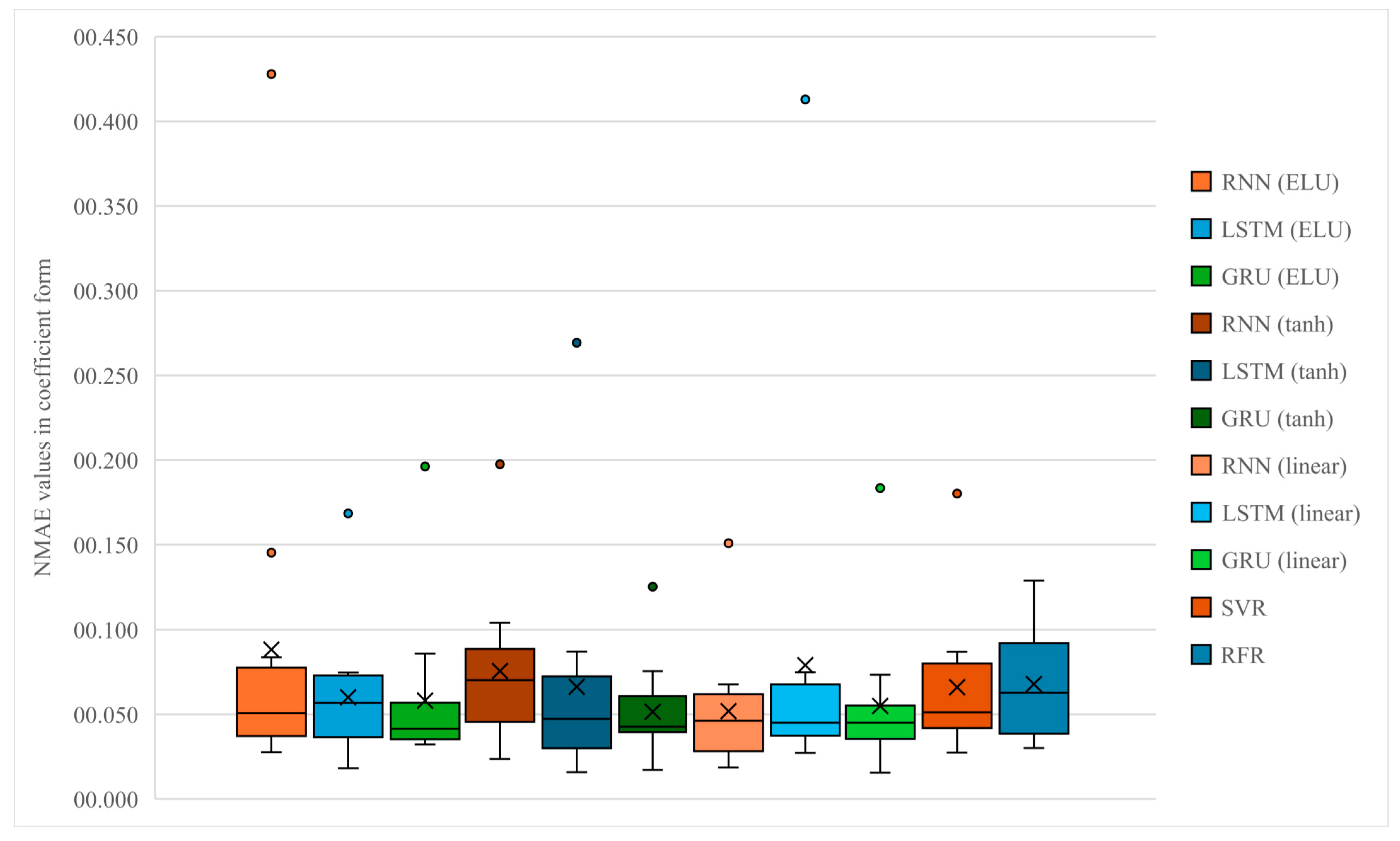
Figure 3 presents the distribution of Normalized Mean Absolute Error (NMAE) values across all forecasting models for the 2023 period. The results reveal a generally higher dispersion of errors compared to earlier periods, reflecting the elevated volatility and uncertainty of the inflation environment during the post-pandemic and geopolitical shock phase. While deep learning models continue to outperform the traditional approaches, the differences among architectures become more pronounced under these unstable conditions. The RNN (tanh) and RNN (linear) models exhibit the lowest median NMAE values, indicating better adaptability to abrupt structural changes in the inflation series. In contrast, LSTM and GRU models, especially those using ELU and tanh activations, show wider interquartile ranges and the presence of outliers, suggesting sensitivity to short-term volatility. Traditional machine learning models, particularly SVR and RFR, perform significantly weaker, with both higher median and mean NMAE values, indicating reduced robustness in highly non-stationary environments. Despite the increased overall error dispersion, nonlinear recurrent models still maintain a relative advantage in stability and predictive accuracy. This pattern underlines the superior flexibility of deep learning architectures in capturing the rapidly changing inflation dynamics characteristic of the 2023 regime.

Across the three examined periods (2009, 2016, and 2023), the evolution of forecasting performance reflects clear links between macroeconomic stability and model accuracy. During the 2009 crisis period, models exhibited higher NMAE dispersion, indicating instability in capturing the rapidly changing inflation dynamics. The 2016 control period showed a noticeable improvement, with all recurrent neural network variants producing more compact error distributions and lower median values, reflecting greater predictability in a stable environment. By contrast, in 2023 forecasting accuracy deteriorated again, and the variance of errors widened significantly. Among the tested models, LSTM and GRU architectures with nonlinear activation functions (particularly tanh and ELU) consistently achieved the most stable results across all regimes. Traditional machine learning methods, especially SVR and RFR, tended to produce larger errors and greater variability, confirming their lower adaptability to nonlinear and volatile inflation patterns. The dispersion in the boxplots across models and categories serves as an empirical proxy for forecast uncertainty, reflecting variation in model-specific error distributions. This dispersion illustrates how uncertainty increases under volatile regimes, while narrowing substantially in periods of macroeconomic stability. Outlier observations were primarily linked to “Miscellaneous goods and services” and, to a lesser extent, “Health”. The concentration of extreme values in these categories especially across LSTM variants implies that model performance was more sensitive to the changing dynamics of these sectors in the post-pandemic period. Overall, the results underline that deep learning approaches are not only superior under stable conditions but also more resilient to economic shocks, capturing complex dependencies that traditional algorithms fail to model effectively.

Table 9. NMAE indicators for the period 2009, 2016, and 2023 in case of HICP.

NMAE	RNN (ELU)	LSTM (ELU)	GRU (ELU)	RNN (tanh)	LSTM (tanh)	GRU (tanh)	RNN (lin)	LSTM (lin)	GRU (lin)	SVR	RFR	Avg.
2009	0.1380	0.2627	0.1644	0.1507	0.1875	0.1542	0.0530	0.2089	0.1388	0.3987	0.3309	0.1989
2016	0.0464	0.0287	0.0320	0.0473	0.0308	0.0319	0.0399	0.0423	0.0291	0.0474	0.0434	0.0381
2023	0.1895	0.1203	0.1789	0.0613	0.0493	0.1333	0.0674	0.0711	0.1366	0.2476	0.3076	0.1421
Average	0.1246	0.1372	0.1251	0.0864	0.0892	0.1065	0.0534	0.1074	0.1015	0.2312	0.2273

Lower NMAE values indicate better forecasting accuracy. To enhance interpretability, the results are displayed using a color scale ranging from dark green (best performance) to dark red (worst performance), allowing for a quick visual comparison across models. Source: own research.

presents the normalized mean absolute error (NMAE) of the HICP inflation forecasts, estimated by the different machine learning models for the three years under study: 2009, 2016, and 2023. For 2009, the errors are relatively high, especially for the SVR (0.3987) and RFR (0.3309) models, while the lowest error is obtained with the RNN linear activation (0.0530). This suggests that the more complex models did not necessarily perform better in the mid-crisis period. By 2016, forecast errors had decreased significantly, with the LSTM (ELU) model achieving the lowest error (0.0287) and the average error for all models decreasing to 0.0381. In 2023, NMAE values increased again, especially for SVR (0.2476) and RFR (0.3076), which can be attributed to the post-pandemic and geopolitically uncertain period. Here again, the best performance was shown by LSTM with tanh activation (0.0493), which proved to be more robust in the changed environment. The year-to-year changes reflect the interaction between the volatility of the inflation environment and the adaptability of the models. Traditional machine learning algorithms, such as SVR and RFR, have consistently performed the poorest, confirming the advantage of recursive neural networks in predicting time-dependent economic time series. Interestingly, in 2016 almost all models performed with exceptionally low error, indicating the stability of inflation trends and the well-learned patterns of the models. Overall, the results suggest that the activation functions and the economic context of the period have a significant impact on the forecasting performance of the models. Simpler, linear RNN-based approaches offer a reliable and robust alternative in turbulent periods.

To ensure comparability with traditional statistical approaches, two benchmark models Seasonal Autoregressive Integrated Moving Average (SARIMA—automatic orders with drift) and Exponential Smoothing (ETS) were also implemented. Both models were estimated using the same 12-month rolling window framework as applied to the machine learning and deep learning approaches, ensuring temporal consistency and preventing information leakage. In addition to the inflation subcomponents, the HICP was also forecasted for each examined period, with all models re-estimated sequentially to capture potential structural changes in the data. The evaluation metrics, including MAE and NMAE, are reported in Appendix A 

Table A5. MAE and NMAE indicators of SARIMA and ETS models for the period 2009, 2016, and 2023 in case of subcomponents and HICP.

	2009				2016				2023
	SARIMA		ETS		SARIMA		ETS		SARIMA		ETS
	MAE	NMAE	MAE	NMAE	MAE	NMAE	MAE	NMAE	MAE	NMAE	MAE	NMAE
Alcoholic beverages, tobacco	0.7138	0.1020	0.6116	0.0874	0.2081	0.0595	0.2500	0.0714	1.7880	0.2838	1.7477	0.2774
Clothing and footwear	0.3456	0.0576	0.2771	0.0462	0.4977	0.0830	0.5456	0.0909	1.1799	0.1229	1.3289	0.1384
Communication	0.8836	0.0982	0.7974	0.0886	0.3862	0.0757	0.1149	0.0225	0.3863	0.0898	0.6296	0.1464
Education	7.4545	0.8192	0.5104	0.0561	0.3474	0.0374	0.3910	0.0420	0.8898	0.1085	0.5010	0.0611
Food and non-alcoholic beverages	2.0776	0.2534	0.7701	0.0939	0.8826	0.1076	0.3418	0.0417	2.9229	0.1571	9.8771	0.5310
Furnishings, household equipment and routine house maintenance	0.5462	0.3414	0.5141	0.3213	0.1650	0.0750	0.5544	0.2520	5.9219	0.6437	6.0449	0.6571
Health	0.6780	0.0892	0.9050	0.1191	0.2030	0.0597	0.1688	0.0497	0.7086	0.2362	0.9770	0.3257
Housing, water, electricity, gas and other fuels	2.3022	0.2709	3.7486	0.4410	0.6761	0.0795	0.5839	0.0687	14.1232	0.4820	2.3557	0.0804
Miscellaneous goods and services	0.1627	0.0904	0.1676	0.0931	0.2519	0.1200	0.2301	0.1096	0.5023	0.0985	0.7207	0.1413
Recreation and culture	0.2770	0.0893	0.3884	0.1253	0.4198	0.0857	1.0785	0.2201	1.5927	0.1991	0.8337	0.1042
Restaurants and hotels	1.5107	0.4196	1.5139	0.4205	0.1108	0.0426	0.0926	0.0356	0.9166	0.1066	2.1562	0.2507
Transport	1.3214	0.1040	2.1421	0.1687	1.5447	0.1216	1.5222	0.1199	5.3045	0.2777	5.1734	0.2709
HICP	1.1258	0.2395	1.3273	0.2824	0.4546	0.0967	0.3057	0.0650	3.1388	0.2803	5.2836	0.4717

Source: own research.

. The results show that neither of the baseline statistical models achieved superior predictive performance compared to the best-performing machine learning models within each regime and inflation category. This finding underscores the added value of advanced data-driven methods in capturing nonlinear and time-varying inflation dynamics that traditional linear frameworks often fail to represent adequately. Overall, the SARIMA and ETS models serve as meaningful benchmarks, confirming the robustness and relative advantage of the applied machine and deep learning architectures.

Building on the model performance comparisons, we calculated the Forecastability Index (FI) to assess the relative predictability of each inflation subcomponents and the overall HICP. This index provides a clear perspective on which categories are easier or more challenging to forecast, complementing the insights gained from the benchmark models.

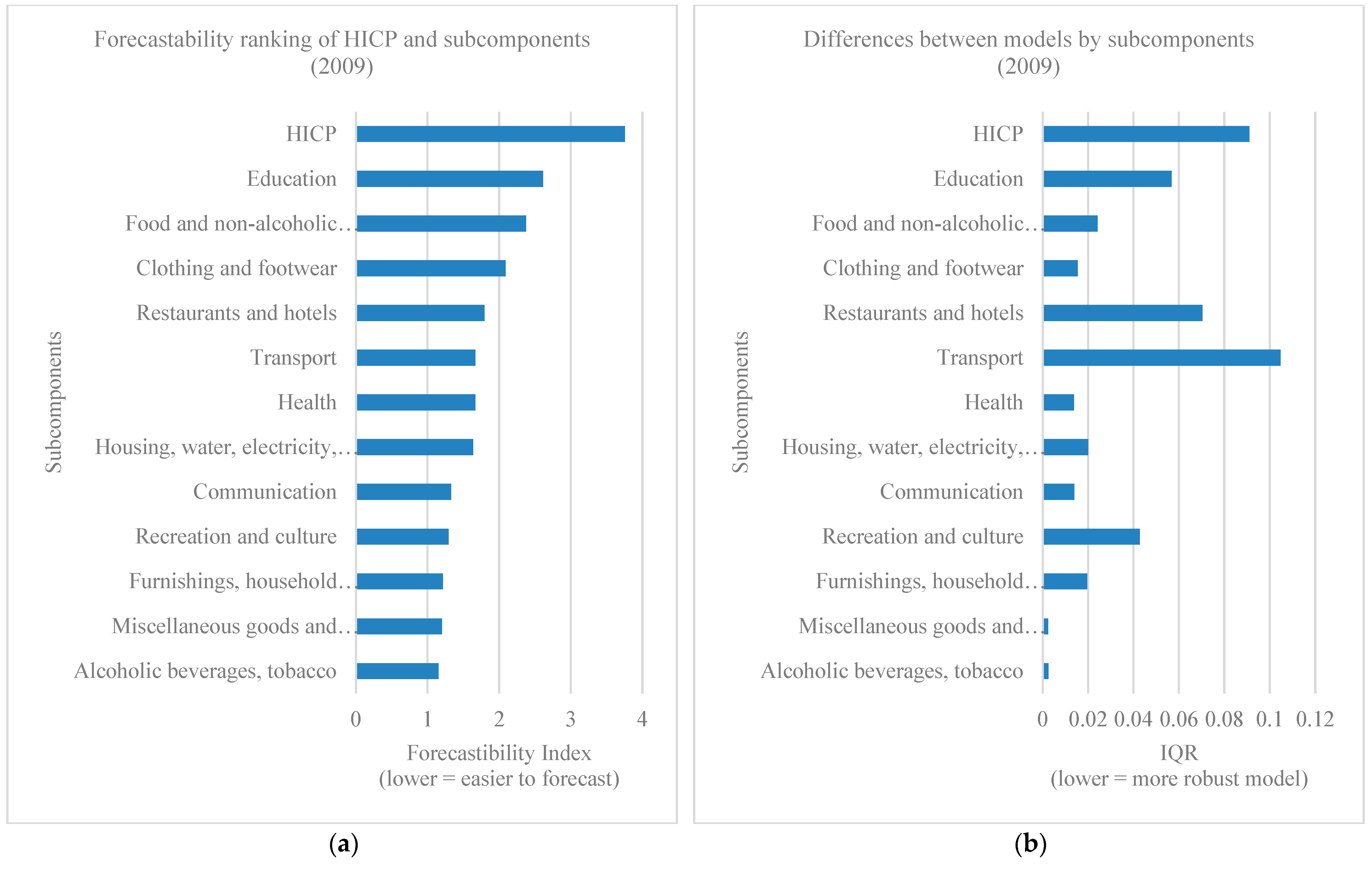
Figure 4 displays the ranking of inflation subcomponents according to their Forecastability Index (FI) and interquartile range (IQR) in 2009. The results show that Alcoholic beverages and tobacco and Miscellaneous goods and services are among the most predictable categories, as indicated by their low FI values. A middle group, including Recreation and culture, Communication, and Housing, water, electricity, gas and other fuels, exhibits moderately higher FI scores, reflecting a greater forecasting challenge. The most difficult components to predict are Clothing and footwear, Food and non-alcoholic beverages, and Education, all of which record FI values well above 2. Finally, the aggregated HICP shows by far the highest FI, suggesting that headline inflation is considerably more difficult to model than its disaggregated subcomponents. The IQR values provide complementary insights into the robustness of forecasting performance. A lower IQR implies that the predictability of a subcomponent is less dependent on the choice of model, while a higher IQR indicates greater variability across models. The findings suggest that categories such as Alcoholic beverages and tobacco and Miscellaneous goods and services are not only easy but also stable to forecast. In contrast, sectors like Transport, Restaurants and hotels, and Education display relatively high IQR values, highlighting that forecasting accuracy for these subcomponents is more sensitive to model specification.

Figure 5 displays the ranking of inflation subcomponents according to their Forecastability Index (FI) and interquartile range (IQR) in 2016. The analysis reveals that Food and non-alcoholic beverages is the most predictable category, with the lowest FI value, followed by the aggregated HICP and Transport, which also fall within the relatively easier-to-forecast group. A mid-range of predictability is observed for Clothing and footwear, Housing, water, electricity, gas and other fuels, and Miscellaneous goods and services, each with FI values between 1.4 and 1.5. Higher forecasting difficulty is associated with categories such as Restaurants and hotels, Alcoholic beverages and tobacco, Furnishings, household equipment and routine house maintenance, Health, and Education, where FI values approach or exceed 1.6–1.7. The most challenging components to predict in this period are Recreation and culture and Communication, both with FI values well above 2, indicating significant forecasting complexity. The IQR results provide additional insight into the robustness of predictions across models. Categories such as Food and non-alcoholic beverages, HICP, and Transport show very low IQR values, suggesting that their forecastability is stable and largely independent of model choice. In contrast, Recreation and culture has by far the highest IQR, underlining considerable dispersion in model performance and a lack of robustness. Moderate IQR values are observed for Clothing and footwear, Miscellaneous goods and services, and Alcoholic beverages and tobacco, pointing to greater sensitivity to model specification. Overall, the IQR analysis highlights that while some subcomponents are consistently predictable across models, others, especially Recreation and culture and Communication, remain both difficult and unstable to forecast.

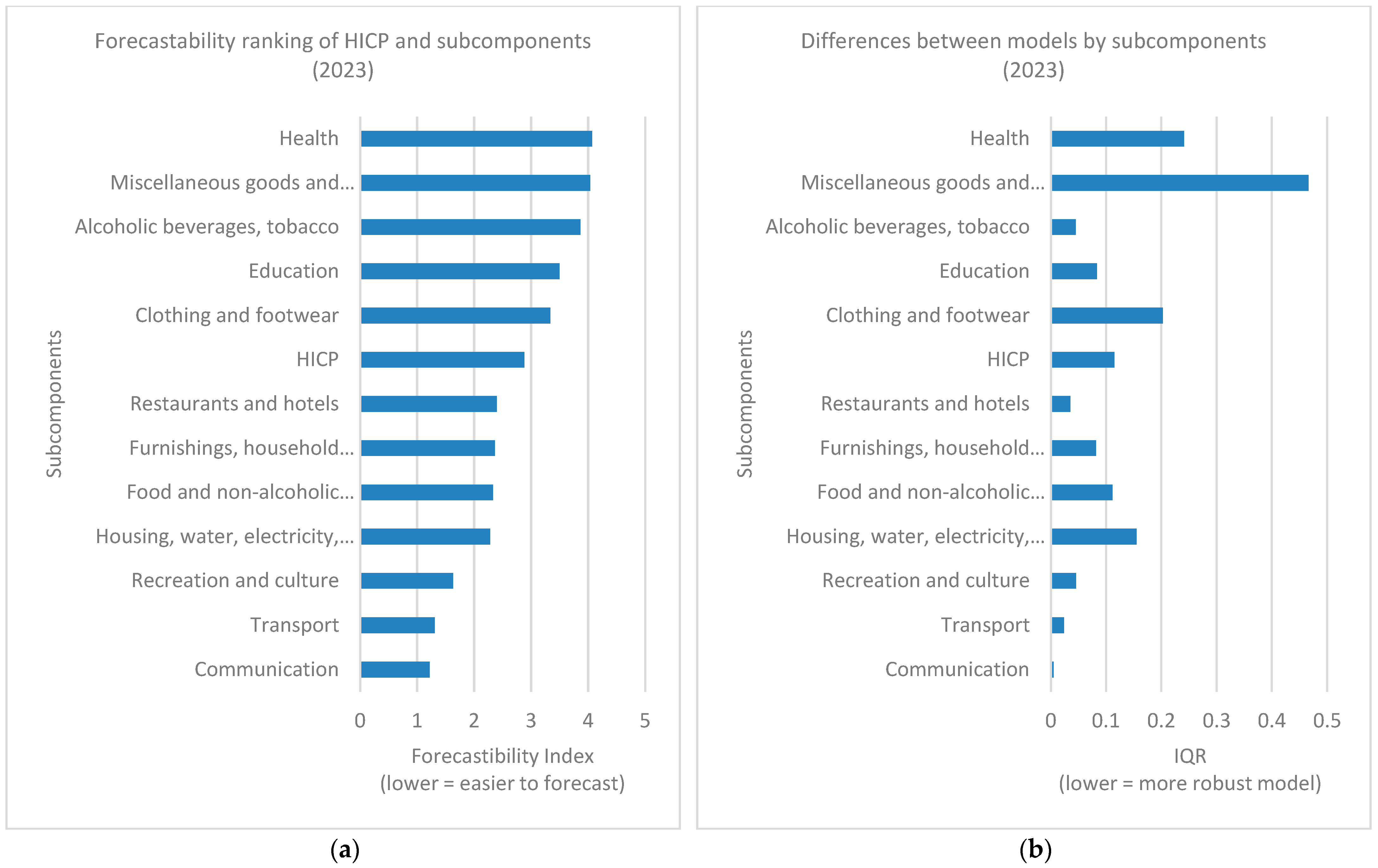
Figure 6 displays the ranking of inflation subcomponents according to their Forecastability Index (FI) and interquartile range (IQR) in 2023. The results indicate that Communication is the most predictable category in this sample, with the lowest FI value, followed by Transport and, to a lesser extent, Recreation and culture. These components can therefore be considered relatively easier to forecast. In contrast, a large group of subcomponents (including Housing, water, electricity, gas and other fuels, Food and non-alcoholic beverages, Furnishings, household equipment and routine house maintenance, and Restaurants and hotels) record substantially higher FI values, ranging between 2.2 and 2.4. The aggregated HICP also appears in this cluster, with an FI close to 2.9. The most difficult categories to forecast are found at the upper end of the ranking: Clothing and footwear, Education, Alcoholic beverages and tobacco, Miscellaneous goods and services, and Health, all of which exceed an FI of 3.0. Notably, Health and Miscellaneous goods and services stand out as particularly challenging, with FI values around 4.0, underscoring the considerable complexity of forecasting these components. The IQR results complement the FI analysis by capturing the robustness of forecasts across models. Communication again demonstrates high stability, with the lowest IQR, followed by Transport and Recreation and culture, where the dispersion of model errors is limited. Conversely, several subcomponents with high FI values also exhibit very large IQRs, indicating not only forecasting difficulty but also strong sensitivity to model choice. In particular, Miscellaneous goods and services and Health show extremely high IQRs (0.47 and 0.24, respectively), highlighting substantial heterogeneity across models. Other categories, such as Clothing and footwear, Food and non-alcoholic beverages, and Housing, water, electricity, gas, and other fuels, also record relatively large IQR values, reinforcing the notion that these subcomponents are both hard to predict and unstable across different model specifications.

As Table 9 presents the NMAE values for the overall HICP, while Table 3, Table 5 and Table 7 detail the same error metrics for various HICP subcategories over the years 2009, 2016, and 2023. In 2009, the subcategories generally show much lower forecast errors compared to the aggregate HICP NMAE of 0.1989. Most subcategories’ errors range between 0.03 and 0.14, with only a few exceptions like “Restaurants and hotels” and “Transport,” which have somewhat higher errors (~0.14–0.15). This contrast indicates that the aggregated inflation measure (HICP) was harder to predict than its individual components, possibly due to the combined volatility and complexity of the overall index. By 2016, both the aggregate HICP and subcategories experienced a marked improvement in forecast accuracy. The average NMAE for subcategories dropped to roughly 0.06, while the overall HICP error was even lower at 0.0381, reflecting a more stable inflation environment. Forecasting models performed consistently well across most subcategories, except for “Recreation and culture,” which exhibited notably higher errors (~0.22). This suggests that during stable economic conditions, models better capture both aggregate and disaggregated inflation dynamics, though some niche areas remain more challenging. The 2023 results show a substantial increase in errors across both HICP and its subcategories. The average NMAE for subcategories rose to about 0.22, while the aggregate HICP error reached 0.1421. Some categories such as “Miscellaneous goods and services” and “Health” had particularly high errors, with averages well above 0.3, indicating increased volatility or model difficulties possibly linked to post-pandemic and geopolitical uncertainties. Nevertheless, other subcategories like “Communication” and “Transport” maintained relatively lower errors (around 0.07–0.11), demonstrating some robustness in prediction. Overall, the results highlight that while individual components may be easier to forecast under normal conditions, in turbulent periods both aggregate and disaggregated inflation indicators face heightened prediction challenges.

4. Discussion

The results of this study provide important insights into the predictability of euro area inflation both at the aggregate level and across individual HICP subcomponents. A central finding is that deep learning models, in particular recurrent neural networks, consistently outperformed traditional machine learning methods such as SVR and RFR. This confirms the importance of using forecasting tools that are capable of capturing nonlinear dynamics and temporal dependencies in inflation data, as also emphasized in recent discussions on the role of expectations and uncertainty in shaping price developments (ECB, 2017; ECB, 2021) [3,4]. The introduction of the Forecastability Index (FI) and the Interquartile Range (IQR) provided a novel framework to evaluate not only forecasting accuracy but also the robustness of results across models. These indicators revealed substantial heterogeneity among inflation categories. While subcomponents such as Health and Education were characterized by lower errors and relatively stable performance across models, others, such as Recreation and culture and Restaurants and hotels, proved considerably more difficult to predict. These findings highlight that inflation should not be treated as a homogeneous process: some categories are inherently more volatile and sensitive to shocks, while others follow more stable and predictable dynamics.

The comparison across three different macroeconomic periods—the post-crisis environment of 2009, the relative stability of 2016, and the recent inflationary shock associated with the Russia–Ukraine conflict—further underlined the role of the broader economic environment in shaping forecastability. Periods of volatility and structural breaks were associated with higher forecasting errors and greater dispersion across models, while stable periods improved accuracy uniformly. This reinforces the importance of considering regime changes and external shocks in the evaluation of inflation forecasts, consistent with the view that expectations and sudden disruptions can amplify inflation dynamics (Binder & Kamdar, 2022; BIS, 2021) [1,2]. From a policy perspective, these results suggest that central banks and governments should not rely exclusively on headline HICP forecasts but also pay attention to subcomponent-level dynamics. Identifying which sectors can be forecast more reliably enables better-targeted interventions, for example, through temporary support measures or price regulation in sectors where price increases have disproportionate social effects, such as energy or food. At the same time, the more volatile categories point to areas where forecasting remains fragile, and where policymakers must account for greater uncertainty in their decision-making. Finally, this research demonstrates the added value of combining advanced modelling approaches with novel evaluation measures. By systematically assessing both the accuracy and stability of inflation forecasts, our findings contribute to a deeper understanding of inflation dynamics in the euro area. They also highlight the practical relevance of inflation subcomponent analysis for policymakers, businesses, and households, who all rely on forecasts to mitigate risks and make informed economic decisions.

5. Limitations and Future Research

Our study has several methodological limitations, which also point to directions for future research. The analysis primarily focused on comparing machine learning and deep learning models and therefore did not extensively cover traditional statistical approaches, such as ARIMA, ARIMAX, or VAR models. While these models are well-suited for time series forecasting, the aim of the present study was to evaluate the advantages and stability of machine learning methods across different macroeconomic environments.

Another limitation is that the models operated in a univariate framework, meaning that other macroeconomic factors (e.g., interest rates, unemployment, or commodity prices) potentially affecting inflation dynamics were not considered. However, it is important to note that previous literature suggests that including exogenous variables does not always lead to significant improvements in model performance, especially when the underlying time series already exhibits strong autocorrelative structures. One of the main advantages of neural network models is their ability to capture hidden, nonlinear patterns and dynamic relationships within the time series, providing effective forecasts even without incorporating external variables.

Furthermore, the study did not explore more recent, time-series-specific architectures, such as Temporal Fusion Transformer (TFT), Temporal Convolutional Network (TCN), Autoformer, Informer, or N-BEATS models, which are specifically designed to handle long-term dependencies and seasonal patterns. Including these models in future research could further enhance the generalizability and robustness of the findings. Future research may also integrate explainable AI methods, enabling better understanding of how specific economic shocks influence subcomponent-level inflation forecasts.

Finally, while the 12-month rolling window and time-based cross-validation used in this study adequately addressed overfitting concerns, experiments with longer time series or alternative validation strategies could provide additional insights into the temporal stability of the models. Overall, our research lays the foundation for understanding the role of machine learning models in inflation forecasting, while leaving multiple avenues open for further development and refinement.

6. Conclusions

This paper has investigated the forecastability of the HICP and its 12 subcomponents using a wide range of machine learning and deep learning models over three distinct macroeconomic periods (2009, 2016, and 2023). By comparing forecasting performance across both models and economic regimes, we aimed to provide a comprehensive understanding of the heterogeneity of inflation dynamics in the euro area. Our results confirm that advanced deep learning architectures, particularly RNN (linear) and LSTM (tanh), consistently achieved lower forecast errors than traditional machine learning techniques such as SVR and RFR. This indicates that models based on recurrent neural networks are better equipped to capture the nonlinearities and temporal dependencies that characterize inflation processes. A further contribution of this study is the introduction of the Forecastability Index (FI) and the Interquartile Range (IQR) as complementary measures of predictive performance. The FI allowed us to systematically rank the predictability of inflation categories, while the IQR provided insights into the robustness of results across models. Together, these indicators revealed clear differences among inflation components. Categories such as Health and Education emerged as the most predictable, with low forecast errors and limited model sensitivity, suggesting that their inflation dynamics are more stable and easier to capture. Conversely, components such as Recreation and culture, Restaurants and hotels, and, in some cases, Clothing and footwear proved particularly difficult to forecast, displaying both high FI values and wide inter-model variation. These results underscore the importance of moving beyond the aggregate HICP in order to better understand the sectoral sources of inflationary volatility.

Our temporal analysis highlights that the broader macroeconomic environment plays a decisive role in forecasting accuracy. Following the 2009 financial crisis, inflation was highly volatile, and forecasting errors increased substantially across all models. The 2016 period of stability represented the most favourable forecasting environment, with consistently lower errors and reduced heterogeneity across methods. Finally, the 2023 inflation shock, driven by the COVID-19 pandemic and the Russia–Ukraine conflict, once again exposed the limitations of conventional models under extreme uncertainty. In these periods of instability, recurrent neural networks and advanced architectures such as LSTM and GRU demonstrated superior adaptability, while classical regression-based models like SVR and RFR recorded significantly higher errors. These findings suggest that deep learning approaches not only outperform in general but are particularly valuable in volatile environments where nonlinear dynamics and structural breaks dominate. For central banks operating under inflation-targeting regimes, the inclusion of advanced machine learning and deep learning models can significantly enhance the timeliness and accuracy of inflation forecasts, especially when traditional models struggle to capture rapidly changing dynamics. This is particularly relevant in periods of crisis, when the credibility of monetary policy depends on responding quickly to shifting inflation expectations. For governments, the disaggregated analysis of inflation is equally important, as it reveals which components can be forecast with greater reliability and where forecasting remains fragile. This information can guide targeted interventions, such as energy price support schemes, subsidies, or temporary price caps, that aim to reduce the social burden of inflation without distorting the entire price system.

The study also has implications for financial institutions and firms. Accurate inflation forecasts affect the pricing of loans, bonds, and other financial instruments, as well as business investment and wage-setting decisions. Companies in inflation-sensitive sectors such as food, energy, housing, and real estate can benefit directly from more reliable forecasts by improving cost planning, supply chain management, and pricing strategies. By identifying which inflation components are systematically harder to predict, firms and investors can also better manage risk exposure in volatile markets.

In conclusion, this study demonstrates that a dual approach combining advanced deep learning methods with new evaluation metrics (FI and IQR) provides richer insights into both the accuracy and robustness of inflation forecasts. By explicitly focusing on subcomponents in addition to the headline HICP, we offer a more granular perspective on the sources of inflationary pressure. Our findings confirm that macroeconomic stability improves forecastability across the board, while periods of crisis and uncertainty amplify errors and model dispersion. Overall, this research not only strengthens the methodological toolkit for forecasting inflation but also contributes to policy debates by identifying which sectors can be forecast with greater confidence and where persistent challenges remain. Future research should continue to explore model innovations and extend the analysis to other economies, thereby improving the resilience of inflation forecasting frameworks in an increasingly uncertain global environment.

Our study paves the way for comparisons with forecasts based on models where predictions are constructed based on the impact of various economic variables. This can inspire debates that focus on analysing the accuracy of models with different approaches.