NCD-Pred: Forecasting Multichannel Shipboard Electrical Power Demand Using Neighborhood-Constrained VMD
Abstract
1. Introduction
1.1. Related Work
1.2. Contribution
2. Materials and Methods
2.1. Forecasting Nomenclature
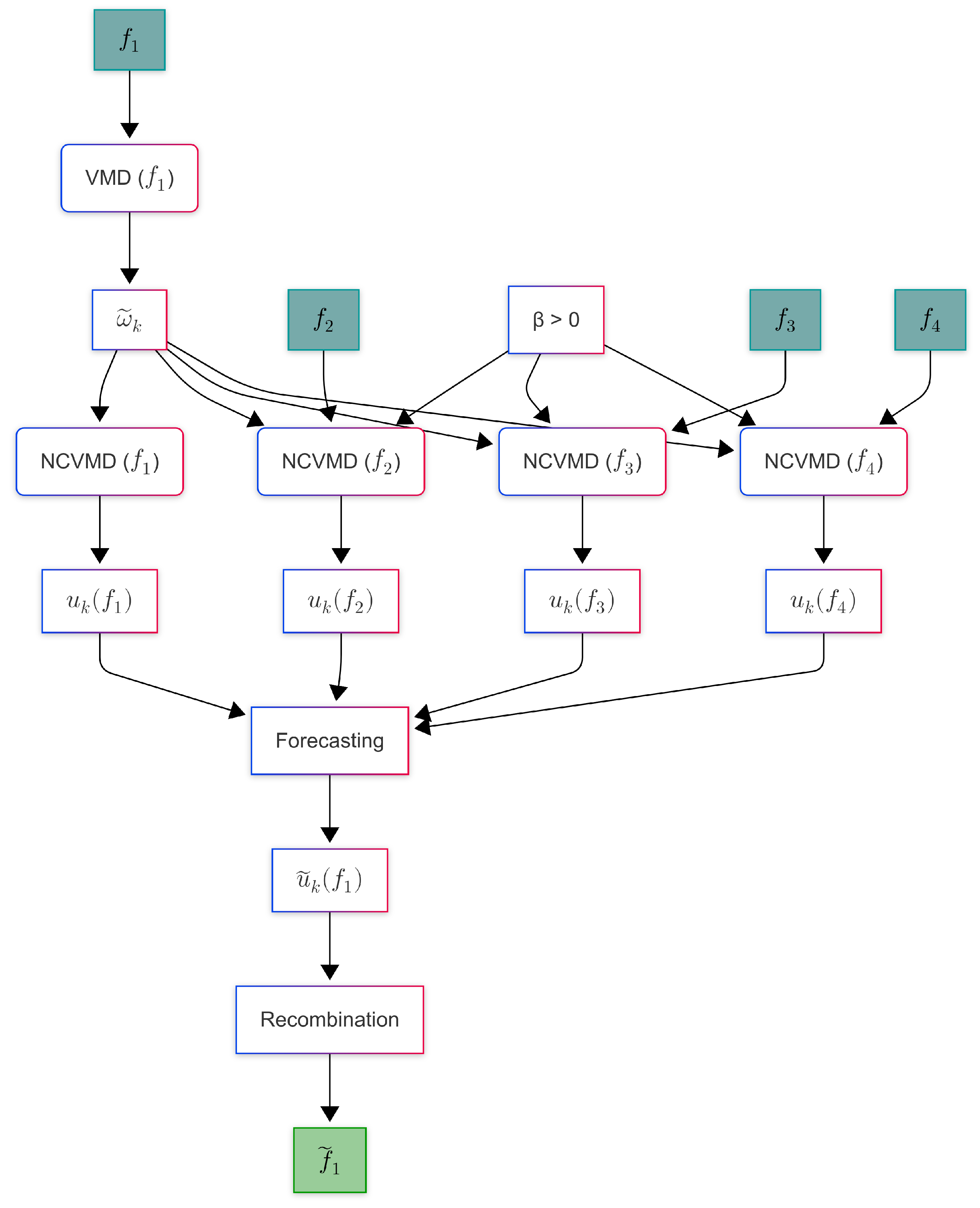
2.2. Neighborhood-Constrained Variational Mode Decomposition (Outline)
2.2.1. Background and Motivation
2.2.2. NCVMD: Core Principles and Formulation
- In a multi-channel forecasting system, the main channel—which contains the primary source of information—should be treated differently from the auxiliary channels, which convey less relevant information.
- Adjustable frequency matching among modes with closely related, yet distinct, spectral content should be supported. This enables a balance between decomposition error and alignment precision, resulting in a more flexible and adaptable algorithm.
- acts as a customizable weight that determines the influence of the neighborhood constraint;
- denotes the central frequency associated with the k-th mode of the main channel;
- weights the influence of the frequency difference.
2.2.3. Update Rules and Implementation
| Algorithm 1 ADMM Optimization of Neighborhood-Constrained Variational Mode Decomposition (NCVMD) |
|
2.2.4. Applications to Multi-Channel Forecasting
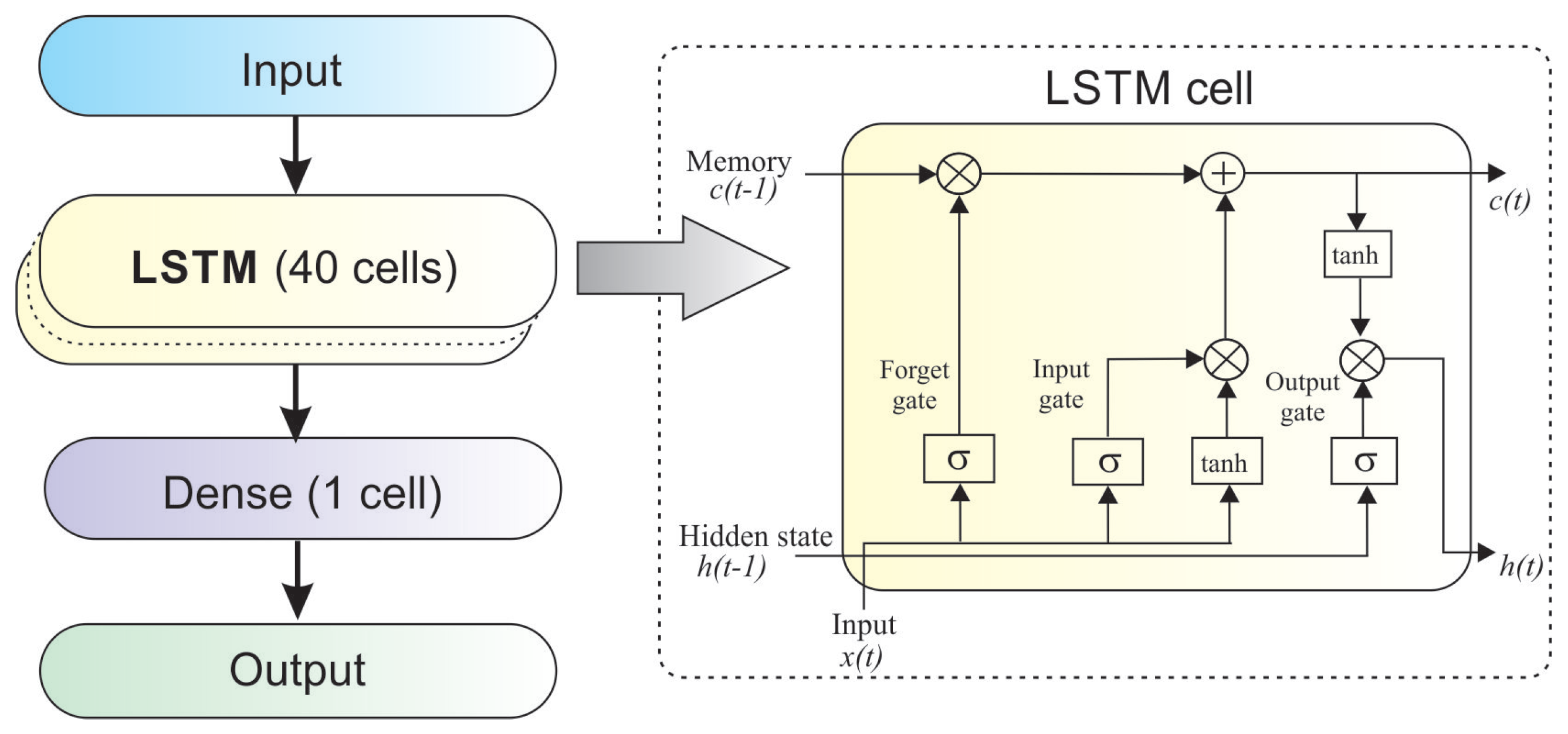
2.2.5. ANN-Based Forecasting and Recombination
2.3. Case Study Framework
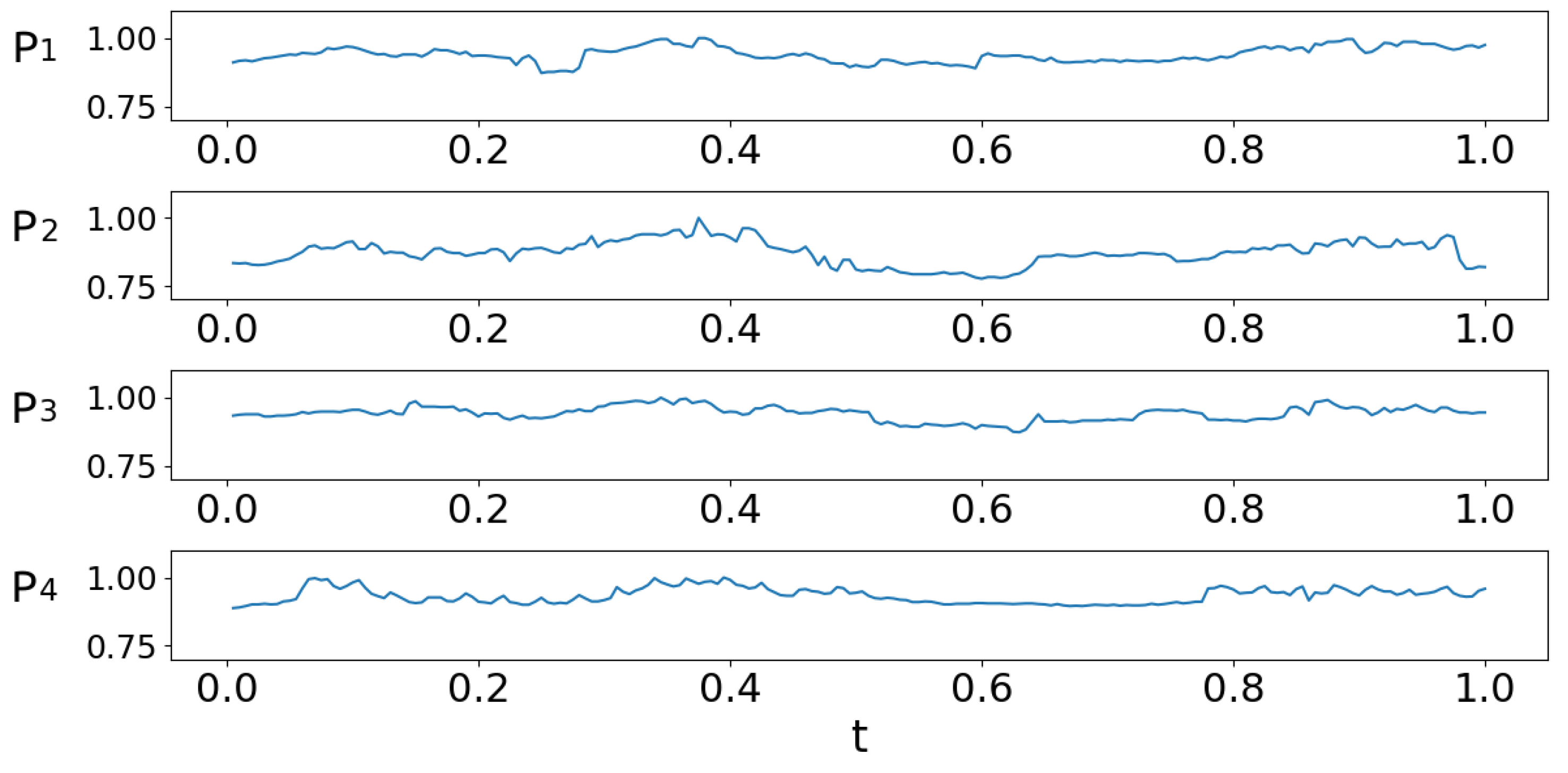
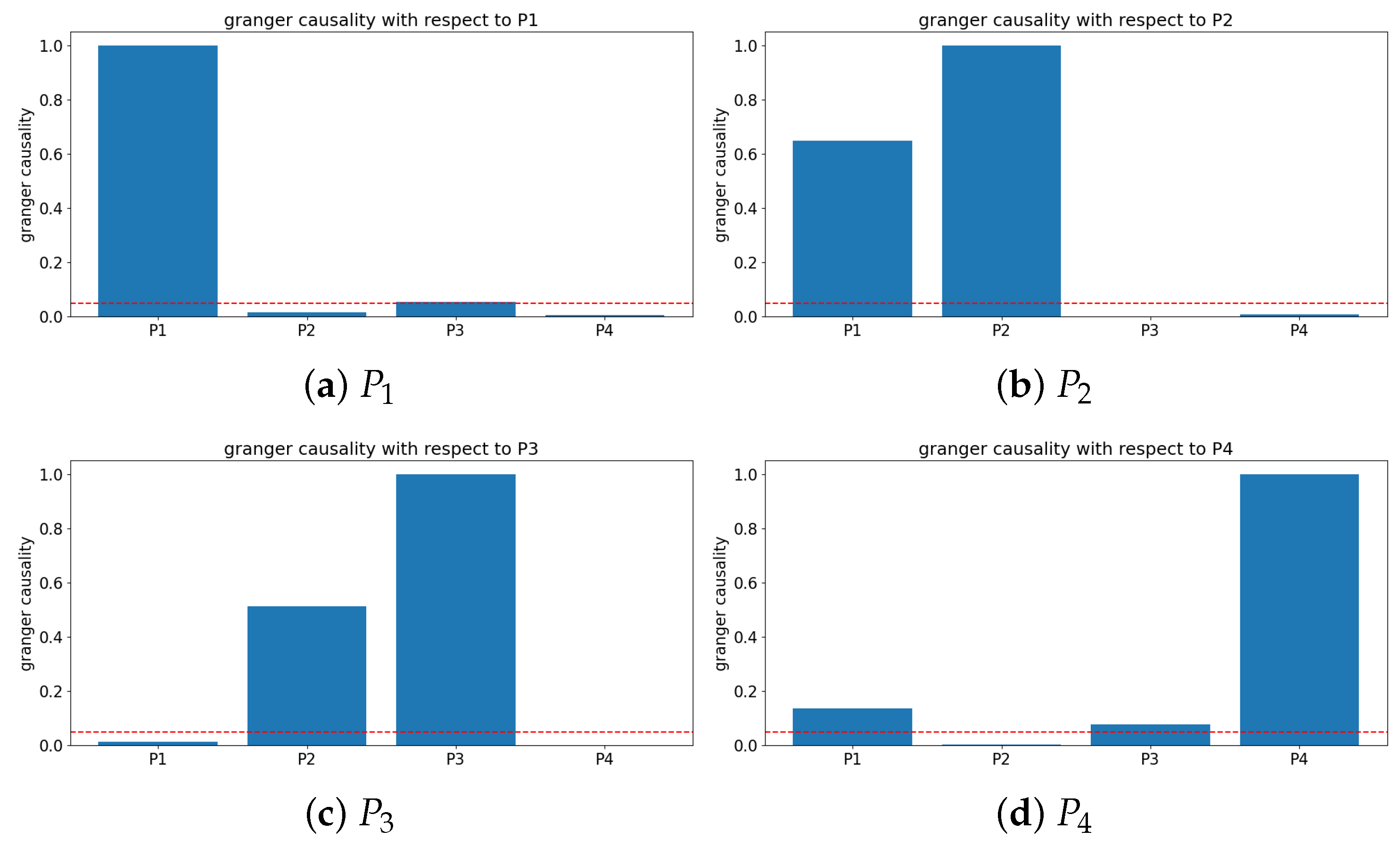
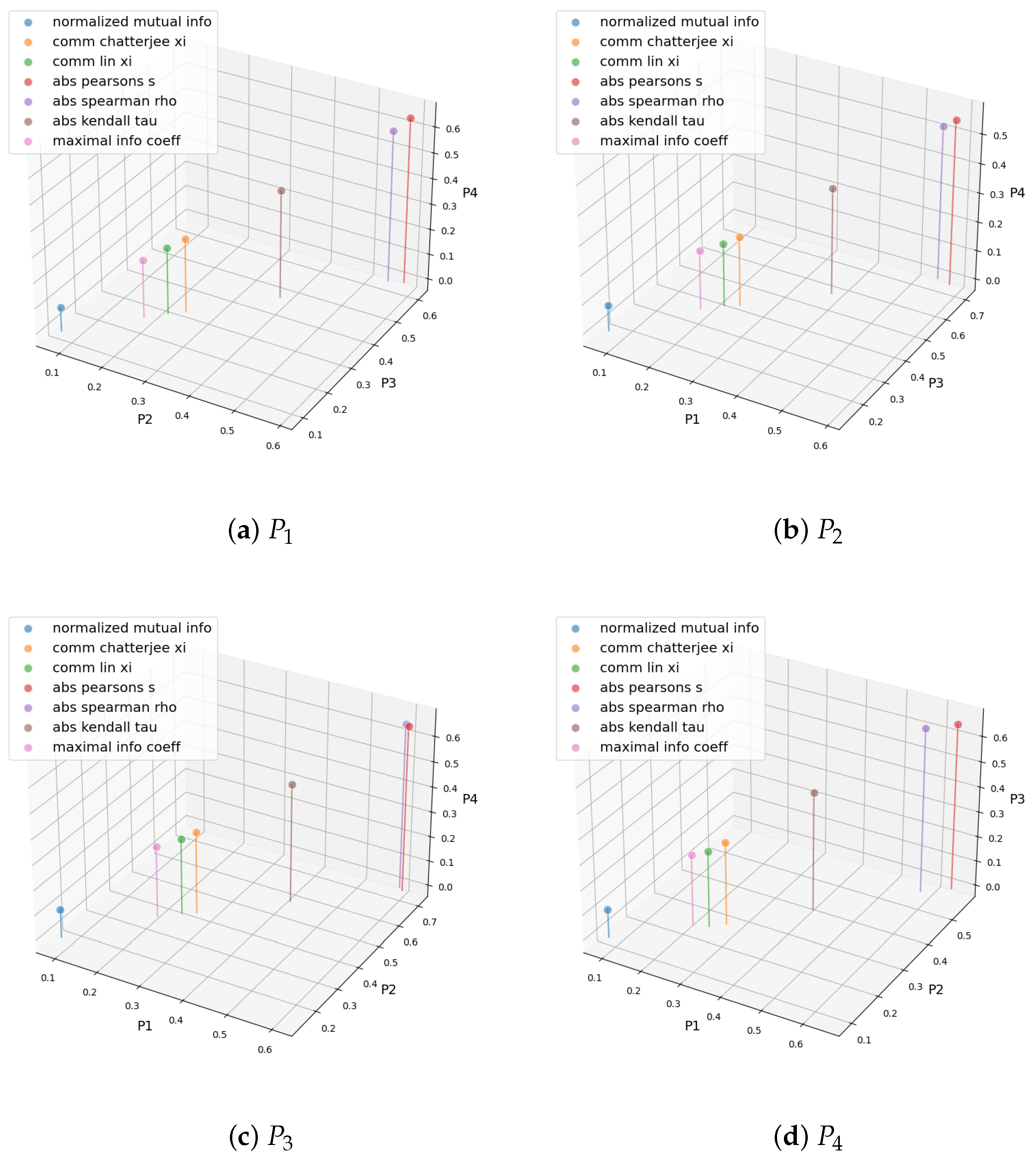
2.3.1. Causation and Correlation Among the Data Channels
2.3.2. Prediction Module Setup
3. Results
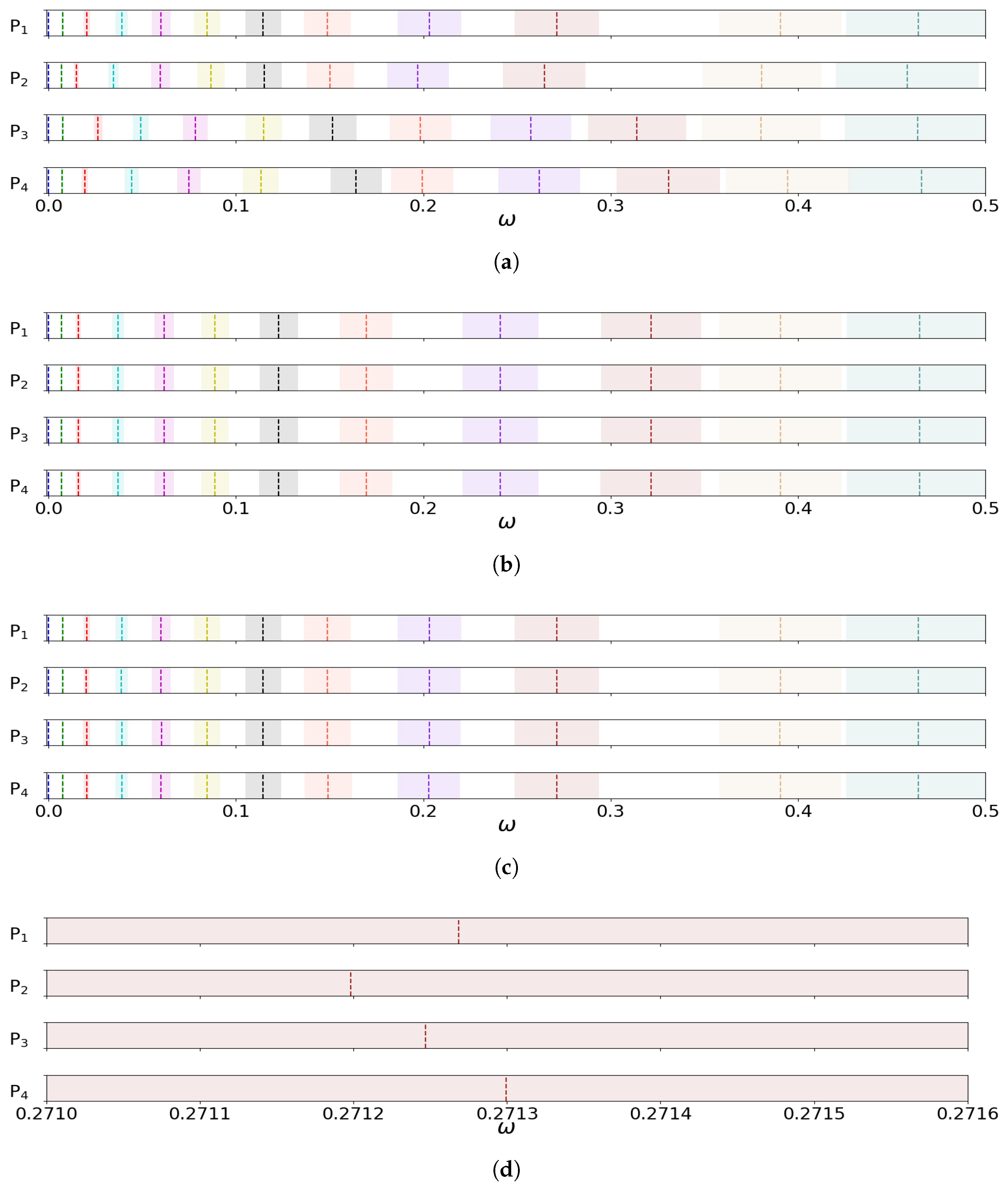
3.1. Decomposition in the Frequency Domain
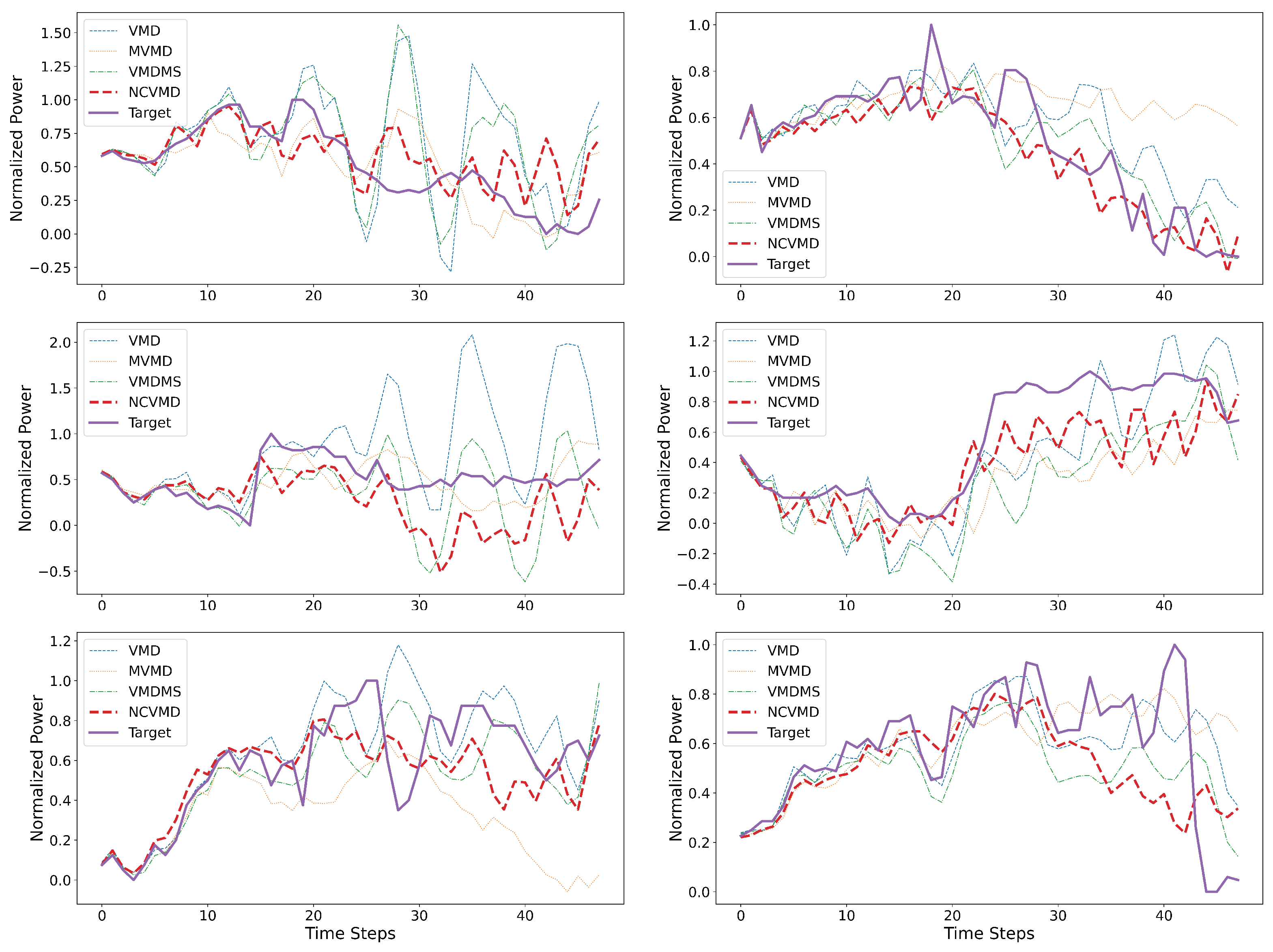
3.2. Forecasting Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rahimi, N.; Park, S.; Choi, W.; Oh, B.; Kim, S.; Cho, Y.h.; Ahn, S.; Chong, C.; Kim, D.; Jin, C.; et al. A Comprehensive Review on Ensemble Solar Power Forecasting Algorithms. J. Electr. Eng. Technol. 2023, 18, 719–733. [Google Scholar] [CrossRef] [PubMed]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Haykal, V.; Cardot, H.; Ragot, N. A Combination of Variational Mode Decomposition with Neural Networks on Household Electricity Consumption Forecast. In Proceedings of the ITISE 2017, Granada, Spain, 18–20 September 2017. [Google Scholar]
- Chao, H.C.; Lin, F.I.; Pan, J.S.; Chien, W.T.; Lai, C.S. Power Load Forecasting Based on VMD and Attention-LSTM. In Proceedings of the 3rd International Conference On Data Science And Information Technology, Xiamen, China, 24–26 July 2020; pp. 19–25. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, Z.; Yu, J.; Dai, X.; Li, Y. Short-term load forecasting based on IPSO-DBiLSTM network with variational mode decomposition and attention mechanism. Appl. Intell. 2023, 53, 12701–12718. [Google Scholar] [CrossRef]
- Fazzini, P.; La Tona, G.; Diez, M.; Di Piazza, M.C. Sailing Towards Efficiency: A Variational Mode Decomposition Based Approach to Forecasting Shipboard Electrical Power Consumption. In Proceedings of the 2024 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Naples, Italy, 26–29 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, F.; Zhou, H.; Li, Z.; Zhao, K. Multi-Step Ahead Short-Term Electricity Load Forecasting Using VMD-TCN and Error Correction Strategy. Energies 2022, 15, 5375. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, J.; Ma, Y.; Li, G.; Ma, J.; Wang, C. Short-term load forecasting method with variational mode decomposition and stacking model fusion. Sustain. Energy Grids Netw. 2022, 30, 100622. [Google Scholar] [CrossRef]
- Xiong, Q.; Liu, M.; Li, Y.; Zheng, C.; Deng, S. Short-Term Load Forecasting Based on VMD and Deep TCN-Based Hybrid Model with Self-Attention Mechanism. Appl. Sci. 2023, 13, 12479. [Google Scholar] [CrossRef]
- Zhang, Z.; Hong, W.; Li, J. Electric Load Forecasting by Hybrid Self-Recurrent Support Vector Regression Model With Variational Mode Decomposition and Improved Cuckoo Search Algorithm. IEEE Access 2020, 8, 14642–14658. [Google Scholar] [CrossRef]
- Zhang, D.; Peng, X.; Pan, K. A Novel Online Method for Wind Speed Forecasting Based on Hybrid Decomposition and OSORELM. In Proceedings of the 2018 International Conference On Power System Technology (POWERCON), Guangzhou, China, 6–9 November 2018; pp. 1797–1804. [Google Scholar] [CrossRef]
- Xia, X.; Wang, X. A Novel Hybrid Model for Short-Term Wind Speed Forecasting Based on Twice Decomposition, PSR, and IMVO-ELM. Complexity 2022, 2022, 1–21. [Google Scholar] [CrossRef]
- Alemu, N.S.; Zheng, D.; Zhang, W.; Teshager, G. Short-term PV power forecasting using variational mode decomposition integrated with Ant colony optimization and neural network. Energy Rep. 2022, 8, 2022–2035. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Du, J.; Wang, Z.; Shao, Q. De-noising magnetotelluric data using variational mode decomposition combined with mathematical morphology filtering and wavelet thresholding. J. Appl. Geophys. 2022, 204, 104751. [Google Scholar] [CrossRef]
- Shi, J.; Zhou, J.; Feng, J.; Chen, H. Network traffic prediction model based on improved VMD and PSO-ELM. Int. J. Commun. Syst. 2023, 36, e5448. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, R.; Wang, P.; Chen, H. A new perspective on air quality index time series forecasting: A ternary interval decomposition ensemble learning paradigm. Technol. Forecast. Soc. Change 2023, 191, 122504. [Google Scholar] [CrossRef]
- Rehman, N.; Aftab, H. Multivariate Variational Mode Decomposition. IEEE Trans. Signal Process. 2019, 67, 6039–6052. [Google Scholar] [CrossRef]
- Huang, Y.; Hasan, N.; Deng, C.; Bao, Y. Multivariate empirical mode decomposition based hybrid model for day-ahead peak load forecasting. Energy 2022, 239, 122245. [Google Scholar] [CrossRef]
- Rehman, N.; Mandic, D.P. Multivariate Empirical Mode Decomposition. Proc. R. Soc. A 2010, 466, 1291–1302. [Google Scholar] [CrossRef]
- International Maritime Organization (IMO). Fourth IMO GHG Study 2020 Full Report; International Maritime Organization (IMO): London, UK, 2021; Volume 6, pp. 951–952. [Google Scholar]
- DNV-GL. MARITIME FORECAST TO 2050—Energy Transition Outlook 2019; Technical Report; DNV-GL: Oslo, Norway, 2019. [Google Scholar]
- IMO. IMO Action to Reduce Greenhouse Gas Emissions from International Shipping; International Maritime Organization (IMO): London, UK, 2019. [Google Scholar]
- Lee, H.; Lee, J.; Roh, G.; Lee, S.; Choung, C.; Kang, H. Comparative Life Cycle Assessments and Economic Analyses of Alternative Marine Fuels: Insights for Practical Strategies. Sustainability 2024, 16, 2114. [Google Scholar] [CrossRef]
- Nivolianiti, E.; Karnavas, Y.L.; Charpentier, J.F. Energy management of shipboard microgrids integrating energy storage systems: A review. Renew. Sustain. Energy Rev. 2024, 189, 114012. [Google Scholar] [CrossRef]
- Di Piazza, M.; La Tona, G.; Luna, M.; Di Piazza, A. A two-stage Energy Management System for smart buildings reducing the impact of demand uncertainty. Energy Build. 2017, 139, 1–9. [Google Scholar] [CrossRef]
- Fazzini, P.; La Tona, G.; Diez, M.; Montuori, M.; Di Piazza, M.C. Multi-Channel Neighborhood-Constrained Variational Mode Decomposition. TechRxiv 2025. [Google Scholar] [CrossRef]
- Fazzini, P.; La Tona, G.; Diez, M.; Di Piazza, M.C. Enhanced forecasting of shipboard electrical power demand using multivariate input and variational mode decomposition with mode selection. Sci. Rep. 2025, 15, 23941. [Google Scholar] [CrossRef]
- Hochreiter, S. Long Short-term Memory. Neural Comput. 1997, 8, 1735–1780. [Google Scholar] [CrossRef]
- Fazzini, P.; Montuori, M.; Pasini, A.; Cuzzucoli, A.; Crotti, I.; Campana, E.F.; Petracchini, F.; Dobricic, S. Forecasting PM10 Levels Using Machine Learning Models in the Arctic: A Comparative Study. Remote Sens. 2023, 15, 3348. [Google Scholar] [CrossRef]
- Sulligoi, G.; Vicenzutti, A.; Menis, R. All-Electric Ship Design: From Electrical Propulsion to Integrated Electrical and Electronic Power Systems. IEEE Trans. Transp. Electrif. 2016, 2, 507–521. [Google Scholar] [CrossRef]
- Patel, M.R. Shipboard Electrical Power Systems; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Chatterjee, S. A New Coefficient of Correlation. J. Am. Stat. Assoc. 2021, 116, 2009–2022. [Google Scholar] [CrossRef]
- Lin, Z.; Han, F. On boosting the power of Chatterjee’s rank correlation. Biometrika 2022, 110, 283–299. [Google Scholar] [CrossRef]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting Novel Associations in Large Data Sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef]

| Hyperparameter | Value |
|---|---|
| Input steps for each mode | 150 140 130 120 100 80 |
| 60 40 30 25 20 20 | |
| Num. of LSTM cells | 40 |
| Epochs | 5 |
| Early Stopping | yes |
| Dense layer activation | tanh() |
| Loss | 0.5 × [Mean Squared Error] + |
| 0.5 × [Mean Cross Entropy] |
| Power/Slot | VMD | MVMD | VMDMS | NCD-Pred |
|---|---|---|---|---|
| —Slot 1 | 4.6589 | 2.6122 | 4.2294 | 2.5818 |
| —Slot 2 | 3.6203 | 1.3934 | 2.4295 | 2.2225 |
| —Slot 3 | 1.7384 | 2.8372 | 1.5922 | 1.4231 |
| —Slot 1 | 3.6461 | 5.7057 | 2.9208 | 2.4994 |
| —Slot 2 | 3.0014 | 3.7965 | 4.0715 | 2.6854 |
| —Slot 3 | 2.6591 | 2.9644 | 2.7849 | 3.0040 |
| —Slot 1 | 1.9280 | 2.1777 | 4.6758 | 2.3759 |
| —Slot 2 | 2.4078 | 3.1866 | 2.1003 | 4.1193 |
| —Slot 3 | 2.8707 | 1.6033 | 3.1776 | 2.0501 |
| —Slot 1 | 3.0211 | 2.4549 | 2.1623 | 2.3475 |
| —Slot 2 | 4.7863 | 1.3101 | 1.9731 | 0.7752 |
| —Slot 3 | 6.0600 | 2.7043 | 4.8644 | 1.9290 |
| Power/Slot | VMD | MVMD | VMDMS | NCD-Pred |
|---|---|---|---|---|
| —Slot 1 | 3.2626 | 1.9528 | 2.9184 | 1.8662 |
| —Slot 2 | 2.3633 | 1.1393 | 1.7758 | 1.7492 |
| —Slot 3 | 1.0969 | 2.1990 | 1.1200 | 1.0671 |
| —Slot 1 | 2.8544 | 3.9373 | 2.1656 | 1.8151 |
| —Slot 2 | 2.3770 | 2.9299 | 3.3518 | 2.1180 |
| —Slot 3 | 1.7455 | 1.8857 | 2.0799 | 2.0606 |
| —Slot 1 | 1.4845 | 1.6552 | 3.6963 | 1.7773 |
| —Slot 2 | 1.8359 | 2.0530 | 1.5778 | 2.7812 |
| —Slot 3 | 2.1858 | 1.1448 | 2.3856 | 1.6204 |
| —Slot 1 | 2.2529 | 1.6142 | 1.4718 | 1.6652 |
| —Slot 2 | 3.3068 | 0.9736 | 1.5554 | 0.5938 |
| —Slot 3 | 4.5394 | 1.7958 | 3.3722 | 1.3942 |
| Power/Slot | VMD | MVMD | VMDMS | NCD-Pred |
|---|---|---|---|---|
| —Slot 1 | 3.4116 | 2.0626 | 3.0553 | 1.9761 |
| —Slot 2 | 2.3691 | 1.1721 | 1.8461 | 1.8225 |
| —Slot 3 | 1.1205 | 2.2893 | 1.1509 | 1.0996 |
| —Slot 1 | 3.1895 | 4.4160 | 2.4075 | 2.0190 |
| —Slot 2 | 2.5111 | 3.0760 | 3.5791 | 2.2223 |
| —Slot 3 | 1.8546 | 2.0061 | 2.2058 | 2.1954 |
| —Slot 1 | 1.5417 | 1.7176 | 3.7745 | 1.8458 |
| —Slot 2 | 1.9458 | 2.1612 | 1.6373 | 2.9368 |
| —Slot 3 | 2.2446 | 1.1900 | 2.4345 | 1.7018 |
| —Slot 1 | 2.3308 | 1.6746 | 1.5228 | 1.7322 |
| —Slot 2 | 3.2893 | 1.0064 | 1.6072 | 0.6115 |
| —Slot 3 | 4.5752 | 1.8136 | 3.4372 | 1.4185 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fazzini, P.; La Tona, G.; Montuori, M.; Diez, M.; Di Piazza, M.C. NCD-Pred: Forecasting Multichannel Shipboard Electrical Power Demand Using Neighborhood-Constrained VMD. Forecasting 2025, 7, 44. https://doi.org/10.3390/forecast7030044
Fazzini P, La Tona G, Montuori M, Diez M, Di Piazza MC. NCD-Pred: Forecasting Multichannel Shipboard Electrical Power Demand Using Neighborhood-Constrained VMD. Forecasting. 2025; 7(3):44. https://doi.org/10.3390/forecast7030044
Chicago/Turabian StyleFazzini, Paolo, Giuseppe La Tona, Marco Montuori, Matteo Diez, and Maria Carmela Di Piazza. 2025. "NCD-Pred: Forecasting Multichannel Shipboard Electrical Power Demand Using Neighborhood-Constrained VMD" Forecasting 7, no. 3: 44. https://doi.org/10.3390/forecast7030044
APA StyleFazzini, P., La Tona, G., Montuori, M., Diez, M., & Di Piazza, M. C. (2025). NCD-Pred: Forecasting Multichannel Shipboard Electrical Power Demand Using Neighborhood-Constrained VMD. Forecasting, 7(3), 44. https://doi.org/10.3390/forecast7030044








