Stochastic Model and Rhythm-Adaptive Technologies of Statistical Analysis and Forecasting of Economic Processes with Cyclic Components
Abstract
1. Introduction
- Software specializing in econometrics, regression analysis, and time series analysis: EViews (Quantitative Micro Software), Stata (StataCorp LLC), Rats (Thomas Doan and Robert Littermn), Micro TSP (David M. Lilien), Gretl (Riccardo “Jack” Lucchetti, Allin Cottrell).
- Software for statistical analysis, descriptive statistics, regression, and factor analysis: IBM SPSS (Normn H.Nie), SAS (James Goodnight), BMDP Statistical Soft¬ware (W.J.Dixon), Minitab (Minitab Inc.).
- Programming languages and libraries for statistics, machine learning, and econometric modeling: Python (Libraries: statsmodels, scikit-learn, pmdarima, PyWavelets), R (packages: forecast, tseries, vars, wavelets).
- Tools for business analytics, financial forecasting, and simulation modeling: Oracle Crystal Ball (Oracle Corporation), Tableau (Tableau Software).
2. Related Work
3. Methodology
3.1. Mathematical Models of a Cyclical Economic Process
3.2. Methods for Processing Cyclical Economic Processes
3.2.1. Method for Estimating the Trend Component of a Cyclic Economic Process
3.2.2. Statistical Methods for Processing the Cyclic Component of an Economic Process
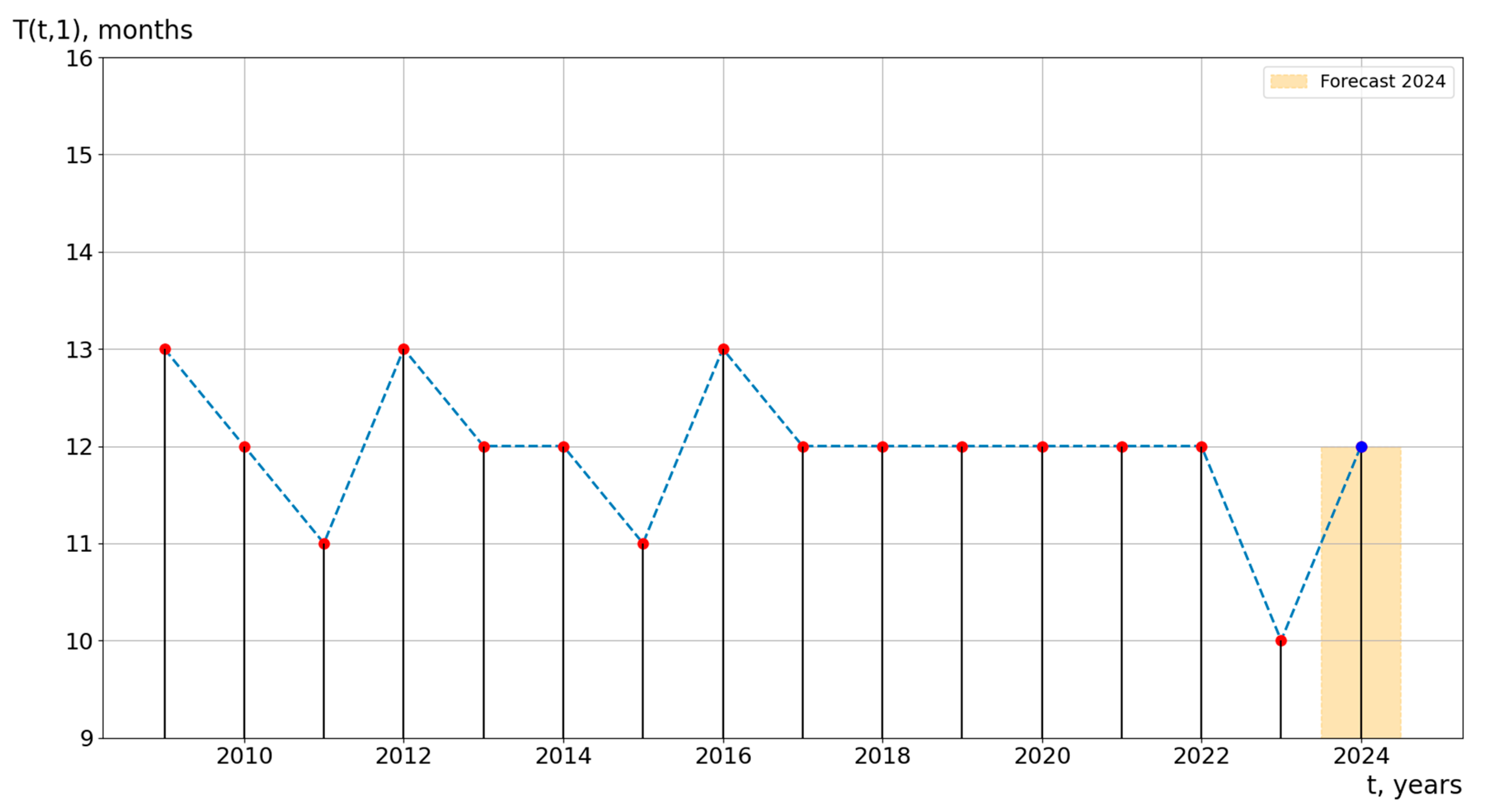
3.2.3. Method for Estimating the Rhythm Function of Cyclic Economic Processes
3.2.4. Method for Forecasting Cyclic Economic Processes Based on a Set of Confidence Intervals
- Forecasting the cyclical component of the economic process.
- Forecasting its trend component.
- Forecasting the cyclical economic process as a whole.
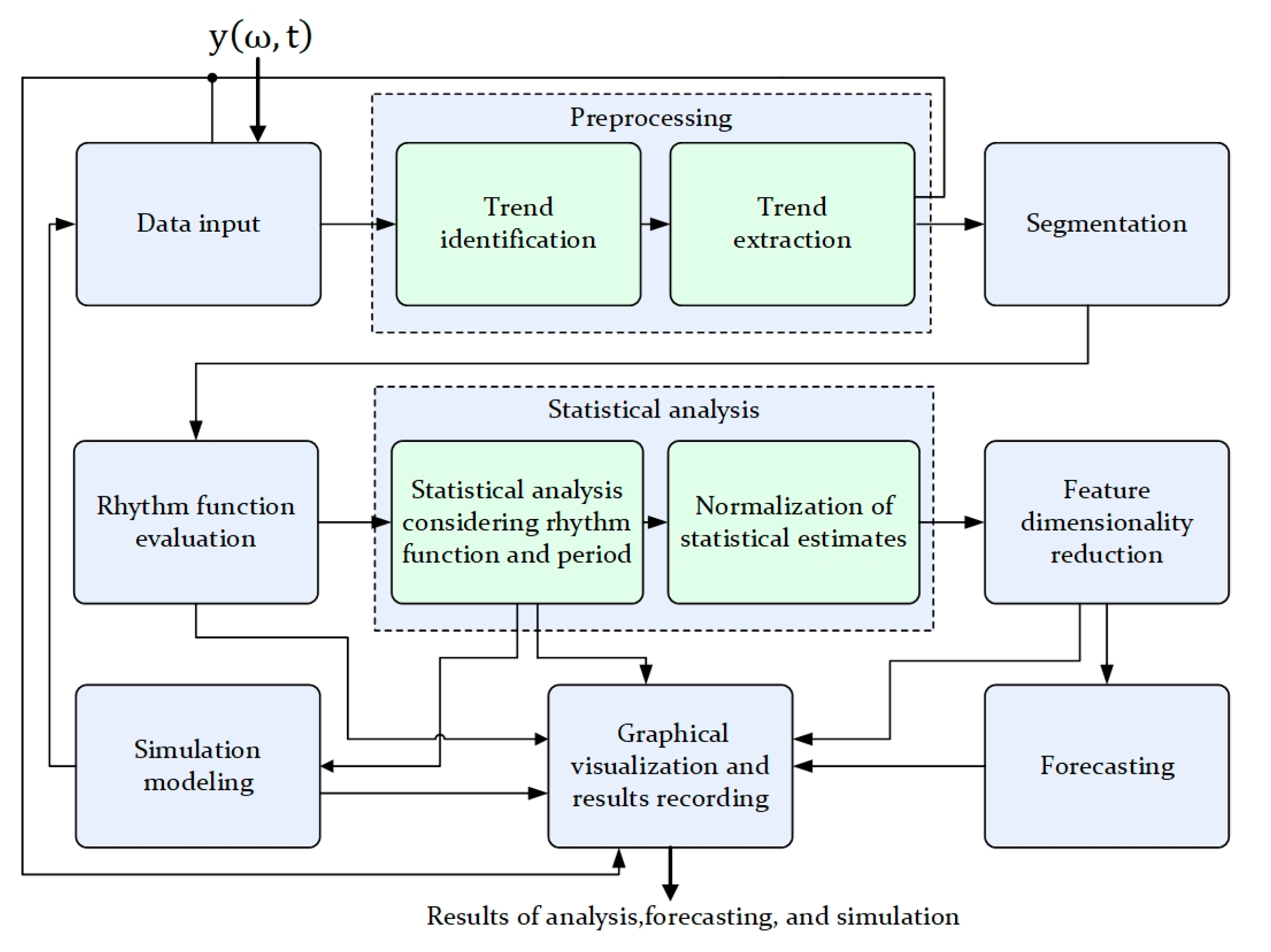
4. The Software System for Modeling, Analysis, and Forecasting of Cyclical Economic Processes as a Component of a Decision Support System
5. Experimental Part
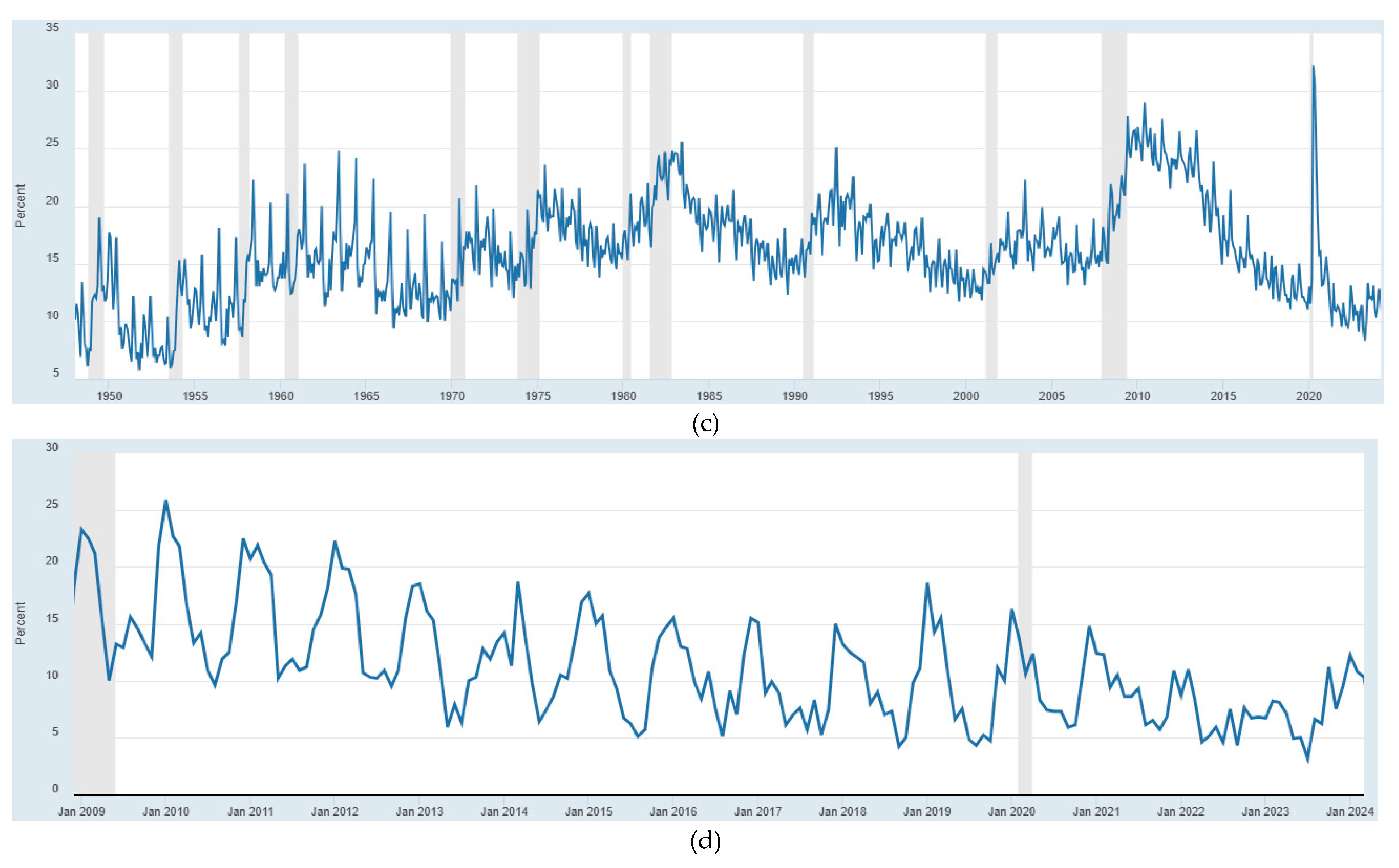
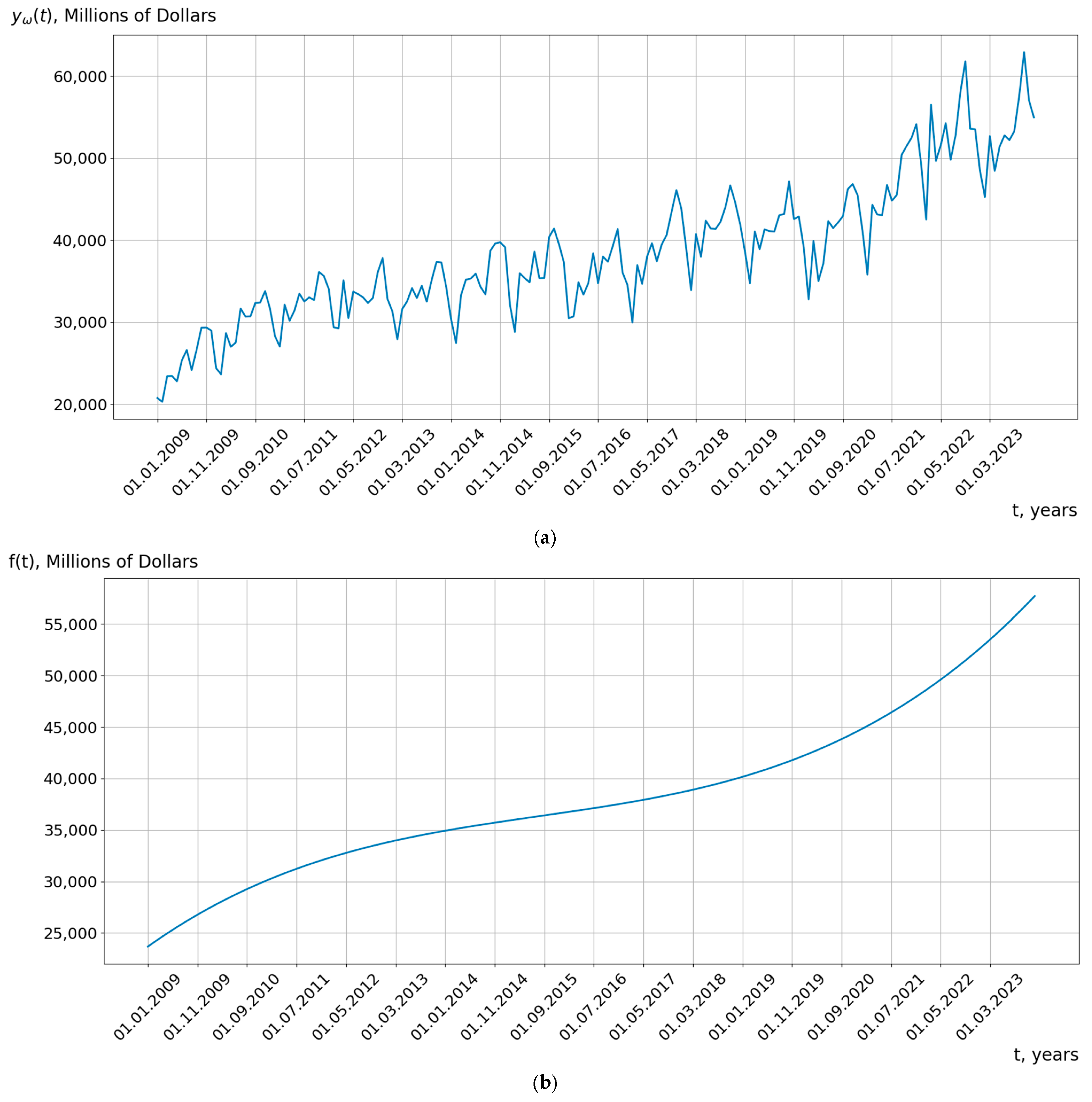
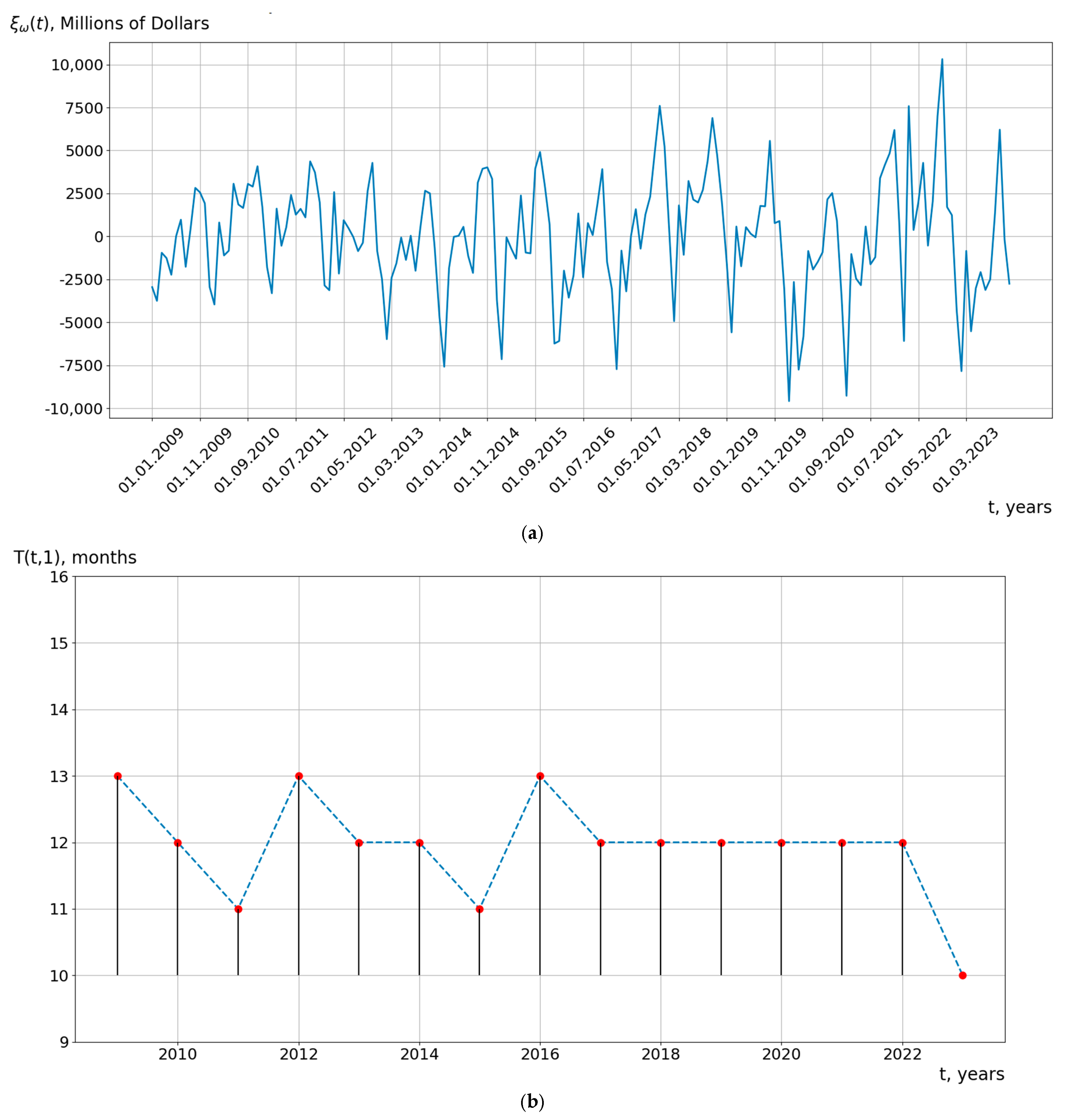
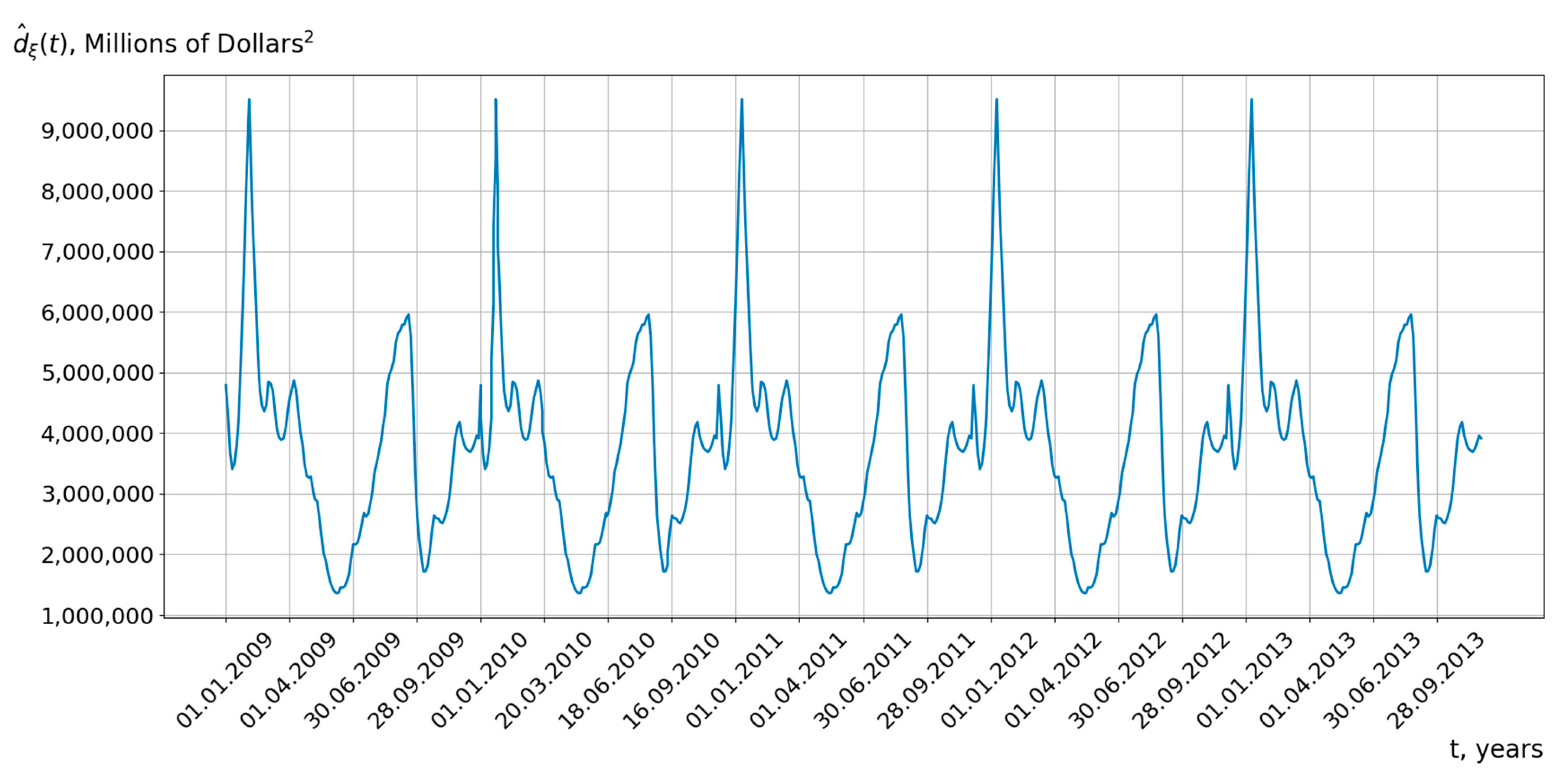
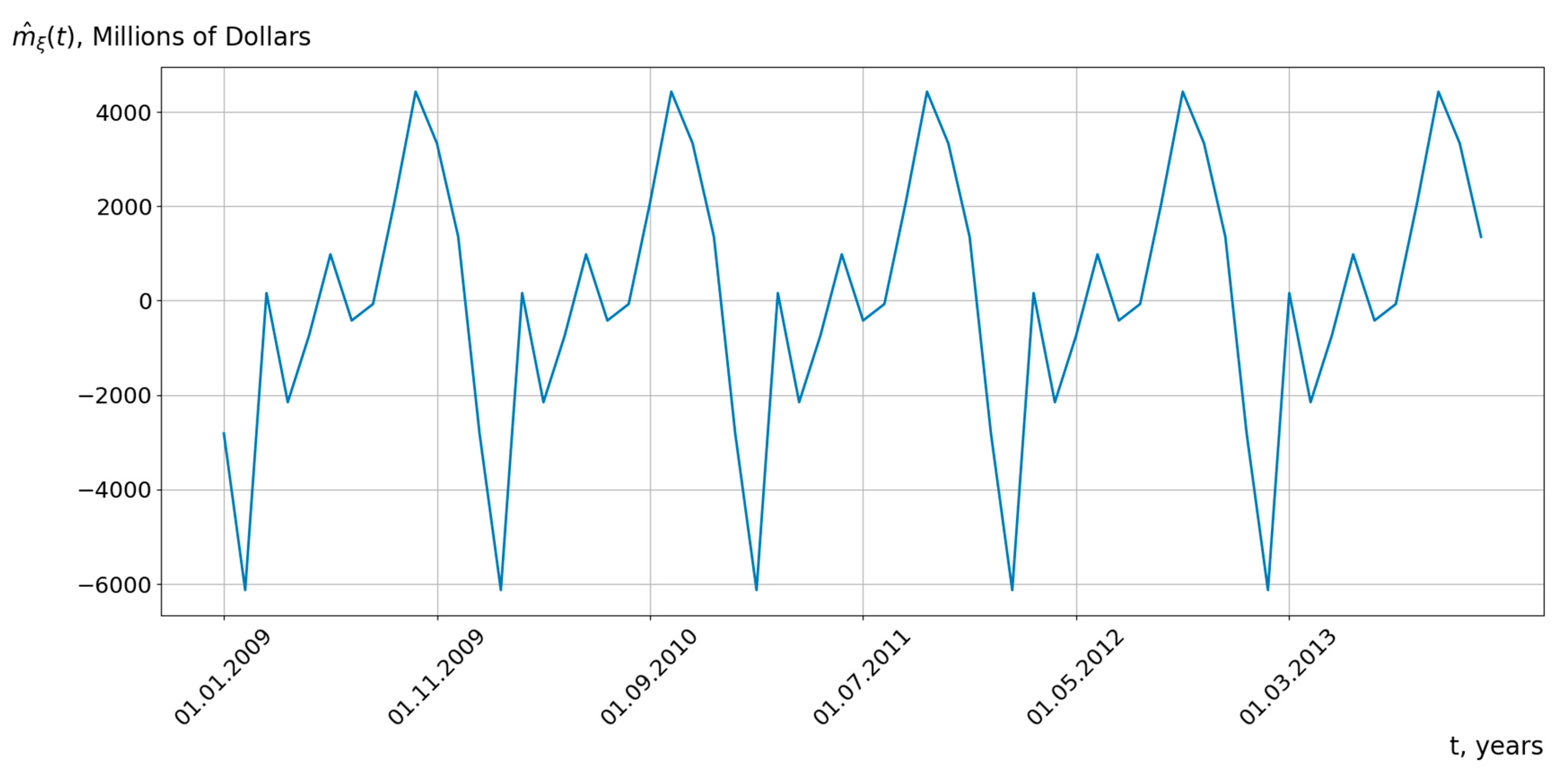
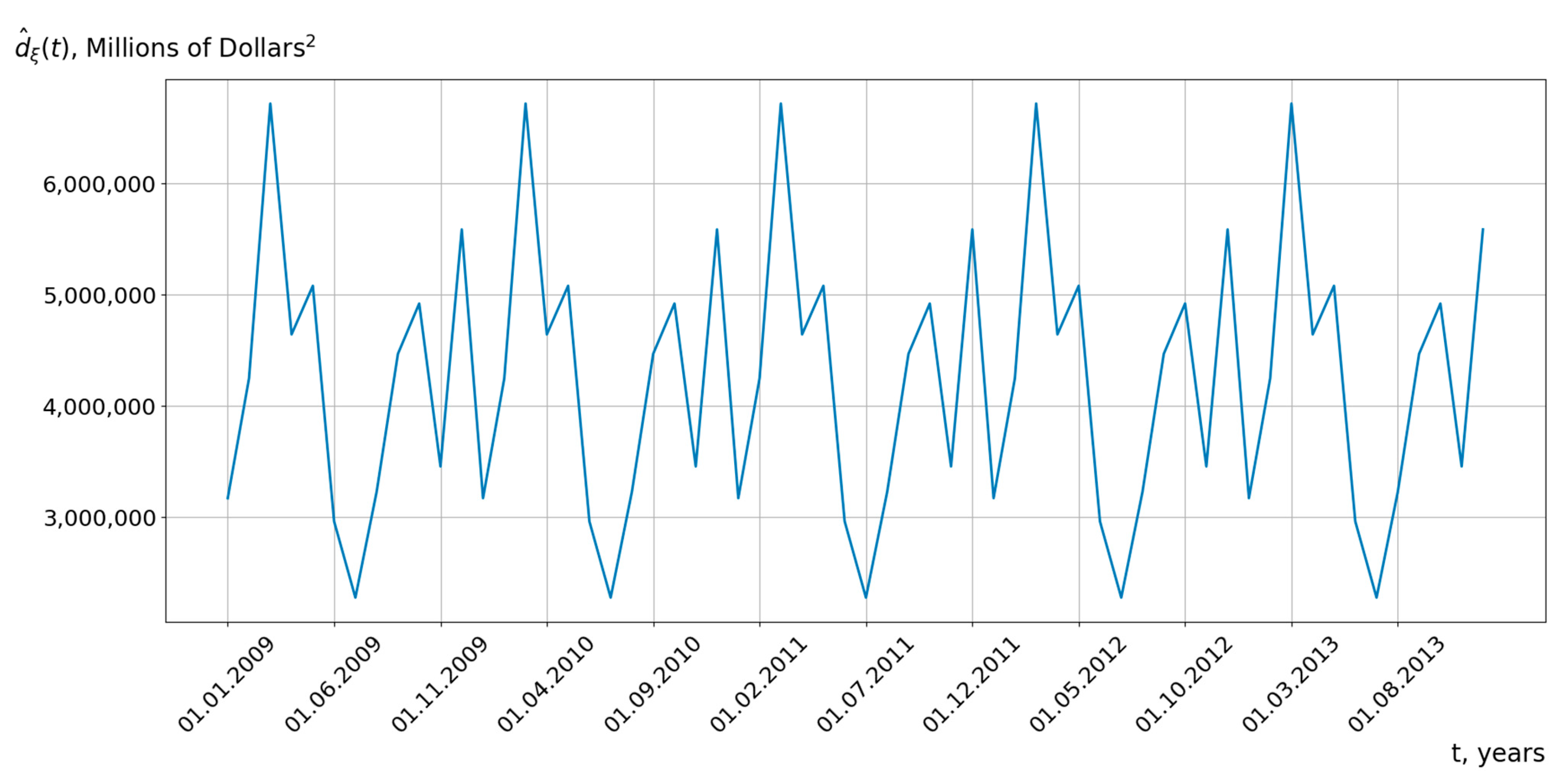
5.1. Results of the Analysis of Cyclical Economic Processes
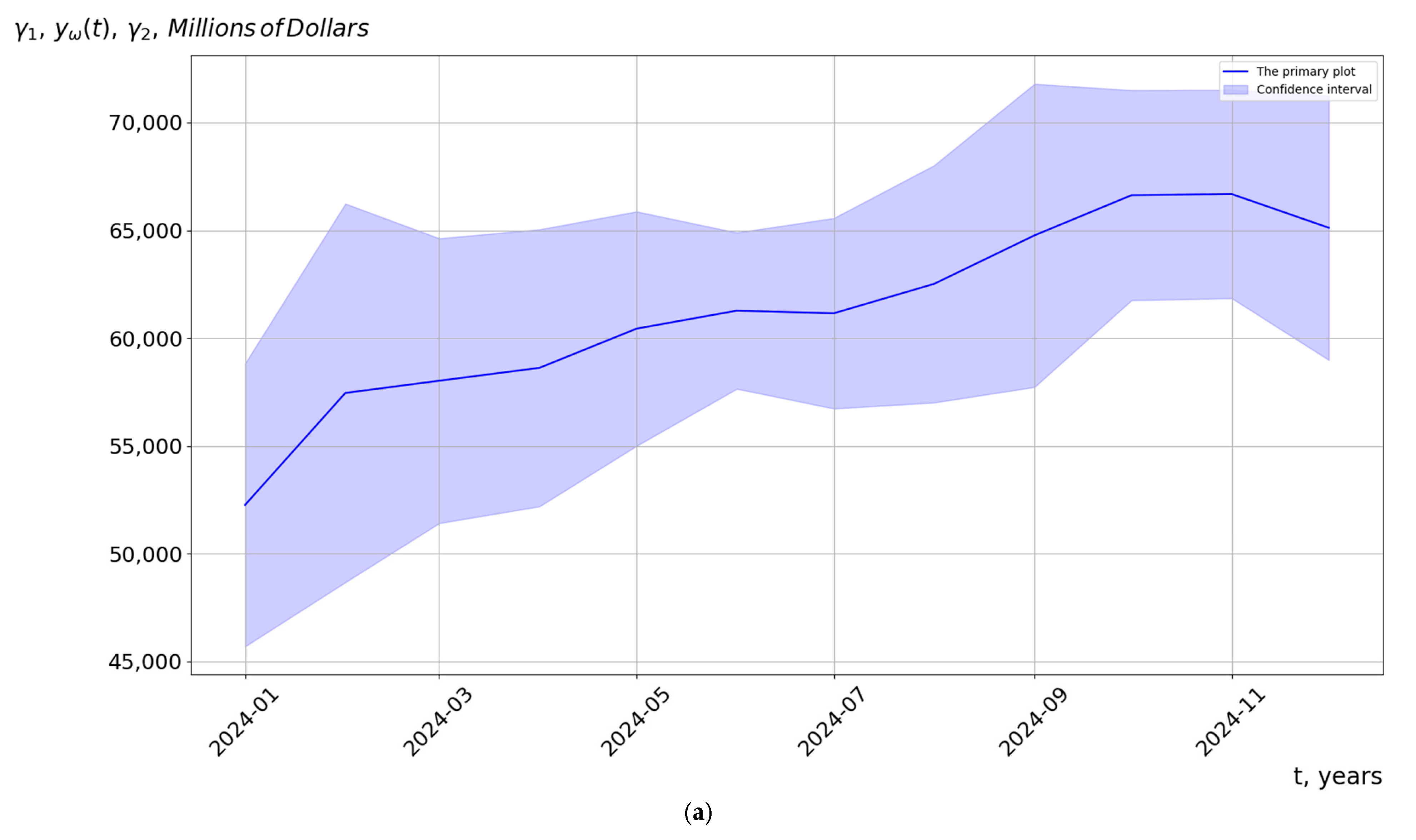
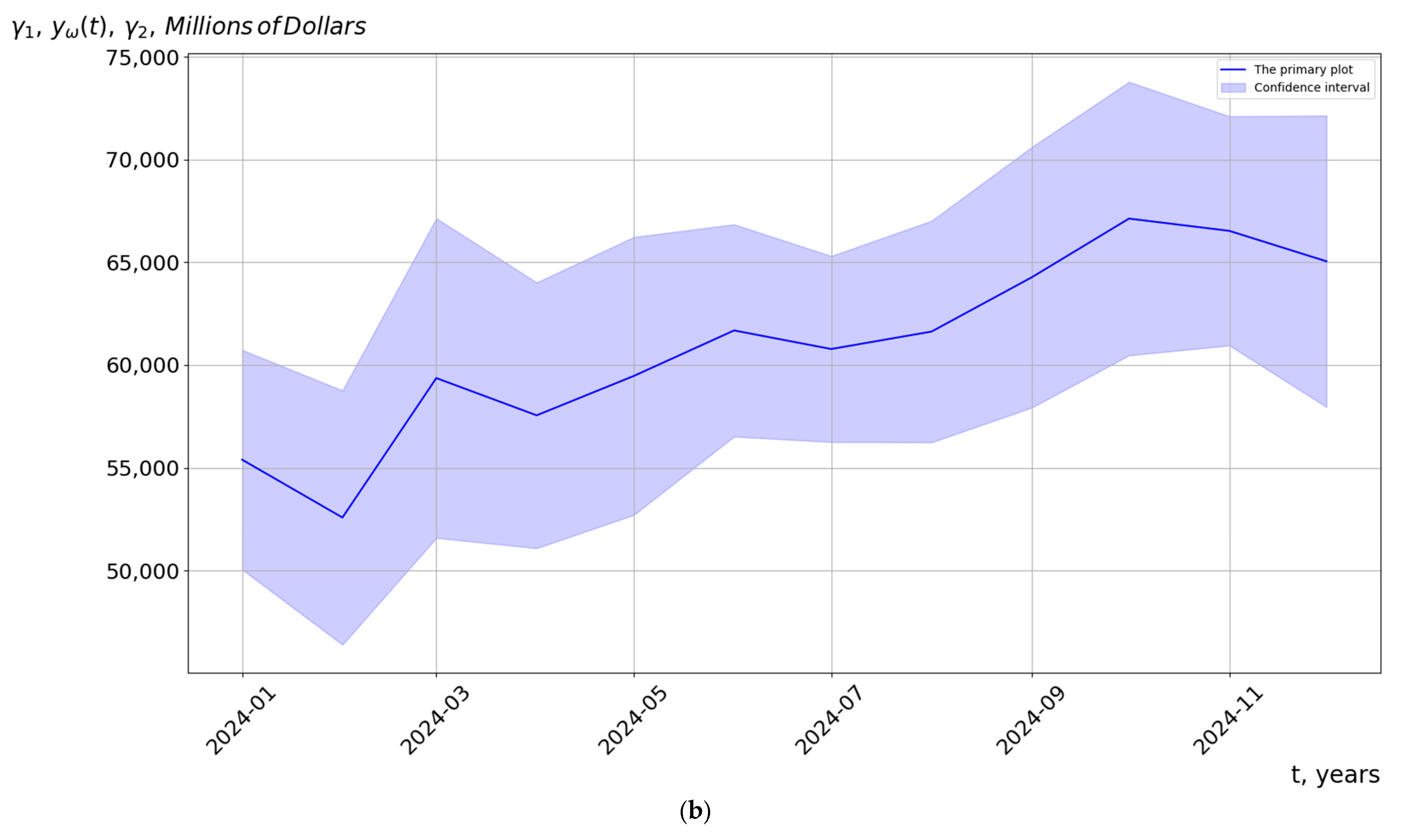
5.2. Results of Forecasting of Cyclical Economic Processes
6. Discussion and Conclusions
- Based on the results of a comprehensive review of the literature, a comparative analysis of existing mathematical models, methods, and software tools for the analysis and forecasting of cyclical economic processes was conducted. This analysis identified a number of shortcomings and outlined the direction for further research.
- A new mathematical model of cyclical economic processes was developed, represented as the sum of a deterministic polynomial function and a cyclical random process. By incorporating trend components, stochasticity, cyclicality, and rhythm variability of cyclical economic processes, this model improved the accuracy, reliability, and informativeness of methods and software tools for their modeling, analysis, and forecasting.
- A new statistical method for processing (analysis and forecasting) cyclical economic processes was substantiated, characterized by enhanced accuracy in estimating probabilistic characteristics of the studied processes through its adaptation to changes in their rhythm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hodrick, R.J. An Exploration of Trend-Cycle Decomposition Methodologies in Simulated Data National Bureau of Economic Research. NBER Working Paper 26750. 2020. Available online: http://www.nber.org/papers/w26750.pdf (accessed on 10 January 2025).
- Kang, N.; Marmer, V. Modeling long cycles. J. Econ. Dyn. Control 2024, 5, 120–163. [Google Scholar] [CrossRef]
- Lenart, Ł.; Kwiatkowski, Ł.; Wróblewska, J. A Bayesian nonlinear stationary model with multiple frequencies for business cycle analysis. arXiv 2024, arXiv:2406.02321. [Google Scholar]
- Krüger, J.J. A wavelet evaluation of some leading business cycle indicators for the German economy. J. Bus. Cycle Res. 2021, 17, 293–319. [Google Scholar] [CrossRef]
- Guvenen, F.; McKay, A.; Ryan, C. A Tractable Income Process for Business Cycle Analysis; National Bureau of Economic Research, Inc.: Cambridge, MA, USA, 2023. [Google Scholar]
- Wildi, M. Business-cycle analysis and zero-crossings of time series: A generalized forecast approach. J. Bus. Cycle Res. 2024, 20, 155–192. [Google Scholar] [CrossRef]
- Bernard, L.; Gevorkyan, A.; Palley, T.; Semmler, W. Long-wave economic cycles: The contributions of Kondratieff, Kuznets, Schumpeter, Kalecki, Goodwin, Kaldor, and Minsky. J. Econ. Dyn. Struct. 2024, 5, 120–163. [Google Scholar]
- Pontes, E.L.; Benjannet, M.; Yung, R. Forecasting Four Business Cycle Phases Using Machine Learning: A Case Study of US and EuroZone. arXiv 2024, arXiv:2405.17170. [Google Scholar]
- Azqueta-Gavaldon, A.; Hirschbühl, D.; Onorante, L.; Saiz, L. Nowcasting Business Cycle Turning Points with Stock Networks and Machine Learning; European Central Bank Working Paper Series #2494; European Central Bank: Frankfurt, Germany, 2020. [Google Scholar]
- Kuntze, V. The Role of Coincident Information in Real-Time Business Cycle Forecasting. SSRN 2024, 4692581. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4692581 (accessed on 21 March 2025). [CrossRef]
- Mariani, M.C.; Bhuiyan, M.A.M.; Tweneboah, O.K.; Beccar-Varela, M.P.; Florescu, I. Analysis of stock market data by using Dynamic Fourier and Wavelets techniques. Phys. A Stat. Mech. Its Appl. 2020, 537, 122785. [Google Scholar] [CrossRef]
- Pisol, M.; Harun, M.; Abdul Latif, R. Utilization of Holt-Winters Exponential Smoothing Model in Forecasting 2023 LZNK Collection. Int. J. Zakat Islam. Philanthr. 2023, 5, 163–172. [Google Scholar]
- Tiao, G.C.; Grupe, M.R. Hidden periodic autoregressive-moving average models in time series data. Biom. 1980, 67, 365–373. [Google Scholar] [CrossRef]
- Todd, R. A Dynamic Equilibrium Model of Seasonal and Cyclical Fluctuations in the Corn–Soybean–Hog Sector; University of Minnesota: Minneapolis, MN, USA, 1983. [Google Scholar]
- Todd, R. Periodic linear–quadratic methods for modeling seasonality. J. Econ. Dyn. Control 1990, 14, 763–795. [Google Scholar] [CrossRef]
- Osborn, D.R. Seasonality and habit persistence in a life cycle model of consumption. J. Appl. Econom. 1988, 3, 255–266. [Google Scholar] [CrossRef]
- Osborn, D.R.; Smith, J.P. The performance of periodic autoregressive models in forecasting seasonal U.K. consumption. J. Bus. Econ. Stat. 1989, 7, 117–128. [Google Scholar] [CrossRef]
- Hansen, L.P.; Sargent, T.J. Recursive Linear Models of Dynamic Economies; Hoover Institution, Stanford University: Stanford, CA, USA, 1990. [Google Scholar]
- Chen, L.; Dolado, J.J.; Gonzalo, J.; Pan, H. Estimation of Characteristics-Based Quantile Factor Models (PHBS Working Paper No. 20220701); Peking University HSBC Business School: Beijing, China, 2022. [Google Scholar]
- Huang, H. Analysis and Forecast of Resource-based City GDP Based on ARIMA Model. Adv. Econ. Bus. Manag. Res. 2019, 76, 210–216. [Google Scholar]
- Eckert, F.; Hyndman, R.J.; Panagiotelis, A. Forecasting Swiss exports using Bayesian forecast reconciliation. Eur. J. Oper. Res. 2021, 291, 693–710. [Google Scholar] [CrossRef]
- Choi, H.K. Stock price correlation coefficient prediction with ARIMA-LSTM hybrid model. arXiv 2018, arXiv:1808.01560. [Google Scholar]
- Krolzig, H.-M. Econometric Modelling of Markov-Switching Vector Autoregressions using MSVAR for Ox (Discussion Paper No. 9802); Nuffield College, University of Oxford: Oxford, UK, 1998. [Google Scholar]
- Amisano, G.; Colavecchio, R. Money Growth and Inflation: Evidence from a Markov Switching Bayesian VAR (Paper No. 4/2013); Department of Socioeconomics, University of Hamburg: Hamburg, Germany, 2013. [Google Scholar]
- Shin, M.; Kim, D.; Wang, Y.; Fan, J. Factor and idiosyncratic VAR-Ito volatility models for heavy-tailed high-frequency financial data. arXiv 2023, arXiv:2109.05227. [Google Scholar]
- Ghysels, E. Are Business Cycle Turning Points Uniformly Distributed Throughout the Year? (Discussion Paper No. 3891); Université de Montréal: Montréal, QC, Canada, 1991. [Google Scholar]
- Ghysels, E. On the Periodic Structure of the Business Cycle (Discussion Paper No. 1028); Cowles Foundation, Yale University: New Haven, CO, USA, 1992. [Google Scholar]
- Hamilton, J.D. Rational-expectations econometric analysis of changes in regime: An investigation of the term structure of interest rates. J. Econ. Dyn. Control 1988, 12, 385–423. [Google Scholar] [CrossRef]
- Hamilton, J.D. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 1989, 57, 357–384. [Google Scholar] [CrossRef]
- Hamilton, J.D. Analysis of time series subject to changes in regime. J. Econom. 1990, 45, 39–70. [Google Scholar] [CrossRef]
- Garcia, R.; Perron, P. An analysis of the real interest rate under regime shifts (Unpublished manuscript); Princeton University: Princeton, NJ, USA, 1989. [Google Scholar]
- Phillips, K.L. A two-country model of stochastic output with changes in regime. J. Int. Econ. 1991, 31, 121–142. [Google Scholar] [CrossRef]
- McCulloch, R.E.; Tsay, R.S. Statistical inference of Markov switching models with applications to US GNP (Technical Report No. 125); Graduate School of Business, University of Chicago: Chicago, IL, USA, 1992. [Google Scholar]
- Albert, J.; Chib, S. Bayes inference via Gibbs sampling of autoregressive time series subject to Markov mean and variance shifts. J. Bus. Econ. Stat. 1993, 11, 1–15. [Google Scholar] [CrossRef]
- McCracken, M.W.; Owyang, M.T.; Sekhposyan, T. Real-time forecasting and scenario analysis using a large mixed-frequency Bayesian VAR. Int. J. Cent. Bank. 2021, 18, 327–355. [Google Scholar]
- Alsinglawi, O.; Aladwan, M.; Alwadi, S.; Alazzam, E. Forecasting Economic Growth and Movements with Wavelet Transform and ARIMA Model. Appl. Math. Inf. Sci. 2023, 17, 817–828. [Google Scholar]
- Vîntu, D. GDP modelling and forecasting using ARIMA: An empirical assessment for innovative economy formation. Eur. J. Econ. Stud. 2021, 10, 29–44. [Google Scholar] [CrossRef]
- Petrova, A.; Deyneka, M. ARIMA-models: Modeling and forecasting prices of stocks. Int. Sci. J. “Internauka” 2022, 2, 1–19. [Google Scholar] [CrossRef]
- Ma, Y. Analysis and Forecasting of GDP Using the ARIMA Model. Inf. Syst. Econ. 2024, 5, 91–97. [Google Scholar]
- Lai, H.; Ng, E. On business cycle forecasting. Front. Bus. Res. China 2020, 14, 17. [Google Scholar] [CrossRef]
- Tran, T.N. The Volatility of the Stock Market and Financial Cycle: GARCH Family Models. J. Ekon. Malays. 2022, 56, 151–168. [Google Scholar]
- Ng, P.; Kwok, M.; Cheng, C. Business Cycle and Early Warning Indicators for the Economy of Hong Kong—Challenges of Forecasting Work amid the COVID-19 Pandemic. J. Bus. Cycle Res. 2024, 20, 123–135. [Google Scholar] [CrossRef]
- Rekova, N.; Telnova, H.; Kachur, O.; Holubkova, I.; Balezentis, T.; Streimikiene, D. Financial sustainability evaluation and forecasting using the Markov chain: The case of the wine business. Sustainability 2020, 12, 6150. [Google Scholar] [CrossRef]
- Lin, Y.; Sung, B.; Park, S. Integrated systematic framework for forecasting China’s consumer confidence: A machine learning approach. Systems 2024, 12, 445. [Google Scholar] [CrossRef]
- Tang, P.; Zhang, Y. China’s business cycle forecasting: A machine learning approach. Comput. Econ. 2024, 64, 2783–2811. [Google Scholar] [CrossRef]
- Masini, R.; Medeiros, M.; Mendes, E. Machine Learning Advances for Time Series Forecasting. J. Econ. Surv. 2023, 37, 76–111. [Google Scholar] [CrossRef]
- Sako, K.; Mpinda, B.; Rodrigues, P. Neural Networks for Financial Time Series Forecasting. Entropy 2022, 24, 657. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, T. A novel deterministic probabilistic forecasting framework for gold price with a new pandemic index based on quantile regression deep learning and multi-objective optimization. Mathematics 2024, 12, 29. [Google Scholar] [CrossRef]
- Arslan, M.; Hunjra, A.; Ahmed, W.; Zaied, Y. Forecasting multi-frequency intraday exchange rates using deep learning models. J. Forecast. 2024, 43, 1338–1355. [Google Scholar] [CrossRef]
- Kinlaw, W.; Kritzman, M.; Turkington, D. A new index of the business cycle. J. Invest. Manag. 2021, 19, 4–19. [Google Scholar] [CrossRef]
- Rademacher, P. Forecasting Recessions in Germany with Machine Learning; DICE Discussion Paper #416; Heinrich Heine University Düsseldorf, Düsseldorf Institute for Competition Economics (DICE): Düsseldorf, Germany, 2024. [Google Scholar]
- Chaiboonsri, C.; Wannapan, S. Big data and machine learning for economic cycle prediction: Application of Thailand’s economy. Lect. Notes Artif. Intell. 2020, 11471, 347–359. [Google Scholar]
- Garg, R.; Sah, A. Cyclical dynamics and co-movement of business, credit, and investment cycles: Empirical evidence from India. Humanit. Soc. Sci. Commun. 2024, 11, 515. [Google Scholar] [CrossRef]
- Chai, S.; Lim, J.; Yoon, H.; Wang, B. A novel methodology for forecasting business cycles using ARIMA and neural network with weighted fuzzy membership functions. Axioms 2024, 13, 56. [Google Scholar] [CrossRef]
- Benrhmach, G.; Namir, K.; Bouyaghroumni, J.; Namir, A. Financial Time Series Prediction Using Wavelet and Artificial Neural Network. J. Math. Comput. Sci. 2021, 11, 5487–5500. [Google Scholar]
- Leventides, J.; Melas, E.; Poulios, C. Extended dynamic mode decomposition for cyclic macroeconomic data. Data Sci. Financ. Econ. 2022, 2, 117–146. [Google Scholar] [CrossRef]
- Lupenko, S. Rhythm-adaptive statistical estimation methods of probabilistic characteristics of cyclic random processes. Digit. Signal Process. 2024, 151, 104563. [Google Scholar] [CrossRef]
- Lupenko, S. Abstract Cyclic Functional Relation and Taxonomies of Cyclic Signals Mathematical Models: Construction, Definitions and Properties. Mathematics 2024, 12, 3084. [Google Scholar] [CrossRef]
- Lupenko, S. The rhythm-adaptive Fourier series decompositions of cyclic numerical functions and one-dimensional probabilistic characteristics of cyclic random processes. Digit. Signal Process. 2023, 140, 104104. [Google Scholar] [CrossRef]
- Lupenko, S.; Butsiy, R.; Shakhovska, N. Advanced Modeling and Signal Processing Methods in Brain–Computer Interfaces Based on a Vector of Cyclic Rhythmically Connected Random Processes. Sensors 2023, 23, 760. [Google Scholar] [CrossRef]
- Lupenko, S.; Butsiy, R. Isomorphic Multidimensional Structures of the Cyclic Random Process in Problems of Modeling Cyclic Signals with Regular and Irregular Rhythms. Fractal Fract. 2024, 8, 203. [Google Scholar] [CrossRef]
- Lupenko, S. The Mathematical Model of Cyclic Signals in Dynamic Systems as a Cyclically Correlated Random Process. Mathematics 2022, 10, 3406. [Google Scholar] [CrossRef]




| Properties of cyclic economic processes accounted for by the mathematical model | |||||||
| Cyclic structure of cyclic economic processes | Randomness of the structure of cyclic economic processes | Variability of rhythm | Commonality of rhythm | Trend components | |||
| Known mathematical models | Deterministic | FOURIER SERIES AND FOURIER TRANSFORM | + | − | − | − | − |
| WAVELET SERIES AND WAVELET TRANSFORM | + | − | + | − | − | ||
| SIMPLE SIGN ACCURACY (SSA) | − | − | − | − | + | ||
| WINTERS’ EQUATIONS | + | − | − | − | + | ||
| Stochastic | REGRESSION MODELS | − | + | − | − | + | |
| STATIONARY RANDOM PROCESS | − | + | − | − | − | ||
| PERIODIC ARMA MODELS | + | + | − | − | − | ||
| ARIMA, SARIMA, ARIMAX | + | + | − | − | + | ||
| GARCH, ARCH, EGARCH | − | + | − | − | − | ||
| VAR, VECM | − | + | − | + | − | ||
| AR-LOGIT-FACTOR-MIDAS | + | + | − | + | + | ||
| PERIODIC MARKOV CHAINS | + | + | − | − | − | ||
| Other models | NEURAL NETWORK MODELS | + | − | − | − | + | |
| MODELS IN THE “CATERPILLAR” METHOD | + | + | − | − | + | ||
| FUZZY MODELS | + | − | − | − | + | ||
| MODELS IN GMDH (GROUP METHOD OF DATA HANDLING) | − | + | − | − | + | ||
| INTERVAL MODELS | − | − | − | − | + | ||
| New models | SUM OF A POLYNOMIAL FUNCTION AND A CYCLIC RANDOM PROCESS | + | + | + | − | + | |
| SUM OF VECTORS OF POLYNOMIAL FUNCTIONS AND A VECTOR OF CYCLICALLY RHYTHMICALLY CONNECTED RANDOM PROCESSES | + | + | + | + | + | ||
| A Forecasting Method Based on a Model in the Form of a Cyclical Random Process. | A Forecasting Method Based on a Model in the Form of a Periodic Random Process. |
|---|---|
| 2925.72 Million USD | 6105.54 Million USD |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lupenko, S.; Horkunenko, A. Stochastic Model and Rhythm-Adaptive Technologies of Statistical Analysis and Forecasting of Economic Processes with Cyclic Components. Forecasting 2025, 7, 20. https://doi.org/10.3390/forecast7020020
Lupenko S, Horkunenko A. Stochastic Model and Rhythm-Adaptive Technologies of Statistical Analysis and Forecasting of Economic Processes with Cyclic Components. Forecasting. 2025; 7(2):20. https://doi.org/10.3390/forecast7020020
Chicago/Turabian StyleLupenko, Serhii, and Andrii Horkunenko. 2025. "Stochastic Model and Rhythm-Adaptive Technologies of Statistical Analysis and Forecasting of Economic Processes with Cyclic Components" Forecasting 7, no. 2: 20. https://doi.org/10.3390/forecast7020020
APA StyleLupenko, S., & Horkunenko, A. (2025). Stochastic Model and Rhythm-Adaptive Technologies of Statistical Analysis and Forecasting of Economic Processes with Cyclic Components. Forecasting, 7(2), 20. https://doi.org/10.3390/forecast7020020







