Cognitive and Spatial Forecasting Model for Maritime Migratory Incidents: SIFM

Abstract

The security challenges associated with maritime migratory incidents in the Mediterranean Sea since the onset of the 21st century are considerable. Reports of such incidents are generated almost daily, leading to significant scientific interest, including that of this manuscript. This article introduces a forecasting model specifically designed to equip maritime security stakeholders around the Mediterranean Sea with a technical instrument for estimating the frequency of maritime migratory incidents. The proposed model, the SIFM, encompasses five methodological steps: Tessellation: The initial step involves partitioning the maritime area affected by these incidents into distinct cells. Subsidiary process: In this phase, the cells are classified according to the year in which incidents were recorded. Containment index: This index quantifies the magnitude of incidents within the designated cells. Incidence growth index: This metric further refines the forecasting methodology. Maritime migration incident forecasting: The concluding step establishes a forecast interval for the anticipated quantity of maritime migratory incidents. This systematic approach aims to enhance the understanding and prediction of maritime migratory incidents within the Mediterranean region.

1. Introduction

The Mediterranean Sea has long been recognized as a crucial conduit for communication, fostering cultural and economic exchanges among civilizations spanning the Middle East [1], Mediterranean Europe [2], and the Maghreb region [3]. This rich historical legacy has greatly contributed to the prosperity of the region. However, in the modern era, marked by continuous economic interactions across these waters, the Mediterranean is beset by pressing challenges related to migratory movements.

Since the dawn of the 21st century, the frequency of maritime migration incidents in the Mediterranean has surged alarmingly, with tragic outcomes now reported almost daily. These incidents have escalated into a significant humanitarian crisis [4], posing formidable political and maritime security challenges for the region [5]. The sheer volume of migration-related maritime incidents [6] has not only garnered extensive media attention but has also underscored the urgent necessity for proactive intervention.

The human toll resulting from these incidents is often exacerbated by multiple factors, including the precarious condition of vessels, the inexperience of pilots, and the impact of hydrodynamic forces [7], particularly under perilous wave conditions [8]. Research by Chalikov [9] and Didenkulova et al. [10] further emphasizes the considerable threat posed by waves, illuminating the various hydrodynamic effects that influence safety within the Mediterranean Sea.

In light of the escalating scale and frequency of these maritime migration incidents, a variety of scientific methodologies—including legal, geopolitical, and medical frameworks—have been proposed to enhance migrant search and rescue efforts and mitigate the associated consequences. Nonetheless, despite their merits, these approaches largely remain reactive and fail to contextualize these incidents within the specific geographical realities of the Mediterranean. This observation has led to the proposition of the SIFM.

The primary objective of this scientific study was to develop a predictive model [11,12] designed to furnish stakeholders involved in maritime security [13,14] and safety [5,15] with estimates of future migratory incidents in the Mediterranean. The model aspires to optimize the organization of interventions and implement measures aimed at reducing both human and material losses associated with maritime migration incidents. To facilitate its practical application, five sequential and interdependent methodological steps have been delineated based on data concerning maritime migration incidents recorded from 2014 to 2024:

• Tessellation process;
• Subsidiary process;
• Calculation of the containment index;
• Calculation of the incidence growth index;
• Forecasting incidents related to maritime migration.

These variables are interactive; without one of them, it would be impossible to determine the others since the model is designed sequentially.

This analytical framework aimed to provide critical insights and actionable strategies for addressing the challenges posed by maritime migration in the Mediterranean, ultimately contributing to the safety and security of those navigating these perilous waters.

2. Literature Review

The 21st century has emerged as a remarkable era characterized by unprecedented economic growth, prosperity, and technological innovation. Yet, it simultaneously grapples with formidable global challenges that threaten to undermine this progress. Among these challenges are the far-reaching effects of climate change [16], the persistent threat of terrorism [17], escalating socioeconomic tensions [18], and geopolitical instability [19]. Additionally, the world faces a series of significant incidents related to natural, anthropogenic, and industrial hazards, with migration crises standing out as a particularly pressing issue, exemplified by the ongoing turmoil in the Mediterranean Sea.

This body of water has tragically become synonymous with the perilous journeys undertaken by illegal migrants from sub-Saharan Africa, the Middle East, and Asia. Each day brings reports of shipwrecks involving overcrowded and unsafe boats, leading to a harrowing toll of thousands of lives lost or missing over the past decade. The Mediterranean now serves as a focal point for a migratory crisis that has evolved into a geopolitical matter, igniting fervent debates not only among the coastal states but also within the broader scientific community, which is increasingly focused on mitigating the impacts of maritime migration incidents.

Prominent scholars (e.g., Gemma Merlode Gloniger [20]) have illuminated the collaborative efforts among governments, intergovernmental organizations, and non-governmental organizations (NGOs) in the search and rescue operations for migrants in the Mediterranean. Similarly, researchers like Michael Briguglio and Maria Brown [21] have underscored the critical interactions between states and NGOs, all aimed at preserving human life in this treacherous environment. Along these lines, Antje Scharenberg and Peter Rees [22] have proposed a legal framework to enhance the process of saving lives at sea, while Giulio Nittari et al. [23] have concentrated on the medical aspects of search and rescue operations.

The collective work of these authors demonstrates a commendable commitment to improving the search and rescue of migrants, recognizing the urgent need to safeguard lives amid such crises. However, there remains a pressing need to expand efforts beyond immediate response mechanisms towards a proactive approach that emphasizes prediction, particularly spatial prediction. This predictive capacity is essential and forms the cornerstone of the model proposed in this article. By investing in predictive methodologies, we can better anticipate and ultimately prevent such tragic incidents, striking a vital balance between immediate humanitarian response and long-term solutions to migration challenges.

3. Materials and Methods

3.1. Study Area

This manuscript endeavors to investigate the maritime migratory incidents that transpired over the course of a decade in the Mediterranean Sea, the central theme of this research study. The Mediterranean Sea, recognized as the largest inland sea globally [24,25] serves as an intercontinental and largely landlocked body of water. It is bordered by Southern Europe, North Africa, and Western Asia, encompassing an area of approximately 2.5 million square kilometers [26,27]. In contemporary times, this region garnered notable geopolitical significance due to the frequent occurrences of maritime migration incidents [28,29]. Such incidents present complex challenges for policymakers tasked with ensuring maritime safety.

Multiple factors contribute to these incidents. Human factors [13], particularly the inadequacy of boat pilots, are of considerable concern. Additionally, technical factors [30] arise from the substandard quality and diminutive size of vessels [31]. 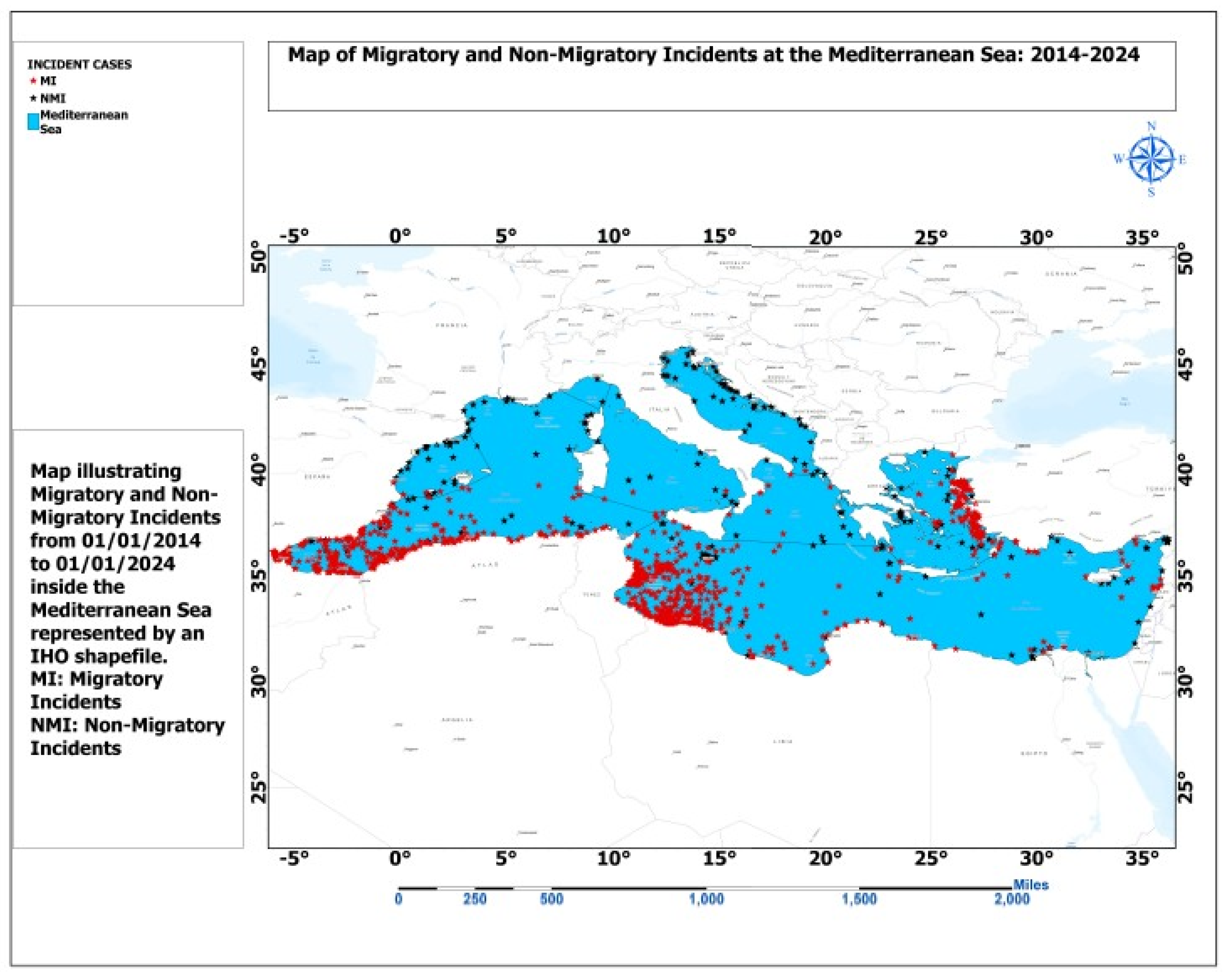These vessels exhibit heightened vulnerability to hydrodynamic forces [32], exacerbated by climate change, along with environmental factors, notably the detrimental impact of elevated wave heights [33] on maritime craft. Data provided by the International Organization for Migration (IOM), represented by small red stars, and the International Maritime Organization (IMO), represented by small black stars, indicate that approximately 90% of incidents in the Mediterranean are associated with maritime migration, while the remaining 10% consist of non-migratory maritime incidents recorded between 2014 and 2024, as shown in Figure 1.

3.2. Research Data

The study of maritime migration incidents (MMIs) [34] presents a comprehensive scientific framework designed to identify and analyze data pertinent to maritime migration incidents, with particular emphasis on the Mediterranean Sea represented by a shapefile from the International Hydrographic Organization (IHO). This research focuses on a specific category of data: maritime migration incident data (MMID); see Figure 2, which has been sourced from the Missing Migrants Project (MMP) platform of the International Organization for Migration (IOM).

The MMID has undergone meticulous processing and analysis with ArcGIS Pro tools in accordance with the proposed methodology, yielding the anticipated results for this academic endeavor. These findings are expected to offer significant insights that will support informed decision making related to maritime migration incidents.

3.3. Epistemological Approach

The proposal for a forecast model [35] focuses on maritime migration incidents in the Mediterranean Sea and is grounded in established Cartesian principles and laws, which are vital for the execution of this research. This study utilizes methodologies from various disciplines, including geometry, geospatial sciences, algebra, financial mathematics, and probability, to develop a Spatial Incident Forecast Model (SIFM).

The SIFM incorporates several advanced processes, including tessellation as described by Shah Wasif Sazzad et al. [36], the subsidiary process [37], the confinement index, and the calculation of the incidence growth index, along with MMI forecasting. This sequence of steps is presented in diagrammatic form in Figure 3.

3.3.1. Tessellation Process

Tessellation is a widely recognized method utilized in the field of geospatial sciences. This technique entails the division of a geometric shape or set {E}, typically represented as a rectangle, into morphologically identical subsets, referred to as cells or pixels {${\mathrm{e}}_{1,},{\mathrm{e}}_2,\dots \dots \dots {\mathrm{e}}_{\mathrm{n}-1},{\mathrm{e}}_{\mathrm{n}}$}. The primary aim of this operation is to adequately prepare the data for subsidiary analytical processes.

Equation (1):

$$\mathrm{E}=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{e}}_{\mathrm{i}}$$

(1)

3.3.2. Subsidiary Process

The Subsidiary process, in this context, is divided into two stages.

The first stage establishes the intersection of a rectangle that has undergone a tessellation process and the shapefile delineating the area of interest, specifically the Mediterranean Sea, as shown in Figure 4. Subsequently, while in the second stage, another intersection is established between the outcomes of the initial intersection and the points shapefile that corresponds to annual maritime migration incidents, as shown in Figure 5 [38].

Equation (2):

$${\mathrm{I}}_1=\mathrm{AOI}\cap \mathrm{E}$$

(2)

Here, AOI.shp indicates the figure or shapefile on which we base ourselves to create the geometric set that will be tessellated. Then, Girded Polygon {E}.shp represents the geometric set to be tessellated (rectangle), while (AOI ∩ {E}).shp is the result of the intersection between AOI.shp and Girded Polygon {E}.shp.

Equation (3):

$${\mathrm{I}}_2={\mathrm{I}}_1\cap \mathrm{M}\mathrm{M}\mathrm{I}\left|\right|{\mathrm{I}}_2=\mathrm{A}\mathrm{O}\mathrm{I}\cap \mathrm{E}\cap \mathrm{M}\mathrm{M}\mathrm{I}$$

(3)

Figure 5 provides a detailed representation of the second stage of the subsidiary process, which is derived from the second intersection. This intersection is evaluated annually to yield yearly subsidiaries; specifically, the intersection of $I_1$ is combined with the total number of maritime migration incidents (MMIs) that were recorded during a year. The primary objective of this methodological approach is to quantify the number of cells that are influenced by events associated with maritime migration incidents. By doing so, this analytical framework seeks to elucidate the spatial relation of maritime migration incidents on specific geographical regions over time [39].

3.3.3. Process for Determining Containment Index (Qi)

A containment index serves as a quantitative metric that assesses the ratio of maritime migratory incidents (denoted as xi) to the number of reporting cells that have documented these incidents within a given year (denoted as yi). The timeframe for this analysis may be tailored to align with specific user objectives, with potential intervals ranging from weekly to monthly or annual assessments, as exemplified in this study.

The index for the initial period is designated as the basic containment index (${\mathrm{Q}}_0$), whereas indices for subsequent periods are referred to as the updated containment index (${\mathrm{Q}}_{\mathrm{n}}$).

Equation (4):

$${\mathrm{Q}}_{\mathrm{i}}={\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\mathrm{x}\mathrm{i}}{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\mathrm{y}\mathrm{i}}}$$

(4)

3.3.4. Process of Deduction of the Incidence Growth Index (${\mathrm{K}}_{\mathrm{i}}$)

The incidence growth index serves as a quantitative measure of the periodic growth rate of maritime migration incidents. The methodology employed for deriving this index is analogous to the process of determining the interest rate of discounted capital (${\mathrm{C}}_{\mathrm{n}})$, a concept prevalent in financial mathematics [40].

Specifically, the determination of discounted capital involves the application of an equation that incorporates the original capital (${\mathrm{C}}_{\mathrm{o}}$), alongside the interest function (${1+\mathrm{i}}^{\mathrm{n}}$), where (i) denotes the interest rate and (n) signifies the annuity [41].

This relationship is expressed in the following equation:

Equation (5):

$${\mathrm{C}}_{\mathrm{n}=}{\mathrm{C}}_{\mathrm{o}}{(1+\mathrm{i})}^{\mathrm{n}}$$

(5)

This research involves a comparison of the updated containment index with the updated capital and the fundamental parameters of the basic containment index. The parameters utilized in the formula for the updated concentration index include the incidence index (k) and the corresponding ranking period or year of incidence (a), whose first year in the series of years has the ranking value of (0). From the equation governing the updated containment index, it is possible to derive the incidence index.

Equation (6):

$${\mathrm{Q}}_{\mathrm{n}}{=\mathrm{Q}}_{\mathrm{o}}{(1+{\mathrm{k}}_{\mathrm{i}})}^{\mathrm{a}}$$

(6)

Equation (7):

$${\mathrm{k}}_{\mathrm{i}}=[{({\displaystyle \frac{{\mathrm{Q}}_{\mathrm{n}}}{{\mathrm{Q}}_{\mathrm{o}}}})}^{1/\mathrm{a}}-1]$$

(7)

The incidence growth indices (ki) thus known, it would also be judicious to define an average incidence growth index ($\overline{\mathrm{K}}$), a lower incidence growth index (${\mathrm{k}}_{\mathrm{l}}$) and a higher incidence growth index (${\mathrm{k}}_{\mathrm{u}}$) whose usefulness is important in the process of posteriori forecasts.

Equation (8):

$$\overline{\mathrm{k}}={\displaystyle \frac{{\sum }_{\mathrm{i}=0}^{\mathrm{n}}\mathrm{k}\mathrm{i}}{\mathrm{a}}}$$

(8)

3.3.5. MMI Forecasting Process

Occurrence probability ${\mathrm{P}}_{{\mathrm{k}}_{\mathrm{i}}}$

The objective of this study is to forecast the number of maritime migratory incidents based on the incident index.

In order to accomplish this forecast, this analysis relies on established probability laws and theories, specifically the probability of detection (POD) [42], as introduced by Bernard Koopman in his seminal work on search theory [43]. This methodology facilitates the estimation of the probability of incident occurrences, designated as (${\mathrm{P}}_{\mathrm{k}\mathrm{i}}$). The selection of this probabilistic method is motivated by its potential to enhance the reliability of the forecast.

The Koopman detection probability is articulated through the following function:

Equation (9):

$$\mathrm{POD}={1-\mathrm{e}}^{-\mathrm{c}}$$

(9)

In this analytical framework, the probability of detection (POD) is effectively replaced by the probability of occurrence (${\mathrm{P}}_{\mathrm{k}}$), while the traditional concept of coverage (C) is reinterpreted through the lens of the incidence growth index (${\mathrm{k}}_{\mathrm{i}}$). This substitution is not merely semantic; it underscores a fundamental relationship between these variables. Just as coverage (C) serves as a pivotal role in the POD formula, the incidence growth index (${\mathrm{k}}_{\mathrm{i}}$) is equally crucial for accurately calculating the probability of occurrence (${\mathrm{P}}_{\mathrm{k}}$).

Both (${\mathrm{k}}_{\mathrm{i}}$) and (C) operate within distinct contexts yet fulfill the same overarching purpose: they are instrumental in estimating probabilities. Importantly, these variables are expressed as ratios, with their outcomes yielding decimal values, which facilitates a consistent framework of analysis. Given this congruence, it is logical to assert that (${\mathrm{k}}_{\mathrm{i}}$) may be more adept at determining (${\mathrm{P}}_{\mathrm{k}}$), thereby facilitating the application of various probability calculation methodologies.

This exploration of the interconnections between these variables not only enriches our understanding of probabilistic modeling but also enhances the precision with which we can assess occurrences across diverse scenarios. In conclusion, the nuanced relationship between C and ${\mathrm{k}}_{\mathrm{i}}$ illustrates the versatility and utility of these metrics in probability estimation.

Equation (10a–c):

$${\mathrm{P}}_{{\mathrm{k}}_{\mathrm{i}}}={1-\mathrm{e}}^{-{\mathrm{k}}_{\mathrm{i}}}$$

(10a)

Forecast values (${\mathrm{X}}_{\mathrm{n}+1}$)

Upon establishing the probability of occurrence of incidents (${\mathrm{P}}_{\mathrm{k}\mathrm{i}}$) it becomes feasible to project the number of migratory incidents for the subsequent year. This projection is made according to the growth indices of “lower (${\mathrm{K}}_{\mathrm{l}}$), means (K) and upper (${\mathrm{K}}_{\mathrm{u}}$)” incidences. Thanks to these different types of indices, it is possible to determine forecast intervals (${\mathrm{I}}_{\mathrm{F}}$) based on the formula of Koopman’s research theory.

$${\mathrm{I}}_{\mathrm{F}}=[{\mathrm{K}}_{\mathrm{l}};\mathrm{K}]\cup [\mathrm{K};{\mathrm{K}}_{\mathrm{u}}\left]\mathrm{or}\right[{\mathrm{K}}_{\mathrm{l}};{\mathrm{K}}_{\mathrm{u}}]$$

(10b)

Any values outside these ranges (${\mathrm{I}}_{\overline{\mathrm{F}}}$) are out of the series and should therefore be added to the annual migration incident data series [44] and then repeat the SIFM forecasting process.

$${\mathrm{I}}_{\overline{\mathrm{F}}}=]\mathrm{\infty }-;{\mathrm{K}}_{\mathrm{l}}[\cup ]{\mathrm{K}}_{\mathrm{u}};+\mathrm{\infty }[$$

(10c)

Equation (11a–e):

Case 1:

$${\mathrm{X}}_{\mathrm{n}+1}={\mathrm{X}}_{\mathrm{n}}[1-({\mathrm{P}}_{{\mathrm{k}}_{\mathrm{l}}}\left)\right]$$

(11a)

Case 2:

$${\mathrm{X}}_{\mathrm{n}+1}={\mathrm{X}}_{\mathrm{n}}[1+({\mathrm{P}}_{\overline{\mathrm{K}}}\left)\right]$$

(11b)

Case 3:

$${\mathrm{X}}_{\mathrm{n}+1}={\mathrm{X}}_{\mathrm{n}}[1+({\mathrm{P}}_{{\mathrm{k}}_{\mathrm{u}}}\left)\right]$$

(11c)

Forecast value

$${\mathrm{X}}_{\mathrm{n}+1}=[{\mathrm{X}}_{\mathrm{n}}+\left(\right({\mathrm{X}}_{\mathrm{n}}\left)\right({\mathrm{P}}_{{\mathrm{k}}_{\mathrm{i}}}\left)\right)]$$

(11d)

$${\mathrm{X}}_{\mathrm{n}+1}={\mathrm{X}}_{\mathrm{n}}[1+({\mathrm{P}}_{{\mathrm{k}}_{\mathrm{i}}}\left)\right]$$

(11e)

4. Results

4.1. Tessellation Process

Tessellation refers to the method of partitioning a polygon into multiple cells. In this context, the polygon is defined by the area of interest (AOI), specifically the Medi-terranean Sea. Given its geographical characteristics, the resultant polygon, designated as {E}, is a rectangle with dimensions of 4100 km by 1600 km. This rectangle is situated between the 29th and 47th parallels and extends longitudinally from the 5° W to the 37° E meridians . To accommodate the form of the Earth, the vertical axis coincides with the meridian 16° E and the horizontal axis coincides with the intersection of this meridian with the parallel 38° N. It comprises a total of 656 cells, with each individual cell meas-uring 100 km by 100 km as shown in Figure 6.

This image above evokes the process of generating the set {E} made of 656 cells based on the figure of the Mediterranean Sea, and of which the first cell (e1) is located at the lower-left end of {E} then the last cell (e656) situated at the upper-right end of {E}.

4.2. Filialization Process

In the second step of the SIFM, the implementation of the subsidiary was conducted in three distinct stages. The first two stages adhered to Equations (2) and (3), while the third stage employed a subdivision method based on incident years, as outlined in the second section of the methodology. The application of Equation (2) in this context entails the intersection of the area of interest (AOI) with the shapefile representing the tessellated set, denoted as {E}. The objective of this process is to generate a pixelated shapefile of the AOI, organized into multiple cells.

Figure 7 presents a detailed analysis of the input data concerning the Mediterranean Sea shapefile, illustrated in parts (a) and (b). Both sections depict the configuration of set E, which is represented through a fishnet shapefile that encapsulates the data necessary for the branching process, specifically the Areas of Interest (AOI) and set E.

Moving to part (c), this section illustrates the intersection process, denoted as AOI ∩ {E}, highlighting the method by which the areas of interest interact with set E. Finally, part (d) displays the outcome of this intersection, offering a visual representation of the data’s alignment and overlap.

This figure serves as a clear illustration of the initial step in the branching process, providing a foundational understanding of how the data sets converge.

The outcome of the initial step is subsequently intersected with the point entities of the MMI. Following this, the resulting data are further subdivided on an annual basis to categorize subsidiaries by year. This approach facilitates the effective determination of the confinement index.

Figure 8 presents a comprehensive visual analysis of the geographic data involved in our study. Panel (a) illustrates the shapefile corresponding to the MMI’s points, while panel (b) displays the shapefile representing the intersection of the Area of Interest (AOI) and the set E. These datasets serve as pivotal input for the branching process denoted as (MMI and AOI ∩ {E}).

In panel (c), we delve into the intersection process itself, represented as (MMI ∩ AOI ∩ {E}), which is crucial for understanding the spatial relationships between the variables at play. Panel (d) provides the resultant shapefile from this intersection, encapsulating the combined data.

The subsequent calculation of Equation (3), denoted as (AOI {E}), is the final step necessary for establishing annual subsidiaries composed of individual cells. The numerical values extracted from these cells will be instrumental in the overarching process of calculating the containment index. This analytical procedure signifies the second crucial step in the branching process, ultimately leading us towards a more refined understanding of the spatial dynamics involved.

Figure 9 displays the annual subsidiaries which are derived from the intersection (MMI ∩ AOI ∩ {E}), from 2014 at the top left on the first line to 2024 at the bottom right on the last line, passing successively through the years (2015 to 2023).

These subsidiaries provide a clear understanding of the number of cells impacted by IMMs, thereby facilitating the calculation of the containment index.

4.3. Containment Index (Qi)

The confinement index quantifies the relationship between the number of maritime migratory incidents and the number of cells that have recorded these incidents. Each cell corresponds to an entire pixel, although some may be reduced due to the intersection process. While these cells can be regarded as representing surface values and interpreted as density, the values of the confinement index are generally quite small. Consequently, it is deemed more appropriate to focus exclusively on the count of cells involved.

Table 1. Qi process table.

Year	MMI/xi	Cells/yi	Qi
2014	53	34	1.56
2015	112	32	3.50
2016	74	24	3.08
2017	108	31	3.48
2018	171	41	4.17
2019	122	42	2.90
2020	154	23	6.70
2021	226	46	4.91
2022	221	66	3.35
2023	221	27	8.19
2024	235	60	3.92

presented below delineates the annual values of Qi, providing a comprehensive overview of its fluctuations over the years. Additionally, Figure 10 visually represents the evolution of Qi across the last several decades, offering valuable insights into its trends and patterns.

4.4. Incidence Index (ki)

This operation underscores the significance of Equation (6), which facilitates the derivation of the incidence growth index from the incident growth index, based on Equation (5). The implementation of Equation (6) within this framework considers the values of (Qi) as well as the annual deviation.

Table 2. (${\mathrm{K}}_{\mathrm{i}}$) Process table showing ${\mathrm{K}}_{\mathrm{u}}$, ${\mathrm{K}}_{\mathrm{l}}$, K.

Year	a	Qi	${\mathbf{K}}_{\mathbf{i}}$$=[{\left(\frac{{\mathbf{Q}}_{\mathbf{n}}}{{\mathbf{Q}}_{\mathbf{o}}}\right)}^{1/\mathbf{a}}-1]$
2014	0	1.56	0.00
$2015\left({\mathrm{K}}_{\mathrm{u}}\right)$	1	3.50	1.25
2016	2	3.08	0.41
2017	3	3.48	0.31
2018	4	4.17	0.28
2019	5	2.90	0.13
2020	6	6.70	0.27
2021	7	4.91	0.18
$2022\left({\mathrm{K}}_{\mathrm{l}}\right)$	8	3.35	0.10
2023	9	8.19	0.20
2024	10	3.92	0.10
K = ${\displaystyle \frac{{\sum }_{\mathrm{i}=0}^{\mathrm{n}}\mathrm{k}\mathrm{i}}{\mathrm{a}}}$			0.32

below presents a comprehensive overview of the annual values of ${\mathrm{K}}_{\mathrm{i}}$ in relation to Qi, providing a clear quantitative analysis of their interdependence. Accompanying this data, Figure 11 graphically depicts the evolution of ${\mathrm{K}}_{\mathrm{i}}$ over the past several decades, offering valuable insights into its trends and fluctuations.

4.5. MMI Forecasting Interval

The determination of the lower (${\mathrm{K}}_{\mathrm{l}}$), mean ($\overline{\mathrm{K}}$), and upper (${\mathrm{K}}_{\mathrm{u}}$) incidence growth indices constitute the key to this stage of the model, based on the Bernard Koopman method in search theory.

Formula	$\mathbf{l}$	$\mathbf{k}$	$\mathbf{u}$
${\mathrm{P}}_{{\mathrm{k}}_{\mathrm{i}}}$$={1-\mathrm{e}}^{-{\mathrm{k}}_{\mathrm{i}}}$	0.10	027	0.71
${\mathrm{X}}_{\mathrm{n}+1}$ = ${\mathrm{X}}_{\mathrm{n}}$ [1 $\pm$ $({\mathrm{P}}_{{\mathrm{k}}_{\mathrm{i}}}$)]	$211.5\cong$ 212	$298.45\cong$ 298	$401.85\cong$ 402
${\mathrm{I}}_{\mathrm{F}}$ = [212; 402].

5. Discussion

The central aim of this study was to forecast maritime migratory incidents (xi) in the years subsequent to the current year, with a particular focus on the upcoming year. The SIFM is established as a crucial framework for estimating the expected volume of maritime migratory incidents in the forthcoming year.

This model builds upon prior research designed to alleviate the repercussions of maritime migration crises, notably the studies conducted by Carlo Amenta et al. [34] and Salvatore Coluccello and Simon Massey [45].

The operationalization of this model begins with an essential process known as tessellation. This step, commonly utilized in geospatial sciences, adeptly filters out non-adjacent regions that are extraneous to the effective functioning of the model.

Following tessellation [46], the model enters the filialization phase, a pivotal element of the SIFM framework. This process is instrumental in deriving a crucial variable: the number of annual cells (yi). This variable plays a significant role in the calculation of various indices and probabilities that form the backbone of the forecasting methodology. Additionally, filialization aids in pinpointing regions annually impacted by these incidents, thus enabling the identification of the most severely affected areas within the Mediterranean Sea.

Once the tessellation and Filialization processes are finalized, the model progresses to the calculation of indices, specifically confinement indices (Qi) and incidence growth indices. In the realm of incident forecasting, the confinement index measures the occupancy rate of cells influenced by maritime migratory incidents, functioning similarly to geographic density.

The incidence growth index is crucial for defining the forecast interval. This index affects both the lower and upper limits of the forecast, potentially minimizing the projected number of maritime migratory incidents at the lower bound while amplifying estimates at the upper bound, consequently influencing the average number of incidents.

Ultimately, probabilities are calculated using the formula proposed by Bernard Koopman in the field of research theory. This approach enables the prediction of future migratory incidents for the subsequent year through the application of three types of incidence growth indices: Ki minima, Ki medium, and Ki maxima. These indices are vital for delineating the forecast interval of the SIFM, ensuring a comprehensive understanding of the potential future landscape of maritime migration incidents.

In summary, this analytical exploration aims to provide a robust methodology for anticipating undefined maritime migratory incidents, thereby contributing valuable insights to the ongoing discourse surrounding maritime migration.

6. Conclusions

In light of the aforementioned considerations, SIFM presents a sophisticated forecasting model tailored to predict the number of migratory incidents occurring in the Mediterranean Sea for the year subsequent to the previous year. Remarkably, this model exhibits adaptability, enabling its application across various maritime regions globally.

This manuscript meticulously delineates the methodological framework essential for the effective implementation of the proposed model, underscoring the robustness of its capability to establish a forecast interval for maritime migration incidents (MMIs). The procedure encompasses several pivotal steps: tessellation, subdivision, the identification of two critical indices (the containment index and the incidence growth index), and the estimation of probabilities necessary for configuring the forecast interval. The overarching objective of this study was to equip maritime security stakeholders and decision makers with advanced analytical tools that empower them to anticipate and respond more effectively to future maritime migration incidents. By enhancing their preparedness, these stakeholders can work diligently to mitigate the tragedies associated with these occurrences—tragedies increasingly recognized as human-induced hazards that starkly reflect the inequalities between developed and developing nations.

In practical terms, this model is designed for seamless integration into various maritime security systems within the Mediterranean context, thereby facilitating not only the prediction of migration incidents but also the assessment of relevant alert levels pertaining to these maritime challenges. However, to enhance the accuracy of these forecasts, comprehensive and transparent data collection from previous years regarding such maritime incidents is imperative. Addressing this data collection challenge will create the foundation for developing a refined version of the model that takes into account the hydro-atmospheric dynamics influencing maritime migratory patterns.

Through these concerted efforts, the model aspires not only to provide a clearer understanding of migration patterns but also to foster proactive measures designed to diminish the scale of tragedies linked to maritime migration. In doing so, it aims to illuminate the complexities of this issue and promote a more equitable discourse on the global challenges of migration, particularly in maritime contexts.