Day-Ahead Energy Price Forecasting with Machine Learning: Role of Endogenous Predictors
Abstract
1. Introduction
2. Materials and Methods
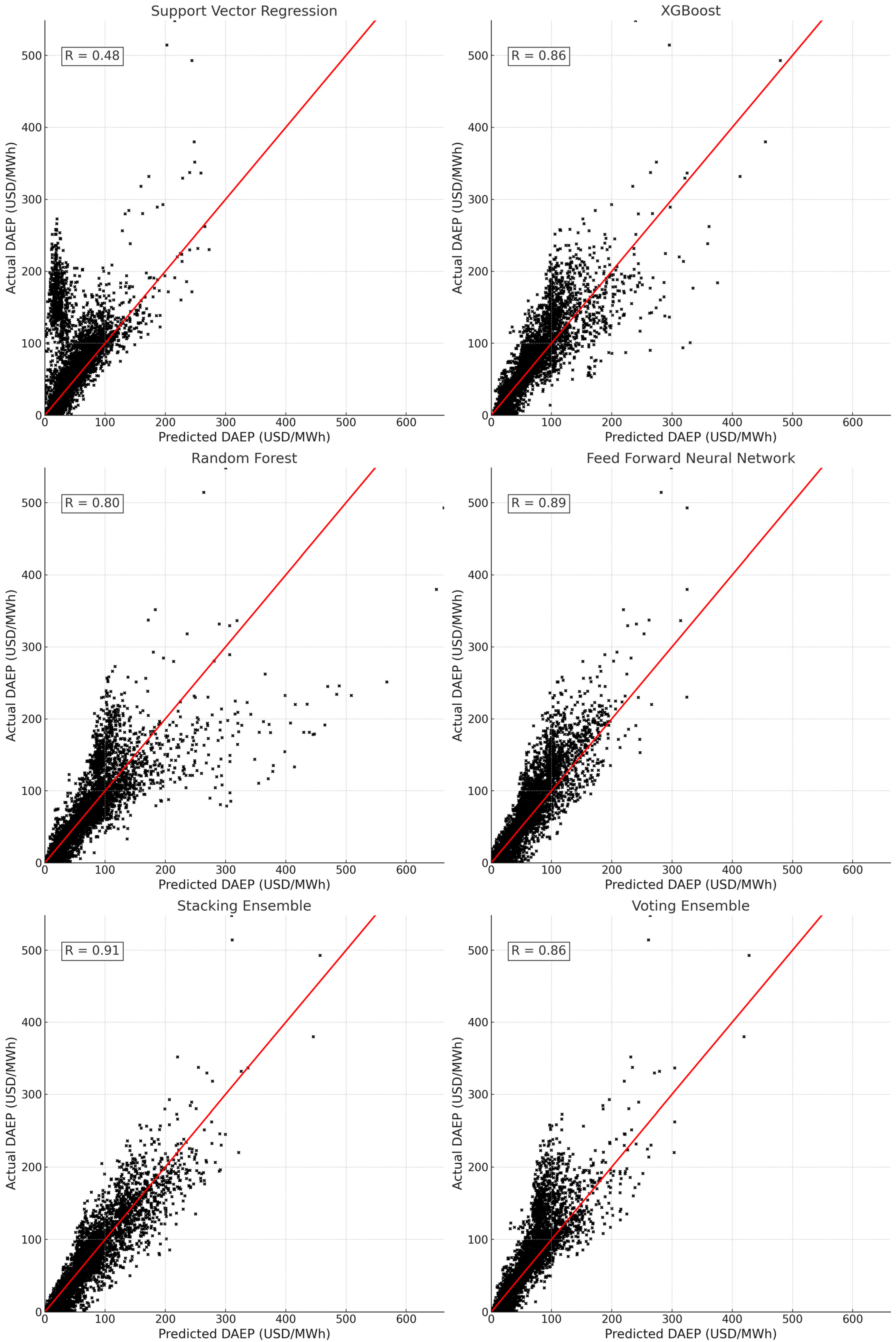
3. Results
4. Discussion
5. Conclusions
- SHAP analysis identified endogenous features, including the DAEP from 1 h ago, 24 h ago, 30-day moving average, day of the week, and DAEP difference between t − 1 and t − 25, as top contributors, driving approximately 60% of model accuracy.
- XGBoost cross-validation across 2372-day folds with a 24 h rolling window achieved a median MAE of 6.26 USD/MWh and RMSE of 8.27 USD/MWh across a highly volatile analysis period.
- The best-performing model varies by forecast model, training period, and test period, highlighting the need for ensemble forecasting using multiple models (e.g., SVR, XGBoost, RF, FFNN), combining the strengths of base models through methods such as voting and stacking, and using a dynamic evaluation period to capture different market conditions.
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
References
- Hassan, Q.; Viktor, P.; Al-Musawi, T.J.; Ali, B.M.; Algburi, S.; Alzoubi, H.M.; Al-Jiboory, A.K.; Sameen, A.Z.; Salman, H.M.; Jaszczur, M. The renewable energy role in the global energy Transformations. Renew. Energy Focus 2024, 48, 100545. [Google Scholar] [CrossRef]
- Safari, A.; Gharehbagh, H.K.; Nazari-Heris, M.; Zare, K. Design of a Dynamic Feedback LSTM Electricity Price Forecast of Smart Grids. In Artificial Intelligence in the Operation and Control of Digitalized Power Systems; Springer Nature: Cham, Switzerland, 2024; pp. 327–344. [Google Scholar]
- Cheng, L.; Huang, P.; Zhang, M.; Yang, R.; Wang, Y. Optimizing Electricity Markets Through Game-Theoretical Methods: Strategic and Policy Implications for Power Purchasing and Generation Enterprises. Mathematics 2025, 13, 373. [Google Scholar] [CrossRef]
- Abidi, I.; Nsaibi, M. Assessing the impact of renewable energy in mitigating climate change: A comprehensive study on effectiveness and adaptation support. Int. J. Energy Econ. Policy 2024, 14, 442–454. [Google Scholar] [CrossRef]
- Strielkowski, W.; Civín, L.; Tarkhanova, E.; Tvaronavičienė, M.; Petrenko, Y. Renewable energy in the sustainable development of electrical power sector: A review. Energies 2021, 14, 8240. [Google Scholar] [CrossRef]
- Constante, D.M.A.; Erazo, C.R.R. The role of renewable energies in the transition to a sustainable energy model: Challenges and opportunities. J. Bus. Entrep. Stud. 2024, 8, 38–48. [Google Scholar]
- Hassan, W.; Elsabbagh, B.; Abdelaziz, A.; Essam, G.; Aboushama, R. Energy Trading Enhancing Sustainability. In Artificial Intelligence and Machine Learning for Sustainable Development: Innovations, Challenges, and Applications; CRC Press: Boca Raton, FL, USA, 2024; p. 33. [Google Scholar]
- Coker, P.J.; Bloomfield, H.C.; Drew, D.R.; Brayshaw, D.J. Interannual weather variability and the challenges for Great Britain’s electricity market design. Renew. Energy 2020, 150, 509–522. [Google Scholar] [CrossRef]
- Gonçalves, A.C.; Costoya, X.; Nieto, R.; Liberato, M.L. Extreme weather events on energy systems: A comprehensive review on impacts, mitigation, and adaptation measures. Sustain. Energy Res. 2024, 11, 4. [Google Scholar] [CrossRef]
- Kumar, R.R.; Sanjai, M.; Sivashanmugam, R.; Saranya, S.; Sinega, S.; Logeswaran, T. Grid integration of renewable energy sources with IoT system. In Proceedings of the 2022 International Conference on Sustainable Computing and Data Communication Systems (ICSCDS), Erode, India, 7–9 April 2022; pp. 1012–1017. [Google Scholar]
- Medina, C.; Ana, C.R.M.; González, G. Transmission grids to foster high penetration of large-scale variable renewable energy sources–A review of challenges, problems, and solutions. Int. J. Renew. Energy Res. 2022, 12, 146–169. [Google Scholar]
- Foster, J.M. Control Systems in Power Markets: Demand Response, Transmission Topology Control, and Renewable Integration. Ph.D. Thesis, Boston University, Boston, MA, USA, 2012. [Google Scholar]
- Welton, S. Electricity markets and the social project of decarbonization. Columbia Law Rev. 2018, 118, 1067–1138. [Google Scholar]
- Ketterer, J.C. The impact of wind power generation on the electricity price in Germany. Energy Econ. 2014, 44, 270–280. [Google Scholar] [CrossRef]
- Van Kuik, G.A.M.; Peinke, J.; Nijssen, R.; Lekou, D.; Mann, J.; Sørensen, J.N.; Ferreira, C.; van Wingerden, J.W.; Schlipf, D.; Gebraad, P.; et al. Long-term research challenges in wind energy—A research agenda by the European Academy of Wind Energy. Wind. Energy Sci. 2016, 1, 1–39. [Google Scholar] [CrossRef]
- Aderibigbe, A.O.; Ani, E.C.; Ohenhen, P.E.; Ohalete, N.C.; Daraojimba, D.O. Enhancing energy efficiency with ai: A review of machine learning models in electricity demand forecasting. Eng. Sci. Technol. J. 2023, 4, 341–356. [Google Scholar] [CrossRef]
- Ibebuchi, C.C.; Richman, M.B. Deep learning with autoencoders and LSTM for ENSO forecasting. Clim. Dyn. 2024, 62, 5683–5697. [Google Scholar] [CrossRef]
- Allal, Z.; Noura, H.N.; Salman, O.; Chahine, K. Machine learning solutions for renewable energy systems: Applications, challenges, limitations, and future directions. J. Environ. Manag. 2024, 354, 120392. [Google Scholar] [CrossRef]
- Rane, N.L.; Choudhary, S.P.; Rane, J. Artificial Intelligence and machine learning in renewable and sustainable energy strategies: A critical review and future perspectives. Partn. Univers. Int. Innov. J. 2024, 2, 80–102. [Google Scholar] [CrossRef]
- Wegener, C.; Ibebuchi, C.C. Application of XGBOOST in Disentangling the Fingerprints of Global Warming and Interdecadal Pacific Oscillation on Seasonal Precipitation Trends in Ohio. Res. Sq. 2024. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R.; Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Manohar, V.J.; Murthy, G.; Royal, N.P.; Binu, B.; Patil, T. Comprehensive Analysis of Energy Demand Prediction Using Advanced Machine Learning Techniques. In Proceedings of the 2nd International Conference on Renewable Energy, Green Computing and Sustainable Development (ICREGCSD 2025), Hyderabad, India, 21–22 February 2025; Volume 616, p. 02027. [Google Scholar]
- Xie, H.; Chen, S.; Lai, C.; Ma, G.; Huang, W. Forecasting the clearing price in the day-ahead spot market using eXtreme Gradient Boosting. Electr. Eng. 2022, 104, 1607–1621. [Google Scholar] [CrossRef]
- Tschora, L.; Pierre, E.; Plantevit, M.; Robardet, C. Electricity price forecasting on the day-ahead market using machine learning. Appl. Energy 2022, 313, 118752. [Google Scholar] [CrossRef]
- Tan, Y.Q.; Shen, Y.X.; Yu, X.Y.; Lu, X. Day-ahead electricity price forecasting employing a novel hybrid frame of deep learning methods: A case study in NSW, Australia. Electr. Power Syst. Res. 2023, 220, 109300. [Google Scholar] [CrossRef]
- Sun, C.; Pan, X.; Li, G.; Li, P.; Gao, G.; Tian, Y.; Xu, G. Day-Ahead Electricity Price Forecasting Strategy Based on Machine Learning and Optimization Algorithm. In Proceedings of the 2022 4th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 25–28 March 2022; pp. 254–259. [Google Scholar]
- Bae, D.J.; Kwon, B.S.; Song, K.B. XGBoost-based day-ahead load forecasting algorithm considering behind-the-meter solar PV generation. Energies 2021, 15, 128. [Google Scholar] [CrossRef]
- Raviv, E.; Bouwman, K.E.; Van Dijk, D. Forecasting day-ahead electricity prices: Utilizing hourly prices. Energy Econ. 2015, 50, 227–239. [Google Scholar] [CrossRef]
- Nohara, Y.; Matsumoto, K.; Soejima, H.; Nakashima, N. Explanation of machine learning models using improved shapley additive explanation. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, Niagara Falls, NY, USA, 7–10 September 2019; p. 546. [Google Scholar]
- Divina, F.; Gilson, A.; Goméz-Vela, F.; García Torres, M.; Torres, J.F. Stacking ensemble learning for short-term electricity consumption forecasting. Energies 2018, 11, 949. [Google Scholar] [CrossRef]
- Solano, E.S.; Affonso, C.M. Solar irradiation forecasting using ensemble voting based on machine learning algorithms. Sustainability 2023, 15, 7943. [Google Scholar] [CrossRef]
- California Independent System Operator (CAISO). CAISO Market Data. 2025. Available online: https://www.caiso.com (accessed on 15 February 2025).
- Ibebuchi, C.C.; Rainey, S.; Obarein, O.A.; Silva, A.; Lee, C.C. Comparison of machine learning models in forecasting different ENSO types. Phys. Scr. 2024, 99, 086007. [Google Scholar] [CrossRef]
- Sahlaoui, H.; Nayyar, A.; Agoujil, S.; Jaber, M.M. Predicting and interpreting student performance using ensemble models and shapley additive explanations. IEEE Access 2021, 9, 152688–152703. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- O’Malley, T.; Bursztein, E.; Long, J.; Chollet, F.; Jin, H. Keras Tuner. 2019. Available online: https://github.com/keras-team/keras-tuner (accessed on 15 February 2025).
- Hodson, T.O. Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. Discuss. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Sharma, N.; Mangla, M.; Mohanty, S.N.; Pattanaik, C.R. Employing stacked ensemble approach for time series forecasting. Int. J. Inf. Technol. 2021, 13, 2075–2080. [Google Scholar] [CrossRef]
- Nyangon, J.; Akintunde, R. Principal component analysis of day-ahead electricity price forecasting in CAISO and its implications for highly integrated renewable energy markets. Wiley Interdiscip. Rev. Energy Environ. 2024, 13, e504. [Google Scholar] [CrossRef]
- Cai, M.; Pipattanasomporn, M.; Rahman, S. Day-ahead building-level load forecasts using deep learning vs. traditional time-series techniques. Appl. Energy 2019, 236, 1078–1088. [Google Scholar] [CrossRef]
- Lago, J.; Marcjasz, G.; De Schutter, B.; Weron, R. Forecasting day-ahead electricity prices: A review of state-of-the-art algorithms, best practices and an open-access benchmark. Appl. Energy 2021, 293, 116983. [Google Scholar] [CrossRef]
- Nizharadze, N.; Farokhi Soofi, A.; Manshadi, S. Predicting the gap in the day-ahead and real-time market prices leveraging exogenous weather data. Algorithms 2023, 16, 508. [Google Scholar] [CrossRef]
- Alkawaz, A.N.; Abdellatif, A.; Kanesan, J.; Khairuddin, A.S.M.; Gheni, H.M. Day-ahead electricity price forecasting based on hybrid regression model. IEEE Access 2022, 10, 108021–108033. [Google Scholar] [CrossRef]
- Zhang, C.; Li, R.; Shi, H.; Li, F. Deep learning for day-ahead electricity price forecasting. IET Smart Grid 2020, 3, 462–469. [Google Scholar] [CrossRef]
- Caffù, D. Explainable Deep Learning Based Electricity Price Forecasting Through SHAP Values for the Extended Cross-Regional Markets Integration. 2021. Available online: https://www.politesi.polimi.it/handle/10589/201356?mode=simple (accessed on 3 April 2025).
- Liu, H.; Shen, X.; Tang, X.; Liu, J. Day-Ahead electricity price probabilistic forecasting based on SHAP feature selection and LSTNet quantile regression. Energies 2023, 16, 5152. [Google Scholar] [CrossRef]
- Kilian, L. The economic effects of energy price shocks. J. Econ. Lit. 2008, 46, 871–909. [Google Scholar] [CrossRef]
- Lehna, M.; Scheller, F.; Herwartz, H. Forecasting day-ahead electricity prices: A comparison of time series and neural network models taking external regressors into account. Energy Econ. 2022, 106, 105742. [Google Scholar] [CrossRef]
- Goodell, J.W.; Corbet, S. The evolving landscape of energy finance: Challenges and opportunities during global uncertainty. In Handbook of Financial Integration; Edward Elgar Publishing: Northampton, MA, USA, 2024; pp. 172–191. [Google Scholar]
- Tan, J.; Yang, J.; Wu, S.; Chen, G.; Zhao, J. A critical look at the current train/test split in machine learning. arXiv 2021, arXiv:2106.04525. [Google Scholar]
- Ferruzzi, G.; Cervone, G.; Delle Monache, L.; Graditi, G.; Jacobone, F. Optimal bidding in a Day-Ahead energy market for Micro Grid under uncertainty in renewable energy production. Energy 2016, 106, 194–202. [Google Scholar] [CrossRef]
- Rahimiyan, M.; Baringo, L. Strategic bidding for a virtual power plant in the day-ahead and real-time markets: A price-taker robust optimization approach. IEEE Trans. Power Syst. 2015, 31, 2676–2687. [Google Scholar] [CrossRef]
- Ibebuchi, C. California Independent System Operator (CAISO) Energy Market Data; Zenodo: Geneva, Switzerland, 2025. [Google Scholar] [CrossRef]
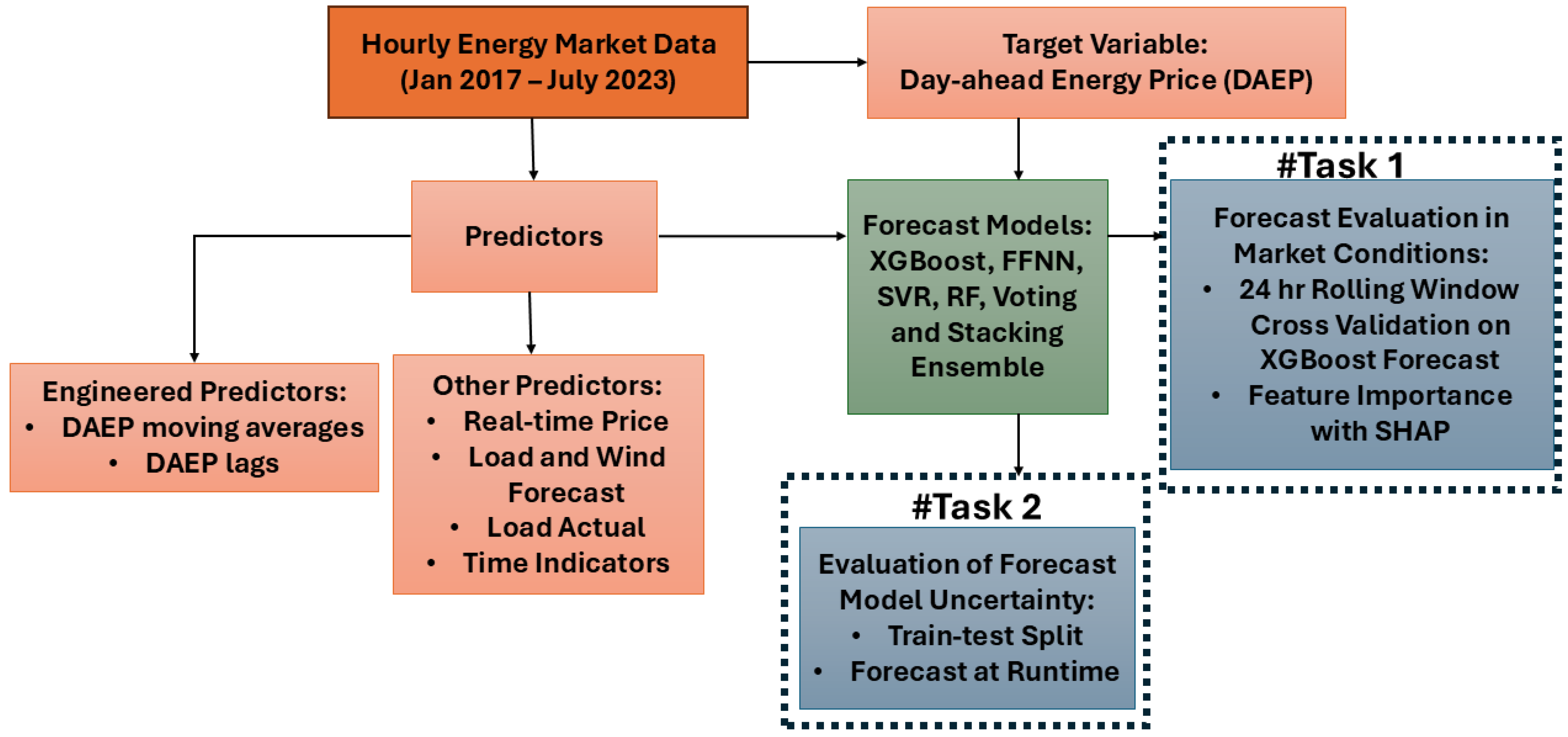
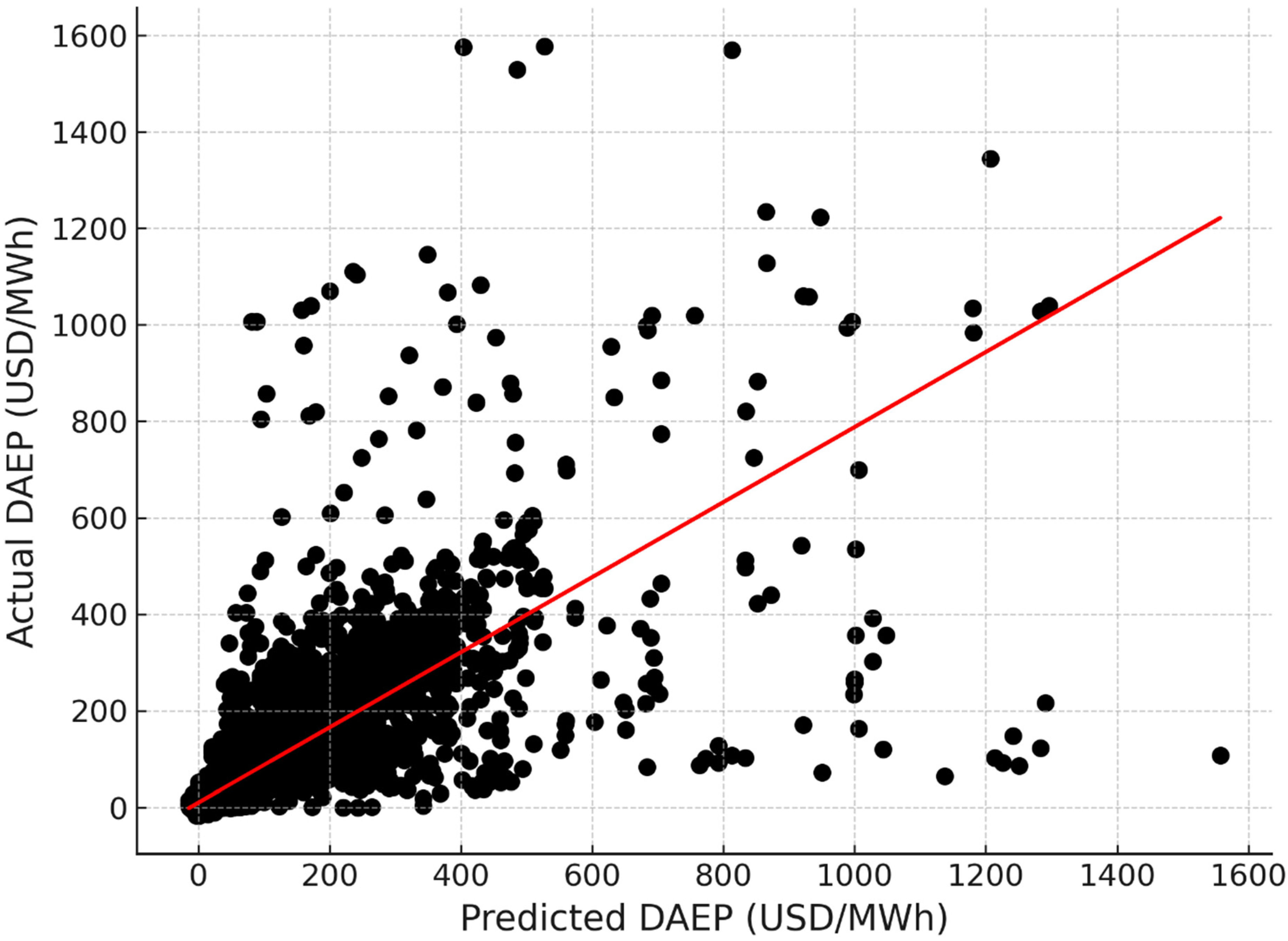
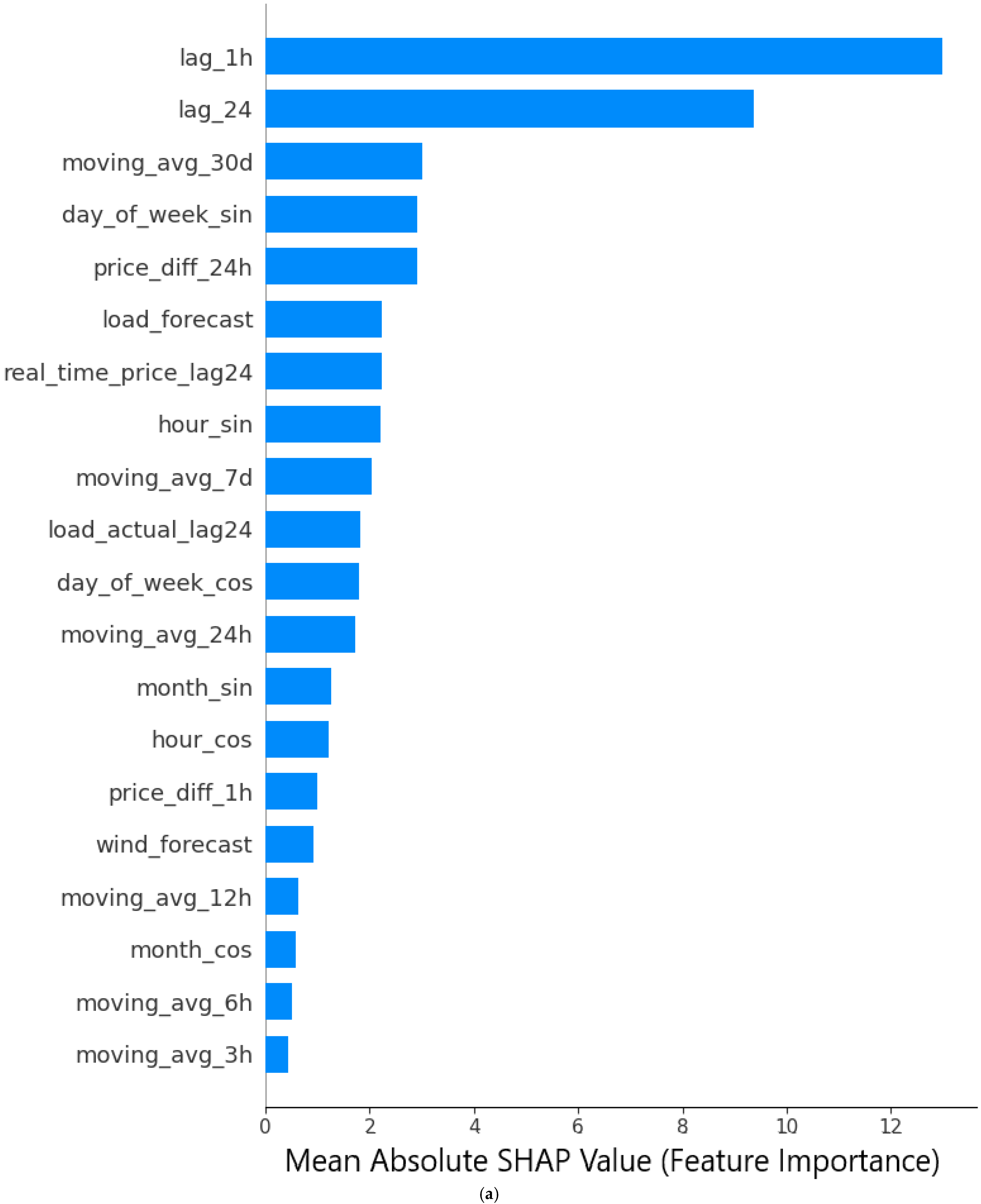

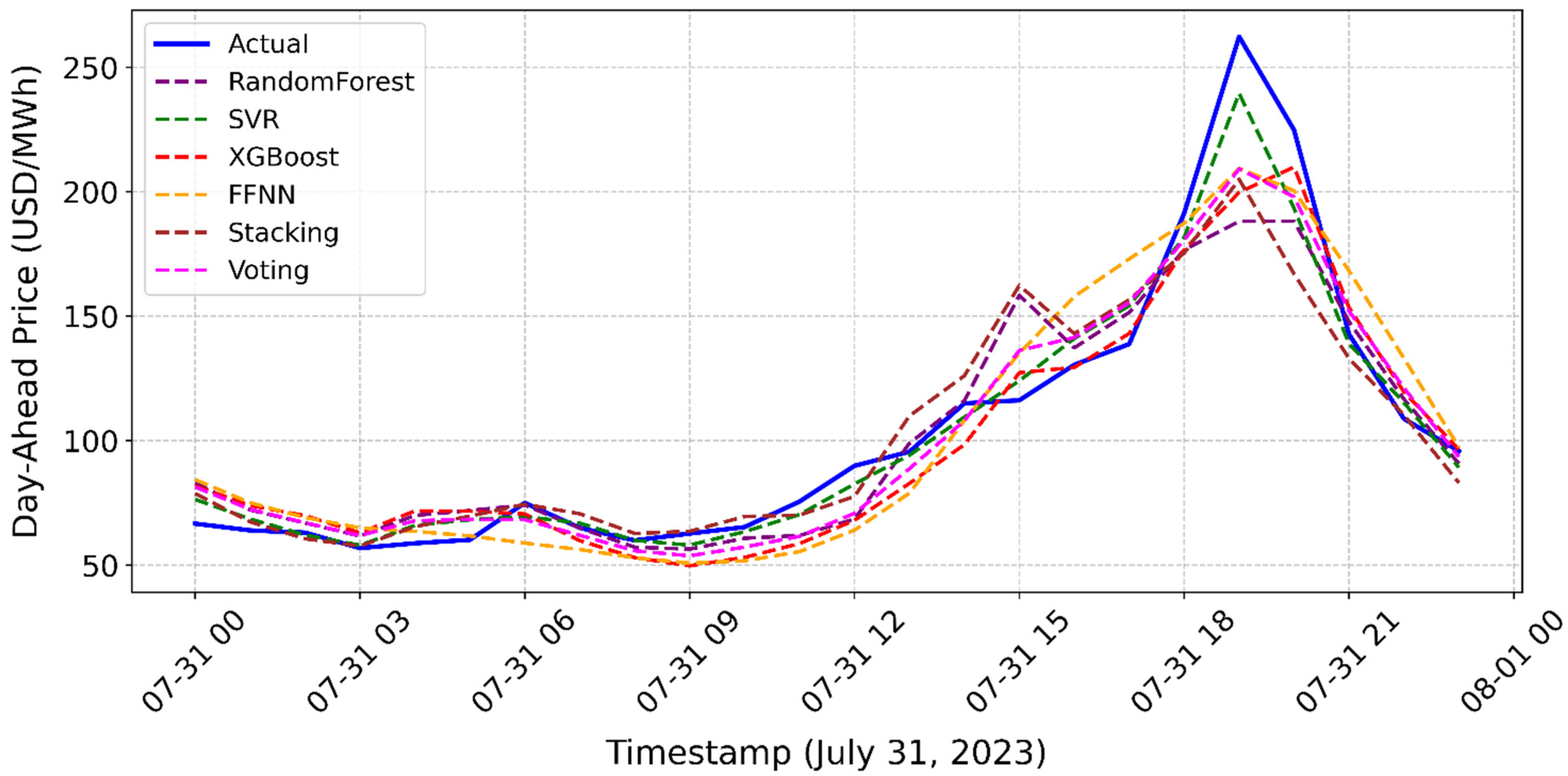
| Predictor | Explanation |
|---|---|
| Wind_forecast | Forecasted wind generation for , available during the forecast |
| Load_forecast | Forecasted electricity demand for , available during the forecast |
| Real_time_price_lag24 | Real-time electricity price (USD/MWh) from |
| Hour | Hour of the day (0–23) at , indicating daily cyclical patterns |
| Day_of_week | Day of the week (0–6, Monday–Sunday) at , capturing weekly cycles |
| Month | Month at , capturing seasonal cycle |
| Is Holiday Target | Binary indicator (1 if is a U.S. federal holiday, 0 otherwise) reflecting holiday effects |
| Load_actual_lag24 | Actual electricity demand (MW) from |
| Lag_1h | Day-ahead price (USD/MWh) from , capturing short-term price trends |
| Lag_24h | Day-ahead price (USD/MWh) from , reflecting daily price persistence |
| Moving_avg_3h | 3 h moving average of day-ahead prices up to , smoothing short-term fluctuations |
| Moving_avg_6h | 6 h moving average of day-ahead prices up to , capturing intraday trends |
| Moving_avg_12h | 12 h moving average of day-ahead prices up to , reflecting half-day patterns |
| Moving_avg_24h | 24 h moving average of day-ahead prices up to , indicating daily trends |
| Moving_avg_7d | 7-day moving average of day-ahead prices up to , capturing weekly trends |
| Moving_avg_30d | 30-day moving average of day-ahead prices up to , smoothing long-term variations |
| Price_diff_1h | Difference in day-ahead prices between and , measuring short-term changes |
| Price_diff_24h | Difference in day-ahead prices between and , capturing daily price shifts |
| Statistic | USD/MWh |
|---|---|
| Mean | 50.5 |
| Standard Deviation | 55.27 |
| 25th Percentile | 26.62 |
| 50th Percentile | 37.72 |
| 75th Percentile | 58.15 |
| 99th Percentile | 269.92 |
| Maximum | 1577.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibebuchi, C.C. Day-Ahead Energy Price Forecasting with Machine Learning: Role of Endogenous Predictors. Forecasting 2025, 7, 18. https://doi.org/10.3390/forecast7020018
Ibebuchi CC. Day-Ahead Energy Price Forecasting with Machine Learning: Role of Endogenous Predictors. Forecasting. 2025; 7(2):18. https://doi.org/10.3390/forecast7020018
Chicago/Turabian StyleIbebuchi, Chibuike Chiedozie. 2025. "Day-Ahead Energy Price Forecasting with Machine Learning: Role of Endogenous Predictors" Forecasting 7, no. 2: 18. https://doi.org/10.3390/forecast7020018
APA StyleIbebuchi, C. C. (2025). Day-Ahead Energy Price Forecasting with Machine Learning: Role of Endogenous Predictors. Forecasting, 7(2), 18. https://doi.org/10.3390/forecast7020018







