1. Introduction
Renewables are a new dawn in energy production, having demonstrated practicality and efficacy. They are projected to surpass coal, the largest global source of electricity generation, by early 2025 [
1]. According to the International Energy Agency (IEA), nearly 60% of the newly installed power capacities by 2040 will be clean and renewable energy technologies [
2]. The Sun, as the most environmentally friendly power source, converts approximately 1–2% of its intensity reaching Earth into wind energy, accounting for around 10 million megawatts [
3]. Perez and Perez estimated that the global wind potential is five times greater than that of a fully electrified global future scenario [
4]. Therefore, this tremendous energy reservoir should be harnessed if a sustainable and better world is the overriding target. Wind technologies are green and mature power producers that have shown their effectiveness in producing electricity. They are continuously experiencing increases in their total installed capacity, as demonstrated in
Figure 1, provided by the Global Wind Energy Council (GWEC) in their 2023 report [
5]. The figure indicates a recent decline in added capacity over the last two years, attributed to delayed project commissioning caused by COVID-19 restrictions; however, experts anticipate a rebound [
6]. The GWEC’s report highlights a total global installed wind capacity of 906 GW, with onshore turbines dominating and offshore technology concentrated in Europe and the Asia-Pacific region, representing 99% of global installations [
5]. In a related study, Tong et al. explored the reliability of renewable energy technologies in 42 countries, addressing a significant concern associated with clean energy machinery. Their findings indicate that wind systems are the most reliable electricity generators, capable of meeting 72–91% of the countries’ demand in hours [
7].
Wind resource assessment is pivotal during the planning phase, particularly for large-scale projects involving multiple megawatts. In other words, evaluating the wind potential at the candidate site is essential, relying on a comprehensive range of models [
8]. Parametric statistical distribution models have long been established to represent or characterize wind speed, serving as a milestone in evaluating the resource efficiency of a prospective area [
9]. The most widely used models for this purpose in the literature include Exponential, Gamma, Generalized Extreme Value, Inverse Gaussian, Lognormal, Rayleigh, and Weibull distributions [
10,
11]. Generally, these frequently used parametric models are categorized into unimodal, where only one model is utilized (such as those mentioned above), and multimodal, which involves a combination of the same models, such as the Gamma–Weibull or the Weibull–Weibull models [
12,
13]. The two-parameter Weibull distribution model, initially introduced by the Swedish physicist Weibull [
14], stands out as the most utilized model in the pertinent literature for characterizing wind speed across diverse global locations [
15,
16,
17,
18]. This preference is attributed to its straightforward and highly flexible density functions, along with efficiently calculable parameters [
19]. However, a notable limitation of this renowned statistical distribution model lies in its inability to effectively forecast or fit low wind speeds below 2 m/s, commonly referred to as null wind speeds. In such instances, the three-parameter Weibull distribution proves to be more effective than the conventional two-parameter model [
20]. It is worth noting that Wang and Okaze showed that the two and three-parameter models described the strong winds around tall buildings with the same accuracy [
21].
Among the numerous methods employed for estimating the parameters of statistical distribution models, numerical methods, notably the maximum likelihood method (MLM), the least squares method (LSE), and the method of moments (MOM), are commonly used [
22,
23,
24,
25,
26]. Additionally, artificial intelligence (AI) methods, primarily driven by heuristic algorithms, have demonstrated superiority over other methods in terms of solution accuracy and wind speed characterization [
27,
28,
29,
30,
31,
32]. In this category, the Cuckoo Search (CS) algorithm was the most frequently used [
33,
34] followed by, in some cases, the genetic algorithm (GA) [
35,
36,
37].
Figure 2 shows the share of each parameter estimation method in 46 studies reviewed by Jung and Schindler [
38]. Furthermore, the literature presents various innovative machine learning approaches aimed at achieving similar objectives in wind speed forecasting, such as long short-term memory (LSTM) neural networks fine-tuned using the modified reptile search algorithm [
39]. Notably, efforts such as those by Ala et al. [
40] have examined and ranked off-the-shelf algorithms based on their ability to generate highly accurate solutions for optimization problems in the field of wind energy. The typical objective functions employed with metaheuristic algorithms to address minimization optimization problems include the root mean square error (RMSE) [
41,
42,
43,
44] or the mean square error (MSE) [
45,
46]. In some instances, researchers relied on maximizing the objective function. For example, Guedes et al. used the coefficient of determination (
R2) to identify the relevant distribution model parameters [
47], and Shin et al. maximized the log-likelihood function [
48].
The firefly algorithm (FA), inspired by the bioluminescent communication between fireflies [
49], is considered an essential tool in the swarm intelligence category. It is characterized by its simplicity, flexibility, and proven efficacy against different optimization problems [
50]. However, it is also known for issues such as stagnation, often associated with unbalanced exploration and exploitation [
51], slow convergence or solution speed [
52,
53], and high dependence on control parameters [
54]. To address these flaws, extensive research has been conducted to either hybridize or improve the classic algorithm, seeking variants with better performance [
55,
56,
57].
Figure 3, adapted from the work of Kumar and Kumar [
58], illustrates a general template for all FA variants. Rizk-Allah et al. hybridized ant colony optimization with FA to benefit from the former’s merits in improving exploration by initializing the ants that wander the entire search space [
59]. The resulting algorithm demonstrated comparable performance to other algorithms when solving benchmark optimization problems. Fister et al. reviewed chaos map-enhanced FA algorithms, which led to high population diversity and improved exploration [
60]. Wang et al. introduced an FA algorithm with adaptive control parameters that produced comparable results to other famous FA variants when tested with benchmark functions [
54]. Hassan developed a chaotic sine–cosine FA that overcame the computational complexity of the standard algorithm, tested against benchmark functions, as customary in this research line [
53]. Ghasemi et al. introduced an enhanced version of the FA that uses different movements to improve global exploration, adding more strength to the algorithm in facing complex engineering problems [
61]. On the exploitation side, Bazi et al. developed a fast version of the FA in which the convergence to the optimal solution was faster than the basic one, while solution accuracy was almost maintained. These results were obtained after testing the algorithm with benchmark functions [
62]. Altabeeb et al. introduced a hybrid version of FA that integrates local search and genetic operators to achieve fast convergence and highly accurate solutions. When tested using benchmark datasets, this new hybridization outperformed other innovative FA approaches [
63]. Wang et al. incorporated a probability method similar to that in this research, which depends on the fitness value obtained from the classic FA to accelerate convergence. The newly developed FA algorithm was tested against recognized benchmark functions and proved superior performance [
64].
Many applications have relied on the FA to identify the parameters of their relevant models, such as the hybrid model of the solar charging station [
65], the capacitated vehicle routing problem [
63], civil engineering, meteorological optimization, and other relevant engineering applications [
58]. It is worth mentioning that the FA algorithm and its variants are not commonly used in wind energy research, with a few exceptions, such as the work conducted by Younis et al. to forecast wind speed based on data from Khartoum, Sudan [
66]; and the study by Shan et al., where they developed a hybrid FA variant used to tune the parameters of a variable pitch wind turbine PID controller [
52].
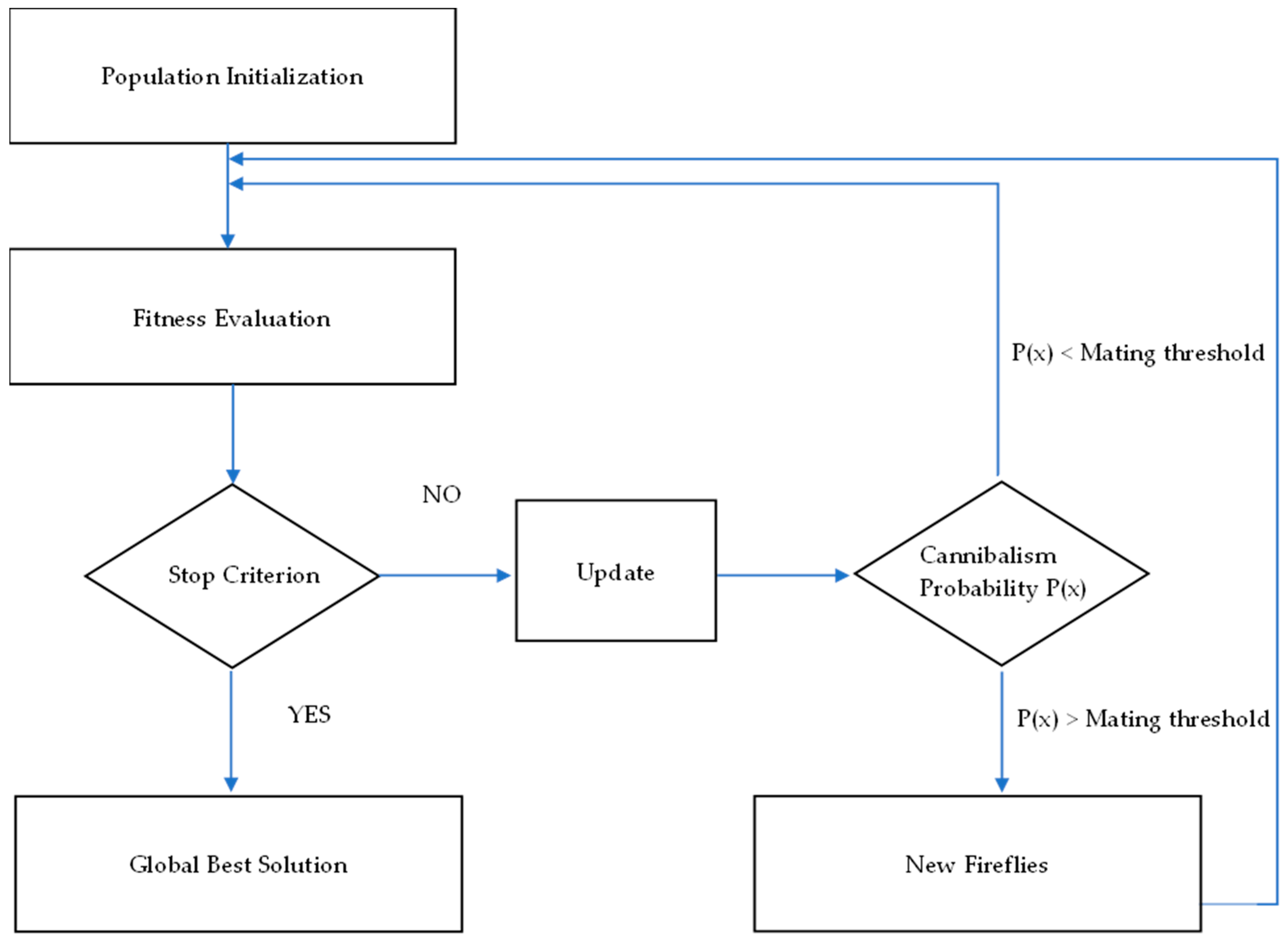
Figure 3.
Universal structure of the firefly algorithms.
Figure 3.
Universal structure of the firefly algorithms.
The current study utilizes the honeybees mating optimizer (HBMO) annealing function to calculate a conditional value representing the small proportion of firefly insects that engage in cannibalism instead of mating. This intricate simulation of biotic interactions between organisms leads to the development of a more robust algorithm in terms of solution accuracy, termed the honeybees mating-inspired firefly algorithm (HBMFA). This algorithm represents a significant step towards garnering attention for firefly algorithm (FA) variants, especially for those seeking straightforward implementation in future optimizers. The methodology of this work focuses on determining the value of this function and integrating it as a condition in the algorithm structure. The newly introduced statement compares the calculated value with an empirical reference value obtained through extensive experimentation or fine-tuning, representing the segment of flesh-eating fireflies. The efficacy of the HBMFA was evaluated through various experiments, including testing on benchmark functions. Statistical analyses, such as two-sample
t-tests and fitness function evaluations, were conducted to validate the optimization capabilities of the algorithm. The study also involved comparing the performance of HBMFA with conventional FA and other optimization algorithms. Additionally, a real-world application using wind speed data from Station SCR-25 in São João do Cariri, Brazil, in 2008 [
47], was conducted to assess the algorithm’s effectiveness, fine-tune control parameters, and achieve optimal solution accuracy for wind speed characterization. The significant contribution of this study is bridging the gap in developing optimization algorithms for wind speed forecasting, aiming for improved accuracy, robustness against various factors such as changing weather conditions and terrain features, and computational efficiency for real-time applications. This endeavor involves effectively incorporating algorithmic modifications and establishing benchmark datasets for fair comparisons. Addressing this research void will not only enhance wind speed forecasting accuracy but also contribute to the more efficient utilization of renewable energy sources. Specifically, employing this innovative FA variant to achieve an accurate global best solution maximizing
R2 as an objective function exemplifies this effort to narrow the disparity.
Therefore, the remaining sections of this article are organized as follows:
Section 2 introduces the new metaheuristic algorithm and the objective function used throughout the study.
Section 3 showcases the wind speed model and benchmark data functions,
Section 4 presents and discusses the results, and
Section 5 concludes.
4. Results and Discussion
The provided results in
Table 3 detail the testing of two optimization algorithms, HBMFA and FA, on the four CEC 2005 benchmark functions (i.e., Function 11 to Function 14). Both algorithms achieved similar best fitness values for each function, indicating comparable performance in optimizing them. However, it is notable that HBMFA consistently demonstrated slightly better performance in terms of best fitness values compared to FA across all tested functions, suggesting its potential for more accurate optimization results. Conversely, FA consistently exhibited faster execution times compared to HBMFA across all tested functions, reflecting its superior computational efficiency.
Furthermore, convergence graphs and box plots of the CEC benchmark functions over independent runs were generated to gain deeper insights into the optimization process.
Figure 9,
Figure 10,
Figure 11 and
Figure 12 depict convergence charts illustrating the progression of the relevant function’s best fitness value over iterations or function evaluations for both HBMFA and FA algorithms. These figures provide visualized information about their convergence behavior and speed. Additionally,
Figure 13 shows box plots summarizing the distribution of the CEC functions’ values obtained from multiple independent runs of the algorithms, allowing for a quantitative assessment of their performance in terms of solution quality and robustness.
To assess the statistical significance of the observed differences, two-sample t-tests were conducted. These tests aimed to determine whether there were significant differences between the algorithms’ best fitness values and execution times. For best fitness values, the t-test results showed t-statistic values within the range of (−1.00000458, −0.00837452), and p-values ranging from (0.35591564, 0.99358968). These results indicated that there was no significant difference between HBMFA and FA in terms of best fitness values, with p-values greater than 0.05 suggesting comparable optimization capabilities. However, for execution times, the t-test results showed a significant difference between HBMFA and FA. The t-statistic value for execution times was within the range of (171.78802293), indicating a notable difference in performance. This was corroborated by very low p-values (close to 0), suggesting that the difference in execution times between the two algorithms was statistically significant.
Additionally, fitness function evaluations (FFE) analysis revealed that both algorithms exhaustively utilized the allowed function evaluations, reaching the maximum of 10,000 for all tested functions. This analysis indicates that both algorithms thoroughly explored the solution space within the given computational constraints.
As the analysis in this study continues to excavate the potentials of the innovative FA variant, the emphasis was put on examining how often the condition of fireflies consuming each other occurs throughout the total number of iterations.
Table 4 provides the mean, median, and mode of instances where the algorithm had to replace eaten fireflies or execute the additional step in the HBMFA. It is evident from these statistics that the predation phenomenon is closely linked to the number of fireflies themselves, which is 13 in our case. The slight variation in statistical measures across a wide range of iterations, such as a difference of three in maximum and minimum averages, is logical, as more fireflies inherently lead to more instances of cannibalism, and vice versa.
The values presented in
Table 5 depict the computational outcomes of the HBMFA algorithm, aimed at maximizing
R2, the objective function in the case of Weibull model parameters extraction based on the earlier mentioned benchmark data. Here, the mating threshold percentage is set to 99.99%, indicating a rare occurrence of cannibalism between firefly pairs. Evidently, the most accurate solution has been consistently achieved since 1000 iterations. When considering both accuracy and execution time, the optimal solution arises at 10,000 iterations, with the time per single iteration being the lowest among the two. This reduction in computational time can be attributed to the algorithm’s memory feature, a common trait in AI, wherein previous iteration results or updated positions are utilized as input for subsequent iterations.
Continuing the investigation into the new algorithm’s performance based on the Brazil benchmark data, it was crucial to compare the results of the HBMFA with those of the standard FA, as presented in
Table 6, to ascertain any performance improvements.
Table 7 provides percentages comparing both algorithms in terms of increased solution accuracy and total execution time across different numbers of iterations. From this table, it is evident that solution accuracy has indeed improved, with an average increase percentage of 0.025%. However, for the second criterion, execution time, the HBMFA lags behind the FA, as illustrated in
Figure 14, with an average increase of 18.74%. For transparency and scientific integrity, it is important to note that the computational study was conducted using a computer equipped with an Intel(R) Core(TM) i9-10850K CPU @ 3.60 GHz processor and 32.0 GB of installed RAM, operating on a 64-bit system.
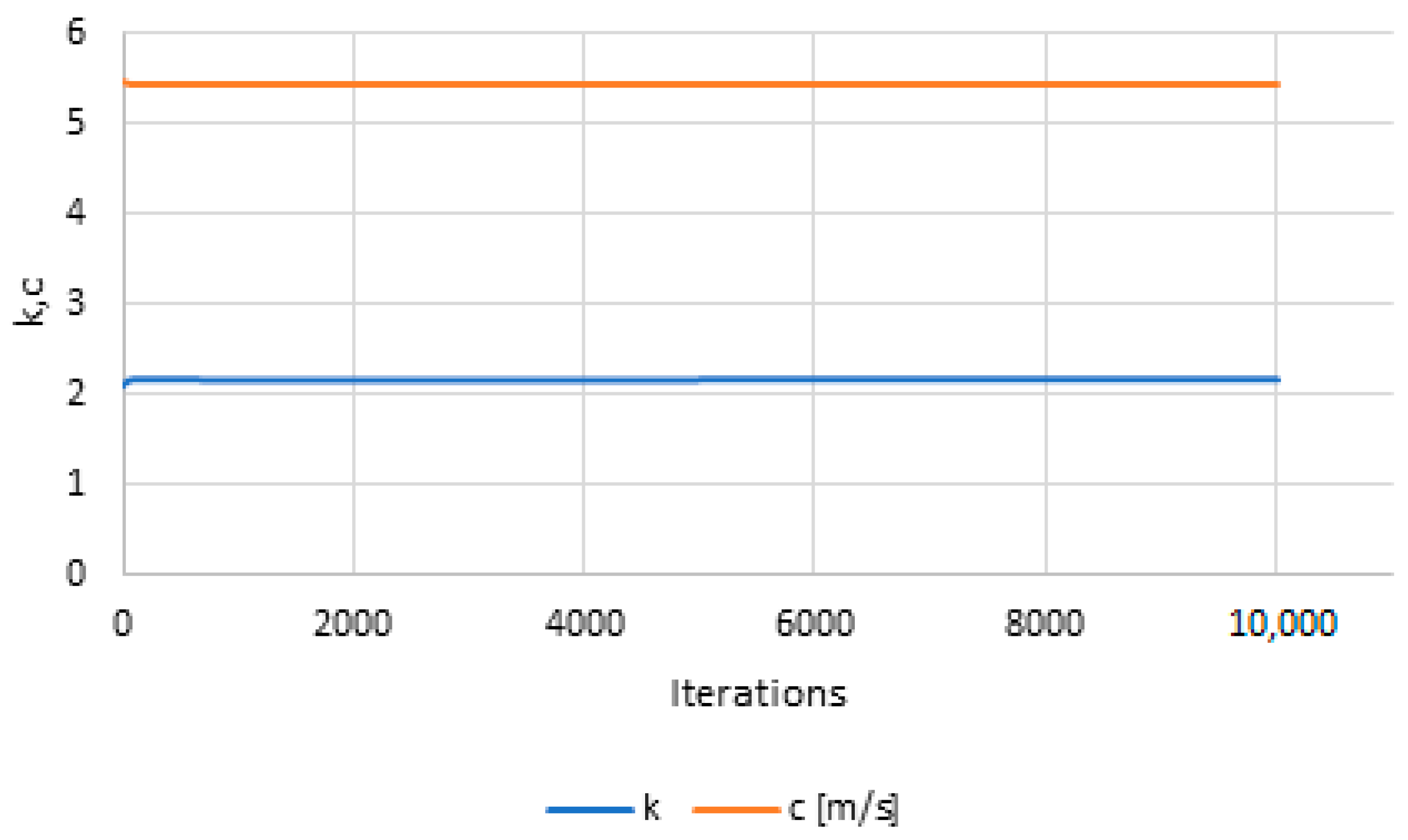
The stability observed in the
R2 values with increasing iterations, as evidenced by the results thus far, along with the consistent k and c values depicted in
Figure 15, suggests a correlation between the increase in the number of iterations and solution stability or convergence. Furthermore,
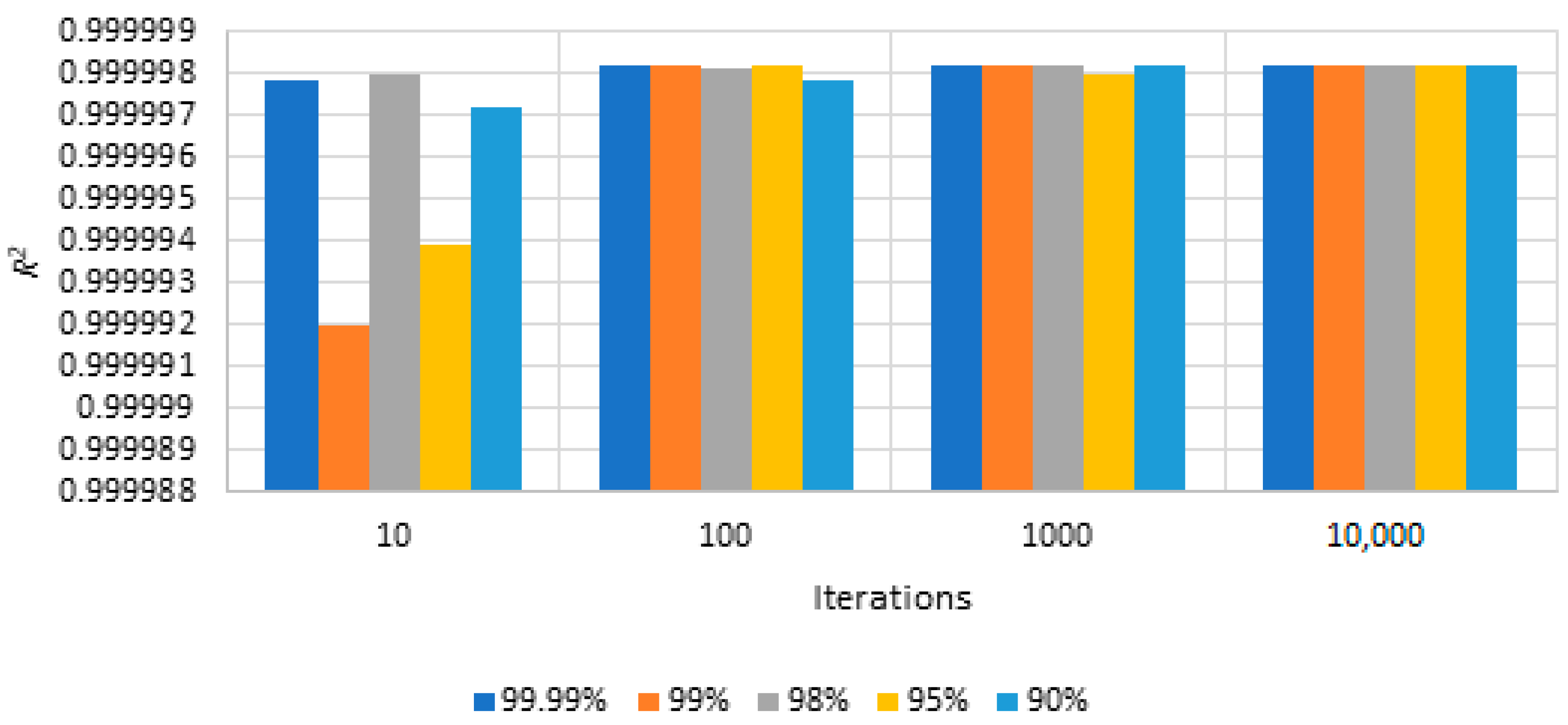
Figure 16 demonstrates that varying mating thresholds can effectively maximize
R2 to the desired value, particularly at high iterations. It is worth noting that, across all cases, the 99.99% threshold consistently yields the highest quality solution. Put simply, the HBMFA is capable of generating similar solutions across a broad spectrum of cannibalism probabilities, especially when the threshold is set at 90% or higher.
Comparative analysis is also crucial for thoroughly assessing the quality and performance of any newly introduced optimization algorithm. In
Table 8, a comparison is provided between the computational results of popular metaheuristic optimization algorithms and HBMFA, all applied to the task of extracting the shape and scale parameters of the two-parameter Weibull model using the same benchmark data, with a unified population size of 13 and a number of iterations of 10,000. The algorithms tested include cuckoo search (CS), genetic algorithm (GA), grey wolf optimizer (GWO), and particle swarm optimization (PSO). Notably, HBMFA achieved the highest
R2 value of 0.999998196, signifying exceptional performance in maximizing the objective function. However, this advantage is accompanied by a longer execution time of 143.317 s compared to other algorithms such as PSO, which achieved a comparable
R2 value with a significantly lower execution time of 0.02336 s. Despite its longer runtime, HBMFA demonstrates promising potential for accurately optimizing the parameters of the Weibull model, offering a trade-off between computational efficiency and optimization effectiveness when compared to existing metaheuristic algorithms.
Finally, in
Table 9, the conveyed
R2 and 1 −
R2 results show that the HBMFA performance exceeds the MBO algorithm in the Guedes et al. [
47] paper by a considerable margin concerning the solution accuracy in the case of excluding the null wind speeds, as the earlier researchers did in their work to ensure the best results out of the two-parameter Weibull model. It is worth noting that due to the unavailability of information regarding the computational time in the study of Guedes et al., the comparison between the two algorithms was conducted only based on solution accuracy.
5. Conclusions
The new HBMFA introduced a novel adjustment to the FA algorithm by incorporating rare instances of cannibalism among fireflies, modeled through a probability threshold. Testing the new algorithm on the CEC 2005 benchmark functions confirmed its efficacy and demonstrated superior performance compared to conventional FA and other common optimization algorithms. Additionally, statistical analyses, including two-sample t-tests and FFE analysis, provided robust validation of the algorithm’s optimization capabilities.
Moreover, the introduced adjustment significantly improved solution accuracy compared to both the conventional FA and the MBO in maximizing the R2 based on the two-parameter Weibull distribution model when the analysis was conducted using wind speed data from the SR-25 station in Brazil for 2008, revealing a notable enhancement in solution accuracy, with an average improvement of 0.025% in the R2 values. Despite an increase in execution time, approximately 18.74%, the HBMFA exhibited outstanding results, yielding an optimal solution with parameters of k = 2.1655 and c = 5.4338 m/s, and R2 values of 0.999998196 and 0.999998825 with and without null speeds, respectively. The HBMFA revealed remarkable stability in solution accuracy, with minimal variation, indicating its robustness across diverse scenarios. The algorithm’s efficient exploitation of the search area led to enhanced R2 values compared to both literature and FA results, underscoring its effectiveness. Nevertheless, higher probabilities of predation between fireflies correlated with decreased solution accuracy.
In summary, this work advanced the state-of-the-art in optimization algorithms by introducing the HBMFA. The integration of rare instances of cannibalism among fireflies enhanced the algorithm’s ability to explore and exploit the search space effectively. Thorough statistical analyses and real-world application using wind speed data demonstrated the algorithm’s robustness and applicability in diverse optimization scenarios. Despite some limitations regarding execution time and statistical significance, the HBMFA’s distinguished solution accuracy underscored its potential for critical engineering applications. Further research will focus on addressing these limitations and exploring the algorithm’s applicability across various engineering domains, ensuring its effectiveness and practical utility.