Forecasting and Anomaly Detection in BEWS: Comparative Study of Theta, Croston, and Prophet Algorithms

Abstract

Evaluation of water quality and accurate prediction of water pollution indicators are key components in water resource management and water pollution control. The use of biological early warning systems (BEWS), in which living organisms are used as biosensors, allows for a comprehensive assessment of the aquatic environment state and a timely response in the event of an emergency. In this paper, we examine three machine learning algorithms (Theta, Croston and Prophet) to forecast bivalves’ activity data obtained from the BEWS developed by the authors. An algorithm for anomalies detection in bivalves’ activity data was developed. Our results showed that for one of the anomalies, Prophet was the best method, and for the other two, the anomaly detection time did not differ between the methods. A comparison of methods in terms of computational speed showed the advantage of the Croston method. This anomaly detection algorithm can be effectively incorporated into the software of biological early warning systems, facilitating rapid responses to changes in the aquatic environment.

1. Introduction

Water, a vital resource for humanity, faces increasing demand due to population growth and economic development. However, the problem is not just the increasing demand for water; poor water quality also makes it unsuitable for many purposes [1]. Therefore, it is important to ensure not only the quantity but also the quality of water to prevent shortages. Thus, the sixth sustainable development goal of the United Nations [2] aims to ensure the availability of water and sanitation, as well as the sustainable management of these resources. Given the presence of more than 350,000 chemicals and their combinations in the world [3], water pollution stands out as one of the key environmental problems we face [4]. This directly affects human health, especially in the context of providing safe drinking water. Given the complexity and diversity of chemicals, analyzing each of them with high frequency is expensive and practically impossible. An alternative to such analysis is the use of living organisms as bioindicators, which provides a comprehensive assessment of the state of the aquatic environment. Biological early warning systems, known as BEWS [5], have become widespread in recent decades in assessing the quality of water resources and activating alarms in emergency situations [6]. Freshwater mussels are a widespread and relatively long-lived group of aquatic organisms [7]. Mussels are considered effective indicators of environmental change, responding to both long-term and acute changes caused by stressors [8]. Behavioral characteristics of mussels, such as valves opening, reflect their natural circadian rhythms, feeding and breathing activity, and can also serve as an indicator of external stress factors [9]. Assessing anomalies from the effects of stress factors using experts is possible, but this approach does not provide a quick response to emergency situations. The key challenge is still to effectively detect abnormal situations and to trigger alarms in a timely manner.

Time series anomaly detection models use a calculated numerical metric, known as an anomaly score, to determine the status of each data point as an anomaly or normal value [10]. The anomaly score is determined based on the difference between the predicted and actual values. If the score value exceeds a set threshold, the data point is classified as an anomaly [11]. In some situations, a static threshold may be applicable, but often, this approach is unsuitable, due to the variability of the variance and the mathematical expectation of the time series.

Machine learning algorithms allow the building of models to predict data with seasonal variability. Algorithms are widely used in making business forecasts, for example, forecasting purchasing power [12], product prices [13,14], and others. In the last decade, algorithms began to be used to predict climatic, environmental, and biological processes. Solving time series forecasting problems is possible using different types of machine learning algorithms, for example, forecasting algorithms, algorithms based on Bayesian statistics, and others. The Prophet forecasting model was used to predict both short-term and long-term air pollution in Seoul, Korea and China [15,16]. Using sensor data from a wastewater treatment plant system, Kramar and Alchakov [17] applied various machine learning methods (seasonal autoregressive integrated moving average SARIMA, Holt–Winters exponential smoothing, ETS, Facebook Prophet, extreme gradient boosting XGBoost, and long short-term memory) for time series forecasting. The XGBoost method turned out to be the best method for their purposes. An important direction for future research is to explore how these approaches can better support forecasting in practice [18]. A Bayesian approach is used to predict the possibility of large earthquakes using thermal anomalies from satellite observations [19].

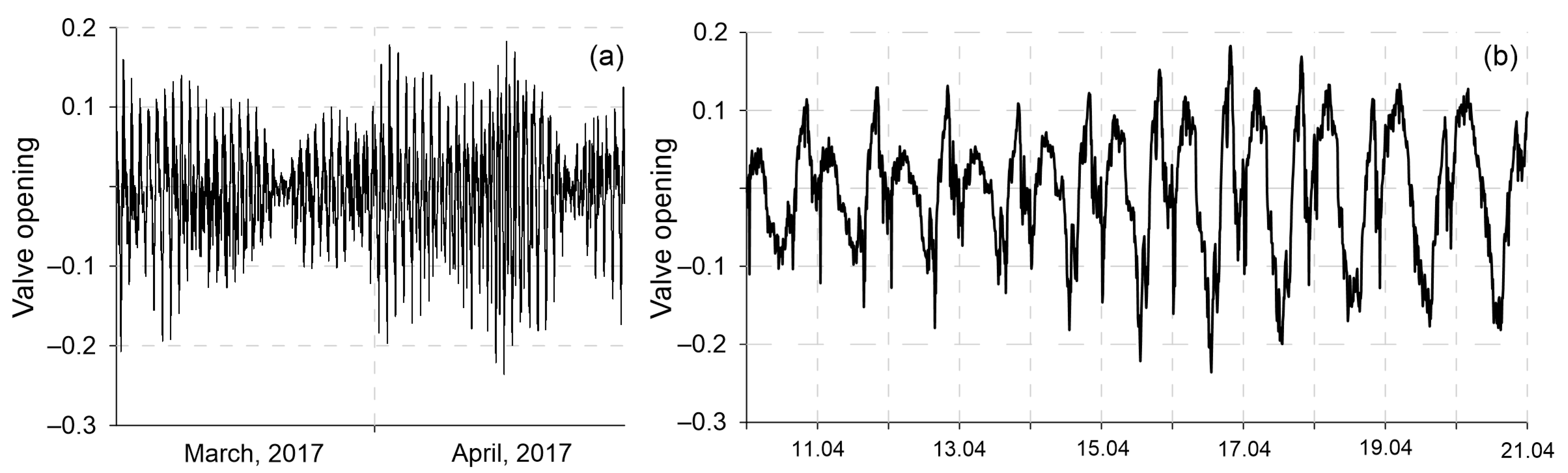
In a previous work, we investigated the ability to detect anomalies in bivalves’ activity data using four unsupervised machine learning algorithms (elliptic envelope, isolation forest (iForest), one-class support vector machine (SVM), and local outlier level (LOF) [20], the autoregressive integrated moving average (ARIMA) forecast model with a seasonal component in the same data [21], obtained by biological early warning system [22]). In this paper, we further analyzed machine learning forecasting algorithms for identifying anomalies and generating alarms in bivalves’ activity data. The main parameter for the success of forecasting the developed models will be the speed of identifying an anomaly, since data from the BEWS is sent to the server in real time, and the algorithm is planned to be implemented in the software of BEWS. In addition, the developed algorithm for detecting an anomaly and subsequently generating an alarm signal should not require significant computing resources. The novelty of the work lies in the application of machine learning algorithms for activity data of bivalve mollusks used as biosensors in the biomonitoring system of water bodies. Previously, Valletta et al. [23] and Bertolini et al. [24] demonstrated the feasibility of using machine learning algorithms in animal behavior studies, particularly to identify consistent behavioral patterns in the activity of the bivalves Mytilus galloprovincialis and Mytilus edulis. Meyer et al. [25] combined statistical-analysis techniques with machine learning approaches to study the prediction of the movement patterns of ruminants. However, to the best of our knowledge, no study has applied machine learning algorithms to forecast bivalves’ activity data.

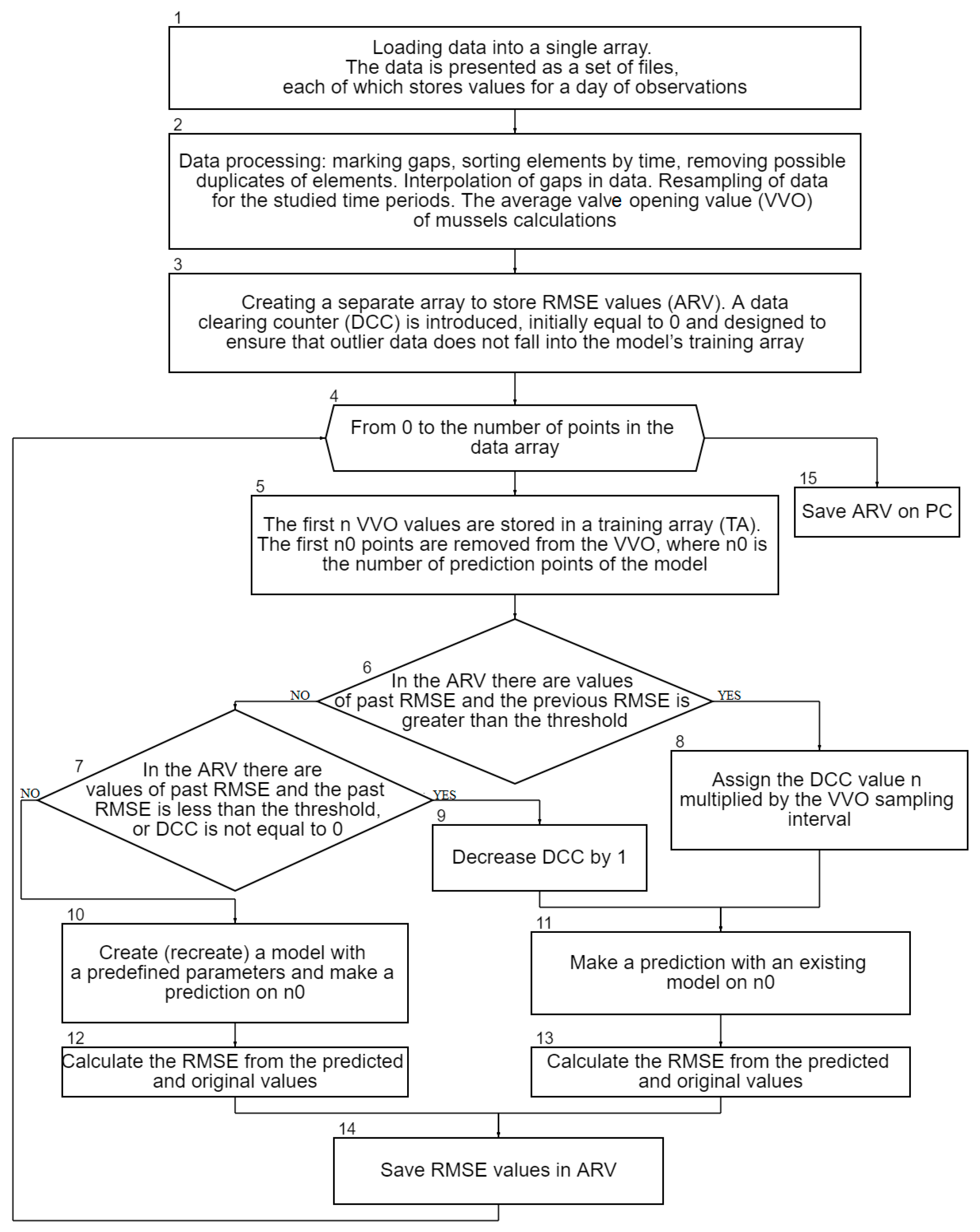
Section 2 describes data, three machine learning algorithms, and data preprocessing. The block diagram of the anomaly detection algorithm is presented. Section 3 provides the main results. The graphical results of choosing a fixed RMSE threshold are given. In Section 4, we discuss results and compare the anomaly detection time obtained by different methods. Finally, Section 4 summarizes the findings and outlines their scope.

2. Materials and Methods

2.1. Data

Measured activity data from the freshwater bivalve Unio pictorum (Linnaeus, 1758) collected between March and April 2017 were used to create forecasting models. The data were obtained using the BEWS developed by the authors, based on recording the behavioral reactions of bivalve mollusks [22]. The BEWS consisted of surface and underwater parts (Figure 1). The system automatically, in real time, provided digital information about the mollusks’ valve movements using Hall sensors and a magnet attached to them (Figure 1b). Individual reactions of 16 animals were recorded simultaneously. The sensitivity of the device was 0.1 mm. Continuous retrieval of information, with the registration of signals, was carried out every 10 s. The synchronous reaction of a group of mollusks (at least 70% of the total number) was an alarm signal. Computer programs allowed the real-time transmission of information in on-line mode. The latent period of the system response to pollution, depending on the nature and concentration, ranged from several seconds to several minutes. The synchronized closing of mollusk valves indicated the occurrence of a stressful situation, in particular, pollution of the aquatic environment [26,27]. In addition, natural factors, such as changes in environmental characteristics, may be the reasons for the reactions of mollusks. In this regard, in addition to the opening amplitude of the valves, the BEWS also measured water temperature and light level.

The biomonitoring complex was deployed at hydroelectric complex No. 14 of the Chernaya River in the city of Sevastopol.

2.2. Machine Learning Algorithms

The following machine learning algorithms were the ones we applied in the investigation presented in this article.

2.2.1. Theta Method

The Theta method, described in [28], is a variant of simple exponential smoothing (SES) that takes into account drift (as shown in [29]). The Theta method is applied to non-seasonal or deseasonalized time series. Multiplicative classical decomposition is often used for deseasonalization. The essence of the method is to decompose the original time series into two new lines using the so-called theta coefficients. The advantage of this approach is the ability to use information that usually cannot be fully taken into account and modeled by extrapolating the original time series [30]. Theta lines can be thought of as separate time series that are extrapolated independently using an appropriate forecasting method.

The Theta method is highly flexible: the number of theta lines, theta coefficients, and extrapolation methods may vary, and they can be combined to obtain reliable forecasts. However, Assimakopoulos and Nikolopoulos [28] proposed a simplified version of the method that uses only two theta lines with predefined coefficients θ. The first theta line with the coefficient θ1 = 0 is extrapolated over time using a linear regression model, while for the second theta line with the coefficient θ2 = 2, the simple exponential smoothing method is applied. The final predictions are generated by combining the predictions of both theta lines with equal weights.

2.2.2. Croston Method

Croston’s method [31] is a modification of simple exponential smoothing (SES), specifically designed for working with discontinuous time series and described by the following equation:

$$y_t=o_t{z}_t$$

(1)

where y_t is the actual observation, o_t is a Bernoulli distributed binary variable that takes a value of one when demand occurs and is zero otherwise, z_t is the potential quantity of demand with a conditional distribution (becomes real only in those moments when o_t =1), and t is the observation time.

Croston proposes dividing the model (1) into two parts, working with each of them separately. This allows us to estimate the probability of demand occurring using intervals between demands [32]. Thus, instead of one series t = 1, …, T, we have two series: demand intervals $q_{j_t}$ and demand sizes $z_{j_t}$, where j_t = 1, …, N reflects the successive numbers of intervals and demand sizes, and N is the number of non-zero demands. If $q_{j_t}$ represents the time since the last non-zero observation and reflects the demand interval, then it serves as an indicator for the next non-zero observation. Croston [31] assumes that the probability of occurrence is constant between non-zero demands, while average demand sizes are assumed to be the same during zero demands. In this method, both demand sizes $z_{j_t}$ and demand intervals $q_{j_t}$ are forecast using SES [33], resulting in the following system of equations:

$$\begin{gathered} {\widehat{y}}_t={\widehat{y}}_{j_t}=\frac{1}{{\widehat{q}}_{j_t}}{\widehat{z}}_{j_t} \\ {\widehat{z}}_{j_t}={\alpha }_z{z}_{j_t-1}+(1-{\alpha }_z){\widehat{z}}_{j_t-1} \\ {\widehat{q}}_{j_t}={\alpha }_q{q}_{j_t-1}+(1+{\alpha }_q){\widehat{q}}_{j_t-1} \\ {j}_t=j_{t-1}+o_t \end{gathered}$$

(2)

where ${\widehat{y}}_{j_t}$ is the projected average demand, ${\widehat{z}}_{j_t}$ is the projected demand size, ${\widehat{q}}_{j_t}$ is the forecast demand interval, and α_q and α_z are the smoothing options for intervals and sizes, respectively. The system of Equation (2) shows how each observation at a certain time t is transformed into the corresponding j_t element of the size and demand interval. Croston’s original formulation assumed that α_q = α_z, but later, Schultz [34] proposed using separate smoothing parameters, which was supported by other researchers [35,36].

However, the Croston method has a significant drawback: the forecast is updated only after periods with positive demand. This means that the method becomes less effective after successive periods of zero demand. Therefore, it cannot be used to assess the risk of product obsolescence or to manage excess inventory [37].

2.2.3. Prophet Method

Prophet is a method for forecasting time series data based on an additive model in which non-linear trends correspond to annual, weekly, and daily seasonality, as well as anomaly effects. It works best with time series that have strong seasonal effects and multiple seasons of historical data. The method is robust to missing data and shifts in trends and generally handles outliers well.

Prophet is an open-source time series regression algorithm originally designed to predict various Facebook data, such as platform usage and growth, and can be used in both Python and R [38].

The proposed approach to time series forecasting uses a decomposable model based on the work of Harvey and Peters [39]. The model consists of three main components: trend, seasonality, and holidays [38]:

$$y\left(t\right)=g\left(t\right)+s\left(t\right)+h\left(t\right)+e\left(t\right)$$

(3)

where y(t) is a value of a time series at a point in time t, g(t) is a trend component taking into account non-periodic changes, s(t) is a seasonal component reflecting periodic changes, h(t) represents the consequences of the holidays, and e(t) is an error term t, which represents any idiosyncratic changes that are not taken into account by the model.

The Prophet algorithm was initially developed for business time series data with annual, seasonal, monthly, daily, or hourly trends, but various recent studies have explored the potential of the Prophet algorithm with environmental time series data.

Unlike ARIMA or SARIMAX, which use autocorrelation and partial autocorrelation to capture temporal dependencies, Prophet decomposes the input time series into additive components [40].

2.3. Data Preprocessing

The activity data of bivalve mollusks in our case were the opening values of the valves (in mm) of 14 mollusks, which were simultaneously recorded and transmitted to the server with a sampling step of 10 s. The average value of the valve openings of all 14 mollusks was used as input data for our models. The data were first checked for omissions and duplicates. Data gaps were filled by interpolation, and duplicates were excluded from the data set. Data gaps were caused by hardware failures.

The ultimate goal of the algorithm is to determine the time of occurrence of the anomaly. The time difference between the detected anomaly point and the actual anomaly point represents a measure of performance. However, the exact time when the anomaly occurred is unknown. The days on which anomalies occurred were identified using the expert assessment method. A biologist and two hydrologists took part in the anomaly analysis. The biologist assessed the monotony of the behavior of mollusks in the daily cycle and determined deviations. Hydrologists assessed the condition of the water (analysis of water turbidity and temperature).

The entire data set (except for anomalies) was divided into intervals from one to five days, with a shift from one minute to an hour. Within each interval, with the exception of the last interval (from one minute to an hour), the models were trained with different data averagings. The final set of variable parameters common to all models was as follows: averaging time (from 10 s to 30 min), number of prediction points (or interval) (from 1 to 6 or from 1 minute to 1 hour), and training sample size (from 1 to 5 days). Multiplying the averaging time and the number of prediction points gave the forecasting horizon (in minutes). The data decompositions studied earlier in the work [21] were used to select the seasonality period parameter required for the Theta and Prophet models. The published article provides a description of the methodology and a detailed analysis of the results. Note that based on the results of the decomposition analysis of the valve opening value (Figure 2), the daily seasonal component of the model was identified (Figure 2b). For the Theta model, the additive method of combining theta lines was used. For the Croston method, the classic version was chosen.

The models were compared with each other based on the time of anomaly detection. The best solution is to detect the anomaly as quickly as possible with a minimum number of false alarms. Thus, the optimal solution is based on a trade-off between detection speed or detection latency and the false alarm rate.

As a measure for detecting anomalies in the data, the root mean squared error (RMSE) was used [41]. The RMSE is the square root of the variance, evaluated by the equation:

$$RMSE=\sqrt{\frac{\sum _{i=1}^n({\widehat{y}}_i-y_i)}{n}}$$

(4)

where y_i and $\widehat{y_i}$ are actual and predicted values, and n is the number of samples.

The calculation of the RMSE was carried out for each prediction interval for all data averaging times. The fact that the threshold value of the RMSE was exceeded was a signal of an anomaly.

The block diagram of the algorithm described above is presented in Figure 3.

Data analysis and implementation of the developed algorithm were carried out in the Python programming language (V 3.9.12) using the machine learning library scikit-learn (V 1.2.2) [42], statistical analysis library statsmodels (V 0.14.0) [43], and library for forecasting and anomaly detection in time series Darts (V 0.27.1) [44].

3. Results

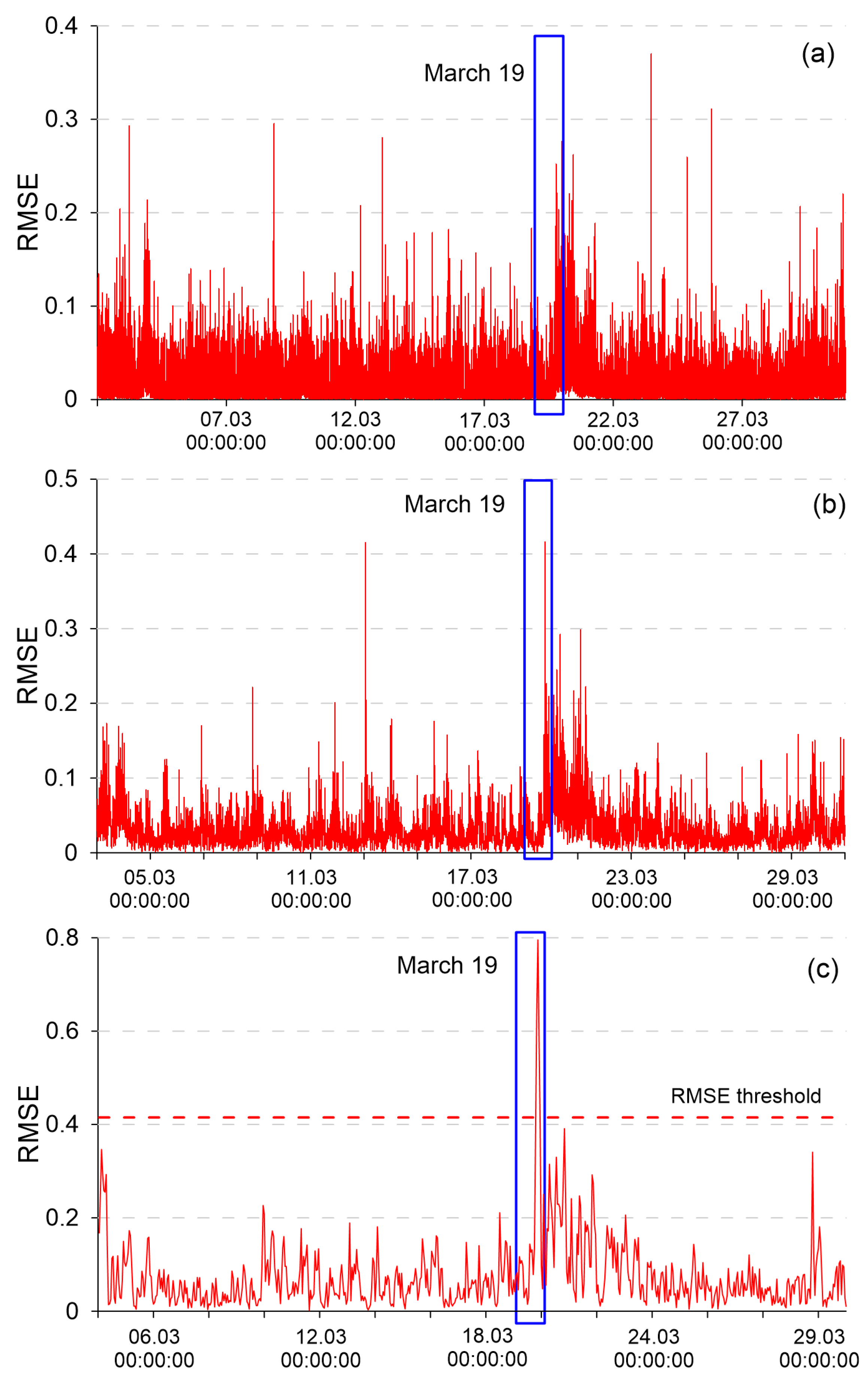
The fixed threshold of the RMSE, at which the largest error occurred in the absence of an anomaly, plus a ten percent safety margin required to work in a real system for each method, was selected to exclude false positives (

Table 1. The RMSE values plus 10% for different averaging times and the number of prediction points using the Theta method.

Averaging Time	Number of Prediction Points	Forecasting Horizon (min)	Training Sample Size, Days
			1	2	3	4	5
10 s	6	1	*	*	*	*	*
1 min	6	6	**	**	**	**	**
5 min	6	30	0.313	0.314	0.314	0.314	0.286
10 min	1	10	**	**	**	**	**
10 min	2	20	0.316	0.314	0.315	0.316	0.275
10 min	3	30	0.295	0.292	0.256	0.253	0.264
10 min	6	60	0.311	0.309	0.213	0.206	0.209
20 min	3	60	0.294	0.289	0.292	0.275	0.286
30 min	2	60	0.243	0.233	0.231	0.231	0.264

* Cannot be distinguished—false positives are higher than real anomalies. ** Cannot be distinguished—false positives at the same level as real anomalies.

,

Table 2. The RMSE values plus 10% for different averaging times and the number of prediction points using the Croston method.

Averaging Time	Number of Prediction Points	Forecasting Horizon (min)	Training Sample Size, Days
			1	2	3	4	5
10 s	6	1	**	**	**	**	**
1 min	6	6	**	**	**	**	**
5 min	6	30	0.322	0.322	0.322	0.322	0.314
10 min	1	10	0.363	0.361	0.361	0.361	0.361
10 min	2	20	0.41	0.41	0.41	0.41	0.41
10 min	3	30	0.313	0.313	0.292	0.292	0.292
10 min	6	60	0.381	0.381	0.481	0.481	0.481
20 min	3	60	0.371	0.571	0.369	0.371	0.373
30 min	2	60	0.52	0.514	0.51	0.52	0.508

** Cannot be distinguished—false positives at the same level as real anomalies.

and

Table 3. The RMSE values plus 10% for different averaging times and the number of prediction points using the Prophet method.

Averaging Time	Number of Prediction Points	Forecasting Horizon (min)	Training Sample Size, Days
			1	2	3	4	5
10 s	6	1	**	**	**	**	**
1 min	6	6	**	**	**	**	**
5 min	6	30	0.281	0.361	0.425	0.491	0.578
10 min	3	30	0.291	0.365	0.491	0.541	0.629
10 min	6	60	0.192	0.323	0.381	0.422	0.496
20 min	3	60	0.191	0.405	0.415	0.486	0.534
30 min	2	60	0.264	0.273	0.290	0.292	0.284

** Cannot be distinguished—false positives at the same level with real anomalies.

). It turned out to be impossible to detect anomalies using the Theta method with a 10 s averaging, since false positives turned out to be higher than real anomalies in the data. With one-minute data averaging, false positives of the models were obtained at the same level with real anomalies by all three methods. For example, Figure 4 shows RMSE graphs for a false alarm above the real anomaly (a) (Theta method, 10 s averaging), for a false alarm at the same level with real anomalies (b) (Prophet method, 1 min data averaging), as well as for the normal operation of the model, where an anomaly was clearly visible in the RMSE values (c) (Prophet, 20 min data averaging).

Using the calculated values of RMSE for certain model settings, the detection times of three anomalies were determined (

Table 4. Anomaly detection time by three algorithms at different data averaging times and number of prediction points.

Averaging Time, Number of Prediction Points	Method
	Theta	Croston	Prophet
Anomaly 1 (19 March 2017)
5 min, 6 points	18:35	18:35	18:35
10 min, 1 point		18:40
10 min, 2 points	18:30	18:30
10 min, 3 points	18:40	18:40	18:40
10 min, 6 points	19:10	18:10	18:10
20 min, 3 points	19:20	18:20	17:20
30 min, 3 points	18:30	19:30	18:30
Anomaly 2 (14 April 2017)
5 min, 6 points	12:05	12:05	12:05
10 min, 1 point		12:30
10 min, 2 points	12:30	12:30
10 min, 3 points	12:40	12:40	12:40
10 min, 6 points	12:10	12:10	12:10
20 min, 3 points	12:20	12:20	12:20
30 min, 3 points	12:30	12:30	12:30
Anomaly 3 (24 April 2017)
5 min, 6 points	17:35	17:35	17:35
10 min, 1 point		17:50
10 min, 2 points	17:50	17:50
10 min, 3 points	17:40	17:40	17:40
10 min, 6 points	17:10	17:10	17:10
20 min, 3 points	17:20	17:20	17:20
30 min, 2 points	17:30	17:30	17:30

The best anomaly detection time is highlighted in red.

). The best time (17:20) for detecting the first anomaly (19 March 2017) was obtained by the Prophet method, with a 20 min averaging and with the number of forecast points equal to 3 (one-hour forecast). The best time to detect the second anomaly (14 April 2017) turned out to be the same for the three methods, with the same model settings (5 min of data averaging and 6 prediction points, with a one-hour forecast). The third anomaly (24 April 2017), similar to the second, was detected using three methods at the same time. The number of days in the training set did not affect the time it took to detect an anomaly, although it did affect the threshold level.

Figure 5 shows the RMSE values and their fixed thresholds for highlighting the anomaly on 19 March 2017.

4. Discussion and Conclusions

The algorithms used separately or together with other models (hybrid approaches) were actively applied to different types of data. For example, algorithms were applied to predict the amount of waste per capita in the states of the European Union using the Prophet model [45]. De Oliviera et al. [46] proposed a new multi-functional methodology based on auto-encoder and traditional time series models, including ARIMA and Prophet, for COVID-19 time series forecasting. Time series forecasting models (SARIMA and Prophet) and technologies based on artificial neural networks were compared to model the dynamics and conditions of soils and the efficiency of agroecosystems [47]. A hybrid model combining wavelet transform, support vector regression (SVR), and Prophet was used for a precipitation forecast [48]. Using several methods, including Croston, an inventory planning system was developed for a tire retailer [49].

In the paper, we compared three machine learning prediction methods (Theta, Croston, and Prophet) for detecting anomalies in bivalves’ activity data. The results showed that for one of the anomalies, Prophet was the best method, and for the other two, the anomaly detection time did not differ between the methods. A comparison of the results obtained in the work with the results of predicting anomalies in the activity data of bivalve mollusks by the SARIMA model [21] showed the preferable use of the selected algorithms. The Prophet method was able to detect the first anomaly 1 hour and 20 min faster than the SARIMA model. The detection time of the second anomaly by the three analyzed algorithms improved by 25 min, and the third anomaly improved by 40 min, compared to the SARIMA model.

The results of the methods in terms of computation time were compared. Calculations were performed on Windows 10 Pro System Version 22H2 Build 19045.4170, processor Intel(R) Core(TM) i5-10500 CPU @ 3.10GHz, RAM 16 GB, NVIDIA GeForce GTX 1650 video card. Croston’s method turned out to be the fastest for all model settings (averaging time and number of prediction points) (

Table 5. Computation time by all methods.

Averaging Time	Method
	Theta	Croston	Prophet	SARIMA
10 s, 6 points	4 h	40 min	1 h 10 min	2 h 22 min
1 min, 6 points	13 min	1 min 25 s	15 min	1 h 43 min
5 min, 6 points	3 min 36 s	40 s	12 min	1 h 40 min
10 min, 1 point	3 min 33 s	55 s	12 min	1 h 27 min
10 min, 2 points	1 min 54 s	37 s	10 min	1 h 10 min
10 min, 3 points	1 min 20 s	33 s	9 min	1 h 2 min
10 min, 6 points	46 s	27 s	7 min	52 min
20 min, 3 points	35 s	23 s	6 min	50 min
30 min, 2 points	29 s	21 s	5 min	44 min

). The computation time for the best model parameters obtained for the second anomaly (5 min, 6 points) showed that the fastest was the Croston method, which was 5.4 times faster compared to the Theta method (40 s, 3 min, and 36 s, respectively) and 18 times faster compared to the Prophet method (40 s and 12 min, respectively). The shortest computation time for the best model parameters obtained for the third anomaly (10 min, 6 points, one-hour forecast) was also obtained for the Croston method (27 s), while the Theta method gave the result in 46 s, and the Prophet in 7 min (Table 5). The SARIMA model turned out to be the slowest computationally. Computation time for the SARIMA model, with settings of averaging time 5 min and 6 forecasting points (the best detection time for the second anomaly by Theta, Croston, and Prophet methods), was 1 h and 40 min.

Comparison with estimates presented in [20], which describes the possibility of detecting anomalies in the same bivalves’ data using four unsupervised machine learning algorithms: elliptic envelope, isolation forest (iForest), one-class support vector machine (SVM), and local outlier level (LOF), showed using the example of the first anomaly (anomaly 3 in [20]) that the use of machine learning algorithms lost by almost an hour in the speed of anomaly detection, compared to the Prophet method (

Table 6. Anomaly detection time for Anomaly 1 (19 March 2017) by Prophet and unsupervised machine learning algorithms.

Method	Anomaly Detection Time	Model Setting (Averaging Time)
Prophet	17:20	20 min
Elliptic envelope	18:30	15 min
iForest	18:15	15 min
LOF	18:35	5 min

).

Thus, the algorithms discussed in the article turned out to be better in terms of anomaly detection time and faster in computational complexity, compared to the SARIMA model.

The advantage of the algorithms used in the article compared to the ARIMA model has been shown in many works using different data. For example, the advantage (less errors) of the Prophet model compared to SARIMA was obtained when predicting solar and wind resources in the Doomadgee area of Far North Queensland, Australia [50]. Despite being extremely useful, empirical evaluations, such as the M4 competition [51], have shown that no automatic selection algorithm (e.g., ETS, or automatic ARIMA) has been able to significantly outperform established benchmarks such as Theta [28], which became popular due to its superiority over other competitors in the M3 competition [52]. Prophet outperformed two other algorithms, ARIMA and ThymeBoost, in predicting monthly rainfall data in India [53]. Xiao et al. [54] found that Prophet improved runoff modeling in the Zhou River Basin. Bolick et al. [55] used the Prophet method to predict hourly water level changes in an urban stream (South Carolina, USA) and obtained very accurate estimates, with coefficient of determination values greater than 0.9.

The work carried out is important for improving the efficiency of forecasting anomalies in the activity data of bivalve mollusks used in the environmental monitoring of the state of the aquatic environment, which will help reduce costs associated with operational, tactical, and strategic planning.