Machine Learning-Enhanced Pairs Trading
Abstract
1. Introduction
- Data availability: Pairs trading relies on identifying correlated or co-integrated securities, which requires access to accurate and timely data. Obtaining and processing this data in real-time can be challenging.
- Execution speed: High-frequency trading requires rapid execution of trades, and delays in executing the pairs trading strategy can result in missed opportunities.
- Transaction costs: High-frequency trading involves frequent trading, which can lead to higher transaction costs as shown by [8]. Such costs can negate the potential profits of pairs trading, suggesting that low-profit trades should be avoided.
A Brief History of Forecasting for Finance
2. Literature Review
2.1. Neural Network Techniques
2.2. Strategies for Pairs Trading
3. Data Source
4. Methodology
4.1. Experimental Framework
4.1.1. Reversion Strategy
4.1.2. Pure Forecasting Strategy
4.1.3. Hybrid Strategy
4.2. Threshold Strategies
4.3. Evaluation Metrics
5. Model Training
5.1. Datasets
- 1.
- The “bbdc3_4” dataset encapsulates the ratio between the financial tickers bbdc3 (ordinary shares) and bbdc4 (preferred shares) from Banco Bradesco stocks.
- 2.
- The “petr3_4” dataset encapsulates the ratio between the financial tickers petr4 (preferred shares) and petr3 (ordinary shares) from Petrobras stocks.
- 3.
- The “itau3_4” dataset encapsulates the ratio between the financial tickers itau4 (preferred shares) and itau3 (ordinary shares) from Banco Itau stocks.
5.2. Training Methodology
6. Threshold-Dependent Hybrid Trading Algorithm
| Algorithm 1 Threshold-Dependent Hybrid Trading Algorithm |
|
7. Results
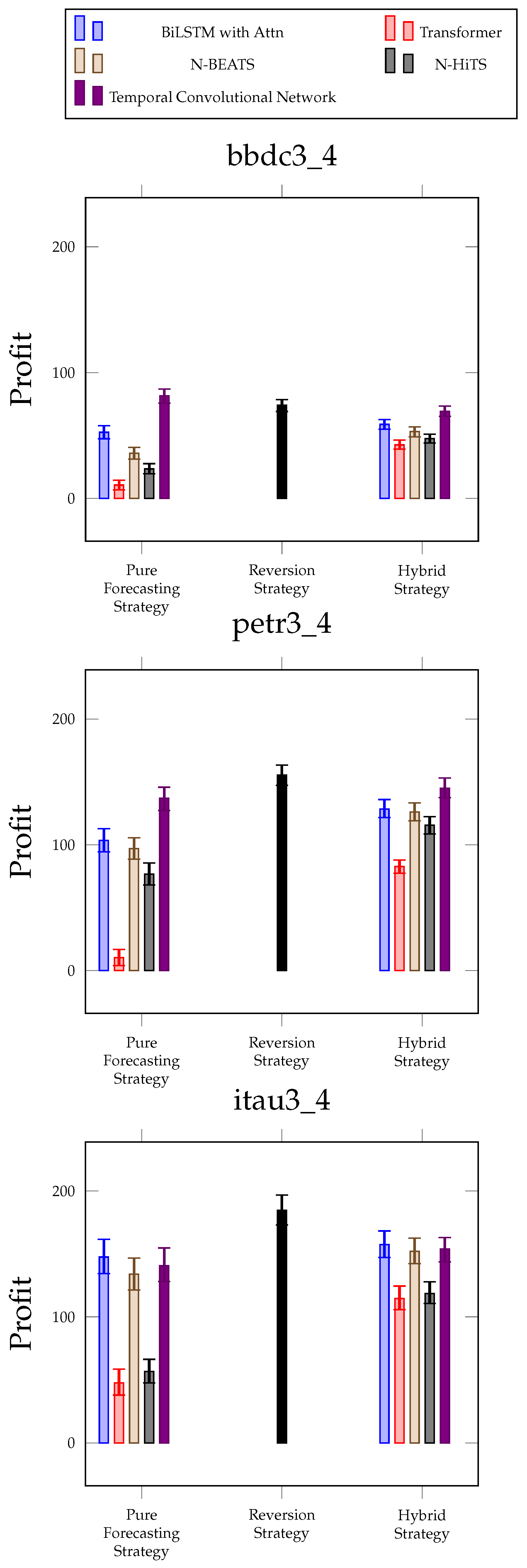
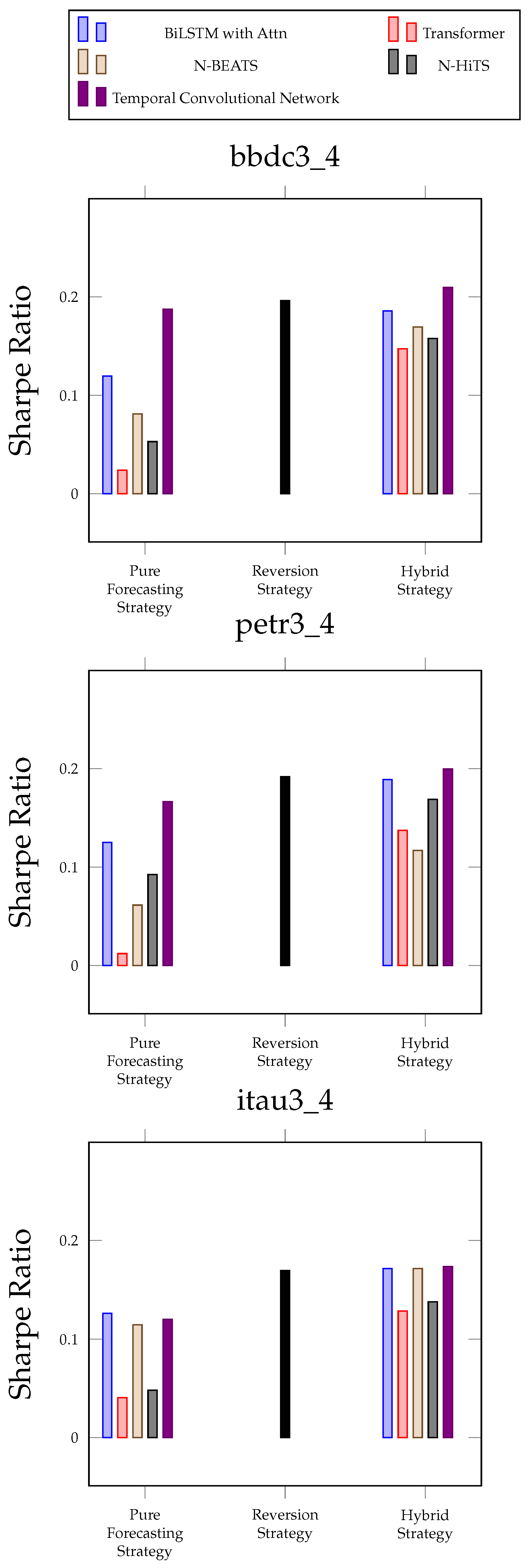
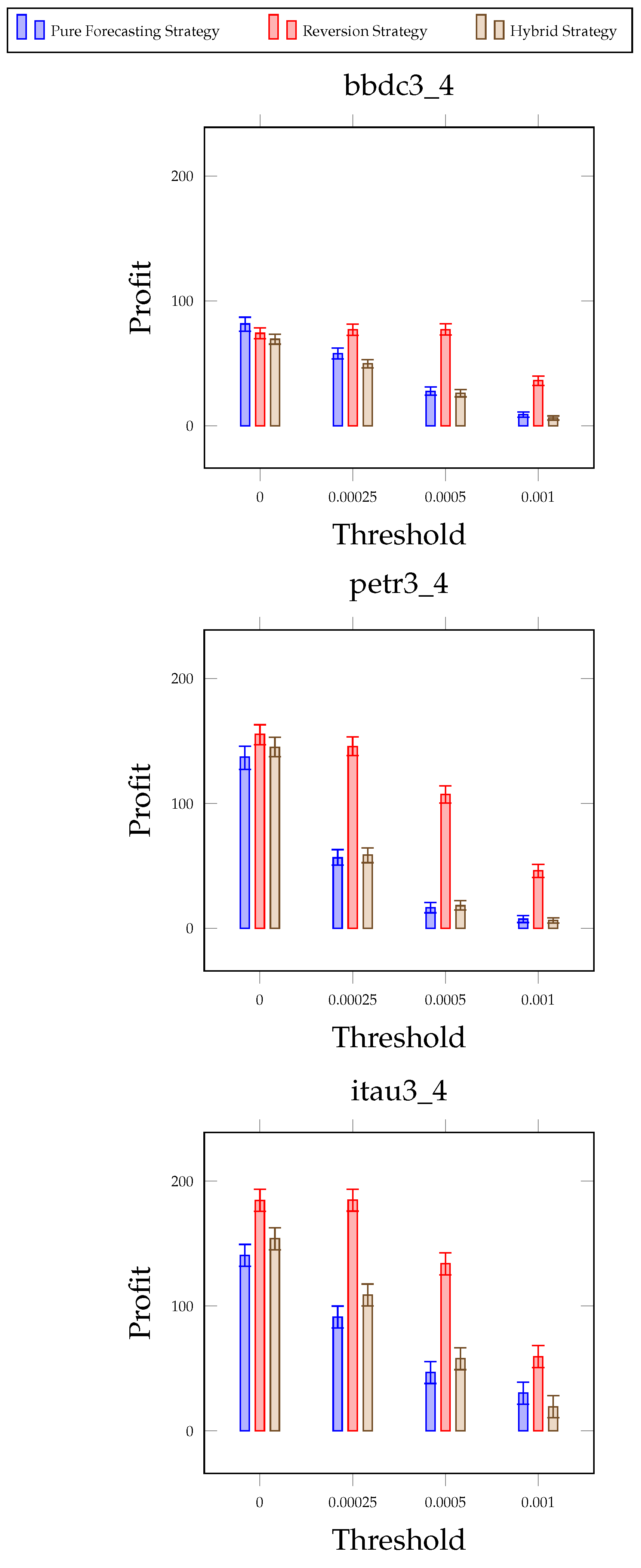
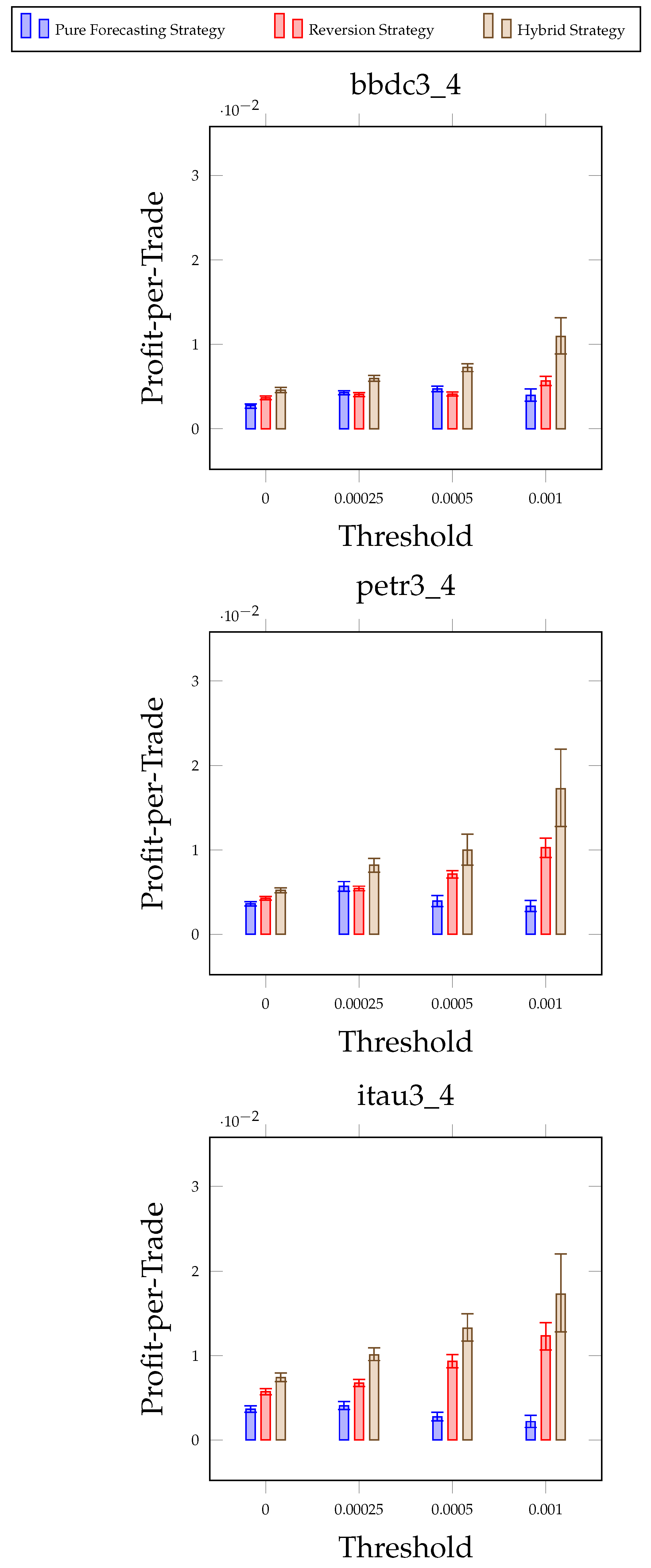
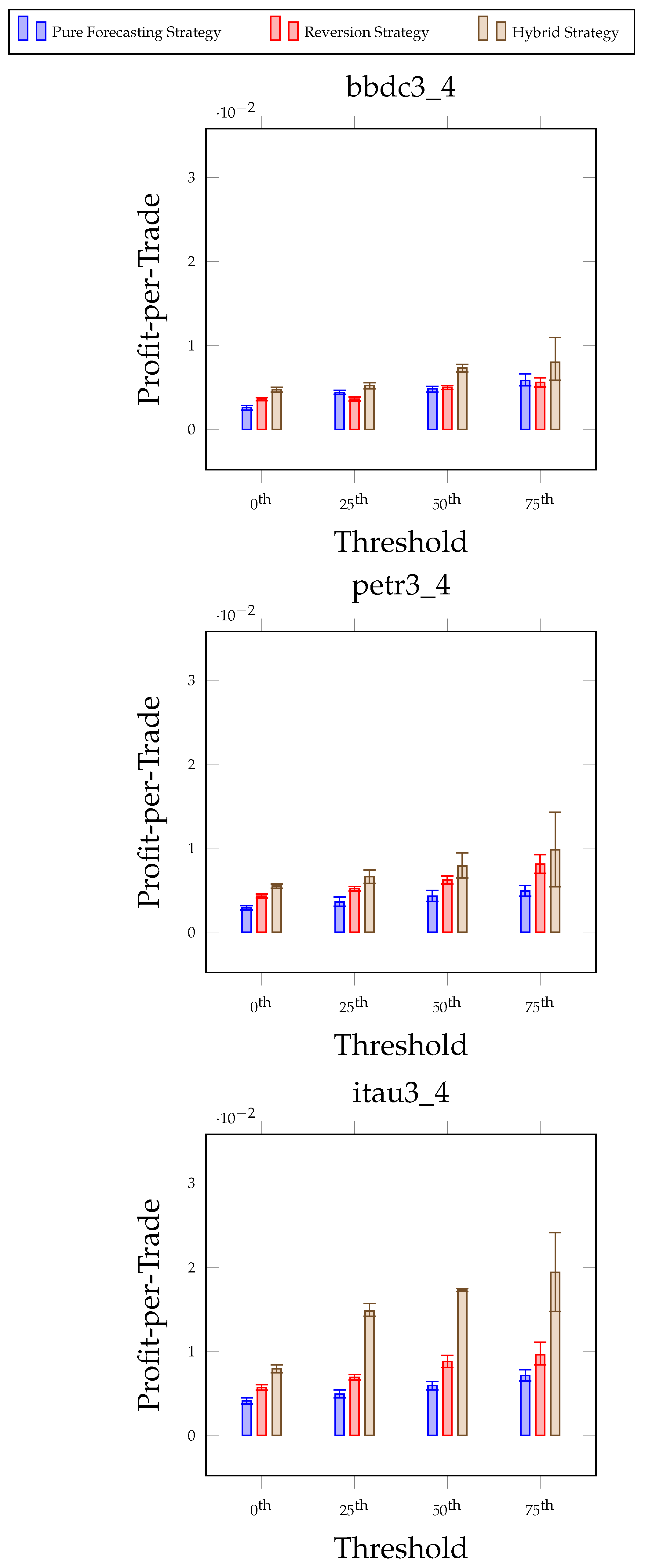
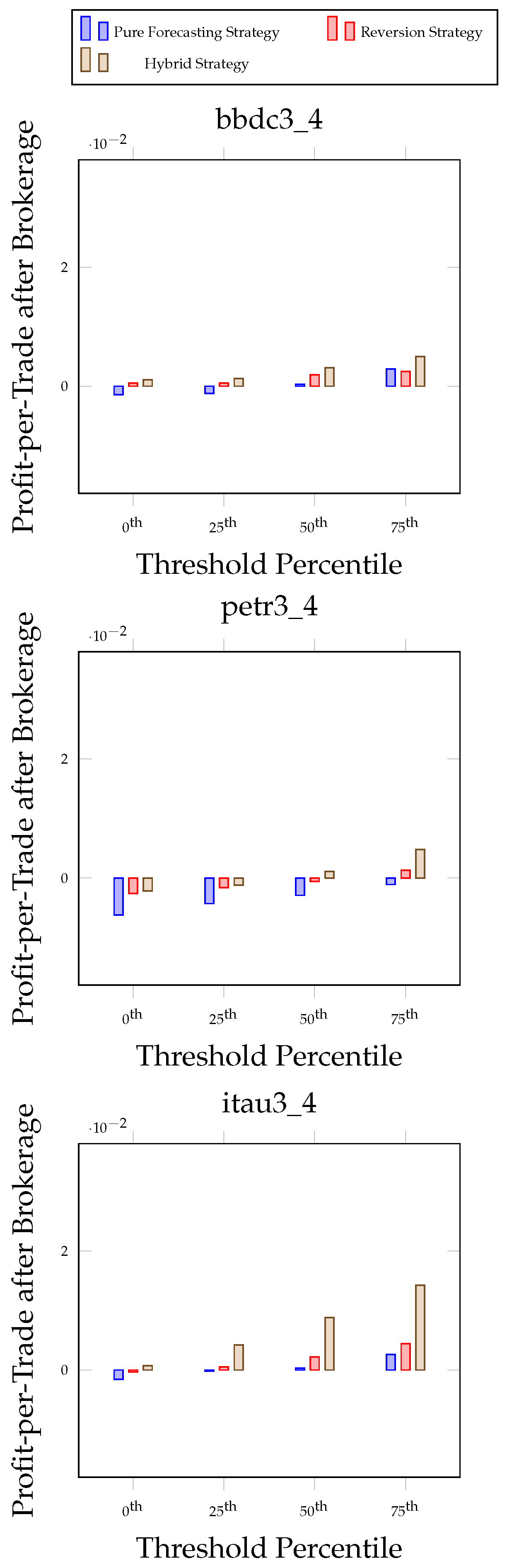
7.1. Threshold Experiments
7.2. Comparison with a Reinforcement Learning Approach
7.3. Practical Implications of Experimental Results
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bookstaber, R.M. A Demon of Our Own Design: Markets, Hedge Funds, and the Perils of Financial Innovation; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Gatev, E.; Goetzmann, W.N.; Rouwenhorst, K.G. Pairs trading: Performance of a relative-value arbitrage rule. Rev. Financ. Stud. 2006, 19, 797–827. [Google Scholar] [CrossRef]
- Lhabitant, F.S.; Gregoriou, G.N. High-frequency trading: Past, present, and future. In Handbook of High Frequency Trading; Academic Press: San Diego, CA, USA, 2015; pp. 155–166. [Google Scholar] [CrossRef]
- Zaharudin, K.Z.; Young, M.R.; Hsu, W.H. High-frequency trading: Definition, implications, and controversies. J. Econ. Surv. 2022, 36, 75–107. [Google Scholar] [CrossRef]
- Virgilio, G. Is high-frequency trading tiering the financial markets? Res. Int. Bus. Financ. 2017, 41, 158–171. [Google Scholar] [CrossRef]
- Bogomolov, T. Pairs trading based on statistical variability of the spread process. Quant. Financ. 2013, 13, 1411–1430. [Google Scholar] [CrossRef]
- Krauss, C. Statistical arbitrage pairs trading strategies: Review and outlook. J. Econ. Surv. 2017, 31, 513–545. [Google Scholar] [CrossRef]
- Tokat, E.; Hayrullahoğlu, A.C. Pairs trading: Is it applicable to exchange-traded funds? Borsa Istanb. Rev. 2022, 22, 743–751. [Google Scholar] [CrossRef]
- Wooldridge, J.M. Introductory Econometrics: A Modern Approach; Nelson Education: Scarborough, ON, Canada, 2015. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Giudici, P. Applied Data Mining: Statistical Methods for Business and Industry; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Shen, Y.; Khorasani, K. Hybrid multi-mode machine learning-based fault diagnosis strategies with application to aircraft gas turbine engines. Neural Netw. 2020, 130, 126–142. [Google Scholar] [CrossRef] [PubMed]
- Tsay, R.S. Analysis of Financial Time Series; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. arXiv 2019, arXiv:1905.10437. [Google Scholar] [CrossRef]
- Oreshkin, B.N.; Dudek, G.; Pełka, P.; Turkina, E. N-BEATS neural network for mid-term electricity load forecasting. Appl. Energy 2021, 293, 116918. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 Competition: 100,000 time series and 61 forecasting methods. Int. J. Forecast. 2020, 36, 54–74. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Elman, J.L. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Malhotra, P.; Vig, L.; Shroff, G.M.; Agarwal, P. Long Short Term Memory Networks for Anomaly Detection in Time Series. In Proceedings of the European Symposium on Artificial Neural Networks, Bruges, Belgium, 22–24 April 2015. [Google Scholar]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 2018, 6, 1662–1669. [Google Scholar] [CrossRef]
- Yunpeng, L.; Di, H.; Junpeng, B.; Yong, Q. Multi-step Ahead Time Series Forecasting for Different Data Patterns Based on LSTM Recurrent Neural Network. In Proceedings of the 2017 14th Web Information Systems and Applications Conference (WISA), Liuzhou, China, 11–12 November 2017; pp. 305–310. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Siami Namin, A. A Comparison of ARIMA and LSTM in Forecasting Time Series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1394–1401. [Google Scholar] [CrossRef]
- Sagheer, A.; Kotb, M. Time series forecasting of petroleum production using deep LSTM recurrent networks. Neurocomputing 2019, 323, 203–213. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, Y.; Dai, F. A LSTM-based method for stock returns prediction: A case study of China stock market. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; pp. 2823–2824. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The Performance of LSTM and BiLSTM in Forecasting Time Series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar] [CrossRef]
- da Silva, D.G.; de Moura Meneses, A.A. Comparing Long Short-Term Memory (LSTM) and bidirectional LSTM deep neural networks for power consumption prediction. Energy Rep. 2023, 10, 3315–3334. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in Time Series: A Survey. arXiv 2023, arXiv:2202.07125. [Google Scholar] [CrossRef]
- Wolf, T.; Debut, L.; Sanh, V.; Chaumond, J.; Delangue, C.; Moi, A.; Cistac, P.; Rault, T.; Louf, R.; Funtowicz, M.; et al. Transformers: State-of-the-Art Natural Language Processing. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, Online, 16–20 November 2020; Liu, Q., Schlangen, D., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 38–45. [Google Scholar] [CrossRef]
- Choi, H.; Cho, K.; Bengio, Y. Fine-grained attention mechanism for neural machine translation. Neurocomputing 2018, 284, 171–176. [Google Scholar] [CrossRef]
- Cholakov, R.; Kolev, T. Transformers predicting the future. Applying attention in next-frame and time series forecasting. arXiv arXiv:2108.08224. [CrossRef]
- Lim, B.; Arık, S.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Challu, C.; Olivares, K.G.; Oreshkin, B.N.; Ramirez, F.G.; Canseco, M.M.; Dubrawski, A. Nhits: Neural hierarchical interpolation for time series forecasting. Proc. AAAI Conf. Artif. Intell. 2023, 37, 6989–6997. [Google Scholar] [CrossRef]
- Benton, G.; Gruver, N.; Maddox, W.; Wilson, A.G. Deep Probabilistic Time Series Forecasting over Long Horizons. 2023. Available online: https://openreview.net/forum?id=22h1XSEiN0 (accessed on 10 March 2023).
- Lea, C.; Flynn, M.D.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal convolutional networks for action segmentation and detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 156–165. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Wan, R.; Mei, S.; Wang, J.; Liu, M.; Yang, F. Multivariate Temporal Convolutional Network: A Deep Neural Networks Approach for Multivariate Time Series Forecasting. Electronics 2019, 8, 876. [Google Scholar] [CrossRef]
- van den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. WaveNet: A Generative Model for Raw Audio. arXiv 2016, arXiv:1609.03499. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Lara-Benítez, P.; Carranza-García, M.; Luna-Romera, J.M.; Riquelme, J.C. Temporal Convolutional Networks Applied to Energy-Related Time Series Forecasting. Appl. Sci. 2020, 10, 2322. [Google Scholar] [CrossRef]
- Koh, B.H.D.; Lim, C.L.P.; Rahimi, H.; Woo, W.L.; Gao, B. Deep Temporal Convolution Network for Time Series Classification. Sensors 2021, 21, 603. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, H.; Wang, X.; Han, S. Time Series Prediction Based on Temporal Convolutional Network. In Proceedings of the 2019 IEEE/ACIS 18th International Conference on Computer and Information Science (ICIS), Beijing, China, 17–19 June 2019; pp. 300–305. [Google Scholar] [CrossRef]
- Liu, B.; Chang, L.B.; Geman, H. Intraday pairs trading strategies on high frequency data: The case of oil companies. Quant. Financ. 2017, 17, 87–100. [Google Scholar] [CrossRef]
- Arumugam, D. Algorithmic trading: Intraday profitability and trading behavior. Econ. Model. 2023, 128, 106521. [Google Scholar] [CrossRef]
- Chen, S.; Chng, M.T.; Liu, Q. The implied arbitrage mechanism in financial markets. J. Econom. 2021, 222, 468–483. [Google Scholar] [CrossRef]
- Gupta, K.; Chatterjee, N. Selecting stock pairs for pairs trading while incorporating lead–lag relationship. Phys. Stat. Mech. Its Appl. 2020, 551, 124103. [Google Scholar] [CrossRef]
- B3. 2023. Available online: https://www.b3.com.br (accessed on 10 March 2023).
- BLK. 2023. Available online: https://www.blk.com.br/ (accessed on 10 March 2023).
- Sharpe, W.F. Adjusting for risk in portfolio performance measurement. J. Portf. Manag. 1975, 1, 29–34. [Google Scholar] [CrossRef]
- Herzen, J.; Lässig, F.; Piazzetta, S.G.; Neuer, T.; Tafti, L.; Raille, G.; Pottelbergh, T.V.; Pasieka, M.; Skrodzki, A.; Huguenin, N.; et al. Darts: User-Friendly Modern Machine Learning for Time Series. J. Mach. Learn. Res. 2022, 23, 1–6. [Google Scholar]
- Xu, Z.; Luo, C. Improved pairs trading strategy using two-level reinforcement learning framework. Eng. Appl. Artif. Intell. 2023, 126, 107148. [Google Scholar] [CrossRef]
- Bacon, P.L.; Harb, J.; Precup, D. The option-critic architecture. Proc. AAAI Conf. Artif. Intell. 2017, 31. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Ansari, A.F.; Stella, L.; Turkmen, C.; Zhang, X.; Mercado, P.; Shen, H.; Shchur, O.; Rangapuram, S.S.; Arango, S.P.; Kapoor, S.; et al. Chronos: Learning the Language of Time Series. arXiv 2024, arXiv:2403.07815. [Google Scholar] [CrossRef]


| Company | Ticker | Type | Sector | Milliseconds Having Trades | Minutes Having Trades |
|---|---|---|---|---|---|
| Petrobras | petr3 | ordinary | gas and oil | 7,602,606 | 95,606 |
| Petrobras | petr4 | preferred | gas and oil | 25,610,052 | 95,853 |
| Banco Itau | itub3 | ordinary | Banks | 4,064,901 | 76,450 |
| Banco Itau | itub4 | preferred | Banks | 12,918,957 | 95,885 |
| Banco Bradesco | bbdc3 | ordinary | Banks | 1,555,960 | 73,266 |
| Banco Bradesco | bbdc4 | preferred | Banks | 11,696,685 | 96,120 |
| Dataset | Prediction Error | Models | ||||
|---|---|---|---|---|---|---|
| Bidirectional LSTM | Transformer | N-BEATS | N-HiTS | Temporal Convolutional Network | ||
| bbdc3_4 | RMSE | 0.00304 | 0.00296 | 0.00131 | 0.00141 | 0.00115 |
| MASE | 13.64749 | 10.58363 | 2.09653 | 2.23407 | 1.47245 | |
| MAPE | 0.16295 | 0.23222 | 0.08583 | 0.09461 | 0.07035 | |
| sMAPE | 0.16274 | 0.23254 | 0.08579 | 0.09455 | 0.07034 | |
| petr3_4 | RMSE | 0.00692 | 0.00302 | 0.00084 | 0.00122 | 0.00097 |
| MASE | 25.86796 | 22.52620 | 2.11696 | 3.14258 | 1.75426 | |
| MAPE | 0.25042 | 0.24915 | 0.05415 | 0.07197 | 0.05509 | |
| sMAPE | 0.24859 | 0.24949 | 0.05416 | 0.07192 | 0.05507 | |
| itau3_4 | RMSE | 0.00319 | 0.00205 | 0.00505 | 0.00431 | 0.00144 |
| MASE | 35.97402 | 23.39049 | 12.67374 | 11.50640 | 3.06157 | |
| MAPE | 0.25089 | 0.20759 | 0.37037 | 0.32999 | 0.12194 | |
| sMAPE | 0.25157 | 0.20787 | 0.37213 | 0.33128 | 0.12206 | |
| Models | Strategy | Predicted Positive | Predicted Negative | F1 Score | ||
|---|---|---|---|---|---|---|
| TP | FP | FN | TN | |||
| Bidirectional LSTM | Pure Forecasting Strategy | 7365 | 6064 | 2696 | 4119 | 0.627 |
| Reversion Strategy | 4704 | 2537 | 2440 | 4715 | 0.654 | |
| Hybrid Strategy | 3779 | 1927 | 1063 | 2561 | 0.716 | |
| Transformer | Pure Forecasting Strategy | 9927 | 9887 | 134 | 296 | 0.664 |
| Reversion Strategy | 4704 | 2537 | 2440 | 4715 | 0.654 | |
| Hybrid Strategy | 4686 | 2521 | 103 | 257 | 0.781 | |
| N-BEATS | Pure Forecasting Strategy | 1272 | 508 | 8789 | 9675 | 0.214 |
| Reversion Strategy | 4704 | 2537 | 2440 | 4715 | 0.654 | |
| Hybrid Strategy | 1158 | 445 | 2416 | 4696 | 0.447 | |
| N-HiTS | Pure Forecasting Strategy | 687 | 271 | 9374 | 9912 | 0.124 |
| Reversion Strategy | 4704 | 2537 | 2440 | 4715 | 0.654 | |
| Hybrid Strategy | 633 | 234 | 2419 | 4702 | 0.323 | |
| Temporal Convolutional Network | Pure Forecasting Strategy | 4747 | 2467 | 5314 | 7716 | 0.549 |
| Reversion Strategy | 4704 | 2537 | 2440 | 4715 | 0.654 | |
| Hybrid Strategy | 3135 | 1341 | 2002 | 4271 | 0.652 | |
| Models | Strategy | Predicted Positive | Predicted Negative | F1 Score | ||
|---|---|---|---|---|---|---|
| TP | FP | FN | TN | |||
| Bidirectional LSTM | Pure Forecasting Strategy | 11,309 | 8921 | 6899 | 9182 | 0.588 |
| Reversion Strategy | 10,512 | 6784 | 6878 | 10,485 | 0.606 | |
| Hybrid Strategy | 7668 | 4598 | 3761 | 6645 | 0.647 | |
| Transformer | Pure Forecasting Strategy | 17,386 | 17,147 | 822 | 956 | 0.659 |
| Reversion Strategy | 10,512 | 6784 | 6878 | 10,485 | 0.606 | |
| Hybrid Strategy | 10,127 | 6542 | 401 | 675 | 0.744 | |
| N-BEATS | Pure Forecasting Strategy | 16,241 | 14,186 | 1967 | 3917 | 0.667 |
| Reversion Strategy | 10,512 | 6784 | 6878 | 10,485 | 0.606 | |
| Hybrid Strategy | 10,454 | 6703 | 1901 | 3821 | 0.708 | |
| N-HiTS | Pure Forecasting Strategy | 3479 | 1948 | 14,729 | 16,155 | 0.294 |
| Reversion Strategy | 10,512 | 6784 | 6878 | 10,485 | 0.606 | |
| Hybrid Strategy | 3285 | 1752 | 6726 | 10,319 | 0.436 | |
| Temporal Convolutional Network | Pure Forecasting Strategy | 10,230 | 7092 | 7978 | 11,011 | 0.575 |
| Reversion Strategy | 10,512 | 6784 | 6878 | 10,485 | 0.606 | |
| Hybrid Strategy | 8048 | 4775 | 5137 | 8542 | 0.618 | |
| Models | Strategy | Predicted Positive | Predicted Negative | F1 Score | ||
|---|---|---|---|---|---|---|
| TP | FP | FN | TN | |||
| Bidirectional LSTM | Pure Forecasting Strategy | 13,076 | 10,122 | 3178 | 5946 | 0.662 |
| Reversion Strategy | 8718 | 4975 | 5100 | 8666 | 0.633 | |
| Hybrid Strategy | 7855 | 3953 | 1727 | 3986 | 0.734 | |
| Transformer | Pure Forecasting Strategy | 15,930 | 15,382 | 324 | 686 | 0.669 |
| Reversion Strategy | 8718 | 4975 | 5100 | 8666 | 0.633 | |
| Hybrid Strategy | 8657 | 4909 | 241 | 582 | 0.770 | |
| N-BEATS | Pure Forecasting Strategy | 11,973 | 9255 | 4281 | 6813 | 0.638 |
| Reversion Strategy | 8718 | 4975 | 5100 | 8666 | 0.633 | |
| Hybrid Strategy | 7553 | 3755 | 2222 | 4431 | 0.716 | |
| N-HiTS | Pure Forecasting Strategy | 15,775 | 14,852 | 479 | 1216 | 0.672 |
| Reversion Strategy | 8718 | 4975 | 5100 | 8666 | 0.633 | |
| Hybrid Strategy | 8674 | 4914 | 394 | 1082 | 0.765 | |
| Temporal Convolutional Network | Pure Forecasting Strategy | 13,195 | 10,308 | 3059 | 5760 | 0.663 |
| Reversion Strategy | 8718 | 4975 | 5100 | 8666 | 0.633 | |
| Hybrid Strategy | 7952 | 4033 | 1739 | 3912 | 0.733 | |
| Pair of Stocks | Strategy | Profit before Fees | Profit after Fees |
|---|---|---|---|
| bbdc3_4 | Pure Forecasting Strategy | 7.8291 | 4.9139 |
| Reversion Strategy | 37.6632 | 16.0140 | |
| Hybrid Strategy | 11.7661 | 7.2873 | |
| petr3_4 | Pure Forecasting Strategy | 64.9675 | 9.4263 |
| Reversion Strategy | 87.0103 | 14.2168 | |
| Hybrid Strategy | 38.4144 | 12.9912 | |
| itau3_4 | Pure Forecasting Strategy | 29.6097 | 17.0472 |
| Reversion Strategy | 86.7440 | 36.9860 | |
| Hybrid Strategy | 32.1873 | 24.7291 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadad, E.; Hodarkar, S.; Lemeneh, B.; Shasha, D. Machine Learning-Enhanced Pairs Trading. Forecasting 2024, 6, 434-455. https://doi.org/10.3390/forecast6020024
Hadad E, Hodarkar S, Lemeneh B, Shasha D. Machine Learning-Enhanced Pairs Trading. Forecasting. 2024; 6(2):434-455. https://doi.org/10.3390/forecast6020024
Chicago/Turabian StyleHadad, Eli, Sohail Hodarkar, Beakal Lemeneh, and Dennis Shasha. 2024. "Machine Learning-Enhanced Pairs Trading" Forecasting 6, no. 2: 434-455. https://doi.org/10.3390/forecast6020024
APA StyleHadad, E., Hodarkar, S., Lemeneh, B., & Shasha, D. (2024). Machine Learning-Enhanced Pairs Trading. Forecasting, 6(2), 434-455. https://doi.org/10.3390/forecast6020024






