Forecasting Daily and Weekly Passenger Demand for Urban Rail Transit Stations Based on a Time Series Model Approach
Abstract
1. Introduction
2. Literature Review
- Accuracy of data aggregation techniques.
- Study the time dependence of URT passenger data before data are input into the model.
- The combined time series forecasting model has become more popular for improving URT passenger forecasting performance over the use of a single model.
- Among several combined time series models, the Box–Jenkins models are more popular and their forecasting efficiency and accuracy have been proven in different studies.
- Future passenger demand forecasting is important to the URT public transportation industry. This point has been proved in several studies on future passenger demand prediction.
3. Data and Methods
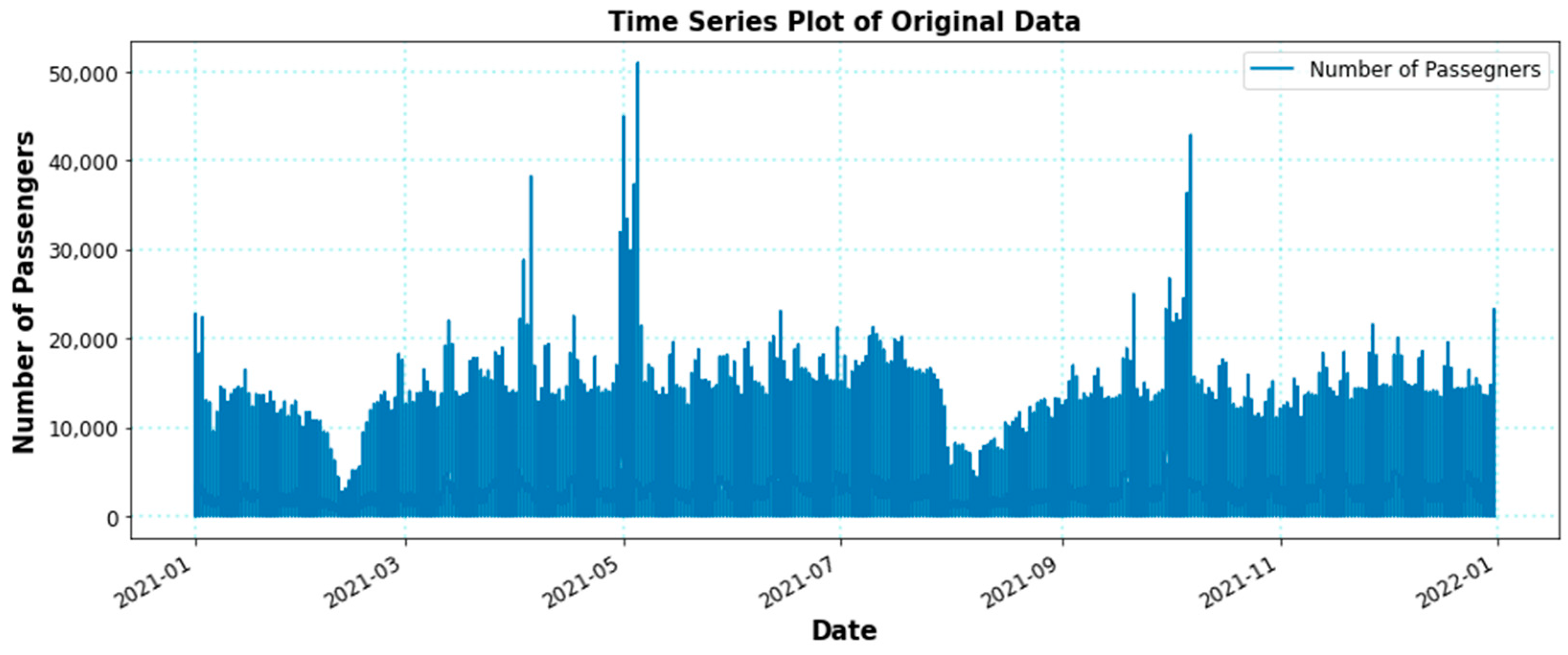
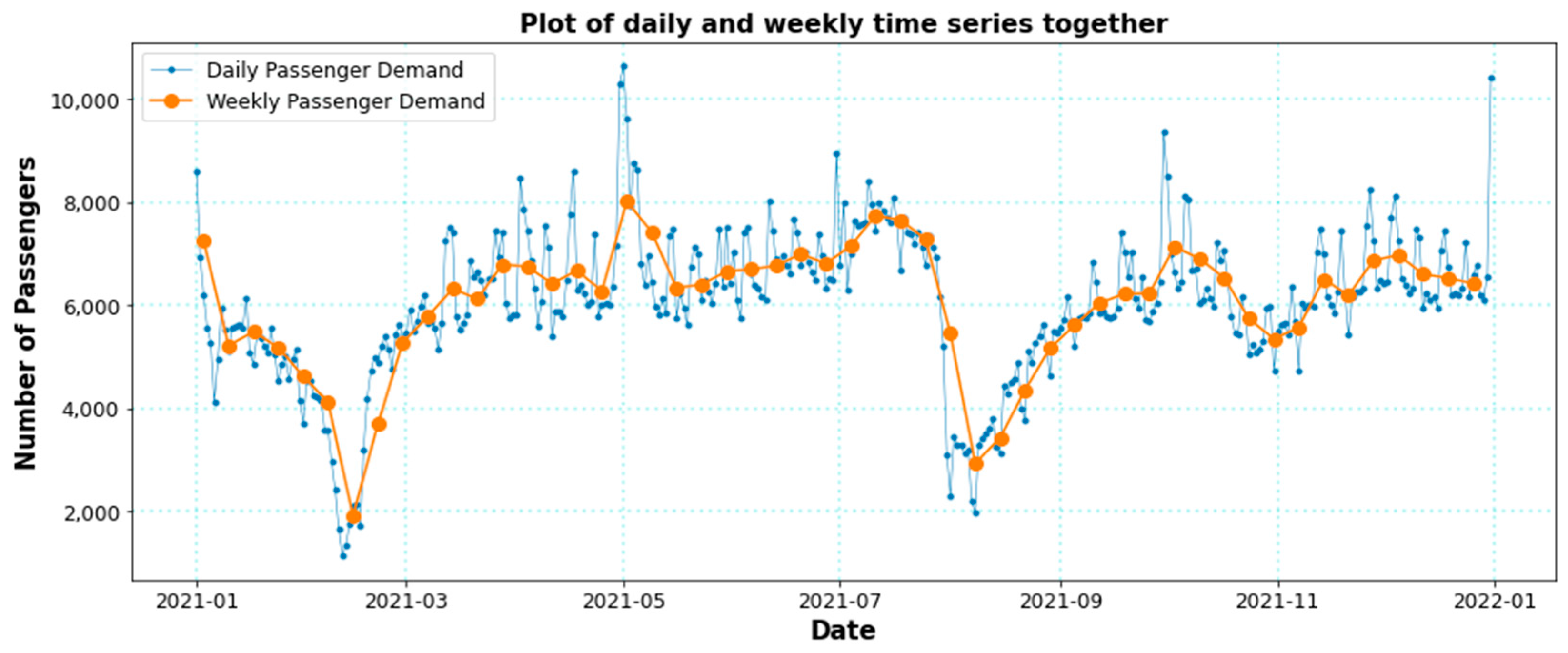
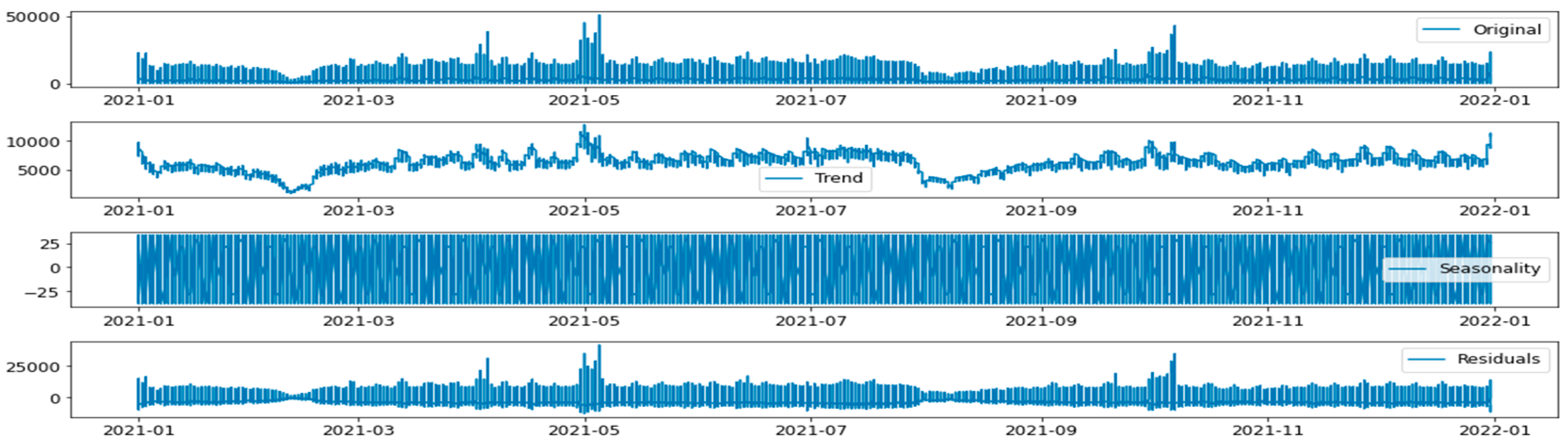
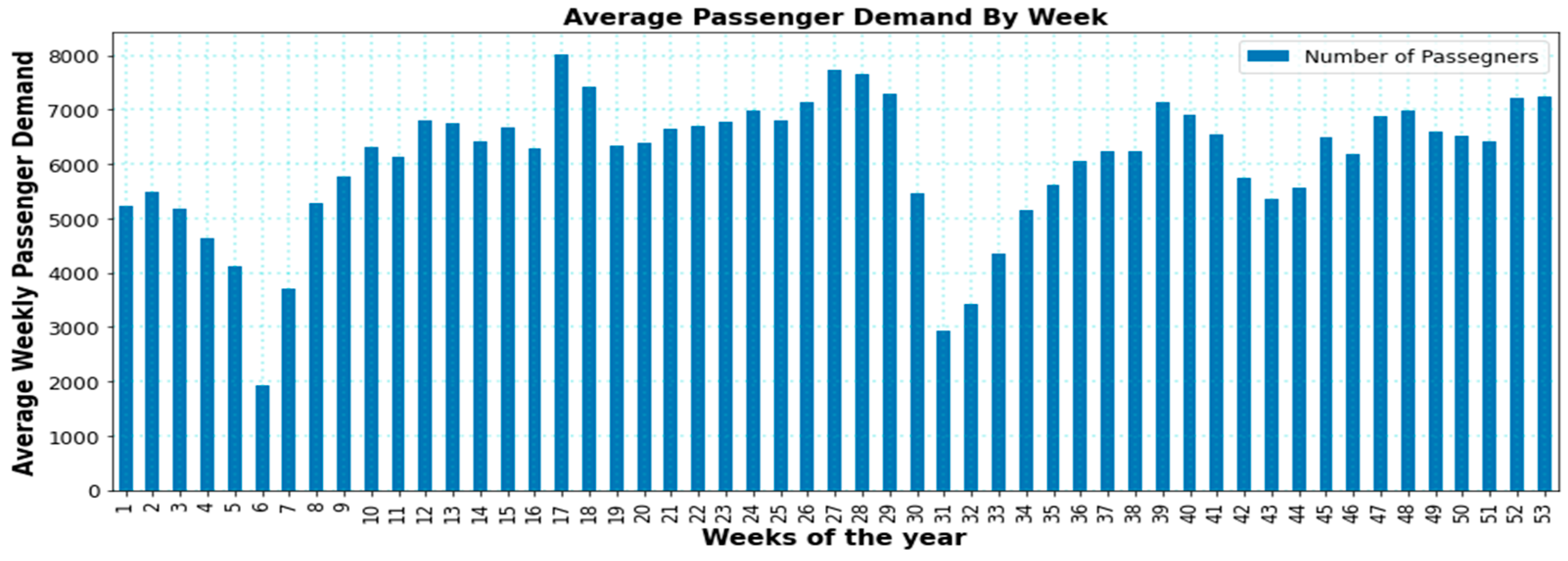
3.1. Data Analysis
3.2. Methodology
3.3. Box–Jenkins Forecasting Models
3.3.1. Autoregressive (AR) (p) Models
3.3.2. Moving Average (MA) (q) Model
3.3.3. Autoregressive Moving Average (ARMA) (p, q) Model
3.3.4. Autoregressive Integrated Moving Average (ARIMA) (p, d, q) Model
3.3.5. Seasonal Autoregressive Integrated Moving Average (SARIMA) Models
3.3.6. Facebook Prophet (FB Prophet) Model
3.4. Forecasting Models Selection
3.4.1. Box–Jenkins Model Selection Criterions
3.4.2. Performance Evaluation Index
4. Results and Discussions
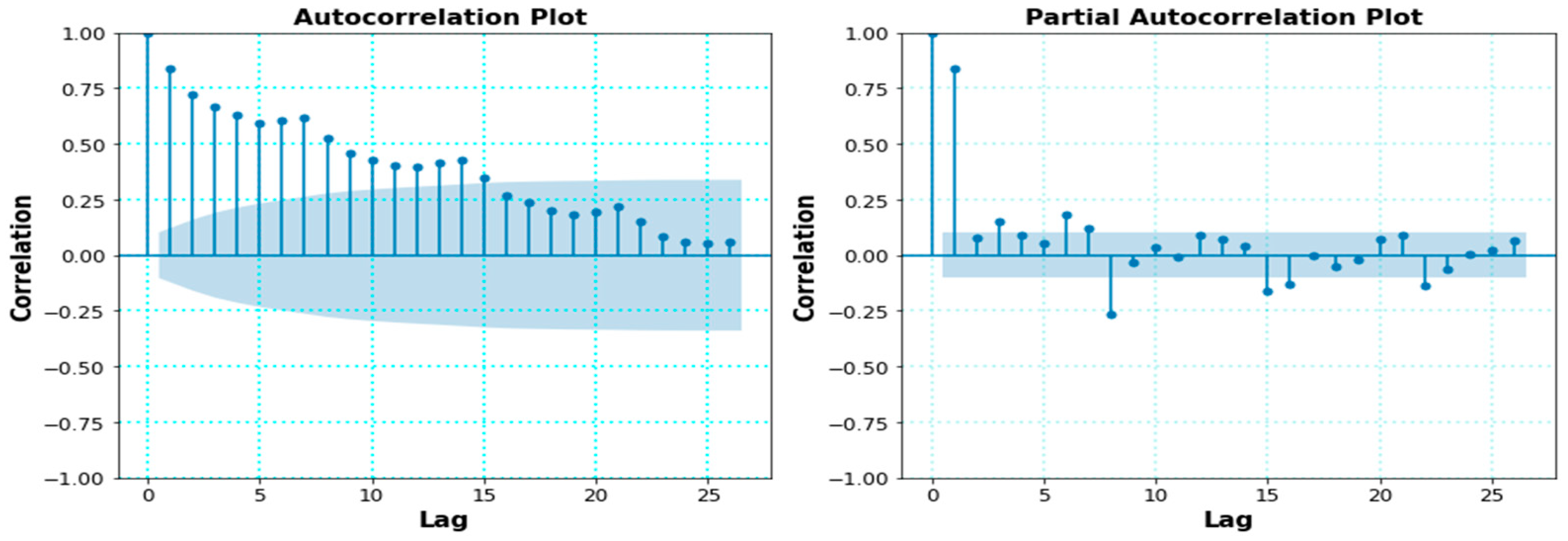
4.1. Time Series Stationarity Test
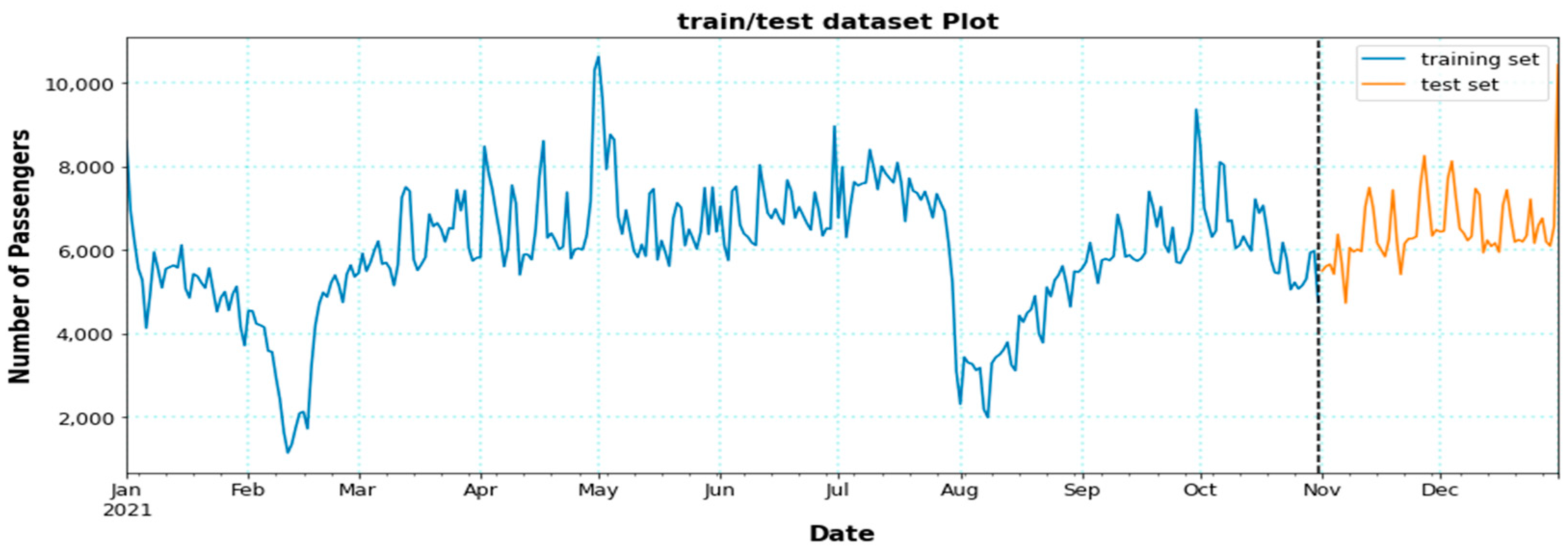
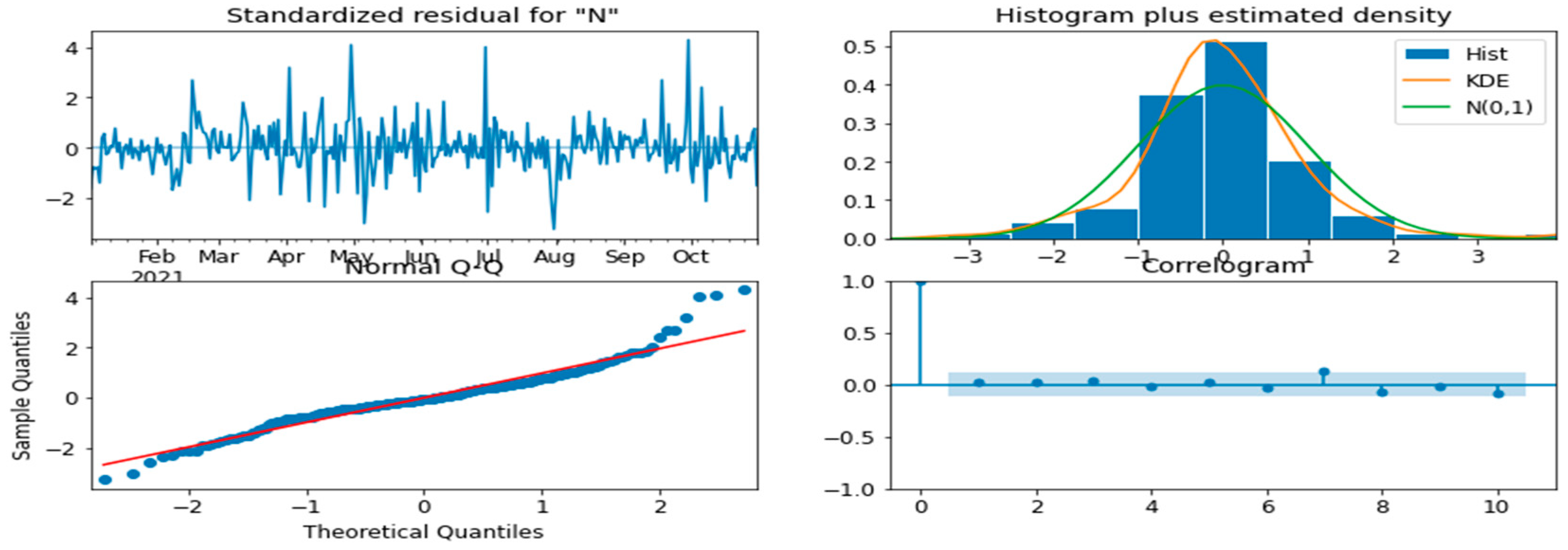
4.2. Daily Time Series Model
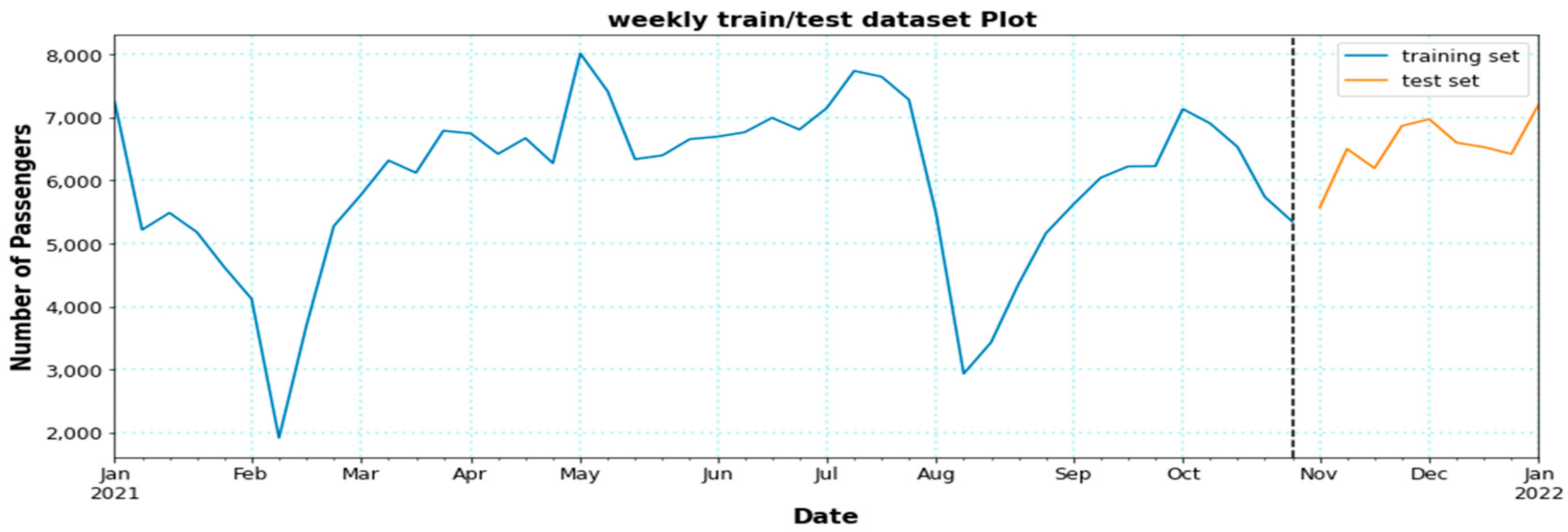
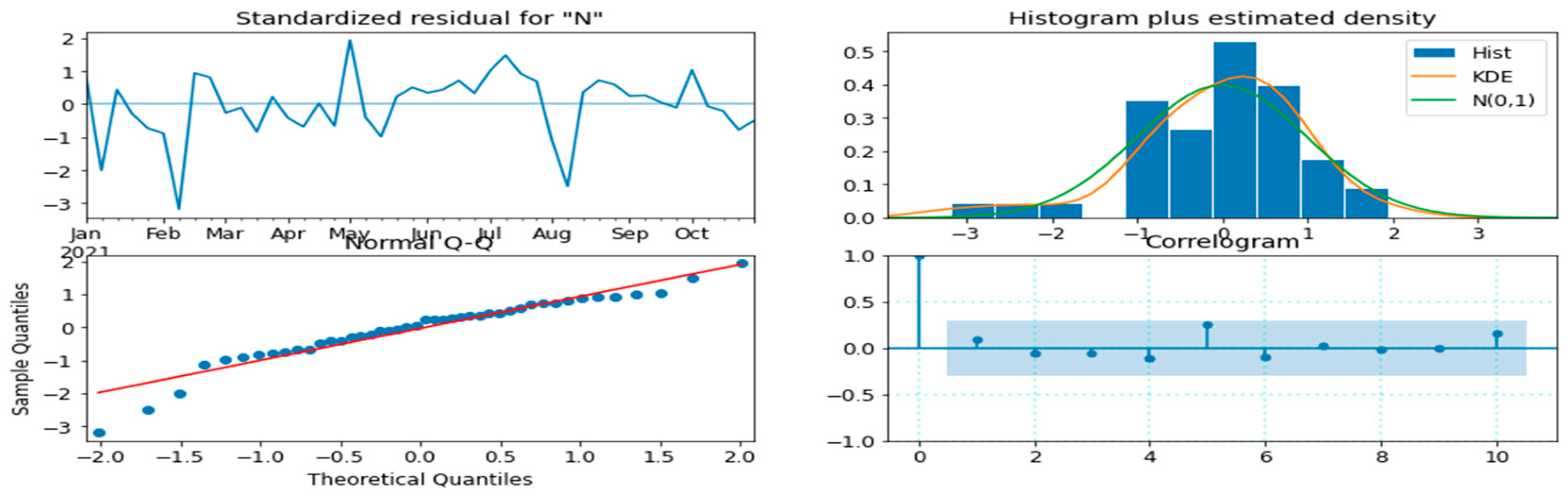
4.3. Weekly Time Series Model
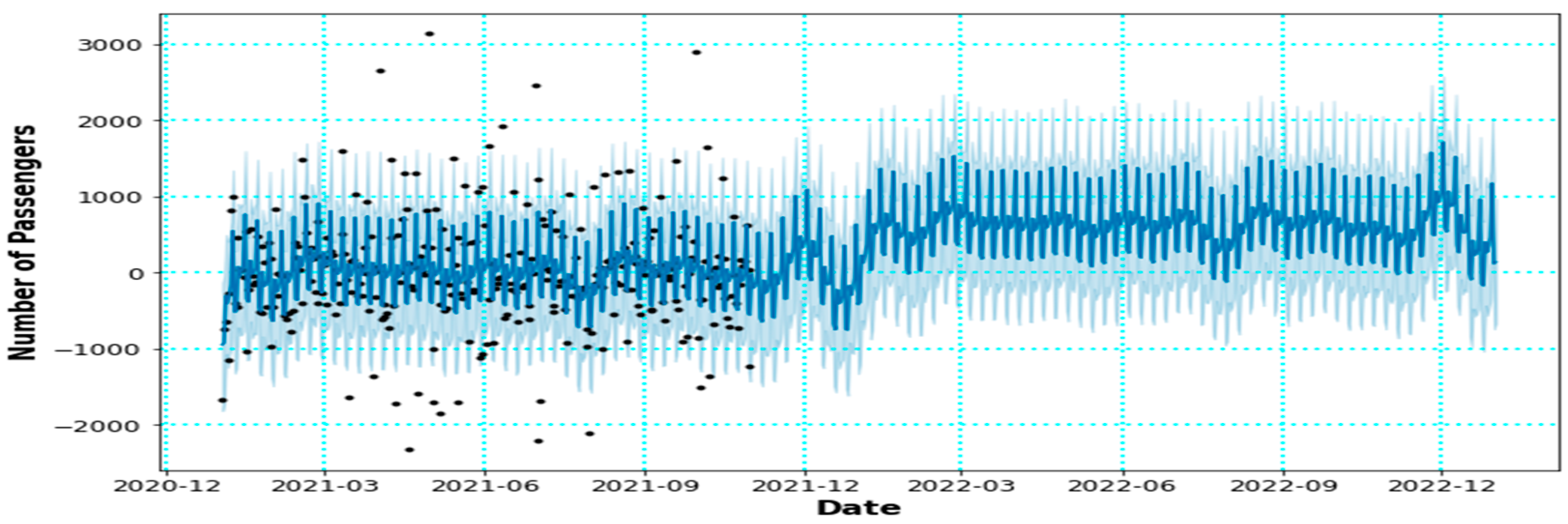
4.4. Forecasting with the Selected Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmed, M.S.; Cook, A.R. Analysis of Freeway Traffic Time-Series Data by Using Box-Jenkins Techniques; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1979. [Google Scholar]
- Ahmed, S.A. On the Estimation of Traffic Occupancy with Application to Freeway Incident Detection. IFAC Proc. Vol. 1982, 15, 819–823. [Google Scholar] [CrossRef]
- Bai, L.; Yao, L.; Kanhere, S.S.; Yang, Z.; Chu, J.; Wang, X. Passenger Demand Forecasting with Multi-Task Convolutional Recurrent Neural Networks. In Advances in Knowledge Discovery and Data Mining; Yang, Q., Zhou, Z.-H., Gong, Z., Zhang, M.-L., Huang, S.J., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 11440, pp. 29–42. ISBN 978-3-030-16144-6. [Google Scholar]
- Chen, C.F.; Chang, Y.H.; Chang, Y.W. Seasonal ARIMA forecasting of inbound air travel arrivals to Taiwan. Transportmetrica 2009, 5, 125–140. [Google Scholar] [CrossRef]
- Chikkakrishna, N.K.; Hardik, C.; Deepika, K.; Sparsha, N. Short-Term Traffic Prediction Using SARIMA and FbPROPHET. In Proceedings of the 2019 IEEE 16th India Council International Conference (INDICON), Rajkot, India, 13–15 December 2019; pp. 1–4. [Google Scholar]
- Fang, Z.; Cheng, Q.; Jia, R.; Liu, Z. Urban Rail Transit Demand Analysis and Prediction: A Review of Recent Studies. In Intelligent Interactive Multimedia Systems and Services; De Pietro, G., Gallo, L., Howlett, R.J., Jain, L.C., Vlacic, L., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 98, pp. 300–309. ISBN 978-3-319-92230-0. [Google Scholar]
- Fathi, O. Time series forecasting using a hybrid ARIMA and LSTM model. Velv. Consult. 2019, 1–7. [Google Scholar]
- Hansen, J.V.; McDonald, J.B.; Nelson, R.D. Time Series Prediction with Genetic-Algorithm Designed Neural Networks: An Empirical Comparison with Modern Statistical Models. Comput. Intell. 1999, 15, 171–184. [Google Scholar] [CrossRef]
- Harvey, A.C.; Peters, S. Estimation Procedures for Structural Time Series Models. J. Forecast. 1990, 9, 21. [Google Scholar] [CrossRef]
- Hong, W.C.; Dong, Y.; Zheng, F.; Lai, C.Y. Forecasting urban traffic flow by SVR with continuous ACO. Appl. Math. Model. 2011, 35, 1282–1291. [Google Scholar] [CrossRef]
- Karlaftis, M.G.; Vlahogianni, E.I. Statistical methods versus neural networks in transportation research: Differences, similarities and some insights. Transp. Res. Part C Emerg. Technol. 2011, 19, 387–399. [Google Scholar] [CrossRef]
- Kumar, S.V.; Vanajakshi, L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data. Eur. Transp. Res. Rev. 2015, 7, 21. [Google Scholar] [CrossRef]
- Lee, S.; Fambro, D.B. Application of Subset Autoregressive Integrated Moving Average Model for Short-Term Freeway Traffic Volume Forecasting. Transp. Res. Rec. 1999, 1678, 179–188. [Google Scholar] [CrossRef]
- Li, W.; Sui, L.; Zhou, M.; Dong, H. Short-term passenger flow forecast for urban rail transit based on multi-source data. EURASIP J. Wirel. Commun. Netw. 2021, 2021, 9. [Google Scholar] [CrossRef]
- Milenković, M.; Švadlenka, L.; Melichar, V.; Bojović, N.; Avramović, Z. SARIMA modelling approach for railway passenger flow forecasting. Transport 2016, 33, 1113–1120. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting; Wiley-Interscience: Hoboken, NJ, USA, 2008; ISBN 978-0-471-65397-4. [Google Scholar]
- Oh, S.; Byon, Y.J.; Jang, K.; Yeo, H. Short-term Travel-time Prediction on Highway: A Review of the Data-driven Approach. Transp. Rev. 2015, 35, 4–32. [Google Scholar] [CrossRef]
- Rabbani, M.B.A.; Musarat, M.A.; Alaloul, W.S.; Rabbani, M.S.; Maqsoom, A.; Ayub, S.; Bukhari, H.; Altaf, M. A Comparison Between Seasonal Autoregressive Integrated Moving Average (SARIMA) and Exponential Smoothing (ES) Based on Time Series Model for Forecasting Road Accidents. Arab. J. Sci. Eng. 2021, 46, 11113–11138. [Google Scholar] [CrossRef]
- Raza, A.; Zhong, M. Lane-based short-term urban traffic forecasting with GA designed ANN and LWR models. Transp. Res. Procedia 2017, 25, 1430–1443. [Google Scholar] [CrossRef]
- Smith, B.L.; Williams, B.M.; Keith Oswald, R. Comparison of parametric and nonparametric models for traffic flow forecasting. Transp. Res. Part C Emerg. Technol. 2002, 10, 303–321. [Google Scholar] [CrossRef]
- Song, H.; Tang, T.; Li, C.; Ding, Y. Short Time Forecasting of Rail Transit Passenger Volume. In The 2nd International Symposium on Rail Transit Comprehensive Development (ISRTCD) Proceedings; Xia, H., Zhang, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 121–130. ISBN 978-3-642-37588-0. [Google Scholar]
- Van Der Voort, M.; Dougherty, M.; Watson, S. Combining Kohonen maps with Arima time series models to forecast traffic flow. Transp. Res. Part C Emerg. Technol. 1996, 4, 307–318. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Golias, J.C.; Karlaftis, M.G. Short-term traffic forecasting: Overview of objectives and methods. Transp. Rev. 2004, 24, 533–557. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, N.; Zhang, Y.; Shi, Z. Forecasting of Short-Term Metro Ridership with Support Vector Machine Online Model. J. Adv. Transp. 2018, 2018, 3189238. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, M.C. Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks. Transp. Res. Part C Emerg. Technol. 2012, 21, 148–162. [Google Scholar] [CrossRef]
- Williams, B.M. Multivariate Vehicular Traffic Flow Prediction: Evaluation of ARIMAX Modeling. Transp. Res. Rec. 2001, 1776, 194–200. [Google Scholar] [CrossRef]
- Williams, B.M.; Durvasula, P.K.; Brown, D.E. Urban Freeway Traffic Flow Prediction: Application of Seasonal Autoregressive Integrated Moving Average and Exponential Smoothing Models. Transp. Res. Rec. 1998, 1644, 132–141. [Google Scholar] [CrossRef]
- Williams, B.M.; Hoel, L.A. Modeling and Forecasting Vehicular Traffic Flow as a Seasonal ARIMA Process: Theoretical Basis and Empirical Results. J. Transp. Eng. 2003, 129, 664–672. [Google Scholar] [CrossRef]
- Yang, J.; Han, L.D.; Freeze, P.B.; Chin, S.M.; Hwang, H.L. Short-Term Freeway Speed Profiling Based on Longitudinal Spatiotemporal Dynamics. Transp. Res. Rec. J. Transp. Res. Board 2014, 2467, 62–72. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, F.; Guo, Y.; Li, X. Multi-graph convolutional network for short-term passenger flow forecasting in urban rail transit. IET Intell. Transp. Syst. 2020, 14, 1210–1217. [Google Scholar] [CrossRef]
- Zhang, M. Time Series: Autoregressive models AR, MA, ARMA, ARIMA; University of Pittsburgh: Pittsburgh, PA, USA, 2018. [Google Scholar]
- Zhao, Y.; Ma, Z.; Yang, Y.; Jiang, W.; Jiang, X. Short-Term Passenger Flow Prediction with Decomposition in Urban Railway Systems. IEEE Access 2020, 8, 107876–107886. [Google Scholar] [CrossRef]
- Zuva, T.; Ngwira, S.M.; Zuva, K.; Ojo, S.O. Effectiveness of Non-Parametric Techniques in Image Retrieval. In Proceedings of the 2014 World Symposium on Computer Applications & Research (WSCAR), Sousse, Tunisia, 18–20 January 2014. [Google Scholar]







| Categories | AR (p) | MA (q) | ARMA (p, q) |
|---|---|---|---|
| ACF | Tails off exponentially | Shuts off after lag q | Tails off exponentially |
| PACF | Shuts off after lag p | Tails off exponentially | Tails off exponentially |
| Model | Parameters | Coefficient | Std Error | z | p-Value | ||
|---|---|---|---|---|---|---|---|
| Daily Time Series Model | SARIMA (5, 1, 3) (1, 0, 0)24 | −0.02 | 0.17 | −0.12 | 0.91 | ||
| −0.81 | 0.11 | −7.06 | 0.00 | *** | |||
| 0.25 | 0.20 | 1.21 | 0.23 | ||||
| −0.08 | 0.07 | −1.23 | 0.22 | ||||
| −0.18 | 0.07 | −2.70 | 0.01 | *** | |||
| −0.17 | 0.17 | −0.99 | 0.32 | ||||
| 0.72 | 0.07 | 9.83 | 0.00 | *** | |||
| −0.56 | 0.16 | −3.46 | 0.00 | *** | |||
| AR.S. L24 | −0.14 | 0.07 | −1.89 | 0.06 | |||
| Weekly Time Series Model | AR (2) | 1.01 | 0.15 | 6.76 | 0.00 | *** | |
| −0.32 | 0.15 | −2.19 | 0.03 | *** | |||
| ARMA (2, 1) | 1.72 | 0.08 | 20.62 | 0.00 | *** | ||
| −0.81 | 0.09 | −9.37 | 0.00 | *** | |||
| −0.99 | 0.07 | −14.86 | 0.00 | *** | |||
| Model | RMSE | MAE | MSLE | RMSLE |
|---|---|---|---|---|
| SARIMA (5, 1, 3) (1, 0, 0) | 1346.908 | 1109.53 | 0.043 | 0.208 |
| AR (2) | 719.674 | 643.19 | 0.013 | 0.113 |
| AR (3) | 719.528 | 645.18 | 0.013 | 0.113 |
| AR (6) | 780.641 | 666.30 | 0.015 | 0.124 |
| ARMA (2, 1) | 469.818 | 360.54 | 0.005 | 0.072 |
| ARMA (0, 3) | 676.571 | 580.62 | 0.011 | 0.105 |
| ARMA (1, 3) | 680.431 | 588.11 | 0.011 | 0.106 |
| Facebook Prophet Time Series Model | ||||
| Daily Time Series | RMSE | MSE | MAE | |
| Baseline Model | 634.47 | 402,553.33 | 421.74 | |
| Baseline Model with Seasonality | 683.96 | 467,800.51 | 475.55 | |
| Weekly Time Series | ||||
| Baseline Model | 844.39 | 712,998.67 | 730.00 | |
| Baseline Model with Seasonality | 6304.62 | 38,497,293.63 | 6161.41 | |
| SARIMA (p, d, q) (P, D, Q)m Models | Daily Time Series | |||
|---|---|---|---|---|
| AIC | BIC | MSE | Log-Likelihood | |
| SARIMA (5, 1, 3) (1, 0, 0)24 | 4828.786 | 4865.923 | 1,814,162.356 | −2404.393 |
| Weekly Time Series | ||||
| AR (2) | 722.86 | 729.99 | 517,930.55 | −357.43 |
| AR (3) | 724.73 | 733.65 | 517,720.89 | −357.36 |
| AR (6) | 723.74 | 738.01 | 609,400.54 | −353.87 |
| ARMA (2, 1) | 722.28 | 731.20 | 220,728.66 | −356.14 |
| ARMA (0, 3) | 720.32 | 729.25 | 457,775.37 | −355.16 |
| ARMA (1, 3) | 721.985 | 732.690 | 462,986.61 | −354.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chuwang, D.D.; Chen, W. Forecasting Daily and Weekly Passenger Demand for Urban Rail Transit Stations Based on a Time Series Model Approach. Forecasting 2022, 4, 904-924. https://doi.org/10.3390/forecast4040049
Chuwang DD, Chen W. Forecasting Daily and Weekly Passenger Demand for Urban Rail Transit Stations Based on a Time Series Model Approach. Forecasting. 2022; 4(4):904-924. https://doi.org/10.3390/forecast4040049
Chicago/Turabian StyleChuwang, Dung David, and Weiya Chen. 2022. "Forecasting Daily and Weekly Passenger Demand for Urban Rail Transit Stations Based on a Time Series Model Approach" Forecasting 4, no. 4: 904-924. https://doi.org/10.3390/forecast4040049
APA StyleChuwang, D. D., & Chen, W. (2022). Forecasting Daily and Weekly Passenger Demand for Urban Rail Transit Stations Based on a Time Series Model Approach. Forecasting, 4(4), 904-924. https://doi.org/10.3390/forecast4040049








