Prevalence and Economic Costs of Absenteeism in an Aging Population—A Quasi-Stochastic Projection for Germany
Abstract
1. Introduction
2. Materials and Methods
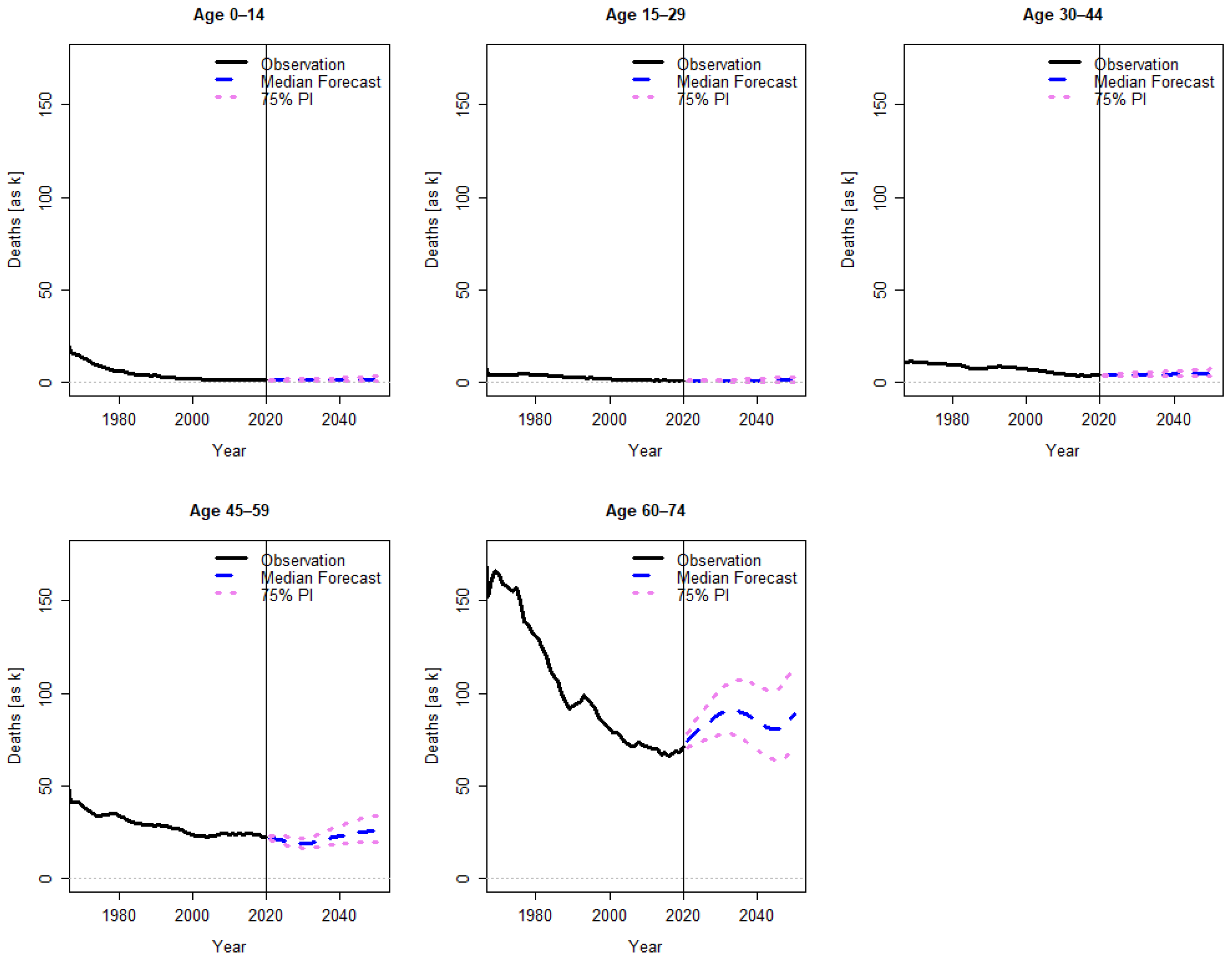
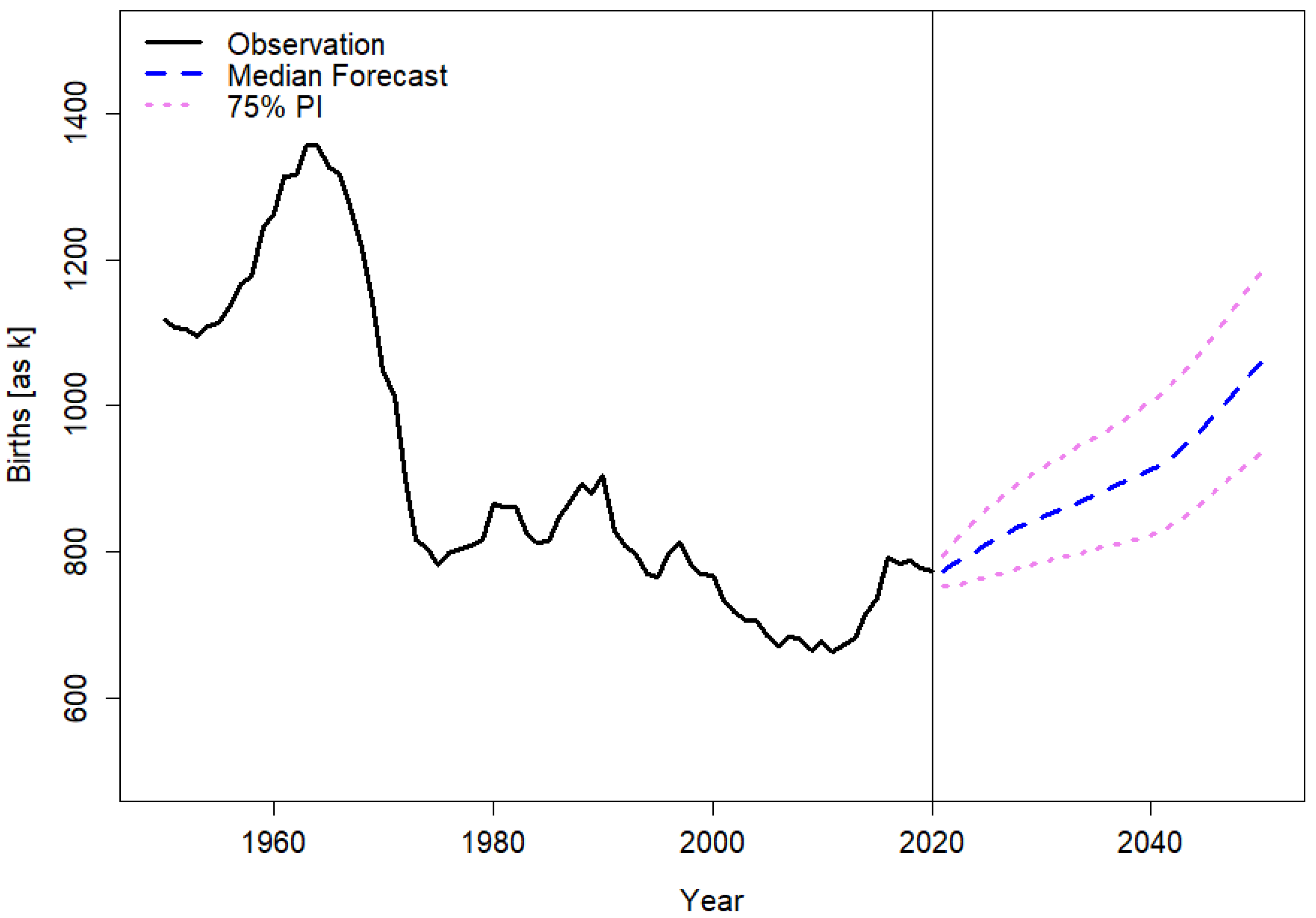
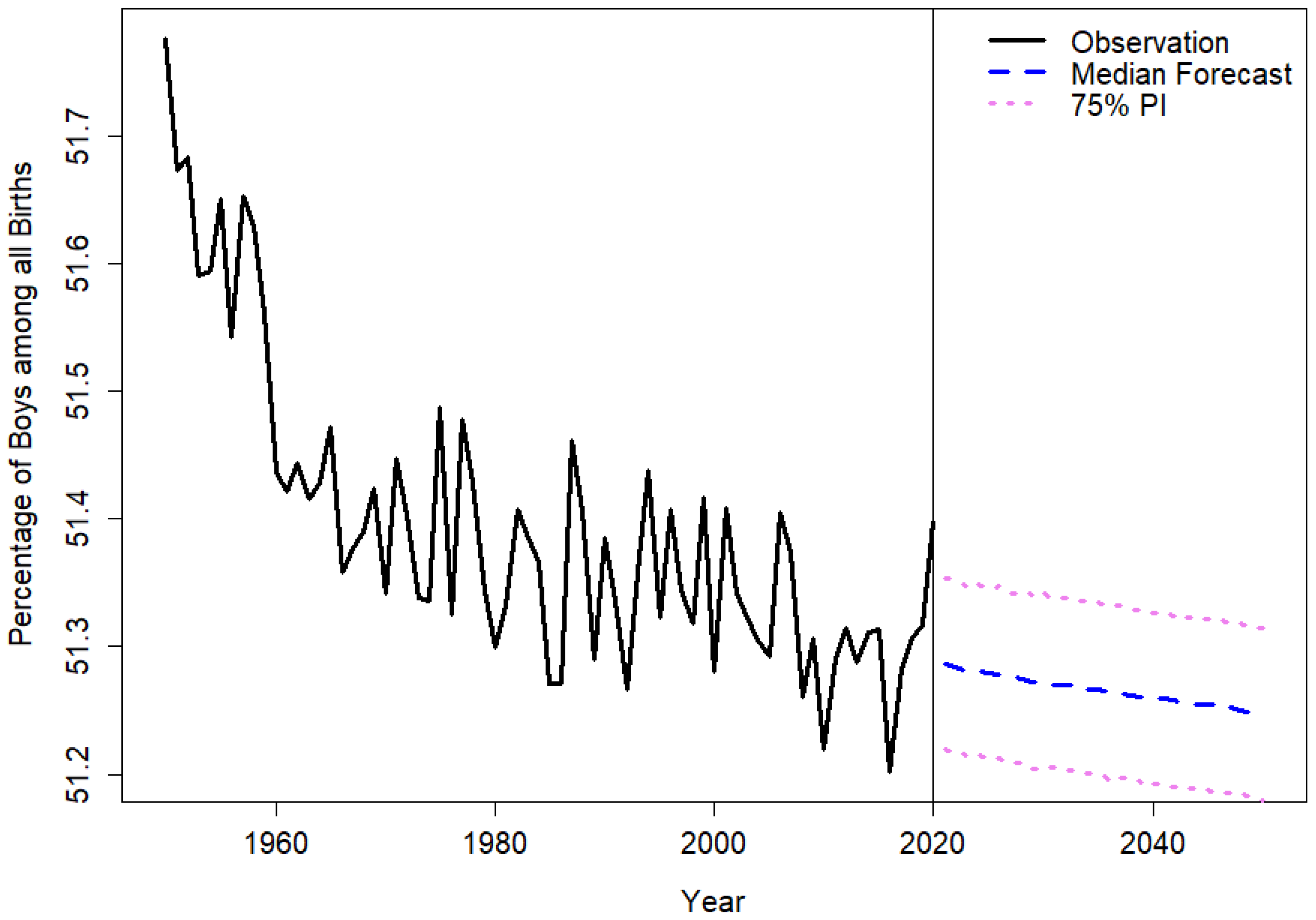
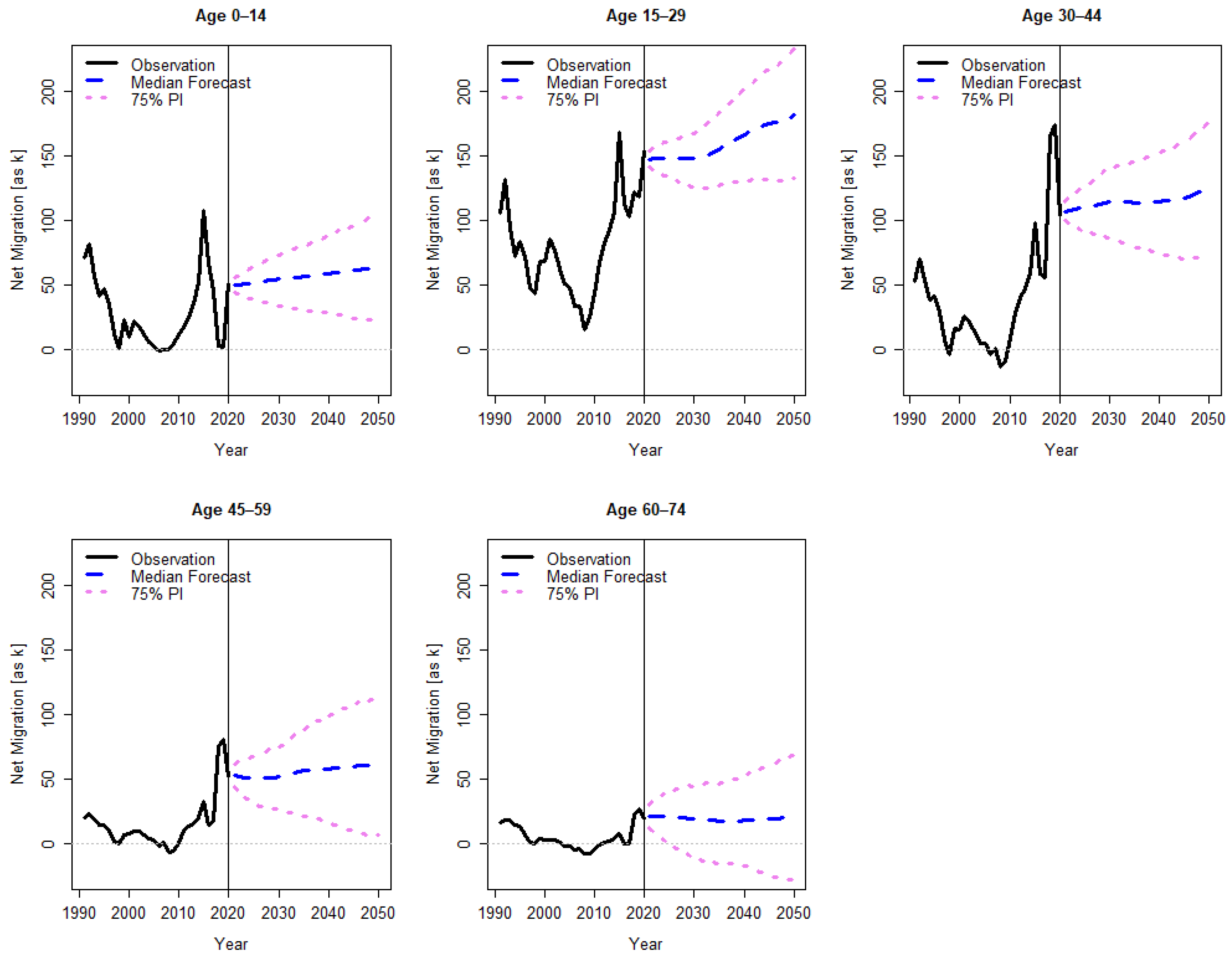
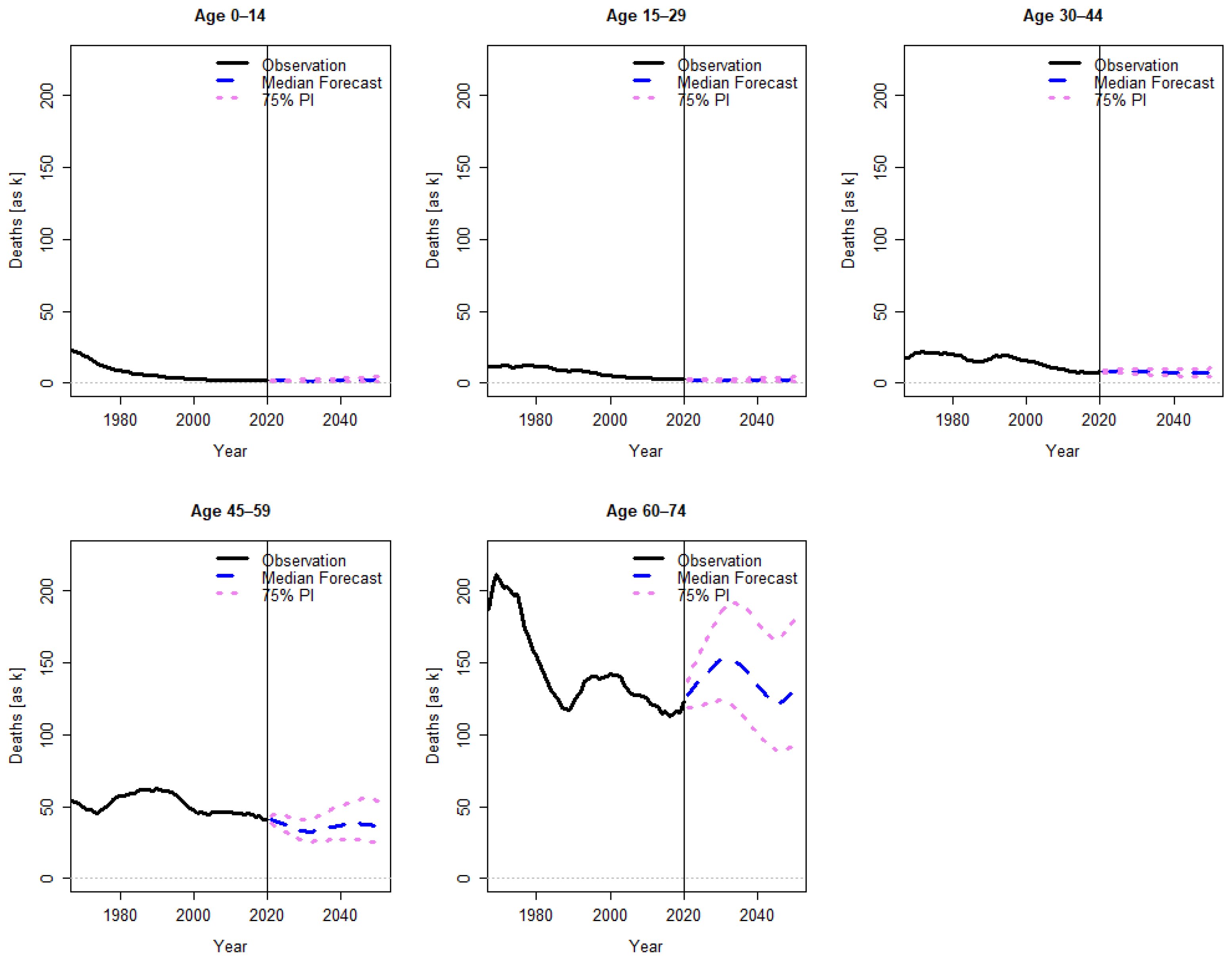
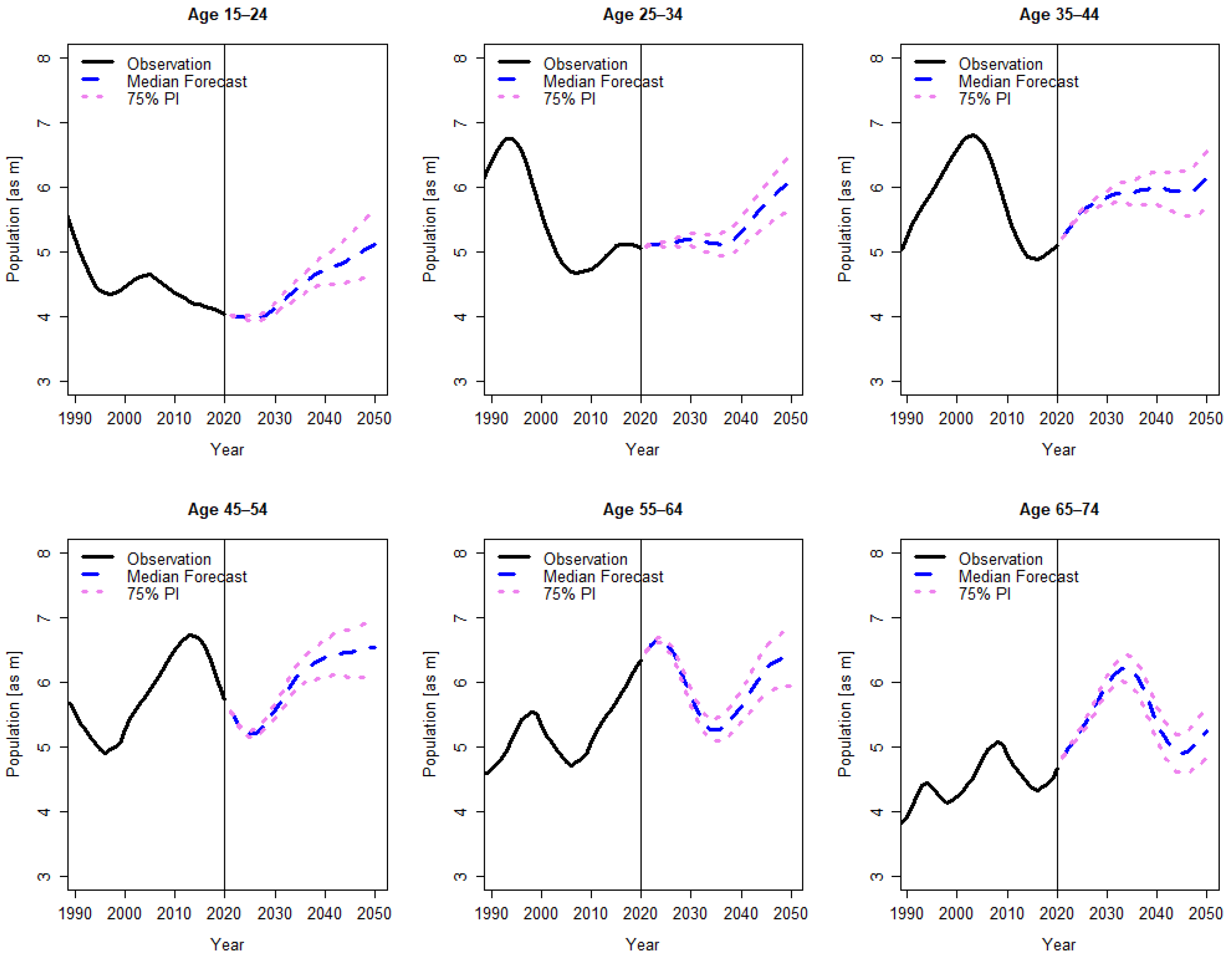
2.1. Stochastic Population Forecast
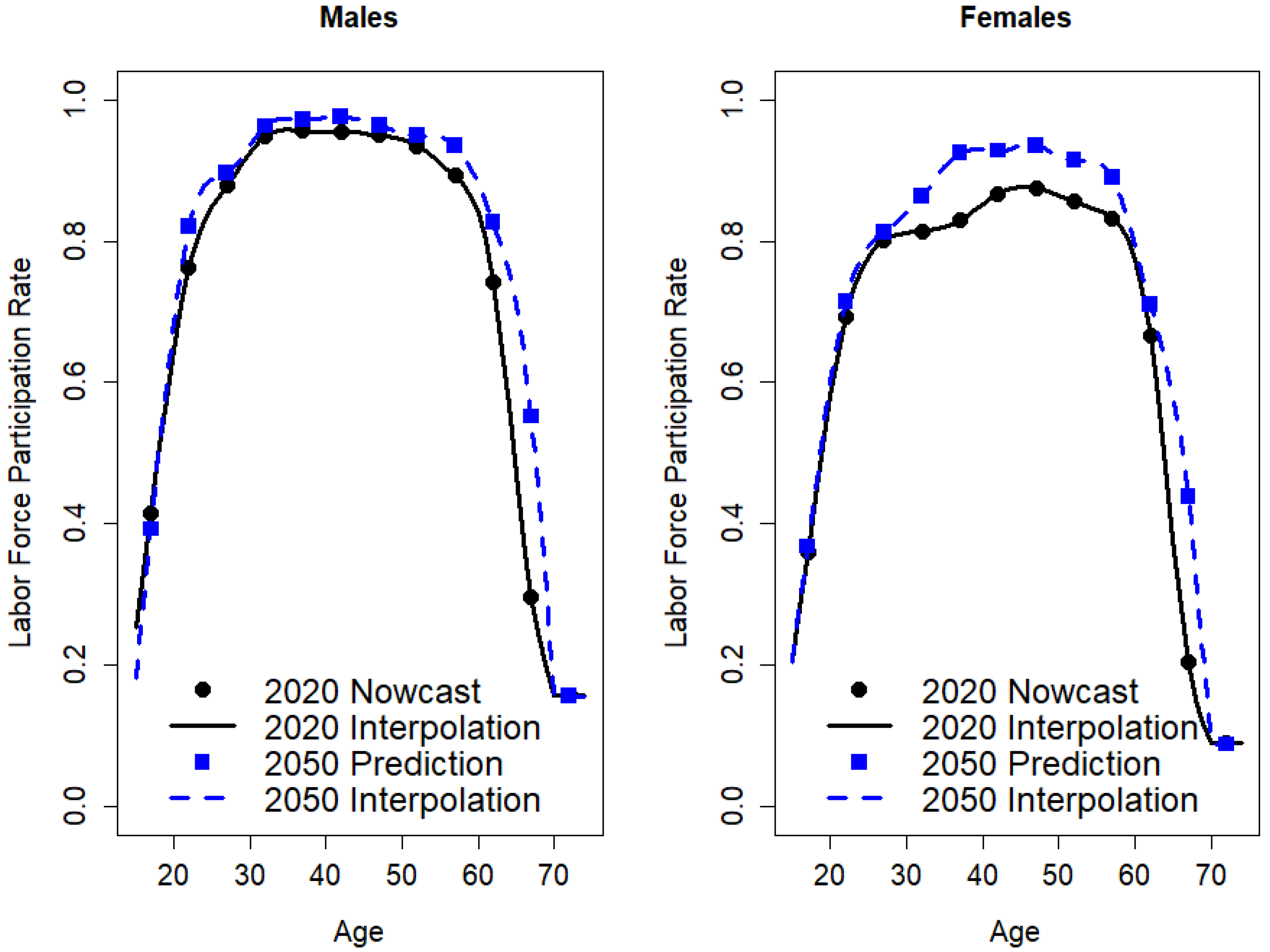
2.2. Projection of Labor Force Participation in the Context of Increasing Retirement Ages
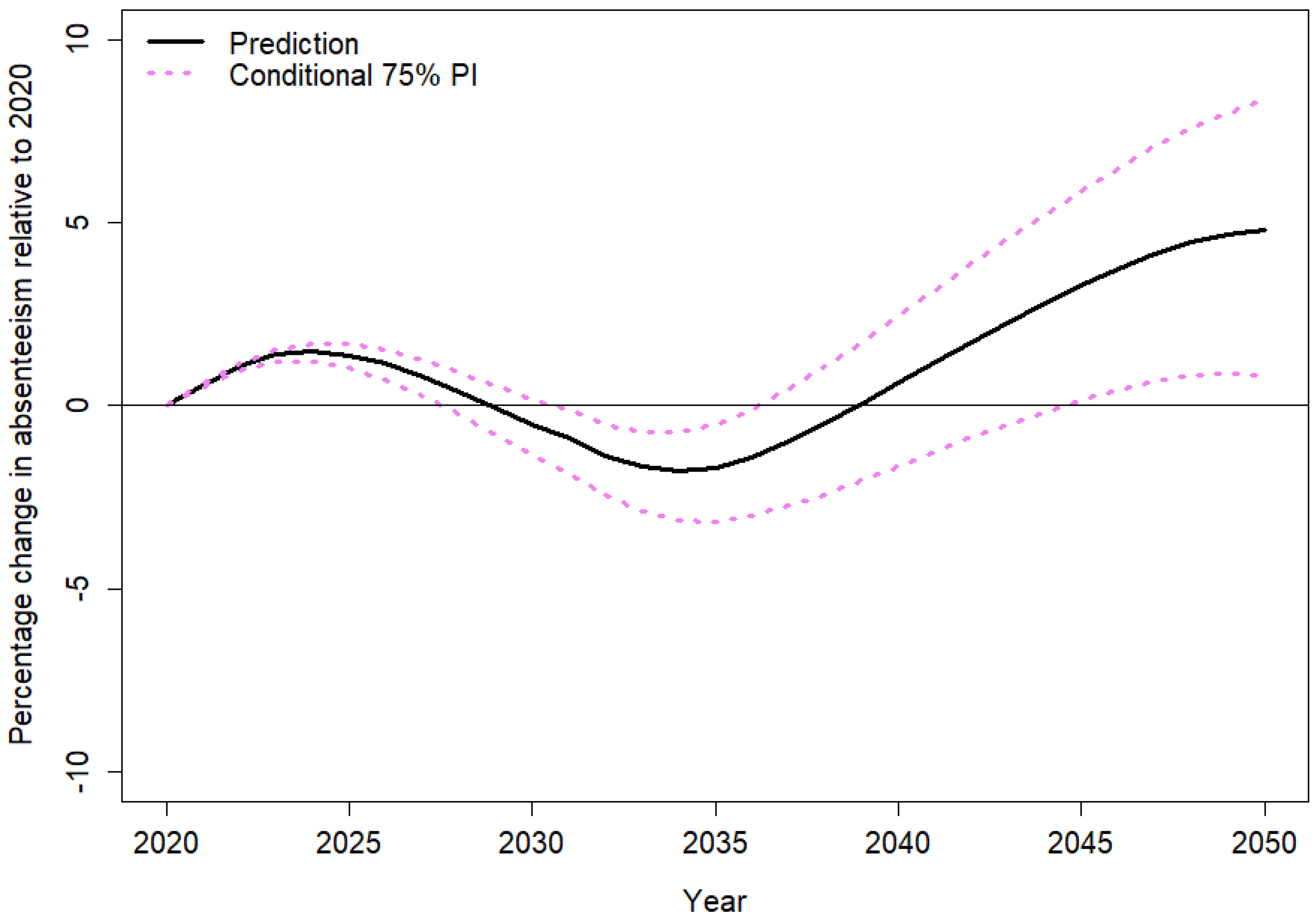
2.3. Projection of Relative Increase in Absenteeism Given Demographic and Economic Trends
2.4. Projection of Relative Increase in Economic Costs by Absenteeism Trends
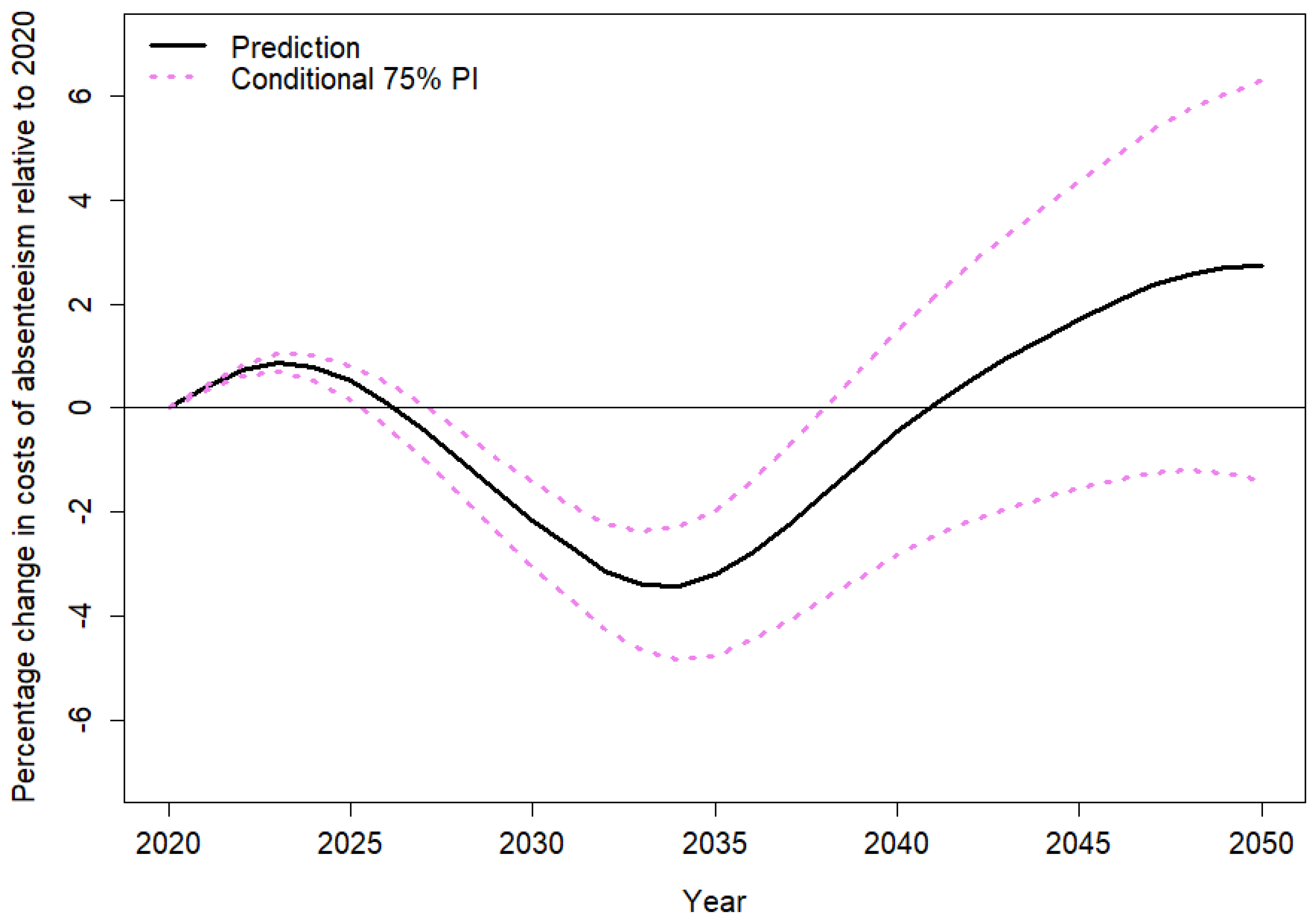
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Further Results

References
- Eurostat. Population Structure Indicators at National Level. Available online: https://ec.europa.eu/eurostat/databrowser/view/DEMO_PJANIND__custom_2133469/default/table?lang=en (accessed on 21 February 2022).
- Statistics Japan. Statistical Handbook of Japan 2021; Ministry of Internal Affairs and Communications Japan, Statistics Bureau: Tokyo, Japan, 2021.
- Fuchs, J.; Sohnlein, D.; Weber, B.; Weber, E. Stochastic Forecasting of Labor Supply and Population: An Integrated Model. Popul. Res. Policy Rev. 2018, 37, 33–58. [Google Scholar] [CrossRef] [PubMed]
- European Union. The 2021 Ageing Report: Economic & Budgetary Projections for the EU Member States (2019–2070); Publications Office of the European Union: Luxembourg, 2021. [Google Scholar] [CrossRef]
- Destatis. Lebendgeborene: Deutschland, Jahre, Geschlecht. Available online: https://www-genesis.destatis.de/genesis/ (accessed on 13 December 2021).
- Vanella, P.; Rodriguez Gonzalez, M.A.; Wilke, C.B. Population Ageing and Future Demand for Old-Age and Disability Pensions in Germany—A Probabilistic Approach. Comp. Popul. Stud. 2022, 47. [Google Scholar] [CrossRef]
- Vanella, P.; Deschermeier, P. A Probabilistic Cohort-Component Model for Population Forecasting—The Case of Germany. J. Popul. Ageing 2020, 13, 513–545. [Google Scholar] [CrossRef]
- Hedges, J.N. Absence from work—A look at some national data. Mon. Labor Rev. 1973, 96, 24–30. [Google Scholar]
- Lusinyan, L.; Bonato, L. Work Absence in Europe. IMF Staff Pap. 2007, 54, 475–538. [Google Scholar] [CrossRef]
- Vanella, P.; Deschermeier, P.; Wilke, C.B. An Overview of Population Projections—Methodological Concepts, International Data Availability, and Use Cases. Forecasting 2020, 2, 346–363. [Google Scholar] [CrossRef]
- Msosa, S.K. A Comparative Trend Analysis of Changes in Teacher Rate of Absenteeism in South Africa. Educ. Sci. 2020, 10, 189. [Google Scholar] [CrossRef]
- Plati, C.; Lanara, V.A.; Katostaras, T.; Mantas, J. Nursing Absenteeism—One Determining Factor for the Staffing Plan. Scand. J. Caring Sci. 1994, 8, 143–148. [Google Scholar] [CrossRef]
- Vanella, P.; Heß, M.; Wilke, C.B. A probabilistic projection of beneficiaries of long-term care insurance in Germany by severity of disability. Qual. Quant. Int. J. Methodol. 2020, 54, 943–974. [Google Scholar] [CrossRef]
- Eurostat. Absence from Work by Main Reason, Sex and Age Group (2006–2020)—Quarterly Data. Available online: https://ec.europa.eu/eurostat/databrowser/view/LFSI_ABS_Q_H__custom_2136298/default/table?lang=en (accessed on 21 February 2022).
- BMAS; BAuA. Sicherheit und Gesundheit bei der Arbeit—Berichtsjahr 2019. Unfallverhütungsbericht Arbeit; BMAS: Paderborn, Germany, 2020. [Google Scholar] [CrossRef]
- Vanella, P.; Deschermeier, P. A Principal Component Simulation of Age-Specific Fertility—Impacts of Family and Social Policy on Reproductive Behavior in Germany. Popul. Rev. 2019, 58, 78–109. [Google Scholar] [CrossRef]
- Vanella, P. A principal component model for forecasting age- and sex-specific survival probabilities in Western Europe. Z. Für Die Gesamte Versicher. (Ger. J. Risk Insur.) 2017, 106, 539–554. [Google Scholar] [CrossRef]
- Wilke, C.B. Volkswirtschaftliche Kosten von Fehlzeiten in einer alternden Gesellschaft. In Zur Relevanz von Bevölkerungsvorausberechnungen für Arbeitsmarkt-, Bildungs- und Regionalpolitik; Deschermeier, P., Fuchs, J., Iwanow, I., Wilke, C.B., Eds.; wbv: Bielefeld, Germany, 2020; pp. 118–139. Available online: https://www.iab.de/651/section.aspx/Publikation/K201014FKE (accessed on 20 January 2022).
- Fuchs, J.; Söhnlein, D.; Vanella, P. Migration Forecasting—Significance and Approaches. Encyclopedia 2021, 1, 689–709. [Google Scholar] [CrossRef]
- Lima, E.; Vieira, T.; de Barros Costa, E. Evaluating deep models for absenteeism prediction of public security agents. Appl. Soft Comput. 2020, 91, 106236. [Google Scholar] [CrossRef]
- Markham, S.E.; Markham, I.S. Biometeorological effects on worker absenteeism. Int. J. Biometeorol. 2005, 49, 317–324. [Google Scholar] [CrossRef] [PubMed]
- van den Dool, H.M. Long-range weather forecasts through numerical and empirical methods. Dyn. Atmos. Ocean. 1994, 20, 247–270. [Google Scholar] [CrossRef]
- Jakovljević, M.; Malmose-Stapelfeldt, C.; Milovanović, O.; Rančić, N.; Bokonjić, D. Disability, Work Absenteeism, Sickness Benefits, and Cancer in Selected European OECD Countries-Forecasts to 2020. Front. Public Health 2017, 5, 23. [Google Scholar] [CrossRef][Green Version]
- BAuA. Arbeitswelt im Wandel: Zahlen-Daten—Fakten; BAuA Ed.: Dortmund, Germany, 2019. [Google Scholar] [CrossRef]
- Fuchs, J.; Söhnlein, D.; Weber, B. Projektion des Erwerbspersonenpotenzials bis 2060: Demografische Entwicklung lässt das Arbeitskräfteangebot stark schrumpfen. IAB-Kurzbericht 2021, 25, 1–12. Available online: https://doku.iab.de/kurzber/2021/kb2021-25.pdf (accessed on 22 December 2021).
- Vanella, P.; Hellwagner, T.; Deschermeier, P. Parsimonious Stochastic Forecasting of International and Internal Migration on the NUTS-3 level—An Outlook of Regional Depopulation Trends in Germany. In Proceedings of the Wittgenstein Centre Conference, Vienna, Austria, 1 December 2021; Available online: https://www.youtube.com/watch?v=QnLHKK4B0EQ (accessed on 20 January 2022).
- Destatis. Lebendgeborene nach dem Alter der Mütter—Insgesamt Alte Bundesländer 1960–1990; Destatis: Wiesbaden, Germany, 2015.
- Destatis. Lebendgeborene nach dem Alter der Mütter—Insgesamt Alte Bundesländer 1961–1989; Destatis: Wiesbaden, Germany, 2018.
- Destatis. Lebendgeborene nach dem Alter der Mütter—Neue Länder und Berlin-Ost. Berichtsjahr: 1990–2000; Destatis: Wiesbaden, Germany, 2018.
- Destatis. Lebendgeborene nach dem Alter der Mütter—Insgesamt Deutschland 1991–2013; Destatis: Wiesbaden, Germany, 2015.
- Destatis. Lebendgeborene: Deutschland, Jahre, Alter der Mutter, Geschlecht der Lebendgeborenen, Familienstand der Eltern; Destatis: Wiesbaden, Germany, 2021.
- Human Mortality Database. East Germany, Population Size (Abridged); University of California: Berkeley, CA, USA; Max Planck Institute for Demographic Research: Rostock, Germany; Available online: https://www.mortality.org/cgi-bin/hmd/country.php?cntr=DEUTE&level=1 (accessed on 17 December 2021).
- Human Mortality Database. Germany, Population Size (Abridged); University of California: Berkeley, CA, USA; Max Planck Institute for Demographic Research: Rostock, Germany; Available online: www.mortality.org (accessed on 17 December 2021).
- Human Mortality Database. West Germany, Population Size (Abridged); University of California: Berkeley, CA, USA; Max Planck Institute for Demographic Research: Rostock, Germany; Available online: https://www.mortality.org/cgi-bin/hmd/country.php?cntr=DEUTW&level=1 (accessed on 17 December 2021).
- Klüsener, S.; Grigoriev, P.; Scholz, R.D.; Jdanov, D.A. Adjusting Inter-censal Population Estimates for Germany 1987-2011: Approaches and Impact on Demographic Indicators. Comp. Popul. Stud. 2018, 43, 31–64. [Google Scholar] [CrossRef]
- Destatis. Bevölkerung am 31.12.2018-2020 nach Alters- und Geburtsjahren; Destatis: Wiesbaden, Germany, 2021.
- Vanella, P. Stochastic Forecasting of Demographic Components Based on Principal Component. Athens J. Sci. 2018, 5, 223–245. [Google Scholar] [CrossRef]
- Vanella, P.; Deschermeier, P.; Greil, A.L. Impacts of the COVID-19 Pandemic on International Fertility—A Stochastic Principal Component Approach. In Proceedings of the MPIDR—Pandemic Babies? The COVID-19 Pandemic and Its Impact on Fertility and Family Dynamics, Rostock, Germany, 14 December 2021; Available online: https://www.demogr.mpg.de/mediacms/16382_main_MPI2021_PV.pdf (accessed on 20 January 2022).
- Destatis. Wanderungen Zwischen Deutschland und dem Ausland 1991–1999 nach Einzelaltersjahren und Geschlecht; Destatis: Wiesbaden, Germany, 2015.
- Destatis. Wanderungen Zwischen Deutschland und dem Ausland: Deutschland, Jahre, Nationalität, Geschlecht, Altersjahre; Destatis: Wiesbaden, Germany, 2021.
- Destatis. Bevölkerung und Erwerbstätigkeit. Gestorbene nach Alters- und Geburtsjahren sowie Familienstand 1948 bis 2003; Destatis: Wiesbaden, Germany, 2016.
- Destatis. Gestorbene 2000–2020 nach Alters- und Geburtsjahren; Destatis: Wiesbaden, Germany, 2021.
- Fritsch, F.N.; Carlson, R.E. Monotone Piecewise Cubic Interpolation. SIAM J. Numer. Anal. 1980, 17, 238–246. [Google Scholar] [CrossRef]
- Kirk, A.; Stamatiadis, N. Crash Rates and Traffic Maneuvers of Younger Drivers. Transp. Res. Rec. J. Transp. Res. Board 2001, 1779, 68–74. [Google Scholar] [CrossRef]
- Beznoska, M.; Pimpertz, J.; Stockhausen, M. Führt eine Bürgerversicherung zu Mehr Solidarität? Eine Vermessung des Solidaritätsprinzips in der Gesetzlichen Krankenversicherung; IW-Analysen: Cologne, Germany, 2021; Volume 143, pp. 1–69. Available online: https://www.iwkoeln.de/studien/martin-beznoska-jochen-pimpertz-maximilian-stockhausen-eine-vermessung-des-solidaritaetsprinzips-in-der-gesetzlichen-krankenversicherung.html (accessed on 17 December 2021).
- Leinert, J. Morbidität als Selektionskriterium. In Fairer Wettbewerb oder Risikoselektion? Analysen zur Gesetzlichen und Privaten Krankenversicherung; Jacobs, K., Klauber, J., Leinert, J., Eds.; Wissenschaftliches Institut der AOK: Bonn, Germany, 2006; pp. 67–76. [Google Scholar]
- Graf von der Schulenburg, J.M.; Lohse, U. Versicherungsökonomik: Ein Leitfaden für Studium und Praxis; Verlag Versicherungswirtschaft: Karlsruhe, Germany, 2014; Volume 2. [Google Scholar]
- Stauder, J.; Kossow, T. Selektion oder bessere Leistungen—Warum sind Privatversicherte gesünder als gesetzlich Versicherte? Gesundheitswesen 2017, 79, 181–187. [Google Scholar] [CrossRef] [PubMed]
- Singh-Manoux, A.; Gueguen, A.; Ferrie, J.; Shipley, M.; Martikainen, P.; Bonenfant, S.; Goldberg, M.; Marmot, M. Gender differences in the association between morbidity and mortality among middle-aged men and women. Am. J. Public Health 2008, 98, 2251–2257. [Google Scholar] [CrossRef] [PubMed]
- Destatis. Studienanfängerquote (Hochschulzugangsberechtigung): Deutschland, Jahre, Geschlecht; Destatis: Wiesbaden, Germany, 2021.
- Fries, J.F. Aging, Natural Death, and the Compression of Morbidity. N. Engl. J. Med. 1980, 303, 130–135. [Google Scholar] [CrossRef]
- Gruenberg, E.M. The Failures of Success. Milbank Q. 2005, 83, 779–800. [Google Scholar] [CrossRef]
- Vanella, P.; Basellini, U.; Lange, B. Assessing excess mortality in times of pandemics based on principal component analysis of weekly mortality data-the case of COVID-19. Genus J. Popul. Sci. 2021, 77, 16. [Google Scholar] [CrossRef]
- Vanella, P.; Wiessner, C.; Holz, A.; Krause, G.; Möhl, A.; Wiegel, S.; Lange, B.; Becher, H. Pitfalls and solutions in case fatality risk estimation—A multi-country analysis on the effects of demographics, surveillance, time lags between case reports and deaths and healthcare system capacity on COVID-19 CFR estimates. Vienna Yearb. Popul. Res. 2022, 20, 1–17. [Google Scholar] [CrossRef]
- Klinger, S.; Fuchs, J. Country report: Germany. In Effects of Population Changes in the Labour Market: An Analysis of Six European Countries; Räisänen, H., Maunu, T., Eds.; Ministry of Economic Affairs and Employment: Helsinki, Finland, 2019; Volume 59, pp. 54–66. [Google Scholar]
- Khailaie, S.; Mitra, T.; Bandyopadhyay, A.; Schips, M.; Mascheroni, P.; Vanella, P.; Lange, B.; Binder, S.C.; Meyer-Hermann, M. Development of the reproduction number from coronavirus SARS-CoV-2 case data in Germany and implications for political measures. BMC Med. 2021, 19, 32. [Google Scholar] [CrossRef]
- Bauer, A.; Weber, E. COVID-19: How much unemployment was caused by the shutdown in Germany? Appl. Econ. Lett. 2020, 28, 1053–1058. [Google Scholar] [CrossRef]
- ILO. Country Profiles: The latest Decent Work Statistics by Country. Available online: https://ilostat.ilo.org/data/country-profiles (accessed on 4 March 2022).

| Age Group | Annual Cases per Capita | Average Days per Case | Average Annual Days per Capita |
|---|---|---|---|
| 15–19 | 2.57 | 5 | 12.85 |
| 20–24 | 2.1 | 6 | 12.6 |
| 25–29 | 1.65 | 8 | 13.2 |
| 30–34 | 1.6 | 9 | 14.4 |
| 35–39 | 1.6 | 10 | 16 |
| 40–44 | 1.53 | 11 | 16.83 |
| 45–49 | 1.48 | 13 | 19.24 |
| 50–54 | 1.53 | 15 | 22.95 |
| 55–59 | 1.65 | 17 | 28.05 |
| 60–64 | 1.74 | 21 | 36.54 |
| 65+ | 0.71 | 23 | 16.33 |
| Age Group | Average Gross Income [as €] | Loss of Productivity by Day [as €] |
|---|---|---|
| 20–24 | 21,246 | 58.21 |
| 25–29 | 31,790 | 87.10 |
| 30–34 | 39,826 | 109.11 |
| 35–39 | 43,083 | 118.04 |
| 40–44 | 45,610 | 124.96 |
| 45–49 | 46,075 | 126.23 |
| 50–54 | 45,972 | 125.95 |
| 55–59 | 43,689 | 119.70 |
| 60–64 | 40,853 | 111.93 |
| 65–69 | 16,233 | 44.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vanella, P.; Wilke, C.B.; Söhnlein, D. Prevalence and Economic Costs of Absenteeism in an Aging Population—A Quasi-Stochastic Projection for Germany. Forecasting 2022, 4, 371-393. https://doi.org/10.3390/forecast4010021
Vanella P, Wilke CB, Söhnlein D. Prevalence and Economic Costs of Absenteeism in an Aging Population—A Quasi-Stochastic Projection for Germany. Forecasting. 2022; 4(1):371-393. https://doi.org/10.3390/forecast4010021
Chicago/Turabian StyleVanella, Patrizio, Christina Benita Wilke, and Doris Söhnlein. 2022. "Prevalence and Economic Costs of Absenteeism in an Aging Population—A Quasi-Stochastic Projection for Germany" Forecasting 4, no. 1: 371-393. https://doi.org/10.3390/forecast4010021
APA StyleVanella, P., Wilke, C. B., & Söhnlein, D. (2022). Prevalence and Economic Costs of Absenteeism in an Aging Population—A Quasi-Stochastic Projection for Germany. Forecasting, 4(1), 371-393. https://doi.org/10.3390/forecast4010021