1. Introduction
The expression
energy transition indicates a long-term structural change in energy systems [
1]. It is not a new phenomenon: man has made several energy transitions in his short history on Earth. One of the most significant was shifting to an energy system based on fossil fuels (coal, oil, and natural gas) from one essentially based on wood; however, since the 1980s, it has been realized that fossil fuels are at the root of climate change due to carbon emissions into the atmosphere [
2]. In short, rapid and deep reductions in greenhouse gas emission are needed to avoid the dangerous effects of climate change and guarantee energy security [
3,
4]. This transition is often referred to as the decarbonization of the energy sector and aims to shift the system to renewable energy technologies (RETs) by also implying a change from centralized to decentralized energy production. As pointed out in [
5], significant reductions can be achieved by using appropriate technologies and policies. Besides a move from fossil fuels to renewable sources, efficiency and savings in the use of energy are seen as complementary viable solutions. In sum, achieving a rapid global decarbonization critically depends on activating contagious and fast-spreading processes of social and technological change within the next few years [
6]. According to the International Renewable Energy Agency (IRENA) [
7], renewable sources and energy efficiency could potentially reduce carbon emissions from the energy sector by 90%.
With the term
renewable energy, we normally refer to all forms of energy present on the planet, whose availability is renewed indefinitely over time, unlike fossil fuels [
8]. Typical renewable sources available today are hydroelectric, wind, and solar energy, but there are also other sources like, e.g., bioenergy generated by the fermentation or combustion of organic mass (such as fertilizer or plants) and geothermal energy, based on heat coming out from Earth’s crust (for example, in the form of a geyser) [
9].
In the case of hydroelectric, wind, and solar power, the energy released is typically converted into electricity, although only 25% of electricity produced worldwide comes from renewables [
8]. Indeed, electrification of the energy system will be necessary to fully exploit the potential of renewables and get the energy transition off the ground [
10], and forecasting electricity consumption becomes critical for improving energy management and planning by supporting a large variety of optimization procedures. Today, there are significant signs that a regime shift is beginning to occur in many countries [
10]. A specific case, analyzed in this paper, is the regime shift in electricity production in Germany. Indeed, Germany has an ambitious plan to realize a transition to sustainable energy with a strong reliance on photovoltaic and wind power for electricity provision [
11]. This plan, called “Energiewende” (the German expression for energy transition), was expected to reach 35% of electricity production from renewable sources by 2020 and 80% by 2050. In this sense, the Energiewende is considered the world’s most extensive embrace of the wind and solar power [
12]. The legal tool behind the Energiewende is the Renewable Energy Act (EEG), promulgated by the German government in 2000. The EEG has favored an exceptional growth in wind and solar energy through the system of
feed-in tariffs [
13]. This mechanism guarantees a minimum purchase price of electricity produced from renewable sources. Three characteristics of German political and cultural history have certainly stimulated the transition: a progressive culture of the environment, legal tools to support RETs, and a historical reluctance towards nuclear energy [
14]. The technical aspects of the current energy scenario in Germany within the goals of the Energiewende program are analyzed for instance in [
15].
The paradigmatic example of energy transition in Germany may be analyzed focusing on the interdependencies between three energy sources for electricity production, namely coal, natural gas and renewables. Specifically, it is interesting to understand whether renewables have a sufficient competitive strength towards fossil fuels.
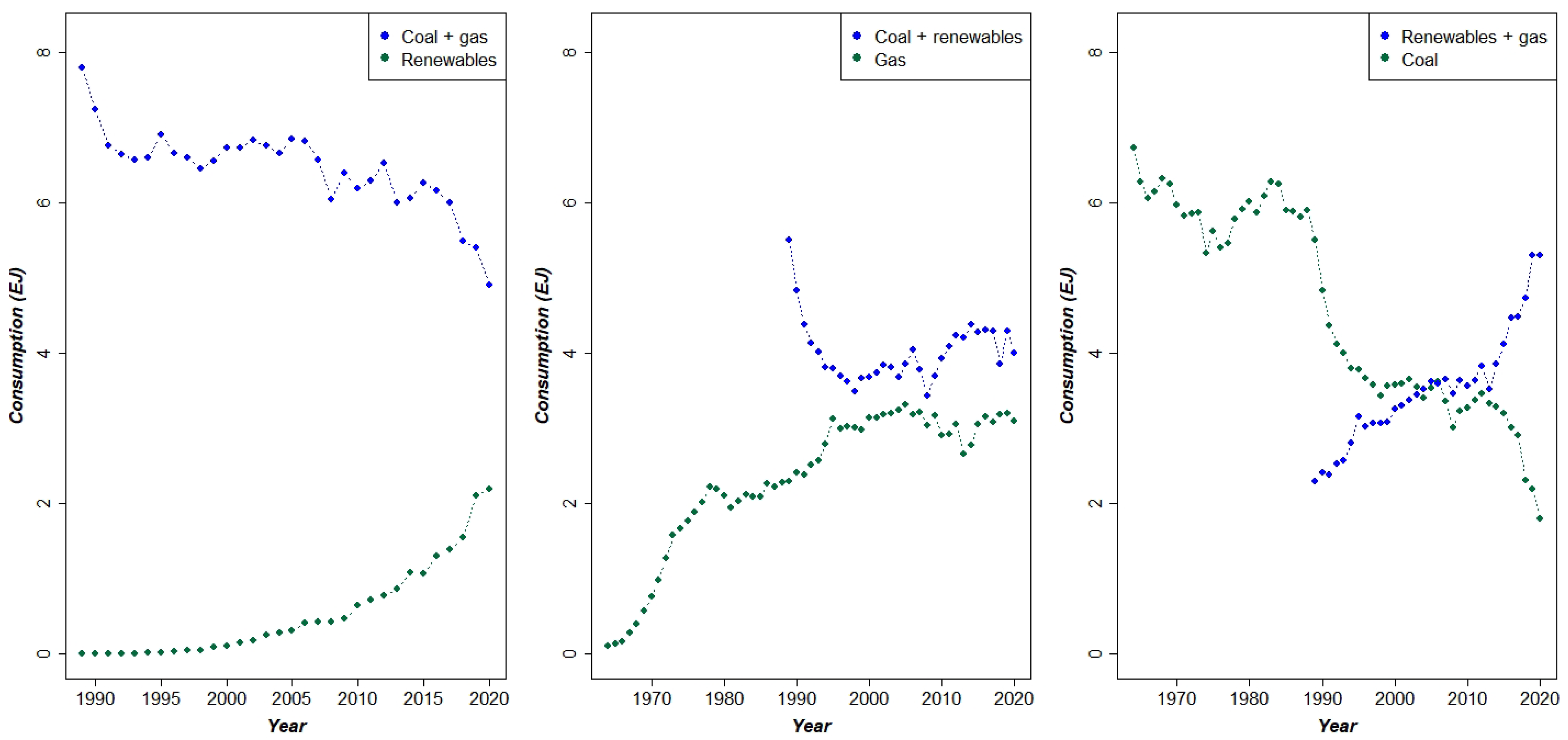
Figure 1 describes the yearly consumption time series in Exajoule (EJ) of coal and natural gas between 1964 and 2020 and of renewables (wind and solar jointly considered) from 1989 to 2020 (source: BP Statistical Review of World Energy [
16]). As may be easily observed, the time series of coal and gas are simultaneous, while renewables have obviously a more recent history. A possible competitive interplay between these series seems to be captured from the visual inspection of data, but the significance and nature of these effects needs to be tested with a suitable model.
A well-established stream of research has analyzed the temporal dynamics of energy sources by employing multivariate innovation diffusion models. In one pioneering contribution on the topic [
17], Marchetti defined energy sources as comparable to commercial products that compete for a market niche, so it is reasonable to analyze the process of adopting a new energy source through diffusion models. Grubler, in [
18], highlighted that energy demand and supply systems co-evolve, with technological innovations mutually enhancing each other.
Within the literature produced in the field, in recent times, several contributions have applied bivariate innovation diffusion models to energy contexts, in order to understand the complex dynamics within energy systems: see for instance [
1], where the case of Germany is analyzed with reference to the competitive relationship between nuclear power and RETs, [
19], which studies the relationship between non-renewable and renewable energy sources in US, Europe, China and India, [
20], focusing on the case of energy transition in Australia by comparing the trends of coal, gas and renewables, and [
10], where bivariate innovation diffusion models are employed to investigate the specific role of gas in the electricity transition.
Grounding on this literature, this paper presents an analysis of the case of Germany, by proposing a multivariate innovation diffusion model, which considers the dynamic interplay between coal, gas and renewables. This model, which is based on a system of differential equations, is then represented within the system dynamics approach, through the Stock-Flow Network (SFN) tool. Such complementary description encourages a deeper understanding of the relationships within the energy market. The SFN representation aids understanding the complex feedback process acting in the system and creates a suitable environment for detecting, simulating and evaluating different policy scenarios able to speed up the renewable energy diffusion.
The rest of the paper is organized as follows.
Section 2 describes the two methodological approaches employed for model development, respectively based on ordinary differential equations (ODE) and system dynamics.
Section 3 describes the Unbalanced Competition among Three Technologies (UCTT) model through its ODE and system dynamics representation, while in
Section 4 the model is applied to the case of Germany’s energy transition, and a detailed discussion of the results is provided. Based on the results obtained, a simulation study is conducted in
Section 5.
Section 6 is left for concluding remarks.
Appendix A compares the UCTT model with the 3PM model proposed by [
21], while
Appendix B discusses some details on the UCTT model.
3. Materials and Methods
3.1. Model Definition with ODE
This section presents the structure of the model for three competitors, according to an ODE representation. The model structure is very similar to the 3PM model proposed by [
21], but also presents some crucial differences. A comparison between the two models to underline similarities and differences is illustrated in
Appendix A.
Given its peculiar features, the model has been called Unbalanced Competition for Three Technologies (UCTT). The UCTT is characterized by two phases: the first one, called competition phase, where two technologies enter the market at the same time and interact with each other, and the second one, called double-competition phase, where the third competitor enters the market and competes against the previous two.
The market potential , which is the maximum level of consumption in that market for the analyzed technologies, takes two different sizes: , the global market potential under the competition phase, and , the global market potential under the double-competition phase. The model assumes a residual market as a common target for each competitor, with denoting common cumulative consumption and , indicating the cumulative consumption of technology i. The common factor corresponds to the residual market share achieved at time t. The model is a system of differential equations where , , and represent instantaneous consumption of the first, of the second, and of the third technology respectively. The third competitor enters the market at time , with , creating the two different phases. The indicator function assumes a value equal to one when the event A occurs or zero otherwise.
Parameters of the UCTT are summarized in
Table 1, by making a distinction between the
competition phase and the
double-competition phase. Parameters referred to as the
competition phase are indicated with the subscript “
c”, while those referred to as the
double-competition phase are indicated with the subscript “
d”.
The system outlines the interaction among the three technologies that could result in competition or collaboration. Each phase is characterized by new parameters referred to both the internal and cross-influence for each technology. The internal growth is described through the
seed coefficient (see
Table 1), which represents the initial dissemination of the technology, and the
internal-influence coefficient (see
Table 1), which modulates the technology-specific growth after the innovation phase. Interaction between competitors is outlined through the
cross-influence coefficient (see
Table 1), which measures the effect of the competitors on the consumption of the considered technology in terms of positive or negative influence. Specifically, under the
double-competition phase, the
cross-influence coefficients describe the two competitors’ effect on a technology. In this case, an assumption is made: that two competitors have the same influence on the third technology (this is a simplifying assumption because it assumes the same effect for two competitors over the third). A negative
cross-influence coefficient implies a dynamic of
competition, while a positive one expresses a mutualistic relationship, termed
collaboration.
3.2. Model Definition with System Dynamics
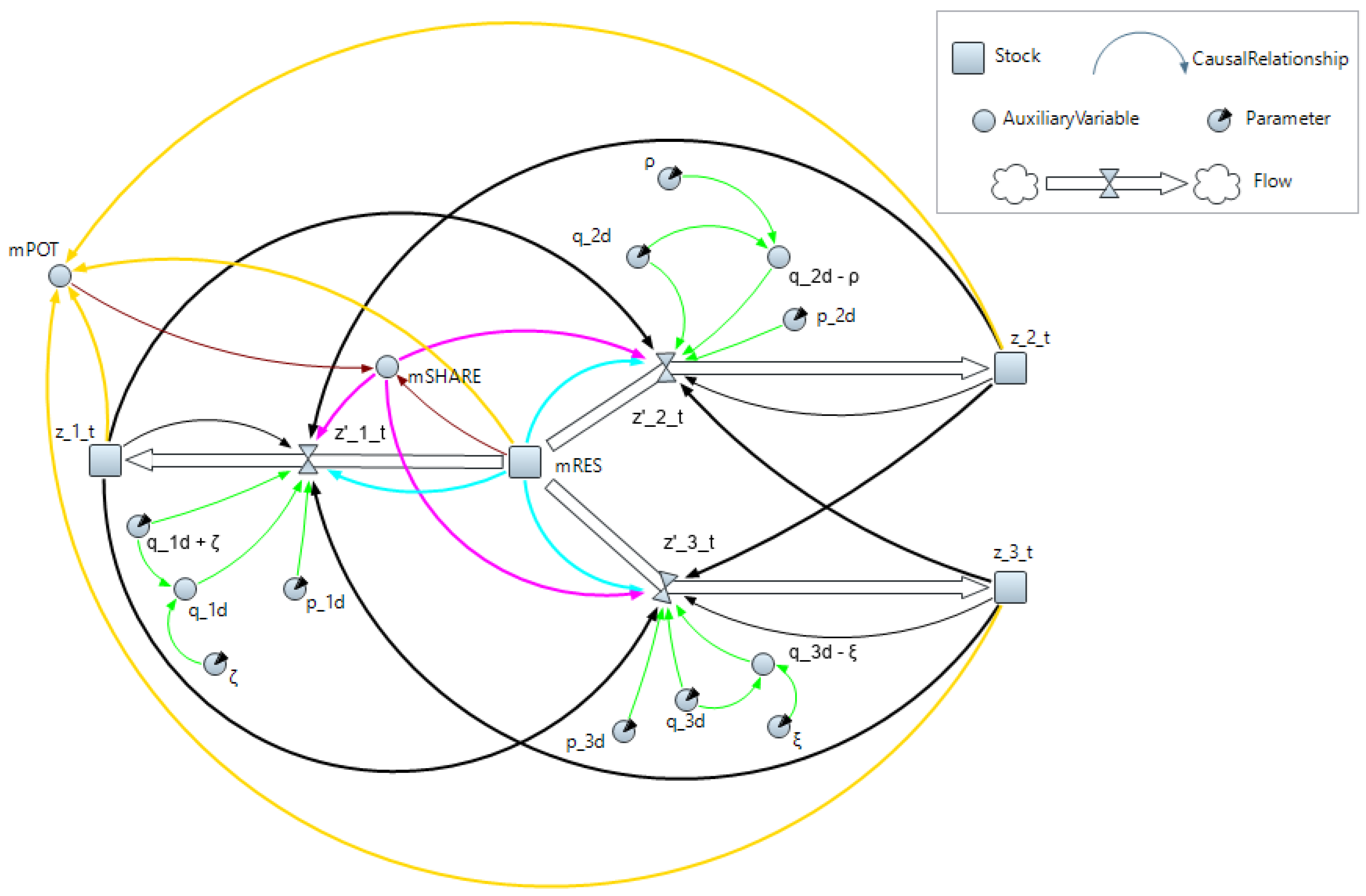
The ODE-based UCTT model may be defined through a System Dynamics approach, with a special focus on the
double-competition phase, where all the technologies exist in the market. This representation allows us to describe how different system variables are interconnected in feedback structures. In particular, this model has been described as a SFN model and it is reported in
Figure 2 (as drawn in its implementation through the simulation software AnyLogic [
47]).
The SFN approach allows defining the presence of cause–effect relationships identifying different types of variables: stocks represent state variables that accumulate or deplete over time and thus have a certain level (or state) at a given time; flows are the variables that alter the stocks and detect their variation per time unit; lastly, some auxiliary variables help improve the system readability making the functions that determine the flows’ structure more explicit [
37].
The system has four stock variables: the residual market, , and the three cumulative consumption flows, , connected by causal links (the flows). These three flows, , represent the instantaneous consumption variables. The flows’ presence explicitly indicates cause–effect relationships that lead to feedback effects, which could be a balancing or reinforcing feedback effect based on the specific case study data. Moreover, several auxiliary variables help to refine the system and are defined as follows. The residual market share, , which influences the instantaneous consumption variables, is determined by the ratio between the residual market, , and the market potential, . The market potential is given by the sum between the residual market and the cumulative consumption of the three technologies, . The cross-influence of each technology is calculated as the difference between its own internal-influence coefficient and the respective parameter, , , . The value of these parameters will be founded on the results of the UCTT model estimation through Nonlinear Least Squares (NLS).
In this way, after identifying the stock and flow system variables, an SFN can be translated into differential equations [
37]. Therefore, what distinguishes these models from many other dynamic models is the specification of the equations that outline the modeling process. All non-trivial models with high order and many non-linearities cannot be solved analytically, but numerical integration methods solve the differential equations. SFN models are generally formulated as high-order, non-linear systems translated into stochastic differential equations.
The equations describing the stock variables and the evolution of the system in quantitative terms are:
The residual market is depleted by the flows that represent the instantaneous consumption of each technology; meanwhile, these flows, that increase the stocks of the cumulative consumption, are characterized by three differential equations that recall the definitions in Equation (
1):
4. Model Application and Results
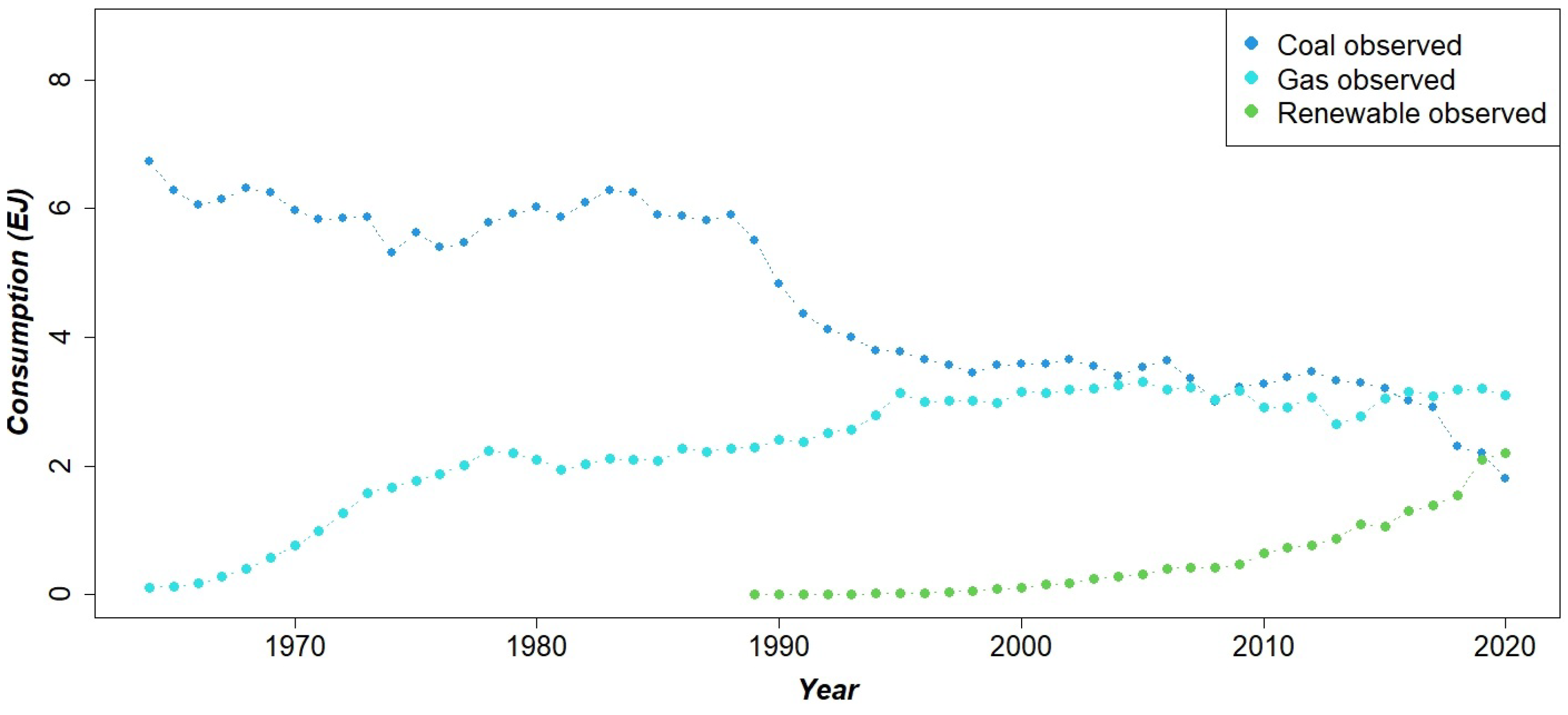
This section presents the results of the UCTT model to the yearly time series of consumption of coal, gas and renewables (solar and wind) in Germany (
Figure 1). The UCTT allows to statistically test the nature and significance of interactions between these three energy sources. The estimates obtained are then employed in the SFN, in order to detect reinforcing and balancing feedback loops and to structure and implement the simulation study.
4.1. UCTT Model Application
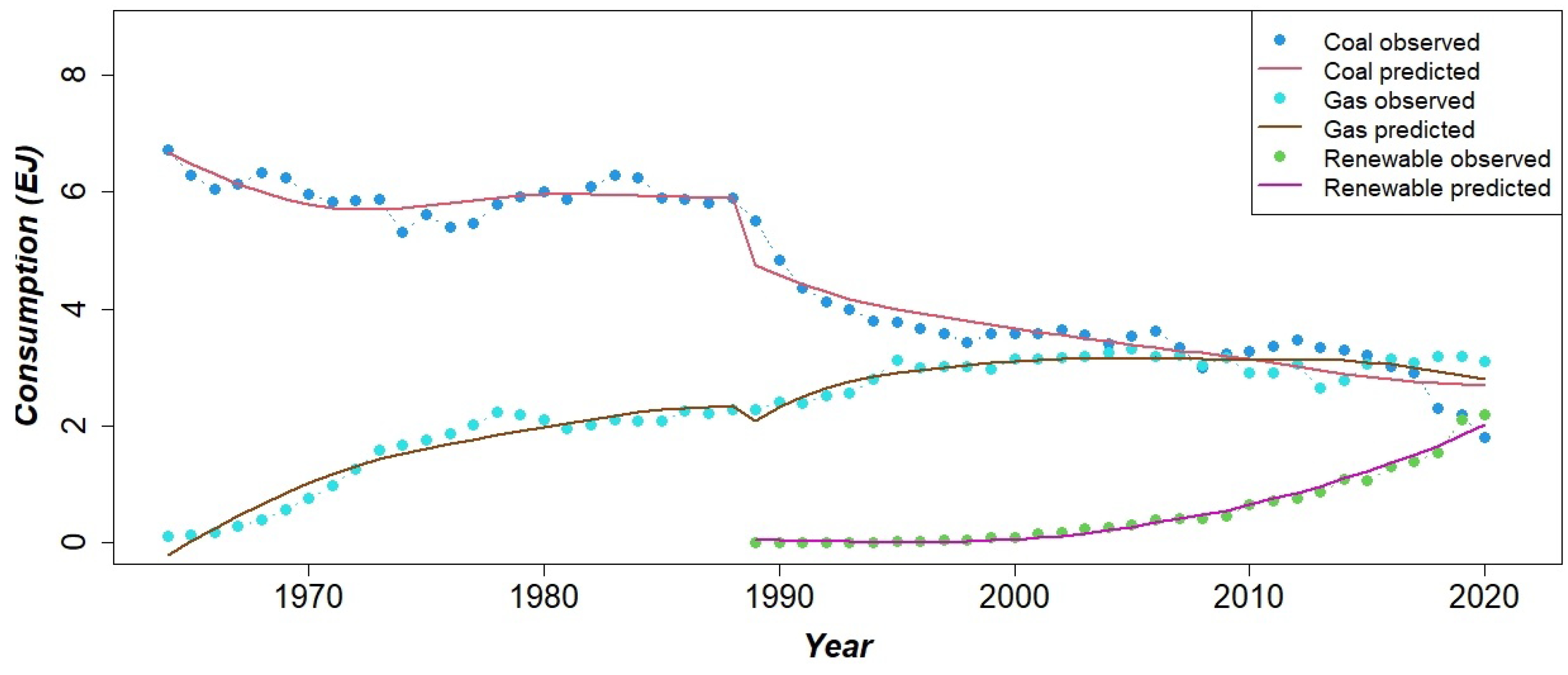
This section describes the application of the UCTT model. The model fitting is illustrated in
Figure 3.
The model obtained a satisfactory result in terms of
goodness-of-fit (
) and significance of parameters as a general outcome. Parameter estimates are outlined in
Table 2. As may be observed, despite some slight instabilities in some parameters concerning the
double-competition phase, namely
,
and
, the model is well identified and the relationships between the three competitors take a clear meaning. A visual inspection of
Figure 3 allows us to appreciate the ability of the model to account for these patterns: renewables exhibit an initial exponential consumption trend that seems to be affecting coal and natural gas trajectories, outlining the decarbonization process. Coal consumption is in a clear decline phase: after an initial period of stability, a sharp decline is evident around the early 1990s; in particular, this is the crucial moment when renewables entered the market. The curve for natural gas also has a particular shape: during the first phase, where it is competing with coal, its consumption is increasing, while it has a more stable structure, around a value of 3 EJ, after the introduction of renewables in the market.
The model allows identifying the main result in terms of “competition-collaboration”, by interpreting the
cross-influence coefficients. These parameter estimates, concerning the
double-competition phase, when coal, gas and renewables are all in the market, are reported in
Table 3.
Analyzing the double-competition phase, the seed coefficients, , and present low values; in particular, for renewables, the weak and not significant value of parameter reflects the initial difficulty of these technologies in entering the market and the subsequent need of incentives to stimulate their initial growth.
After the innovation phase, renewables have been experiencing a strong internal growth, as testified by the high value of the internal-influence coefficient, . At the same time, the corresponding estimates for coal and natural gas are negative and relatively weak, , , which is coherent with the declining trend of both series. Specifically, the internal-influence parameter for gas is not significant, a reasonable outcome given its stable trend in this phase.
Regarding the interplay between the three technologies, the cross-influence coefficients help interpret how the three technologies interplay. Coal and natural gas are characterized by a positive cross-influence effect, i.e., and , which highlights that the competitors collaborate with coal and gas; in particular, renewables do not seem to be able to exert a sufficiently strong competitive power. In contrast, renewables are characterized by a negative, but weak, cross-influence parameter, , which shows that coal and natural gas compete with the new entrant technologies, trying to limit their expansion. However, it should be remarked that renewables are characterized by a strong and rapid growth, as already noticed from the value of the internal-influence parameter, .
A similar result concerning renewables was evidenced in [
1], where the interplay between nuclear and renewables was studied through the UCRCD model. The UCRCD model made it possible to uncover the direct relationship between the nuclear and renewables in terms of internal and cross influence. Specifically, the authors found that renewables exerted a significant and measurable effect in determining the observed decline of nuclear power consumption.
The UCTT model deals with a more complex case, where the action of three energy sources is considered.
4.2. UCTT—SFN Model Application
Based on the estimates obtained, it is interesting to analyze the cause–effect interdependencies between the entities and recognize the feedback acting in the system. In particular, after assigning the estimated value found through the UCTT model (see
Table 2) to each entity of the SFN model in
Figure 2, balancing and reinforcing feedback may be captured. Coal, gas, and renewables are, respectively, referred to elements 1, 2, and 3 of
Figure 2. The relevant feedback loops of the SFN for the UCTT model for the German case are reported in
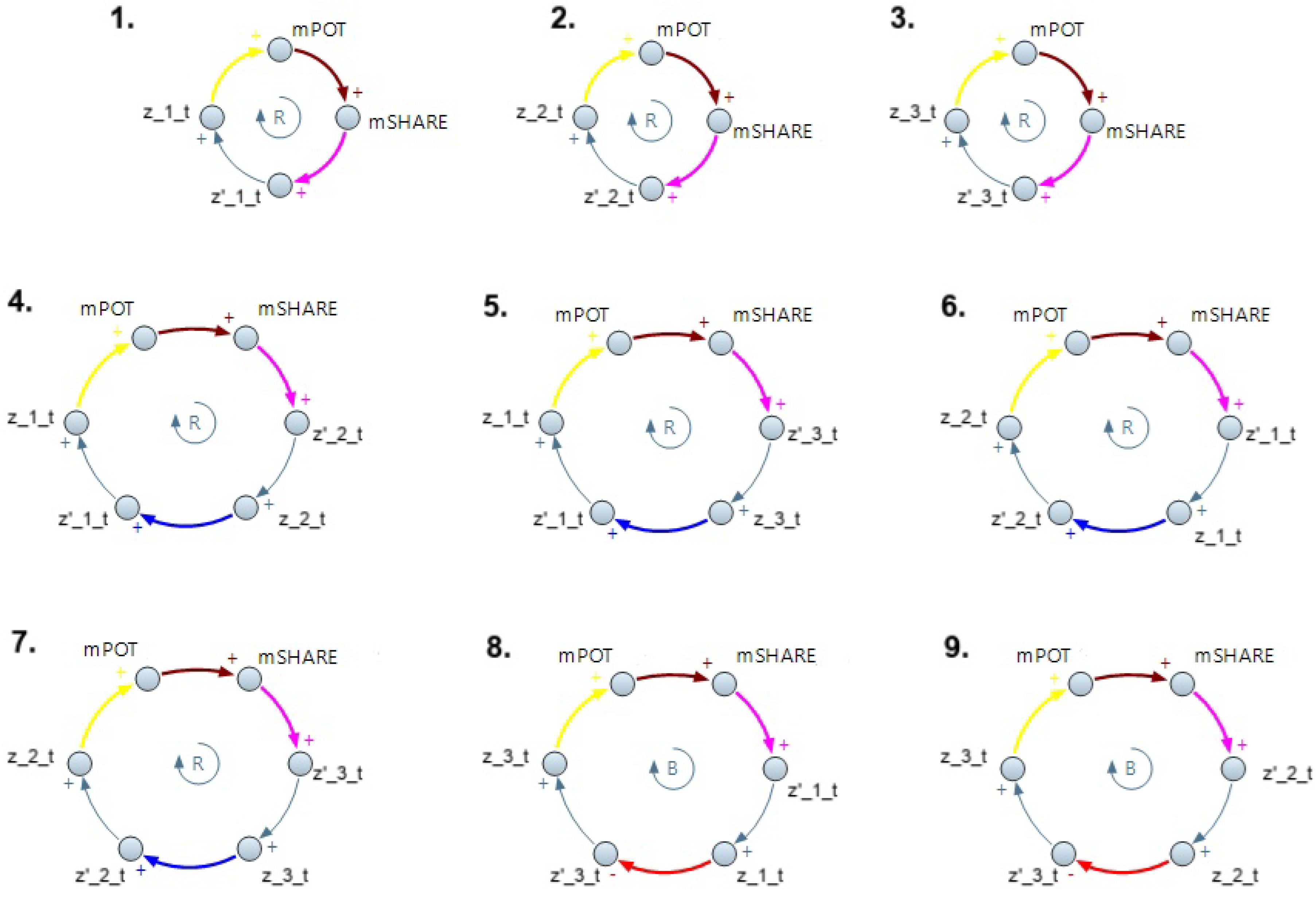
Figure 4. These elements will be essential to make dynamic hypotheses on the system evolution and identify where to take action to reinforce or balance specific tendencies.
The first three feedback loops describe each technology’s dynamic as reinforce feedback: an increase of the potential market generates an expansion of the market share, implying an increase of instantaneous consumption that elicits a push on effect-variable, i.e., the cumulative consumption, causing an increase in the market potential.
The following feedback loops are the ones that determine the interaction between the three energy sources. The most critical element is the connector that goes from the cumulative consumption of an energy source to the instantaneous consumption of the other technology (the connectors from z_i_t to z’_j_t, with
) representing the cross-influence, which defines the relationship between the two competitors. These connectors are colored in blue or red in
Figure 4 depending on the parameter estimates in
Table 2 and
Table 3: the blue link defines a positive cause–effect relationship, while the red one underlines the presence of a negative cause–effect relationship.
In this way, loops 4, 5, 6, 7 represent reinforcing feedback (highlighted with a “R” in the center) and explain how the instantaneous consumptions of coal and natural gas are affected positively by the competitors’ consumption in a cooperative manner. According to feedback loops 4 and 5, for example, an increase in natural gas and renewable energy consumption helps the consumption expansion of coal, and an increase in coal and renewable energy values “reinforces” the diffusion of natural gas. An increase in renewable energy consumption stimulates growth even in gas consumption and vice versa, due to the presence of the reinforcing feedback loop 7. We notice that the cross-influence connector that identifies a positive relationship of renewables over gas plays a key role in this loop.
The last two feedback loops, 8 and 9, present a red arrow that defines a competitive situation for renewable energy. These are balancing feedback loops (highlighted with a "B" in the centre) that point out how the other two technologies hold back the expansion of the renewable source. For example, balancing feedback loop 8 suggests that an increase in coal consumption may even cause renewables’ dampening. Furthermore, an increase in renewables consumption will affect coal consumption in turn, as a brake on this spread.
The initial value of the three stock variables, representing the cumulative consumption, is the first available value for each technology series in the double-competition phase (the value observed of yearly consumption in 1989). The initial value of the potential market is calculated by the difference between the
value in
Table 2 and the first values of the other three stocks. Furthermore, even the auxiliaries variables or parameters values are taken from
Table 2. After assigning each entity of this system the correctly estimated value, the SFN, implemented and run in AnyLogic [
47], allows us to simulate the double-competition phase case.
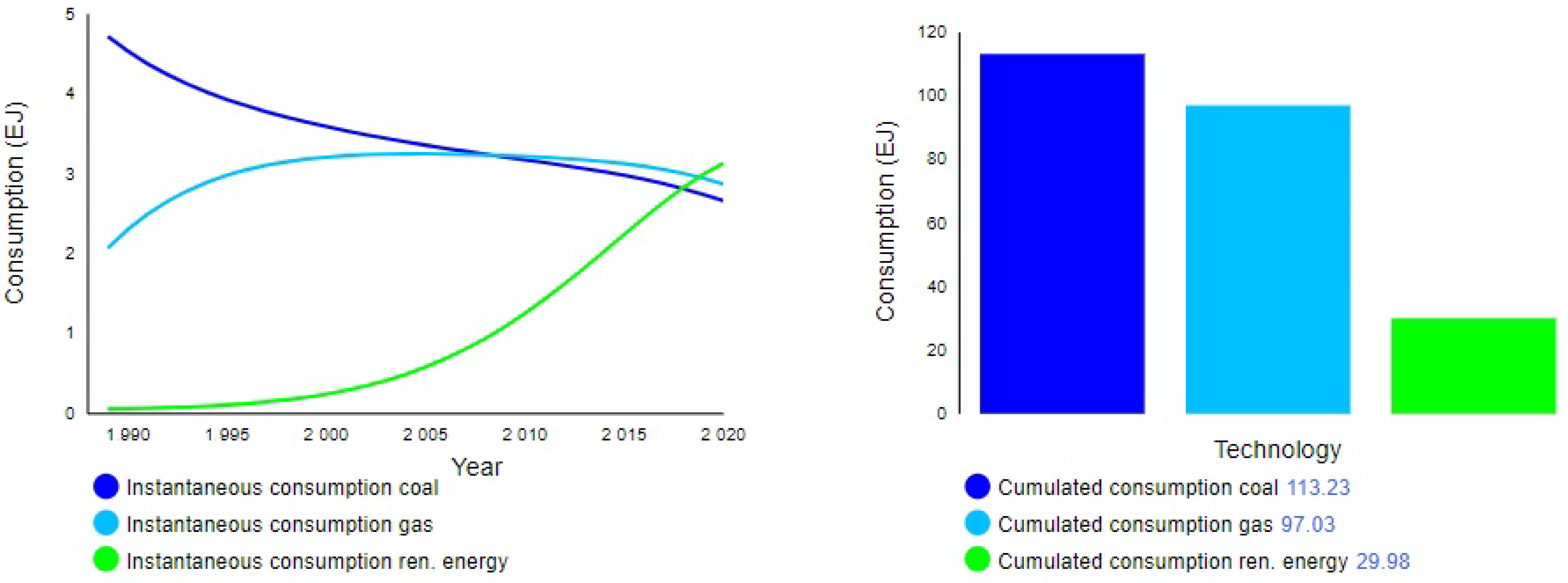
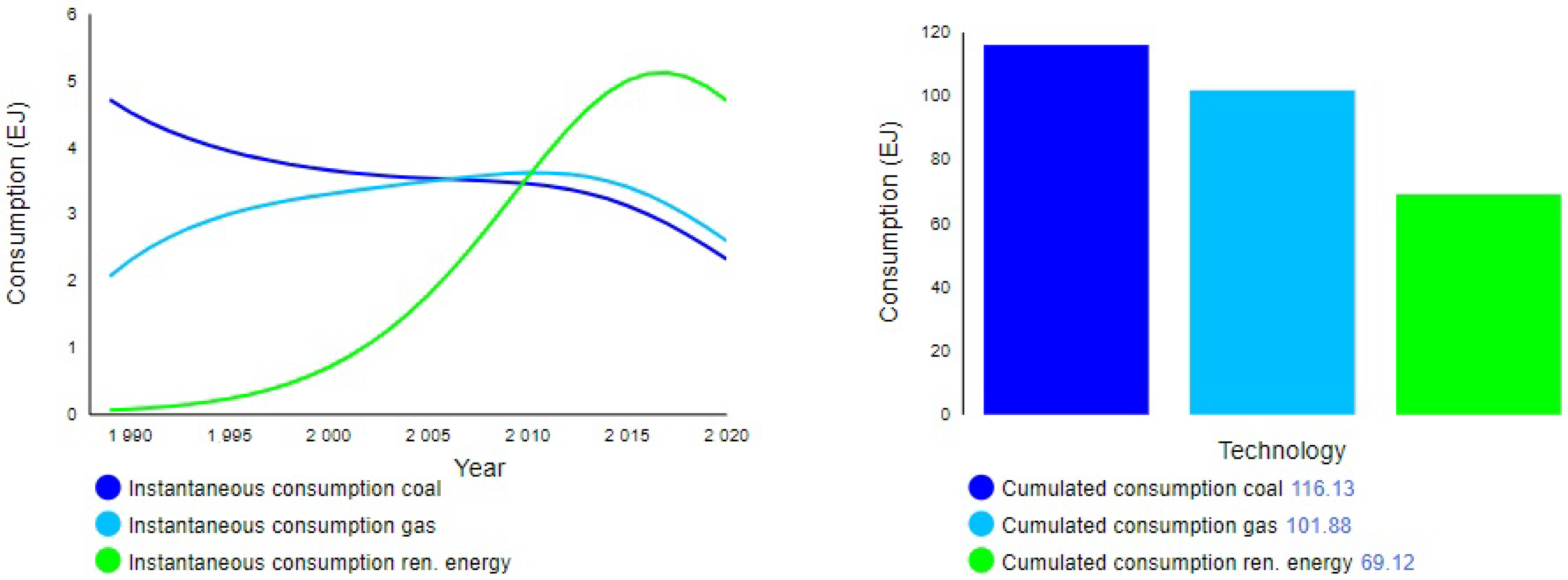
Figure 5 illustrates the trajectories of the instantaneous consumption of the three technologies. The curves on the time plot are very similar to the predicted ones in
Figure 3, since the differential equations that determine the instantaneous consumption are similar to those in System (1). In addition to the time plot, it is provided a bar chart that highlights the EJ cumulative consumption of each energy source: coal and natural gas dominate the market; however, renewable energy is spreading quickly.
6. Conclusions
Achieving sustainable, stable and secure energy systems is reaching the top of many countries’ agendas in recent years. Besides climate change problems, the COVID-19 pandemic, with the long periods of lockdowns imposed on populations, has strongly highlighted the critical importance of resilient and affordable electricity systems. Moreover, energy security is increasingly becoming a major issue. At the time of writing this paper, the world’s attention is focused on the terrible events occurring in Ukraine. While there is no certainty on how this situation will evolve in the future and the need to find a solution to the conflict is the priority, one point that has become clearer than ever, especially to European countries, is that energy independence from oil and gas is a primary objective in the short-term. The importance of an energy transition, by investing in renewables growth, has become central in the public discourse in the last few weeks.
In March 2022, right after the outbreak of war in Ukraine, the IEA provided a 10-point plan for the European Union, in order to reduce consumption of Russian gas and support the European Green Deal [
48]. One of the points foresees an acceleration in the deployment of new wind and solar projects. At the same time, the report clearly states that the process of cut imports of Russian gas will not be simple. Two major aspects will be crucial for a successful implementation according to [
48], (i) a concerted and sustained policy effort with a strong dialogue on energy market and security, and (ii) a clear communication between governments, industry and consumers.
The analysis conducted in this paper obviously does not consider these recent events, but it may provide a useful mean to describe and study, in a relatively simplified way, the dynamics occurring between these critical energy sources. We selected the paradigmatic case of Germany which, thanks to the Energiewende, is projected to become a low-carbon, nuclear-free energy system by the middle of the century [
15]. Focusing on the interdependencies between renewables and the most used sources for electricity production, gas and coal, the UCTT model indicated that renewables are strongly growing and sustained by a widespread belief of people towards sustainability objectives. This essentially confirms the findings of [
1]. On the other hand, the model suggested the presence of a significantly negative effect played by gas and coal on renewables, limiting their expansion, while there appeared to be a kind of “collaboration” between coal and gas, testified by the positive sign of the respective cross-influence parameters, giving rise to a lock-in situation [
10]. This is a different and more complex outcome with respect to that observed in [
1], where renewables were found to have a significantly negative strength on nuclear power. However, in [
1], it was also acknowledged that Germany was ready to implement policies to accelerate the regime shift favoring renewables at the expense of nuclear consumption well before the Fukushima disaster influence.
This stresses the essential role played by policies, helping Germany in realizing a cost-efficient, fair and sustainable path towards its very ambitious energy transition goals [
49]. The SFN approach yielded significant results both qualitatively and quantitatively. The most interesting qualitative result is the direct identification of further feedback compared to the ODE approach: the feedback loops of
Figure 4 allowed a preliminary contextual analysis of the cause–effect relationship acting in the system, the related feedback and interplay, as well as their role in determining the dynamic of the energy market. This analysis helps to identify the points where to act in order to reinforce or balance consumptions’ trends, and can be conveniently exploited for the preparation of policy scenarios. From a quantitative point of view, the SFN model allowed measuring the cause–effect relationships, which is the base for scenarios simulation. This aids evaluations on how possible changes could influence the consumptions trends. In this perspective, the results of the SFN model and the related simulation analysis may be a useful tool to study and forecast the technology trends in the following years, by analyzing different market scenarios based on well-defined policies. In our paper, the most important result deriving from the simulation exercise is the emphasis on the central role of social forces and demand dynamics in renewable energies adoption: both increasing renewable energy incentives and restricting coal and natural gas use would have accelerated the decarbonization in Germany and the energy transition towards renewable sources. Comparing
Figure 6 and
Figure 7, Policy 2 appears to be more promising and conducive to an expansion of renewables. The analysis of the SFN model suggests that this occurs because Policy 2 affects connectors representing causal relationships observed in many of the feedback loops compared to Policy 1.
A limitation of the analysis proposed in this paper is the lack of a forecasting exercise on future evolution of this market, with a specific attention to renewables. Indeed, forecasting the diffusion of renewables is critical for planning a suitable energy agenda and setting achievable targets in terms of electricity generation, although the available time series are typically short and pose some difficulty in modeling [
50]. A further development of this work should certainly try to employ the UCTT-SFN model for scenario building and forecasting, by also extending its application to a wide number of countries. This could offer a larger perspective on decarbonization and sustainability aims, by accounting for the uncertainties and perturbations to energy systems occurring in the upcoming years.