Bankruptcy Prediction: The Case of the Greek Market

Abstract

Financial bankruptcy prediction is an essential issue in emerging economies taking into consideration the economic upheaval that can be caused by business failures. The research on bankruptcy prediction is of the utmost importance as it aims to build statistical models that can distinguish healthy firms from financially distressed ones. This paper explores the applicability of the four most used approaches to predict financial bankruptcy using data concerning the case of Greece. A comparison of linear discriminant analysis, logit, decision trees and neural networks is performed. The results show that discriminant analysis is slightly superior to the other methods.

1. Introduction

Lately, one of the most unique and intense global health crises is leading to an extreme financial crisis as already stock markets are falling, and several industries seem to face significant problems [1]. As it is natural, when there is an intense crisis in an area, corporate companies tend to go bankrupt more easily as the instability problems increase, and liquidity difficulties usually arise [2]. Although there is a plethora of studies that are trying to explain business failure for different countries under normal circumstances, there are limited studies that focus on the company’s business failure for a country under crisis [3].

Business failure can be described in different ways, since it mainly depends on the specific condition the company deals with, during a specific period. For example, if a firm operates for a short period, it is more common to face difficulties than a well-established one [4]. In general, failure is the condition where a firm has problems that do not allow it to continue operation. These problems can be, for instance, related to incapability of paying debts which lead a company to be bankrupt by law. As du Jardin [5] contended, a business that cannot successfully meet its objectives and satisfy its needs might find itself in a critical situation, which can lead to failure in the worst case. Several studies describe failure as the act of filing for liquidation or bankruptcy [6,7]. Within the same vein, other studies define failure as the inability of firms to pay their financial obligations [8].

Altman [9] was a pioneer on bankruptcy prediction; he classified the corporate management system into a binary predefined classification: non-failed companies and failed companies. To better understand this meaning of failure, one needs to consider the condition of a firm in question and the objectives of the study. This way, a baseline is set, that helps to tell apart failed firms from successful ones. In the present day, failure is often used as a substitute and meaning of bankruptcy. A serious form of failure usually leads to the collapse of some business organizations which might, in turn, generate serious problems of liquidity and solvency [10,11]. The use of liquidity and solvency, as baseline metrics of bankruptcy, offers a well-defined dichotomy that helps to conduct an objective assessment of a firm’s financial situation. In addition, these baseline metrics help to have timely insights into a firm’s financial situation. Consequently, one can easily classify firms as failed or healthy, using bankruptcy baseline metrics [12,13]. Besides the long and dominated stance of the baseline bankruptcy measures, they remain limited, because they do not take into account whether the bankruptcy declaration is associated with financial signs of failure or other causes, such as management failure.

Some studies use the terms of financial distress and failure interchangeably, to describe the situation of businesses that are struggling to fulfill their obligations or, in other words, businesses that are facing serious financial difficulties [14]. To this end, financial distress can be used to describe the situation of a business that has to face several years of negative net operating income, major restructuring, layoffs, or suspension of dividend payments [15]. Nevertheless, the meaning conferred to financial distress raises some concerns since this meaning is used arbitrarily. Moreover, the benchmark to discriminate between firms and assign businesses to a category for a given period, say failed or non-failed, is subjective and depends entirely on how some authors conceptualize financial distress. Studies conferring this definition of failure to describe the situation of companies with financial difficulties, therefore, require careful evaluation since the subjective attribution to financial distress may produce biased results [3]. As a result, the notion of bankruptcy remains the most suitable illustration of corporate failure as it offers an objective discrimination criterion stemming from an empirical research viewpoint that can be used for more model development regarding this notion.

Forecasting is the practice of making predictions of the future based on past and present data and most commonly by analysis of trends. Following Sanders [16], one can establish several specific principles that are common to every forecasting procedure:

• Forecasts are hardly accurate. An accurate forecast is rare because there are too many factors within a business environment that cannot be predicted with near certainty.
• The level of accuracy of forecasts tends to be higher for groups of items than for individual ones as items that are grouped tend to cancel out their values.
• As data do not change much in the short run, the forecasting is more accurate for a shorter time horizon. Thereby, the shorter the time horizon of the forecast, the lower the degree of uncertainty.

One of the main disadvantages of all forecasting models is the fact that none of them can predict the future with absolute certainty, particularly the vulnerabilities of real economic conditions. Moreover, unforeseen events can make a forecast model useless regardless of the quality of the data collected. Often, this happens because in any economic environment every company is unique and there are different types of companies, and each of them operates in a different condition with a unique structure, making the analysis more complex. Using the general meaning of failure, Inmaculada [17] pointed out that companies can be classified into three failure categories, namely, revenue financing, failure company chronic failure company, and an acute failure company.

The time horizon is an important factor that is associated with accurate forecasting [15]. In most cases, an increase in the time horizon may result in a decrease in the accuracy of a forecasting model. While many different kinds of forecast models exist, the vast majority can be classified into two different categories, namely, statistical models and theoretical models [18]:

• Statistical models attempt to detect the most common warning sign exhibited by companies that went bankrupt, and then use this past information to assess the likelihood that a specific company will go bankrupt.
• Theoretical models assess the likelihood of bankruptcy by trying to identify the underlying factors associated with instances of bankruptcy.

Several researchers in Greece contacted studies related to bankruptcy prediction using a plethora of models. One of the latest studies, used a probit model to explore how bankruptcy in Greece is predicted in different sectors [19]. In their study, Charalambakis and Garrett [20] used a multi-period logit model to investigate corporate financial distress. In another study, by Doumpos and Kosmidou [21], a comparison of discriminant, logit, and probit analysis was conducted, regarding corporate companies in Greece. Although there are several studies utilizing different methodologies on bankruptcy prediction problems in Greece [22,23,24,25], none of them managed to predict satisfactorily the corporate crisis of 2008 [26].

Based on a review of Greek studies that examined corporate business failure in Greece, it was found that the most commonly used ratio is the Return of Total Assets [27,28,29,30]. Other important ratios in Greek bibliography are Current Ratio, Debt Ratio and Quick Ratio, among others.

In view of the above, the main objective of this study is the development of forecasting models for small and medium Greek companies. We aim to investigate which variables are the most appropriate for model development. Another goal is to compare different models and recognize each model’s effectiveness. Finally, our last objective is a comparison analysis among the different models to understand which one is the most suitable for the Greek market.

In Greek-related corporate failure bibliography, there are almost thirty studies that are using different methods of bankruptcy prediction and they have their own strengths and weaknesses. Some of them use a single prediction method, such as logit or probit, while few of them use more advanced methodologies, such as neural networks or fuzzy logic. Most of these studies are focusing on listed companies, as it is easier to possess their information through specific databases. The main innovation of our study is the examination of small and medium companies in Greece, which is lacking from the literature. Further, four different methodologies are compared in this study: three statistical ones and one advanced method, namely, the neural networks. Although similar methodologies have been previously applied in other countries, very few studies made such comparisons based on samples from Greece.

2. Materials and Methods

In this section, the sample selection and the methodology for predicting the bankruptcy of a firm is explained in detail. First, the preliminary analysis of the data is discussed. Then, the four statistical methods used for forming the prediction models are described: linear discriminant analysis, logistic regression or logit, decision trees and neural networks. These methods are among the most popular ones for bankruptcy prediction.

2.1. Data

The sample consists of small and medium Greek private firms that operate in Greece. Data are obtained from the court of first instance database. Court of first instance contains publicly available information derived from financial statements for Greek private firms. In the analysis, fifty (50) financial ratios are considered, as displayed in

Table 1. The ensemble of ratios used in the analysis.

Profitability Ratios	Gross earnings (EBIT)/Total Assets
	Net Earnings/Total Assets
	EBIT/Sales
	Net Earnings/Sales
	EBIT/Capital employed
	Net Earnings/Total Equity
	EBT/Total Equity
	Total Equity/Total Liabilities
	Profitability Net Earnings/Current Liabilities
	Retained Earnings/Total Assets
	Gross Profit Margin (Revenue—COGS)/Revenue
	Gross Earnings/Total Asset
Liquidity Ratios	Current Assets/Current Liabilities
	Current Assets/Total Assets
	Working Capital/Total Assets
	Working Capital/Total Equity
	(Accounts Receivable + Cash and Cash Equivalent)/Current Assets
	Total Equity/Working Capital
	Sales/Current Liabilities
	Capital Employed/Fixed Assets
	Reserves/Total Assets
	Net Earnings/Working Capital
	Cash and Cash Equivalent/Capital Employed
	(Current Assets–Inventory)/Current Liabilities
	Current Liabilities/Total Assets
	Inventories/Working Capital
Contribution and Efficiency Ratios	Interest Paid/Sales
	Sales/Total Assets
	Sales/Total Equity
	Sales/Capital Employed
	Net Earnings/Gross Earnings(Accounts Receivables x 365 Days)/Sales
Leverage Ratios	Total Liabilities/Total Equity
	Total Equity/Fixed Assets
	Non-Current Liabilities/Common Stock Total Equity/Total Assets
	(Distributable Earnings-(Reserves and Directors’ Reimbursement) + Depreciation)/Total Liabilities
	EBITDA/Total Liabilities
	Non-Current Liabilities/Total Liabilities
	Current Liabilities/Total Equity
	Total Equity/Capital Employed
	Total Liabilities/Total Assets
	EBT/Interest Paid in Notes
	Payable/Total Assets
	Non-Current Liabilities/Total Assets
Other Financial Ratios	Reserves/Common Stock
	Natural Logarithm of Trade Creditors/(COGS—Depreciation) × 360 Days
	(Annual Sales(t)–Annual Sales(t−1))/Annual Sales(t−1)
	Fixed Assets/Total Assets

.

We exclude firm-year observations for which we do not have available data. We also lag the time-varying covariates so as to predict financial distress more efficiently. To forecast corporate business failure, we need to define which firms for this study are considered as bankrupt. We consider a Greek private firm to be financially distressed if:

(a)

It has been declared as bankrupt or

(b)

It has been inactive or liquidated or dissolved and concurrently its common equity is less than fifty percent of its share capital.

The sample companies are grouped into two categories according to whether a company is bankrupt or not. Companies are “paired” in the sense that each bankrupt company has similarities with a non-bankrupt company, such as volume of total assets, type of industry, etc. Bankrupt companies were examined for the last 3 years of operation before they went bankrupt. In this study, financial data are collected 3 years before the company is bankrupt. Let the year when a company is bankrupt be denoted as the benchmark year t, then, (t−1), (t−2) and (t−3), respectively, represents 1, 2 and 3 years before the event of bankruptcy. Whether a company is treated as a bankrupt company or not is determined by the financial public report of year (t−1), etc.

The balance sheet of the companies used was from the years 2010 to 2012. The sample consists of 100 bankrupt and 100 non-bankrupt paired Greek companies from each considered year. One year before bankruptcy is used as a reference year, and companies in this year are divided into 2 subsets: one is used as a training set, consisting of 40 bankrupt companies and 40 healthy ones; the remaining sample is the testing set consisting of 60 bankrupt companies and 60 healthy ones. For the time periods of 2 and 3 years before bankruptcy, the testing sets are comprised by 100 bankrupt and 100 healthy companies.

2.2. Preliminary Analysis

To form the predictive models, some preliminary steps are required for processing with the analysis. First, all the missing values are replaced. Then, the dimensionality of the analysis is reduced by selecting the most informative ratios that will be used to form the predictive models. Therefore, the first issue that is dealt is the incomplete data, a problem which is interpreted as loss of information and, consequently, as loss of efficiency. One way to handle this problem is the adoption of imputation techniques [31]. The missing values are replaced using different techniques, such as using an interpolation method or by the sample mean. Although there are many different techniques to handle missing data, linear interpolation method is simple and effective [32]. In this case, the missing values are replaced with the mean of the two values of the variable before and after the missing one (Figure 1).

The second step in the preliminary analysis is to reduce the dimensionality of the original data set, i.e., the dimensionality of the learning set, by selecting the most effective ratios for bankruptcy prediction. For this, independent samples t-tests (Student′s t-tests) are performed based on the learning set in order to check whether the mean values of a ratio from the two groups, i.e., from the bankrupt and the healthy companies, are statistically different. If there is a statistical difference between the means of the two groups, then this ratio will be used in the predictive model. The assumptions for performing a t-test can be summarized to the following:

• The scale of measurement of the data should be a continuous or ordinal scale.
• The data should be collected from a representative, randomly selected portion of the total population.
• The data should be normally distributed.
• The sample size should be large enough.
• The final assumption is that the homogeneity of variance, i.e., the variances of the different groups should be equal.

The rules of thumb that are usually considered though in real applications are the following: each group should have at least 6 subjects and the design of the analysis is balanced, i.e., the same number of subjects is considered in each group.

Before running the independent samples t-test, one needs to check whether the two groups have equal variances or not (homogeneity of variance). Levene′s test examines the null hypothesis that the population variances of the two groups are equal [33]. It requires two assumptions: the independence of the observations and the test variable to be quantitative. Levene′s test is equivalent to a 1-way between-groups analysis of variance (ANOVA), where the dependent variable is the absolute value of the difference between a score and the mean of the group to which the score belongs: $Z_{ij}=\left|Y_{ij}-{\overline{Y}}_i\right|$, where $Y_{ij}$ is the value of the measured variable for the $j$-th case from the $i$-th group and ${\overline{Y}}_i$ is the mean of each group. The test statistic is defined as

$$W=\left(n-2\right)\frac{{{\displaystyle \sum }}_{i=1}^2{N}_i{\left(Z_i-Z\right)}^2}{{{\displaystyle \sum }}_{i=1}^2{{\displaystyle \sum }}_{j=1}^{N_i}{\left(Z_{ij}-Z_i\right)}^2},$$

(1)

where $N_i$ is the number of different groups to which the sampled cases belong, $n$ is the total number of cases in all groups, $Z_i$ is the mean of the $i$-th group ($Z_i=\frac{1}{N_i}{\displaystyle \sum }_{i=1}^{N_i}{Z}_{ij}$), and $Z$ is the mean of all $Z_{ij}$ ($Z=\frac{1}{n}{\displaystyle \sum }_{i=1}^2{\displaystyle \sum }_{j=1}^{N_i}{Z}_{ij}$). The estimated test statistic $W$ is approximately $F$-distributed with 1 and $n-2$ degrees of freedom, and hence its values is compared with the critical value $F\left(a,1,n-2\right)$ from the $F$ Table, for a chosen level of significance $a$ (we set $a=0.05$ for all tests). If the calculated $W$ value is greater than the critical value $F\left(a,1,n-2\right)$, then we reject the null hypothesis of equal variances.

The null hypothesis of the Student’s t-test is that the two population means (by group) are equal. If the null hypothesis of Levene′s test is rejected, then the variances of the two groups cannot be considered to be equal, and the homogeneity of variances assumption is violated. If the variances of the two groups are equally assumed based on Levene′s test, then the test statistic of the Students t-test is computed as

$$t=\frac{{\overline{x}}_1-{\overline{x}}_2}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}},$$

(2)

where ${\overline{x}}_1$ and ${\overline{x}}_2$ are the means of each sample (group), $n_1 \mathrm{and} n_2$ are the sample sizes of each group, and $s_p$ is the pooled standard deviation expressed as

$$s_p=\sqrt{\frac{\left(n_1-1\right)s_1^2+\left(n_2-1\right)s_2^2}{n_1+n_2-2}},$$

(3)

where $s_1 \mathrm{and} s_2$ are the standard deviations of each sample. The calculated value of the test statistic is then compared to the critical t value from the t distribution table with degrees of freedom $df=n_1+n_2-2$. If the calculated t value is greater than the critical t value, then we reject the null hypothesis of equal means.

If the variances of the two groups are not equally assumed based on Levene′s test, then the test statistic of the Student’s t-test is computed as

$$t=\frac{{\overline{x}}_1-{\overline{x}}_2}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}.$$

(4)

The calculated value of the test statistic is then compared to the critical t value from the t distribution table with degrees of freedom

$$df=\frac{{(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2})}^2}{\frac{1}{n_1-1}{(\frac{s_1^2}{n_1})}^2+\frac{1}{n_2-1}{(\frac{s_2^2}{n_2})}^2}.$$

(5)

If the calculated t value is greater than the critical t value, then we reject the null hypothesis of equal means.

2.3. Linear Discriminant Analysis

Linear discriminant analysis is a classification method originally developed in 1936 by Fisher [34]. It is a widespread method used to predict group membership (dependent variable) from several independent variables. More specifically, it allows us to find a linear combination of features that characterizes two or more classes of objects. It is applicable when the independent variables are continuous and well-distributed while the dependent variable is categorical. Linear discriminant analysis unfolds the difference between the different groups of data.

This method was the first one applied in bankruptcy prediction to forecast which firms may go bankrupt and which seem to be healthy. In bankruptcy prediction, the predictors are various financial variables and accounting ratios. Altman′s model based on linear discriminant analysis has been the leading model in practical applications these last few decades and is still being utilized either for reaching conclusions or for comparative reasons [9]. Unlike logistic regression, it is not limited to a dichotomous dependent variable.

Linear discriminant analysis can be used when the groups of the categorical variable are known a priori. Each case must have a score on one or more quantitative predictor measures, and a score on a group measure. The analysis is sensitive to the existence of outliers, and the size of the smallest group must be larger than the number of the predictors [35]. A list of assumptions should be satisfied for running linear discriminant analysis, although it has been shown to remain robust to slight violations of these assumptions [36]. A fundamental assumption is that the independent variables should be normally distributed. The variances among the group variables should be the same across the different levels of the predictors. Multicollinearity affects the performance of the method; its predictive power decreases if the predictors are correlated. Finally, the independence assumption should be satisfied: independent variables are assumed to be randomly sampled.

In its simplest form, it searches for a linear combination of variables (predictors):

$$Z={\beta }_1{x}_1+\dots +{\beta }_k{x}_k,$$

(6)

that best separates two groups. In our case, the two groups of interest are the bankrupt and healthy companies. To decide on the group that a new value may belong, a cut-off point or discriminant threshold is set, and the estimated $Z$ value is compared with the cut-off point. To capture the notion of separability, Fisher defined the score function as

$$s\left(\beta \right)=\frac{{\beta }^{{\rm T}}{\mu }_1-{\beta }^{{\rm T}}{\mu }_2}{{\beta }^{{\rm T}}C \beta },$$

(7)

where ${\mu }_1$ and ${\mu }_2$ are the means of the two groups, $n_1 \mathrm{and} n_2$ are the number of samples of each group, $C$ is the pooled covariance matrix

$$C=\frac{1}{n_1+n_2}\left(n_1{C}_1+n_2{C}_2\right),$$

(8)

$C_1 \mathrm{and} C_2$ are the covariance matrices of each group, and $\beta$ is the model coefficient:

$$\beta =C^{-1}\left({\mu }_1-{\mu }_2\right).$$

(9)

To assessing the effectiveness of the discrimination is to calculate the Mahalanobis distance ($\Delta$) between the two groups [37], where

$${\Delta }^2={\beta }^{{\rm T}}\left({\mu }_1-{\mu }_2\right).$$

(10)

A distance greater than 3 means that two averages differ by more than 3 standard deviations and there is small overlap of the two groups. A new point can be classified by projecting it onto a maximally separating direction and classifying it in the first group if

$${\beta }^{{\rm T}}\left(x-\left(\frac{{\mu }_1+{\mu }_2}{2}\right)\right)>-log\frac{p\left(c_1\right)}{p\left(c_2\right)},$$

(11)

where $p\left(c_1\right)\mathrm{and}p\left(c_2\right)$ are each group probability.

In its more general form, the goal of the linear discriminant analysis is to project the original data matrix onto a lower dimensional space. Let us suppose we have a set of $N$ samples, $X=\left\{x_1,x_2,\dots ,x_N\right\}$ is the data matrix where $x_i$ represents the $i$-th sample, the number of the different groups that the data are partitioned is $c$ ($X=\left[{\omega }_1,\dots ,{\omega }_c\right]$) and the original data matrix can be represented as

$$X=\left[\begin{array}{ccc}{x}_{11}& \cdots & x_{1M}\\ ⋮& \ddots & ⋮\\ x_{N1}& \cdots & x_{NM}\end{array}\right]$$

(12)

(size $NxM$). Each sample is represented as a point in the $M$-dimensional space ($x_i$∈${\mathcal{R}}^M$) and $n_i$ represents the number of samples of the $i$-th group/class. Therefore, the total number of samples is $N=\sum n_i$. First, one should calculate the mean of each group ${\mu }_i$ ($1xM$) as

$${\mu }_j=\frac{1}{n_j}{\displaystyle \sum }_{x_iϵ{\omega }_j}{x}_i,$$

(13)

and the total mean $\mu$ ($1xM$) of the data as

$$\mu =\frac{1}{N}{\displaystyle \sum }_{i=1}^N{x}_i={\displaystyle \sum }_{i=1}^c\frac{n_i}{N}{\mu }_i.$$

(14)

The between-group variance is then estimated as

$$S_B={\displaystyle \sum }_{i=1}^c{n}_i\left({\mu }_i-\mu \right){\left({\mu }_i-\mu \right)}^{{\rm T}}.$$

(15)

The within-group variance in then computed as

$$S_W={\displaystyle \sum }_{j=1}^c{\displaystyle \sum }_{i=1}^{n_j}{\displaystyle \sum }_{i=1}^{n_j}\left(x_{ij}-{\mu }_j\right){\left(x_{ij}-{\mu }_j\right)}^{{\rm T}},$$

(16)

where $x_{ij}$ is the $i$-th sample in the $j$-th group. From the above two equations (estimation of $S_B$ and $S_W$), the matrix $W$ that maximizes the Fisher’s formula

$$arg ma{x}_W\frac{W^{{\rm T}}{S}_{B}W}{W^{{\rm T}}{S}_{W}W}$$

(17)

is extracted as

$$W=S_W^{-1}{S}_B.$$

(18)

If $S_W$ is non-singular, then the eigenvalues ($\lambda$) and eigenvectors ($V$) of $W$ can be then exported as a conventional eigenvalue problem. One should sort the eigenvectors in descending order according to their corresponding eigenvalues. The first $k$ eigenvectors are then used to form a lower dimensional space ($V_kϵ{\mathcal{R}}^{Mxk}$). The dimension of the original data matrix $Xϵ{\mathcal{R}}^{NxM}$ is reduced by projecting in onto the lower dimensional space $V_kϵ{\mathcal{R}}^{Mxk}$. The dimension of the data after the projection is $k$ because $M-k$ features are ignored or deleted from each sample. The original samples are projected to the lower dimensional space based on the following equation

$$Y=X{V}_k.$$

(19)

Finally, to classify a new value in a group, one utilizes the classification equations or discriminant functions

$$D_k=x^{\prime }{S}_W^{-1}{\mu }_k-\frac{1}{2}{\mu }_k{S}_W^{-1}{\mu }_k+log\frac{n_i}{N}.$$

(20)

We always get $c-1$ discriminant equations where $c$ is the number of groups that the dependent variable has.

2.4. Logistic Regression

Logistic regression has been suggested as an alternative technique to linear discriminant analysis for cases where the normality assumption of the independent variables is not satisfied. As linear discriminant analysis, the logistic regression explains a categorical variable by the values of continuous independent variables. However, it is only suitable for dichotomous categorical variables, i.e., cannot be used if the dependent variable has more than two classes.

A logistic regression produces a logistic curve, which is limited to values between 0 and 1. This curve is constructed using the natural logarithm of the odds of the dependent variable. The odds of the dependent variable equaling $a$ is equivalent to the exponential function of the linear regression expression. The independent variables do not have to be normally distributed and it is not required to have equal variances in each group. The logistic regression equation can be written as an odds ratio

$$\frac{p}{1-p}=\exp \left(b_0+b_1{x}_1+\dots +b_{{\rm M}}{x}_M\right),$$

(21)

which can be converted into a linear form by taking the natural logarithm in both sides

$$logit \epsilon \left({\rm Y}\right)=\ln \left(\frac{p}{1-p}\right)=b_0+b_1{x}_1+\dots +b_{{\rm M}}{x}_M,$$

(22)

where ${\rm Y}$ is the Bernoulli-distributed dependent variable and $x_1,\dots ,x_M$ are the independent variables. The model coefficients are obtained based on the maximum likelihood estimation

$$b={\left[X’X\right]}^{-1}{X}^{\prime }y.$$

(23)

We expect our classifier to give us a set of outputs or groups based on probability when we pass the inputs through a prediction function and returns a probability score between 0 and 1. A threshold/cut-off point helps us decide on the classification of new values.

The Wald statistic (the square of the t-statistic) is used to assess the significance of coefficients of the regression model

$$W_j=\frac{{\beta }_j^2}{S_{{\beta }_j}^2},$$

(24)

where $S_{{\beta }_j}^2$ is the estimated variance of the coefficients. A likelihood ratio test can be used to examine the overall performance of the model

$$D=-2ln\frac{likelihood of the fitted model}{likelihood of the saturated model},$$

(25)

where $D$ represents deviance and approximately follows a chi-squared distribution.

2.5. Decision Trees

Decision trees are among the most popular predictive modelling approaches from the field of machine learning. They aim to achieve optimal classification with the minimal number of decisions. The main advantages of this method can be summarized as the following:

• The assumption of normality of the data is not required;
• If there is a high non-linearity and complex relationship between dependent and independent variables, a tree model will outperform a classical regression method;
• Decision tree models are easily interpreted;
• Unimportant features are excluded.

On the other hand, decision tree models are often biased toward splits on features having a large number of levels, they are easy to overfit, while small changes in the training data can result in large changes to decision logic.

At each level (step) of the algorithm, an attribute or value is selected along the dimension that gives the “best” split of groups (classes). Based on each split, child nodes are created. The same procedure is repeated from each child node until a stopping criterion is reached. Decision trees use the tree representation to solve a problem in which each leaf node corresponds to a class label and attributes are represented on the internal node of the tree.

Tree models where the target (dependent) variable can take a discrete set of values, such as in bankruptcy prediction problems, are called classification trees. In the tree structure, the leaves represent class labels and branches represent connections of features that lead to those class labels. A branch represents the different possibilities that this node could lead to (Figure 2). Based on the tree classification model, one can predict values of a target variable based on values of predictor variables. New values are classified to a class (group) based on a set of decision rules. There are no restrictions regarding the dependent and independent variables; they can be either categorical or numerical.

Initially, the learning data are sorted for every attribute at the beginning of the tree growth phase. There are many different growing methods of the trees, i.e., splitting criteria. In this study, results have been exported using the Classification and Regression Trees (C&RT) method [38]. This is a binary tree algorithm that partitions data and produces accurate homogeneous subsets. It splits the data into segments that are as homogeneous as possible with respect to the dependent variable. A terminal node in which all cases have the same value for the dependent variable is a homogenous node that requires no further splitting.

C&RT algorithm tries to make splits that maximize the homogeneity of child nodes with respect to the value of the dependent variable. An impurity measure shows the extent to which a node does not represent a homogenous subset of cases. Gini index can used as an impurity measure that measures how much every mentioned specification is directly affecting the resultant case. Gini is based on the squared probabilities of membership for each category of the dependent variable. If all the data belong to a single class, then it can be called pure. It is expressed as

$$Gini=1-{\displaystyle \sum }_{i=1}^C{\left(p_i\right)}^2,$$

(26)

where $p_i$ is the probability of an object being classified to a particular group. Gini takes values between zero and one; zero values mean that all data belong to the single class/variable, while one value means the data belong to the different group.

2.6. Neural Networks

Neural networks are used for statistical analysis and data modelling, as an alternative to standard nonlinear regression or cluster analysis techniques [39]. Odom and Sharda [40] first proposed using neural networks to build the bankruptcy prediction models and concluded that neural networks are at least as accurate as discriminant analysis. The neural network approach has significant advantages over other prediction methods since it does not require any restrictive assumptions such as linearity, normality, and independence between variables. It is a nonlinear computational algorithm providing a high level of accuracy.

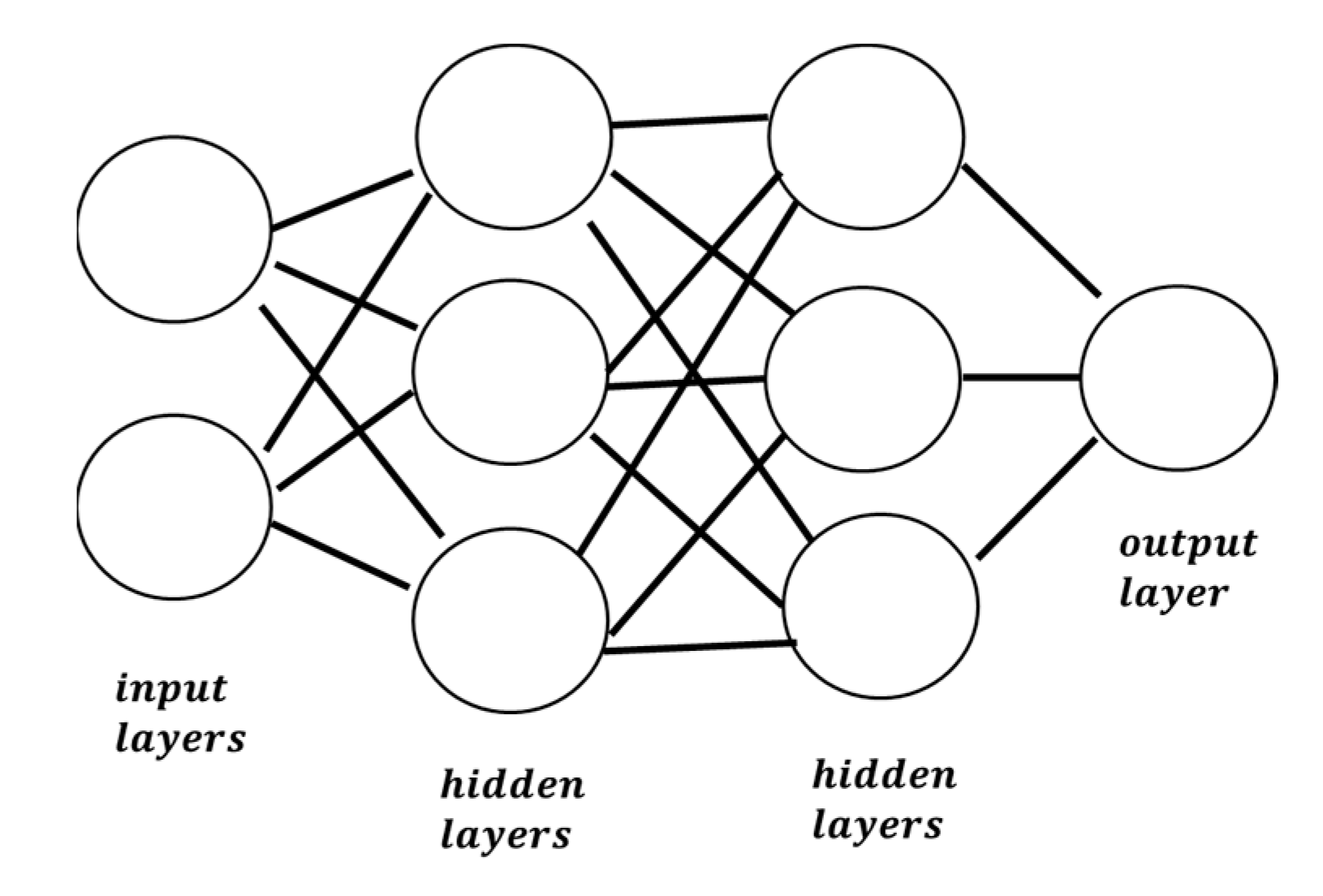
The basic unit of computation in a neural network is the neuron, called a node or unit. A neural network is an interconnected assembly of simple processing nodes (Figure 3). Each collection of these neurons is called a layer. It receives input from some other nodes, or from an external source and computes an output. Each input has an associated weight, which is assigned based on its relative importance to other inputs. The node applies a function to the weighted sum of its inputs and produces the output based on the model

$$y_i={{\displaystyle \sum }}_{i=1}^{n}f\left(w_{ij}{x}_i\right)+b_j,$$

(27)

where $w_{ij}$ are the weight coefficients of neuron $i$ which is connected to neuron $j$, $n$ is a number of inputs for each neuron of the network, $b_j$ is a bias vector for neuron $j$, and $f$ is the activation function. The activation function limits the amplitude of the output of the neuron, i.e., it normalizes the output to a selected interval. The bias vector accelerates the learning process by adding a fixed amount to the sum of the product of the weights of input vectors.

Results here are exported based on radial basis function networks, which are supervised in the sense that the model-predicted results can be compared against known values of the target variables. The connections in the network flow forward from the input layer to the output layer without any feedback loops. The input layer contains the predictors. The hidden layer contains unobservable nodes. The procedure creates a neural network with one hidden radial basis function layer. The activation function for the hidden layers is a hyperbolic tangent

$$f\left(c\right)=\tanh \left(c\right)=\frac{e^c-e^{-c}}{e^c+e^{-c}}.$$

(28)

It takes real-valued arguments and transforms them to the range (–1, 1). The output layer contains the target variable. The output layer contains the responses. The activation function links the weighted sums of units in a layer to the values of units in the succeeding layer and is of the form

$$f\left(c\right)=c.$$

(29)

2.7. Effectiveness of Prediction Models

To decide on the effectiveness of a prediction model and for comparing the different prediction models, three statistical measures are estimated from the testing set: Type I error, Type II error, and overall effectiveness. We test the out-of-sample predictive accuracy of the examined models. The Type I error is computed as

$$E_1=\frac{D_1}{BR}\ast 100\%,$$

(30)

where D₁ is the number of bankrupt companies classified by the prediction model as healthy, BR is the number of bankrupt companies in the testing set. The Type II error is found as

$$E_2=\frac{D_2}{NBR}\ast 100\%,$$

(31)

where D₂ is the number of healthy companies classified by the prediction model as bankrupt, NBR is the number of healthy companies in the testing set. Finally, the overall effectiveness of a prediction model is estimated as

$$S=\left(1-\frac{D_1+D_2}{BR+NBR}\right)\ast 100\%.$$

(32)

3. Results

The subsequent subsections present in detail the results of the different statistical methods in financial bankruptcy prediction using the two samples of firms described above. All the results have been extracted using the IBM SPSS Statistics 25. The efficiency of each method is presented only for the testing set (and not for the learning set).

3.1. Results from Preliminay Analyis

The first step in the analysis is related to the missing values and the employment of the linear interpolation method to the learning set. The number of missing values for each ratio for healthy and bankrupt companies vary from 0 to 5 (out of the 80 companies included in the learning set) before filling them using an imputation technique.

The second step of preliminary analysis is to run the independent samples t-test along with Levene’s test for the equality of the variances of the ratios by group. Again, only the learning set is used for these estimations. The rules of thumb are satisfied for the learning set: each group has 40 subjects and therefore the design of the analysis is balanced.

Table 2. Results from Levene’s test and the Students’ t-test for the learning set. The statistically significant results from the Student’s t-test are denoted with an asterisk.

Variable		Levene′s Test for Equality of Variances		t-test for Equality of Means
		F	Sig.	t	df	Sig. (2-Tailed)	Mean Difference	Std. Error Difference	95% Confidence Interval of the Difference
									Lower	Upper
X1	Equal variances assumed	3.166	0.079	2.025	78	0.046	0.1936	0.0956	0.0032	0.3839
	Equal variances not assumed			2.025	62.914	0.047 *	0.1936	0.0956	0.0025	0.3846
X2	Equal variances assumed	12.035	0.001	2.132	78	0.036	1.0779	0.5056	0.0713	2.0845
	Equal variances not assumed			2.132	43.129	0.039 *	1.0779	0.5056567	0.0584	2.0975
X3	Equal variances assumed	3.280	0.074	2.137	78	0.036	0.1992	0.0932	0.0137	0.3848
	Equal variances not assumed			2.137	62.864	0.036 *	0.1992	0.0932	0.0130	0.3855
X4	Equal variances assumed	0.339	0.562	2.964	78	0.004	1.3471	0.4545	0.4423	2.2519
	Equal variances not assumed			2.964	69.660	0.004 *	1.3471	0.4545	0.4406	2.2536
X5	Equal variances assumed	13.018	0.001	3.937	78	0.000	0.3833	0.0974	0.1895	0.5771
	Equal variances not assumed			3.937	56.372	0.000 *	0.3833	0.0974	0.1883	0.5783
X6	Equal variances assumed	8.552	0.005	2.132	78	0.036	2.9845	1.4001	0.1971	5.7720
	Equal variances not assumed			2.132	39.388	0.039 *	2.9845	1.4001	0.1534	5.8156
X7	Equal variances assumed	19.761	0.000	−2.821	78	0.006	−0.0842	0.0298	−0.1436	−0.0248
	Equal variances not assumed			−2.821	59.106	0.007 *	−0.0842	0.0298	−0.1439	−0.0245
X8	Equal variances assumed	4.346	0.040	2.321	78	0.023	0.0464	0.0200	0.0066	0.0862
	Equal variances not assumed			2.321	71.792	0.023 *	0.0464	0.0200	0.0066	0.0863
X9	Equal variances assumed	9.380	0.003	4.017	78	0.000	0.2645	0.0658	0.1334	0.3956
	Equal variances not assumed			4.017	69.591	0.000 *	0.2645	0.0658	0.1332	0.3959

displays the results from Levene’s test and the Student’s t-test for the statistically significant results. Based on the results shown in this table, the ratios with significantly different means for healthy and bankrupted companies (Sig. < 0.05) are the following:

X1	EBIT/Total Assets;	X6	Total Equities/Total Liabilities;
X2	Current Assets/Current Liabilities;	X7	Notes Payable/Total Assets;
X3	Net Earning/Total Assets;	X8	Reserves/Total Assets;
X4	Total Equity/Fixed Assets;	X9	Total Equity/Total Assets.
X5	Fixed Assets/Total Assets;

The descriptive statistics of these nine variables are displayed in

Table 3. Descriptive statistics of the nine variables extracted from the preliminary analysis of the learning set.

Ratios	Statistics	Good	Bankrupt	Ratios	Statistics	Good	Bankrupt
X1	Mean	0.022	−0.172	X6	Mean	3.361	0.3764
	Median	0.036	0.020		Median	0.808	0.232
	Std. Deviation	0.305	0.272		Std. Deviation	8.833	0.623
	Minimum	−1.039	−2.059		Minimum	−0.183	−0.343
	Maximum	0.766	0.498		Maximum	54.879	2.895
	Interquartile Range	0.212	0.202		Interquartile Range	3.318	0.442
	Skewness	−1.046	−2.716		Skewness	5.372	3.079
	Kurtosis	4.031	7.439		Kurtosis	31.418	10.555
X2	Mean	2.331	1.253	X7	Mean	0.050	0.134
	Median	1.176	1.021		Median	0.016	0.052
	Std. Deviation	3.116	0.718		Std. Deviation	0.088	0.167
	Minimum	0.045	0.028		Minimum	0.000	0.000
	Maximum	16.856	3.872		Maximum	0.491	0.628
	Interquartile Range	1.315	0.530		Interquartile Range	0.078	0.224
	Skewness	3.309	2.037		Skewness	3.576	1.273
	Kurtosis	12.541	4.852		Kurtosis	16.132	0.814
X3	Mean	−0.004	−0.203	X8	Mean	0.084	0.037
	Median	0.006	−0.006		Median	0.050	0.010
	Std. Deviation	0.298	0.509		Std. Deviation	0.102	0.075
	Minimum	−1.071	−2.059		Minimum	0.000	0.000
	Maximum	0.706	0.476		Maximum	0.381	0.348
	Interquartile Range	0.162	0.216		Interquartile Range	0.090	0.029
	Skewness	−1.229	−2.719		Skewness	1.591	3.014
	Kurtosis	4.451	7.613		Kurtosis	1.690	9.044
X4	Mean	1.202	−0.145	X9	Mean	0.452	0.188
	Median	0.602	0.027		Median	0.409	0.162
	Std. Deviation	1.644	2.358		Std. Deviation	0.342	0.238
	Minimum	−0.406	−8.354		Minimum	−0.222	−0.520
	Maximum	8.507	5.583		Maximum	1.089	0.743
	Interquartile Range	1.506	0.919		Interquartile Range	0.597	0.281
	Skewness	2.746	−0.880		Skewness	0.056	0.185
	Kurtosis	9.642	4.748		Kurtosis	−1.005	1.900
X5	Mean	0.676	0.292
	Median	0.536	0.233
	Std. Deviation	0.554	0.269
	Minimum	0.060	0.004
	Maximum	2.345	1.006
	Range	2.285	1.002
	Interquartile Range	0.738	0.281
	Skewness	1.295	1.249
	Kurtosis	1.476	0.879

, for the two groups, i.e., healthy and bankrupt companies, to demonstrate the basic features of the variables in the sample.

3.2. Results from Linear Discriminat Analyis

Based on the nine ratios extracted from the preliminary analysis, we form the discriminant prediction model and explore its effectiveness. The discrimination model is expressed as:

$$\begin{array}{c}D=-0.5-10.668X1-0.002X2+11.286X3+0.261X4+1.275X5-0.007X6\\ -3.017X7+1.519X8+0.990X9.\end{array}$$

(33)

Centroids are the mean discriminant scores for each group. Group centroids are the group means of canonical variables.

Table 4. Functions at group centroids from discriminant analysis.

Groups	Function
	1
good	0.794
bankrupt	−0.794
Unstandardized canonical discriminant functions evaluated at group means.

is used to establish the cutting point for classifying cases. If the two groups are of equal size, the best cutting point is half-way between the values of the functions at group centroids, i.e., the average. For our case, the cut-off point is equal to zero.

Table 5. Classification results from discriminant analysis.

Period		Groups	Predicted Group Membership		Total
			Good	Bankrupt
1 year before bankruptcy	Count	good	38	22	60
		bankrupt	13	47	60
	%	good	63.3	36.7	100
		bankrupt	21.7	78.3	100
2 years before bankruptcy	Count/%	good	60	40	100
		bankrupt	34	66	100
3 years before bankruptcy	Count/%	good	60	40	100
		bankrupt	19	81	100

summarizes the classification results. This table is used to assess how well the discriminant function works, and if it works equally well for each group of the dependent variable. The performance of the discriminant function is presented the testing sets from three periods, i.e., 1, 2 and 3 years before bankruptcy. As already mentioned, the performance of the discrimination model is displayed for the testing test (slightly higher performance is obtained for the learning set).

3.3. Results from Logit

As for the discriminant analysis, to export the discrimination ability of a logit analysis, the nine ratios extracted from the preliminary analysis are again used. First, we examine the efficacy of the logit model based on the data from 1 year before bankruptcy. The prediction equation is

$$\begin{array}{c}\log \left(\frac{p}{1}-p\right)=0.58+14.391X1+0.425X2-15.977X3-0.554X4-2.852X5\\ +5.291X6-0.967X7-0.693X8\end{array}$$

(34)

where $p$ is the probability of being in each group.

Table 6. Variables in the equation of logit model.

Variables	Coefficients (B)	S.E.	Wald	df	Sig.	Exp(B)
X1	14.391	10.999	1.712	1	0.191	178.231
X2	0.425	0.600	0.501	1	0.479	1.529
X3	−15.977	11.337	1.986	1	0.159	0.000
X4	−0.554	0.231	5.768	1	0.016	0.575
X5	−2.852	1.238	5.310	1	0.021	0.058
X6	−0.515	0.735	0.491	1	0.483	0.598
X7	5.291	3.071	2.967	1	0.085	198.450
X8	−0.967	3.615	0.071	1	0.789	0.380
X9	−0.693	2.147	0.104	1	0.747	0.500
Constant	0.580	0.915	0.402	1	0.526	1.787

provides the regression coefficients and the Wald statistic for testing the statistical significance. In addition, the odds ratio (column Exp(B)) for each variable category is displayed; it indicates how much the odds of an outcome occurring may increase or decrease when there is a unit change in the associated explanatory variable. Results suggest that only the variables X4 and X5 are statistically significant (sig < 0.05). The classification table (

Table 7. Classification results from logit.

Period		Groups	Predicted Group Membership		Total
			Good	Bankrupt
1 year before bankruptcy	Count	good	37	23	60
		bankrupt	18	42	60
	%	good	61.67	38.33	100.0
		bankrupt	30	70	100.0
2 years before bankruptcy	Count/%	good	63	37	100
		bankrupt	38	62	100
3 years before bankruptcy	Count/%	good	62	38	100
		bankrupt	26	74	100

) displays the predicted values of the dependent variable based on the full logistic regression model. Again, the performance of the testing sample is presented.

3.4. Results from Decision Trees

The predictability of the methodology of decision tress for bankrupt prediction is tested for the ensemble of the ratios. The decision tree starts with the root node, which simply shows the distribution of the outcome field. The data are then split based on the statistical significance by the predictor with the strongest relationship with the target field (financial aid in this case). In Figure 4, the extracted decision trees are shown for the testing set from 1 year before bankruptcy. The classification table (

Table 8. Classification results from decision trees.

Period		Groups	Predicted Group Membership		Total
			Good	Bankrupt
1 year before bankruptcy	Count	good	24	36	60
		bankrupt	9	51	60
	%	good	40	60	100
		bankrupt	15	85	100
2 years before bankruptcy	Count/%	good	39	61	100
		bankrupt	15	85	100
3 years before bankruptcy	Count/%	good	37	63	100
		bankrupt	15	85	100

) shows the number of cases classified correctly and incorrectly for each category of the dependent variable. The results are presented for the testing set of each period.

3.5. Results from Neural Networks

Finally, neural networks are used to predict the bankruptcy of a company. Three cases are again examined, with testing data from 1, 2 and 3 years before bankrupt, respectively. All ratios are included in the analysis, as for the decision trees. Regarding the architecture of the neural network, the input layer contains the predictors, the hidden layer contains unobservable nodes, and the output layer contains the responses.

Table 9. Classification results from neural networks.

Period		Groups	Predicted Group Membership		Total
			Good	Bankrupt
1 year before bankruptcy	Count	good	41	19	60
		bankrupt	17	43	60
	%	good	68.33	31.66	100.0
		bankrupt	28.33	71.66	100.0
2 years before bankruptcy	Count/%	good	69	31	100
		bankrupt	37	61	100
3 years before bankruptcy	Count/%	good	63	37	100
		bankrupt	32	68	100

presents the classification results for the dependent variable. The number of cases and the percentages classified correctly and incorrectly for each category of dependent variable are shown (for the testing set of each period).

4. Discussion and Conclusions

In this study, two traditional statistical models (discriminant and logit analysis), one non-traditional statistical model (decision trees) and one non-statistical model (neural model), are utilized for inferring about companies’ possible bankruptcy during the Greek ongoing crisis. As mentioned in du Jardin [41], when unexpected situations are developed in a market, making significant changes to the economic environment, there are significant problems for the firms that operate there and failure-based models are expected to have more accurate forecasts than traditional models. The problem is that the time horizon in such cases is not satisfactory and the stability of the extracted models over time is questionable. The time horizon is an important factor that is associated with accurate forecasting [15]. In most cases, an increase in the time horizon may result in a decrease in the accuracy of a forecasting model.

All the exported results from the analysis, as described above for each method, are summarized in

Table 10. Aggregate classification results.

Method	Function	Period	E1	E2	S
Discriminant Analysis	Function: $D=-0.5-10.668X1-0.002X2+11.286X3$ $+0.261X4+1.275X5-0.007X6-3.017X7$ $+1.519X8+0.990X9$	1 year before	21.7%	36.7%	70.8%
		2 years before	34%	40%	63%
		3 years before	19%	40%	70.5%
Logit	Function: $\log \left(\frac{p}{1}-p\right)=0.58+14.391X1+0.425X2$ $-15.977X3-0.554X4-2.852X5$ $+5.291X6-0.967X7-0.693X8$	1 year before	30%	38.3%	65.8%
		2 years before	38%	37%	62.5%
		3 years before	26%	38%	68%
Decision Trees	Importance to the model: EBIT to Total Assets, Net Earnings to Sales, EBITDA to Total Liabilities, Interest Paid to Total Assets, Current Assets Inventory to Current Liabilities	1 year before	15%	60%	62.5%
		2 years before	15%	61%	62%
		3 years before	15%	63%	61%
Neural Network	Importance to the model: EBIT to Interest Paid, Net Earnings to Current Liabilities, Net Earnings to Gross Earnings, Total Equity to Total Liabilities	1 year before	29.3%	32.7%	70%
		2 years before	37%	31%	65.7%
		3 years before	32%	37%	65.5%

, i.e., E1 (type I error), E2 (type II error), and S (overall performance). Results are displayed for the testing set of each period. The linear discriminant analysis seems to be slightly overall better than the rest of the methods.

Regarding the predictive efficiency of the examined methods based on the sample from 1 year before bankrupt, linear discriminant analysis scores first with an overall performance of 70.8%. The method of neural networks closely follows, succeeding an overall performance of 70%, logit achieves 65.8%, and finally, the decision trees attain a total predictiveness equal to 62.5%. When testing the period of 2 years before bankrupt, neural networks outstand the remaining methods, attaining an overall effectiveness of 65.7%. Discriminant analysis scores next (63%), and closely follow the remaining two methods. Finally, for the period of 3 years before bankrupt, discriminant analysis accomplishes 70.5% overall performance, logit follows with 68%, then neural networks with 65.5% and decision trees are again at the last position. The mean effectiveness of the four methods over the three examined periods is 68.1% (linear discriminant analysis), 67.07% (neural networks), 65.43% (logit), and 61.8% (decision trees), respectively.

There is a diversity of different results regarding the effectiveness of the different predictive models for bankruptcy prediction. It seems that the effectiveness of each method is sample based, i.e., dependent on the learning and testing set, the examined time period, and the considered financial ratios. For example, our results are in agreement with Barreda et al. [42], that found that the discriminant model is more accurate than the logit for the bankruptcy prediction of hospitality firms within U.S. equity markets for the period 1992–2010. However, our results are in disagreement with Pereira et al. [13], that concluded that the discriminant and logit model have similar predictive ability when examining the business failure in the hospitality industry for the period 2009–2013 in Portugal. Mihalovič [43] inferred that the logit model outperforms the discriminant model, when examining the prediction ability of the two models based on healthy and bankrupt companies for the year 2014 in Slovak Republic.

In one of the first studies regarding bankruptcy prediction in Greece, Grammatikos and Gloupos [27] compared multivariate discriminant analysis and linear probability model during the period 1977–1981 and they found out that the linear probability model is a better method than multivariate discriminant analysis. Zopounidis and Doumpos [24], concluded in their study that logit is found to be superior to discriminant analysis, using a sample from the period 1986–1990. The same period was examined by Tsakonas et al. [44]; they found out that evolutionary neural logic networks are more superior than other methods. In a more recent study, Charalambakis [45] explored Greek listed companies from 2002 to 2010 and found out that that a “model that incorporates sales to total assets profitability and financial risk with market capitalization, excess returns, and stock return volatility, best depicts the probability of financial distress for Greek firms” (p. 426).

Further, in several international studies it is claimed that neural networks reach much better results than logit or discriminant or decision trees, such as in Barreda [42]. A possible explanation is that a sufficient samples size is required to train a relatively stable neural model [46]. One of the limitations for a study such as ours, which is concerned with a small country, is the difficulty to find a sufficient sample of bankrupt companies.

The extracted results are important both from an academic and managerial point of view. From an academic point of view, it is interesting to find out that a traditional method such as discriminant analysis is the most accurate for predicting the bankruptcy in a country such as Greece, because it is a country based on micro, small and medium enterprises that are trying to survive despite the turbulence they have faced for more than a decade. Of course, it would have been good to examine in the future what might be the results by using more sophisticated methods, such as random forests or fuzzy logic.

Regarding managerial implications, we concluded that the majority of the ratios entering the discriminant and logit models that are important in the methods of decision trees and neural networks, are either profitability ratios or liquidity ratios. These results delineate that micro, small and medium size companies in Greece (and most probably in other similar settlements) should be extremely careful with their liquidity capability as it affects their future. Companies should constantly follow their liquidity, so they can be considered reliable and make better decisions. Another important issue for the evolution of a company, based on our results, is its profitability. Profitability ratios are included in the exported predictive models; they indicate how well a firm uses its assets to generate revenue and value. Future studies could include both financial and non-financial ratios so they can explore their relationship and help in the further development of the industry.