Secondly, once potential customers have reached a webstore, they need to be “encouraged” to actually convert from visitor to buyer. In the literature, there can be found various discussions on how to increase this conversion rate. For once, especially in the earlier days of e-commerce, trust played an important role and could be increased by investing in the general design of an online shop to project the ability of a certain quality in terms of products and services (cf. [
8,
9,
10,
11,
12,
13]). However, the detailed shape, style and content of a website or a shop can also boost the conversion rate if it fits to the characteristics of the targeted customer group (cf. [
14]). This can go as far as having a webstore that automatically “morphs” to match the suspected needs of each specific visitor (cf. [
15]). In this context, based on their generated clickstream data (i.e., how they move through a webpage), customers can be characterized either by statistical methods or, more dynamically, by certain learning models (cf. [
16]) in order to specifically target them with in-store marketing.
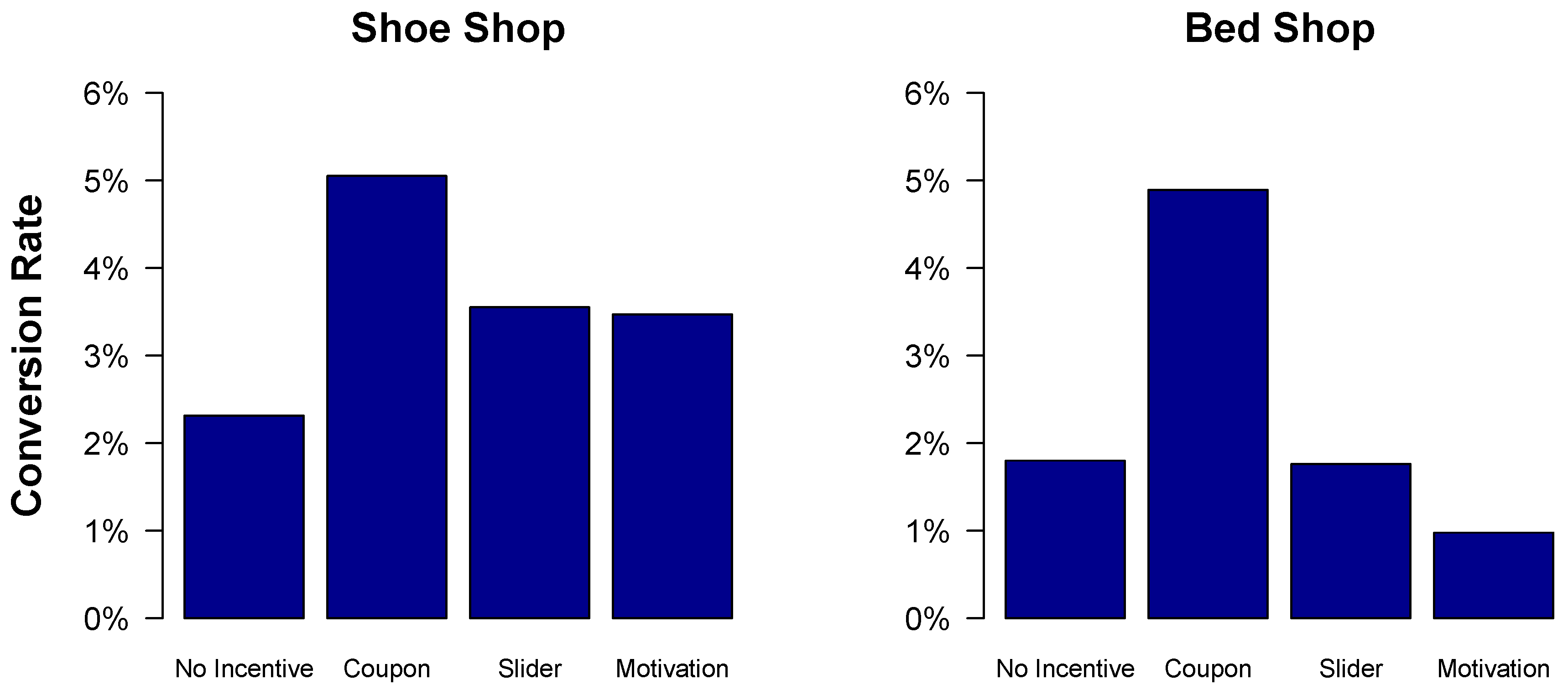
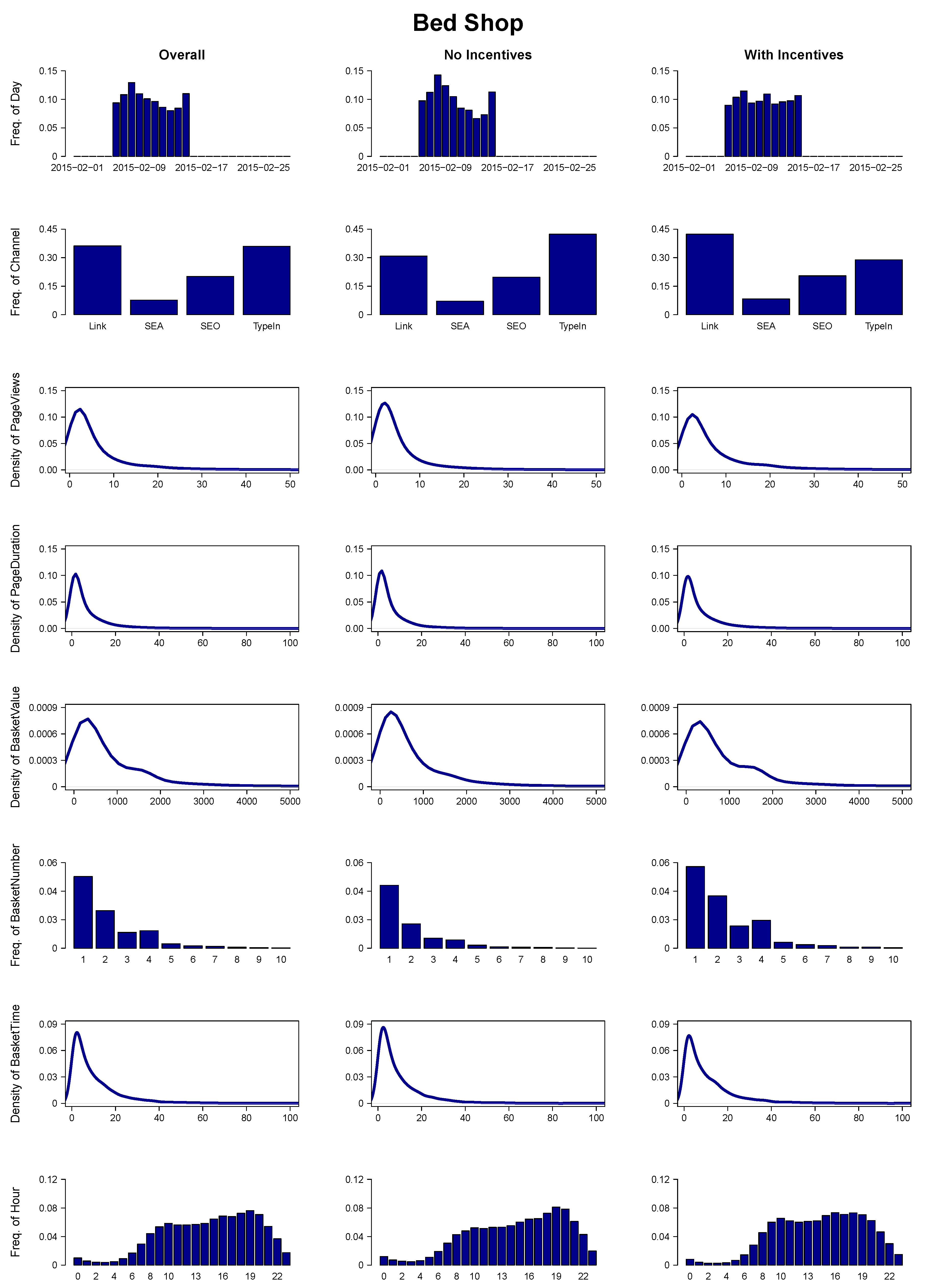
However, due to the rare academic availability of such clickstream data containing in-webstore marketing campaigns, the relevant literature here is still scarce. However, by partnering up with a digital consulting start-up that specializes in increasing the effectiveness of webshops by boosting their conversion rates, we were able to obtain such a unique data set from two stores in the online retail space—a shoe and a bed shop. This provides us with the possibility to investigate two very different product types as shoes and beds differ significantly in various characteristics (price, duration of use, etc.).
Our work adds to current research in two ways: to the best of our knowledge, this is the first time that the effects of in-webstore marketing approaches like coupons have been empirically measured via clickstream data. Additionally, we suggest certain data-driven hypotheses built from our data on how such purchasing incentives could be used best in practice.
The structure of our article is as follows: after a thorough literature review carried out in the next section (“Relevant Literature”), we discuss the present data set and investigate the potential effects of purchasing incentives from a more descriptive standpoint in “Data”. To address any bias in statistical tests due to potentially non-random selection of control and target groups in our data, we invoke classical generalized models of the logit-type (“Statistical Model Setup”). We present our results in “Empirical Findings” and extensively discuss the impact of certain purchasing incentives allowing possible interactions with other exogenous variables. Finally, in “Conclusions and Implications”, we summarize our approach and give recommendations on how to generally identify customer groups which can be purposely targeted to boost an online shop’s conversion rate.
All statistical analyses in the present paper have been carried out with the software package R-3.5.1.
Relevant Literature
A first step towards selling products and services online is obviously taken by attracting users to a webshop which can, e.g., either be done via SEO, contextual SEA (cf., e.g., [
22,
23,
24]) or (graphical) banner ads. With the availability of various types of clickstream data, i.e., information about how users move through the web, a large part of online advertising research has focussed on such contextual and graphical ads, although it might be difficult to deduce direct effects: in this context, Xu et al. [
25] find that banner ads have a rather low impact on direct conversion rates but might encourage future site visits via different advertising formats. Their study is, however, limited in the sense that their data does not contain visits resulting from non-paid search engine results or direct URL type-ins.
An important insight was that, due to some kind of information overflow, the use of display ads is accompanied by the risk of avoidance (cf. [
3]). In order to counteract this effect, such ads can be customized or personalized to catch the attention of users (cf. [
4,
6,
7,
26,
27,
28] or the recent study of [
14]). In addition, one can increase the obtrusiveness of ads which has been shown to positively impact visitors’ purchase intentions even though a combination of both approaches might be harmful due to privacy concerns (cf. [
5,
28,
29]).
In general, behavioural targeting, personalized advertising or so-called website morphing (cf. [
15]) has become a deeply investigated research stream.
However, all of these studies focus somewhat on increasing conversion rates by attracting users to a webstore. Therefore, in a second step, one might also ask how in-webstore advertising might be helpful to convert users which have already found their way to a shop by, e.g., offering time-limited price discounts or luring visitors to view certain products in more detail. The effect of such coupons and general in-store marketing campaigns has already been extensively studied in real-world offline stores over the last decades:
As it is well-known, one advantage of coupons lies in their simplicity as a marketing tool (cf. [
30]). At first, to asses their effectiveness, several authors considered just the pure redemption rate, i.e., the number of coupons which are being used compared to the amount which has been distributed (see [
31]). In addition, Reibstein and Traver [
31] developed a model to determine various factors which influence the redemption rate, namely (amongst other things) the method of distribution, the face value of coupons and the discount offered by the coupon.
However, later on, Bawa and Shoemaker [
32] pointed out that redemption rates as a single measure of success are misleading as high rates are not equal to profitability (cf. [
33]). They suggested to rather focus on incremental sales and tried to identify target households which are most lucrative.
Dhar and Hoch [
34] concluded that the effect of in-store coupons for grocery chains might be larger than the one for off-the-shelf price discounts while [
35] pointed out that the mere exposure to customized coupons might have a positive effect on sales and profitability while such coupons work better when they are unexpected.
In a more recent study, Reichhart et al. [
36] compared digital e-mail and mobile text message coupons by conducting a field experiment with exposed users from an opt-in database. They could find that text message delivery caused better conversion rates even though the response rates proofed to be lower. In a similar context, Danaher et al. [
37] conducted a two-year trial in a shopping mall with similar text message coupons and found that traditional offline coupon characteristics, e.g., face value, are again the main influencing factor for coupon effectiveness. In addition, the authors found that location and time of delivery influence redemption, e.g., customers tend to redeem a coupon more often if the corresponding store is closer. Additionally, they suggest that a shorter expiration length has a positive effect as they signal urgency to customers.
Next to coupons, more general in-store marketing campaigns are in the focus of current research, as well. For example, Chandon et al. [
38] conducted an eye-tracking experiment and concluded that, even though the number of product facings has a positive effect on conversion rate for certain types of shop visitors, gaining attention is itself not always sufficient to increase sales. Inman et al. [
39] carried out several intercept interviews and identified characteristics of shop visitors that tend to make unplanned purchases.
More recently, Hui et al. [
40,
41] investigated visitors of a grocery store by video-tracking and identified product categories that are more likely to elicit unplanned purchases than others. Additionally, they suggest that coupons which tempt customers to deviate from their determined in-store travel path are nearly twice as effective as those who do not. Furthermore, Zhang et al. [
42] concluded that interactive social influences can positively affect sales as well, especially when shoppers show certain behavioral cues.
Having all the above mentioned in-store marketing research available, it might be an obvious step to straightforwardly transfer these results to webstores. However, as Bucklin et al. [
43] pointed out, there are major differences between the choice making processes of online customers and classical real-life shop visitors that can influence the impact of customized promotions (see, e.g., [
44]). As a consequence, it is not clear if obtained results on coupons and in-store marketing do hold in a digital world. In fact, the relevant literature does not yet provide a final answer.
As the conversion rate of a typical online shop rarely exceeds 5% (cf. [
17]), a large part of early studies focussed on identifying visitors who are more likely to buy than others. In this context, based on clickstream data for an online-shop selling cars, Sismeiro and Bucklin [
19] decomposed the purchasing process into several steps describing each one with a probit model. In particular, they find that repeated visits do per se not go hand in hand with a higher conversion rate—even though an earlier study suggested that browsing behaviour might change in such situations (see [
45]). In more detail, Moe and Fader [
17,
18] found evidence that even though customers who visit an retail online-store more frequently tend to have a higher conversion rate, this is mainly due to the subgroup of shoppers whose frequency behaviour actually increased over time.
In terms of directly increasing conversion rates, Wilson [
46] suggested potential positive impacts of easier and more transparent purchase/checkout processes as well as free-shipping promotions in a B2B context even though their study is only based on several hundred shop visitors.
More generally speaking, an understanding of customer decision rules in online stores (cf. [
20]) could be used for individual promotional targeting. In this context, Schellong et al. [
21] (extending an earlier study of [
47]) try to classify the in-store shopping behaviour of a fashion retailer’s visitors by clustering browsing and search patterns.
Still, while several of the above studies already suggested that targeted in-store marketing based on clickstream data might be a fruitful approach, detailed empirical evidence on various such techniques has been scare. One of the few exceptions is the study of [
48] who investigate the effect of showing visitors personalized product recommendations. In the following, by partnering up with a digital consulting start-up, we aim to further close this research gap by studying the effects of various in-store marketing campaigns, especially the impact of time-limited discounts in the form of coupons and certain types of product recommendations.