Forecasting International Tourism Demand Using a Non-Linear Autoregressive Neural Network and Genetic Programming
Abstract
:1. Introduction
- -
- First, the use of artificial neural networks and SARIMA models are common in tourism forecasting; however, the use of GP is still very scarce. There are not many studies that have analyzed and compared the predictive performance of GP in tourism time series.
- -
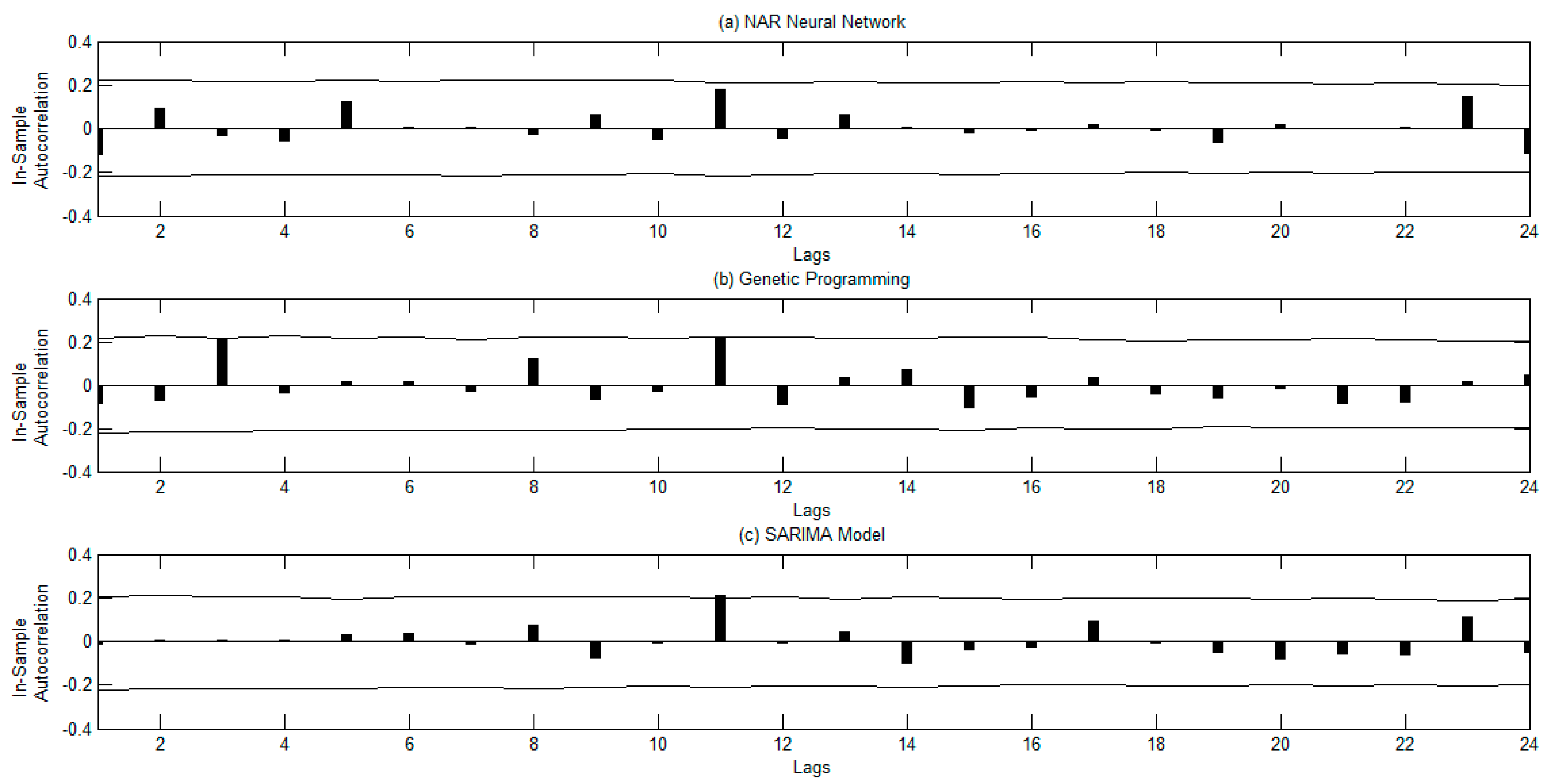
- Second, the robustness of the forecasting methods is checked by using the autocorrelation function of the residuals and the surrogate method. The diagnosis checking is a necessary step frequently omitted in tourism forecasting.
- -
- Third, we check if there are statistical differences between the forecasts of the two competing methods by using a novel approach based on the bootstrap method and on the estimation of empirical distributions of probability through the kernel method.
- -
- Last but not least, the forecasting study presented here is based on a data set related to the international demand for tourism to Spain. International tourism demand in Spain has grown rapidly in recent decades, becoming one of the most important sectors for the Spanish economy. Even more important, the economic contribution of international tourism is playing a proactive role to fuel the economy of Spain, and mitigate the negative effects of the deep economic crisis that hit the country in recent years. For all these reasons, international tourism demand forecasting has become a specific focal point of interest for Spanish policymakers.
2. Forecasting Methods
2.1. Artificial Neural Networks
2.2. Genetic Programming
3. Results
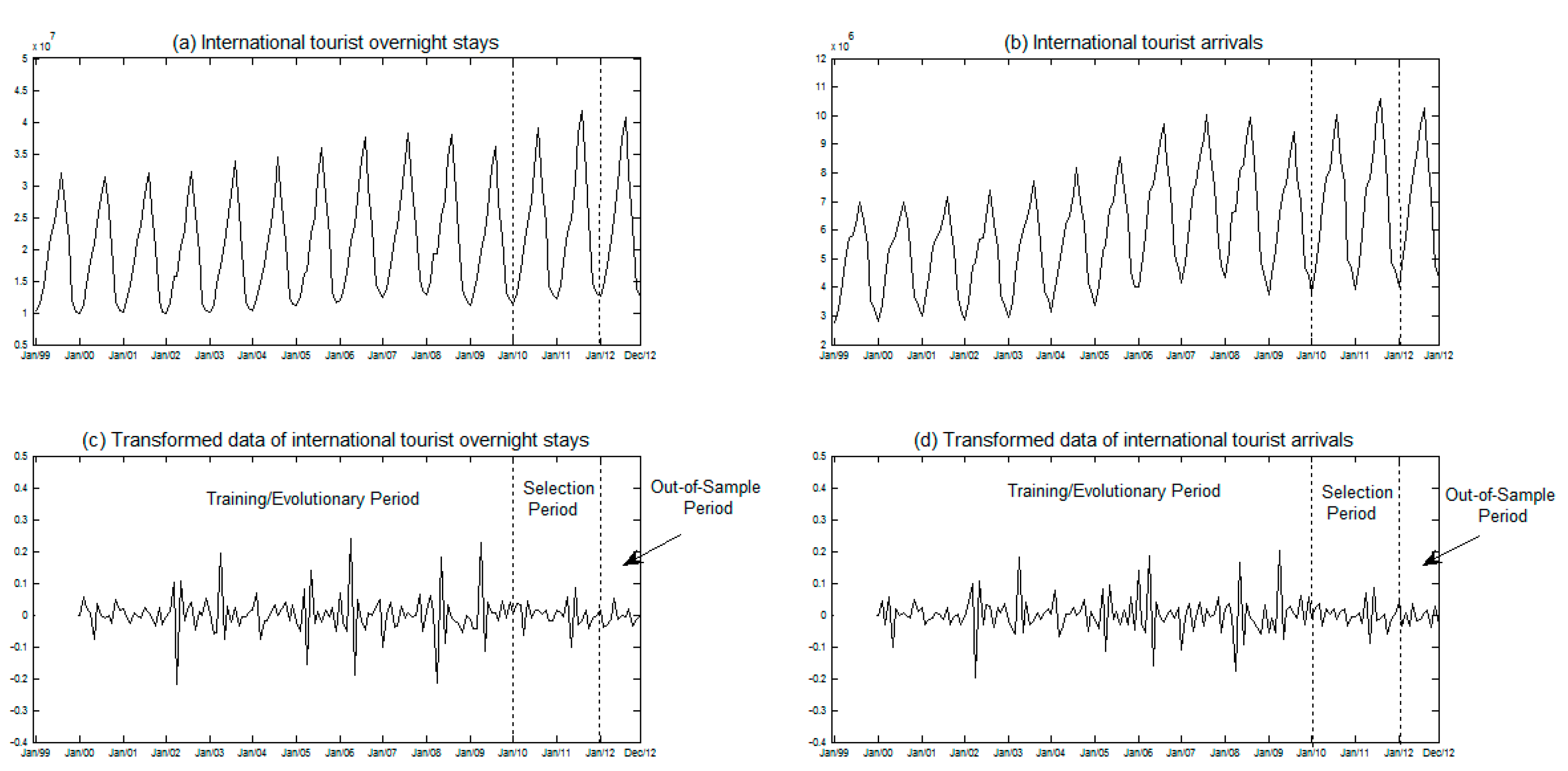
3.1. Data and Assesment of Forecasting Performance
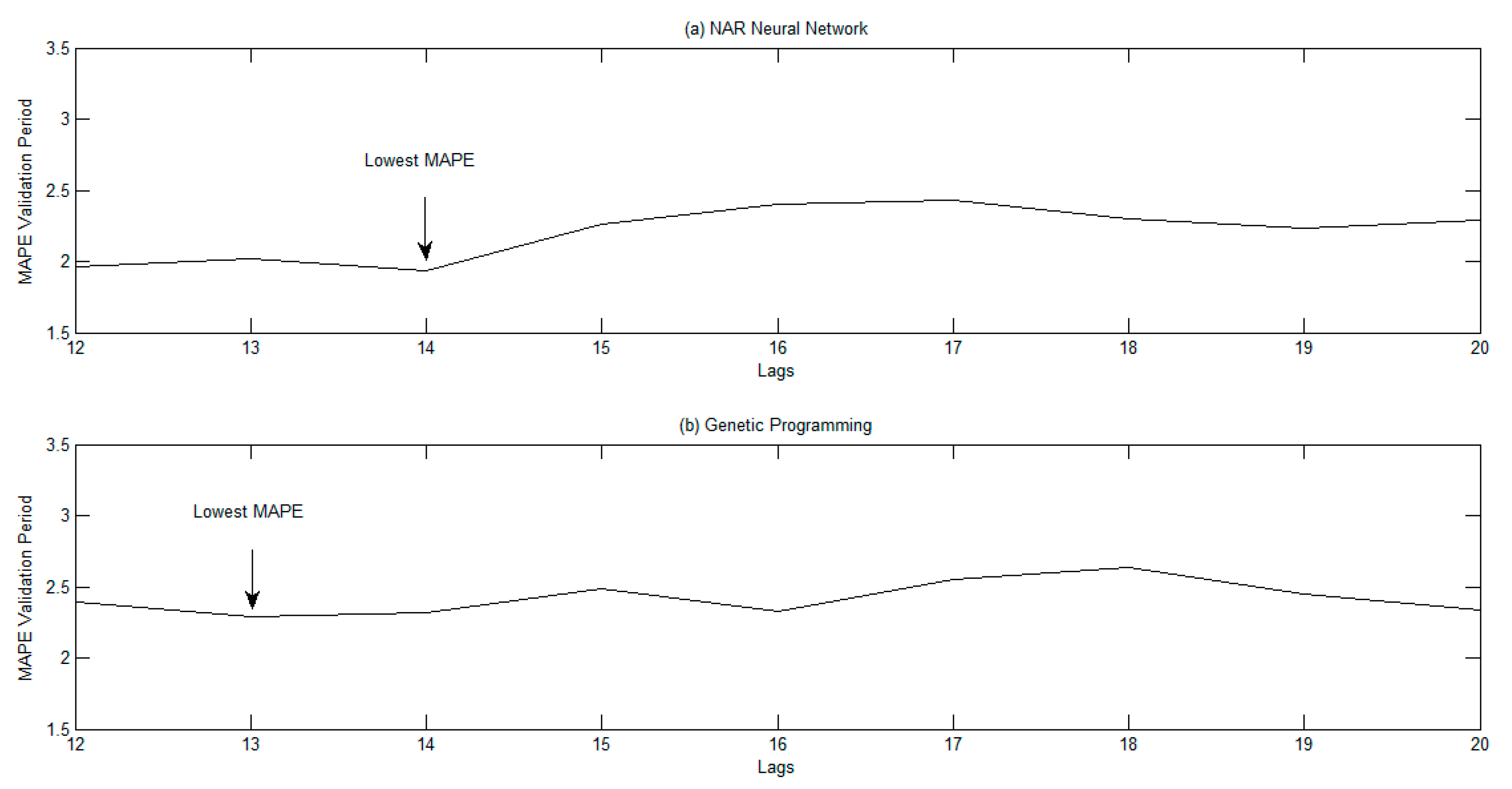
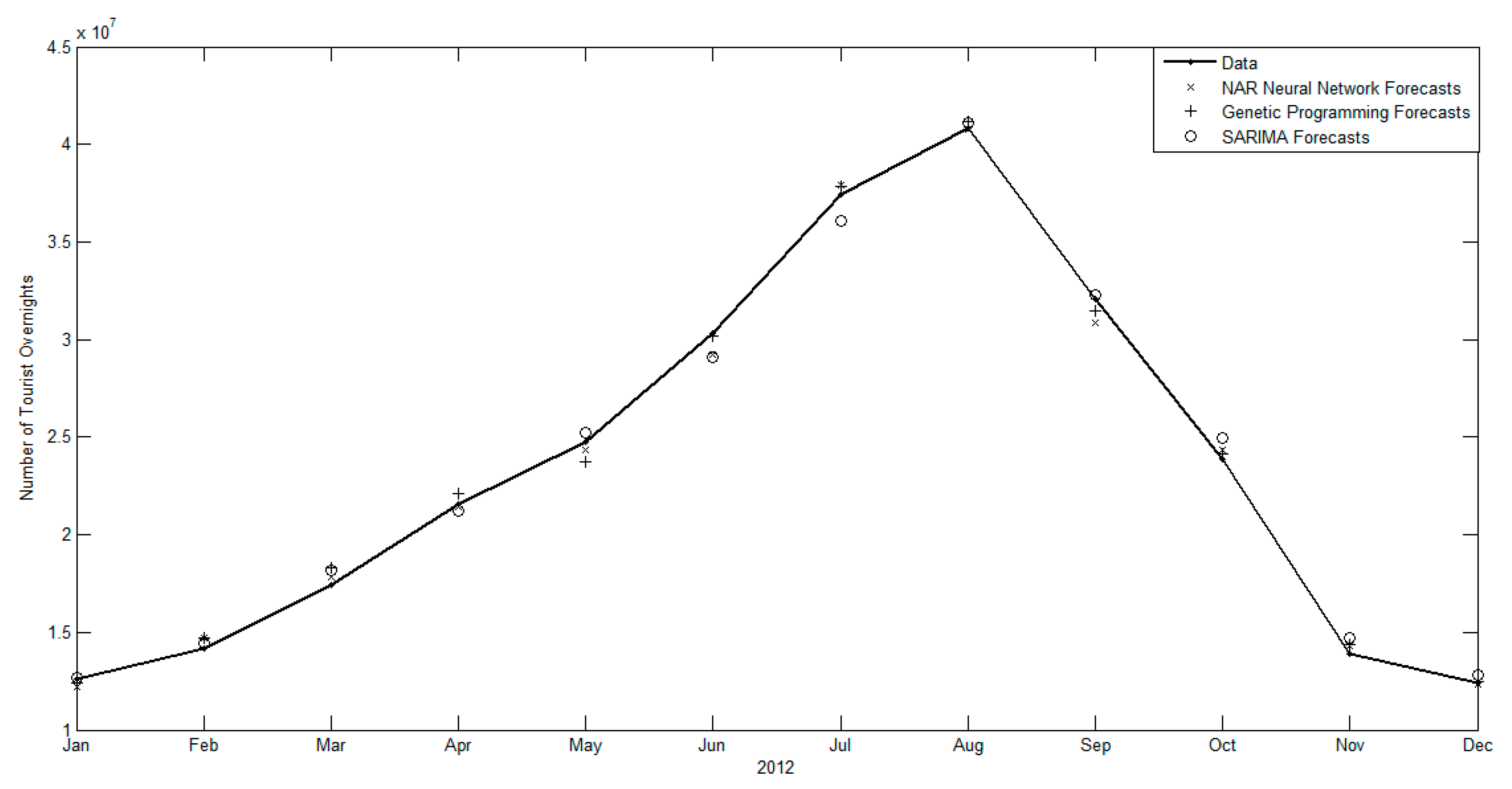
3.2. Forecasting Results
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Frechtling, D. Assessing the impact of travel and tourism—Measuring economic benefits. In Travel, Tourism and Hospitality Research: A Handbook for Managers and Researchers, 2nd ed.; Ritchie, J.B., Goeldner, C.R., Eds.; John Wiley & Sons: New York, NY, USA, 1987; ISBN 978-0-471-58248-9. [Google Scholar]
- Song, H.; Li, G. Tourism demand modelling and forecasting—A review of recent research. Tour. Manag. 2008, 29, 203–220. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Song, H.; Witt, S.F. Recent developments in econometric modelling and forecasting. J. Travel Res. 2005, 44, 82–99. [Google Scholar] [CrossRef] [Green Version]
- Otero-Giráldez, M.; Álvarez-Díaz, M.; González-Gómez, M. Estimating the Long-run Effects of socio-economic and meteorological factors on the domestic tourism demand for Galicia (Spain). Tour. Manag. 2012, 33, 1301–1308. [Google Scholar] [CrossRef]
- Petropoulos, C.; Nikolopoulos, K.; Patelis, A.; Assimakopoulos, V. A technical analysis approach to tourism demand forecasting. Appl. Econ. Lett. 2005, 12, 327–333. [Google Scholar] [CrossRef]
- Martin, C.A.; Witt, S.F. Forecasting tourism demand: A comparison of the accuracy of several quantitative methods. Int. J. Forecast. 1989, 5, 7–10. [Google Scholar] [CrossRef]
- Witt, S.F.; Witt, C.A. Modeling and Forecasting Demand in Tourism; Academic Press: London, UK, 1992; ISBN 10: 0127607404. [Google Scholar]
- Witt, S.F.; Witt, C.A. Forecasting tourism demand: A review of empirical research. Int. J. Forecast. 1995, 11, 447–475. [Google Scholar] [CrossRef]
- Song, H.; Witt, S.F. Tourism Demand Modelling and Forecasting: Modern Econometric Approaches, 1st ed.; Pergamon: Cambridge, UK, 2000; ISBN 1136353550. [Google Scholar]
- Kulendran, N.; Witt, S.F. Cointegration versus least squares regression. Ann. Tour. Res. 2001, 28, 291–311. [Google Scholar] [CrossRef]
- Athanasopoulos, G.; Hyndman, R.J.; Song, H.; Wu, D.C. The tourism forecasting competition. Int. J. Forecast. 2011, 27, 822–844. [Google Scholar] [CrossRef] [Green Version]
- Dharmaratne, G.S. Forecasting Tourist Arrivals to Barbados. Ann. Tour. Res. 1995, 22, 804–818. [Google Scholar] [CrossRef]
- Du Preez, J.; Witt, S.F. Univariate versus multivariate time series forecasting: An application to international tourism demand. Int. J. Forecast. 2003, 19, 435–451. [Google Scholar] [CrossRef]
- Brida, J.G.; Risso, W.A. Research Note: Tourism Demand Forecasting with SARIMA Models—The Case of South Tyrol. Tour. Econ. 2011, 17, 209–221. [Google Scholar] [CrossRef]
- Álvarez-Díaz, M.; Mateu-Sbert, J. Forecasting Daily air arrivals to Mallorca Island using nearest neighbor methods. Tour. Econ. 2011, 17, 191–208. [Google Scholar] [CrossRef]
- Olmedo, E. Comparison of near neighbour and neural network in travel forecasting. J. Forecast. 2016, 35, 217–223. [Google Scholar] [CrossRef]
- Chu, F.L. Forecasting tourism demand: A cubic polynomial approach. Tour. Manag. 2004, 25, 209–218. [Google Scholar] [CrossRef]
- Zhang, G.P.; Patuwo, E.B.; Hu, M.Y. A simulation study of artificial neural networks for nonlinear time-series forecasting. Comput. Oper. Res. 2001, 28, 381–396. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; The MIT Press: Cambridge, UK, 1992; ISBN-10: 0262111705. [Google Scholar]
- Szpiro, G. Forecasting chaotic time series with genetic algorithm. Phys. Rev. E 1997, 55, 2557–2568. [Google Scholar] [CrossRef]
- Yadavalli, V.K.; Dahule, R.K.; Tambe, S.S.; Kulkarni, B.D. Obtaining functional form for chaotic time series evolution using genetic algorithm. Chaos 1999, 9, 789–794. [Google Scholar] [CrossRef] [PubMed]
- Álvarez, A.; Orfila, A.; Tintoré, J. DARWIN—An evolutionary program for nonlinear modeling of chaotic time series. Comput. Phys. Commun. 2001, 136, 334–349. [Google Scholar] [CrossRef]
- Cho, V. A comparison of three different approaches to tourist arrival forecasting. Tour. Manag. 2003, 24, 323–330. [Google Scholar] [CrossRef] [Green Version]
- Law, R. Back-propagation learning in improving the accuracy of neural network based tourism demand forecasting. Tour. Manag. 2000, 21, 331–340. [Google Scholar] [CrossRef]
- Law, R.; Au, N. A neural network model to forecast Japanese demand for travel to Hong Kong. Tour. Manag. 1999, 20, 89–97. [Google Scholar] [CrossRef]
- Aslanargun, A.; Mammadov, M.; Yazici, B.; Yolacan, S. Comparison of ARIMA, neural networks and hybrid models in time series: Tourist arrival forecasting. J. Stat. Comput. Simul. 2007, 77, 29–53. [Google Scholar] [CrossRef]
- Fernandes, P.O.; Teixeira, J.P.; Ferreira, J.J.; Azevedo, S.G. Modelling tourism demand: A comparative study between artificial neural networks and the Box-Jenkins methodology. Rom. J. Econ. Forecast. 2008, 3, 30–50. [Google Scholar]
- Lin, C.J.; Chen, H.F.; Lee, T.S. Forecasting tourism demand using time series, artificial neural networks and multivariate adaptive regression splines: Evidence from Taiwan. Int. J. Bus. Admin. 2011, 2, 14–24. [Google Scholar] [CrossRef]
- Claveria, O.; Torra, S. Forecasting tourism demand to Catalonia: Neural networks vs. time series models. Econ. Model. 2014, 36, 220–228. [Google Scholar] [CrossRef] [Green Version]
- Saayman, A.; Botha, I. Non-linear models for tourism demand forecasting. Tour. Econ. 2017, 23, 594–613. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995; ISBN-10: 0198538642. [Google Scholar]
- Smith, M. Neural Networks for Statistical Modelling; Van Nostrand Reinhold: New York, NY, USA, 1995; ISBN-10: 0442013108. [Google Scholar]
- Trippi, R.R.; Turban, E. (Eds.) Neural Networks in Finance and Investment; McGraw-Hill: New York, NY, USA, 1996; ISBN 1557384525. [Google Scholar]
- Refenes, A. Neural Networks in the Capital Markets; John William and Sons: Chichester, UK, 1995; ISBN 0471943649. [Google Scholar]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Palmer, A.; Montaño, J.J.; Sesé, A. Designing an artificial neural network for forecasting tourism time series. Tour. Manag. 2006, 27, 781–790. [Google Scholar] [CrossRef]
- Kon, S.C.; Turner, W.L. Neural network forecasting of tourism demand. Tour. Econ. 2005, 11, 301–328. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superposition of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- White, H. Connectionist nonparametric regresion multilayer feedforward networks can learn arbitrary mappings. Neural Netw. 1990, 3, 535–549. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by backpropagation errors. Nature 1986, 323, 536. [Google Scholar] [CrossRef]
- Zhang, G.P.; Kline, D. Quarterly time-series forecasting with neural networks. IEEE Trans. Neural Netw. 2007, 18, 1800–1814. [Google Scholar] [CrossRef]
- Kaastra, I.; Boyd, M. Designing a neural network for forecasting financial and economic time series. Neurocomputing 1996, 10, 215–236. [Google Scholar] [CrossRef] [Green Version]
- Álvarez, A.; López, C.; Riera, M.; Hernández, E.; Tintoré, J. Forecasting the SST space-time variability of the Alboran Sea with genetic algorithms. Geophys. Res. Lett. 2000, 27, 2709–2712. [Google Scholar] [CrossRef]
- Álvarez-Díaz, M.; Gupta, R. Forecasting the US Consumer Price Index: Does Nonlinearity Matter? Appl. Econ. 2016, 48, 4462–4475. [Google Scholar] [CrossRef]
- Garín-Muñoz, T. Tourism in Galicia: Foreign and domestic demand. Tour. Econ. 2009, 15, 753–769. [Google Scholar] [CrossRef]
- Lim, C.; McAleer, M. A seasonal analysis of Asian tourist arrivals to Australia. Appl. Econ. 2000, 32, 499–509. [Google Scholar] [CrossRef]
- Alleyne, D. Can seasonal unit root testing improve the forecasting accuracy of tourist arrivals? Tour. Econ. 2006, 12, 45–64. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef] [Green Version]
- Granger, C.W.J.; Newbold, P. Spurious regressions in econometrics. J. Econometr. 1974, 2, 111–120. [Google Scholar] [CrossRef] [Green Version]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B. Testing for Nonlinearity in Time Series: The Method of Surrogate Data. Physica D 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Shen, S.; Li, G.; Song, H. An Assessment of Combining Tourism Demand Forecasts over Different Time Horizons. J. Travel Res. 2008, 47, 197–207. [Google Scholar] [CrossRef] [Green Version]
- Theiler, J.; Eubank, S. Don’t bleach chaotic data. Chaos 1993, 3, 771–782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lewis, C.D. Industrial and Business Forecasting Methods; Butterworths: London, UK, 1982; ISBN-13: 978-0408005593. [Google Scholar]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 1994, 3, 253–263. [Google Scholar] [CrossRef]
- Ferson, W.; Nallareddy, S.; Xie, B. The “out-of-sample” performance of long run risk models. J. Financ. 2013, 107, 537–556. [Google Scholar] [CrossRef]
- Harvey, D.I.; Leybourne, S.J.; Newbold, P. Testing the Equality of Prediction Mean Squared Errors. Int. J. Forecast. 1997, 13, 281–291. [Google Scholar] [CrossRef]
- Bowman, A.W.; Azzalini, A. Applied Smoothing Techniques for Data Analysis; Oxford University Press: New York, NY, USA, 1997; ISBN-13: 978-0198523963. [Google Scholar]
- Chen, K.Y.; Wang, C.H. Support vector regression with genetic algorithms in forecasting tourism demand. Tour. Manag. 2007, 28, 215–226. [Google Scholar] [CrossRef]
- Chen, R.; Liang, C.-Y.; Hong, W.-C.; Gu, D.-X. Forecasting holiday daily tourist flow based on seasonal support vector regression with adaptive genetic algorithm. Appl. Soft Comput. 2015, 26, 435–443. [Google Scholar] [CrossRef]
- Hong, W.C.; Dong, Y.; Chen, L.Y.; Wei, S.Y. SVR with hybrid chaotic genetic algorithms for tourism demand forecasting. Appl. Soft Comput. 2011, 11, 1881–1890. [Google Scholar] [CrossRef]



| Forecasting Methods | MAPE (%) | ||
|---|---|---|---|
| In-Sample Period | Out-of-Sample Period | ||
| Training | Validation | ||
| NAR Neural Network | 3.24 | 1.93 | 2.10 |
| Genetic Programming | 3.36 | 2.29 | 2.18 |
| SARIMA(0,1,2)x(0,1,1) | 2.60 | 2.72 | |
| Comparison between Methods | International Tourist Overnight Stays | |
|---|---|---|
| Diebold-Mariano Test (Bootstrapped p-Value) | Bootstrap Confidence Interval | |
| NAR Neural Network vs. SARIMA | −1.08 (0.23) | (−3.65, 1.07) |
| Genetic Programming vs. SARIMA | −0.92 (0.31) | (−2.70, 1.19) |
| NAR Neural Network vs. Genetic Programming | −0.08 (0.92) | (−2.01, 2.12) |
| Forecasting Methods | MAPE (%) | ||
|---|---|---|---|
| In-Sample Period | Out-of-Sample Period | ||
| Training | Validation | ||
| NAR Neural Network | 2.58 | 1.85 | 2.02 |
| Genetic Programming | 3.33 | 2.33 | 2.05 |
| SARIMA(0,1,2)x(1,1,1) | 2.54 | 2.45 | |
| Comparison between Methods | International Tourist Arrivals | |
|---|---|---|
| Diebold-Mariano Test (Bootstrapped p-Value) | Bootstrap Confidence Interval | |
| NAR Neural Network vs. SARIMA | −1.48 (0.13) | (−3.65, 0.51) |
| Genetic Programming vs. SARIMA | −1.08 (0.25) | (−3.5, 0.66) |
| NAR Neural Network vs. Genetic Programming | −0.43 (0.64) | (−2.46, 1.62) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Álvarez-Díaz, M.; González-Gómez, M.; Otero-Giráldez, M.S. Forecasting International Tourism Demand Using a Non-Linear Autoregressive Neural Network and Genetic Programming. Forecasting 2019, 1, 90-106. https://doi.org/10.3390/forecast1010007
Álvarez-Díaz M, González-Gómez M, Otero-Giráldez MS. Forecasting International Tourism Demand Using a Non-Linear Autoregressive Neural Network and Genetic Programming. Forecasting. 2019; 1(1):90-106. https://doi.org/10.3390/forecast1010007
Chicago/Turabian StyleÁlvarez-Díaz, Marcos, Manuel González-Gómez, and María Soledad Otero-Giráldez. 2019. "Forecasting International Tourism Demand Using a Non-Linear Autoregressive Neural Network and Genetic Programming" Forecasting 1, no. 1: 90-106. https://doi.org/10.3390/forecast1010007
APA StyleÁlvarez-Díaz, M., González-Gómez, M., & Otero-Giráldez, M. S. (2019). Forecasting International Tourism Demand Using a Non-Linear Autoregressive Neural Network and Genetic Programming. Forecasting, 1(1), 90-106. https://doi.org/10.3390/forecast1010007




