Intracranial Pressure Forecasting in Children Using Dynamic Averaging of Time Series Data
Abstract
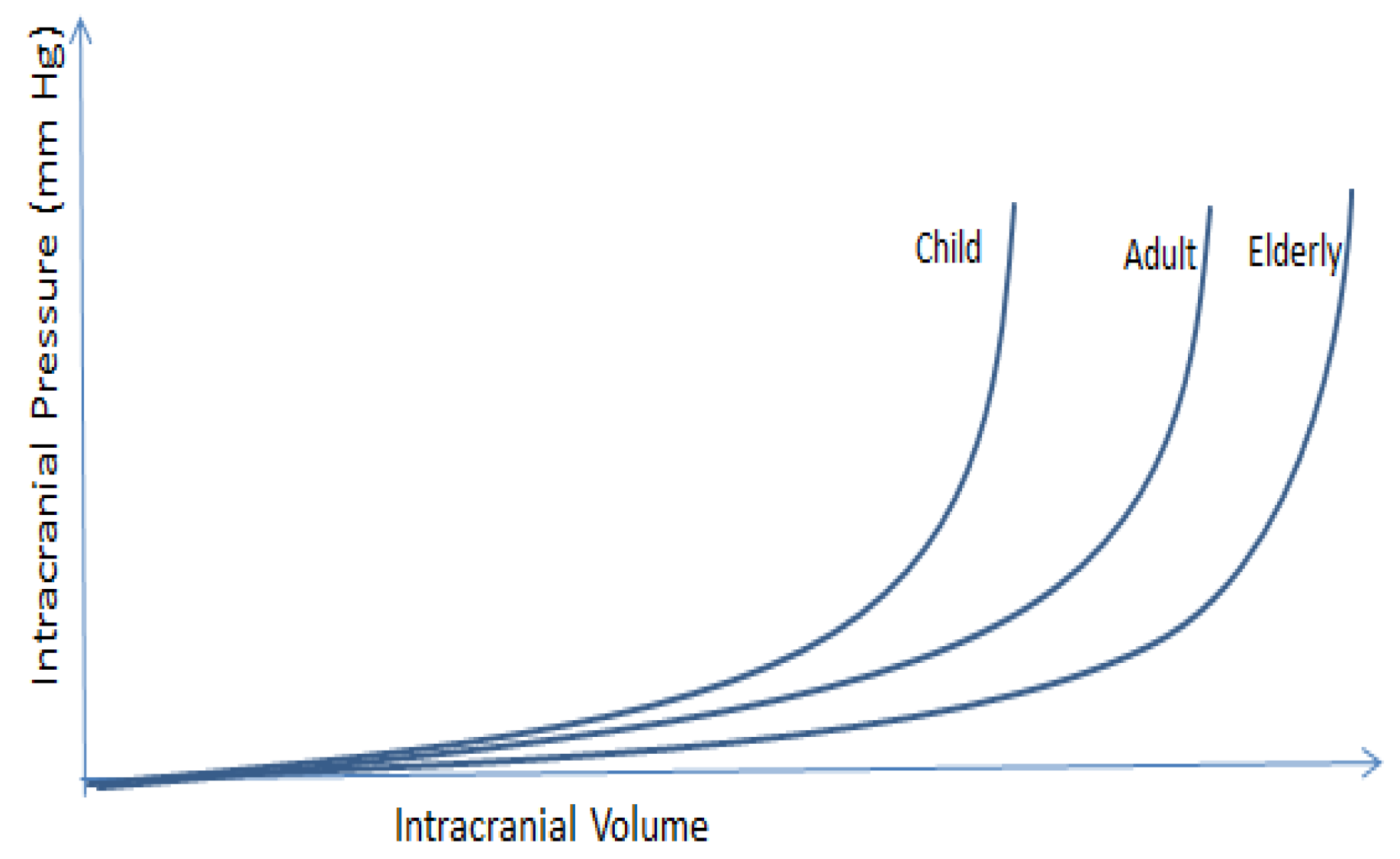
:1. Introduction
2. Methods
2.1. Data Acquisition and Preprocessing
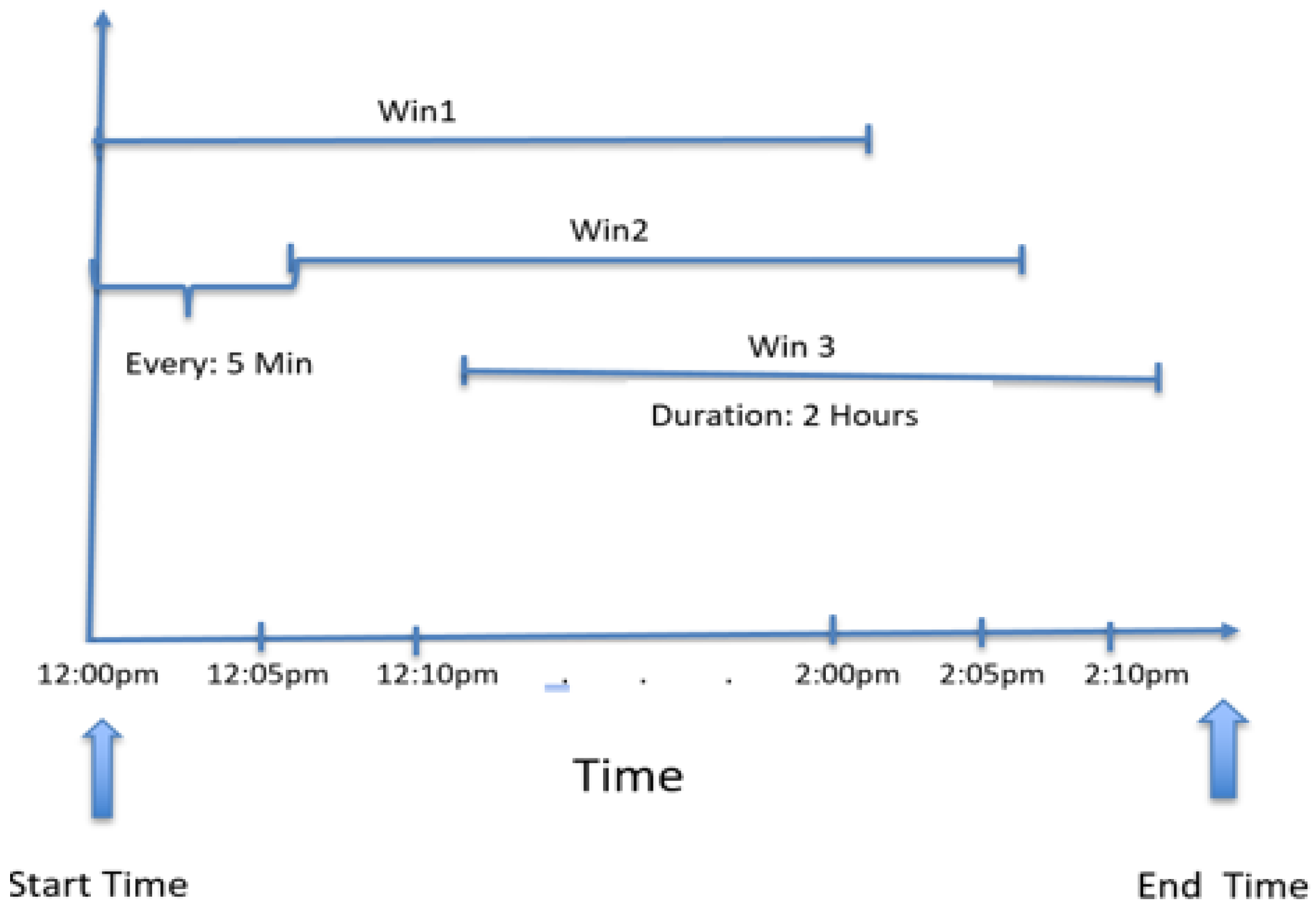
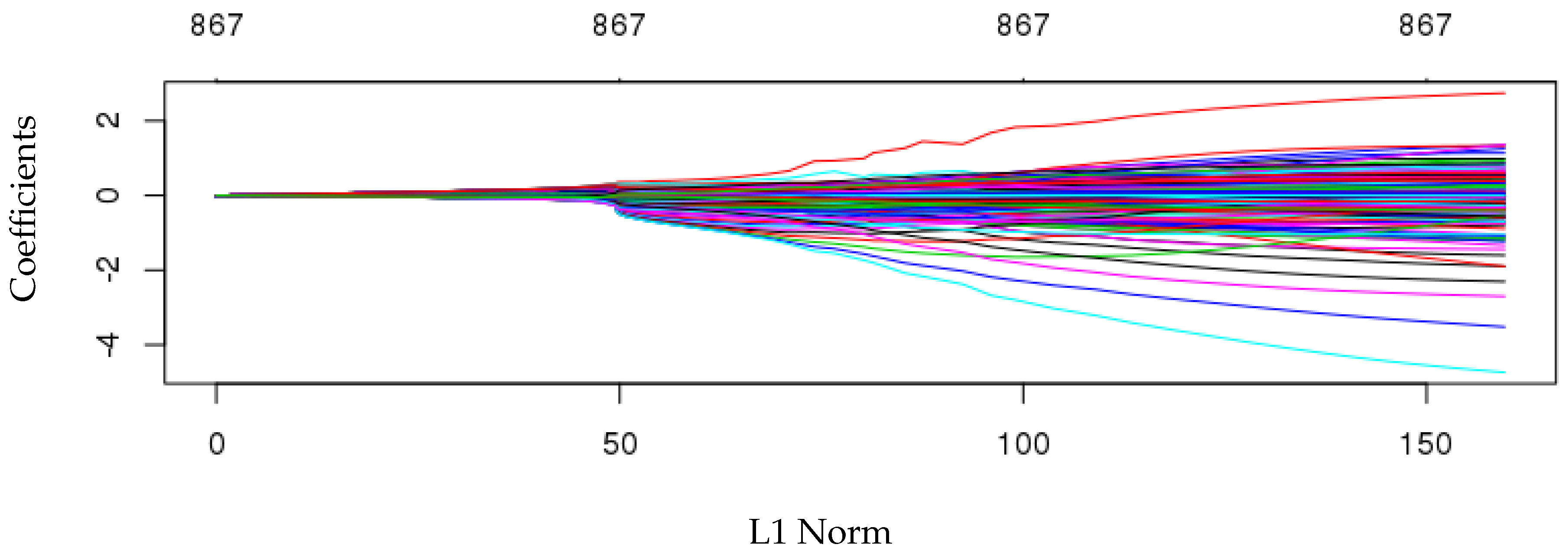
2.2. Statistical Analysis and Machine Learning
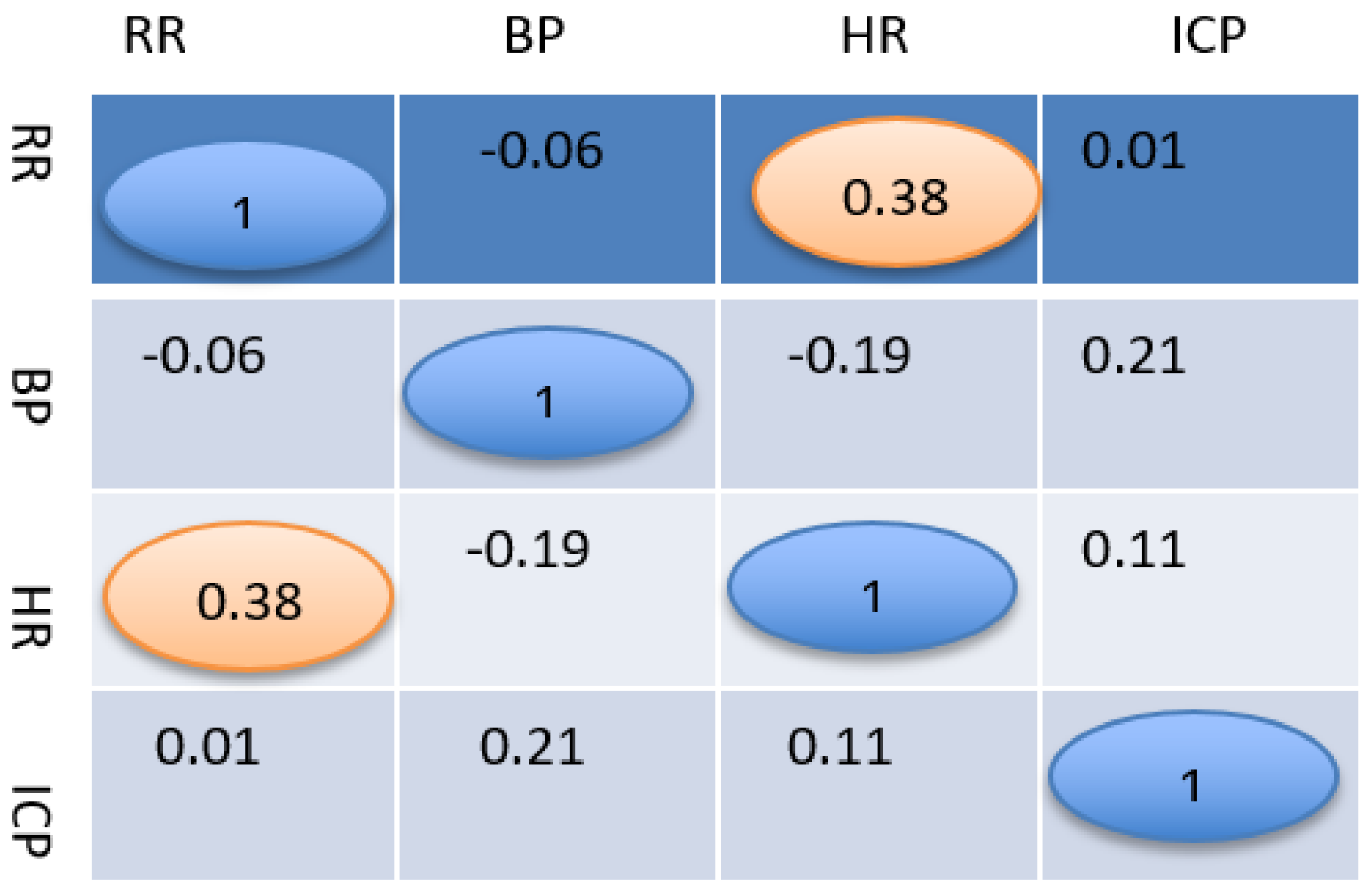
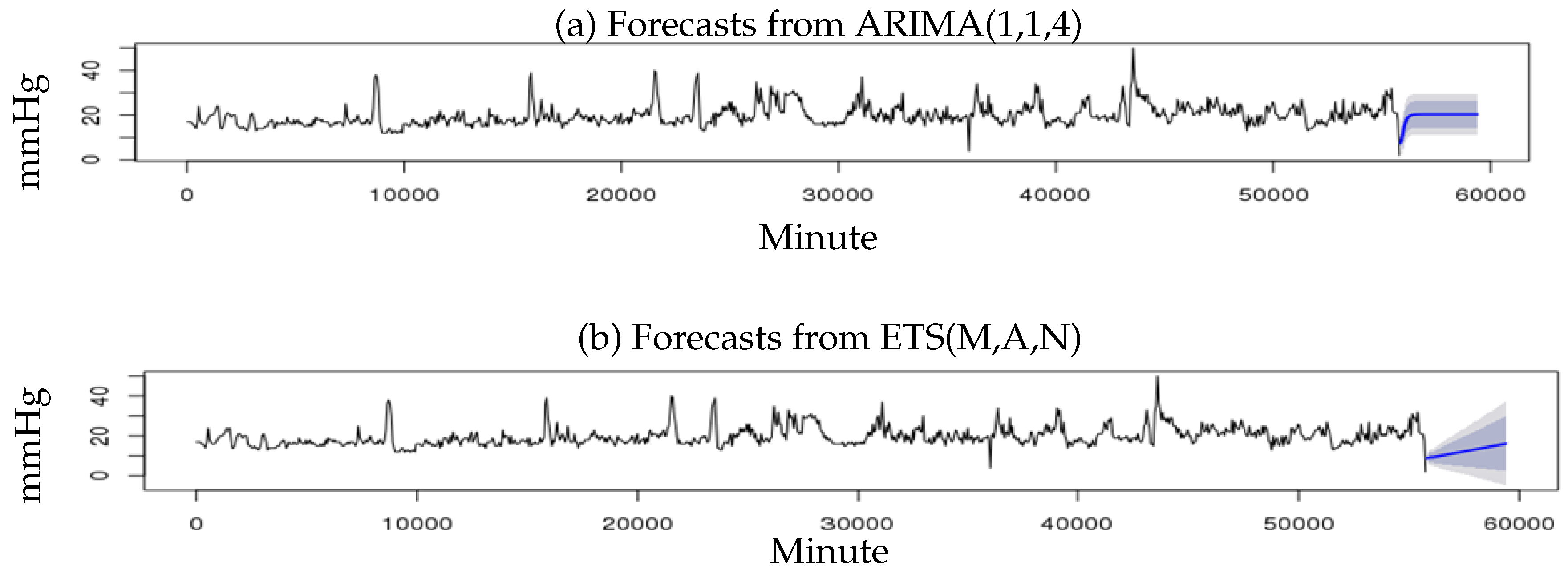
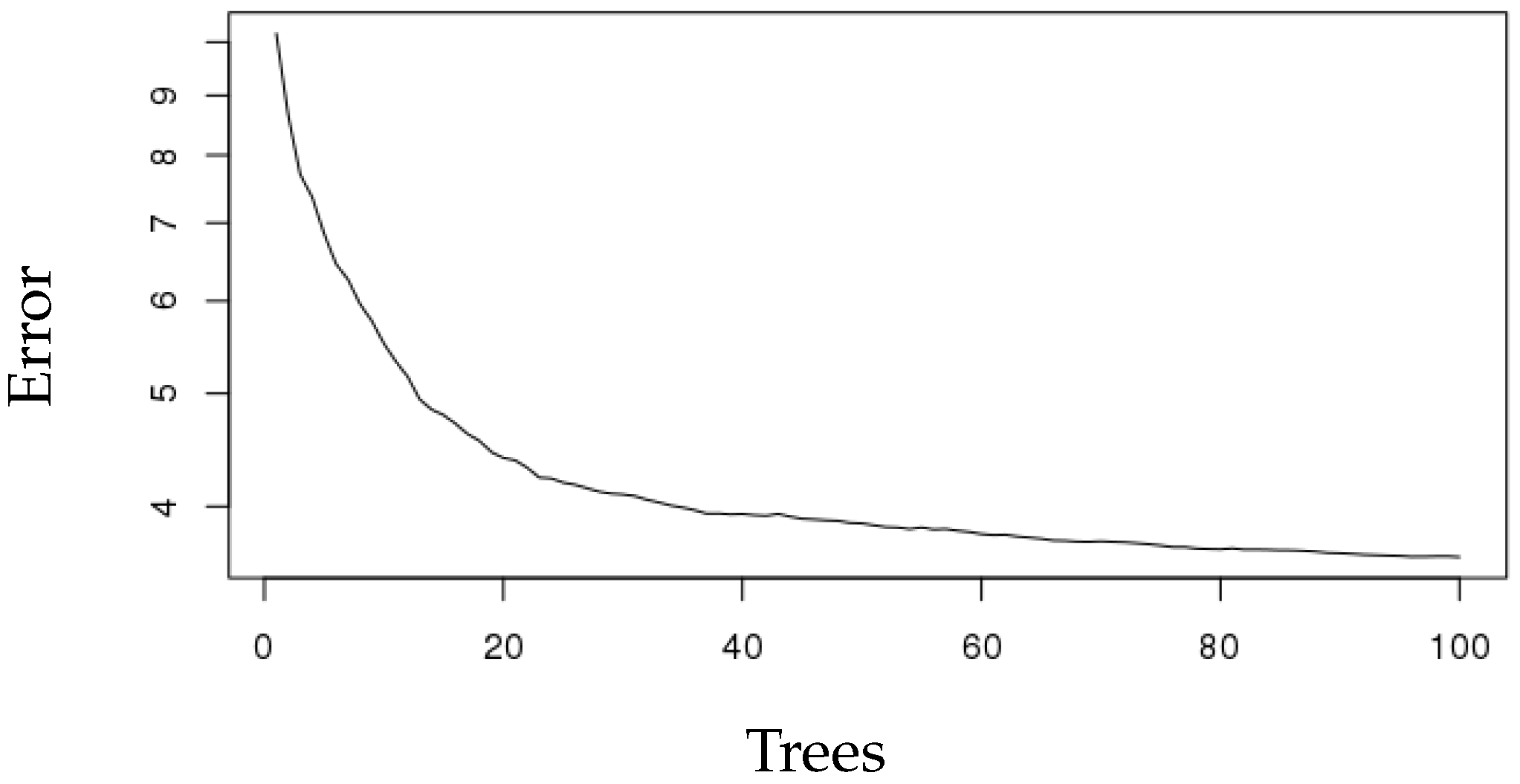
3. Results
4. Discussion
5. Limitations of the Study
6. Conclusions and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Linn, K. Acute Pediatric Neurology. Eur. J. Paediatr. Neurol. 2014, 18, 828. [Google Scholar] [CrossRef]
- Sankhyan, N.; Raju, K.V.; Sharma, S.; Gulati, S. Management of raised intracranial pressure. Indian J. Pediatr. 2010, 77, 1409–1416. [Google Scholar] [CrossRef] [PubMed]
- Palmer, J. Management of raised intracranial pressure in children. Intensive Crit. Care Nurs. 2000, 16, 319–327. [Google Scholar] [CrossRef] [PubMed]
- Klose, M.; Juul, A.; Poulsgaard, L.; Kosteljanetz, M.; Brennum, J.; Feldt-Rasmussen, U. Prevalence and predictive factors of post-traumatic hypopituitarism. Clin. Endocrinol. 2007, 67, 193–201. [Google Scholar] [CrossRef] [PubMed]
- Chambers, I.R.; Jones, P.A.; Lo, T.M.; Forsyth, R.J.; Fulton, B.; Andrews, P.J.; Mendelow, A.D.; Minns, R.A. Critical thresholds of intracranial pressure and cerebral perfusion pressure related to age in paediatric head injury. J. Neurol. Neurosurg. Psychiatry 2006, 77, 234–240. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riordan, M.; Chin, L. Intracranial Pressure Monitors. In Adjuncts for Care of the Surgical Patient, An Issue of Atlas of the Oral & Maxillofacial Surgery Clinics 23-2, E-Book; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Adams, H.; Kolias, A.G.; Hutchinson, P.J. The role of surgical intervention in traumatic brain injury. Neurosurg. Clin. 2016, 27, 519–528. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Xu, P.; Scalzo, F.; Vespa, P.; Bergsneider, M. Morphological clustering and analysis of continuous intracranial pressure. IEEE Trans. Biomed. Eng. 2009, 56, 696–705. [Google Scholar] [PubMed]
- Farhadi, A.; Lloyd, B.; Groat, D.; Mirkovic, J.; Cook, C.B.; Grando, A. iDECIDE: A Mobile Application for Pre-Meal Insulin Dosing Using an Evidence Based Equation to Account for Patient Preferences. In Proceedings of the AMIA, Washington, DC, USA, 14–18 November 2014. [Google Scholar]
- Ursino, M.; Lodi, C.A. A simple mathematical model of the interaction between intracranial pressure and cerebral hemodynamics. J. Appl. Physiol. 1997, 82, 1256–1269. [Google Scholar] [CrossRef] [PubMed]
- Evans, D.; Drapaca, C.; Cusumano, J. Dynamics and Bifurcations in Low-Dimensional Models of Intracranial Pressure. In Mathematical and Computational Approaches in Advancing Modern Science and Engineering; Springer: Berlin, Germany, 2016; pp. 223–232. [Google Scholar]
- Güiza, F.; Depreitere, B.; Piper, I.; Van den Berghe, G.; Meyfroidt, G. Novel methods to predict increased intracranial pressure during intensive care and long-term neurologic outcome after traumatic brain injury: Development and validation in a multicenter dataset. Crit. Care Med. 2013, 41, 554–564. [Google Scholar] [CrossRef] [PubMed]
- Stonebraker, M. Is MR a DBMS? MIT Computer Science and AI Lab: Cambridge, MA, USA, 1993. [Google Scholar]
- Farhadi, A.; Ahmadi, M. The Information Security Needs in Radiological Information Systems—An Insight on State Hospitals of Iran, 2012. J. Digit. Imag. 2013, 26, 1040–1044. [Google Scholar] [CrossRef] [PubMed]
- Kang, H. The prevention and handling of the missing data. Korean J. Anesthesiol. 2013, 64, 402–406. [Google Scholar] [CrossRef] [PubMed]
- Efron, B. Missing data, imputation, and the bootstrap. J. Am. Stat. Assoc. 1994, 89, 463–475. [Google Scholar] [CrossRef]
- Mahmoudi, M. Three Essays in Macroeconomics. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 2017. [Google Scholar]
- Jain, G.; Mallick, B. A study of time series models ARIMA and ETS. SSRN Electron. J. 2017. [Google Scholar] [CrossRef]
- Hassani, H.; Webster, A.; Silva, E.S.; Heravi, S. Forecasting US tourist arrivals using optimal singular spectrum analysis. Tour. Manag. 2015, 46, 322–335. [Google Scholar] [CrossRef]
- Lee, T.F.; Chao, P.J.; Ting, H.M.; Chang, L.; Huang, Y.J.; Wu, J.M.; Wang, H.Y.; Horng, M.F.; Chang, C.M.; Lan, J.H.; et al. Using multivariate regression model with least absolute shrinkage and selection operator (Lasso) to predict the incidence of Xerostomia after intensity-modulated radiotherapy for head and neck cancer. PloS ONE 2014, 9, e89700. [Google Scholar] [CrossRef] [PubMed]
- Vasquez, M.M.; Hu, C.; Roe, D.J.; Chen, Z.; Halonen, M.; Guerra, S. Least absolute shrinkage and selection operator type methods for the identification of serum biomarkers of overweight and obesity: Simulation and application. BMC Med. Res. Methodol. 2016, 16, 154. [Google Scholar] [CrossRef] [PubMed]
- Singer, M.; Deutschman, C.S.; Seymour, C.W.; Shankar-Hari, M.; Annane, D.; Bauer, M.; Bellomo, R.; Bernard, G.R.; Chiche, J.D.; Coopersmith, C.M.; et al. The third international consensus definitions for sepsis and septic shock (sepsis-3). JAMA 2016, 315, 801–810. [Google Scholar] [CrossRef] [PubMed]
- Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998; Volume 1. [Google Scholar]
- Min, J.H.; Lee, Y.C. Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters. Expert Syst. Appl. 2005, 28, 603–614. [Google Scholar] [CrossRef]
- Stone, C.J.; Friedman, J.; Breiman, L.; Olshen, R. Classification and regression trees. Wadsworth Int. Group 1984, 8, 452–456. [Google Scholar]
- Ellis, K.; Kerr, J.; Godbole, S.; Lanckriet, G.; Wing, D.; Marshall, S. A random forest classifier for the prediction of energy expenditure and type of physical activity from wrist and hip accelerometers. Physiol. Meas. 2014, 35, 2191. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Leung, K.S.; Wong, M.H.; Ballester, P.J. Substituting random forest for multiple linear regression improves binding affinity prediction of scoring functions: Cyscore as a case study. BMC Bioinform. 2014, 15, 291. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hunt, R. Percent agreement, Pearson’s correlation, and kappa as measures of inter-examiner reliability. J. Dent. Res. 1986, 65, 128–130. [Google Scholar] [CrossRef] [PubMed]
- Ogutu, J.O.; Schulz-Streeck, T.; Piepho, H.P. Genomic selection using regularized linear regression models: ridge regression, Lasso, elastic net and their extensions. BMC Proc. BioMed Central 2012, 6, S10. [Google Scholar] [CrossRef] [PubMed]
- Smith, M. Monitoring intracranial pressure in traumatic brain injury. Anesth. Analg. 2008, 106, 240–248. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, K.; Morris, W.; Teo, C. Intracranial hypertension: Mechanisms and management. In Pediatric Neurosurgery. Surgery of the Developing Nervous System; WB Saunders: Philadelphia, PA, USA, 1994; pp. 307–319. [Google Scholar]
- Hu, X.; Xu, P.; Asgari, S.; Vespa, P.; Bergsneider, M. Forecasting ICP elevation based on prescient changes of intracranial pressure waveform morphology. IEEE Trans. Biomed. Eng. 2010, 57, 1070–1078. [Google Scholar] [PubMed]
- Swiercz, M.; Mariak, Z.; Krejza, J.; Lewko, J.; Szydlik, P. Intracranial pressure processing with artificial neural networks: Prediction of ICP trends. Acta Neurochir. 2000, 142, 401–406. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Thenmozhi, M. Forecasting stock index movement: A comparison of support vector machines and random forest. SSRN Electron. J. 2006. [Google Scholar] [CrossRef]
- Mahmoudi, M.; Guerrero, F. The transmission of the US stock market crash of 2008 to the European stock markets: An applied time series investigation. Am. J. Econ. 2016, 6, 216–225. [Google Scholar]
- Mayer, S.A.; Dennis, L.J. Management of Increased Intracranial Pressure. Neurologist 1998, 4, 2–12. [Google Scholar] [CrossRef]
| Patients | Total Mean/SD | Training Set (n = 52) | Testing Set (n = 26) |
|---|---|---|---|
| Age: 0 to 2 | 5 | 3 | 2 |
| Age: 2 to 8 | 39 | 25 | 14 |
| Age >8 | 34 | 24 | 10 |
| Sex: Male | 42 | 26 | 16 |
| Sex: Female | 36 | 21 | 15 |
| Days of ICP recordings | 17/14 | 17/16 | 17/19 |
| ICP (mmHg) | 15.3/16.4 | 15.5/18 | 16.3/17.1 |
| Algorithm | CC | MAE | RMSE | RRSE |
|---|---|---|---|---|
| linear Regression | 0.97 | 2.39 | 4.13 | 23.2% |
| ETS | 0.97 | 2.15 | 3.3 | 20.2% |
| ARIMA | 0.97 | 1.89 | 3.0 | 18.7% |
| Lasso Regression | 0.98 | 1.80 | 2.76 | 21.5% |
| Support Vector Machine | 0.98 | 1.59 | 2.74 | 14.25% |
| Random Forest | 0.99 | 0.59 | 0.89 | 5.7% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhadi, A.; Chern, J.J.; Hirsh, D.; Davis, T.; Jo, M.; Maier, F.; Rasheed, K. Intracranial Pressure Forecasting in Children Using Dynamic Averaging of Time Series Data. Forecasting 2019, 1, 47-58. https://doi.org/10.3390/forecast1010004
Farhadi A, Chern JJ, Hirsh D, Davis T, Jo M, Maier F, Rasheed K. Intracranial Pressure Forecasting in Children Using Dynamic Averaging of Time Series Data. Forecasting. 2019; 1(1):47-58. https://doi.org/10.3390/forecast1010004
Chicago/Turabian StyleFarhadi, Akram, Joshua J. Chern, Daniel Hirsh, Tod Davis, Mingyoung Jo, Frederick Maier, and Khaled Rasheed. 2019. "Intracranial Pressure Forecasting in Children Using Dynamic Averaging of Time Series Data" Forecasting 1, no. 1: 47-58. https://doi.org/10.3390/forecast1010004




