Abstract
The literature on discrete valued time series is expanding very fast. Very often we see new models with very similar properties to the existing ones. A natural question that arises is whether the multitude of models with very similar properties can really have a practical purpose or if they mostly present theoretical interest. In the present paper, we consider four models that have negative binomial marginal distributions and are autoregressive in order 1 behavior, but they have a very different generating mechanism. Then we try to answer the question whether we can distinguish between them with real data. Extensive simulations show that while the differences are small, we still can discriminate between the models with relatively moderate sample sizes. However, the mean forecasts are expected to be almost identical for all models.
1. Introduction
The time series of observed counts arise in many real-life applications. Some motivating examples include the daily number of road traffic accidents and injuries, the intra-day transactions of stocks in the financial markets, the weekly number of infected cases following outbreak of a virus and many other applications in different fields. Usually, these series of counts exhibit significant serial auto-correlation and are overdispersed, namely, the observed variance is larger than the sample mean. Thus, it is required to construct a time-series model that can accommodate the features related to discreteness, autocorrelation and overdispersion.
The first papers that popularized the discrete-valued time-series model were by McKenzie [1] and Al-Zaid and Alosh [2]. They introduced the integer-valued auto-regressive model of order one (INAR(1)) with marginal distributions that were Poisson, negative-binomial (NB) and geometric marginal distributions. In the INAR(1) model, the current and the previous-lagged observation are inter-linked using a binomial thinning operator [3], which also serves to ensure the discreteness of the model.
After this initial attempt, many other models have been proposed. For a broad review, see the book of Weib [4]. Sometimes the proposed models, while they are based on a different generating mechanism, share common properties with respect to the marginal distributions and/or the autocorrelation function.
In this paper, we are particularly interested in the INAR(1) model with NB marginal distribution (i.e, NB-INAR(1) process). Initially, McKenzie [1] proposed the NB-INAR(1) with a random binomial thinning operator where the binomial probability follows a Beta distribution. Over the years, other authors have reconsidered other alternative NB-INAR(1) models with some alternative thinning mechanism, such as, for example, the negative binomial thinning defined in Ristic et al. [5].
The present paper intends to provide a comprehensive review of the different representations of the NB-INAR(1)s and compare some NB-INAR(1) models. Ultimately, it is interesting to understand whether we can distinguish (if we can) between these different models that have very similar properties but different generating mechanisms.
The organization of the paper is as follows: Section 2 reviews the models we are going to use for our comparison. Section 3 provides some theoretical comparison between the models, while Section 4 reports the results from simulations to examine whether we can recognize the true underline model that generated the data. Furthermore, a comparison of the forecasts based on the four models is provided. A real data application with the models is described in Section 5, and some concluding remarks can be found in Section 6.
2. Materials and Methods
2.1. Some Background
Al-Osh and Alzaid [2] and McKenzie [6] introduced the integer autoregressive (INAR) model mimicking the well-known AR model for continuous series but preserving the discrete nature of the data. Suppose a sequence of random variables with . Their model assumed that
where ∘ is the binomial thinning operator, defined in Steutel and Van Harn [3] as or, equivalently, that if and 0 otherwise, where ’s are independent Bernoulli () random variables. in the above formulation is an innovation term that follows a discrete distribution. The model has found tremendous extensions in several aspects, considering several different choices of innovation distributions but also by extending the thinning operation in several different directions. An interpretation of the model with binomial thinning is that from those individuals existing at time , some of them survive up to the next time point while new cases arrive.
The above thinning operator has been extended to several different directions [7,8]. A natural idea is to consider a different choice for ’s, also called the counting series, leading to different distributions than the binomial but also allowing for quite different interpretations. An alternative approach can be based on the idea of assuming a non constant in the binomial thinning. A natural way to carry this out is to assume some distribution, for example, a beta, leading to a beta-binomial thinning. Other ideas are to consider some kind of correlation in the counting series, more complicated operations, etc., leading to a wide range of possible approaches.
In the next section, we consider different thinning operators that can lead to negative binomial marginal stationary distributions.
2.2. The Model in McKenzie [1]
The model in Mckenzie [1] is based on binomial thinning, but we further assume that is random and it follows a beta distribution. In particular, if we denote as the distribution with density , , then we obtain a beta binomial thinning operator. We denote this as and then the pmf of Y conditional on X is
For the above beta binomial distribution, the mean is . The model, based on the additive property of the negative binomial distribution, assumes that
where , and is some innovation term. Based on this, we can write the model using the beta binomial thinning as
where . The marginal stationary distribution of is an distribution.
In this paper, we denote as the negative binomial distribution with size parameter and probability parameter p, with pmf given by
.
The conditional distribution is a convolution of a beta binomial with a negative binomial distribution. It is given as
The conditional expectation is , which is obviously linear with respect to the value of . The autocorrelation of order 1 is given as .
For more information about the model, see McKenzie [1] and Jowaheer and Sutradhar [9].
2.3. The Model in Ristic et al. [10]
In this section, we briefly introduce the stationary integer-valued autoregressive process of the first order with negative binomial marginals defined in Ristic et al. [10].
The model is based on the negative binomial thinning operator [5] to replace the binomial thinning. The negative binomial thinning operator is defined as , where is a sequence of independent identically distributed (i.i.d.) random variables with geometric distribution. Therefore, the distribution of is a negative binomial distribution, which is why we call it negative binomial thinning.
The model takes the form
where is an innovation process of i.i.d. random variables independent of , and the random variables and are independent for . With the above specification, the marginal stationary distribution is an distribution.
In this case, the distribution of the innovation is given by the recursive formula
For this distribution, we have and .
The conditional distribution is now given as a convolution of the distribution in (3) and a negative binomial distribution. The conditional expectation of the process is given by
and it is linear with respect to the value of . Note that is the autocorrelation at lag 1, while the autocorrelation is decreasing exponentially.
An interesting interpretation of the negative binomial thinning is that if we have members at time , then each one spreads for the next time point t a random number of offspring and not, as for the binomial thinning, only 0 or 1. Such interpretations for the generating mechanism of the data can be very useful.
The model was also mentioned in Zhu and Joe [11].
2.4. The Model of Al-Osh and Aly [12]
The model proposed by Al-Osh and Aly [12,13,14,15] has a negative binomial marginal distribution, autoregressive structure and linear conditional expectations.
It uses a different thinning operator, namely, the iterated-thinning operator “⊛”. It can be understood as two nested thinning operations [7], where first a binomial thinning ∘ with parameter is applied, and then, another operator ∗ with parameter such that holds. More precisely,
where the i.i.d. counting series of the second operator has the mean . Conditional on , we have .
In Al-Osh and Aly [12] and Weib [7], the special case of iterated thinning together with a geometric counting series is considered.
Following Aleksandrov et al. [16], we denote the following:
and then, the conditional mean is simply .
Then, Al-Osh and Aly [12] defined a model as
where the innovations follow an distribution with mean and . All the thinnings are performed independently.
An alternative representation of the model is
where , and . Furthermore, due to the property of the negative binomial, we can further split as , where , and , and thus,
which resembles more the time-series representation given in Edwards and Gurland [17].
The model is based on the bivariate negative binomial distribution in Edwards and Gurland [17] and the conditional distribution, as can be seen from the above representation, is the convolution of three variables. Note that the innovation is independent of the others, but depends on . The model has linear conditional mean and negative binomial marginal distribution, i.e., with mean and variance , while the autocorrelation function is at lag h.
2.5. A Copula Based Model
Finally, we propose a model based on copulas. The idea is based on an alternative representation of the models through the conditional distribution of given . The motivation is that since we want to have known marginal distribution (negative binomial in our case), one may consider a bivariate negative binomial distribution defined through copulas. To achieve the AR(1) property it suffices to consider a multivariate copula based model, where all the marginal distributions are the same and the multivariate copula has an AR(1) structure of covariance. We have used a Gaussian copula with AR correlation structure to define the joint distribution.
A d-dimensional Gaussian copula has cumulative distribution function (cdf) given by
where is the inverse cumulative distribution function of a standard normal distribution and is the joint cumulative distribution function of a multivariate normal distribution with mean vector zero and covariance matrix equal to .
As such, one can derive the conditional distribution of given , denoted as , simply as
where denotes the joint distribution of two random variables. Note that in the bivariate case, we have
so is the autocorrelation parameter.
For a discrete distribution the joint probability function can be derived with finite differences, namely.
where and are the marginal cdfs for X and Y respectively and is any copula (see [18]).
We assume that the marginal distributions are negative binomial distributions with size parameter and probability , namely, based on the representation in (1).
The conditional expectation is not linear (see, e.g., [19]). For our case, one can derive the conditional expectation numerically.
Therefore, the above representation allows us to create models with given marginals in a rigorous way, removing the need to specify the thinning operation.
Remark 1.
Note that many models can be derived this way. For example, the celebrated Poisson INAR model of Al-Osh and Alzaid [2] and McKenzie [6] can be seen as a model with a bivariate Poisson distribution, defined in Kocherlakota and Kocherlakota [20] as the joint distribution that gives rise to a conditional distribution as a convolution of a binomial and a Poisson, exactly as the binomial thinning representation dictates. Furthermore, the model defined in Section 2.4 is based on a bivariate negative binomial joint distribution, given in Edwards and Gurland [17].
Remark 2.
The model above can be seen as related to what is described in Escarela et al. [21] for a binary time series. For more details about models defined based on Markov properties, see the work in Joe [22]. For a recent work on count time series based on copulas, see Zhang et al. [23].
2.6. Some Comments
In order to sum up this Section, we remark that for all the four models the marginal distribution is a negative binomial distribution, while the autocorrelation structure is autoregressive of an order 1 process. On the other hand, the generating mechanism is different. The McKenzie model assumes a random binomial thinning, i.e., for each time point the thinning probability changes based on a beta distribution. The model of Ristic is based on a different thinning, namely, the negative binomial thinning. Compared to binomial thinning. the negative binomial thinning allows more than one offspring to appear in the next time points. The model of Al-Osh and Aly assumes some thinning that depends on the previous observation, which is quite a different assumption from those in the previous models. Finally, the copula-based model assumes a conditional distribution that is based on a copula, and its conditional expectation is not linear, as all the other models assume. In practical terms, the different models can describe different situations and generating mechanisms, and therefore, it is a challenging question whether one can recognize the underlying mechanism from the available data.
2.7. Final Remarks and More Models
We have presented four models that lead to marginal negative binomial distribution and have an autoregressive structure of order 1. For all of them, the generating mechanism is different, and hence, it provides different insights.
We know that in the literature, there are more models that lead to negative binomial marginals while maintaining the autoregressive structure. Zhu and Joe [11] described more models based on other thinning operators. Furthermore, one can find alternative derivations in Gourieroux and Lu [24] and Leonenko et al. [25]. We have selected the four models in order to examine how easy it is to identify the correct model from real data while maintaining a reasonable level of interpretation. For some models, the underlying assumptions are hard to interpret.
3. Results and Discussion: Some Comparisons
The aim of this section is to examine whether we can recognize the underlying model in the available data. Note that in Zhu and Joe [11], four models with negative binomial marginal distribution were also examined based on their theoretical properties. In our case, we go further by examining the models (which are not the same as those in Zhu and Joe [11]) from an applied point of view, namely, whether we can discriminate the underlying model from real data and whether the forecasting ability of the models differs.
We consider conditional maximum likelihood estimation. The reason is that when basing estimation on moments, the four models share a lot of common moments; hence, it would have been impossible to recognize them. On the other hand, the conditional maximum likelihood approach is based on the conditional distribution, which contains the information about the generating mechanism of the models, and therefore, it differs. It is a matter of investigation how much they differ, and this is the purpose of the present section.
Given data , the conditional log-likelihood is given by
where denotes the totality of the parameters. It is interesting to point out that all four models have the same number of parameters, namely, three.
As a first idea, in Figure 1 and Figure 2, we plotted the conditional distribution for all models under the assumption that the autocorrelation at lag 1 is 0.2 and 0.5 and that the stationary marginal distribution is (in all cases) a negative binomial distribution with mean equal to 6 and variance equal to 18. Figure 1 and Figure 2 present all the conditional distributions given where the previous value was y, i.e., this is . The four models are labeled hereafter as ALY for the model in [12], GC for the model with the Gaussian copula, MC for the model in [1] and NA for the model in [10].
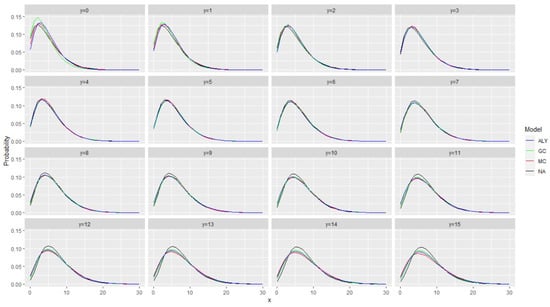
Figure 1.
The conditional distribution for all models under the assumption that the autocorrelation at lag 1 is 0.2 and that the stationary marginal distribution is (in all cases) a negative binomial distribution with mean equal to 6 and variance equal to 18. The figure presents all the conditional distributions given where the previous value was y. The models are labeled as ALY for the model in [12], GC for the model with the Gaussian copula, MC for the model in [1] and NA for the model in [10].
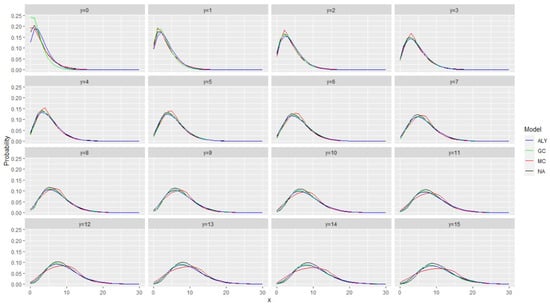
Figure 2.
The conditional distribution for all models under the assumption that the autocorrelation at lag 1 is 0.5 and that the stationary marginal distribution is (in all cases) a negative binomial distribution with mean equal to 6 and variance equal to 18. The figure presents all the conditional distributions given where the previous value was y. The models are labeled as ALY for the model in [12], GC for the model with the Gaussian copula, MC for the model in [1] and NA for the model in [10].
Figure 1 and Figure 2 show that the probability distributions are very close with minor discrepancies. The closeness, however, depends on the value of y (the conditioning value). This gives some idea (and hope) that the log-likelihood will be able to separate the different models and recognize the correct one. A final point is that we have noticed that when the autocorrelation decreases, the differences between the conditional distributions are also decreasing. One can notice that the discrepancies in the case of autocorrelation equal to 0.2 are smaller.
To further support the idea, we have also plotted in Figure 2, for all the distributions, the conditional mean and variance for all the values of . Again, all the marginal distributions are negative binomials with mean equal to 6 and variance equal to 18, and the autocorrelation was the same and equal to 0.5. Similar behavior is observed for autocorrelation 0.2 so we do not present the plots.
Figure 3 shows the conditional expectation and the conditional variance. Not surprisingly, the expectation of the three models are identical and hard to discern. All three have a linear conditional expectation with the same slope, which is the autocorrelation parameter.
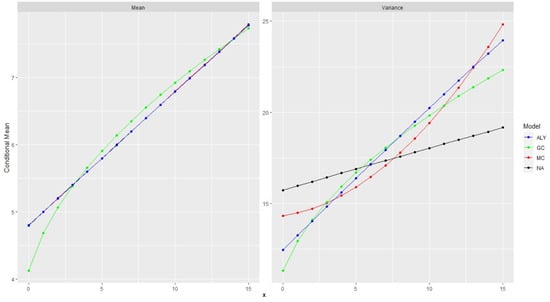
Figure 3.
Conditional expectations and conditional variances for all the 4 models. We have assumed for all of them that the marginal distributions are the same negative binomials and the autocorrelation was set to 0.5.
Only the one with the Gaussian copula shows a slightly curved expectation. This is interesting since the one-step-ahead forecast is simply the conditional expectation, and hence, they provide the same forecast. The case with the variance is different. For some methods, when the conditional variance is linear, the slope differs and, in general, the four models are very different with respect to the conditional variance. Furthermore, the shape is different between the methods. This implies that in the case of probabilistic forecasts, like forecasts with confidence intervals, the methods may differ.
4. Results and Discussion: Simulations
4.1. Discriminating between the Models
In order to see whether we can distinguish between the four different models, we run the following simulation experiment. We have simulated data with different sample sizes, and 500, using the same negative binomial marginal distribution, namely, one with mean equal to 6 and variance equal to 18. We also considered two values for the autocorrelation parameter, namely, 0.2 and 0.5.
Then, from each model, with the given sample size and autocorrelation, we took 500 samples and, applying conditional ML, we checked which model provided better conditional log-likelihood. One would expect to find the true model, namely, the one used to simulate the data, as the one with better log-likelihood. Table 1 reports the number of times each model was selected in the above experiment. For example, one can see that if the true model was the McKenzie model (MC), and the autocorrelation was 0.5, as the sample size increased, we selected the true model in almost all cases. This was the best success rate. For smaller autocorrelations, we had more problems identifying the true model. Recall that for smaller autocorrelations, the conditional distributions were closer.

Table 1.
Number of times each model was selected in 500 replications. The true model that generated the data is the one under the column “Model”. We used different autocorrelation parameter values, namely, and .
For a small sample size and little autocorrelation, it is not easy to distinguish between the models. For , the McKenzie and Ristic models can be selected correctly more frequently.
It seems that the relationships between models depend on the sample size and the autocorrelation in the sense that the model that was selected more frequently after the original model varies based on them.
To sum up the experiment, it seems that with a relatively moderate sample size, we can select the true underlying model very often. The size of the autocorrelation is also important for that; the larger the autocorrelation, the more probable a correct selection.
4.2. Forecasting
Forecasting could be pursued within the usual framework of conditional expectations. In general, the h-step ahead forecast, when T periods are used in fitting, is given by , which leads to minimum mean squared error forecasts. Depending on the model used to fit the data, different estimated conditional mean functions arise. In our case, we focus on one-step-ahead forecasts, so , and as we have seen, the conditional expectations are linear for the three models and non-linear for the Gaussian copula model. Unlike the Box Jenkins time-series models, which usually predict real values via the conditional mean, this is not suitable in our case due to the discreteness of the data. We consider alternative approaches aiming at applying coherent forecasting in order to obtain an integer forecast. The authors of [26] proposed the use of the median of the forecasting distribution, which is an integer. More details about coherent forecasting for integer valued time series can be found in [26,27,28].
Here, we use as median the minimum value for which the cumulative distribution is larger than 0.5. It is also possible to show that the median has the optimality property of minimizing the expected absolute error [26]. Alternatively, one may use the mode of the conditional distribution. We do not report results with the mode since they consistently gave the worst forecasts.
To sum up, we have used two different forecasts. The first is the typical mean prediction, i.e., we used the . We have also used the median of the predictive distribution as a forecast. The one-step predictive distribution is the conditional distribution, and hence, we can easily calculate this.
In order to compare the different models for their forecasting potential, we have also run a forecasting simulation. We simulated 500 samples from each model using the same structure as before, namely, two different levels of autocorrelation , three sample sizes and chosen parameters so as to have the same negative binomial distributions with mean equal to 6 and variance equal to 18.
For each sample of size T, we kept the first observations to fit the models and then we used the last observation for forecasting based on the estimated model. Here, we report the mean absolute error:
where is the number of samples taken, and denotes the T-th (last) observation taken from the i-th replication sample, and denotes the forecast of the observation based on the past observation of the sample.
The results are reported in Table 2. The reported values are the MAE from the 500 simulations. We report both the mean forecasts and the median forecasts for all the models. The column data present the true model from which we have simulated the data. It is very interesting to see that the different models provide the same forecasts for both methods. It is very hard to find a winner. Moreover, note that median forecasting has slightly smaller MAE in most cases.

Table 2.
MAE results from the simulation experiments. We report both the mean forecasts and the median forecasts for all the models. The column data present the true model from which we have simulated the data.
Figure 4 shows a scatter matrix from one of the experiments. The data were generated from the McKenzie model with and sample size . The data refer to the 500 one-step-ahead forecasts made by all methods using the mean prediction. We see that all cases are highly correlated. The Pearson correlation is larger than 0.98 in all pairs. One can see also that only for the Gaussian copula, we have a slight deviation from a straight line, since the conditional expectations are not linear. We can have similar plots from all other configurations. This is a very strong indication about the agreement of the forecasts with the different models. In practice, it is too hard to select one model among the others for its ability to forecast. Moreover, note that as we have seen in Figure 3, the conditional expectations coincide, but here, the estimated parameters have minor differences, producing the minor differences in the forecasts.
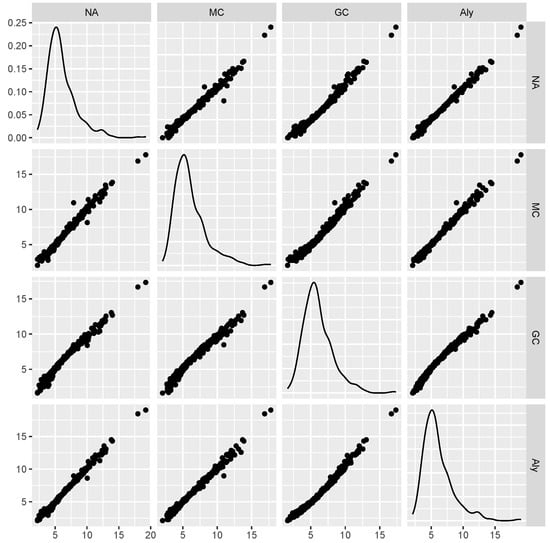
Figure 4.
Scatter matrix from one of the experiments, namely, data were generated from the McKenzie model with and sample size . The data refer to the 500 one-step-ahead forecasts made by all methods using the mean prediction. We see that all cases are highly correlated.
The above results reveal that the one-step forecasts from the different models are relatively the same, and it is very hard to say which method performed better since the errors are very close. Even when we forecast with the true model that generated the data, it is hard to see any differences. Perhaps we may need a much larger sample size before being able to select one model, but this is perhaps not realistic with the usual sample sizes we have. What is really interesting is that in all configurations, the usage of the median as forecast provided smaller MAE for all methods, sample sizes and values of the autocorrelation parameter. Perhaps it can be advised to prefer the median from the mean at the cost of the extra effort to derive the forecast distribution needed to calculate the median.
5. Results and Discussion: Real Data Application
In this section, we fit the four models to a well-known data set in order to see their fit and forecasting ability. We make use of the campylobacter data set [29] that refers to the number of cases of campylobacter infections in the north of the province Quebec (Canada) in four week intervals from January 1990 to the end of October 2000. It has 13 observations per year and 140 observations in total. Campylobacterosis is an acute bacterial infectious disease attacking the digestive system. The data and their autocorrelation are shown in Figure 5 and were first reported by [30]. The data show overdispersion (mean = 11.54, variance = 53.24), and they also have autocorrelation.
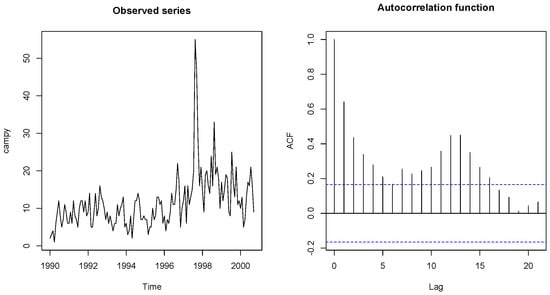
Figure 5.
Campylobacterosis dataset and its autocorrelation function.
We fitted all four models in the data using the conditional ML method. The estimated parameters and their standard errors can be seen in Table 3. We used the optim function in R for the optimization and the Hessian to derive the standard errors. The log-likelihood of all the models is quite close, while the Ristic model provides slightly better log-likelihood, but the differences are small. Moreover, note that the estimated autocorrelation at lag 1 is slightly different between the models. For McKenzie, this is ; for Ristic, it is ; for the Al-Osh and Aly model, it is ; and finally, for the copula model, it is . Note that for the copula model, the parameter is not exactly the autocorrelation but that of the underlying Gaussian copula, so we expect it to be somewhat smaller. The observed autocorrelation is 0.642. The minor differences in the estimated autocorrelation may also explain the differences in the one-step-ahead forecasts.

Table 3.
The fitted models. Parameter estimates and their standard errors. We also report the log-likelihood of the models.
The goodness-of-fit for the models is an interesting issue. Here, since all models share the same properties for the marginal distribution and the autocorrelations, tests that make use of the conditional or joint distributions are needed in order to be able to recognize the underlying models. On the other hand, for small to moderate sample sizes, it is very difficult to accomplish.
We also calculated the one-step-ahead prediction for the last observation. We fitted the models without the last observation, and then we derived the conditional distributions for . The distributions can be seen in Figure 6. One can see that the agreement is quite large, but minor differences are present. The vertical line is the observed value (.
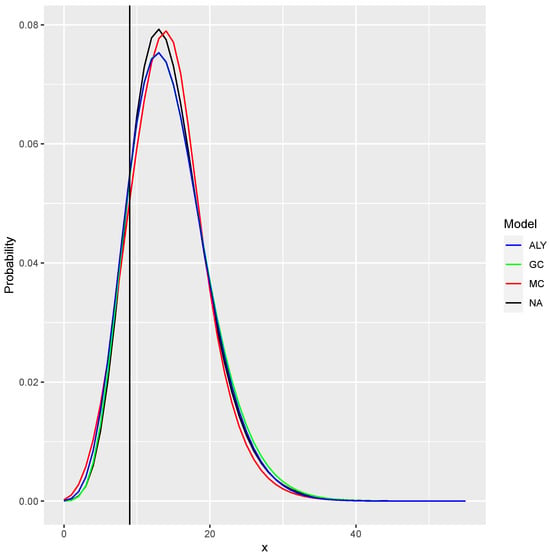
Figure 6.
The conditional distribution for given that . All four models provide very close conditional distribution. The vertical line is the observed value.
The conditional mean and the conditional variance for the four models can be read in Table 4. We have also reported the confidence interval as follows: We aim for a 95% confidence interval. The discrete nature of the data do not allow for an exact 95% interval, so we report an interval that is smaller than 95% but as close to 95% as possible. We also report the level, i.e., the probability that the interval covers.

Table 4.
Ahead forecasts derived through simulation from all models. We report the mean, the variance and the median for each time point.
Finally, we also attempted to forecast in a greater horizon. The conditional distributions for k-steps ahead are not always available, so we used a simulation-based approach. Based on the estimated parameters, we simulated paths up to 10-steps ahead from each model. We replicated this procedure 10,000 times and we report the mean, the variance and the median found. The results are reported in Table 4. One can see that there are minor differences in the mean and recall, as well as some Monte Carlo error. Looking at the variance, the differences are more prominent.
6. Conclusions
In this paper, we compared different autoregressive models that provide AR structure and marginal distribution of the data, which is a negative binomial distribution. We used four such models while there are more in the literature with the above characteristics. The aim was to examine whether we can separate/recognize the true model from the data since all the models have very similar characteristics.
The results show that there is a very large overlap between the models, and it is hard to recognize them from the real data, while the forecasting provided by the different models is pretty much the same. What makes the problem even more challenging is the fact that the generating mechanism of the different models is quite different, giving rise to different insights. For example, the model of McKenzie [1] assumes a beta binomial thinning, which can be interpreted as a mechanism that each value provides at the next time point for some offspring but the probability of surviving is a random following beta distribution. This is the extension of the binomial thinning interpretation. On the other hand, the model of Ristic et al. [10] with the negative binomial thinning implies that each value can produce a different number of offspring at the next period, which is a very different interpretation. The model of Al-Osh and Aly [12] implies that the innovations may depend on the value at the previous time points, which is also a very different way to see the generating mechanism. Recognizing the underlying model could have provided insights on the underlying mechanism. The results show that this is hard.
Another approach to select among the models is their ability to extend, either to higher order models but also to the case when regressors can be used. In this case, some external information can improve the models. Introducing regressors is not difficult for all the models in the sense that typically this is carried out on the innovation part of the model. For the model in McKenzie [1] and Al-Osh and Alzaid [2], this is easy since the innovations are following a negative binomial distribution. However, since the regressors typically apply on the mean of the distribution, the model specification may create difficulties in embedding such information. The model based on the Gaussian copula is more straightforward on how to carry this out. As far as computational complexity, all models are relatively simple to work with since the conditional distributions can be derived, if not in closed form, with rather simple computations. Moreover, note that the conditional distribution is a convolution, and as such, it can be calculated rather easily. For more details see [31].
Our analysis showed that while the conditional mean is almost identical for all models (truly identical for three of them), the conditional variance differs, and this can be the basis to distinguish between the models. We believe that since we can define a large range of different models with very close properties, we need to emphasize the interpretations provided by the model and the insights that this can generate.
Finally, we believe that based on the used models and as a scope for future work, one can consider other families of models, such as, for example, bivariate INAR models with bivariate negative binomial marginals but also univariate models with given marginal distributions other than the negative binomial.
Author Contributions
Conceptualization, D.K.; methodology, N.M.K.; software, D.K.; validation, N.M.K. and Y.S.; formal analysis, D.K.; investigation, Y.S.; resources, D.K.; data curation, D.K.; writing—original draft preparation, D.K.; writing—review and editing, N.M.K. and Y.S.; visualization, Y.S.; supervision, D.K.; project administration, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors hereby declare that there is no funding statement to disclose for this research 428 and the APC was funded by a discount voucher.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
We make use of the campylobacter data set (Liboschik, T.; Fokianos, 432 K.; Fried, R. tscount: An R package for analysis of count time series following generalized linear 433 models. J. Stat. Softw. 2017, 82, 1–51).
Conflicts of Interest
The authors declare that there was no conflict of interest.
References
- McKenzie, E. Autoregressive moving-average processes with negative-binomial and geometric marginal distributions. Adv. Appl. Probab. 1986, 18, 679–705. [Google Scholar] [CrossRef]
- Al-Osh, M.A.; Alzaid, A.A. First-order integer-valued autoregressive (INAR (1)) process. J. Time Ser. Anal. 1987, 8, 261–275. [Google Scholar] [CrossRef]
- Steutel, F.W.; van Harn, K. Discrete analogues of self-decomposability and stability. Ann. Probab. 1979, 7, 893–899. [Google Scholar] [CrossRef]
- Weiß, C.H. An Introduction to Discrete-Valued Time Series; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Ristić, M.M.; Bakouch, H.S.; Nastić, A.S. A new geometric first-order integer-valued autoregressive (NGINAR (1)) process. J. Stat. Plan. Inference 2009, 139, 2218–2226. [Google Scholar] [CrossRef]
- McKenzie, E. Some simple models for discrete variate time series 1. J. Am. Water Resour. Assoc. 1985, 21, 645–650. [Google Scholar] [CrossRef]
- Weiß, C.H. Thinning operations for modeling time series of counts—a survey. AStA Adv. Stat. Anal. 2008, 92, 319–341. [Google Scholar] [CrossRef]
- Scotto, M.G.; Weiss, C.H.; Gouveia, S. Thinning-based models in the analysis of integer-valued time series: A review. Stat. Model. 2015, 15, 590–618. [Google Scholar] [CrossRef]
- Jowaheer, V.; Sutradhar, B.C. Analysing longitudinal count data with overdispersion. Biometrika 2002, 89, 389–399. [Google Scholar] [CrossRef]
- Ristić, M.M.; Nastić, A.S.; Bakouch, H.S. Estimation in an integer-valued autoregressive process with negative binomial marginals (NBINAR (1)). Commun. Stat.-Theory Methods 2012, 41, 606–618. [Google Scholar] [CrossRef]
- Zhu, R.; Joe, H. Negative binomial time series models based on expectation thinning operators. J. Stat. Plan. Inference 2010, 140, 1874–1888. [Google Scholar] [CrossRef]
- Al-Osh, M.A.; Aly, E.E.A. First order autoregressive time series with negative binomial and geometric marginals. Commun. Stat.-Theory Methods 1992, 21, 2483–2492. [Google Scholar] [CrossRef]
- Wolpert, R.L.; Brown, L.D. Markov infinitely-divisible stationary time-reversible integer-valued processes. arXiv 2021, arXiv:2105.14591. [Google Scholar]
- Leisen, F.; Mena, R.H.; Palma, F.; Rossini, L. On a flexible construction of a negative binomial model. Stat. Probab. Lett. 2019, 152, 1–8. [Google Scholar] [CrossRef]
- Guerrero, M.B.; Barreto-Souza, W.; Ombao, H. Integer-valued autoregressive processes with prespecified marginal and innovation distributions: A novel perspective. Stoch. Model. 2022, 38, 70–90. [Google Scholar] [CrossRef]
- Aleksandrov, B.; Weiß, C.H.; Nik, S.; Faymonville, M.; Jentsch, C. Modelling and diagnostic tests for Poisson and negative-binomial count time series. Metrika 2023, 1–45. [Google Scholar] [CrossRef]
- Edwards, C.B.; Gurland, J. A class of distributions applicable to accidents. J. Am. Stat. Assoc. 1961, 56, 503–517. [Google Scholar] [CrossRef]
- Nikoloulopoulos, A.K. Copula-based models for multivariate discrete response data. In Proceedings of the Copulae in Mathematical and Quantitative Finance: Proceedings of the Workshop, Cracow, Poland, 10–11 July 2012; Springer: Berlin/Heidelberg, Germany, 2013; pp. 231–249. [Google Scholar]
- Crane, G.J.; Hoek, J.v.d. Conditional expectation formulae for copulas. Aust. N. Z. J. Stat. 2008, 50, 53–67. [Google Scholar] [CrossRef]
- Kocherlakota, S.; Kocherlakota, K. Bivariate Discrete Distributions; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Escarela, G.; Perez-Ruiz, L.C.; Bowater, R.J. A copula-based Markov chain model for the analysis of binary longitudinal data. J. Appl. Stat. 2009, 36, 647–657. [Google Scholar] [CrossRef]
- Joe, H. Markov models for count time series. In Handbook of Discrete-Valued Time Series; Chapman and Hall/CRC: New York, NY, USA, 2016; pp. 49–70. [Google Scholar]
- Zhang, M.; Wang, H.J.; Livsey, J. Copula Based Analysis for Count Time Series. Stat. Sin. 2024, prepint. [Google Scholar] [CrossRef]
- Gouriéroux, C.; Lu, Y. Negative binomial autoregressive process with stochastic intensity. J. Time Ser. Anal. 2019, 40, 225–247. [Google Scholar] [CrossRef]
- Leonenko, N.N.; Savani, V.; Zhigljavsky, A.A. Autoregressive negative binomial processes. Ann. l’ISUP 2007, 51, 25–47. [Google Scholar]
- Freeland, R.K.; McCabe, B.P. Forecasting discrete valued low count time series. Int. J. Forecast. 2004, 20, 427–434. [Google Scholar] [CrossRef]
- Maiti, R.; Biswas, A. Coherent forecasting for over-dispersed time series of count data. Braz. J. Probab. Stat. 2015, 29, 747–766. [Google Scholar] [CrossRef]
- Jung, R.C.; Tremayne, A.R. Coherent forecasting in integer time series models. Int. J. Forecast. 2006, 22, 223–238. [Google Scholar] [CrossRef]
- Liboschik, T.; Fokianos, K.; Fried, R. tscount: An R package for analysis of count time series following generalized linear models. J. Stat. Softw. 2017, 82, 1–51. [Google Scholar] [CrossRef]
- Ferland, R.; Latour, A.; Oraichi, D. Integer-valued GARCH process. J. Time Ser. Anal. 2006, 27, 923–942. [Google Scholar] [CrossRef]
- Karlis, D.; Chutoo, A.; Mamode Khan, N.; Jowaheer, V. The multilateral spatial integer-valued process of order 1. Stat. Neerl. 2024, 78, 4–24. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).