Prepivoted Augmented Dickey-Fuller Test with Bootstrap-Assisted Lag Length Selection

Abstract

We investigate the application of prepivoting in conjunction with lag length selection to correct the size and power performance of the Augmented Dickey-Fuller test for a unit root. The bootstrap methodology used to perform the prepivoting is a residual based AR bootstrap that ensures that bootstrap replicate time series are created under the null irrespective of whether the originally observed series obeys the null hypothesis or not. Simulation studies wherein we examine the performance of our proposed method are given; we evaluate our method’s performance on ARMA(1,1) models with varying configurations for size and power performance. We also propose a novel data dependent lag selection technique that uses bootstrap data under the null to select an optimal lag length; the performance of our method is compared to existing lag length selection criteria.

1. Introduction

Unit root testing is a central problem of time series and econometric analysis. For example, the presence (or not) of a unit root in time series data has huge repercussions in forecasting applications. In econometric analyses, unit roots render the data to be highly sensitive to shocks; while stationary processes tend to revert to the mean in the presence of shocks, random walks tend to diverge.

The primary approaches to unit root testing include the augmented Dickey-Fuller (henceforth referred to as ADF) test [1], and the Phillips-Perron (PP) test [2]. Extensive literature including the work of Schwert (1989) [3], Perron and Ng (1996) [4] as well as Davidson and MacKinnon (2004) [5] point to evidence that PP tests underperform with respect to size in finite samples compared to ADF tests since PP tests are highly reliant on asymptotic results; additionally PP tests suffer from severe size distortions in the presence of negative moving average errors. However, the ADF test may suffer from reduced power; see Paparoditis and Politis (2018) [6] and references therein.

The ADF test examines the presence of a unit root in a stretch of time series data $X_1,X_2,\dots X_n$ by focusing on the Ordinary Least Squares (OLS) estimate $\widehat{\rho }$ of $\rho$ in the regression equation

$$X_t=\rho X_{t-1}+\sum _{i=1}^q{a}_{j,q}\Delta X_{t-i}+e_{t,q}$$

(1)

fitted to the observed data. In the above equation, we use the notation $\Delta X_t=X_t-X_{t-1}$. Additionally, note that the number of lagged differences (denoted by q) is allowed to vary with the sample size n, and thus q is an abbreviated notation for $q_n$. The null and alternative hypotheses for the ADF testing framework are as follows.

$$\begin{array}{cc}\hfill {\mathrm{H}}_0& :X_t=X_{t-1}+U_t\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\mathrm{H}}_a& :X_t=U_t\hfill \end{array}$$

(3)

A typical assumption in the above is that $U_t={\sum }_{j=1}^{\infty }{a}_j{U}_{t-j}+e_t$, where the $a_j$ are autoregressive (AR) coefficients, and $e_t$ is a sequence of independent, identically distributed (i.i.d.) mean zero random variables with finite (and nonzero) variance, denoted by ${\sigma }_e^2$; however, the i.i.d. assumption on $e_t$ can be relaxed as discussed in Section 2. To elaborate, the hypotheses are essentially that under the null, the series $X_t$ is obtained by integrating an infinite order autoregressive process, while the alternative is that the series is a de facto infinite order autoregressive process. The process $U_t$ can be guaranteed to be stationary and causal by imposing conditions on its coefficients, namely ${\sum }_{j=1}^{\infty }{\left|j\right|}^s\left|a_j\right|<\infty$ for some $s\ge 1$ and that ${\sum }_{j=1}^{\infty }{a}_j{z}^j\ne 0$ for all $\left|z\right|\le 1$.

In their seminal work on the topic, Dickey and Fuller (1979) [1] suggested the studentized statistic

$$t_{n,q}={\displaystyle \frac{{\widehat{\rho }}_n-1}{\widehat{\mathrm{Std}}\left({\widehat{\rho }}_n\right)}}$$

with $\widehat{\mathrm{Std}}\left({\widehat{\rho }}_n\right)$ used to denote the estimated standard deviation of the OLS estimator of $\rho$. We explicitly denote the importance of the lag length q by using the notation $t_{n,q}$ to denote the ADF test statistic as opposed to $t_n$. The distribution of this studentized statistic under the null is non-standard/non-normal; however, it is free of unknown parameters, and has been promulgated in econometric and statistics literature. Assumptions under which this distribution is valid have been progressively relaxed since Dickey and Fuller’s original work in 1979; see [6] for a chronological account.

The ADF test has been demonstrated to have less than ideal size and power performance in real world applications. It is well examined in literature [3,7] that the presence of negative MA coefficients in the data generating process causes severe size distortions, while the work of Paparoditis and Politis [6] offers a concrete real world example wherein the power performance is poor. The latter work also provides evidence of the asymptotic collinearity problem in the ADF regression; the collinearity becomes more prominent for large q, in which case loss of power ensues. The issue is then how to work with a moderate value of q while still achieving a (close to) nominal size of the ADF test.

A succinct summary justifying the choice of adopting the prepivoting framework for the ADF test comes from Section 3 of Beran (1988) [8], where the author demonstrates that (under regularity conditions and in the case where the asymptotic null distribution of the test statistic is independent of the unknown parameters) prepivoted tests have smaller order errors in rejection probability than that of the asymptotic theory test. Since the asymptotic null distribution of the OLS estimate ${\widehat{\rho }}_n$ from the ADF regression is independent of $\rho$, the ADF test belongs to the category of hypothesis tests that stand to benefit from the prepivoting framework.

The remainder of this paper is organized as follows. Section 2 reviews the asymptotic properties of the ADF test statistic, along with conditions on $q_n$ for good size and power. We also demonstrate that the AR-sieve bootstrap of Paparoditis and Politis [9] is a prepivoted test in the sense of Beran [8]. Section 3 highlights the consistency of the prepivoted ADF test against fixed and local alternatives. Section 4 details the results of numerical experiments wherein we study the empirical performance of the prepivoted ADF test for different lag length specifications. Section 5 introduces a novel bootstrap-based tuning parameter selection algorithm and its application to the prepivoted ADF test, along with numerical experiments that demonstrate its efficacy with respect to both size and power.

2. Asymptotic Properties of the ADF Test

The asymptotic properties of the ADF test primarily hinge upon the convergence results of the test statistic $t_{n,q}$ under the null and the alternative, as well as the conditions governing the underlying stationary process $U_t$. In what follows, we proffer a brief summary of the relaxations to assumptions under which the convergence result of the test statistic $t_{n,q}$ under the null. Dickey and Fuller [1] initially derived the non-standard null distribution of the statistic under the assumption that the underlying process is autoregressive with known and finite order. The result was consequently extended in 1984 by Said and Dickey [10] to the setup where the innovation process $U_t$ is an invertible ARMA process; the latter can be expressed as an AR$(\infty )$ process with exponentially decaying coefficients. Further relaxations to conditions have been examined in literature with Chang and Park (2002) [11] considering the case that $\left\{e_t\right\}$ is a martingale difference sequence and in 2018, Paparoditis and Politis [6] showed the convergence under the sole provision that the innovation process $U_t$ has a continuous spectral density that is strictly positive; this is can also be stated in the equivalent form that the process $U_t$ has a Wold-type AR representation with respect to just white noise errors, allowing for a much larger class of time series versus hitherto linear AR$(\infty )$ processes with i.i.d. or martingale difference innovations. The following subsections review the two main asymptotic results of the ADF test statistic from the work of Paparoditis and Politis (2018) [6].

2.1. Behaviour of the Test Statistic Under the Null

We now describe the convergence behavior of the test statistic $t_{n,q}$. We adopt the general framework of Paparoditis and Politis [6], and assume that $U_t$ is a mean zero weakly stationary process with autocovariance function ${\gamma }_U\left(h\right)=\mathrm{Cov}(U_0,U_h)$ that is absolutely summable; hence, the spectral density $f_U\left(w\right)={\left(2\pi \right)}^{-1}{\sum }_{h=-\infty }^{\infty }{\gamma }_U\left(h\right)e^{iwh}$ is well-defined. We also assume that the logarithm of the spectral density $f_U$ is integrable, and therefore $U_t$ admits the Wold representation

$$U_t=\sum _{j=1}^{\infty }{\alpha }_j{ϵ}_{t-j}+{ϵ}_t$$

where ${\sum }_{j=1}^{\infty }{\alpha }_j^2<\infty$ and ${ϵ}_t$ is a white noise, i.e., a weakly stationary process with zero mean, common variance and $\mathrm{Cov}({ϵ}_t,{ϵ}_k)=0$ for $t\ne k$; see Brockwell and Davis [12].

If we further assume that $f_U\left(w\right)>0$ for all w, then $U_t$ also admits the Wold-type AR representation:

$$U_t=\sum _{j=1}^{\infty }{b}_j{U}_{t-j}+{ϵ}_t$$

(4)

where ${ϵ}_t$ is the same white noise process as above, and the coefficients $b_j$ are absolutely summable. Additionally, $b\left(z\right)=1-{\sum }_{k=1}^{\infty }{b}_j{z}^j\ne 0$ for $\left|z\right|\le 1$; see [6] for details. The assumption of positive spectral density of the underlying innovation process is a sine qua non for an AR(∞) approximation to the spectral density to be consistent; this assumption has been used by Paparoditis and Politis (2018) [6] and Kreiss, Paparoditis and Politis (2011) [13] and has not been found to be a limitation for practical applications and has not been found to be a limitation for practical applications.

Under all the above assumptions, and recalling the ADF regression (1) used to test unit root hypothesis $H_0$, the following result is true. To state it, we require an extra assumption on the white noise process appearing in (4), namely:

$${\displaystyle \mathbb{E}\left({ϵ}_t^4\right)<\infty \mathrm{and}\sum _{n=1}^{\infty }n\parallel {\mathcal{P}}_1\left({ϵ}_n\right)\parallel <\infty }$$

(5)

where ${\mathcal{P}}_t\left(Y\right)=\mathbb{E}\left[Y\right|{\mathcal{F}}_t]-\mathbb{E}\left[Y\right|{\mathcal{F}}_{t-1}]$, ${\mathcal{F}}_s$ is the $\sigma$-field generated by $({ϵ}_t$ for $t\le s)$, and the norm $\parallel ·\parallel$ is the $L_p$ norm with $p=4$.

Theorem 1

(Paparoditis and Politis (2018) [6]). Assume $f_U\left(w\right)>0$ for all w, and Equations (4) and (5). If $p_n\to \infty$ as $n\to \infty$ such that ${\displaystyle \frac{p_n}{\sqrt{n}}}\to 0$, then

$$t_{n,q}\stackrel{d}{\to }{\displaystyle \frac{{\int }_0^{1}W\left(t\right)dW\left(t\right)}{{\left({\int }_0^1{\left(W\left(t\right)\right)}^{2}dt\right)}^{\frac{1}{2}}}}$$

when $H_0$ is true; here $W\left(t\right),t\in [0,1]$ is the standard Wiener process on $[0,1]$, and $\stackrel{d}{\to }$ denotes convergence in distribution.

The $\alpha$ level ADF test therefore rejects the null $H_0$ whenever the test statistic $t_{n,q}$ is smaller than $C_{\alpha }$ where $C_{\alpha }$ is the lower $\alpha$ percentile of the above distribution.

Theorem 1 can be further extended to the cases wherein (1) is modified to include an affine time trend; the same limit result except that the standard Wiener process is replaced by

$${\tilde{W}}_t=W_t+(6t-4){\int }_0^{1}W\left(s\right)ds-(12t-6){\int }_0^{1}sW\left(s\right)ds$$

For a case by case analysis of intercept/trend inclusion, the reader is referred to the book of Hamilton [14].

2.2. Behaviour Under the Alternative

The limiting distribution of the test statistic $t_{n,q}$ under the alternative is more straightforward; the limiting distribution is normal albeit dependent on the true $\rho$ in (1). The work of Paparoditis and Politis [6] establishes this limiting behavior even under their relaxed requirement where the underlying innovation process is just assumed to possess a continuous spectral density which is strictly positive; they also discuss the problem of asymptotic collinearity in the ADF regression where increasing the number of lagged differences leads to a reduction in power. In essence, as the chosen number of lags q increases, the regressors in the ADF regression (1) become asymptotically collinear, leading to slow rate of convergence of the estimator ${\widehat{\rho }}_n$. This directly leads to a loss of power of the ADF test. We comment on this behaviour of the prepivoted ADF test further in the following sections.

Under the same assumptions on the innovation process $U_t$ used in Theorem 1 the limiting behaviour of the test statistic under the alternative hypothesis $H_a$ is as follows.

Theorem 2

(Paparoditis and Politis (2018) [6]). Assume $X_t=U_t$ is true with $U_t$ such that $f_U\left(w\right)>0$ for all w, and Equations (4) and (5). Let $q=q_n\to \infty$ as $n\to \infty$ in such a way that ${\displaystyle \frac{q_n^4}{n}}\to 0$ and $\sqrt{n}{\sum }_{j=q+1}^{\infty }\left|a_j\right|\to 0$. Then, as $n\to \infty$

1. 

${\displaystyle \frac{n}{q}}Var\left({\widehat{\rho }}_n\right)\to {(1-\rho )}^2$ in probability

2. 

$\sqrt{{\displaystyle \frac{n}{q}}}({\widehat{\rho }}_n-\rho )\stackrel{d}{\to }\mathcal{N}(0,{(1-\rho )}^2)$.

3. Power of the Prepivoted Test

Prepivoting, as introduced by Beran [8], is the mapping of the test statistic $t_{n,q}$ to a new test statistic $F^{\ast }\left(t_{n,q}\right)$, where $F^{\ast }(·)$ is a consistent estimator of the distribution function of $t_{n,q}$ computed from the data $(X_1,\cdots ,X_n)$; typically, $F^{\ast }(·)$ will be based on some kind of bootstrap procedure. We will adopt the residual AR bootstrap of Paparoditis and Politis [9] to generate the ith bootstrap sample denoted by $(X_{1,i}^{\ast },\cdots ,X_{n,i}^{\ast })$ where $i=1,\dots ,B$. Applying the ADF regression(1) to each of these B samples, we obtain B bootstrap ADF statistics $t_{n,q}^{\ast }$; this allows us to compute the bootstrap estimate of the CDF, denoted by $F^{\ast }(·)$. Thus, the prepivoted test statistic is $F^{\ast }\left(t_{n,q}\right)={\displaystyle \frac{1}{B}}{\sum }_{i=1}^B{\mathbb{1}}_{\{t_{n,q}^{\ast }<t_{n,q}\}}$. The prepivoted ADF test rejects the null hypothesis if $F^{\ast }\left(t_{n,q}\right)<\alpha$, the nominal level of the test.

In this section, we briefly discuss the power of the prepivoted ADF test. In particular, we show that it is consistent against the alternative hypothesis $\rho <1$. We build upon the result of Theorem 2 and obtain the following novel result.

Theorem 3.

If $q=q_n\to \infty$ as $n\to \infty$ such that ${\displaystyle \frac{q_n^4}{n}}\to 0$ and $\sqrt{n}{\sum }_{j=q+1}^{\infty }\left|a_j\right|\to 0$, then the prepivoted ADF test is consistent where the alternative is that ρ is any fixed value less than 1.

Proof. 

From Theorem 2 we have that $\sqrt{{\displaystyle \frac{n}{q}}}({\widehat{\rho }}_n-\rho )\stackrel{d}{\to }\mathcal{N}(0,{(1-\rho )}^2)$. Observe that the ADF test statistic can be written as

$$t_{n,q}={\displaystyle \frac{{\widehat{\rho }}_n-1}{\widehat{\mathrm{Std}}\left(\widehat{\rho }\right)}}={\displaystyle \frac{{\widehat{\rho }}_n-\rho +\rho -1}{\widehat{\mathrm{Std}}\left(\widehat{\rho }\right)}}$$

The power of the prepivoted test is given by the probability of correct rejection of the test, i.e., $\mathbb{P}(F^{\ast }\left(t_{n,q}\right)<\alpha |H_a)$ where $F^{\ast }$ is the bootstrap estimate of the CDF of $t_{n,q}$. Let $C_{\alpha }^{\ast }$ be an $\alpha$ quantile of $F^{\ast }$.

Then,

$$\begin{array}{cc}\hfill \mathbb{P}(F^{\ast }\left(t_{n,q}\right)<\alpha |H_a)& =\mathbb{P}(t_{n,q}<C_{\alpha }^{\ast }|H_a)\hfill \\ \hfill & =\mathbb{P}(({\widehat{\rho }}_n-1)<C_{\alpha }^{\ast }\widehat{\mathrm{Std}}\left({\widehat{\rho }}_n\right)|H_a)\hfill \\ \hfill & =\mathbb{P}({\widehat{\rho }}_n-\rho <C_{\alpha }^{\ast }\widehat{\mathrm{Std}}\left({\widehat{\rho }}_n\right)+(1-\rho )|H_a)\hfill \\ \hfill & =\mathbb{P}\left(\sqrt{{\displaystyle \frac{n}{q}}}{\displaystyle \frac{{\widehat{\rho }}_n-\rho }{1-\rho }}<C_{\alpha }^{\ast }\sqrt{{\displaystyle \frac{n}{q}}}{\displaystyle \frac{\widehat{\mathrm{Std}}\left({\widehat{\rho }}_n\right)}{1-\rho }}+\sqrt{{\displaystyle \frac{n}{q}}}|H_a\right)\hfill \\ \hfill & =\Phi \left(C_{\alpha }^{\ast }\sqrt{{\displaystyle \frac{n}{q}}}{\displaystyle \frac{\widehat{\mathrm{Std}}\left({\widehat{\rho }}_n\right)}{1-\rho }}+\sqrt{{\displaystyle \frac{n}{q}}}\right)\hfill \end{array}$$

Now since $\widehat{\mathrm{Std}}\left(\widehat{\rho }\right)=\sqrt{{\displaystyle \frac{q}{n}}}(1-\rho )+o_p(\sqrt{{\displaystyle \frac{q}{n}}})$ and using consistency of bootstrap quantiles (cf. Lemma 1.2.1 of Politis, Romano and Wolf [15]) and the continuous mapping theorem, we have

$$\Phi \left(C_{\alpha }^{\ast }\sqrt{{\displaystyle \frac{n}{q}}}{\displaystyle \frac{\widehat{\mathrm{Std}}\left({\widehat{\rho }}_n\right)}{1-\rho }}+\sqrt{{\displaystyle \frac{n}{q}}}\right)\approx \Phi \left(C_{\alpha }+\sqrt{{\displaystyle \frac{n}{q}}}\right)$$

(6)

where $C_{\alpha }$ is the $\alpha$ quantile of the Dickey-Fuller distribution. Observe therefore, that the power of the prepivoted test tends to 1 as $n\to \infty$.

While it is not immediately clear from this expression, the prepivoted ADF test in fact has better power than the asymptotic ADF test. We demonstrate the same through numerical experiments in the next two sections.    □

We briefly discuss the behavior of the prepivoted ADF test in the local alternative framework. We build upon the theorem of Aylar, Westerlund and Smeekes [16], where they derive the limiting distribution of the ADF test statistic $t_{n,q}$ under the local alternative $\rho =1+{\displaystyle \frac{c}{n}}$ for some fixed $c<0$ to demonstrate non-trivial power of the prepivoted ADF test. Their notation and assumptions are briefly reviewed as follows. The DGP under consideration is $X_t=\rho X_{t-1}+U_t$ with $U_t=\pi \left(L\right){ϵ}_t$. It is assumed that ${ϵ}_t$ is a martingale difference sequence with some filtration ${\mathcal{F}}_t$ with $E\left({ϵ}_t^2\right)={\sigma }^2$, ${\displaystyle \frac{1}{n}}{\sum }_{t=1}^n{ϵ}_t^2{\to }_p{\sigma }^2$ and $E\left(\right|{ϵ}_t^4\left|\right)<\infty$. Assume $\pi \left(z\right)\ne 0$ for all $\left|z\right|\le 1$, and ${\sum }_{k=0}^{\infty }{\left|k\right|}^s\left|{\pi }_k\right|<\infty$ for some $s\ge 1$. They then assume $\rho =1+{\displaystyle \frac{c}{n}}$ with $c<0$, and ${\displaystyle \frac{q}{\sqrt{n}}}\to 0$ as $n\to \infty$. Then, they claim that

$$t_{n,q}\stackrel{d}{\to }{\displaystyle \frac{{\int }_0^1{J}_c\left(r\right)dW\left(r\right)}{{\left({\int }_0^1{J}_c^2\left(r\right)dr\right)}^{\frac{1}{2}}}}+c\underset{q\to \infty }{lim}(1-{\delta }_q\left(1\right))\pi \left(1\right){\left({\int }_0^1{J}_c^2\left(r\right)dr\right)}^{{\displaystyle \frac{1}{2}}}$$

(7)

In the above Equation (7), $J_c\left(r\right)={\int }_{v=0}^{r}exp\left(c(r-v)\right)dW\left(v\right)$ where $W\left(r\right)$ is the standard Wiener process on $[0,1]$. Additionally, ${\delta }_q\left(L\right)={\sum }_{k=1}^q{\theta }_k{L}^{k-1}$, where $\theta \left(L\right)=\pi {\left(L\right)}^{-1}=1-{\sum }_{k=1}^{\infty }{\theta }_k{L}^k$. Given this setup, we have the following result.

Theorem 4.

Under the above assumptions, the prepivoted ADF test has non-trivial power against a local alternative of the form $\rho =1+{\displaystyle \frac{c}{n}}$ where c is a negative constant.

Proof. 

Let $G(·)$ be the continuous CDF of the limiting distribution given in (7). Note that $J_c\left(r\right)\sim \mathcal{N}(0,{\displaystyle \frac{e^{2rc}-1}{2c}})$ for $r\in [0,1]$ and is an Ornstein-Uhlenbeck process that solves $d{J}_c\left(r\right)=c{J}_c\left(r\right)+dW\left(r\right)$ with $J_c\left(0\right)=0$. Let $H_{\mathrm{loc}}$ denote the local alternative hypothesis. Then,

$$\begin{array}{cc}\hfill \mathbb{P}(F^{\ast }\left(t_{n,q}\right)<\alpha |H_{\mathrm{loc}})& =\mathbb{P}(t_{n,q}<C_{\alpha }^{\ast }|H_{\mathrm{loc}})\hfill \\ \hfill & \approx P(t_{n,q}<C_{\alpha }|H_{\mathrm{loc}})+O_P(C_{\alpha }^{\ast }-C_{\alpha })\approx G\left(C_{\alpha }\right)\ne 0\hfill \end{array}$$

where the last line follows since $G(·)$ has infinite support.    □

Remark 1.

The above mentioned result of Aylar, Smeekes and Westerlund fails to capture the loss of power with increasing q. The asymptotic collinearity problem is empirically verified in Paparoditis and Politis [6] as well as the later sections of the paper at hand. Nevertheless, the result does allow us to demonstrate that the prepivoted ADF test has non-trivial power against local alternatives—which can be seen in Section 4 and Section 5, in particular Tables 3 and 4.

4. Numerical Experiments

In this section we provide the results of a numerical experiment. The setup is similar to that of Paparoditis and Politis [6], wherein the authors consider the ARMA(1,1) model to be the data generating process i.e., $X_t-\varphi X_{t-1}=Z_t+\theta Z_{t-1}$ with $Z_t\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }N(0,1)$. We consider six different combinations of the ARMA parameters $\varphi$ and $\theta$; two that yield samples under the unit root hypothesis and four that yield samples under the alternative hypothesis. For each sample size n, we generate 10,000 time series each of length n.

This simulation allowed us to compute the empirical rejection probabilities of the prepivoted ADF test at the nominal level $0.05$. We use a ‘tuning parameter sweep’ approach to select the lag lengths for the experiment in this section: we used the formula $q=n^a$ with varying values of a. Note that the lag length used was the same for both the ADF regression on the original data as well as the ADF regression on the bootstrap samples.

The bootstrap methodology selected to generate bootstrap samples under the null is from Section 2.2 of Paparoditis and Politis [9]. This is a bootstrap approach that is based on unrestricted residuals, and the resultant bootstrap samples are generated under the null irrespective of whether the original data obey the null or not.

Table 1. Entries represent empirical rejection probabilities of the prepivoted ADF test with q = $n^a$ for various values of a. The data generating process was ARMA(1,1) with $(\varphi ,\theta )=(1,0.5)$.

a =	0.09	0.13	0.17	0.21	0.25	0.29	0.33	0.37	0.41	0.45	0.49
n = 50	0.0845	0.0916	0.0848	0.0380	0.0390	0.0585	0.0583	0.0478	0.0471	0.0510	0.0474
n = 100	0.0884	0.0898	0.0341	0.0390	0.0594	0.0615	0.0484	0.0525	0.0494	0.0552	0.0514
n = 200	0.0949	0.0944	0.0417	0.0590	0.0650	0.0492	0.0555	0.0494	0.0495	0.0552	0.0514
n = 400	0.0938	0.0382	0.0382	0.0611	0.0471	0.0537	0.0515	0.0485	0.0519	0.0542	0.0494
n = 800	0.0915	0.0354	0.0613	0.0437	0.0515	0.0496	0.0533	0.0522	0.0495	0.0505	0.0527
n = 1600	0.0886	0.0424	0.0595	0.0470	0.0527	0.0476	0.0511	0.0502	0.0489	0.0515	0.0507

and

Table 2. Entries represent empirical rejection probabilities of the prepivoted ADF test with q = $n^a$ for various values of a. The data generating process was ARMA(1,1) with $(\varphi ,\theta )=(1,-0.5)$.

a =	0.09	0.13	0.17	0.21	0.25	0.29	0.33	0.37	0.41	0.45	0.49
n = 50	0.1712	0.1675	0.1706	0.1001	0.0958	0.0708	0.0743	0.0576	0.0619	0.0541	0.0489
n = 100	0.1837	0.1844	0.1075	0.1027	0.0710	0.0767	0.0648	0.0619	0.0501	0.0501	0.0514
n = 200	0.1915	0.1953	0.1074	0.0778	0.0776	0.0635	0.0569	0.0522	0.0503	0.0528	0.0542
n = 400	0.1992	0.1083	0.1077	0.0748	0.0622	0.0571	0.0518	0.0520	0.0495	0.0527	0.0513
n = 800	0.2037	0.1128	0.0737	0.0680	0.0555	0.0553	0.0503	0.0490	0.0530	0.0534	0.0502
n = 1600	0.2118	0.1140	0.0797	0.0660	0.0568	0.0571	0.0517	0.0515	0.0550	0.0561	0.0472

correspond to the setting where $\left\{X_t\right\}$ has a unit root. The resulting empirical rejection probabilities should be close to the nominal level of the test i.e., $0.05$. The entry closest to $0.05$ is presented in bold face. As opposed to [6], the column $a=0.05$ is omitted in all the Tables—the entries in all 6 Tables corresponding to $a=0.05$ were very similar to those of $a=0.09$.

From the results of Table 1 and Table 2, we observe that the prepivoted ADF test yields accurate size when the lag length is large. The test has good size in the presence of the negative MA parameter $\theta =-0.5$ when lags are large, but suffers from severe over-rejection of the null when the lag lengths are short. The test is able to achieve accurate size for all sample sizes.

Table 3. Entries represent empirical rejection probabilities of the prepivoted ADF test with q = $n^a$ for various values of a. The data generating process was ARMA(1,1) with $(\varphi ,\theta )=(0.985,0.5)$.

a =	0.09	0.13	0.17	0.21	0.25	0.29	0.33	0.37	0.41	0.45	0.49
n = 50	0.1150	0.1150	0.1130	0.0851	0.0843	0.0958	0.0894	0.0902	0.0875	0.0890	0.0805
n = 100	0.1752	0.1741	0.1147	0.1078	0.1408	0.1288	0.1145	0.1229	0.1161	0.1172	0.1170
n = 200	0.3044	0.2986	0.1781	0.2271	0.2283	0.1949	0.2035	0.2037	0.1983	0.1887	0.1881
n = 400	0.6175	0.3756	0.3579	0.4897	0.4308	0.4494	0.4239	0.4117	0.4084	0.3781	0.3692
n = 800	0.9593	0.8139	0.8981	0.8501	0.8673	0.8525	0.8380	0.8265	0.8074	0.7712	0.7408
n = 1600	1.0000	0.9992	1.0000	0.9993	0.9987	0.9993	0.9986	0.9975	0.9961	0.9932	0.9855

,

Table 4. Entries represent empirical rejection probabilities of the prepivoted ADF test with q = $n^a$ for various values of a. The data generating process was ARMA(1,1) with $(\varphi ,\theta )=(0.985,-0.5)$.

a =	0.09	0.13	0.17	0.21	0.25	0.29	0.33	0.37	0.41	0.45	0.49
n = 50	0.1884	0.1901	0.1821	0.1243	0.1238	0.1000	0.1038	0.0942	0.0961	0.0939	0.0911
n = 100	0.3074	0.3091	0.1948	0.1973	0.1489	0.1546	0.1367	0.1226	0.1199	0.1241	0.1195
n = 200	0.5455	0.5417	0.3550	0.2777	0.2686	0.2420	0.2193	0.2076	0.1983	0.2001	0.1947
n = 400	0.8786	0.6832	0.6819	0.5686	0.4975	0.4629	0.4379	0.4171	0.4168	0.3876	0.3851
n = 800	0.9989	0.9813	0.9458	0.9182	0.8920	0.8736	0.8533	0.8419	0.8162	0.7875	0.7546
n = 1600	1.0000	1.0000	0.9999	0.9998	1.0000	0.9990	0.9984	0.9975	0.9974	0.9939	0.9861

,

Table 5. Entries represent empirical rejection probabilities of the prepivoted ADF test with q = $n^a$ for various values of a. The data generating process was ARMA(1,1) with $(\varphi ,\theta )=(0.97,0.5)$.

a =	0.09	0.13	0.17	0.21	0.25	0.29	0.33	0.37	0.41	0.45	0.49
n = 50	0.1668	0.1740	0.1728	0.1069	0.1047	0.1253	0.1267	0.1115	0.1091	0.1085	0.1171
n = 100	0.3033	0.3033	0.1644	0.1700	0.2153	0.2139	0.1877	0.1936	0.1808	0.1898	0.1764
n = 200	0.5977	0.5960	0.3511	0.4549	0.4522	0.3890	0.4117	0.3889	0.3813	0.3607	0.3346
n = 400	0.9600	0.7989	0.7913	0.8787	0.8264	0.8441	0.8129	0.7859	0.7601	0.7357	0.6897
n = 800	1.0000	0.9978	0.9998	0.9985	0.9987	0.9976	0.9982	0.9950	0.9906	0.9832	0.9730
n = 1600	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0.9999

and

Table 6. Entries represent empirical rejection probabilities of the prepivoted ADF test with q = $n^a$ for various values of a. The data generating process was ARMA(1,1) with $(\varphi ,\theta )=(0.97,-0.5)$.

a =	0.09	0.13	0.17	0.21	0.25	0.29	0.33	0.37	0.41	0.45	0.49
n = 50	0.2861	0.2871	0.2817	0.1854	0.1793	0.1536	0.1500	0.1308	0.1311	0.1225	0.1151
n = 100	0.5246	0.5194	0.3356	0.3326	0.2614	0.2654	0.2336	0.2076	0.2009	0.1856	0.1817
n = 200	0.8698	0.8712	0.6678	0.5514	0.5507	0.4752	0.4482	0.4060	0.3993	0.3376	0.3516
n = 400	0.9987	0.9762	0.9774	0.9421	0.9003	0.8723	0.8372	0.8102	0.7898	0.7592	0.7092
n = 800	1.0000	1.0000	0.9999	1.0000	0.9993	0.9994	0.9983	0.9975	0.9951	0.9870	0.9775
n = 1600	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0.9999	0.9998

correspond to the setting where $\left\{X_t\right\}$ does not have a unit root and is under the alternative hypothesis. These empirical rejection probabilities therefore represent the power of the prepivoted ADF test, and should ideally be as large as possible. The largest entries in each row are represented in boldface.

The results of Table 3, Table 4, Table 5 and Table 6 are encouraging. While the finite sample power of the prepivoted ADF test is fairly low, it is much higher than the power of the asymptotic ADF test for the same specifications. We observe that the power tends to 1 as the sample size increases—empirically verifying the theoretical consistency of the test. Unfortunately, we see that the lag length chosen to optimize size does not also optimize power—the power of the test appears to be highest when the chosen lag length is short. We also see the manifestation of the asymptotic collinearity problem from Paparoditis and Politis [6] when the lag lengths are allowed to increase, we observe that the power of the test reduces. In the next section, we will develop a bootstrap method with the goal of choosing a lag length that optimizes power while securing a size close to nominal.

5. Bootstrap Selection of Tuning Parameters for Hypothesis Tests

In this section, we propose a state of the art tuning parameter selection algorithm for general hypothesis tests, and apply it to the case of lag length selection for the prepivoted ADF test. The general algorithm proceeds as follows. Given time series data $(X_1,\cdots X_n)$ from an assumed model, and a test statistic $t_{n,q}$ where a tuning parameter q is involved, the procedure is as follows:

Bootstrap Algorithm for Tuning Parameter Selection for Hypothesis Tests

• Use an information-based choice of q from the sample $(X_1,\cdots X_n)$ to obtain initial parameter estimates for the assumed model.
• Use the estimated parameters to compute residuals that are not restricted to be under the null.
• Bootstrap the residuals to construct B stretches of bootstrap data under the null.
• Compute the test statistic $t_{n,q}^{\ast }$ from each of the B bootstrap samples across the range of acceptable values of the tuning parameter. Collect the acceptance/rejections of these bootstrap tests as a matrix of 0s and 1s.
• Select the tuning parameter that has empirical rejection probability closest to the nominal level of the test; this is essentially done by computing the column averages of the matrix generated in the previous step and selecting the index with column average closest to the nominal level. If there is more than one such choice, select the tuning parameter associated with the smallest fitted model.
• The above is the optimal tuning parameter called $q^{\ast }$.
• The optimal tuning parameter is fed back to the original data and the hypothesis test is performed with $q^{\ast }$, i.e., computing $t_{n,q^{\ast }}$ on $(X_1,\cdots X_n)$.
• Reject the null hypothesis if the p value of the test based on $t_{n,q^{\ast }}$ is less than the nominal level.

Occam’s razor postulates that if two models are equally apt in explaining a phenomenon at hand, then the smallest, i.e., least complex, model is preferable. Step 5 of the above algorithm encapsulates our preference for smaller, more parsimonious models. There are several instances in the literature of applying some form of bootstrap with the purpose of choosing a tuning parameter, see Leger and Romano [17], Fenga and Politis [18] and Shao [19]. However, it is important to note that our bootstrap algorithm of Section 5 is novel. As far as we know, no other work has proposed to generate bootstrap samples that obey the null (whether the data obey the null or not) with the purpose of choosing the smallest model order that still yields size close to nominal. In the next subsection, we will apply this algorithm to the ADF test in which case, as we have shown, using a smaller model generally leads to better power.

5.1. ADF with Bootstrap-Assisted Lag Choice

In this subsection, we apply the above general bootstrap algorithm for tuning parameter selection to the prepivoted ADF test. We perform numerical experiments to empirically verify the size and power properties of our algorithm and report the results. As per the work of Paparoditis and Politis [6], we observe that the Akaike Information Criterion (AIC) works reasonably well with regards to both size and power of the ADF test in the case of positive MA parameters. In the case of negative MA parameters, the AIC based tests suffer from over-rejection of the null. The Modified AIC (MAIC) due to Ng and Perron [7] was designed specifically to ameliorate the ADF test’s over-rejection of the null in the presence of negative MA parameters. Their method uses a combination of GLS detrending along with a modified information criterion to select the optimal lag length for the ADF test. The MAIC is designed to favor larger lag lengths in the presence of a negative MA parameter, but as shown by Paparoditis and Politis [6], this can hurt the power performance of the test due to the asymptotic collinearity effect.

Our lag length selection algorithm, dubbed the ‘bootstrap-assisted lag choice’ (BALC) is given below; it uses the residual AR bootstrap of Paparoditis and Politis [9] along with the prepivoting idea of Beran [8] with the aim of selecting lag lengths that yield both good size and power. We performed numerical experiments using an ARMA(1,1) data generating process with six different combinations of the ARMA parameters $\varphi$ and $\theta$. For each ARMA(1,1) configuration and sample size n, we generated 10,000 different time series and recorded the performance of our novel lag length selection algorithm. This allowed us to compute the empirical rejection probabilities corresponding to our algorithm at the nominal level $0.05$. We compare the results of our novel lag length selection method with prepivoted ADF tests with lag lengths selected by AIC and MAIC optimality. The experimental design is as follows:

Bootstrap Assisted Lag Choice Algorithm for the ADF Test

• We are given a stretch of time series data $X_1,\cdots X_n$ to be tested for a possible unit root.
• Run the ADF regression (1) on this data with lag length q selected by AIC. AIC minimization is done over the range 1 to $\sqrt{n}$. Denote the selected lag by $q_{AIC}$.
• Use the estimated parameters and centered residuals from the ADF regression to construct $B_1$ bootstrap samples under the null, using the AR bootstrap of Paparoditis and Politis [9].
• For each of the bootstrap samples, perform a prepivoted ADF test with varying lag lengths. The bootstrap methodology for the prepivoted test also uses the AR bootstrap of Paparoditis and Politis [9], and generates $B_2$ bootstrap samples for each q. The range of values for q we chose was from $\lfloor 0.5·q_{AIC}\rfloor$ to $\lceil 1.5·q_{AIC}\rceil$. The result of these tests is stored in a 0–1 matrix with $B_1$ rows and appropriate number of columns.
• The optimal $q^{\ast }$ is then picked by using the value of q that yields smallest type-1 error for all of the bootstrap samples i.e., the value of q that yields column average closest to the nominal level $0.05$.
• We then perform a prepivoted ADF test with $B_2$ bootstrap samples on the original data with number of lags equal to $q^{\ast }$.
• The unit root null hypothesis is rejected if the p-value is less than the nominal level $0.05$.

5.2. Discussion of Simulation Results

The Tables below list the empirical rejection probabilities of the prepivoted ADF test with lag lengths selected by three different data dependent approaches. We list the results of our algorithm and compare them with those with lags selected by AIC, BIC and MAIC optimality. AIC optimization is carried out over lag lengths q ranging from 1 to $\sqrt{n}$, while MAIC optimization is carried out over q ranging from 1 to $\lfloor 12·{\left({\displaystyle \frac{n+1}{100}}\right)}^{0.25}\rfloor$ as per Schwert [3]. For our experiments, the values of $B_1,B_2$ were set to 250 and 100 respectively in the interest of computational parsimony since our simulation involved 10,000 replications; in practice, given a single dataset in hand, the values of $B_1,B_2$ can easily become of the order of 1000. In terms of computational efficiency, for a single dataset, the computational complexity is entirely determined by the values of $B_1$ and $B_2$ and the lag length initially chosen by AIC. More specifically, the ADF regression is performed is $1+B_1{B}_2{q}_{AIC}+B_2$ times. Step 4 from the algorithm is highly conducive to parallelization—the search can be run over all candidate values for $q^{\ast }$ at the same time since the results from one candidate value of $q^{\ast }$ are independent of those for other candidate values—thereby improving the computational efficiency and runtime of the algorithm.

Table 7. $(\varphi ,\theta )=(1,0.5)$.

n =	50	100	200	400	800	1600
AIC	0.0578	0.0512	0.0511	0.0522	0.0526	0.0544
BIC	0.0706	0.0644	0.0537	0.0499	0.0543	0.0526
MAIC	0.0465	0.0500	0.0463	0.0497	0.0541	0.0506
BALC	0.0612	0.0582	0.0541	0.0526	0.0514	0.0495

and

Table 8. $(\varphi ,\theta )=(1,-0.5)$.

n =	50	100	200	400	800	1600
AIC	0.0964	0.0864	0.0714	0.0656	0.0593	0.0528
BIC	0.1152	0.1286	0.1101	0.0945	0.0782	0.0704
MAIC	0.0673	0.0650	0.0631	0.0602	0.0588	0.0528
BALC	0.1174	0.1056	0.1049	0.0966	0.0842	0.0761

correspond to the setting wherein the data $\left\{X_t\right\}$ have a unit root. The entries therefore list the rejection probabilities under the null, and should ideally be as close to the nominal level $0.05$ as possible. For each sample size in each Table, the rejection probability closest to the nominal level is presented in bold.

Putting together the results of Table 7 and Table 8, we see that the performance of our method is comparable to that of AIC and MAIC. It is clear from the Tables that tests achieve more accurate size for larger sample sizes. Not surprisingly, the bootstrap selection method also suffers from over-rejection of the null hypothesis in the presence of negative MA parameter.

Table 9. $(\varphi ,\theta )=(0.985,0.5)$.

n =	50	100	200	400	800	1600
AIC	0.0931	0.1166	0.1892	0.4162	0.8375	0.9987
BIC	0.1008	0.1232	0.1928	0.3812	0.8402	0.9995
MAIC	0.0893	0.1133	0.1965	0.4239	0.8462	0.9983
BALC	0.0965	0.1215	0.2113	0.4391	0.8407	0.9989

,

Table 10. $(\varphi ,\theta )=(0.985,-0.5)$.

n =	50	100	200	400	800	1600
AIC	0.1199	0.1586	0.2429	0.4837	0.8712	0.9991
BIC	0.1432	0.2207	0.3348	0.5862	0.9290	0.9998
MAIC	0.1067	0.1395	0.2313	0.4707	0.8678	0.9985
BALC	0.1378	0.2049	0.3245	0.5769	0.8972	0.9992

,

Table 11. $(\varphi ,\theta )=(0.97,0.5)$.

n =	50	100	200	400	800	1600
AIC	0.1142	0.1829	0.3786	0.7974	0.9955	1.0000
BIC	0.1286	0.2100	0.3902	0.7965	0.9958	1.0000
MAIC	0.1127	0.1819	0.3799	0.7910	0.9947	0.9999
BALC	0.1364	0.2198	0.4336	0.8205	0.9963	1.0000

and

Table 12. $(\varphi ,\theta )=(0.97,-0.5)$.

n =	50	100	200	400	800	1600
AIC	0.1689	0.2713	0.4869	0.8521	0.9980	1.0000
BIC	0.2218	0.3721	0.6242	0.9299	0.9997	1.0000
MAIC	0.1530	0.2242	0.4499	0.8343	0.9940	1.0000
BALC	0.2071	0.3409	0.5874	0.8959	0.9993	1.0000

correspond to the setting wherein the data $\left\{X_t\right\}$ obey the alternative hypothesis. The entries therefore correspond to the power of the prepivoted ADF test, and should be as high as possible. For each sample size in each Table, the highest rejection probability is presented in bold.

These results allow us to draw the following conclusions. First, it appears that our method performs reasonably well with respect to finite sample power. The power of the BALC test is higher than the power of the prepivoted test with AIC or MAIC lag lengths. We also note that the method is consistent as its power approaches 1 with increasing sample size. Additionally, we observe that Table 10, Table 11 and Table 12 show significant increases in the power of our method compared to the two information based criteria. What is interesting is that the biggest improvements are seen for intermediate sample sizes. In particular, we observe that our method outperforms the MAIC vis-à-vis power. This can primarily be attributed to the fact that our method is designed to favor shorter lags (provided their associated size is close to nominal), thereby avoiding the asymptotic collinearity problem under the alternative hypothesis. It appears that our proposed bootstrap-assisted lag choice (BALC) generally outperforms AIC and MAIC in the cases of size and power, with the exception that the MAIC achieves better size in the well-known problematic case of a negative MA parameter. The prepivoted test with lag length selected by BIC provides a comparable but slightly higher power in the presence of a negative MA parameter as compared to our BALC based test.

All in all, it appears that the BALC method works well at arriving at a compromise between size and power performance. Our lag selection method yields accurate size as well as improved power over the information based lag length selection criteria. The lag length selection idea along with prepivoting appears to yield appreciable improvements over the asymptotic ADF test.

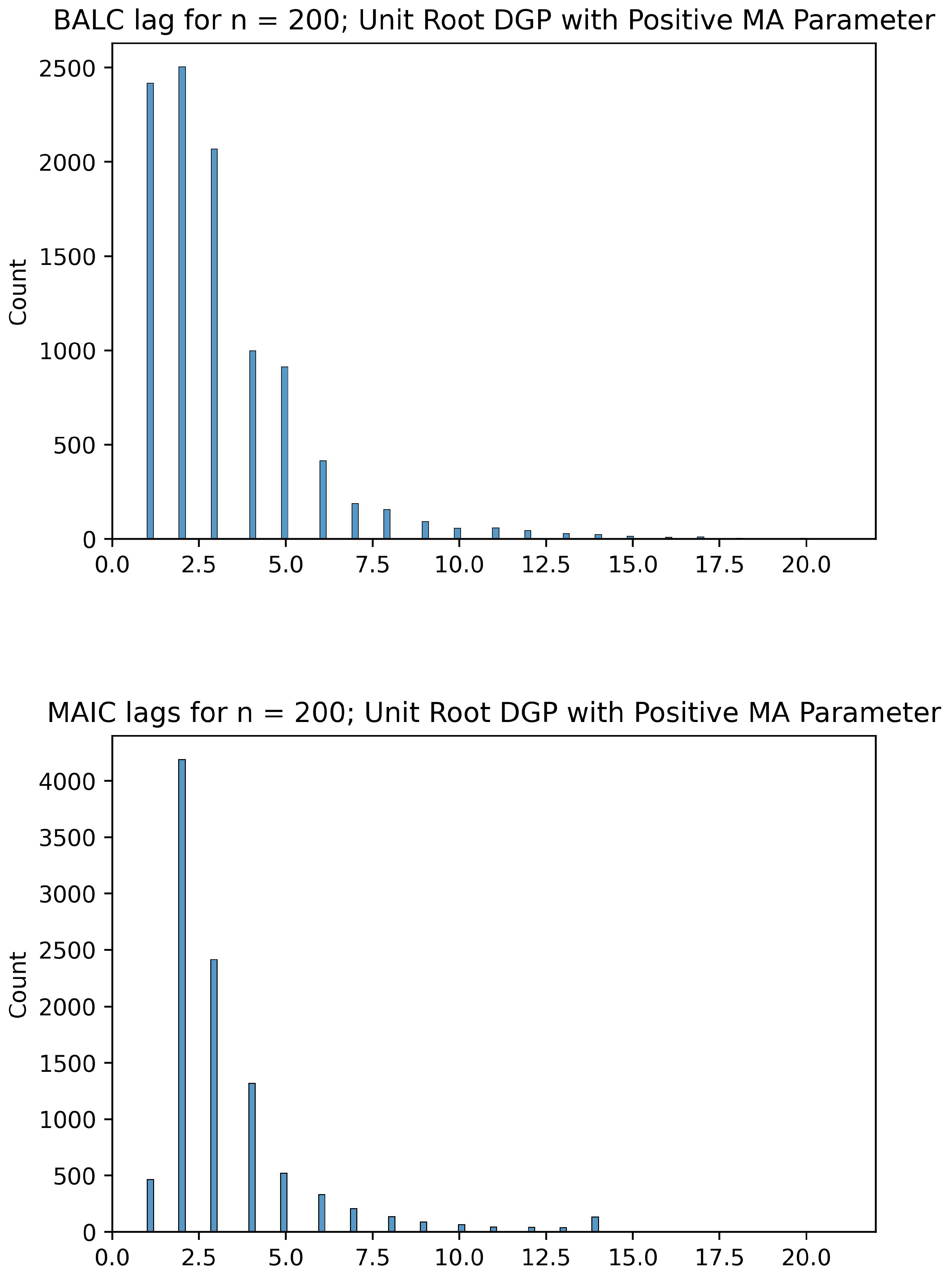
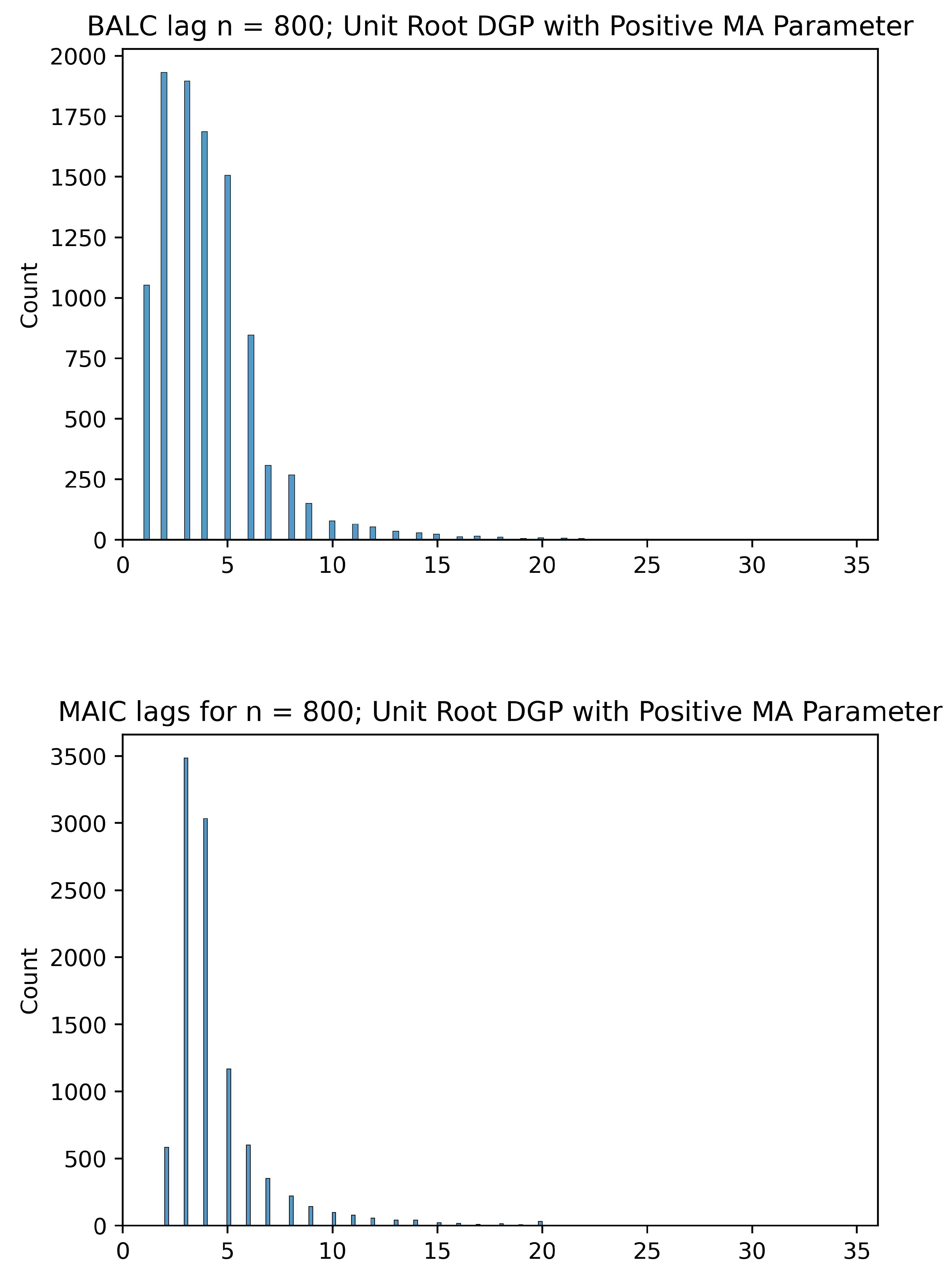
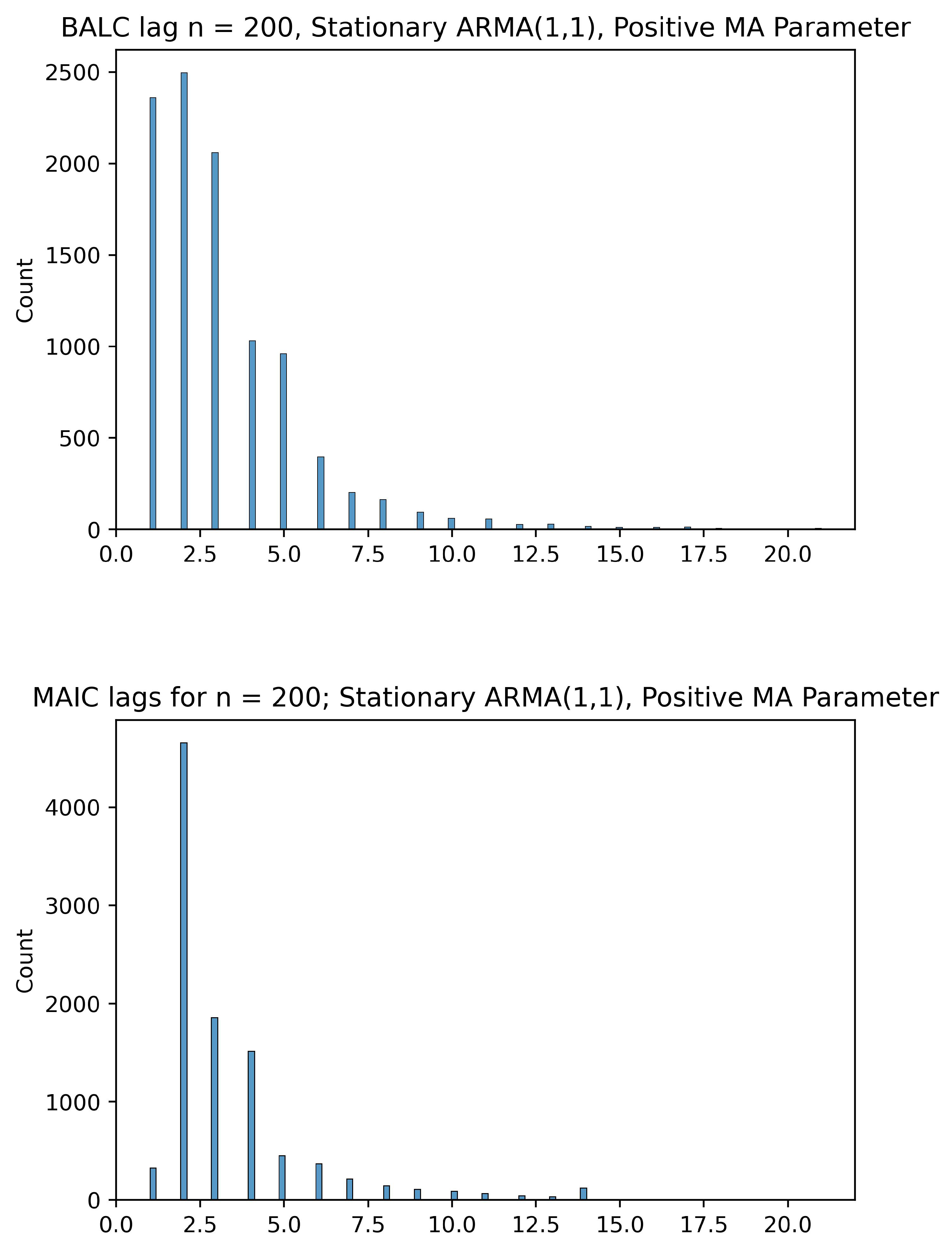
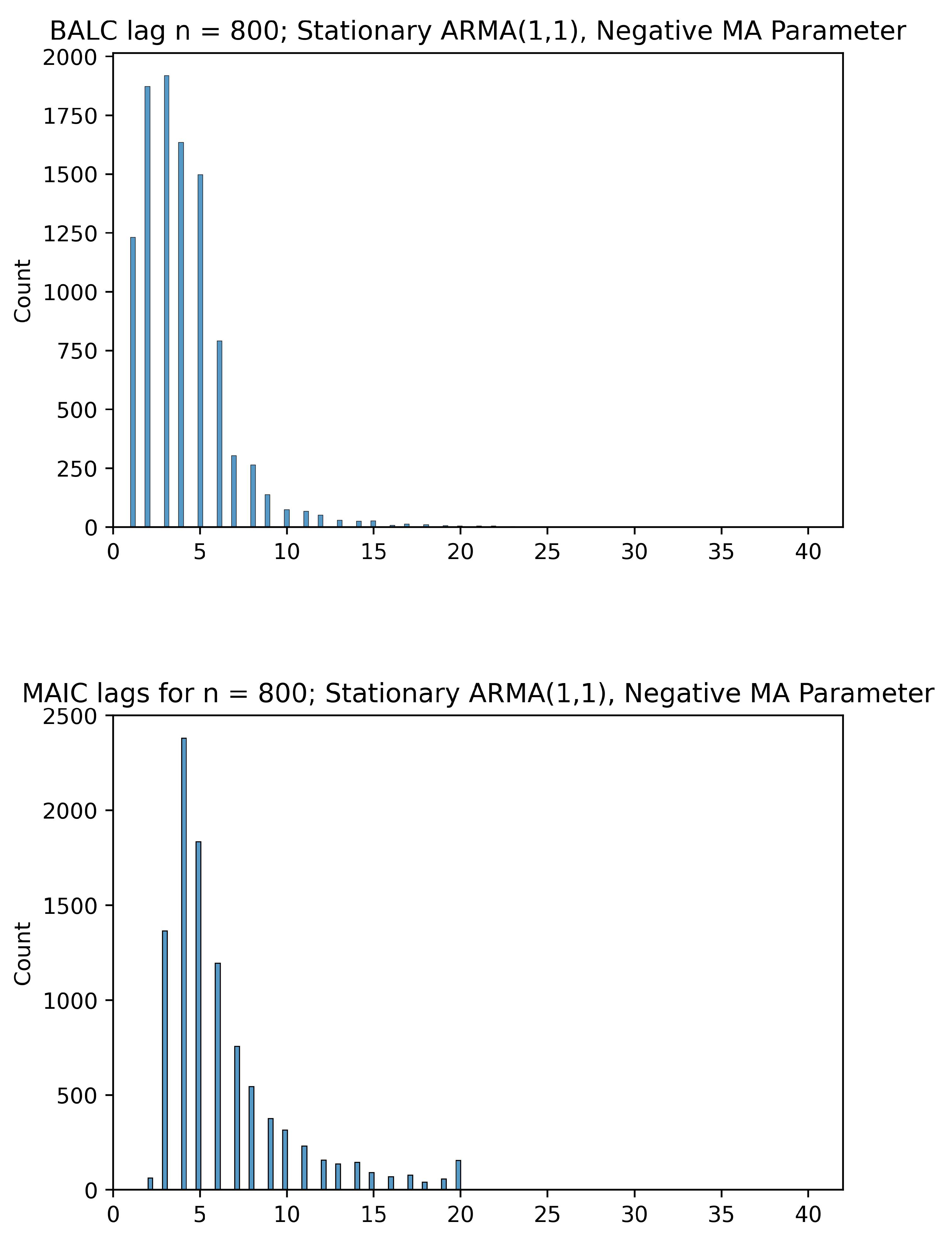
5.3. Comparing the BALC Lag Lengths to MAIC

Given below are histograms comparing the optimal lags selected by our BALC algorithm and lags selected by MAIC optimality. They serve as evidence of the fact that the BALC tends to pick lower lags than MAIC, while still searching in a range higher than the lags selected by AIC—therefore splitting the difference between AIC and MAIC. The lag lengths selected by BALC are generally shorter than those selected by MAIC. Although there is a stochastic component to the BALC framework, we observe that the choice to cut off the search for lags at $1.5\ast q_{\mathrm{AIC}}$ allows us to inflate the search space from just the value selected by AIC while simultaneously preventing the asymptotic collinearity problem. The asymptotic collinearity problem stems from the fact that as the number of lags q increases, the regressors in the ADF regression become asymptotically collinear—this is the reason for the loss in power of the ADF test as pointed out in Paparoditis and Politis (2018) [6]. If a regression is collinear, then the OLS estimator is ill-conditioned/non-unique; fortunately, here we have only approximate/asymptotic collinearity (under the alternative) whose effect can be mitigated by choosing the smallest q possible. This issue is demonstrated in Figure 1, Figure 2, Figure 3 and Figure 4 and best visualized in Figure 5 and Figure 6, where the MAIC picks fairly large lag lengths for a significant proportion of the 10,000 DGPs whereas the BALC algorithm avoids larger lag lengths.

5.4. A Real Data Application

Lastly, we apply our novel lag selection method to a real data example. We apply our BALC testing procedure to the dataset of Figure 7 that is discussed in the textbook on time series analysis by Shumway and Stoffer (2017) [20]. The dataset represents the yearly average global temperature deviations from 1880 to 2009, with the deviations measured in degrees Celsius with respect to the average temperature between 1951 and 1980. In Section 3 of Paparoditis and Politis [6], the authors comment on the failure of the tseries implementation of the ADF test to reject the null, as a consequence of selecting too many lags. As per their discussion and diagnostic figures, there is strong evidence that the detrended data do not contain any strong evidence for a unit root, and therefore obeys the alternative hypothesis—evidenced by the ACF plot of the detrended data given in Figure 8. The BALC method yields an optimal lag length of 3, compared to the tseries ADF function’s recommendation of 5. The prepivoted ADF test with lag length $q=3$ then rejects the unit root null hypothesis, which is the expected result. In contrast, the asymptotic ADF test with $q=q_{AIC}$ (which also equals 5) fails to reject the null.

6. Discussion

In this paper, we have presented a novel bootstrap assisted lag length selection criterion for the ADF test. As the asymptotic theory shows, the choice of lag length for the ADF test significantly affects its size and power properties. The convergence rate of the ADF estimator is different under the null and under the alternative. In addition, there is a tug-of-war: we need a large q to ensure size close to nominal while we need a smaller q (still diverging though) to have good power. The practical implementation of the ADF test requires the practitioner to choose the q to use in the ADF test without knowing whether the null or the alternative holds as this is the very question of the test. Given this difficult situation, our paper proposes a bootstrap-based algorithm that helps the practitioner choose a value of q that is the smallest among all q values that achieve size close to nominal. Our Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12 show that our algorithm works well in practice as it automatically adapts to the underlying data structure without the need for the practitioner to choose q in an ad hoc way, e.g., by minimizing a criterion such as AIC, BIC, MAIC, etc.