1. Introduction
Seismic hazard evaluation is always considered to be a problem of high scientific importance due to the consequences that are often associated with earthquake occurrence. Central and South America are considered to be regions with very high seismicity levels. In fact, the two strongest shocks ever recorded occurred in this region: in particular, in Chile, with magnitudes of
(1960) and
(2010) on the Richter scale. It should be noted that, based on their seismicity levels, Chile and Peru have been placed in second and fourth place, respectively, among 50 seismogenic countries [
1]. The region of Central America is known to be less seismogenic compared to South America. Indeed, large shocks like the one in the year 2012 with a magnitude of
rarely occur, but shocks with magnitudes from
to
are frequently recorded.
The tectonics of the abovementioned areas are characterized by an underthrust process by the underlying Nazca (South America) and Cocos (Central America) Plates. Reverse faults prevail in both areas, and almost all of the seismicity occurs along the west coasts [
2]. The high seismicity indicates that almost 90% of the deformation is released by the earthquakes [
3,
4,
5]. Convergent velocity values of approximately 9.0 cm/year are present in these regions [
6,
7].
The high seismicity and related phenomena—like deformation, among others—indicate that the Nazca Plate is a complicated tectonic structure [
8]. The Cocos Plate, which was created by seafloor spread along the East Pacific Rise, also forms a complicated tectonic plate; it was created almost 23 million years ago when the Faralon Plate broke into two pieces [
9]. Note that the Cocos Plate broke into two pieces (see [
9]), creating the small Rivera Plate, which is bounded by the North American and Caribbean Plates (northeast), the Pacific Plate (west), and the Nazca Plate (south) (see
Figure 1).
Several researchers have worked on various aspects of seismic activity. For example, Ruiz and Madariaga [
11] focused on historical and recent megathrust earthquakes in Chile to identify seismic gaps, earthquake periodicity, and potential precursors of such events. In contrast, Tsapanos [
12] analyzed the return periods of earthquakes in South America based on different seismicity parameters at various focal depths. More recently, several authors [
13,
14,
15] have studied seismic activity in South and Central America.
From a mathematical perspective, physical phenomena such as earthquake activity are often described by deterministic models when the temporal evolution is known, or stochastic models when the time evolution is unknown. Stochastic processes are classic examples of functions of time that can represent the evolution of a system of random values over time. One such process, with numerous applications, is the Markov chain, which transitions from one state to another among a finite number of states. Vere-Jones in [
16] presented a model for aftershocks in which successive aftershocks are seen as transitions of an active system from one state to another, with these states linked in a Markov chain. The states include aftershock frequency, energy release, and the frequency-magnitude law. However, these models are not very satisfactory as they are not tied to a specific theory of earthquake mechanisms, limiting their effectiveness.
A Markov chain was recently used by Nava et. al in [
17] for seismic risk assessment in Japan by modeling the transition probabilities of different types of seismicity in a geographic area over a time interval. The resulting high transition probabilities provided satisfactory predictions for the Japan area. In South America, Tsapanos in [
18] applied the Markov model and successfully predicted earthquakes of 2001 and 2010 with magnitudes
and
, respectively (
: Moment magnitude scale). While Markov models are effective, they are limited in terms of the distribution of waiting times.
Alternatives to Markov models include semi-Markov and hidden Markov models (HMM), both of which have various applications, including in seismology. A hidden Markov model consists of hidden states, observed values, and transition probabilities. Researchers have used the hidden Markov methodology to compute earthquake occurrence probabilities [
19]. Granat and Donnellan in [
20] applied HMM to earthquake data in Southern California to estimate earthquake magnitudes above a certain threshold. Ebel et al. [
21] used HMM to predict future earthquakes based on available data. Chambers et al. [
22] developed a new method based on HMM for earthquake prediction in Southern California and Western Nevada. Li and Anderson-Spencer in [
23] proposed using HMM to estimate the distribution of waiting times for earthquake swarms, focusing on the largest swarms in the Yellowstone region. Semi-Markov models allow for any underlying distribution but do not consider hidden states that may affect seismic activity, which is the primary focus of this work, with each hidden state representing the mean of a Poisson distribution.
This paper focuses on evaluating earthquake occurrence probabilities in the seismic zones that cover parts of Central and South America. The evaluation is done by implementing the hidden Markov model, specifically the Poisson HMM (PHMM), which is a dual discrete-time stochastic process. The parameters of the underlying Poisson distributions represent the hidden states of the process. The methodology is discussed in
Section 2, while
Section 3 is dedicated to implementing the PHMM methodology for the regions of Central and South America. Conclusions and a discussion are provided in
Section 4.
2. The HMM Methodology
Hidden Markov models (HMM) are statistical models proposed by Baum and Petrie in [
24] and have been applied in various scientific fields such as biology, gesture and speech recognition, economics, bioinformatics, and seismology.
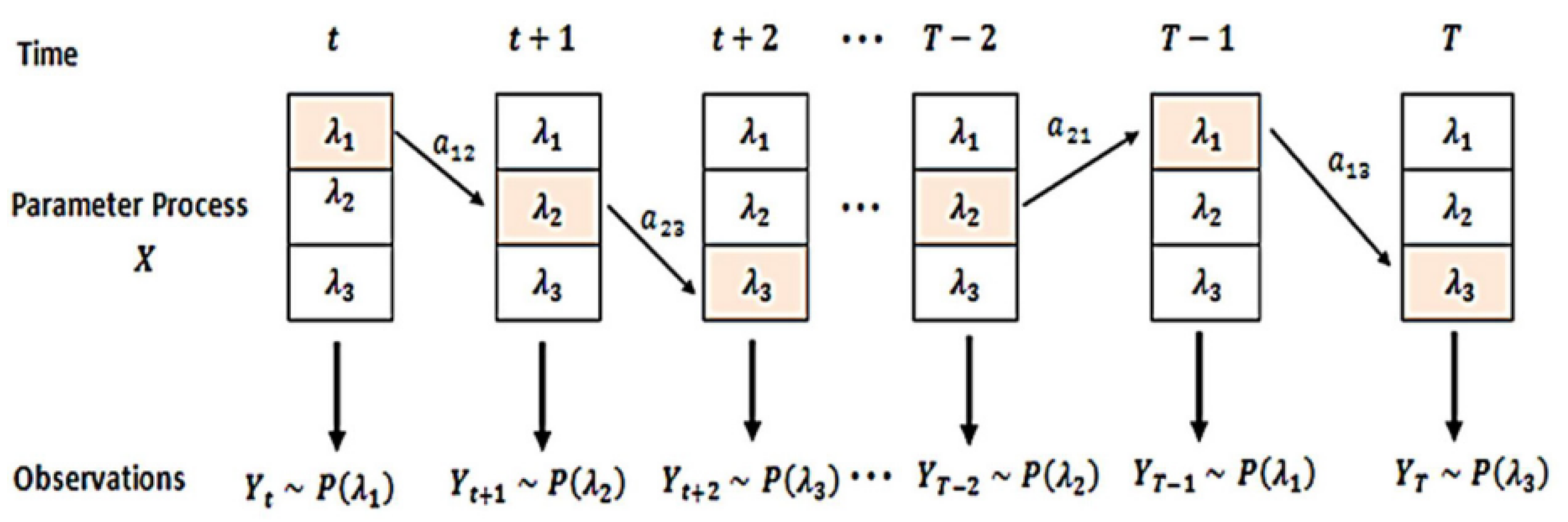
A hidden Markov model is a double stochastic process which consists of the underlying process which is a Markov process with state space where N is the number of hidden states and of the observation process i.e., a sequence of random variables that take values from the space where M is the number of observations which not necessarily coincides with N. The underlying process cannot be observed unlike the observation process. More specifically, the observable sequence of states is produced by and depends on the states of the Markov chain.
A Poisson hidden Markov model (PHMM) is a dual discrete-time stochastic process consisting of the finite-space underlying Markov process
,
and an observable stochastic process
,
, taking values in the
and
O sets, respectively (
Figure 2). The observed process is
where each one is associated with the process
and each
is associated with one of
N states
,
(see also
Figure 3 where the same hidden states can be revisited during the realization of the process
). A PHMM is characterized by the following five elements:
The number of hidden states (N): Each observation at the time point t, comes from one of N Poisson distributions but the state of , is not directly observed, i.e., it is hidden. The unobserved hidden state corresponding to at the time point t of the underlying homogeneous Markov Chain, is the mean , of the associated Poisson distribution. The N states of a PHMM are denoted by where the state represents the rate of occurrence of events associated with the specific state.
The transition probability matrix (
P): Each element of the transition probability matrix
P expresses the probability of transition in one step, from state
at time
t to state
at time
.
The following matrix shows the transition probabilities matrix for
N hidden states:
- 3.
Observations , , are non-negative integer values.
- 4.
When the system is in state
at time
t the observed value
comes from a Poisson distribution with parameter
. Thus, the distribution of
conditional on the state
, is defined as follows:
The above conditional probabilities for each y and i are often viewed as the elements of a matrix known as the emission probability matrix denoted by B. Note that in theory there is no upper bound on the value that the r.v. can take on but depending on the situation the probabilities eventually get tiny for large values of . Nevertheless, we could choose a large value for T for all practical purposes.
- 5.
The
N dimensional row vector
, namely the initial distribution which consists of the elements
, representing the probability that the Markov process starts from state
, that is
The PHMM with the above characteristics is often represented by
.
Figure 3 indicates a 3-state PHMM with the relevant parameters and the associated transition probabilities.
There have been a few applications of PHMM on earthquake problems. For instance, Can et al. in [
25] used PHMM for prediction of earthquake hazard around Bilecik (NW Turkey) and Orfanogiannaki et al. in [
26] applied PHMM to identify seismicity levels in the seismogenic area of Killini (Ionian Sea).
2.1. The Three Main Issues of HMM
According to [
27], when dealing with the observation sequence
and the model
, using HMM in real applications involves solving three fundamental issues. These are:
- (1)
The Estimation problem, which involves calculating the probability , i.e., the probability that the observation sequence was produced by the given model. This helps in selecting the model that best fits the observations when multiple models are considered.
- (2)
The Learning problem, which focuses on maximizing the probability by determining the optimal parameters of the model.
- (3)
The Decoding problem, which is about finding the optimal sequence of states for the Markov process, i.e., the sequence of Poisson distributions that generate the given observations.
2.2. The Implementation of the PHMM
To begin, the number
N of hidden states must be determined for each seismic zone. This number represents the different Poisson distributions generating the observations
, which express the annual number of earthquakes in each seismic zone. Due to the dataset’s size, it is more appropriate to work with annual events rather than monthly or daily ones. The researcher’s goal is to identify the optimal number of hidden states and their parameter values
,…,
to accurately describe how the observations were generated. The Baum-Welch algorithm [
28], a form of the Expectation Maximization (EM) algorithm (see [
29]), is used to determine these parameters iteratively through the E-step and M-step until convergence is achieved. The Baum-Welch algorithm is repeated for various values of
N to identify candidate models. Model selection criteria, such as the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC), are then used to choose the best-fitting model. The model with the lowest criterion value is selected as the most suitable one. It is noted that the R software is employed for implementing the PHMM.
After determining the ideal model, the steady state probabilities (
) need to be calculated. These probabilities represent the long-term probabilities of the system being in each state. For this, the following is calculated:
where
P the transition probability matrix given in (
2).
Let
the number of transitions from hidden state
i to hidden state
j and
the number of exits from hidden state
i. The estimated transition probabilities are defined by
and are used as initial values for the implementation of Baum–Welch algorithm under the package “HMMpa” of R software. The likelihood associated with the classical Poisson model is defines as
while in the complex cases with
hidden states the likelihood is formulated accordingly taking into account all the parameters
involved.
The PHMM combined with the EM algorithm and the AIC and BIC criteria will be applied in the following section for the Central and South American regions.
4. Discussion and Conclusions
Stochastic processes like Markov chains have been proven to be useful tools with numerous applications, including seismic hazard evaluation. This process transitions from one state/zone to another, between a finite number of states/zones according to a transition probability matrix. In this work, a Poisson hidden Markov model (PHMM) is presented and implemented for seismic activity in Central and South America. The choice of these regions was not random. Both areas are characterized by a high degree of tectonics, with mainly two subduction tectonic plates: the Nazca plate under South America and the Cocos plate under Central America. These tectonics result in a significant number of large earthquakes. The largest earthquake ever recorded globally occurred in South America in 1960 with a magnitude of . Additionally, a large earthquake in 2010 with a magnitude of occurred in the same area.
After identifying the number of hidden states and estimating the parameters of the selected model(s) for each zone separately using the EM algorithm and Information Criteria AIC and BIC, several conclusions were reached.
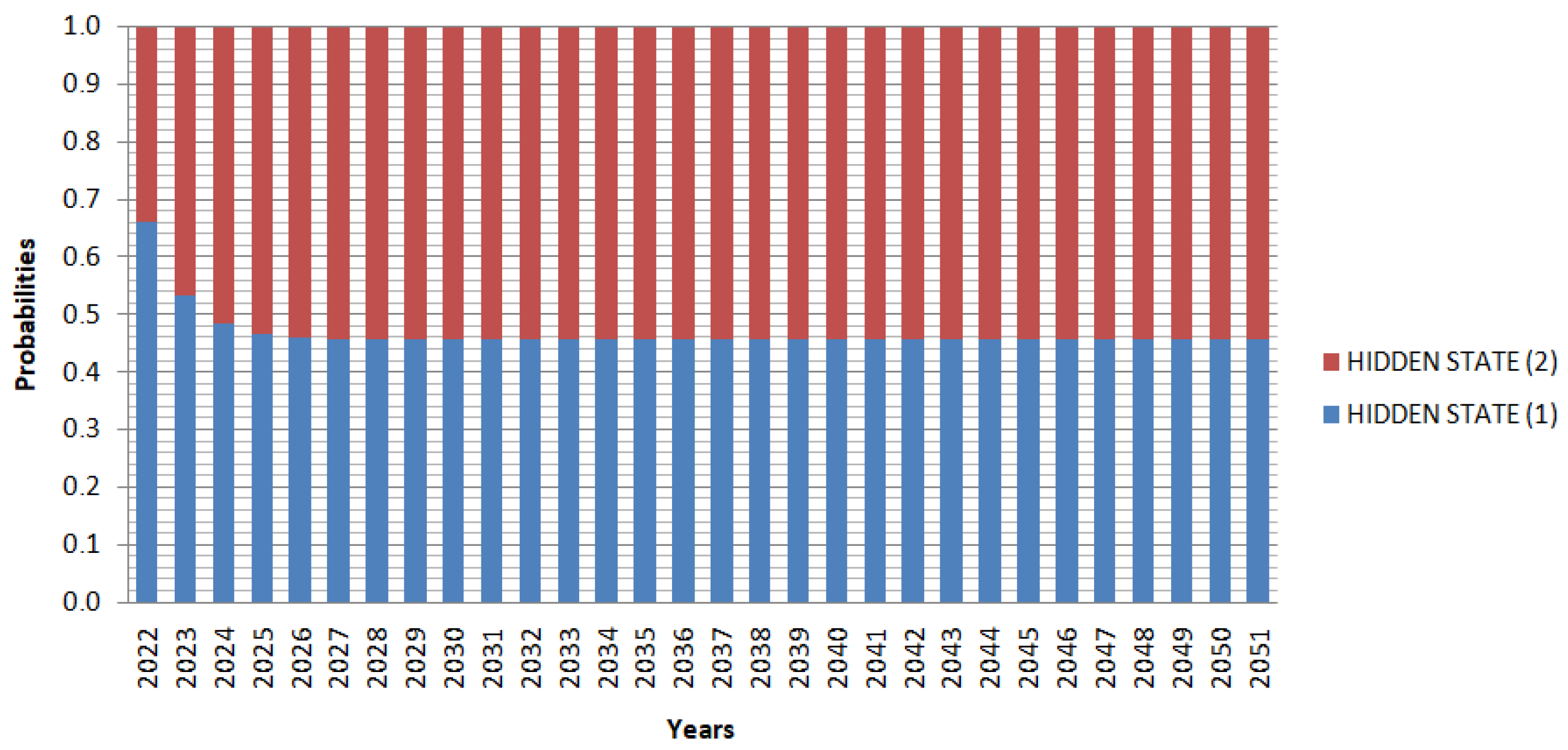
Seismic activity in most zones follows the PHMM for the geographical area under investigation, with the classical Poisson model chosen only for zone 3 and only by BIC. The steady state probabilities vary for different zones. For zones 4 and 7, which are fully presented in this work, the probabilities stabilize quite early (after 10 and 6 years, respectively). While for most zones, stabilization occurs within 3–10 years, zones 2 and 9 require more than 15 years for the steady-state distribution to be realized. Additionally, although the selection criteria recommend different models for zones 3, 6, 7, and 9, the differences are relatively small.
In most zones, the system remains in the first state for the next 30 years. In zone 7 (similar to zones 6 and 9), the system remains in the second state for the next 30 years (see e.g.,
Figure 8 and
Figure 9 and matrix in (
11)).
The methodology presented in this work demonstrates that the models used are reliable for estimating seismic activity in Central and South America. While classical Poisson-type models like the Generalized Poisson or Negative Binomial models often work well, PHMMs provide researchers with a way to capture autocorrelation in the data, resulting in an adequate representation of the phenomenon under investigation. It is worth noting that PHMMs can also be used for other aspects of seismic activity, such as estimating horizontal acceleration of an earthquake, which is crucial for designing large engineering projects. The seismicity of the regions investigated in this work is considered one of the most active in the world, with frequent large and destructive earthquakes. Due to the highly reliable results, the implementation of the proposed methodology is recommended for other geographical regions with varying levels of seismic activity.