Adjustment of Anticipatory Covariates in Retrospective Surveys: An Expected Likelihood Approach
Abstract
:1. Introduction
2. The Multiplicative Two-Factor Hazard Model
3. Adjusting for Anticipatory Covariates
3.1. Expected Likelihood
3.2. Parameter Estimation in the Expected Likelihood
4. Illustration: Effect of Education on Divorce
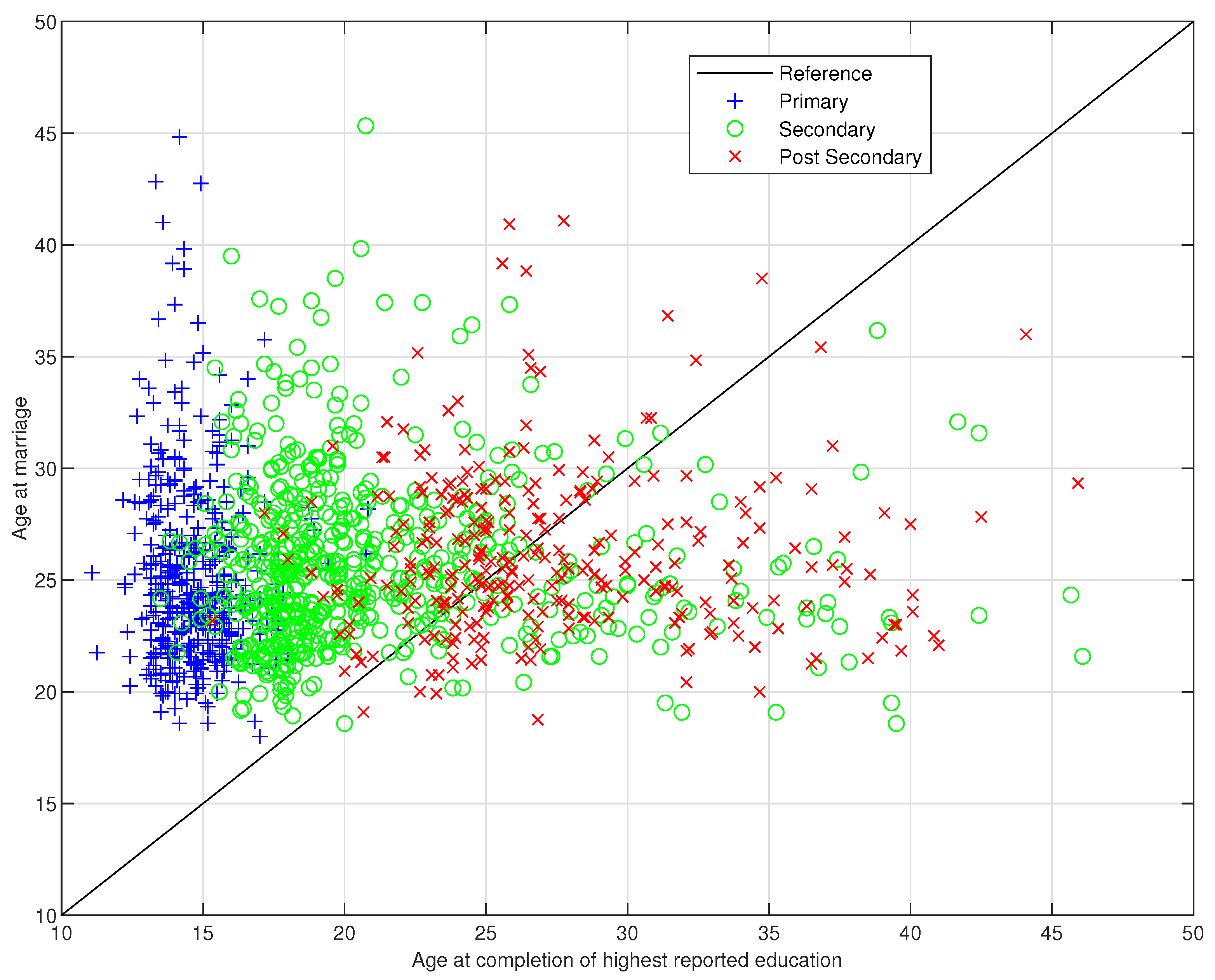
4.1. Data set
4.2. Models
4.3. Numerical Considerations
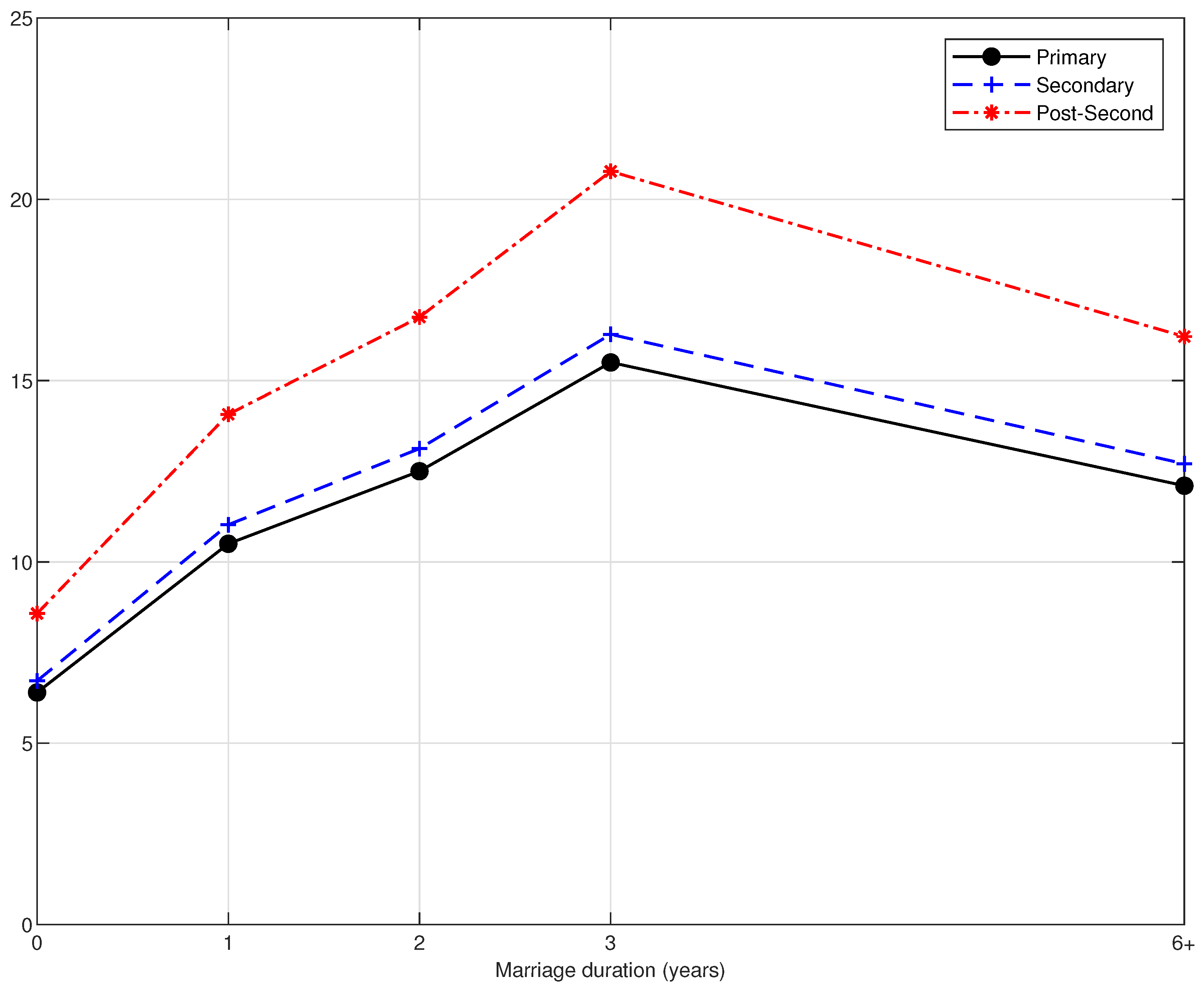
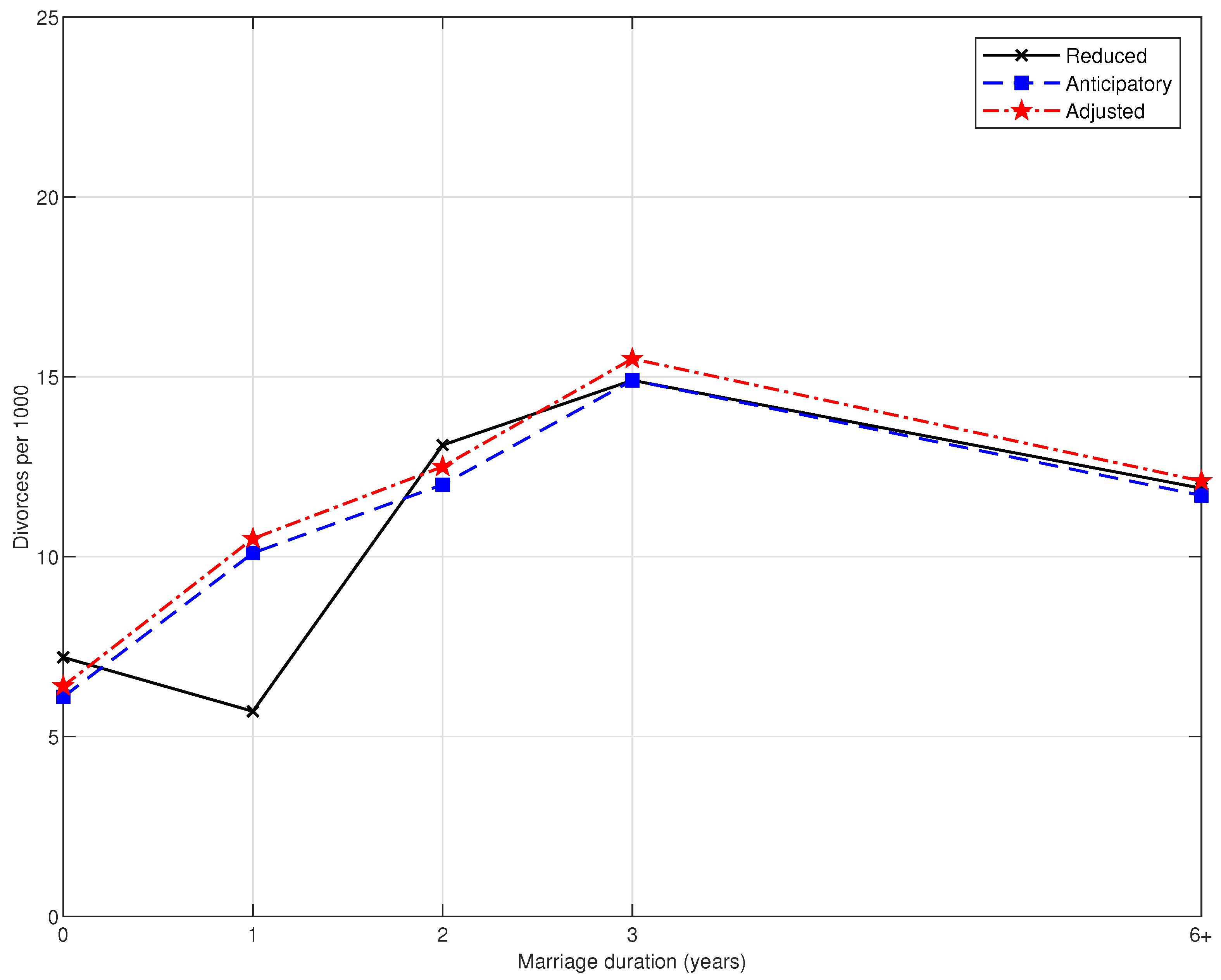
4.4. Results
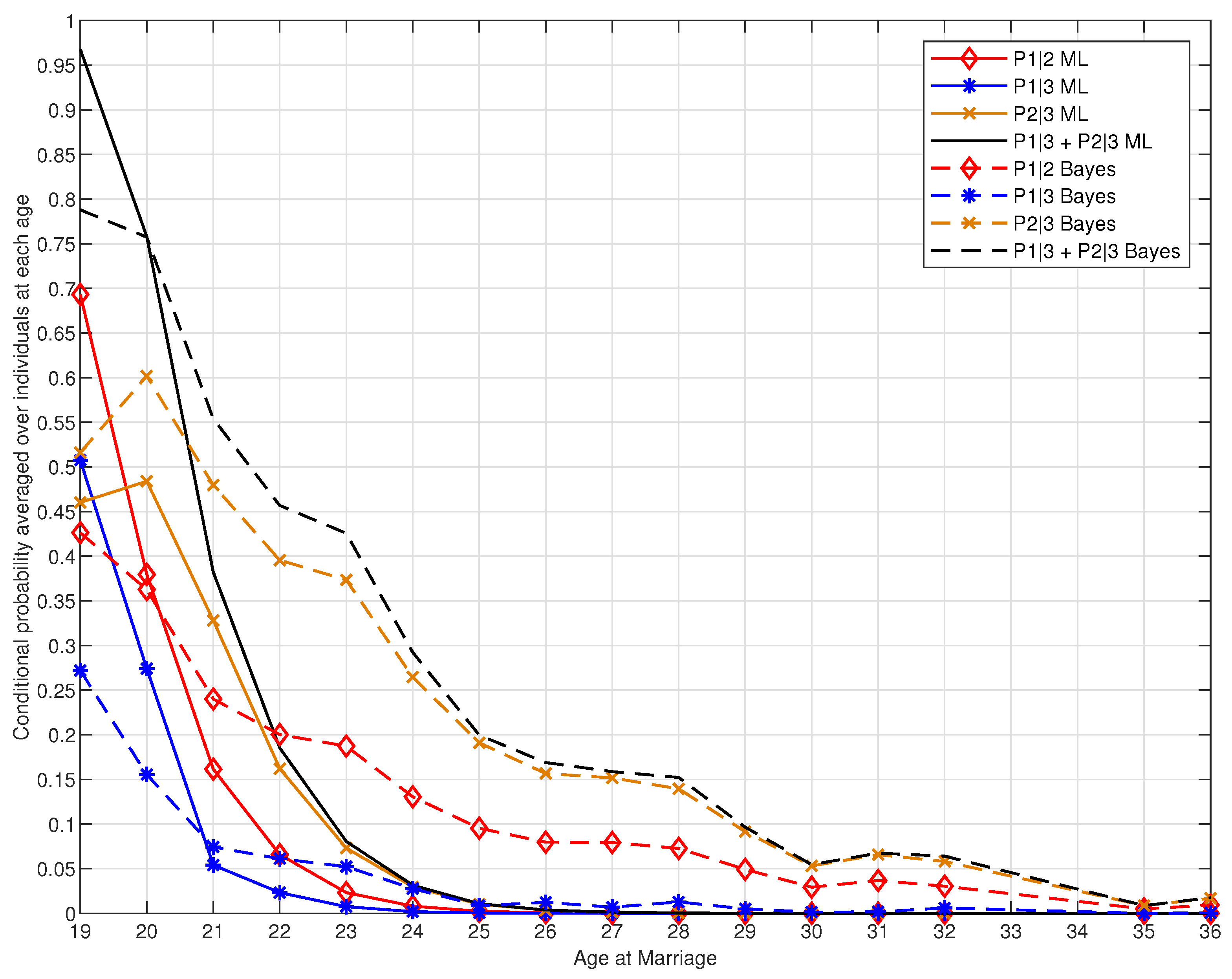
4.4.1. Conditional Probabilities
4.4.2. Model Parameters
4.4.3. Covariate-Model Parameters
5. Summary and Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Omitted Proofs & Tables and Figures of Empirical Results
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Proposition 2
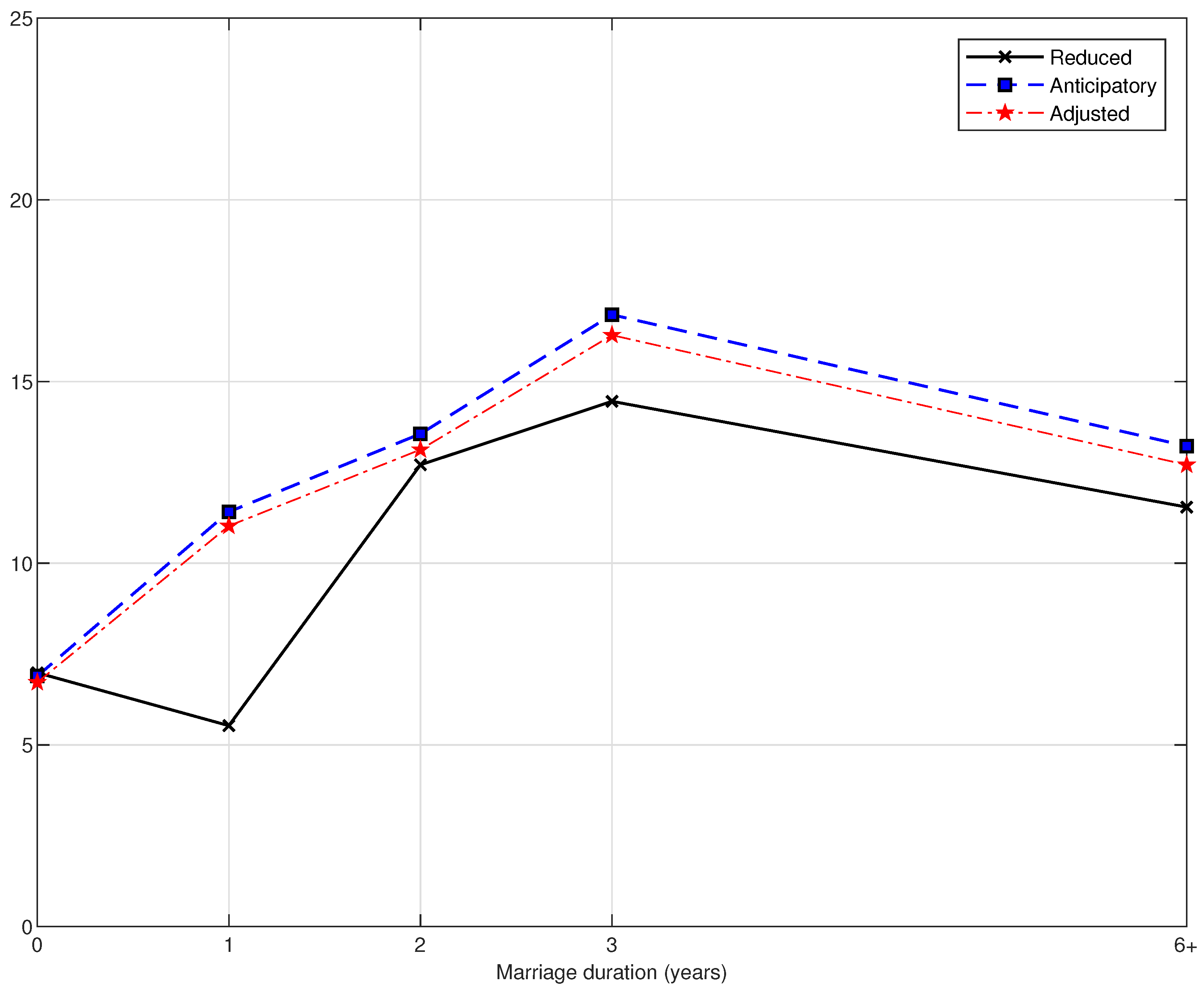
Appendix A.3. Tables and Figures of Empirical Results
| Status | |||||
|---|---|---|---|---|---|
| Still Married | Divorced | Total | % Divorced | ||
| Non-Anticip | Primary | 371 | 71 | 442 | 16 |
| Secondary | 433 | 55 | 488 | 11 | |
| Post Secon. | 116 | 21 | 137 | 15 | |
| 920 | 147 | 1067 | 14 | ||
| Anticipatory | Primary | - | - | - | - |
| Secondary | 66 | 28 | 94 | 30 | |
| Post-Secon. | 120 | 31 | 151 | 21 | |
| 186 | 59 | 245 | 24 | ||
| Total | 1106 | 206 | 1312 | 16 |
| Reduced | Anticip | Adjusted | |
|---|---|---|---|
| - | - | 34,900 (21,600, 36,900) | |
| - | - | ||
| - | - | ||
| - | - | 2130 | |
| - | - | ||
| - | - |
| Estimate | 80% Confidence Interval | ||
|---|---|---|---|
| Primary | |||
| Secondary | |||
| Post-secondary |
| Estimate | 80% Confidence Interval | ||
|---|---|---|---|
| Primary | |||
| Secondary |
| 6.4 | |
| 10.5 | |
| 12.6 | |
| 15.6 | |
| 12.2 | |
| 1.07 | |
| 1.30 |
| Model | Education | G & K [7] | M & G [8] | Present Study |
|---|---|---|---|---|
| Reduced | Primary (ref) | 1 | 1 | 1 |
| Model | Second. | 0.96 (0.66, 1.35) | 0.93 (0.40, 2.22) | 0.97 (0.67, 1.39) |
| Post-Sec. | 1.59 (1.23, 1.86) | 1.08 (0.72, 1.73) | 1.57 (0.90, 2.51) | |
| Anticip. | Primary (ref) | 1 | 1 | 1 |
| Model | Second. | 1.12 (0.81, 1.54) | 1.12 (0.52, 2.38) | 1.13 (0.83, 1.57) |
| Post-Sec. | 1.36 (1.02, 1.76) | 1.31 (0.66, 2.45) | 1.35 (0.93, 1.92) | |
| Adjusted | Primary (ref) | 1 | 1 | 1 |
| Model | Second. | 0.98 (0.71, 1.30) | 0.94 (0.41, 2.13) | 1.05 (0.78, 1.44) |
| Post-Sec. | 1.07 (0.84, 1.27) | 1.26 (1.19 1.48) | 1.34 (0.91, 1.92) |



References
- Hoem, J.M. The harmfulness and harmlessness of using anticipatory regressor. How dangerous is it to use education achieved as of 1990 in the analysis of divorce risks in earlier years. Finn. Yearb. Popul. Res. 1996, 33, 34–43. [Google Scholar] [CrossRef]
- Arulampalam, W.; Bhalotra, S. Sibling death clustering in India: State dependence versus unobserved heterogeneity. J. R. Stat. Soc. Ser. A Stat. Soc. 2006, 169, 829–848. [Google Scholar] [CrossRef]
- Hoem, J.M.; Kreyenfeld, M. Anticipatory Analysis and its Alternatives in Life-Course Research. Part 1: The Role of Education in the Study of First Childbearing. Demogr. Res. 2006, 15, 461–484. [Google Scholar] [CrossRef]
- Hoem, J.M.; Kreyenfeld, M. Anticipatory Analysis and its Alternatives in Life-Course Research. Part 2: Two Interacting Processes. Demogr. Res. 2006, 15, 485–498. [Google Scholar] [CrossRef]
- Faucett, C.L.; Schenker, N.; Elashoff, R.M. Analysis of Censored Survival Data with Intermittently Observed Time-Dependent Binary Covariates. J. Am. Stat. Assoc. 1998, 93, 427–437. [Google Scholar] [CrossRef]
- Todesco, L. A Matter of Number, Age or Marriage? Children and Marital Dissolution in Italy. Popul. Res. Policy Rev. 2011, 30, 313–332. [Google Scholar] [CrossRef]
- Ghilagaber, G.; Koskinen, J.H. Bayesian Adjustment of Anticipatory Covariates in Analyzing Retrospective Survey Data. Math. Popul. Stud. 2009, 16, 105–130. [Google Scholar] [CrossRef]
- Munezero, P.; Ghilagaber, G. Dynamic Bayesian Adjustment of Anticipatory Covariates in Retrospective Data: Application to the Effect of Education on Divorce Risk. J. Appl. Stat. 2022, 49, 1382–1401. [Google Scholar] [CrossRef] [PubMed]
- Hoem, J.M.; Nedoluzhko, L. The dangers of using‘negative durations’to estimate pre- and post-migration fertility. Popul. Stud. 2016, 70, 359–363. [Google Scholar] [CrossRef] [PubMed]
- Pina-Sánchez, J.; Koskinen, J.; Plewis, I. Adjusting for Measurement Error in Retrospectively Reported Work Histories: An Analysis Using Swedish Register Data. J. Off. Stat. 2019, 35, 203–229. [Google Scholar] [CrossRef]
- Breslow, N.E.; Day, N.E. Indirect standardization and multiplicative models for rates with reference to the age adjustment of cancer incidence and relative frequency data. J. Chronic. Dis. 1975, 28, 289–303. [Google Scholar] [CrossRef] [PubMed]
- Hoem, J.M. Statistical analysis of a multiplicative model and its application to the standardization of vital rates: A review. Int. Stat. Rev. 1987, 55, 119–152. [Google Scholar] [CrossRef]
- Orchard, T.; Woodbury, M.A. A missing information principle: Theory and applications. In Proceedings of the 6th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 19–21 July 1971; Volume 6.1, pp. 697–715. [Google Scholar]
- Ghilagaber, G.; Larsson, R. Maximum Likelihood Adjustment of Anticipatory Covariates in the Analysis of Retrospective Data; Research Report 2019:1; Department of Statistics, Stockholm University: Stockholm, Sweden, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghilagaber, G.; Larsson, R. Adjustment of Anticipatory Covariates in Retrospective Surveys: An Expected Likelihood Approach. Stats 2023, 6, 1179-1197. https://doi.org/10.3390/stats6040074
Ghilagaber G, Larsson R. Adjustment of Anticipatory Covariates in Retrospective Surveys: An Expected Likelihood Approach. Stats. 2023; 6(4):1179-1197. https://doi.org/10.3390/stats6040074
Chicago/Turabian StyleGhilagaber, Gebrenegus, and Rolf Larsson. 2023. "Adjustment of Anticipatory Covariates in Retrospective Surveys: An Expected Likelihood Approach" Stats 6, no. 4: 1179-1197. https://doi.org/10.3390/stats6040074
APA StyleGhilagaber, G., & Larsson, R. (2023). Adjustment of Anticipatory Covariates in Retrospective Surveys: An Expected Likelihood Approach. Stats, 6(4), 1179-1197. https://doi.org/10.3390/stats6040074






