Effective Sample Size with the Bivariate Gaussian Common Component Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Bivariate Gaussian Spatial Model
2.2. Univariate and Bivariate Effective Sample Size
- decreases as the spatial correlation increases;
- when there is a perfect spatial correlation between all pairs of observations;
- when there is no spatial correlation between the pairs of observations, where is the number of georeferenced observations of the variable;
- grows as increases;
- .
2.3. Description of the Simulation Study
2.4. Description of the Actual Data Study

2.5. Computational Resources
3. Results
3.1. Simulated Data: Properties (i) to (iv) of
3.2. Algebraic Verification of Property (v)
3.3. Application to the Organic Matter and Sum of Bases Data in an Agricultural Area Cultivated with Soybean
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BCRM | Bivariate coregionalization model |
| BGCCM | Bivariate Gaussian common component model |
| CEC | Cation exchange capacity |
| Ca | Calcium |
| ESS | Effective sample size |
| Bivariate effective sample size | |
| K | Potassium |
| MAE | Mean absolute error |
| Mg | Magnesium |
| OA | Overall accuracy |
| OM | Organic matter |
| SB | Sum of bases |
| SD | Standard deviation |
References
- Brus, D.J. Spatial Sampling with R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2022. [Google Scholar] [CrossRef]
- Griffith, D.A. Effective geographic sample size in the presence of spatial autocorrelation. Ann. Am. Assoc. Geogr. 2005, 95, 740–760. [Google Scholar] [CrossRef]
- Griffith, D.A.; Plant, R.E. Statistical Analysis in the Presence of Spatial Autocorrelation: Selected Sampling Strategy Effects. Stats 2022, 5, 1334–1353. [Google Scholar] [CrossRef]
- Vallejos, R.; Osorio, F. Effective sample size of spatial process models. Spat. Stat. 2014, 9, 66–92. [Google Scholar] [CrossRef]
- Vallejos, R.; Osorio, F.; Bevilacqua, M. Spatial Relationships between Two Georeferenced Variables: With applications in R; Springer: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Vallejos, R.; Acosta, J. The effective sample size for multivariate spatial processes with an application to soil contamination. Nat. Resour. Model. 2021, 34, e12322. [Google Scholar] [CrossRef]
- Watson, S.I. Efficient design of geographically-defined clusters with spatial autocorrelation. J. Appl. Stat. 2021, 49, 3300–3318. [Google Scholar] [CrossRef]
- Acosta, J.; Osorio, F.; Vallejos, R. Effective sample size for line transect sampling models with an application to marine macroalgae. J. Agric. Biol. Environ. Stat. 2016, 21, 407–425. [Google Scholar] [CrossRef]
- Acosta, J.; Vallejos, R. Effective sample size for spatial regression models. Electron. J. Stat. 2018, 12, 3147–3180. [Google Scholar] [CrossRef]
- Canton, L.E.D.; Guedes, L.P.C.; Uribe-Opazo, M.A.; Assumpção, R.A.B.; Maltauro, T.C. Sampling redesign of soil penetration resistance in spatial t-Student models. Span. J. Agric. Res. 2021, 19, e0202. [Google Scholar] [CrossRef]
- Canton, L.E.D.; Guedes, L.P.C.; Uribe-Opazo, M.A. Reduction of sample size in the soil physical-chemical attributes using the multivariate effective sample size. J. Agric. Stud. 2021, 9, 357–376. [Google Scholar] [CrossRef]
- Canton, L.E.D.; Maltauro, T.C.; Guedes, L.P.C.; Uribe-Opazo, M.A. Bivariate spatial correlation between soil attributes and soybean productivity in an agricultural area with Dystroferric Red Latosol. Aust. J. Crop Sci. 2023, 17, 20–27. [Google Scholar] [CrossRef]
- Mengel, K.; Kirkby, E. Principles of Plant Nutrition, 5th ed.; Kluwer Academic Publishers: Boston, MA, USA, 2001. [Google Scholar]
- Fonseca, B. Um Estudo Sobre Estimação e Predição em Modelos Geoestatísticos Bivariados. Master’s Thesis, Escola Superior de Agricultura Luiz de Queiroz, São Paulo, Brazil, 2008. [Google Scholar] [CrossRef]
- Diggle, P.J.; Ribeiro, P.J., Jr. Model Based Geostatistics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Fanshawe, T.R.; Diggle, P.J. Bivariate geostatistical modelling: A review and an application to spatial variation in radon concentrations. Environ. Ecol. Stat. 2012, 19, 139–160. [Google Scholar] [CrossRef]
- Righetto, A. Avaliação de Modelos Geoestatísticos Multivariados. Master’s Thesis, Escola Superior de Agricultura Luiz de Queiroz, São Paulo, Brazil, 2012. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Statistics for Spatial Data, 1st ed.; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Pavan, M.; Bloch, M.; Zempulski, H.; Miyazawa, M.; Zocoler, D. Manual de Análise Química de Solo e Controle de Qualidade; Instituto Agronômico do Paraná: Londrina, Brazil, 1992. [Google Scholar]
- Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter and a proposed modification of the chromic acid titration method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- De Bastiani, F.; Cysneiros, A.F.J.; Cysneiros, A.H.M.; Uribe-Opazo, M.A.; Galea, M. Infuence diagnostics in elliptical spatial linear models. Test 2015, 24, 322–340. [Google Scholar] [CrossRef]
- Anderson, J.R.; Hardy, E.E.; Roach, J.T.; Witmer, R.E. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; U.S. Government Print Office: Washington, DC, USA, 2001.
- R Development Core Team. R: A Language and Environment for Statistical Computing, version 4.1.1; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.r-project.org/ (accessed on 1 November 2022).
- Ribeiro, P.J., Jr.; Diggle, P.J. geoR: A Package for Geostatistical Analysis. R-NEWS 2001, 1, 15–18. [Google Scholar]
- SBCS-NEPAR. Manual de Adubação e Calagem para o Estado do Paraná; Sociedade Brasileira de Ciência do Solo—Núcleo Estadual do Paraná: Curitiba, Brazil, 2017. [Google Scholar]
- Gomes, F.P.; Garcia, C. Estatística Aplicada a Experimentos Agronômicos e Florestais; Fundação de Estudos Agrários Luiz de Queiroz: Piracicaba, Brazil, 2002. [Google Scholar]
- Faraco, M.A.; Uribe-Opazo, M.A.; Silva, E.A.A.; Johann, J.A.; Borssoi, J.A. Seleção de modelos de variabilidade espacial para elaboração de mapas temáticos de atributos físicos do solo e produtividade da soja. Rev. Bras. Ciênc. Solo 2008, 32, 463–476. [Google Scholar] [CrossRef]
- Krippendorff, K. Content Analysis: An Introduction to Its Methodology; Sage Publications: Beverly Hills, CA, USA, 2004. [Google Scholar]
- Ma, Z.; Redmond, R.L. Tau coefficients for accuracy assessment of classification of remote sensing data. Photogramm. Eng. Remote Sens. 1995, 61, 435–439. [Google Scholar]
- Kestring, F.B.; Guedes, L.P.C.; De Bastiani, F.; Uribe-Opazo, M.A. Comparação de mapas temáticos de diferentes grades amostrais para a produtividade da soja. Eng. Agric. 2015, 35, 733–743. [Google Scholar] [CrossRef][Green Version]
- Maltauro, T.C.; Guedes, L.P.C.; Uribe-Opazo, M.A.; Canton, L.E.D. A genetic algorithm for resizing and sampling reduction of non-stationary soil chemical attributes optimizing spatial prediction. Span. J. Agric. Res. 2021, 19, e0210. [Google Scholar] [CrossRef]
- Maltauro, T.C.; Guedes, L.P.C.; Uribe-Opazo, M.A.; Canton, L.E.D. Spatial multivariate optimization for a sampling redesign with a reduced sample size of soil chemical properties. Rev. Bras. Cienc. Solo 2023, 47, e0220072. [Google Scholar] [CrossRef]
- El Saeiti, R.; García-Fiñana, M.; Hughes, D.M. The effect of random-effects misspecification on classification accuracy. Int. J. Biostat. 2021, 18, 279–292. [Google Scholar] [CrossRef]
- Sheng, Y.; Yang, C.; Curhan, S.; Curhan, G.; Wang, M. Analytical methods for correlated data arising from multicenter hearing studies. Stat. Med. 2022, 41, 5335–5348. [Google Scholar] [CrossRef] [PubMed]
- Schemmer, R.C.; Uribe-Opazo, M.A.; Galea, M.; Assumpção, R.A.B. Spatial variability of soybean yield through a reparameterized t-student model. Eng. Agríc. 2017, 37, 760–770. [Google Scholar] [CrossRef]
- Garcia-Papani, F.; Leiva, V.; Uribe-Opazo, M.A.; Aykroyd, R.G. Birnbaum-Saunders spatial regression models: Diagnostics and application to chemical data. Chemom. Intell. Lab. Syst. 2018, 177, 114–128. [Google Scholar] [CrossRef]

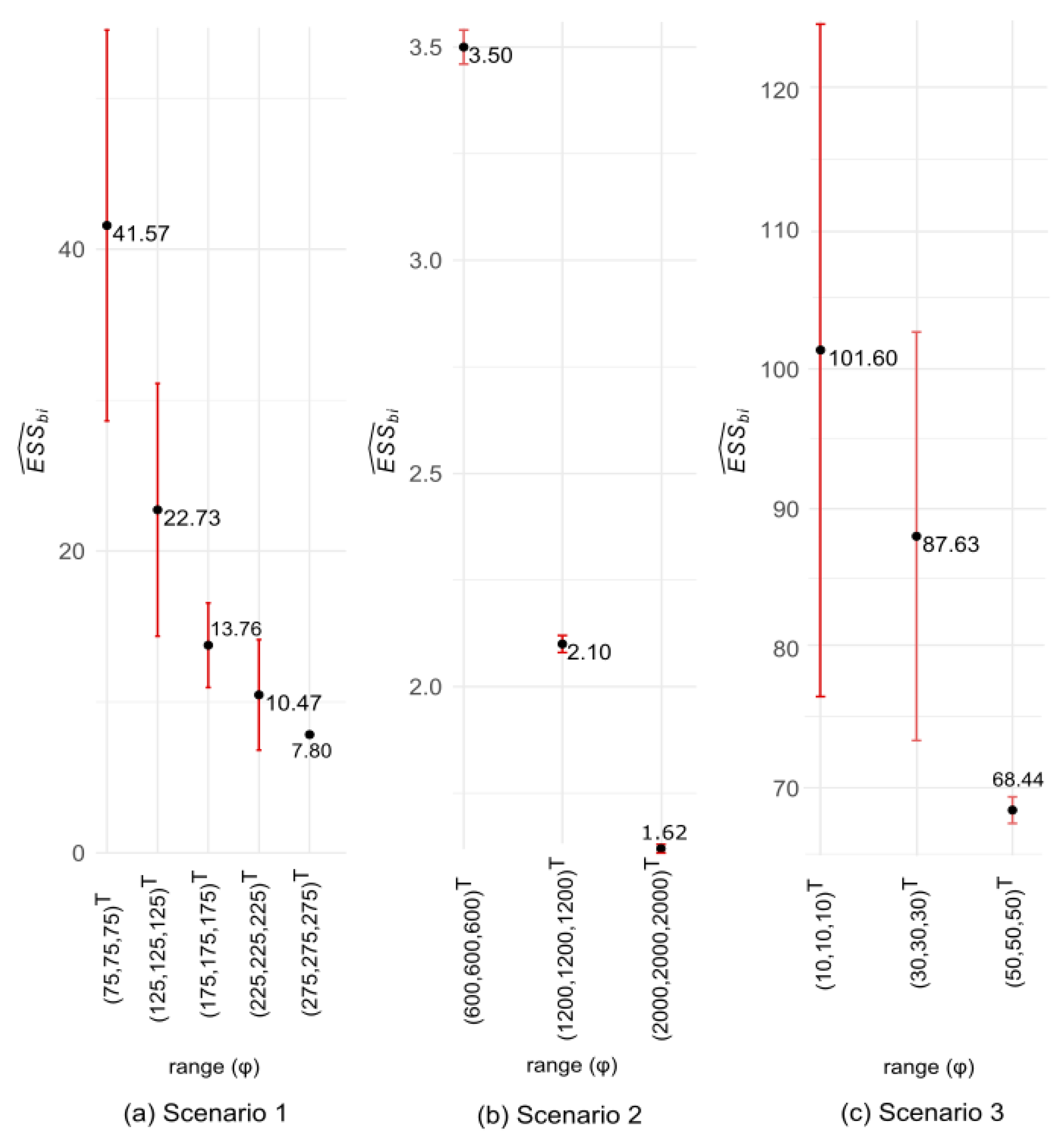
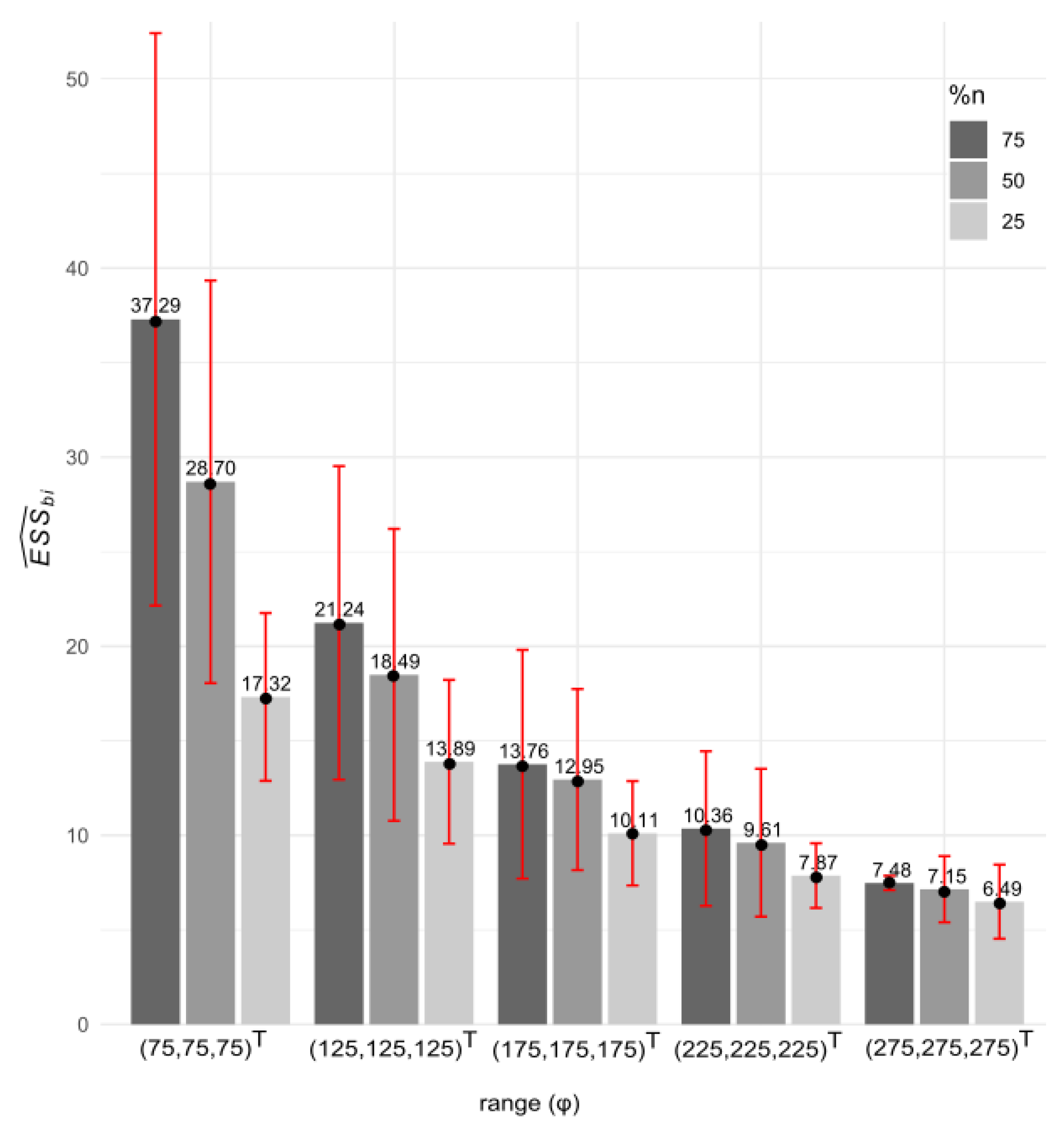
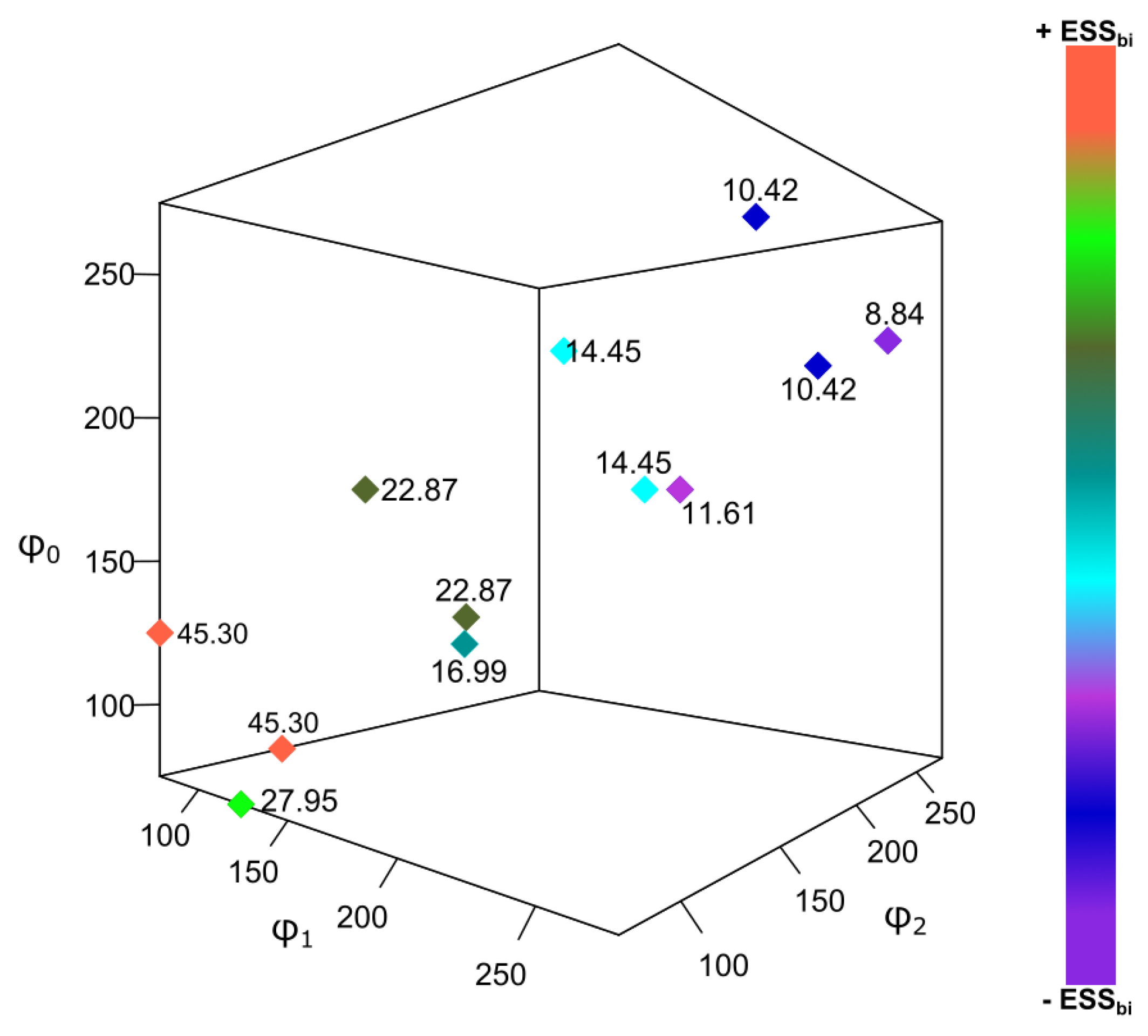
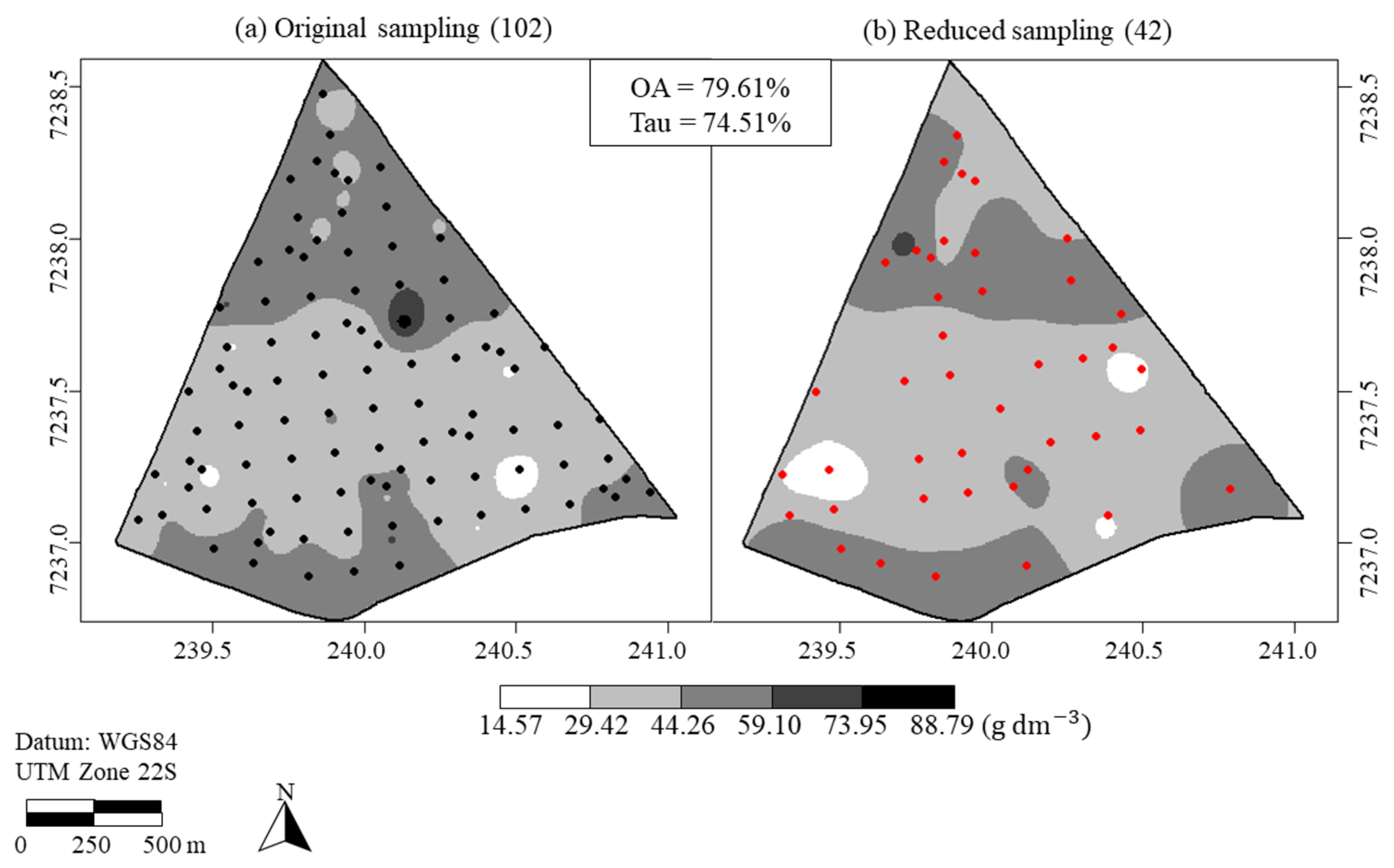
| Trial: | ||||||||
|---|---|---|---|---|---|---|---|---|
| Scenario 1 | T1: | 0.47 | 6.19 | 2.58 | 4.29 | 92.35 | 68.97 | 74.50 |
| (1.66) | (1.60) | (2.29) | (2.40) | (27.59) | (18.58) | (39.63) | ||
| T2: | 0.46 | 4.79 | 1.33 | 4.27 | 137.05 | 118.65 | 120.47 | |
| (1.76) | (2.28) | (2.13) | (2.77) | (32.28) | (28.25) | (26.61) | ||
| T3: | 0.10 | 1.79 | 0.38 | 1.93 | 186.79 | 170.75 | 178.63 | |
| (1.90) | (3.80) | (1.93) | (4.02) | (19.60) | (17.37) | (13.46) | ||
| T4: | 0.01 | 0.37 | 0.17 | 0.55 | 233.12 | 221.01 | 232.02 | |
| (1.98) | (4.63) | (2.02) | (4.78) | (15.39) | (11.20) | (11.14) | ||
| T5: | 2.40 | 1.95 | 5.72 | 1.70 | 285.98 | 278.75 | 279.28 | |
| (≈2.00) | (≈5.00) | (≈2.00) | (≈5.00) | (11.24) | (5.78) | (7.05) | ||
| Scenario 2 | T1: | 2.11 | 3.19 | 2.28 | 4.54 | 629.67 | 607.81 | 608.75 |
| (≈2.00) | (≈5.00) | (≈2.00) | (≈5.00) | (30.58) | (12.21) | (10.94) | ||
| T2: | 4.16 | 1.83 | 2.17 | 2.81 | 1278.03 | 1208.10 | 1213.74 | |
| (≈2.00) | (≈5.00) | (≈2.00) | (≈5.00) | (79.63) | (14.33) | (17.08) | ||
| T3: | 1.55 | 1.87 | 1.34 | 1.59 | 2171.38 | 2004.29 | 1987.34 | |
| (≈2.00) | (≈5.00) | (≈2.00) | (≈5.00) | (171.37) | (20.99) | (37.28) | ||
| Scenario 3 | T1: | 1.14 | 5.83 | 0.63 | 6.27 | 6.75 | 12.77 | 14.63 |
| (1.49) | (1.59) | (1.65) | (1.65) | (7.60) | (9.79) | (12.01) | ||
| T2: | 1.40 | 5.43 | 1.35 | 5.63 | 32.50 | 29.43 | 29.86 | |
| (1.57) | (1.62) | (2.20) | (2.35) | (16.53) | (12.45) | (14.21) | ||
| T3: | 0.58 | 6.15 | 2.95 | 3.96 | 54.89 | 46.43 | 46.58 | |
| (1.66) | (1.62) | (2.65) | (2.75) | (18.62) | (17.76) | (23.72) |
| Trial: | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario 4 | n = 77 (75%) | T1: | 0.62 | 5.92 | 2.46 | 4.40 | 97.23 | 65.68 | 66.01 |
| (1.75) | (1.66) | (2.31) | (2.54) | (31.01) | (23.74) | (34.59) | |||
| T2: | 0.52 | 4.86 | 2.12 | 3.70 | 170.52 | 113.90 | 110.08 | ||
| (1.88) | (2.11) | (2.35) | (2.90) | (62.89) | (36.66) | (37.20) | |||
| T3: | 0.16 | 2.44 | 0.97 | 2.15 | 194.16 | 164.61 | 168.25 | ||
| (1.91) | (3.33) | (2.22) | (3.69) | (36.29) | (25.51) | (30.24) | |||
| T4: | 0. 05 | 0.87 | 0.53 | 0.90 | 232.28 | 217.20 | 230.40 | ||
| (1.97) | (4.35) | (2.08) | (4.49) | (21.83) | (18.97) | (14.37) | |||
| T5: | 0.02 | 0.24 | 0.08 | 0.33 | 289.19 | 275.68 | 278.30 | ||
| (1.97) | (4.78) | (2.02) | (4.85) | (15.77) | (11.37) | (9.47) | |||
| n = 51 (50%) | T1: | 0.46 | 5.83 | 2.82 | 3.91 | 101.36 | 60.82 | 67.28 | |
| (1.63) | (1.78) | (2.58) | (2.68) | (36.02) | (30.88) | (40.64) | |||
| T2: | 0.37 | 4.97 | 2.44 | 3.54 | 157.02 | 105.98 | 116.42 | ||
| (1.76) | (2.04) | (2.54) | (2.81) | (52.68) | (33.94) | (59.92) | |||
| T3: | 0.22 | 3.30 | 1.26 | 2.96 | 197.72 | 158.68 | 165.81 | ||
| (1.88) | (2.88) | (2.26) | (3.32) | (40.72) | (36.87) | (41.87) | |||
| T4: | 0.04 | 1.61 | 0.78 | 1.66 | 242.50 | 209.03 | 230.76 | ||
| (1.95) | (3.81) | (2.05) | (4.23) | (38.88) | (25.06) | (33.36) | |||
| T5: | 0.02 | 1.02 | 0.62 | 1.10 | 306.30 | 257.65 | 283.61 | ||
| (1.98) | (4.16) | (2.21) | (4.24) | (44.91) | (28.52) | (30.98) | |||
| n = 26 (25%) | T1: | 0.86 | 5.44 | 2.68 | 4.02 | 110.17 | 53.43 | 65.70 | |
| (1.69) | (2.05) | (2.63) | (2.51) | (45.52) | (39.03) | (41.70) | |||
| T2: | 0.76 | 4.35 | 2.40 | 3.51 | 145.37 | 102.18 | 106.91 | ||
| (1.77) | (2.13) | (2.38) | (2.95) | (50.08) | (49.69) | (58.19) | |||
| T3: | 0.43 | 3.60 | 2.12 | 2.44 | 205.45 | 149.13 | 178.98 | ||
| (1.91) | (2.67) | (2.62) | (3.45) | (55.01) | (52.66) | (84.78) | |||
| T4: | 0.12 | 3.07 | 1.25 | 2.36 | 255.67 | 190.27 | 187.42 | ||
| (1.88) | (2.93) | (2.16) | (3.34) | (48.83) | (60.70) | (54.76) | |||
| T5: | 0.11 | 2.53 | 1.23 | 2.04 | 303.92 | 236.79 | 255.68 | ||
| (1.91) | (3.29) | (2.31) | (3.52) | (59.50) | (62.18) | (61.41) |
| Trial: | |||||
|---|---|---|---|---|---|
| Scenario 5 | T1: | 0.38 | 5.68 | 1.78 | 4.52 |
| (1.71) | (1.85) | (2.17) | (2.43) | ||
| T2: | 0.29 | 6.39 | 2.16 | 4.62 | |
| (1.70) | (1.66) | (2.13) | (2.08) | ||
| T3: | 0.25 | 6.37 | 2.73 | 4.24 | |
| (1.76) | (1.41) | (1.93) | (1.94) | ||
| T4: | 0.25 | 2.76 | 1.08 | 2.54 | |
| (1.85) | (3.07) | (2.25) | (3.53) | ||
| T5: | 0.35 | 3.80 | 0.81 | 3.59 | |
| (1.78) | (2.81) | (2.05) | (3.12) | ||
| T6: | 0.24 | 5.52 | 1.03 | 5.07 | |
| (1.76) | (2.00) | (1.76) | (2.31) | ||
| T7: | 0.14 | 1.23 | 0.46 | 1.34 | |
| (2.01) | (4.18) | (2.03) | (4.33) | ||
| T8: | 0.09 | 1.62 | 0.36 | 1.72 | |
| (1.90) | (3.93) | (1.99) | (4.20) | ||
| T9: | 0.05 | 2.20 | 0.61 | 2.15 | |
| (1.94) | (3.68) | (2.01) | (3.92) | ||
| T10: | 0.02 | 0.36 | 0.28 | 0.50 | |
| (1.97) | (4.67) | (2.09) | (4.84) | ||
| T11: | 0.01 | 0.52 | 0.33 | 0.49 | |
| (1.98) | (4.73) | (2.10) | (4.68) | ||
| T12: | 0.003 | 0.49 | 0.34 | 0.53 | |
| (1.99) | (4.61) | (2.05) | (4.73) |
| Sample Size | Attributes | Minimum | Maximum | Mean | SD | CV (%) |
|---|---|---|---|---|---|---|
| OM | 13.40 | 89.80 | 42.14 | 10.51 | 24.93 | |
| SB | 2.55 | 9.65 | 6.05 | 1.38 | 22.83 | |
| OM | 22.78 | 57.63 | 41.87 | 9.19 | 21.96 | |
| SB | 2.55 | 9.65 | 6.32 | 1.52 | 24.03 |
| Geostatistical Model (Sample Configuration) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Exponential (Original) | 43.95 | 6.14 | 3.14 | 1.91 | 1.87 | 5.78 | 79.43 (237.97) | 269.28 (806.70) | 296.02 (886.81) |
| Matérn 2.5 (Reduced) | 51.22 | 2.81 | 4.88 | 7.94 | 1.65 | 1.96 | 162.39 (961.15) | 241.63 (1430.16) | 241.69 (1430.51) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Canton, L.E.D.; Guedes, L.P.C.; Uribe-Opazo, M.A.; Maltauro, T.C. Effective Sample Size with the Bivariate Gaussian Common Component Model. Stats 2023, 6, 1019-1036. https://doi.org/10.3390/stats6040064
Canton LED, Guedes LPC, Uribe-Opazo MA, Maltauro TC. Effective Sample Size with the Bivariate Gaussian Common Component Model. Stats. 2023; 6(4):1019-1036. https://doi.org/10.3390/stats6040064
Chicago/Turabian StyleCanton, Letícia Ellen Dal, Luciana Pagliosa Carvalho Guedes, Miguel Angel Uribe-Opazo, and Tamara Cantu Maltauro. 2023. "Effective Sample Size with the Bivariate Gaussian Common Component Model" Stats 6, no. 4: 1019-1036. https://doi.org/10.3390/stats6040064
APA StyleCanton, L. E. D., Guedes, L. P. C., Uribe-Opazo, M. A., & Maltauro, T. C. (2023). Effective Sample Size with the Bivariate Gaussian Common Component Model. Stats, 6(4), 1019-1036. https://doi.org/10.3390/stats6040064






