A Shared Frailty Model for Left-Truncated and Right-Censored Under-Five Child Mortality Data in South Africa
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Source and Study Variables
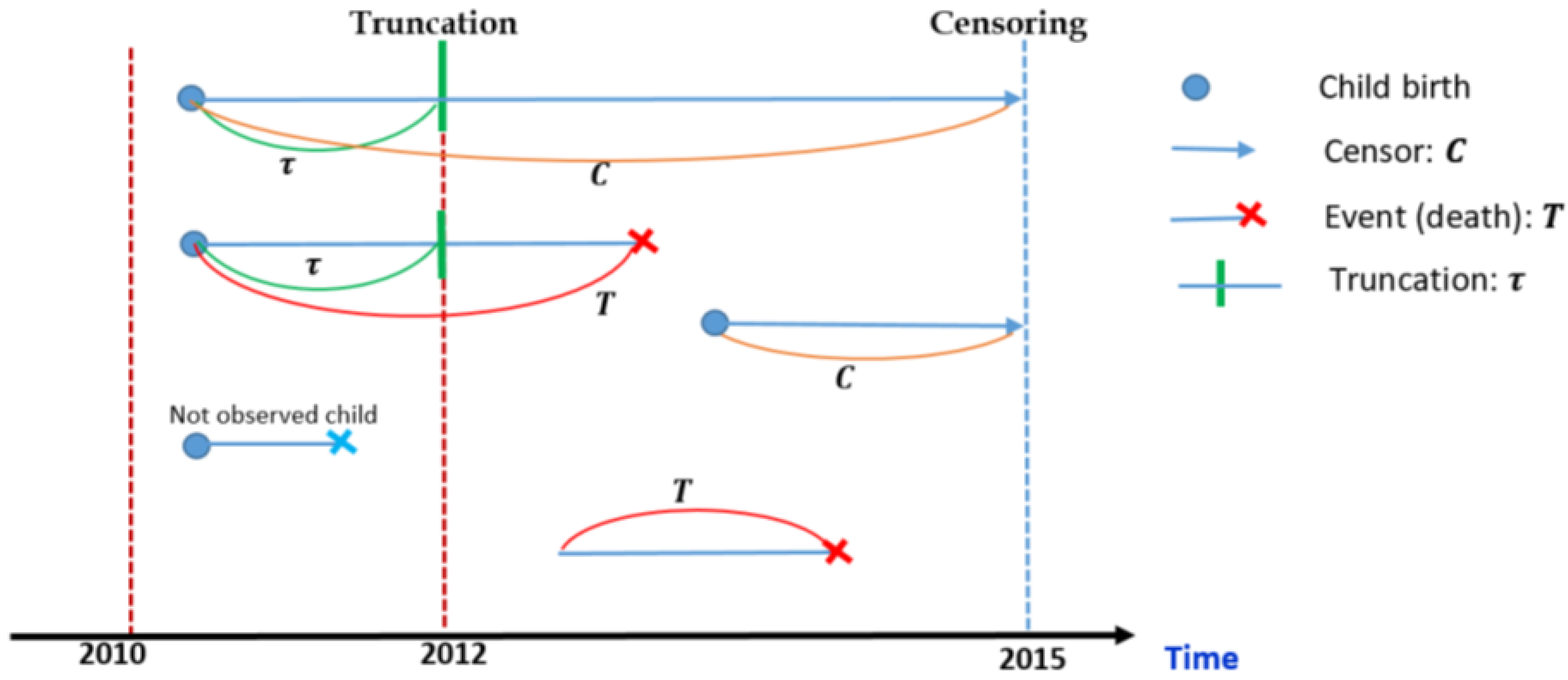
Dataset
2.2. Methods of Data Analysis
2.2.1. Cox Proportional Hazards Model
2.2.2. Shared Frailty Model
3. Results
4. Discussion
5. Conclusions
Study Limitation
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIC | Akaike Information Criterion |
| HR | Hazard ratio |
| LCV | Likelihood cross-validation |
| MDG | Millennium Development Goal |
| PH | Proportional hazards |
| SDG | Sustainable Development Goal |
| Stats SA | Statistics South Africa |
| U5CM | Under-five child mortality |
References
- Munyamahoro, F. Copula-Based Dependence Measures for Under-Five Mortality Rate in Rwanda. Arch. Med. 2016, 2, 34. [Google Scholar] [CrossRef]
- Bryce, J.; Terreri, N.; Victora, C.G.; Mason, E.; Daelmans, B.; Bhutta, Z.A.; Bustreo, F.; Songane, F.; Salama, P.; Wardlaw, T. Countdown to 2015: Tracking intervention coverage for child survival. Lancet 2006, 368, 1067–1076. [Google Scholar] [CrossRef] [PubMed]
- United Nations Development Programme. Sustainable Development Goals—Good Health and Wellbeing; United Nations Development Programme: New York, NY, USA, 2019. [Google Scholar]
- Bamford, L.; McKerrow, N.; Barron, P.; Aung, Y. Child mortality in South Africa: Fewer deaths, but better data are needed. S. Afr. Med. J. 2018, 108, 25–32. [Google Scholar] [CrossRef]
- Schober, P.; Vetter, T.R. Survival analysis and interpretation of time-to-event data: The tortoise and the hare. Anesth. Analg. 2018, 127, 792. [Google Scholar] [CrossRef] [PubMed]
- Guo, G.; Rodriguez, G. Estimating a multivariate proportional hazards model for clustered data using the EM algorithm, with an application to child survival in Guatemala. J. Am. Stat. Assoc. 1992, 87, 969–976. [Google Scholar] [CrossRef]
- Cesar, C.C.; Palloni, A.; Rafalimanana, H. Analysis of Child Mortality with Clustered Aata: A Review of Alternative Models and Procedures; Center for Demography and Ecology, University of Wisconsin–Madison: Madison, WI, USA, 1997. [Google Scholar]
- Duchateau, L.; Janssen, P. The Frailty Model; Springer: New York, NY, USA, 2008. [Google Scholar]
- Zhang, H.; Schaubel, D.E.; Kalbfleisch, J.D. Proportional hazards regression for the analysis of clustered survival data from case–cohort studies. Biometrics 2011, 67, 18–28. [Google Scholar] [CrossRef]
- Spiekerman, C.; Lin, D. Marginal Regression Models for Multivariate Failure Time Data. J. Am. Stat. Assoc. 1998, 93, 1164–1175. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. (Methodol.) 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Wienke, A. Frailty Models in Survival Analysis, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2010. [Google Scholar]
- Hanagal, D.D.; Sharma, R. Modeling heterogeneity for bivariate survival data by shared gamma frailty regression model. Model Assist. Stat. Appl. 2013, 8, 85–102. [Google Scholar] [CrossRef]
- Kifle, Y.; Janssen, P.; Yewhalaw, D.; Speybroeck, N.; Duchateau, L. Coping with time and space in modelling malaria incidence: A comparison of survival and count regression models. Stat. Med. 2013, 32, 3224–3233. [Google Scholar]
- Goethals, K. Multivariate Survival Models for Interval-Censored udder Quarter Infection Times. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2011. [Google Scholar]
- Simon, R.M.; Subramanian, J.; Li, M.C.; Menezes, S. Using cross-validation to evaluate predictive accuracy of survival risk classifiers based on high-dimensional data. Brief. Bioinform. 2011, 12, 203–214. [Google Scholar] [CrossRef]
- Rondeau, V.; Marzroui, Y.; Gonzalez, J.R. frailtypack: An R package for the analysis of correlated survival data with frailty models using penalized likelihood estimation or parametrical estimation. J. Stat. Softw. 2012, 47, 1–28. [Google Scholar] [CrossRef]
- Legrand, C. Advanced Survival Models; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Gachau, W.S. Frailty Models with Applications in Medical Research: Observed and Simulated Data. Ph.D. Thesis, University of Nairobi, Nairobi, Kenya, 2014. [Google Scholar]
- Kifle, Y.G.; Chen, D.G.; Haileyesus, M.T. Multivariate frailty models using survey weights with applications to twins infant mortality in Ethiopia. Stat. Interface 2023, 16, 493–502. [Google Scholar] [CrossRef]
- Legrand, C.; Duchateau, L.; Sylvester, R.; Janssen, P.; van der Hage, J.A.; Van de Velde, C.J.; Therasse, P. Heterogeneity in disease free survival between centers: Lessons learned from an EORTC breast cancer trial. Clin. Trials 2006, 3, 10–18. [Google Scholar] [CrossRef] [PubMed]
- Goethals, K.; Janssen, P.; Duchateau, L. Frailty models and copulas: Similarities and differences. J. Appl. Stat. 2008, 35, 1071–1079. [Google Scholar] [CrossRef]
- Srivastava, S.; Upadhyay, S.K.; Chauhan, S.; Alagarajan, M. Preceding child survival status and its effect on infant and child mortality in India: An evidence from National Family Health Survey 2015–16. BMC Public Health 2021, 21, 1577. [Google Scholar] [CrossRef]
- Khan, J.R.; Awan, N. A comprehensive analysis on child mortality and its determinants in Bangladesh using frailty models. Arch. Public Health 2017, 75, 58. [Google Scholar] [CrossRef]
- Nasejje, J. Application of Survival Analysis Methods to Study Under-five Child Mortality in Uganda. Ph.D. Thesis, University of KwaZulu-Natal, Pietermaritzburg, South Africa, 2013. [Google Scholar]
- Zike, D.T.; Fenta, H.M.; Workie, D.L.; Swain, P.K. Determinants of Under-Five Mortality in Ethiopia: An Application of Cox Proportional Hazard and Frailty Models. Turk. Klin. J. Biostat. 2018, 10, 123–136. [Google Scholar] [CrossRef]
- Ezeh, O.K.; Agho, K.E.; Dibley, M.J.; Hall, J.J.; Page, A.N. Risk factors for postneonatal, infant, child and under-5 mortality in Nigeria: A pooled cross-sectional analysis. BMJ Open 2015, 5, e006779. [Google Scholar] [CrossRef]
- Seçkin, N. Determinants of Infant Mortality in Turkey. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2009. [Google Scholar]
- Pongou, R. Why is infant mortality higher in boys than in girls? A new hypothesis based on preconception environment and evidence from a large sample of twins. Demography 2013, 50, 421–444. [Google Scholar] [CrossRef]
- Becher, H.; Müller, O.; Jahn, A.; Gbangou, A.; Kynast-Wolf, G.; Kouyaté, B. Risk factors of infant and child mortality in rural Burkina Faso. Bull. World Health Organ. 2004, 82, 265–273. [Google Scholar] [PubMed]
- Liu, L.; Wolfe, R.A.; Huang, X. Shared frailty models for recurrent events and a terminal event. Biometrics 2004, 60, 747–756. [Google Scholar] [CrossRef] [PubMed]
| Variables | ||
|---|---|---|
| Name | Description | Category |
| Gender | Child gender | Female or Male |
| Province | Birth province | Limpopo, Eastern Cape, Free State, Gauteng KwaZulu Natal, Mpumalanga, North West Northern Cape, Western Cape |
| Year | Birth year | 2009–2015 |
| Twin | Twin identifier | Belonging to a twin pair or not |
| Birth order | Previous number of living children | Eldest, second, third, fourth, fifth, etc. |
| Status | Survival status indicator | Dead or alive |
| Time | Follow-up time (in days) | Duration in days between birth date and day of death or censoring |
| TrunTime | Time for left truncation | Number of days between birth date and day of truncation (31 December 2012) |
| ClusterId | For distinguishing siblings born to the same mother | |
| Factors | Levels | Total (%) | Death N (%) | Censored N (%) | Left Truncated N (%) |
|---|---|---|---|---|---|
| Gender | Female | 124,901 (49.9%) | 2482 (2.0%) | 122,419 (98.0%) | 15,282 (50%) |
| Male | 125,359 (50.1%) | 2720 (2.2%) | 122,639 (97.8%) | 15,274 (50%) | |
| Province | Limpopo | 29,779 (11.9%) | 824 (2.8%) | 28,955 (97.2%) | 3189 (10.4%) |
| Eastern Cape | 33,146 (13.2%) | 598 (1.8%) | 32,548 (98.2%) | 4761 (15.6%) | |
| Free State | 11,299 (4.5%) | 402 (3.6%) | 10,897 (96.4%) | 997 (3.3%) | |
| Gauteng | 51,328 (20.5%) | 1047 (2.0%) | 50,281 (98.0%) | 4812 (15.7%) | |
| KwaZulu | 59,876 (23.9%) | 766 (1.3%) | 59,110 (98.7%) | 9425 (30.8%) | |
| Mpumalanga | 21,073 (8.4%) | 458 (2.2%) | 20,615 (97.8%) | 2705 (8.9%) | |
| North West | 15,530 (6.2%) | 517 (3.3%) | 15,013 (96.7%) | 2431 (8.0%) | |
| Northern Cape | 5782 (2.3%) | 249 (4.3%) | 5533 (95.7%) | 1703 (5.6%) | |
| Western Cape | 22,447 (9.0%) | 341 (1.5%) | 22,106 (98.5%) | 533 (1.7%) | |
| Year | 2010 | 6887 (2.8%) | 11 (0.2%) | 6876 (99.8%) | 6887 (22.5%) |
| 2011 | 8676 (3.5%) | 24 (0.3%) | 8652 (99.7%) | 8676 (28.4%) | |
| 2012 | 14,993 (6.0%) | 189 (1.3%) | 14,804 (98.7%) | 14,993 (49.1%) | |
| 2013 | 103,811 (41.5%) | 3624 (3.5%) | 100,187 (96.5%) | 0 (0%) | |
| 2014 | 12,694 (5.1%) | 191 (1.5%) | 12,503 (98.5%) | 0 (0%) | |
| 2015 | 103,199 (41.2%) | 1163 (1.1%) | 102,036 (98.9%) | 0 (0%) | |
| Twin | Yes | 197,956 (79.1%) | 3775 (1.9%) | 194,181 (98.1%) | 28,781 (94.2%) |
| No | 52,304 (20.9%) | 1427 (2.7%) | 50,877 (97.3%) | 1775 (5.8%) | |
| Order | 0 (No ordering) | 147,274 (58.8%) | 4073 (2.8%) | 143,201 (97.2%) | 27,525 (90.1%) |
| 1 | 100,424 (40.1%) | 1098 (1.1%) | 99,326 (98.9%) | 3000 (9.8%) | |
| 2 | 2504 (1.0%) | 29 (1.2%) | 2475 (98.8%) | 31 (0.1%) | |
| 3 | 55 (0.0%) | 2 (3.6%) | 53 (96.4%) | 0 (0%) | |
| 4 | 3 (0.0%) | 0 (0.0%) | 3 (100.0%) | 0 (0%) |
| Factors | Levels | Coef | Hazard Ratio HR | Unadjusted SE (Robust SE) | p-Value | ||
|---|---|---|---|---|---|---|---|
| Gender | Female (Ref) | ||||||
| Male | 0.0946 | 1.0992 | 0.0278 (0.0280) | 0.0007 | |||
| Province | Limpopo (Ref) | ||||||
| Eastern Cape | −0.3899 | 0.6771 | 0.0538 (0.0552) | <0.0001 | |||
| Free State | 0.2512 | 1.2856 | 0.0609 (0.0622) | <0.0001 | |||
| Gauteng | −0.3311 | 0.7181 | 0.0466 (0.0477) | <0.0001 | |||
| KwaZulu | −0.7372 | 0.4785 | 0.0520 (0.0533) | <0.0001 | |||
| Mpumalanga | −0.2208 | 0.8019 | 0.0583 (0.0597) | 0.00022 | |||
| North West | 0.2594 | 1.2962 | 0.0562 (0.0569) | <0.0001 | |||
| Northern Cape | 0.4782 | 1.6131 | 0.0724 (0.0746) | <0.0001 | |||
| Western Cape | −0.6318 | 0.5317 | 0.0644 (0.0650) | <0.0001 | |||
| Year | 2010 (Ref) | ||||||
| 2011 | 0.8213 | 2.2731 | 0.293 (0.3102) | 0.0051 | |||
| 2012 | 1.2830 | 3.6090 | 0.324 (0.3340) | <0.0001 | |||
| 2013 | 1.8350 | 6.2644 | 0.342 (0.3520) | <0.0001 | |||
| 2014 | 1.4220 | 4.1460 | 0.325 (0.3622) | <0.0001 | |||
| 2015 | 1.6871 | 5.4060 | 0.346 (0.3500) | <0.0001 | |||
| Twin | No (Ref) | ||||||
| Yes | 0.1672 | 1.1820 | 0.0345 (0.0363) | <0.0001 | |||
| Order | No (Ref) | ||||||
| ≥1 | −0.3667 | 0.6929 | 0.0475 (0.0506) | <0.0001 | |||
| Likelihood ratio test | 1075 (p < 0.0001) | ||||||
| Wald test | 1047 (p < 0.0001) | ||||||
| Score test | 1096 (p < 0.0001) | ||||||
| Penalized marginal log-likelihood | −55,833.07 | ||||||
| LCV | 0.2232 | ||||||
| Factors | Levels | Shared Frailty Model | |||||
|---|---|---|---|---|---|---|---|
| Coef | Hazard Ratio | Standard Error | p-Value | ||||
| Gender | Female (Ref) | ||||||
| Male | 0.096 | 1.100 | 0.029 | 0.0010 | |||
| Province | Limpopo (Ref) | ||||||
| Eastern Cape | −0.404 | 0.667 | 0.062 | <0.0001 | |||
| Free State | 0.268 | 1.308 | 0.070 | 0.0001 | |||
| Gauteng | −0.336 | 0.714 | 0.054 | <0.0001 | |||
| KwaZulu | −0.758 | 0.468 | 0.055 | <0.0001 | |||
| Mpumalanga | −0.226 | 0.798 | 0.066 | 0.0007 | |||
| North West | 0.270 | 1.310 | 0.066 | <0.0001 | |||
| Northern Cape | 0.517 | 1.678 | 0.083 | <0.0001 | |||
| Western Cape | −0.646 | 0.524 | 0.071 | <0.0001 | |||
| Year | 2010 (Ref) | ||||||
| 2011 | 0.824 | 2.279 | 0.497 | 0.0972 | |||
| 2012 | 1.288 | 3.626 | 0.192 | <0.0001 | |||
| 2013 | 1.883 | 6.577 | 0.175 | <0.0001 | |||
| 2014 | 1.446 | 4.247 | 0.197 | <0.0001 | |||
| 2015 | 1.723 | 5.603 | 0.180 | <0.0001 | |||
| Twin | No (Ref) | ||||||
| Yes | 0.180 | 1.197 | 0.037 | <0.0001 | |||
| Order | 0 (Ref) | ||||||
| ≥1 | −0.372 | 0.690 | 0.049 | <0.0001 | |||
| (p-value) | 2.342 (p < 0.0001) | ||||||
| Penalised marginal log-likelihood | −55,742.73 | ||||||
| LCV | 0.2228 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mulaudzi, T.B.; Kifle, Y.G.; Braekers, R. A Shared Frailty Model for Left-Truncated and Right-Censored Under-Five Child Mortality Data in South Africa. Stats 2023, 6, 1008-1018. https://doi.org/10.3390/stats6040063
Mulaudzi TB, Kifle YG, Braekers R. A Shared Frailty Model for Left-Truncated and Right-Censored Under-Five Child Mortality Data in South Africa. Stats. 2023; 6(4):1008-1018. https://doi.org/10.3390/stats6040063
Chicago/Turabian StyleMulaudzi, Tshilidzi Benedicta, Yehenew Getachew Kifle, and Roel Braekers. 2023. "A Shared Frailty Model for Left-Truncated and Right-Censored Under-Five Child Mortality Data in South Africa" Stats 6, no. 4: 1008-1018. https://doi.org/10.3390/stats6040063
APA StyleMulaudzi, T. B., Kifle, Y. G., & Braekers, R. (2023). A Shared Frailty Model for Left-Truncated and Right-Censored Under-Five Child Mortality Data in South Africa. Stats, 6(4), 1008-1018. https://doi.org/10.3390/stats6040063






