Change Point Detection by State Space Modeling of Long-Term Air Temperature Series in Europe

Abstract

This work presents the statistical analysis of a monthly average temperatures time series in several European cities using a state space approach, which considers models with a deterministic seasonal component and a stochastic trend. Temperature rise rates in Europe seem to have increased in the last decades when compared with longer periods. Therefore, change point detection methods, both parametric and non-parametric methods, were applied to the standardized residuals of the state space models (or some other related component) in order to identify these possible changes in the monthly temperature rise rates. All of the used methods have identified at least one change point in each of the temperature time series, particularly in the late 1980s or early 1990s. The differences in the average temperature trend are more evident in Eastern European cities than in Western Europe. The smoother-based t-test framework proposed in this work showed an advantage over the other methods, precisely because it considers the time correlation presented in time series. Moreover, this framework focuses the change point detection on the stochastic trend component.

1. Introduction

The Secretary-General of the United Nations, António Guterres, claimed that “We are still significantly off-schedule to meet the goals of the Paris Agreement. Unless there are immediate, rapid and large-scale reductions in greenhouse gas emissions, limiting warming to 1.5 °C will be impossible, with catastrophic consequences for people and the planet on which we depend” [1].

However, changes in Earth’s climate have different effects in different areas of the world with different regional impacts. Although the Intergovernmental Panel on Climate Change reports that the world’s greenhouse gas emissions are continuing to increase and predicts that, at this rate, the global temperature rise will far exceed the two degrees Celsius limit goal that countries have agreed, in Europe, the greenhouse gas emissions have had a decreasing trend at least since the year 1990, as presented in the Trends and Projections in Europe 2021, EEA Report N. 13/2021, [2]. In the same sense, Europe has stable emissions of nitrous oxide (N₂O), often as a result of reductions in industrial emissions (through emission abatement technologies) and increased nitrogen use efficiency in agriculture, [3].

Several works or reports from world institutions present the last numbers of global surface temperatures in the context of climate change. For instance, [4] indicates that, in 2019, the global land and ocean surface temperature was 0.44 °C–0.56 °C above the 1981–2010 average. Moreover and according to three independent in situ analyses, 2019 was one of the top-three warmest years since global records have begun, in the mid-to-late 1800s. Some results about different anomalies of temperature are presented, e.g., whereas the Northern Hemisphere, where distinctive warmer and cooler regions can be identified, namely, Alaska, Greenland, and Europe (except the Northeast), clearly show positive anomalies, Tibet and parts of North America show clear negative anomalies [4].

From another perspective, some works focus on a single or on a few temperature time series in a limited analysis, in general related to a country [5] or a time series modeling of a single series [6]. At a regional level, ref. [7] analyzed the time horizon dynamics of crop and climate variables in India employing Bai–Perron structural break and continuous wavelet transform methods. Also at a regional level and using a spatio-temporal approach, the work of [8] focuses on daily temperature modeling in the Aragón region, Spain, to study the summer period over 60 years and [9] proposed a fully stochastic hierarchical model that incorporates relationships between climate, time, and space to study the annual profiles of temperature across the Eastern United States over the period 1963–2012.

A review of methods applied to the trend analysis of climate time series is presented in [10], based on regression models as linear, nonlinear and nonparametric models with application to the GISTEMP time series of global surface temperature. Ref. [11] proposed a new class of long-memory models with time-varying fractional parameters, with an application to the analysis of series of monthly global historical surface temperature anomalies regarding the 1961–1990 reference period contained in the data set HadCRUT4.

A statistical analysis of long-term air temperatures in Europe, a densely populated and highly industrialized continent, can contribute to improving the monitoring of the rising air temperature in a regional approach. It is very important to analyze air temperature trends and, in case these occur, to identify any change-points in these time series. This information can be useful for scientists and in political decision-making contexts. In fact, on 14 July 2021, the European Commission adopted a series of legislative proposals setting out how it intends to achieve climate neutrality in the EU by 2050, including the intermediate target of at least 55% net reduction in greenhouse gas emissions by 2030. On the other hand, it is useful to form an accurate view of trends and changes, if any of these occur.

In order to contribute to the monitoring of this major and urgent problem, which is global climate change, with a particular focus on Europe, this work performs a time series analysis of temperature data of several European cities for which data are available. In combination with the national strategies of each country, the statistical analysis of various temperature series contributes to the monitoring of this process, as it is framed by the European Commission Climate Action (https://ec.europa.eu/clima/index_pt, accessed on 22 July 2022).

To achieve this goal, credible data access as well as the adoption of suitable statistical methodologies to address the problem are required. Therefore, this work consists of an analysis of a significant data set obtained from the Climate Data Online (CDO) portal, a platform that provides free access to archives of the National Oceanic and Atmospheric Administration (NOAA)’s National Climatic Data Center (NCDC), where global historical weather, climate data, and station history information are available for consultation (https://www.ncei.noaa.gov/, accessed on 10 May 2022).

This work focuses on time series modeling in view of the change-point detection in temperature trends in several European cities. It proposes an integrated approach, which combines the state space modeling of time series with the change-point detection in trends from Kalman smoothers prediction of unobservable stochastic components or in a residuals analysis.

State space models have been successfully applied in both environment or ecological time series [12,13]. A review for ecologists to create state space models was presented in [14] since these models are robust to common, and often hidden, estimation problems; moreover, the model selection and validation tools can help them assess how well these models fit their data. In order to account for the impact of seasonality in the soybean crush spread, ref. [15] proposed a time series model with co-integration that allows for a time-varying covariance structure and a time-varying intercept. Ref. [16] considered a state space framework for modeling and grouping time series of water quality monitoring variables. State space models and the Kalman filter were applied to merge weather radar and rain gauge measurements in order to improve area rainfall estimates in [13]. A mixed-effect state-space model was considered to model both historical climate data as well as dynamically derived mean climate change projection information obtained from global climate models in [17]. The state space modeling, in a periodic framework, was performed to long temperature time series in Portuguese cities (Lisbon, Coimbra and Porto) in a study by [5], where it was concluded that Porto has a temperature growth rate, per century, substantially different from the other cities. In [18], the application of state space models to long series of air temperature, together with cluster procedures, enabled the identification of temperature growth rates patterns in several cities in Europe.

However, modeling time series of climate variables is not sufficient to monitor the changes in climate and its change points. Accordingly, additional structural break detection methodologies are needed, a view that is supported by the vast literature on the subject [19,20,21]. Much of the methodology was first developed for a sequence of independent and identically distributed (i.i.d.) random variables and a large part of the literature is devoted to CUSUM-type and likelihood ratio procedures based on distributional assumptions (usually Gaussian) to test for a change in the mean and or in variance. Comparison analyses between methods to detect changes in mean are made in [22].

When no knowledge about the distributional form of the phenomenon under analysis is available, nonparametric change detection methods can be used to identify these changes. Ref. [23] considers methods that take well-established nonparametric tests for location and scale comparisons into consideration and [24] developed an R package with the implementation of several change points detection methods. The existence of serial dependence in many applications led to the development of methodologies to deal with change points in time series. Several approaches can be used in this context, for example, test statistics developed for the independent setting to the underlying innovation process can be applied or one can try to quantify the effect of dependence on these test statistics depending on the model structure that is considered. There are several works on change point detection in climate or environmental data. For instance, ref. [25] applied several change points procedures to Klementinum temperature. However, ref. [25] analyzed the mean annual temperatures assuming that these variables are a sequence of independent random variables, not taking the time correlation usually present in time series into consideration. In contrast, this paper considers statistical procedures for detecting change points that take temporal correlation into account.

This work contributes with an exhaustive analysis based on the detection of change points in a very significant set of time series of monthly average temperatures of European cities with a significant dispersion and geographic coverage. The proposed approach in this work of applying the change point detection methods on the stochastic trend component, an approach that allows for the incorporation of temporal correlation from the state equation of the state space model, shall be discussed. This aspect is particularly relevant in a time series analysis focusing on climate change analysis. This innovative approach to detecting points of change in non-observable variables takes temporal correlation into account and, once the assumptions of the considered method are verified, it is possible to identify the points of change focusing on the stochastic trend component.

In this work, the authors considered both parametric and nonparametric statistical tests with the application of the maximum type statistics to the innovation processes predictions, which are obtained by the Kalman filter algorithm for the temperature time series in Europe. All statistical and calculation procedures were developed in the R environment, [26], and it was considered a maximum significance level of 5% in all statistical tests.

2. Materials and Methods

2.1. Study Area and Data Used

The data set comprises the period between January 1900 and December 2017, in a total of 1416 observations of the monthly average air temperature of fifteen European cities, in fifteen different countries (Figure 1). These cities cover the European continent with a reasonable geographic dispersion from northwest to northeast. Moreover, these time series were selected from the CDO portal since they are the most complete time series, i.e., only with a small number of missing values, without compromising both the geographic dispersion and European representation. To fill the missing values, in each time series, a multiple linear regression using time and months as independent variables were applied considering the five years preceding and following the missing value.

Data descriptive statistics can be found in

Table 1. Characterization of time series data set.

City (Country)	Min	Max	Min	Max	Min	Max	Min	Max	Average	Average	Average	Average	Missing
	1900		1900		1918		2000		1900	1900	1918	2000	Values
	to 2017		to 1917		to 1999		to 2017		to 2017	to 1917	to 1999	to 2017	(%)
Berlin (Germany)	−10.7	23.0	−4.2	20.5	−10.7	22.5	−4.8	23.0	8.6	8.3	8.5	9.8	2.3
Bucharest (Romania)	−11.5	27.5	−8.4	23.6	−11.5	27.5	−6.6	26.5	10.1	9.5	9.8	11.0	2.6
Copenhagen (Denmark)	−6.7	21.6	−3.0	20.6	−6.7	21.6	−3.1	21.6	8.5	8.2	8.4	9.6	0.4
Dublin (Ireland)	0.0	17.1	2.0	16.5	0.4	17.1	0.0	17.0	9.2	9.2	8.9	9.6	2.2
Kiev (Ukraine)	−15.3	26.0	−10.4	22.4	−15.3	26.0	−10.0	24.7	7.9	7.7	7.9	9.4	0.9
Lisbon (Portugal)	8.0	25.1	9.0	23.6	8.0	25.1	9.4	25.1	16.9	16.8	16.4	17.4	3.4
Minsk (Belarus)	−16.8	22.6	−11.6	20.0	−16.8	22.0	−11.1	22.6	6.1	5.9	5.8	7.4	1.8
Nantes (France)	−1.2	23.3	2.1	22.4	−1.2	23.2	2.5	23.3	12.0	11.6	11.9	12.5	0.4
Prague (Czech Rep.)	−13.1	22.0	−6.9	19.6	−13.1	21.7	−5.5	22.0	7.7	7.3	7.6	9.0	8.2
S. Petersburg (Russia)	−18.3	24.4	−14.00	21.6	−18.3	22.4	−12.1	24.4	5.1	4.8	5.1	6.5	0.0
Talin (Estonia)	−15.5	21.5	−9.0	21.2	−15.5	20.3	−11	21.5	5.2	4.9	5.1	6.4	5.4
Vienna (Austria)	−9.5	24.4	−4.2	21.7	−9.5	24.4	−3.4	24.1	10.0	9.7	9.9	11.2	0.2
Vilnius (Lithuania)	−17.1	21.8	−11.9	20.0	−17.1	20.4	−10.4	21.8	5.6	5.2	5.6	7.2	2.6
Zagreb (Croatia)	−7.0	25.9	−4.0	23.7	−7.0	25.9	−2.5	25.7	11.8	11.7	11.5	13.0	1.4
Zurich (Switzerland)	−8.7	22.4	−4.7	20.4	−8.7	21.8	−3.6	22.4	8.5	8.5	8.1	9.7	0.0

, which contains the minimum, maximum and average temperature for all periods and also the same statistics for the period before the year 2000 and the second millennium. The cutoff point was chosen to separate centuries. For comparative purposes, the same statistics are also presented for the period 1900–1917. With the exception of Ireland, the global minimums occurred in the time period from 1918 to 1999, whereas, in two-thirds of the series, the global maximums were reached between 2000 to 2017, with the other third being reached in a longer period. For all the cities analyzed, the increase in average temperatures in recent years is quite evident.

2.2. State Space Modeling

Environmental data have three main properties that characterize their temporal evolution: seasonality, skewed distribution and dependence besides non-stationarity [27]. In this context, state space models are very flexible to accommodate these properties and the Kalman filter algorithm is very useful even in the case of non-normality, since its predictions are the best linear unbiased estimators. Following the work of [18], we consider a state space model that highlights the trend component by an unobservable stochastic process, the state, and deals with the monthly seasonality in a deterministic component, in a simple way based on dummy variables.

Under the assumption of no change points, for each European city, we consider the state space model defined by the equations:

$$\begin{array}{ccc}\hfill Y_t& =& {\tau }_t+\sum _{i=1}^{12}{\beta }_i{S}_{t,i}+e_{1,t}\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill {\tau }_t& =& \mu +\varphi ({\tau }_{t-1}-\mu )+e_{2,t},\hfill \end{array}$$

(2)

where $Y_t$ represents the monthly average air temperature in the time t, with $t=1,...,n$, and ${\beta }_i$ with $i=1,2,...,12$ is the seasonal coefficient associated to the month $t=i+12j$, for some $j=0,1,2,...$, and $S_{t,i}$ is an indicative function defined such that

$$S_{t,i}=\left\{\begin{array}{ccc}1\hfill & \mathrm{if}& t=i+12j,\mathrm{for}\mathrm{some}j=0,1,2,...\hfill \\ 0\hfill & & \mathrm{otherwise}.\hfill \end{array}\right.$$

(3)

The $\left\{{\tau }_t\right\}$ process represents a stochastic trend component, the state, that follows a stationary autoregressive process of order 1, $\left\{{\tau }_t\right\}\sim \mathrm{AR}\left(1\right)$, with mean $\mu$ with autoregressive parameter $\mid \varphi \mid <1$; errors $e_{i,t}$, with $i=1,2$, following uncorrelated white noise processes with variances $var\left(e_{i,t}\right)={\sigma }_i^2$ and $E\left(e_{i,t}{e}_{i,r}\right)=0$, for $t\ne r$, in the sense that $E\left(e_{1,t}{e}_{2,r}\right)=0$, $\forall t,r$.

The error $e_{1,t}$ is considered the observational error and can be seen as a measurement error, whereas the error $e_{2,t}$ is considered the state error and and translates the randomness of the trend component.

Note that the state $\left\{{\tau }_t\right\}$ is an unobservable process and its predictions must be obtained. Kalman filter algorithms provide optimal unbiased estimators for the state ${\tau }_t$; ${\widehat{\tau }}_{t\mid t-1}$ for one-step-ahead prediction, ${\widehat{\tau }}_{t\mid t}$ for Kalman filter update and ${\widehat{\tau }}_{t\mid n}$ for Kalman smoother predictions [28].

It is worth noting that no assumptions are made about the distributional form of both errors. Nevertheless, there are several situations (not the case here) where the Gaussian distribution of the errors, that is, $e_{i,t}\sim N(0,{\sigma }_i^2)$, with $i=1,2$, is considered mainly for inferences goals. When the transition probability density is unknown and possibly degenerate it can be considered a robust state space filtering problem that has a Kalman-like structure and solves a minimax game [29,30].

2.3. Predictions of the Unobservable State—The Kalman Filter Algorithm

As the trend component is not observable it must be predicted. The most usual algorithm to perform this task is the Kalman filter algorithm which computes, at each time t, the optimal linear estimator of the state based on the available information until t. In the context of the linear state space models, the Kalman filter produces the best linear unbiased estimators; and, when the errors and the initial state are Gaussian, the Kalman filter predictors are the best unbiased estimators in the sense of the minimum mean square error, assuming that all model’s parameters $\Theta$ are known.

The Kalman filter equations provide optimal unbiased linear one-step-ahead and updated estimates of the unobservable state ${\tau }_t$ which is given by the orthogonal projection of the state onto the observed variables up to that time. Let ${\widehat{\tau }}_{t\mid t-1}$ denote the estimator of ${\tau }_t$ based on the observations $Y_1,Y_2,...,Y_{t-1}$ and let $P_{t\mid t-1}$ be its mean square error (MSE), i.e., $E\left[{({\widehat{\tau }}_{t\mid t-1}-{\tau }_t)}^2\right]$. Since the orthogonal projection is a linear estimator, the forecast of the observable vector $Y_t$ is given by

$${\widehat{Y}}_{t\mid t-1}={\widehat{\tau }}_{t\mid t-1}+\sum _{i=1}^{12}{\beta }_i{S}_{t,i},$$

(4)

with an MSE of ${\widehat{Y}}_{t\mid t-1}$ given by ${\omega }_t=P_{t\mid t-1}+{\sigma }_1^2$. When $Y_t$ is available, the prediction error or innovation, ${\eta }_t=Y_t-{\widehat{Y}}_{t\mid t-1}$, is used to update the estimate of ${\tau }_t$ through the equation

$${\widehat{\tau }}_{t\mid t}={\widehat{\tau }}_{t\mid t-1}+k_t{\eta }_t,$$

(5)

where $k_t$ is called the Kalman gain and is given by $k_t=P_{t\mid t-1}{\omega }_t^{-1}$. Furthermore, the MSE of the updated estimator ${\widehat{\tau }}_{t\mid t}$, represented by $P_{t\mid t}$, verifies the relationship $P_{t\mid t}=P_{t\mid t-1}-k_t{P}_{t\mid t-1}$.

On the other hand, the forecast for the state ${\tau }_{t+1\mid t}$ is given by the equation

$$\begin{array}{c}\hfill {\widehat{\tau }}_{t+1\mid t}=\mu +\varphi ({\widehat{\tau }}_{t\mid t}-\mu ),\end{array}$$

(6)

and its MSE is $P_{t+1\mid t}={\varphi }^2{P}_{t\mid t}+{\sigma }_2^2$.

The Kalman filter algorithm is initialized with ${\tau }_{1\mid 0}$ and $P_{1\mid 0}$. As the state process is assumed to be stationary, the Kalman filter algorithm can be initialized considering that initial state ${\widehat{\tau }}_{1\mid 0}=\mu$ and its mean square error by $P_{1\mid 0}={\sigma }_2^2{(1-{\varphi }^2)}^{-1}$.

When the entire time series $y_1,y_2,...,y_n$ is available, the best estimators of the state ${\tau }_t$ based on all data are the Kalman smoothers ${\widehat{\tau }}_{t\mid n}$. These estimators can be obtained recursively through the equations

$${\widehat{\tau }}_{t-1\mid n}={\widehat{\tau }}_{t-1\mid t-1}+J_{t-1}\left({\widehat{\tau }}_{t\mid n}-{\widehat{\tau }}_{t\mid t-1}\right),$$

(7)

and $P_{t-1\mid n}=P_{t-1\mid t-1}+J_{t-1}^2\left(P_{t\mid n}-P_{t-1\mid n}\right)$, where $J_{t-1}=P_{t-1\mid t-1}\varphi P_{t\mid t-1}^{-1}$ [28], using the initial conditions ${\widehat{\tau }}_{n\mid n}$ and $P_{n\mid n}$ obtained from the Kalman filter.

2.4. Parameter Estimation

The estimation of the vector $\Theta$ of unknown parameters in state space models is usually performed by the Gaussian maximum likelihood estimation method in cases when it can be assumed that the initial state is normal and $e_{i,t}\sim N(0,{\sigma }_i^2)$, with $t=1,2$. In this case, the likelihood is computed using the innovations ${\eta }_1,{\eta }_2,...,{\eta }_n$ with ${\eta }_t=Y_t-{\widehat{Y}}_{t\mid t-1}$, which are independent Gaussian random variables with mean square error given by ${\sigma }_{{\eta }_t}^2=P_{t\mid t-1}+{\sigma }_1^2$. However, the likelihood $L_Y(\Theta )$ is a highly nonlinear function of the unknown parameters [28]. A Newton–Raphson algorithm or an estimation procedure based on the Baum–Welch algorithm, also known as the EM (expectation–maximization) algorithm, can be adopted. Technical indications can be obtained from [28].

However, it often happens that the normality assumption is not verified when analyzing the innovations ${\widehat{\eta }}_t$, with $t=1,...,n$ at the stage of evaluating the model’s assumptions. This occurs mainly because their distribution has heavy tails or is asymmetric, or because there are change points associated to change in some parameters of the model. In these cases, distribution-free estimators can be adopted, for example, those proposed by [31] for univariate models and later generalized to multivariate models in [16]. On the one hand, these estimators are consistent and, therefore, a good option specially for large samples or long time series. On the other hand, these estimators do not assume any knowledge of the error distribution, whereas other proposals assume some of the information (for instance, Refs. [32,33]). However, some robust EM algorithms can mitigate some of these problems in the estimation procedure of unknown parameters as suggested in [34].

In this work, the complexity of the estimation process was reduced by adopting a decomposition procedure, that is, by estimating the parameters associated with seasonality ${\beta }_i$, with $i=1,...,12$ using the least squares method, as suggested by [35], p. 23, and [5]. In fact, in this case, the focus is not on determining changes in seasonal patterns over the decades, but mainly on the trend, so this approach is even more suitable for the purpose of this paper since it simplifies the estimation process. To avoid having to make assumptions about the error distributions, the remaining parameters are obtained by using the distribution-free estimators proposed by [31].

2.5. Change Point Detection Approaches

In this paper, we propose that structural change in a long-term temperature time series can be detected through two complementary approaches: (1) by analyzing the series of innovations and (2) by analyzing the series of the Kalman smoothers of the trend process, ${\widehat{\tau }}_{t\mid n}$.

We will start with the description of the procedures to detect a single change point, by two approaches, which will be later used on the possible detection of multiple change points.

In order to identify an abrupt change in the behavior of the temperature time series, a statistical test of the maximum type is applied to detect a change in the location of innovations or in the Kalman smoothers [27]. In a first stage, this type of test is developed assuming that the time c, where the change may have occurred, is known and, in a second phase, the test statistic is computed for all the possibilities of c and its maximum is determined.

On the one hand, if no change point exists, the innovations are uncorrelated and identically distributed. Thus, one approach is the innovations analysis and detection of change point. If a change point exists at some time c in the location of innovations, it indicates that after that time point at least one parameter of model Equations (1)–(2) changed [23], since from the innovations one can evaluate the quality of the model fit. On the other hand, if there are no structural changes in the temperature trend, it is expected that the process $\left\{{\tau }_t\right\}$ has no changes over time in its location, namely in its mean $\mu$. Thus, the second approach will be the detection of change point in the trend component, $\left\{{\tau }_t\right\}$.

Therefore, considering that it is intended to test if the change point occurs at the unknown time point c, the statistical hypotheses on a process $\left\{X_t\right\}$ and its distribution $F(x;\theta )$ in function on parameters $\Theta$, that can be the innovations or the Kalman smoothers processes, are:

$H_0$:	$X_t\sim F_0(x;{\theta }_0)$ for $\forall t=1,...,n$
$vs$
$H_1$:	$X_t\sim F_0(x;{\theta }_0)$ for $t\le c$ and $X_t\sim F_1(x;{\theta }_1)$, for $t>c$.

Under the non-existence of a change points hypothesis, tests in both parametric and nonparametric approaches can be applied maximum type. If the statistic test exceeds some appropriately chosen threshold, then the null hypothesis that the two samples have identical distributions is rejected, and we conclude that a change point has occurred immediately after c time.

Since it is not known in advance where the change point occurs, the c time is unknown and the statistic test is evaluated at every value $1<c<n$, and the maximum value is used. The following subsection presents the two parametric and non-parametric approaches that can be applied to detect a change point in the sample location.

2.5.1. Maximum Type T Test—CUSUM

Under the normality assumption and independence of variables $X_i$, that is, $X_i\sim N({\mu }_X,{\sigma }_X^2)$, with $i=1,...,n$, whose variance is assumed to be unknown, the statistic $T\left(n\right)$ to test the null hypothesis of no change point in the mean ${\mu }_X$ is the maximum of the absolute values of two samples t-test statistics,

$${\displaystyle T\left(n\right)=\underset{1\le r<n}{max}\mid T_r\mid =\underset{1\le r<n}{max}\sqrt{\frac{(n-r)}{n}} \frac{\mid {\overline{X}}_r-{\overline{X}}_r^{*}\mid }{s_r},}$$

where

$${\overline{X}}_r=\frac{1}{r}\sum _{i=1}^r{X}_i, {\overline{X}}_r^{*}=\frac{1}{n-r}\sum _{i=r+1}^n{X}_i$$

and

$$s_r=\sqrt{\frac{1}{n-2}\left[\sum _{i=1}^r{\left(X_i-{\overline{X}}_r\right)}^2+\sum _{i=r+1}^n{\left(X_i-{\overline{X}}_r^{*}\right)}^2\right]}.$$

The null hypothesis can be rejected if the statistic $T\left(n\right)$ is greater than the critical value. The exact distribution of $T\left(n\right)$, for independent variables, is very complex and [36] was able to calculate the true critical values only for the number of observations n under 10. Alternatively, approximate critical values can be computed by other methods such as the Bonferroni inequality, simulation or the asymptotic distribution.

When random variables $X_1$, $X_2$, …, $X_n$ are not independent but form an ARMA process, then the asymptotic critical values of the test statistics considering independence have to be multiplied by $\sqrt{2\pi f\left(0\right)/\gamma }$, where $\gamma =var\left(X_t\right)$ and $f(·)$ denotes the spectral density function of the corresponding ARMA process [37]. Especially for an AR(1) sequence, the critical values should be multiplied by ${\left[(1+\varphi ){(1-\varphi )}^{-1}\right]}^{1/2}$ where $\varphi$ is the first autoregressive coefficient [27].

2.5.2. Maximum Type Mann-Whitney Test

In the nonparametric framework, at each r point, $1<r<n$, the two-sample Mann–Whitney test statistic $D_{r;n}$ can be computed. The variance of $D_{r;n}$ depends on the value r, so the test statistic is obtained through the maximization of the standardized $D_{r,n}$ to have mean 0 and variance 1 [24],

$${\displaystyle D_n=\underset{r=2,...,n-1}{max}{\tilde{D}}_{r,n}=\frac{\mid D_{r,n}-{\mu }_{D_{r,n}}\mid }{{\sigma }_{D_{r,n}}}.}$$

(8)

The standardizing of ${\tilde{D}}_{r,n}$ is computed by subtracting their means ${\mu }_{{\tilde{D}}_{r,n}}$ and dividing by their standard deviations ${\sigma }_{{\tilde{D}}_{r,n}}$ and taking the absolute value. The moments of the distribution of the Mann-Whitney test statistic are known under the null hypothesis [24].

The null hypothesis of no change is then rejected if $D_n>h_n$ for some appropriately chosen threshold $h_n$, which is the upper $\alpha$ quantile of the distribution of $D_n$ under the null hypothesis. This distribution does not have an analytic finite-sample form and for the case of the Mann–Whitney statistics, the asymptotic distribution of $D_n$ can be written. However, these asymptotic distributions may not be accurate when considering finite length sequences, and so numerical simulation may be required in order to estimate the distribution, an approach that is used in the cpm R package for change point detection [24]. The best estimate of the change point location will be immediately followed by the value of r, which maximizes ${\tilde{D}}_{n,r}$.

2.6. Multiple Change Point Detection

In order to detect multiple change points, this work adopts the binary segmentation proposed by [38]. Binary segmentation is a generic technique for multiple change-point detection in which, initially, the entire dataset is searched for one change-point and when a change point is detected, the data are split into two subsegments, defined by the detected change-point. A similar search is then performed on each sub-segment, possibly resulting in further splits. The recursion on a given segment continues until a certain criterion is satisfied [39]. For high dimensional time series, ref. [40] considered a segmentation of the second-order structure via a sparsified binary segmentation. This approach is, thus, a very often applied approach due to its simplicity.

Consider $S{T}_s^e\left(X\right)$ to be one of the statistic tests defined in Section 2.5.1 and Section 2.5.2 using the series X at times between s and e. The following algorithm (Algorithm 1) summarizes the adopted recursive procedure, being initialized with $s=1$ and $e=n$, and a value $\alpha$ for the significance level test.

Algorithm 1 Multiple change point detection.

procedureBinarySegm(X, s, e)

if $e-s<1$ then

STOP

else

Compute $S{T}_s^e\left(X\right)$

Compute $Cv$, the critical value for the test

if $S{T}_s^e\left(X\right)>Cv$ then

$c<-argmaxS{T}_s^e\left(X\right)$

include c in the set of change points

BINARYSEGM(X, s, c)

BINARYSEGM(X, $c+1$, e)

else

STOP

end if

end if

end procedure

3. Results

In a first step, seasonal parameters ${\beta }_i$, with $i=1,...,12$, were estimated using the method of least squares for each of the 15 time series in a classical decomposition perspective, and then the remaining parameters associated with the state space model were estimated using distribution free estimators (see [13] for details). These methods are useful when convergence problems associated with likelihood optimization arise or when it is not possible to guarantee the absolute maximum of the likelihood function. These situations may occur either due to the fact that the errors cannot be Gaussian or other predefined distribution, or due to the existence of change points that hinder the convergence of numerical processes for the adjustment of an inadequate model.

The estimation parameters were obtained based on a VBA macro developed in the work of [31]. The results of the estimation procedure are presented in

Table 2. Parameter estimates of the initial state space model for the temperature time series in the fifteen European cities.

City	${\widehat{\mathit{\beta }}}_{\mathit{i}}$												$\widehat{\mathit{\mu }}$	$\widehat{\mathit{\varphi }}$	${\widehat{\mathit{\sigma }}}_1^2$	${\widehat{\mathit{\sigma }}}_2^2$	${\widehat{\mathit{\sigma }}}_{{\mathit{Y}}_{\mathit{t}}}^2$
	Jan.	Feb.	Mar.	Apr.	May	Jun.	Jul.	Aug.	Sep.	Oct.	Nov.	Dec.
Berlin	−1.2	−0.4	3.0	7.6	12.7	15.8	17.5	16.6	12.9	8.1	3.2	0.1	0.709	0.576	1.937	1.319	3.912
Bucharest	−3.9	−1.7	3.6	9.9	15.3	19.1	21.3	20.7	16.0	9.8	3.8	−1.4	0.611	0.537	1.989	1.653	4.311
Copenhagen	0.0	−0.2	1.9	6.1	11.2	14.9	16.9	16.4	13.0	8.7	4.5	1.7	0.655	0.711	1.128	0.836	2.815
Dublin	4.4	4.5	5.6	7.3	9.9	12.7	14.5	14.2	12.3	9.6	6.3	5.0	0.383	0.521	0.704	0.484	1.369
Kiev	−5.5	−4.7	0.2	8.0	14.6	17.9	19.6	18.7	13.7	7.4	1.4	−3.1	0.732	0.583	2.735	1.893	5.601
Lisbon	10.9	11.6	13.4	14.9	17.0	19.9	21.8	22.3	20.9	17.9	14.0	11.6	0.510	0.771	0.859	0.179	1.299
Minsk	−7.1	−6.4	−2.1	5.3	11.8	15.4	17.0	16.0	11.1	5.2	−0.3	−4.6	0.954	0.679	3.377	1.299	5.788
Nantes	5.2	5.7	7.9	10.2	13.6	16.6	18.6	18.3	16.0	12.2	8.0	5.8	0.478	0.439	1.385	0.785	2.357
Prague	−2.8	−1.8	2.0	6.7	11.9	15.1	16.9	16.2	12.3	7.1	1.9	−1.4	0.797	0.701	2.506	0.674	3.831
S. Petersburg	−7.5	−7.5	−3.4	3.3	9.9	14.8	17.7	15.9	10.7	4.8	−0.6	−4.9	0.843	0.607	3.232	2.100	6.560
Talin	−5.5	−6.0	−2.8	2.7	8.6	13.2	16.0	15.0	10.5	5.3	0.5	−3.0	0.800	0.648	2.181	1.844	5.360
Vienna	−1.0	0.5	4.6	9.5	14.3	17.5	19.4	18.7	14.7	9.4	4.3	0.6	0.710	0.559	2.043	1.086	3.624
Vilnius	−6.7	−5.9	−2.3	4.5	11.0	14.3	16.2	15.1	10.4	4.9	−0.4	−4.3	1.132	0.821	3.487	0.782	5.889
Zagreb	0.3	2.4	6.9	11.5	16.0	19.4	21.4	20.8	16.7	11.4	6.2	1.9	0.572	0.606	2.258	1.044	3.907
Zurich	−1.2	0.0	3.8	7.5	11.9	15.1	16.9	16.3	13.1	8.2	3.1	−0.1	0.763	0.653	2.302	0.591	3.331

. Seasonal coefficients, as expected, show different seasonal curves; while Lisbon has the highest coefficient in the warm months, namely 22.3 °C in August, the coldest city in winter is St. Petersburg with seasonal coefficients for January and February equal to −7.5 °C.

Analyzing the parameters associated with the state space model, we find that all estimates of the autoregressive parameters, $\varphi$, verify the stationary condition of the AR(1) process and the smallest estimate of the mean of the stochastic trend level is 0.383 in Dublin (Ireland) whereas the largest is 1.132 in Vilnius (Lithuania).

The analysis of residuals, ${\eta }_t=Y_t-{\widehat{Y}}_{t\mid t-1}$, shows that, for the majority of cities, there is no serial correlation up to lag 12 when considering a significance of 1%. The exception is the city of Lisbon which presents no serial correlation only up to lag 3. Thus, there is no correlation structure in innovation showing that the model captured the time-dependent structure of the series.

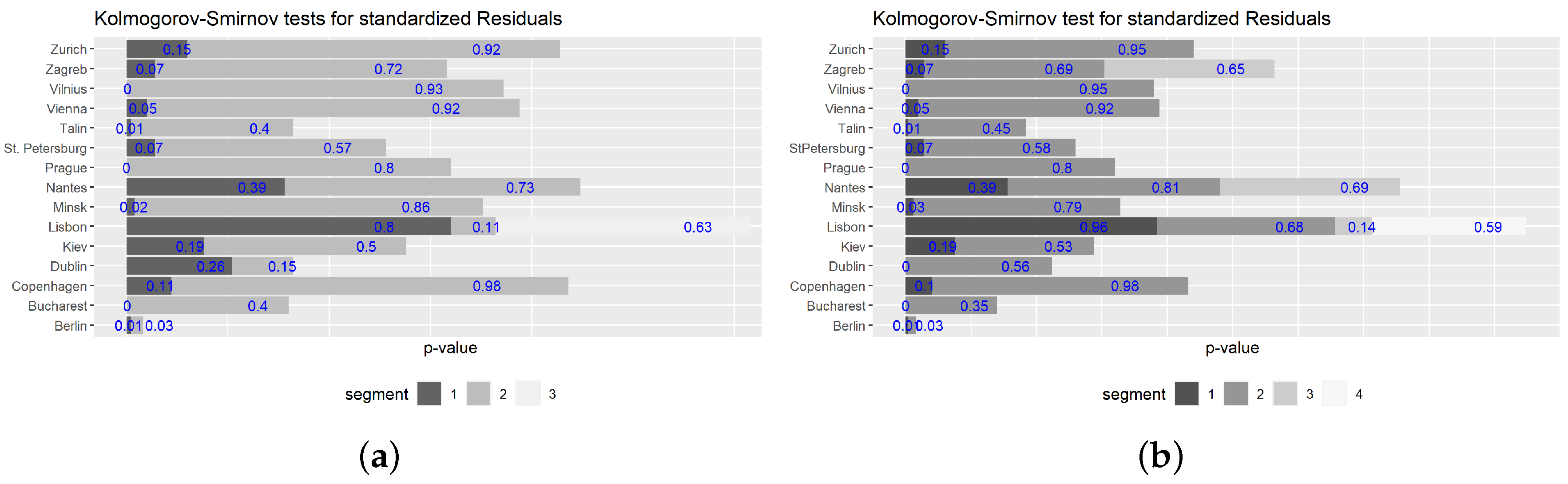
Although the model parameters estimation step has been performed without considering any distribution for the errors, the normality was tested through the application of a Lilliefors-corrected Kolmogorov–Smirnov test to standardized residuals, that is, ${\eta }_t^{*}={\eta }_t/\sqrt{{\omega }_t}$, which leads to the rejection of this assumption in the majority of the cities. This situation is not unusual and can be caused by many factors: the errors are not normally distributed, the tests reject the normality because they are performed on large sample sizes leading to rejection of the null hypothesis, or normality is challenged by the presence of change points. In the latter case, the normality can be re-examined after the points of change have been identified.

For each city, we have considered three situations: the maximum-type test using Mann–Whitney tests and also t-test applied to the standardized residuals; the application of the maximum-type t-test applied to smoother predictions of the latent process $\left\{{\tau }_t\right\}$ which represents the trend of the temperature. For each city and method, the cpm package of the software R was used in order to identify each change point. Since $\left\{{\tau }_t\right\}$ has an autoregressive structure of order 1, it was necessary to adjust, for each series, the critical value of the test using the estimates of the autoregressive parameters. In all series, for each of the approaches considered, a first change point was detected. From this point onwards, binary segmentation was used, with each segment being modeled separately and to which the previous procedures were applied. The results of the multiple change point detections are presented in

Table 3. Multiple change points for each city with each method.

	Change Point Detection							Methods Comparison
City (Country)	M1		M2		M3			Similar
	M-W Test		t-Test		t-Test (Smoother)			Change Points
	Change Points		Change Points		Change Points			Results
	Month/Year		Month/Year		Month/Year			M1	M2	M3	Group
Berlin	Aug./87		Aug./87		Sep./87			X	X	X	1
Bucharest	Sep./06		Dec./06		Sep./06			X	X	X	1
Copenhagen	Aug./87		Aug./87		Sep./87			X	X	X	1
Dublin	Oct./31	Sep./88	Sep./88		Oct./31	Oct./88		X	–	X	3
Kiev	Dec./98		Nov./88		Dec./88			–	X	X	2
Lisbon	Jan./45	Apr./86	Aug./42	Jun./78	Apr./31	Sep./42	Jul./78	–	–	–	4
Minsk	Oct./87		Nov./88		Nov./87			X	X	X	1
Nantes	Jul./81	Aug./17	Jun./87	Aug./17	Jul./87	Sep./17		–	X	X	2
Prague	Apr./29	Nov./97	Aug./87		Aug./87			–	X	X	2
S. Petersburg	Dec/87		Dec./87		Dec./87			X	X	X	1
Talin	Sep./87		Sep./87		Dec./87			X	X	X	1
Vienna	Aug./87	Jun./13	Aug./87		Aug./87			–	X	X	2
Vilnius	Jun./82		Sep./87		Nov./87			–	X	X	2
Zagreb	Dec./91	Aug./06	Dec./91		Dec./91	Aug./06		X	–	X	3
Zurich	Feb./42	Jul./97	Jun./87	Jun./13	Aug./87			–	–	–	4

together with the methods comparison. We grouped the cities according to the detection results achieved by each of the approaches used. For instance, group 1 is composed of those cities where all methods produced similar results. In half of the cities, only one change point was detected regardless of the method used. In 80% of the cities, the t-test approaches detected a change point in the late eighties while the M-W test detected a change point in this period only for about 50% of the cities.

The three methods detected similar change points in Berlin, Bucharest, Copenhagen, Minsk, St. Petersburg and Talin (group 1). All these cities detected only a single change point. In Bucharest, the change point was identified in the year 2006 while, in the other cities, it was between 1987 and 1988. In addition to the cities already mentioned, methods using the t-test detected the same change points in Kyiv, Nantes, Prague, Vienna and Vilnius (group 2). For these cities, only a single change point was detected by these methods in the late eighties, except for Nantes, where a second point at the end of the period under analysis was still detected. The M-W methods and the t-test based on smoothers estimates produced the same results in Dublin and Zagreb, where two change points were detected (group 3).

In Lisbon and Zurich, the three methods produced different results (group 4). Whereas the smoother based t-test detected three change points in Lisbon, the t-test method based on standard residuals detected two change points, specifically, the last ones detected by the former method. In order to identify geographical patterns in the similarity of change point detection by the three methods, Figure 2 presents the location of cities according to the groups presented in Table 3. In general, the cities that belong to group 1, where all methods show similar results, are located in Northern Europe. Bucharest deviates from this pattern. The cities in the group where only the t-tests show similar results are mostly in Central Europe. Cities in groups 3 and 4 are located further west, with Croatia slightly further east.

Performing a global analysis, the first method (M-W test) presents similar results with at least one of the other methods in eight series, while the second and the third method present eleven and thirteen series, respectively, which indicates an advantage of the t-test method based on smoothers over the others.

After the change point analysis, standardized residuals were analysed in each segment and for each of the approaches. The standardized residuals did not present significant serial correlation for a significance level of 1%, up to lag 12, on the various approaches used, see Figure 3. The only discordant case was Vilnius, in the second segment.

The normality of the standardized residuals obtained in the t-test based approaches was also assessed, see Figure 4. For the majority of the series and segments, the normality was not rejected for a significance level of 1% in both t-test approaches.

The exceptions were Bucharest, Minsk, Prague and Vilnius, where the Lilliefors-corrected Kolmogorov–Smirnov test rejected, for a significance level of 1%, the normality of the standardized residuals in the first segment for both t-test approaches. In Dublin, the normality was rejected for the smoother based t-test approach in the first segment. In Nantes, the third segment only had three observations and, for this reason, it was not analyzed in terms of normality and also correlation.

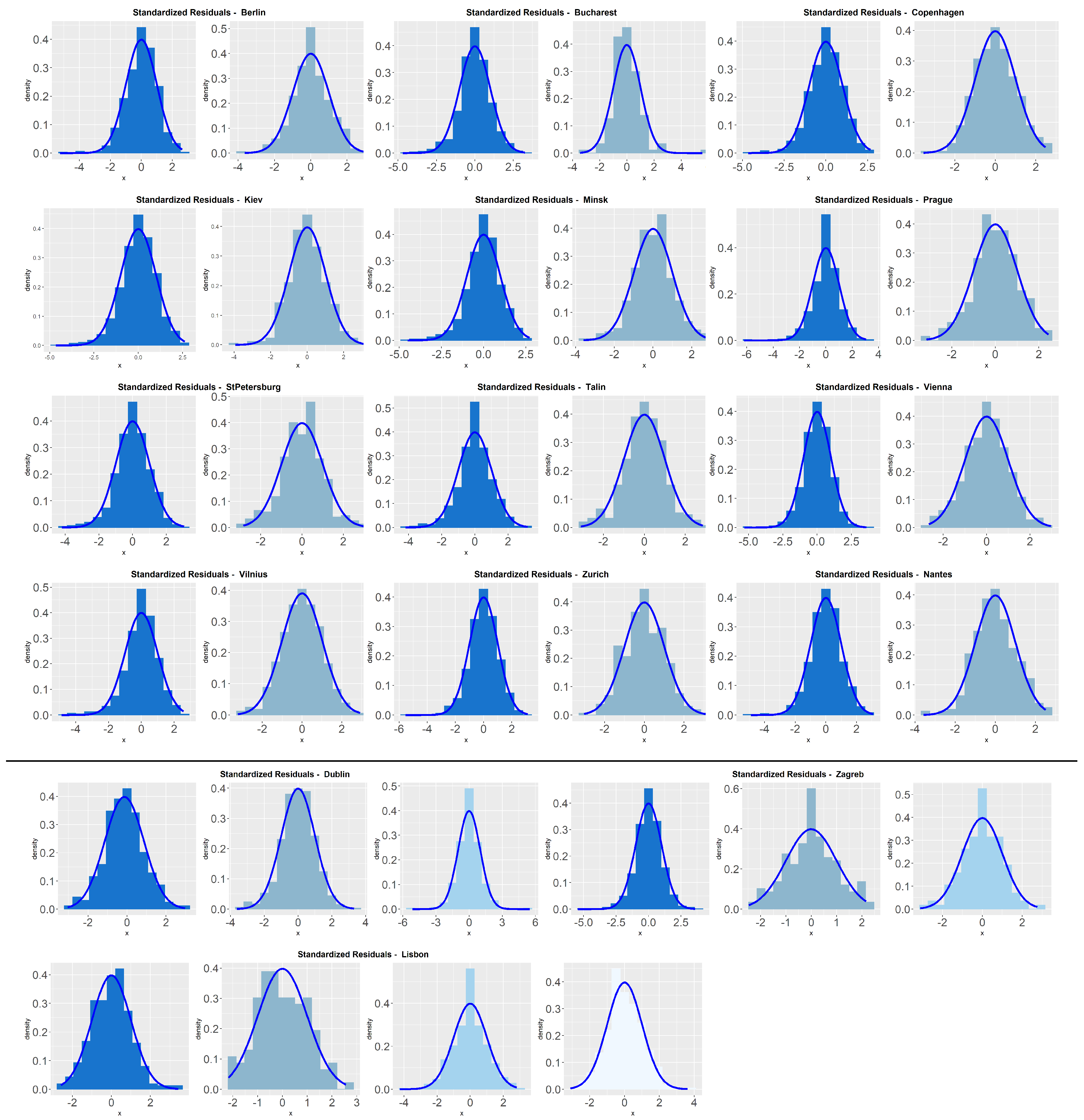
Figure 5 presents standardized residual histograms for each segment identified by the smoother based t-test approach for each city. We can see that histograms present the shape of the normal distribution, even in the cases where the Lilliefors-corrected Kolmogorov–Smirnov test rejected the normal distribution. This can be explained by the fact that the majority of the cities in the first segment of the series has a high dimension, above 1000 observations, easily leading to the rejection of the usual tests for normality.

The analysis of the histograms obtained by the other t-test approach is similar to the one presented here. Given that in most situations normality was not rejected and that method 3, the smoother based t-test approach, is the one with more similarities with the other two methods in terms of change point detection results, it is considered that these change points should be taken into account to better assess the mean temperature growth rates before and after change points, using the mean estimate of the trend component.

Table 4. $\widehat{\mu }$ of the trend component before and after change point times defined by smoother based t-test.

City	Segment 1	Segment 2	Segment 3	Segment 4
Berlin	0.433	1.627
Bucharest	0.493	2.056
Copenhagen	0.388	1.465
Dublin	0.247	0.347
Kiev	0.447	1.677
Lisboa	0.251	−0.154	0.524	0.931
Minsk	0.579	2.050
Nantes	0.293	0.973
Prague	0.484	1.687
St. Petersburg	0.507	1.843
Talin	0.463	1.718
Vienna	0.450	1.518
Vilnius	0.654	2.503
Zagreb	0.327	1.169	1.978
Zurich	0.489	1.603

summarizes this information. With the exception of Lisbon for the period between May 1931 and September 1942, when compared to the older segments, the most recent segments show larger estimates for the mean of the trend component. Eastern cities show larger differences while western European cities, which are closest to the Atlantic Ocean and its currents, show smaller differences. Based on the models used, these findings corroborate that, in recent decades, there is an increase in temperatures in this part of the globe, which should cause greater concern, especially in Eastern Europe. As an illustration, we present in Figure 6 the one-step predictors of the trend component for the cities of Berlin, Kyiv, Dublin and Lisbon, one city from each of the previously identified groups, in each of the segments identified by the change points detection procedure 3. In all graphs presented, the change in the trend component means in recent years is clearly visible.

4. Conclusions

In this work, we applied three methodologies to detect change points, two based on the model residuals (one in a parametric and the other in a non-parametric approach), and a third based on the smoother predictions of the stochastic trend. It was possible to conclude that all of them detected at least one change point in each city, suggesting that there was effectively a change in temperature in each of the cities. In 40% of cities, the methods detected only one change point corresponding to the same year. The t-test based on the smoothers methodology was considered the most appropriate as it detected change points similar to the other two methods and, in most cities, the standardized residuals were uncorrelated and the Lilliefors-corrected Kolmogorov–Smirnov test did not reject their normal distribution. The analysis of the results of the aforementioned method allows us to conclude that, in most cities, there is a change point in the late 1980s or early 1990s. With the detection of all change points before 1980, Lisbon does not match this pattern, as well as Bucharest, also with the detection in the middle of the 2000s. In most cities, the average estimates in the most recent years, after the change point detection, are much higher than in the immediately preceding period, showing greater differences in the cities located in Eastern Europe.

From a methodological point of view, in six of the fifteen series analyzed, the three methods considered had similar change points, as identified in Table 3, and in another five there are similar results between the methods based on the t-test on innovations and predictions smoothed out of the trend. Globally, in 11 of the 15 series, the methods based on the CUSUM test had identical results. Differences between the non-parametric method and the other two parametric methods are justified by the fact that the test based on non-parametric statistics does not consider temporal correlation, while the CUSUM test, on innovations or on smoothed trend predictions, is applied with corrected p-values for correlation. Therefore, the test based on smoothed trend predictions is particularly focused on the component of interest for the analysis of climate change without neglecting the incorporation of temporal correlation in the inferential process.