Assessing Area under the Curve as an Alternative to Latent Growth Curve Modeling for Repeated Measures Zero-Inflated Poisson Data: A Simulation Study
Abstract
1. Introduction
2. Methods
2.1. ZIP LGCM
2.2. AUC
3. Results
3.1. Area under the Curve
3.2. Case Examples
4. Discussions
4.1. Limitations and Conclusions
4.2. Software
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| GEE | General Estimating Equation |
| LGCM | Latent Growth Curve Model |
| ZIP | Zero-Inflated Poisson |
| SEM | Structural Equation Modeling |
| AUC | Area Under the Curve |
| AUC—g | Area Under the Curve with respect to ground |
| AUC—i | Area Under the Curve with respect to the increase |
| ROC | Receiver Operating Characteristic |
References
- Liang, K.-Y.; Zeger, S.L. Longitudinal data analysis using generalized linear models. Biometrika 1986, 73, 13–22. [Google Scholar] [CrossRef]
- Robins, J.M.; Rotnitzky, A.; Zhao, L.P. Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. J. Am. Stat. Assoc. 1995, 90, 106–121. [Google Scholar] [CrossRef]
- Sarvi, F.; Moghimbeigi, A.; Mahjub, H. GEE-based zero-inflated generalized Poisson model for clustered over or under-dispersed count data. J. Stat. Comput. Simul. 2019, 89, 2711–2732. [Google Scholar] [CrossRef]
- Yang, C.; Diao, L.; Cook, R.J. Adaptive response-dependent two-phase designs: Some results on robustness and efficiency. Stat. Med. 2022, 41, 4403–4425. [Google Scholar] [CrossRef]
- Morrell, C.H.; Pearson, J.D.; Brant, L.J.; Gordon-Salant, S. Construction of hearing percentiles in women with non-constant variance from the linear mixed-effects model. Stat. Med. 1997, 16, 2475–2488. [Google Scholar] [CrossRef]
- Feldman, B.J.; Masyn, K.E.; Conger, R.D. New approaches to studying problem behaviors: A comparison of methods for modeling longitudinal, categorical adolescent drinking data. Dev. Psychol. 2009, 45, 652–676. [Google Scholar] [CrossRef]
- Mehta, P.D.; Neale, M.C.; Flay, B.R. Squeezing interval change from ordinal panel data: Latent growth curves with ordinal outcomes. Psychol. Methods 2004, 9, 301–333. [Google Scholar] [CrossRef]
- Hogg, R.; McKean, J.; Craig, A. Introduction to Mathematical Statistics, 6th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Homish, G.G.; Edwards, E.P.; Eiden, R.D.; Leonard, K.E. Analyzing family data: A GEE approach for substance use researchers. Addict. Behav. 2010, 35, 558–563. [Google Scholar] [CrossRef]
- Sellers, K.F.; Raim, A. A flexible zero-inflated model to address data dispersion. Comput. Stat. Data Anal. 2016, 99, 68–80. [Google Scholar] [CrossRef]
- Winkelmann, R.; Zimmermann, K.F. Count data models for demographic data∗. Math. Popul. Stud. 1994, 4, 205–221. [Google Scholar] [CrossRef]
- Beckett, S.; Jee, J.; Ncube, T.; Pompilus, S.; Washington, Q.; Singh, A.; Pal, N. Zero-inflated Poisson (ZIP) distribution: Parameter estimation and applications to model data from natural calamities. Involv. A J. Math. 2014, 7, 751–767. [Google Scholar] [CrossRef]
- Grimm, K.J.; Stegmann, G. Modeling change trajectories with count and zero-inflated outcomes: Challenges and recommendations. Addict. Behav. 2019, 94, 4–15. [Google Scholar] [CrossRef]
- Vel, K.; Bharathiar University; Tha, C. Estimation of Zero-Inflation Parameter in Zero-Inflated Poisson Model. Int. J. Math. Trends Technol. 2018, 56, 135–140. [Google Scholar] [CrossRef]
- Hua, H.E.; Wan, T.A.N.G.; Wenjuan, W.A.N.G.; Crits-Christoph, P. Structural zeroes and zero-inflated models. Shanghai Arch. Psychiatry 2014, 26, 236. [Google Scholar]
- Liu, H. Growth Curve Models for Zero-Inflated Count Data: An Application to Smoking Behavior. Struct. Equ. Model. A Multidiscip. J. 2007, 14, 247–279. [Google Scholar] [CrossRef]
- Olsen, M.K.; Schafer, J.L. A Two-Part Random-Effects Model for Semicontinuous Longitudinal Data. J. Am. Stat. Assoc. 2001, 96, 730–745. [Google Scholar] [CrossRef]
- Colder, C.R.; Frndak, S.; Lengua, L.J.; Read, J.P.; Hawk, L.W.; Wieczorek, W.F. Internalizing and Externalizing Problem Behavior: A Test of a Latent Variable Interaction Predicting a Two-Part Growth Model of Adolescent Substance Use. J. Abnorm. Child Psychol. 2018, 46, 319–330. [Google Scholar] [CrossRef]
- Henry, K.L.; Tran, T.P.; Agbeke, D.V.; Lee, H.; Williford, A.; Dziak, J.J. Two-Part Models for Father–Child Relationship Variables: Presence in the Child’s Life and Quality of the Relationship Conditional on Some Presence. J. Soc. Soc. Work. Res. 2022, 13, 409–430. [Google Scholar] [CrossRef]
- Petras, H.; Nieuwbeerta, P.; Piquero, A.R. Participation and Frequency during Criminal Careers across the Life Span*. Criminology 2010, 48, 607–637. [Google Scholar] [CrossRef]
- Fekedulegn, D.B.; Andrew, M.E.; Burchfiel, C.M.; Violanti, J.M.; Hartley, T.A.; Charles, L.E.; Miller, D.B. Area Under the Curve and Other Summary Indicators of Repeated Waking Cortisol Measurements. Psychosom. Med. 2007, 69, 651–659. [Google Scholar] [CrossRef]
- McCanlies, E.; Leppma, M.; Mnatsakanova, A.; Allison, P.; Fekedulegn, D.; Andrew, M.; Violanti, J. Associations of burnout with awakening and diurnal cortisol among police officers. Compr. Psychoneuroendocrinol. 2020, 4, 100016. [Google Scholar] [CrossRef]
- Jain, S.; Bharathi, D. Receiver Operating Characteristic Curve Analysis and its Application in Dentistry. J. Adv. Med. Dent. Sci. Res. 2020, 8, 152–155. [Google Scholar]
- Mandrekar, J.N. Receiver Operating Characteristic Curve in Diagnostic Test Assessment. J. Thorac. Oncol. 2010, 5, 1315–1316. [Google Scholar] [CrossRef] [PubMed]
- Tafiadis, D.; Chronopoulos, S.K.; Kosma, E.I.; Voniati, L.; Raptis, V.; Siafaka, V.; Ziavra, N. Using Receiver Operating Characteristic Curve to Define the Cutoff Points of Voice Handicap Index Applied to Young Adult Male Smokers. J. Voice 2018, 32, 443–448. [Google Scholar] [CrossRef] [PubMed]
- Campbell, R.L.; Cloutier, R.; Bynion, T.M.; Nguyen, A.; Blumenthal, H.; Feldner, M.T.; Leen-Feldner, E.W. Greater adolescent tiredness is related to more emotional arousal during a hyperventilation task: An area under the curve approach. J. Adolesc. 2021, 90, 45–52. [Google Scholar] [CrossRef] [PubMed]
- Jordan, K.H.; Long, D.L.; Mcgwin, G., Jr.; Childers, N.K. Average area under the curve: An alternative method for quantifying the dental caries experience in longitudinal studies. Community Dent. Oral Epidemiol. 2019, 47, 441–447. [Google Scholar] [CrossRef] [PubMed]
- Pruessner, J.C.; Kirschbaum, C.; Meinlschmid, G.; Hellhammer, D.H. Two formulas for computation of the area under the curve represent measures of total hormone concentration versus time-dependent change. Psychoneuroendocrinology 2003, 28, 916–931. [Google Scholar] [CrossRef] [PubMed]
- Muthén, L.K.; Muthén, B.O. Mplus User’s Guide, 8th ed.; Los Angeles, 1998–2017; Available online: https://www.statmodel.com/download/usersguide/MplusUserGuideVer_8.pdf (accessed on 27 January 2023).
- Duncan, T.E.; Duncan, S.C. An introduction to latent growth curve modeling. Behav. Ther. 2004, 35, 333–363. [Google Scholar] [CrossRef]
- Rodriguez, D. Research Methods. In Dubuque, IA; Kendall Hunt Publishing Company: Dubuque, IA, USA, 2021. [Google Scholar]
- Rodriguez, D. Core Statistics: Practical Knowledge for the Health Sciences; Kendall Hunt Publishing Company: Dubuque, IA, USA, 2020. [Google Scholar]
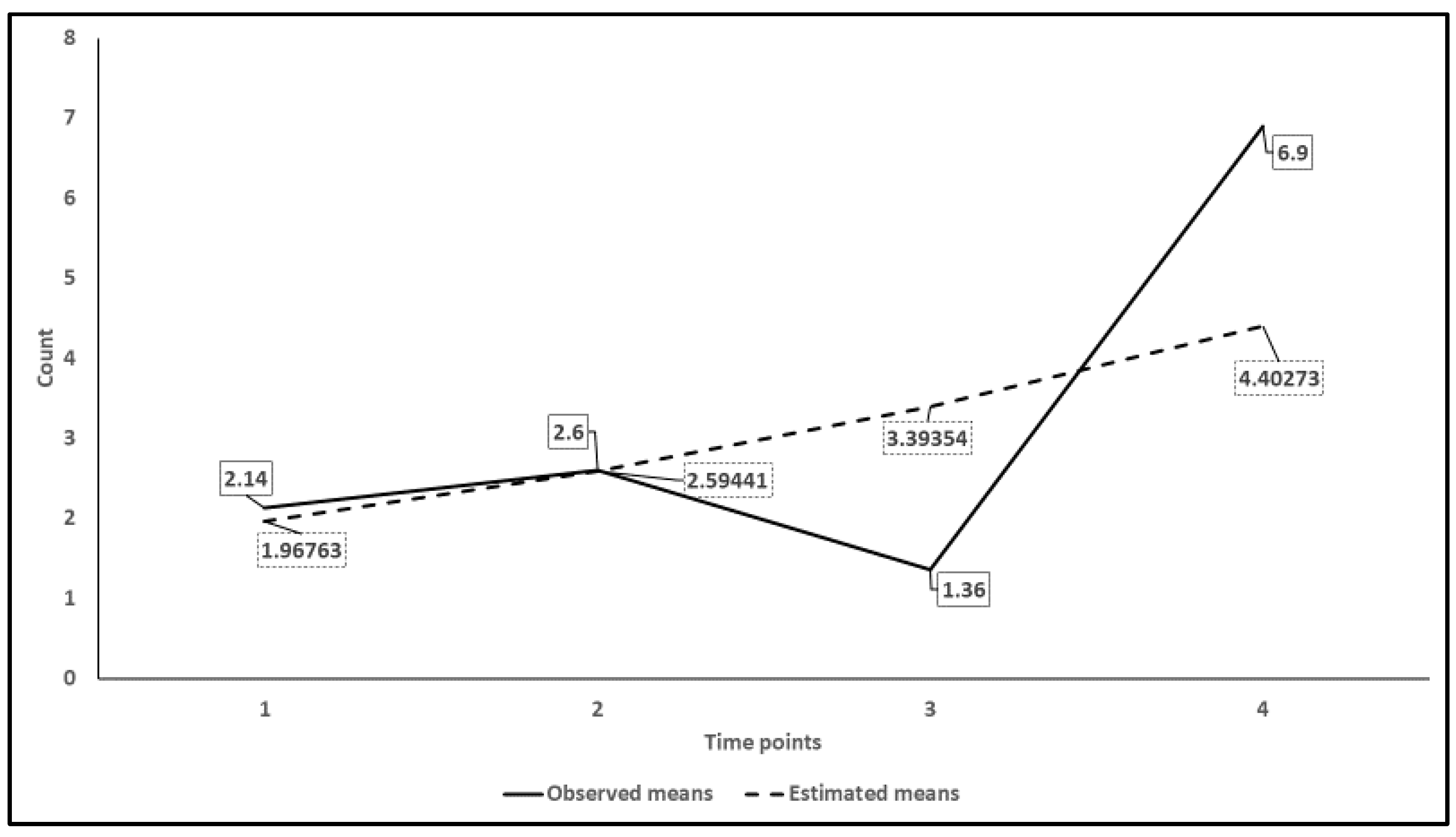
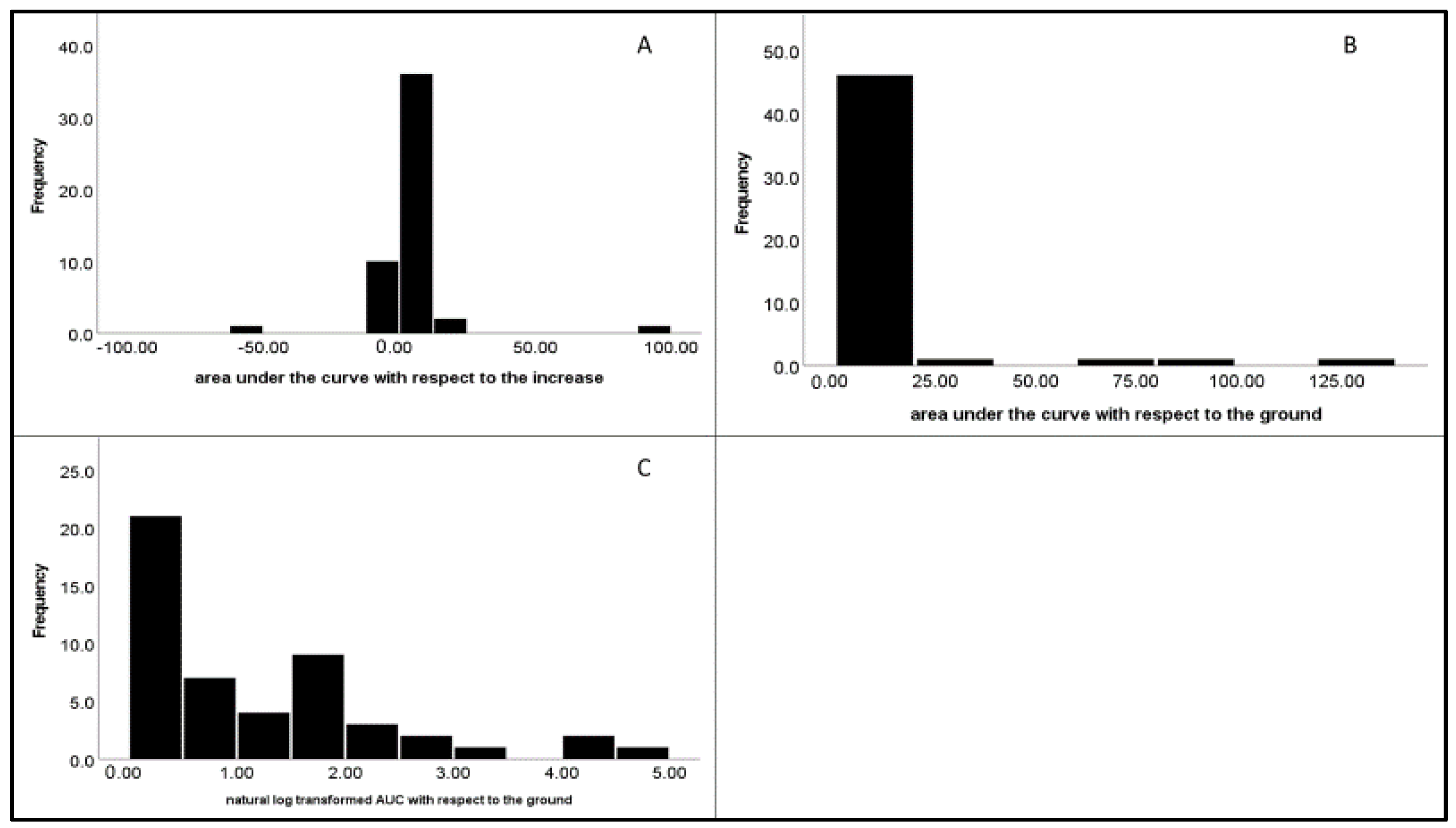
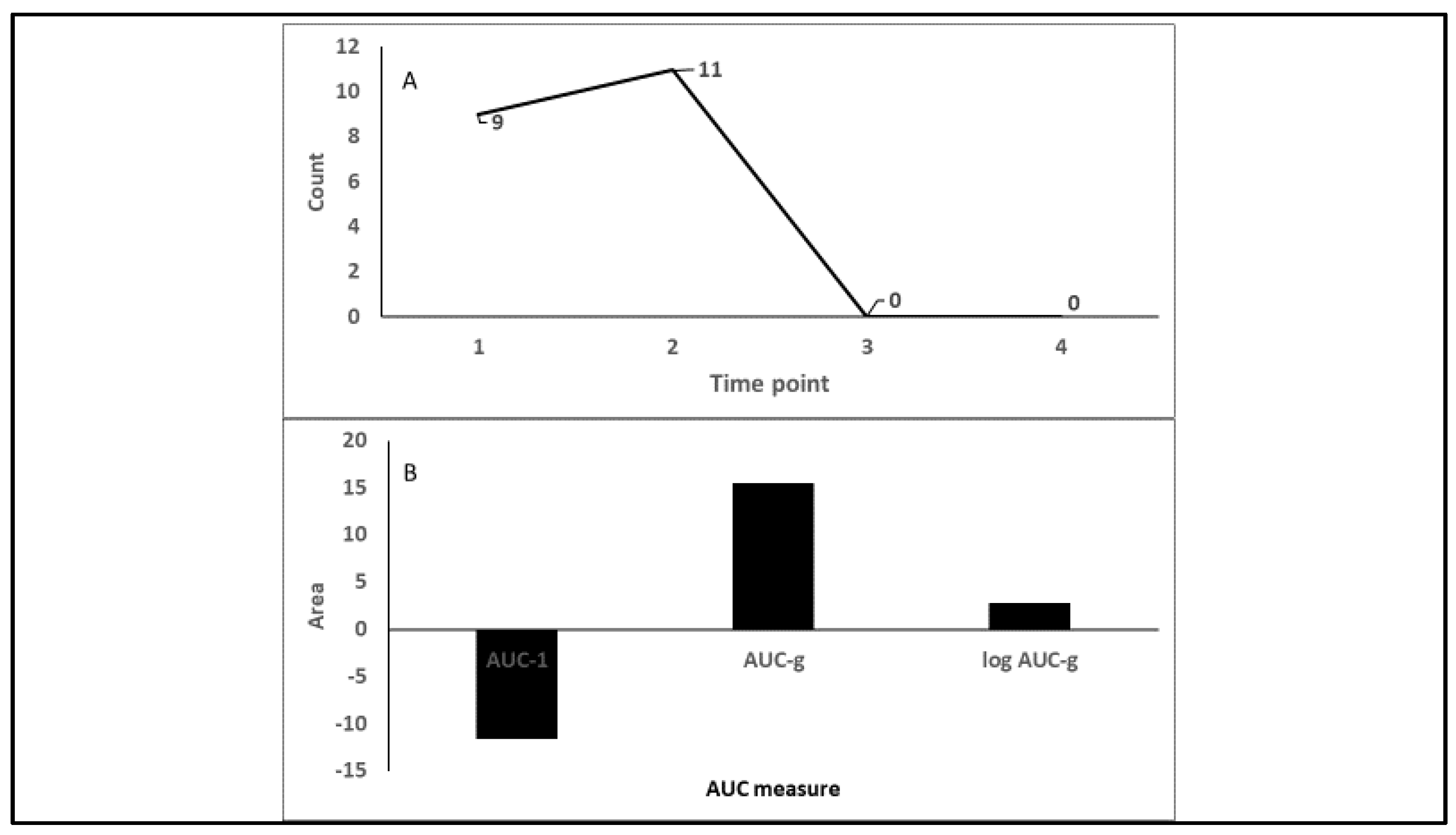
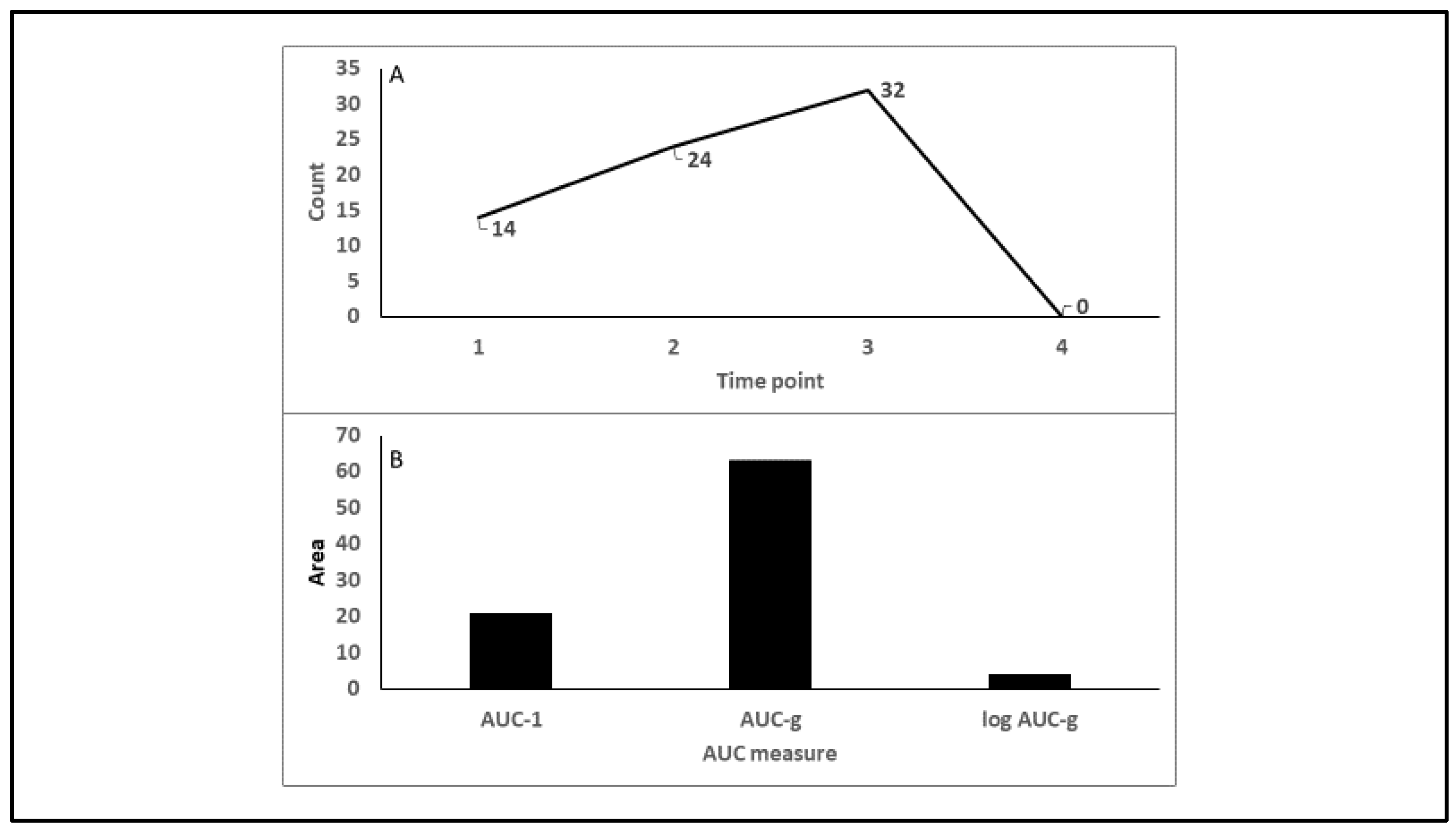
| N | Wave | Minimum | Maximum | Mean | SD | λ | π |
|---|---|---|---|---|---|---|---|
| 500 | Time 1 | 0 | 83 | 1.93 | 7.419 | 29.45 | 0.93 |
| Time 2 | 0 | 107 | 2.06 | 8.064 | 32.78 | 0.94 | |
| Time 3 | 0 | 475 | 2.54 | 21.662 | 186.28 | 0.99 | |
| Time 4 | 0 | 206 | 2.57 | 14.417 | 82.45 | 0.97 | |
| 250 | Time 1 | 0 | 83 | 2.17 | 8.341 | 33.23 | 0.93 |
| Time 2 | 0 | 106 | 2.31 | 8.636 | 33.60 | 0.93 | |
| Time 3 | 0 | 38 | 1.73 | 5.153 | 16.08 | 0.89 | |
| Time 4 | 0 | 206 | 3.26 | 18.248 | 104.71 | 0.97 | |
| 100 | Time 1 | 0 | 63 | 2.15 | 8.964 | 38.524 | 0.94 |
| Time 2 | 0 | 43 | 2.04 | 5.605 | 16.440 | 0.88 | |
| Time 3 | 0 | 38 | 2.00 | 5.944 | 18.666 | 0.89 | |
| Time 4 | 0 | 206 | 4.27 | 22.431 | 121.104 | 0.96 | |
| 50 | Time 1 | 0 | 63 | 2.14 | 9.165 | 40.391 | 0.95 |
| Time 2 | 0 | 43 | 2.60 | 7.100 | 20.989 | 0.95 | |
| Time 3 | 0 | 32 | 1.36 | 4.681 | 16.472 | 0.92 | |
| Time 4 | 0 | 206 | 6.90 | 31.403 | 148.820 | 0.95 |
| Count Intercept 1 | Binary Intercept 2 | Count Trend 3 | Binary Trend 4 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| n | Measures 5 | X1 | X2 | X1 | X2 | X1 | X2 | X1 | X2 |
| 500 | Average | 1.0009 | −0.9993 | 0.5091 | −0.509 | 0.0998 | −0.1002 | 0.3545 | −0.3537 |
| %Bias | 0.09 | −0.07 | 1.82 | 0.018 | −0.2 | 0.2 | 1.2857 | 1.0571 | |
| MSE | 0.0032 | 0.0032 | 0.0331 | 0.331 | 0.0005 | 0.0005 | 0.106 | 0.011 | |
| Coverage | 0.942 | 0.943 | 0.95 | 0.946 | 0.93 | 0.931 | 0.952 | 0.943 | |
| Power | 1.00 | 1.00 | 0.829 | 0.846 | 0.992 | 0.992 | 0.939 | 0.933 | |
| 250 | Average | 1.0022 | −0.9996 | 0.5257 | −0.5203 | 0.1001 | −0.1007 | 0.3595 | −0.3609 |
| %Bias | 0.22 | −0.04 | 5.14 | 4.06 | 0.1 | 0.7 | 2.7143 | 3.1143 | |
| MSE | 0.0066 | 0.0067 | 0.0738 | 0.0732 | 0.001 | 0.0011 | 0.0229 | 0.0237 | |
| Coverage | 0.934 | 0.939 | 0.943 | 0.949 | 0.924 | 0.925 | 0.948 | 0.945 | |
| Power | 1.0 | 1.0 | 0.524 | 0.514 | 0.882 | 0.888 | 0.691 | 0.692 | |
| 100 | Average | 1.0039 | −1.004 | 0.5705 | −0.5599 | 0.1013 | −0.1015 | 0.3804 | −0.3846 |
| %Bias | 0.39 | 0.4 | 14.1 | 11.98 | 1.3 | 1.5 | 8.6857 | 9.8857 | |
| MSE | 0.0193 | 0.0187 | 0.2371 | 0.2274 | 0.0034 | 0.0032 | 0.0735 | 0.0737 | |
| Coverage | 0.922 | 0.923 | 0.942 | 0.95 | 0.901 | 0.905 | 0.936 | 0.943 | |
| Power | 1 | 1 | 0.203 | 0.189 | 0.543 | 0.543 | 0.347 | 0.348 | |
| 50 | Average | 1.0131 | −1.0123 | 5.2436 | −3.6967 | 0.1007 | −0.102 | −0.1756 | −0.18 |
| %Bias | 1.31 | 1.23 | 948.72 | 639.34 | 0.7 | 2.00 | −150.171 | −48.571 | |
| MSE | 0.0494 | 0.0473 | 25461.42 | 7943.048 | 0.0093 | 0.0092 | 1909.731 | 409.3025 | |
| Coverage | 0.893 | 0.9 | 0.935 | 0.937 | 0.886 | 0.886 | 0.923 | 0.921 | |
| Power | 0.986 | 0.985 | 0.112 | 0.111 | 0.334 | 0.343 | 0.205 | 0.204 | |
| n | AUC Measure | Mean | SD | Skewness | Kurtosis | Median | IQR 1 |
|---|---|---|---|---|---|---|---|
| 500 | AUC—i | 1.061 | 25.589 | 12.146 | 240.570 | 0.00 | 2.00 |
| AUC—g | 6.857 | 26.907 | 12.565 | 196.822 | 1.50 | 4.50 | |
| LN AUC—g | 1.11 | 1.13 | 1.089 | 1.067 | 0.916 | ||
| 250 | AUC—i | 0.24 | 16.343 | −3.515 | 45.006 | 0.00 | 2.50 |
| AUC—g | 6.756 | 20.107 | 7.818 | 77.213 | 1.50 | 5.00 | |
| LN AUC—g | 1.158 | 1.135 | 0.991 | 0.709 | 0.916 | 1.79 | |
| 100 | AUC—i | 0.8 | 20.416 | −3.714 | 38.084 | 0.00 | 2.50 |
| AUC—g | 7.25 | 18.484 | 4.754 | 26.398 | 1.50 | 4.50 | |
| LN AUC—g | 1.164 | 1.181 | 1.087 | 0.708 | 0.916 | 1.70 | |
| 50 | AUC—i | 2.06 | 15.441 | 22.673 | 8.48 | 0.00 | 4.13 |
| AUC—g | 8.48 | 23.780 | 18.467 | 1.105 | 1.250 | 4.13 | |
| LN AUC—g | 1.105 | 1.251 | 1.340 | 1.535 | 0.805 | 1.63 |
| AUC—g 1 | AUC—i | ||||
|---|---|---|---|---|---|
| n | Measures | X1 | X2 | X1 | X2 |
| 500 | Average | 0.3282 | −0.4147 | 0.9069 | −1.4914 |
| Bias | −0.243 | −0.072 | −2.274 | −0.441 | |
| MSE | 0.0021 | 0.0018 | 1.3694 | 1.1977 | |
| Coverage | 0.945 | 0.95 | 0.946 | 0.95 | |
| Power | 1 | 1 | 0.134 | 0.283 | |
| 250 | Average | 0.2924 | −0.4504 | −0.5813 | 0.0029 |
| Bias | −0.205 | 0.0889 | 1.6259 | −71 | |
| MSE | 0.0045 | 0.004 | 1.1947 | 1.0654 | |
| Coverage | 0.947 | 0.948 | 0.947 | 0.948 | |
| Power | 0.991 | 1 | 0.091 | 0.051 | |
| 100 | Average | 0.3167 | −0.4294 | −2.9642 | −2.0807 |
| Bias | −0.409 | −0.14 | 0.8918 | −0.54 | |
| MSE | 0.0115 | 0.01 | 4.448 | 3.8672 | |
| Coverage | 0.941 | 0.944 | 0.941 | 0.944 | |
| Power | 0.845 | 0.986 | 0.313 | 0.195 | |
| 50 | Average | 0.4064 | −0.4795 | 0.1414 | −1.385 |
| Bias | −0.392 | 0.1044 | −14.303 | 0.581 | |
| MSE | 0.0226 | 0.021 | 4.7604 | 4.4243 | |
| Coverage | 0.936 | 0.929 | 0.936 | 0.928 | |
| Power | 0.802 | 0.924 | 0.069 | 0.125 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez, D. Assessing Area under the Curve as an Alternative to Latent Growth Curve Modeling for Repeated Measures Zero-Inflated Poisson Data: A Simulation Study. Stats 2023, 6, 354-364. https://doi.org/10.3390/stats6010022
Rodriguez D. Assessing Area under the Curve as an Alternative to Latent Growth Curve Modeling for Repeated Measures Zero-Inflated Poisson Data: A Simulation Study. Stats. 2023; 6(1):354-364. https://doi.org/10.3390/stats6010022
Chicago/Turabian StyleRodriguez, Daniel. 2023. "Assessing Area under the Curve as an Alternative to Latent Growth Curve Modeling for Repeated Measures Zero-Inflated Poisson Data: A Simulation Study" Stats 6, no. 1: 354-364. https://doi.org/10.3390/stats6010022
APA StyleRodriguez, D. (2023). Assessing Area under the Curve as an Alternative to Latent Growth Curve Modeling for Repeated Measures Zero-Inflated Poisson Data: A Simulation Study. Stats, 6(1), 354-364. https://doi.org/10.3390/stats6010022






