Statistical Analysis in the Presence of Spatial Autocorrelation: Selected Sampling Strategy Effects

Abstract

Fundamental to most classical data collection sampling theory development is the random drawings assumption requiring that each targeted population member has a known sample selection (i.e., inclusion) probability. Frequently, however, unrestricted random sampling of spatially autocorrelated data is impractical and/or inefficient. Instead, randomly choosing a population subset accounts for its exhibited spatial pattern by utilizing a grid, which often provides improved parameter estimates, such as the geographic landscape mean, at least via its precision. Unfortunately, spatial autocorrelation latent in these data can produce a questionable mean and/or standard error estimate because each sampled population member contains information about its nearby members, a data feature explicitly acknowledged in model-based inference, but ignored in design-based inference. This autocorrelation effect prompted the development of formulae for calculating an effective sample size (i.e., the equivalent number of sample selections from a geographically randomly distributed population that would yield the same sampling error) estimate. Some researchers recently challenged this and other aspects of spatial statistics as being incorrect/invalid/misleading. This paper seeks to address this category of misconceptions, demonstrating that the effective geographic sample size is a valid and useful concept regardless of the inferential basis invoked. Its spatial statistical methodology builds upon the preceding ingredients.

1. Introduction

Recent literature claims “persistent misconceptions” exist about the interpretation of data obtained from sampling of spatially autocorrelated phenomena. In spatially autocorrelated data, values at each sample location provide information about the values of neighboring locations as well as the sampled location itself. The supposed misconceptions include the calculation of a quantity called the effective sample size, the focus of this paper, which is a measure of the loss of information attributable to the effects of positive spatial autocorrelation (SA; similar neighboring values cluster on a map). Brus [1], for example, contends that effective sample size calculations are inappropriate in a design-based analysis, in part because it considers attribute values as fixed rather than random quantities. The main objective of this paper is to demonstrate that this specific contention is incorrect, and that effective sample size is a meaningful quantity even with a random sampling selection implementation; the discussion here begins by briefly contextualizing it within a broader set of controversies about spatial statistical analyses.

Correlated data theory and practice has a history dating back to the early 1800s, with Laplace’s initial recognition of its presence in time series (e.g., [2]). The addition of SA to this raw dependent data family did not occur until the early 1900s, with its popularization failing to materialize until roughly 1970. Its transition from a tacit to a mathematically formulated conceptualization was not without controversy. Lebart [3], for example, used first spatial differences, fundamentally describing SA as being perfectly positive for each and every attribute variable in a dataset, to reduce/remove spatial dependence effects from factor analysis applications later, Besag et al. [4] formulated the improper conditional autoregressive (ICAR) model partly in this manner, but retained an uncorrelated component coupled with the spatial differencing term in order to preserve the almost always prevailing less-than-perfect positive SA. Because his overcorrection was incapable of aptly capturing the exhibited latent degree of SA—moving data from zero, past intermediate, and to perfect positive SA—this transformation created little difference between the factor structures he calculated for these spatially adjusted variates and their corresponding unadjusted sources, discouraging many quantitative researchers at that time from pursuing emerging non-point pattern spatial statistics themes of that era. Since then, a number of other scholars directed criticisms at spatial statistical approaches to georeferenced data analyses. Wall [5], for example, carefully scrutinizes the spatial correlation structures implied by two of the most commonly employed spatial regression models within the context of an irregular lattice geographic structure of areal units, concluding that they produce many counterintuitive or impractical, and hence essentially unintelligible, consequences (e.g., adjacent polygons with a relatively small SA degree, perhaps because of spatial heterogeneity effects). Furthermore, Wakefield [6] argues that respecifying models to properly capture spatial dependence often is unwarranted for ecological regression analysis of geospatial environmental exposure and other epidemiological health data (e.g., because of data quality issues).

The spatial statistics/econometrics literature is replete with SA impact claims, the foremost being variance inflation. The publication of papers evaluating such assertions is one critical reaction to these allegations. Along these lines, Hawkins et al. [7] appraise the contention found in the ecological literature that SA in standard ordinary least squares (OLS) estimated linear regression residuals results in shifts in the equation’s partial coefficients, which bias an interpretation of the role of covariates vis-à-vis response variable map patterns. Their validation study confirms what mathematical statistics already declared, namely that OLS yields unbiased linear regression coefficient estimates for both independent and spatially autocorrelated observations, cautioning that interpretation requires an explicit awareness of both geographic scale and resolution. Meanwhile, acknowledging the contemporary popularity of mixed models in statistics in general, and spatial statistics/econometrics in particular, which involves adding a spatially autocorrelated random effects term to a regression model specification (e.g., re [4]), Hodges and Reich [8] show how to avoid spatial confounding, which they attribute to, at least in part, the presence of collinearity in data arising from the tendency for measures taken at locations nearby each other to be more similar than measures taken at more distant locations. Hodges and Reich [8] (p. 326) contend that they “debunk the common belief that introducing a spatially-correlated random effect adjusts fixed-effect estimates for spatially-structured missing covariates”.

Accompanying debates such as the preceding spatial confounding argument is one about the functional organization connecting locations in a SA conceptualization. Echoing Griffith and Lagona [9], LeSage and Pace [10] counter a nearly universal consensus, distinct from the concern about endogeneity, that estimates and inferences from spatial regression models are sensitive to even moderate changes in the definition governing this articulation. Nevertheless, for model identification issues affiliated with this linkage system and other reasons, Partridge et al. [11] note that econometricians remain skeptical about spatial econometric approaches that utilize SA effects to estimate geographic spillovers in regional outcomes. This type of skepticism also appears in the spatial sampling literature. Lark and Cullis [12] insist that the inferential basis supporting standard OLS estimation for a linear regression model is design-based, requiring that the collection of georeferenced data be in accordance with an appropriate random-grounded sampling design, a protocol rarely used for gathering soil data; hence, they conclude that OLS methods are not applicable for analyzing such data. In the same vein, Brus [1], for example, challenges declarations pertaining to sampling and variance inflation, and hence the use of other designs apart from simple random sampling (RS) for compiling geospatial data, as well as the application of the independent and identically distributed (iid) assumption to parent populations in such data analyses.

The primary objective of this paper is to augment the general literature in defense of spatial statistics/econometrics, and to reenforce earlier rebuttals such as those already reiterated here. Specifically, we address the debatable contentions posited by Brus with a goal of furnishing further clarification about them; at least part of this difference of opinion reflects that between the design- and model-based inference approaches (e.g., see [13,14]). Part of our underlying viewpoint emphasizes that iid random variables (RVs) provide a mathematical framework for RS, which is a special (not the sole) case of this concept’s implementation: knowing the output of one iid RV, whether for a population or a sample (à la [15]), supplies no information about the outputs of the others. After all, joint distributions for independent RVs differ from those for conditionally dependent RVs. Products of probability density/mass functions conceptualize this former, whereas Markov chain Monte Carlo (MCMC; [16]) formulations, for example, conceptualize this latter, situation. In addition, not only real-world geographic landscapes, but also time series, matched/correlated/paired/dependent observational units, and social network collections of phenomena, rarely constitute random mixtures (see [17]); rather, they embrace trans-observational structure meriting quantitative recognition similar to calculating means, variances, and skewness and kurtosis measures.

2. The Case Brus Promotes: A Summary and Traditional Numerical Counterexamples

Brus [1] (pp. 689, 694, 696) raises provocative points about geographic probability sampling when he states.

• Remarkably, in other publications we can read that the classical formula [for finite population sampling?] for the variance of the estimated population mean with SRS [simple RS] underestimates the true variance for populations showing spatial structure (see for instance Griffith [17] and Plant [18]). The reasoning is that due to the spatial structure there is less information in the sample data about the population mean.
• Another persistent misconception is that when estimating the variance of the estimated mean of a spatial population or the correlation of two variables of a population we must account for autocorrelation of the sample data. This misconception occurs, for instance, in [17] and in [18]). The reasoning is that, due to the [SA] in the sample data, there is less information in the data about the parameter of interest, and so the effective sample size is smaller than the actual sample size.
• … Griffith [17] confused the population mean and the model mean, Wang et al. [19] confused the population variance with the sill variance (a priori variance) of the random process that has generated the population [20].

A focal point in this set of disputes is variance inflation.

This section encapsulates output from Monte Carlo simulation experiments employing pseudo-random numbers that characterize two conventional numerical illustrations often anecdotally presented in pedagogic circumstances to exemplify variance inflation. The first is the instance of doubling to n an original sample of size n/2 drawn according to a SRS design by repeating each of its selected entries; educators can devise similar demonstrations for other sampling designs. The next subsection extends this pretend prospect to legitimate matched observations schemes. The third is the instance of a sample of size n comprising two distinct and unmistakably separated clusters of n/2 values, a data configuration resembling two repeated measures plagued by measurement error.

2.1. Samples Artificially Enlarged by Repeating Each of Their Selected Observations

One simulation experiment engages correlated data, with n/2 pairs of perfectly correlated (i.e., ρ = 1) observations. For simplicity, the synthetic data consist of pseudo-random numbers drawn from a normal distribution with μ = 0 and σ = 1. This experiment has 10,000 replications, and affords a comparison of output for this contrived sample with a SRS sample of size n; each sample contains the same initial n/2 SRS selections. The only factor manipulated in this experiment was sample composition.

Table 1. A SRS and correlated data simulation experiment synopsis; 10,000 replications.

n	Central Limit Theorem		n/2 SRS Selections Doubled		n SRS Selections		${\left(\frac{{\hat{\mathsf{\sigma }}}_{\overline{\mathbf{y}}}^{*}}{{\hat{\mathsf{\sigma }}}_{\overline{\mathbf{y}}}}\right)}^2$
	${\mathsf{\mu }}_{\overline{\mathbf{y}}}$	${\mathsf{\sigma }}_{\overline{\mathrm{y}}}$	${\widehat{\mathsf{\mu }}}_{\overline{\mathrm{y}}}^{*}$	${\widehat{\mathsf{\sigma }}}_{\overline{\mathrm{y}}}^{*}$	${\widehat{\mathsf{\mu }}}_{\overline{\mathrm{y}}}$	${\widehat{\mathsf{\sigma }}}_{\overline{\mathrm{y}}}$
30	0	0.18257	0.00359	0.25759	0.00337	0.18197	2.00382
100	0	0.10000	0.00021	0.14135	0.00082	0.10085	1.96444
500	0	0.04472	0.00026	0.06272	0.00026	0.04433	2.00178
1000	0	0.03162	−0.00013	0.04428	0.00015	0.03148	1.97854
5000	0	0.01414	−0.00016	0.01995	−0.00012	0.01404	2.01907

tabulations summarize selected output from this simulation experiment. One finding gleaned from this table is the well-known confirmation that SRS yields results consistent with the central limit theorem (CLT); slight differences appearing between the two sets of calculations are attributable to sampling error. Another finding is variance inflation attributable to correlated observations, the same variety discussed by Griffith [17], Plant [18], and Wang et al. [19], and discounted by Brus [1]; Griffith [17] treats this specific source within the context of the effective sample size notion. Indeed, this particular variance inflation, as indexed by the reported estimated sampling distribution variance ratios, reveals the actual sample size doubling that occurs in the contrived cases.

In summary, evidence exists advocating that assumption violations unintentionally induced by correlated data make alterations to conventional SRS design statistical theory. Ensuing sections of this paper substantiate that this property extends to geographic sampling settings involving SA.

2.2. Ignoring the Correlation in Correlated/Paired/Matched Samples

The preceding example imitates real-world possibilities, such as the genuine traditional testing of the difference between two population means hypothesis that is an exemplar of the investigation of an average outcome before and after an intervention. An analyst may manage this situation in one of two general ways: (1) draw two independent random samples, each of size n for balance, one before and the other after some controlled or natural disruption; or, (2) draw a single random sample of n matched/correlated/paired/dependent observations, recording each pair of before and after measurements. This second choice helps to control for certain potential sources of unwanted variation. The design-based approach acknowledges the latent temporal autocorrelation here by adopting the orthodox practice of analyzing the differences of before–after value pairings, setting, conceding, and perpetuating a habit of handling autocorrelation when sampling.

Table 2. Simulated CLT results for the difference of two means sampling distributions, with ρ = 0.9 for the correlated samples; 10,000 replications.

Sampling Design	nk	Difference of Means: μ1 − μ2 = 0	Standard Error † for σ1 = σ2	P(K–S) ‡ Normality Diagnostic
two independent samples	30	0.0002	0.2595	> 0.15
one correlated sample		–0.0002	0.0818	0.1362
two independent samples	100	–0.0009	0.1414	> 0.15
one correlated sample		–0.0006	0.0443	0.1269

^† the CLT values here are $\sqrt{2/{\mathrm{n}}_{\mathrm{k}}}$ (i.e., respectively, 0.2582 and 0.1414) for independent samples, and $\sqrt{2\left(1-\mathsf{\rho }\right)/{\mathrm{n}}_{\mathrm{k}}}$ (i.e., respectively, 0.0816 and 0.0447) for correlated samples. ^‡ denotes the probability of the Kolmogorov–Smirnov(K–S) normality goodness-of-fit diagnostic statistic.

summarizes output for a basic second simulation experiment exemplifying this latter approach. As in the preceding section, Table 2 discloses marked variance inflation attributable to correlated observations.

In this longstanding statistical problem, dating back to work by Hotelling around 1930, the independence affiliated with RS differs from the pairwise observational correlation attributable to matching/pairing, a standing analogous to that of SA in geospatial data. Nonetheless, the RS design embraces it (e.g., collecting pre- and post-event measurements requires a coordinated effort beyond simple/unconstrained RS) in order to decrease the sampling distribution variance, here by about one third—again, design-based approaches customarily account for this in their variance estimation via differencing. Ignoring this sampling design facet would allow an analyst to pretend that a sample size has twice as many entries as it truly has (i.e., the effective sample size here is n_k, not 2n_k), and that the difference of two means standard error is nearly three times greater than its true magnitude. A real-world example of this possibility occurred during the early years of the United States Environmental Protection Agency’s Environmental Monitoring and Assessment Program (US EPA EMAP), underwater soil samples collected from the Chesapeake Bay and other near-coastal water sea beds along the US Atlantic Ocean and Gulf of Mexico shorelines were coded and then distributed to private chemistry laboratories for assaying, with the goal of determining which companies should receive subsequent government contracts through this project. For quality control purposes, both the same and different laboratories received sets of soil sample bags with some containing near-duplicate (i.e., some would say SA, whereas others would say measurement error, at work) content because of their side-by-side borehole locations. One entrepreneur deciphered the adopted code, and merely again reported first replicate bag results rather than assaying duplicate samples: he treated a sample smaller than n as being of size n. Because he reported identical results for replicate bags, project scientists detected his deception, preventing him from receiving a subsequent project contract. Recognizing and accounting for correlation in observations matters!

2.3. Samples Grouping into Two Equal-Sized Disparate-Valued Subsets of Observation

A third simulation experiment was bivariate in nature, and involved clustered data grouped into two clearly distinct subsets, each with n/2 pairs of uncorrelated (i.e., ρ = 0) observations. Once more, for simplicity, the synthetic data consist of pseudo-random numbers drawn from a normal distribution with (μ_x,1, μ_y,1) = (5, 5) and (μ_x,2, μ_y,2) = (10, 10), and σ_x = σ_y = 0.5; this chosen variance ensures that the two subset clusters are distinct and concentrated. The experiment had 10,000 replications, and supported comparing output for a SRS sample of size n with a stratified sample of size four. The only factor manipulated in this experiment was the design sample size.

Geometrically speaking, the pedagogic feature of interest here is that determining a straight line linear regression on a two-dimensional scatterplot requires only two different points, which always are collinear; by reducing one of the two point clouds to a single point, this specimen also more commonly offers an excellent illustration about the influence of outliers on linear correlation and regression estimation. Maintaining a minimum number of degrees of freedom as well as a balanced design in an affiliated simulation experiment requires increasing each minimum stratified RS stratum sample size n_k, where k denotes the number of strata, here from one to two (i.e., two draws from each cluster).

Table 3. Varying n SRS versus fixed small n stratified RS; population: β₀ = 0, β₁ = 1, R² = 1, and CV = 1; 10,000 replications.

n	SRS				n1 = n2 = 2 stratified RS				variance ratios
	${\widehat{\mathsf{\beta }}}_0$	${\widehat{\mathsf{\beta }}}_1$	R2	CV	${\widehat{\mathsf{\beta }}}_0$	${\widehat{\mathsf{\beta }}}_1$	R2	CV	${\widehat{\mathsf{\beta }}}_0$	${\widehat{\mathsf{\beta }}}_1$	R2	CV
4	4.740	0.683	0.778	350.016	0.025	0.997	0.990	4.020	201.8	112.9	1191.1	1.9 $\times$ 1010
30	1.165	0.921	0.906	1.605	0.011	0.999	0.990	4.021	22.0	12.3	511.1	1600.2
100	0.619	0.957	0.934	1.091	0.017	0.998	0.990	4.020	7.4	4.1	224.7	49.0
500	0.439	0.969	0.945	1.011	0.026	0.997	0.990	4.021	2.5	1.4	107.0	0.3
1000	0.428	0.969	0.945	1.005	0.037	0.997	0.990	4.021	2.1	1.1	107.3	<0.1
5000	0.424	0.969	0.944	1.001	0.023	0.998	0.990	4.020	1.7	0.9	95.7	<0.1

NOTE: CV = PRESS/ESS denotes leave-one-out cross-validation; ESS denotes error sum of squares; and PRESS denotes predicted ESS.

tabulations report selected summary output from the simulation experiment. One finding gleaned from this table is the well-known confirmation that SRS yields results that improve in accuracy and precision by increasing sample size n, with trajectories converging upon their corresponding population parameter values. Another corroborated well-known finding is that stratified RS is capable of furnishing more representative samples that can better estimate population parameters with smaller sampling variances; this trait, although not guaranteed to arise, holds for the relatively larger sample sizes sometimes utilized in soil science research, for example.

In closing this section, evidence exists endorsing the common practice of using stratified RS designs for more efficient data collection. However, the illustration in this section is for emphasis only; no inconsistencies exist between what design- and model-based approaches tell the scientific community (e.g., see [21], ([22], §13.2)). Ensuing sections of this paper substantiate that this property also extends to geographic sampling venues involving SA. As with the preceding exemplar, variance inflation occurs in SRS vis-à-vis stratified RS, a similar kind to that discussed by Griffith [17], Plant [18], and Wang et al. [19], and denigrated by Brus [1].

3. SA Effects in Spatial Sampling Designs

The three preceding instructional simulation experiment studies establish a foundation for examining effective geographic sample size, following in the footsteps of Fisher [23] (p. 506) when he mentored Tedin [24] to confirm SA impacts upon variance estimation within the context of randomization [25]. Probability sampling in general encounters correlation in at least three distinct ways. First, if RS is without replacement and from a finite population, then, for a population of size N, the sampling probabilities become increasingly conspicuously conditional probabilities with each draw, decreasing in magnitude from 1/N to 1/(N − n). This change in probabilities results in a modified classical CLT in which the square root of the correction factor (N − n)/(N − 1) pre-multiplies the conventional standard error [26] (p. 24), especially for samples of size n/N > 5%. Of note, however, is that these draw-by-draw selection probabilities do not impact the properties of a final simple random sample in the design-based setting because estimator calculations use inclusion probabilities instead. A second correlation source is RV attributes in a typical multicollinearity setting. One of its widely recognized consequences is variance inflation of, for example, linear regression standard errors. Third, if RS draws correlated observations, such as matched pairs or those tied together with spatial or temporal (or other, such as social networking) dependencies, then the sample size or degrees of freedom arguably are not what they naïvely appear to be. An extreme example of this possibility is to augment an original sample of size n with itself (with survey nonresponse/suppression substitutions from responses or imputations being a less hypothetical version of this possibility), creating an enlarged sample of size 2n comprising n perfectly correlated pairs of observations—this is the theme of §2.1; not only does this sample, whose size is artificially inflated by repetition, fail to contain any new information after duplication, but its unbiased variance estimate, for example, also is incorrect, at least for small sample sizes. This situation epitomizes the underpinnings of an effective geographic sample size concept.

3.1. What Some Experts Say

Brus [1] comments that Griffith [17], Plant [18], and Wang et al. [19] advance misconceptions about sampling variance in the presence of SA. However, many other scholars address the effective sample size (i.e., the number of equivalent iid observations/degrees of freedom) concept; §2.1 alludes to this view, with Table 1 documenting a carefully crafted but intentionally bogus sample composition numerically illustrating it. Furthermore, in classical statistics, matched/correlated/paired/dependent observations constitute routine practice that treats 2n as n observations (see §2.2), frequently measurements taken before and after some intervention/event/treatment; their latent pairwise correlations reduce them to an effective sample size of n. This size reduction is true for both parametric and nonparametric techniques evaluating the same statistical null hypothesis. Its correlation is a feature of both a random sample—as a sample statistic—and its parent population—as a parameter. One generic statistical product is a suite of problem-specific statistical techniques that properly analyze such correlated observations.

Spatial scientists are among those scholars acknowledging correlated data impacts, even ones pertinent to sampling designs (e.g., [27]). Cressie [28] (pp. 15, 272–273) discusses the equivalent number of independent observations, noting that SA has impacts in both small and large sample contexts. Shabenberger and Gotway [29] (pp. 31–34) pursue this SA effect on statistical inference lines of reasoning. Clifford et al. [30] (p. 123) initiated a sequence of papers presenting a similar inspection of the Pearson product–moment correlation coefficient for georeferenced RVs in terms of degrees of freedom; this effort helped spawn other papers, such as several by Acosta and Vallejos (e.g., [31,32]). Ditulleul et al. [33] broaden this treatment to embrace the linear regression multiple correlation coefficient. Dale and Fortin [34] investigate two related SA effective sample size adjustments for correcting statistical tests applied to data collected with one-dimensional sampling schemes, such as the transects used in plant ecology. Finally, although not comprehensively, Renner et al. [35] extend this notion to Poisson point process models. To these publications can be added one by de Gruijter et al. [36], as noted in Brus [1]. Although this appeal to authority logic is not definitive, most notable is that each member in this community of autonomous thinkers more or less individually derived similar conclusions. Therefore, the expert opinion it represents bolsters claims by Griffith [17], Plant [18], and Wang et al. [19], helping to rebuff objections by Brus [1].

In summary, a diverse group of researchers, many of whom are recognized spatial statistics experts, not just Griffith, Plant, and Wang and his article co-authors, promote the idea of effective geographic sample size. Acosta et al. [37] establish a sampling distribution framework for it, Acosta and Vallejos [31] expand it to regression, Vallejos and Acosta [32] expand it to multivariate spatial data analyses, with special reference to soils, and Acosta et al. [38] expand it to massive georeferenced datasets. Consequently, widely promulgated arguments by this assembly of academics warrant more detailed examination vis-à-vis Brus’s critique, which is one of the objectives of this paper.

3.2. About Variance

The analysis of SRS impacts upon a true spatially structured population variance estimate is complicated, more so than Brus [1] acknowledges (see Appendix A). More specifically, technically, Brus does not misrepresent the design-based definition of variance, although he overlooks that it is a definition the model-based approach does not accept. Griffith [17] emphasizes the variance inflation effects of SA. Plant [18] follows Cressie’s [28] (pp. 14–15) line of reasoning: a failure to account for positive SA in geospatial data produces a confidence interval that is too narrow. Cressie couches his statistical inference coverage contention within the context of effective geographic sample size (i.e., recapitulating its preceding definition, the equivalent number of independent observations [28] (pp. 15, 272–273)), noting that SA effects differ between internal (i.e., more pronounced impacts) and boundary/external (i.e., less pronounced impacts because of edge effects) locations when sampling in a geographic landscape.

Table 3 alludes to, and the ensuing

Table 4. Sampling design comparisons in the presence of SA: a specimen 200-by-200 regular square tessellation geographic landscape; Y~N(μ = 25, σ = 5); 10,000 replications.

n	CLT: ${\mathsf{\sigma }}_{\overline{\mathrm{y}}}^{*}$	Near-Maximum Positive SA (MC ≈ 1, GR ≈ 0.03)			Near-Zero Positive SA (MC ≈ 0, GR ≈1)			${\left(\frac{{\hat{\mathsf{\sigma }}}_{\overline{\mathbf{y}}}^{*}}{{\hat{\mathsf{\sigma }}}_{\overline{\mathbf{y}}}}\right)}^2$
		Stratified RS		SRS	Stratified RS		SRS
		$\overline{\overline{\mathrm{y}}}$	$s_{\overline{\mathrm{y}}}$	$s_{\overline{\mathrm{y}}}$	$\overline{\overline{\mathrm{y}}}$*	$s_{\overline{\mathrm{y}}}^{*}$	$s_{\overline{\mathrm{y}}}^{*}$
25	1.000	24.99683	0.42343	1.01057	24.98502	0.99711	0.99236	5.54527
64	0.625	25.00073	0.19666	0.62203	24.99690	0.62707	0.62656	10.16717
100	0.500	25.00156	0.13642	0.50118	24.99648	0.50005	0.50507	13.43602
400	0.250	25.00080	0.05437	0.24656	25.00249	0.24988	0.24887	21.12245
625	0.200	25.00006	0.04171	0.19917	24.99697	0.20093	0.19827	23.20648
1600	0.125	24.99974	0.02448	0.12267	25.00148	0.12364	0.12104	25.50910

NOTE: increasing the replications to 100,000 results in trivial changes; increasing n to 90% of the population size still retains the correct finite population correction factor variance.

demonstrates, this conception in terms of stratified RS. Further reinforcing it, Webster and Oliver [20] (p. 33) spotlight that

• If there is any spatial dependence then [the pooled within strata variance] will be less than s², and so the variance and standard error of … stratified [RS] will be less than that of a simple random sample for the same effort, the same size of sample. … If we were happy with the precision achieved by [SRS] then we could get the same precision by stratification with a smaller sample [size]. Stratified [RS] is more efficient by the [multiplicative] factor

[n_random/n_stratified],

a fraction resembling the model-based inference design effect outlook sometimes translated into the equivalent sample size of SRS with the same standard error as the employed stratified design—this is the effective geographic sample size of interest in this paper. This ratio Webster and Oliver report is analogous to the one appearing in Table 1, and, as stated, relates to the effective sample size perspective. Furthermore, in the earlier first edition of their book, they state that [20] (p. 33) “There is another disadvantage of systematic sampling. The method gives no entirely valid estimate of the sampling error [i.e., sampling variance], since the sampling points are not located at random within the strata. Nevertheless, there is considerable empirical evidence to show that systematic sampling is more precise than [SRS].” Again, they advocate for approximate methods to estimate a variance component in the presence of SA. As before, an effective sample size, in turn, is computable using such estimates.

In summary, Webster and Oliver, among others, highlight the well-recognized design-based systematic sampling weakness that it does not provide a correct variance estimate when SA prevails, bringing into question the universality of what is known as variance. Because the general meaning of this term is well established in statistical theory and practice, with a presumed uniformly recognized interpretation, the communication problem arising pertains to one that avoids referring to focused forms of this calculated quantity without a qualifier. The source of design-based variance is solely sampling, and its emphasis strictly is on unbiasedness—Appendix A outlines the comparative situation for design- and model-based inference. Meanwhile, Rubin [39], for example, argues that Bayesian statistics offers yet another focal definition of variance. Therefore, attaching the phrase “effective sample size” to a variance, which also has an established interpretation even if its corresponding variance is not a true variance, is more appropriate. Accordingly, Brus [1] is mistaken in his failure to recognize this distinction. To their credit, Webster and Oliver point out a different sampling design contrast of it in each edition of their book, as the two preceding quotations attest.

3.3. Classical CLT Stipulated Calculations and $\overline{y}$ Behavior in the Presence of SA

Further pursuing geographic variance complications, this section sketches a findings assessment for a fourth Monte Carlo simulation experiment, one pertaining to both conventional simple and unconstrained RS, and now focusing on the sampling distribution of some RV Y’s mean, $\overline{\mathrm{y}}$, whose estimation is often the intention of a study (but perhaps in its nonconstant regression version). The source correlation is SA latent in a given attribute. Regardless of whether or not a geographic distribution contains SA, classical RS with (out) replacement creates a sampling distribution described by the CLT, or its modified adaptation incorporating a finite population correction factor, both of which can embrace variance inflation. Dozens of simulation experiments confirm this affirmation (e.g., Table 4). Therefore, SA does not impact computational aspects produced by SRS, even though it ignores the prevailing nonrandom mixture of phenomena across entire geographic landscapes, and overlooks both variance inflation and potentially poor geographic sampling coverage of this landscape (i.e., SRS of two-dimensional points from a coterminous region generates a Poisson distribution, with patches of over- and under-sampling). However, Table 1 and Table 2 validate that exploiting latent observational correlation in data harvests benefits; by extension, this is true for SA, as well.

Table 4 summarizes output from a simulation experiment in keeping with Overton and Stehman [40]. The synthetic georeferenced attribute is proportional to the second eigenvector of a doubly centered spatial weights matrix constructed with the rook adjacency definition [41] for a large regular square tessellation containing 40,000 pixels (i.e., near-maximum positive SA). The smallest sample size represents roughly the minimum acceptable expedient sample size for which one can begin to invoke the CLT; i.e., one nearly equal to 30 that still conveniently allows the surface partitioning tessellation strata to have an equal number of pixels. The largest is close to, but less than, the maximum allowable sample size without needing to apply a finite population adjustment factor when sampling without replacement; i.e., an n still satisfying the 5% sample size upper limit constraint for finite populations. The sample sampling distribution means are nearly identical to their parent population mean, as anticipated. The sample mean standard errors are nearly identical to those given by the CLT for the zero SA dataset: stratification does not alter SRS outcomes for a completely random mixture of values. In contrast, the nonzero SA tessellation stratified dataset shows dramatic variance reduction (see the preceding section).

This consequence is as expected. Sample entry drawings involve an independent selection process that ignores SA. Accordingly, the presence of either zero or non-zero SA does not alter the resulting composite sampling distribution, as Brus [1] (p. 687) underscores, preserving the CLT’s description. As the preceding sections ultimately imply, it may shuffle a sample composition selection ordering, rearranging where specific samples place themselves within their sampling distribution, without affecting the resulting aggregate mean, variance, or bell-shaped form. Nevertheless, SA does indirectly, if not directly, impact any such sampling undertaking, as the already mentioned tessellation stratified RS results indicate; the CLT fails to render the true sample mean variability. Acknowledging SA means recognizing its variance inflation repercussions, which is the georeferenced data element referred to by Griffith [17], Plant [18], and Wang et al. [19], and dismissed by Brus [1]. It is not a misconception or confusion. Instead, it is a detection of a data ingredient that can compromise statistical inferences, with the magnitudes appearing in Table 4 implying serious corruption given variance inflation factors as large as nearly 26 (exceeding the threshold values indicating problematic, let alone serious, concerning, or considerable, collinearity [42,43,44]). As the strata shrink in size, this inflation factor increases because the degree of SA retained in samples concomitantly increases (i.e., the average distance between adjacent strata pixels decreases); nonetheless, even n = 25 (i.e., strata sizes of 1600) reflects a concerning level of variance inflation.

Given Table 4, and letting κ be the variance inflation factor, for the coarsest strata geographic resolution case of n = 25, the SRS arithmetic mean standard error may be written as κ(5/κ)/5 = 1, whereas the SA adjusted variance is approximately (5/κ)/5 ≈ 0.42. This second equivalence implies that κ ≈ 1/0.42 ≈ 2.4, which is a variance inflation factor of the same degree as found in §2.1 by artificially doubling a sample size. Thus, its effective geographic sample size, say n*, is roughly 4.5.

4. Alternative Sampling Designs and Model-Based Inference

For a variety of reasons, not all data collection profits from, nor do collected data automatically relate to, SRS or its alternative data randomization procedures. Correlated data in general, and the presence of SA in particular, furnish(es) one justification for departure from an all-encompassing exploitation of randomness.

When planning data collection, a principal reason to sample is to engage in an efficient and effective use of finite resources while surveying a population. A sample size n should be large enough to make a statement about given parameters describing its parent population with a pre-specified precision and a stipulated resources cost. The arithmetic mean CLT, for example, enables such an outcome. However, researchers end up with only a single, but not necessarily a typical, sample, whose data also may need to display bonus salient features to bolster its value. Seeking such desirable add-ons motivated the invention of more sophisticated designs, such as stratified RS, whose important supplemental quality is improved representativeness (see Table 3 and Table 4)—chiefly by reducing the selection probability of certain anomalous sample composition possibilities, sometimes to zero, while (perhaps uniformly) increasing the probability of all achievable samples.

After collecting data, whose gathering was potentially in some non- or constrained random fashion (e.g., its sampling design deviates from SRS), a researcher has the option to shift to model-based inference. Relocating the all-important random aspect for scientific research from probability sampling to the obtained attribute values themselves, a sample becomes a realization of a joint distribution of RVs, the superpopulation, a notion apparently first put forth by Cochran [26], and the fundamental basis of most time series analyses as well as MCMC methods especially popular in Bayesian map analysis and frequentist spatial statistics. In its traditional version of this context, variance estimation derives from OLS theory, and thus, variance heteroscedasticity replaces known, and appealingly equally likely, probabilities as the primary worry. The resulting inferential basis has a model validity foundation, emphatically accenting the adequacy of its description via goodness-of-fit and other diagnostics. Randomness here stems from the assumption of the existence of a superpopulation, and hence some stochastic process producing an observed realization, not from a sampling design. SRS requires independent probabilities in its selection of observations (e.g., all possible samples of size n have an equal probability of being selected), whereas this model-based approach requires independence among the observations themselves; accordingly, the presence of nonzero SA necessitates the adoption of appropriate techniques to account for it. Although they are functional in their individual forms, coupling design- and model-based strategies has at least one synergistic advantage, namely that their combination allows inferences to be robust with respect to possible model misspecification.

4.1. Some Reasons Why Designs Utilize Other Than Simple/Unrestricted RS

In response to representativeness needs, statistically informed experimental designs embracing more than RS strive to plan data collection efficiently and effectively, within a sampling framework, in such a way that subsequent statistical analysis of any sampled data yields valid and objective statistical inferences. In doing so, each strategy essentially pre-determines the appropriate statistical techniques for subsequently analyzing data collected with its implemented strategy. Balance frequently is one of the important elements: an equal number of observations drawn from various segments of a population to enhance statistical power, to improve efficiency of sampling estimates, and to create certain data analytic orthogonality conditions. Unbalanced data have a skewed distribution of observations across targeted population subgroups, with methodologists habitually describing such unbalanced datasets as being messy [45]. Areal unit dependencies (e.g., SA) and/or nonlinear relationships (e.g., the specification and estimation of auto- models [46]) tend to permeate such untidy sample data, a common hallmark of observational studies, increasing the risk of promoting inexplicable model specifications (e.g., re the spatial autoregressive critique by Wall [4]). A balanced geospatial sample data assemblage scheme relates directly to the Horvitz–Thompson estimators, for which balance ensures that picked auxiliary variable sample totals are the same or almost the same as their true population counterparts. Balance introduces the importance of a design establishing a suitable sample size for achieving not only satisfactory population coverage (e.g., a need for the full range of interpoint distances to estimate a semivariogram model; see [47]), but also a particular degree of statistical power.

Real-world sample data also tend to be what methodologists label dirty (i.e., are incomplete and/or include outliers/anomalies; e.g., [48]). Such data may contain corruptions from inaccuracies and/or inconsistencies, or may mandate variance-stabilizing transformations, both of which necessitate remedial action by an analyst. This context certainly impacts any determination of the appropriate subsequent statistical techniques for analyzing data collected with an implemented plan. SA plays a role here, as espoused by, for example, Griffith and Liau [49]. Geostatistical kriging, which exploits SA, symbolizes the importance of missing data imputation.

An adequate sample size, vis-à-vis statistical power [50], combines with methodologists’ impressions of noisy data: numerical facts and figures characterized by unsystematic uncertainty/variability/stochastic error, containing obscured/masked trends of various degrees that conceal a true alternate hypothesis. This issue partners with the contemporary debate about substantive significance (e.g., [51]), namely the size of a(n) effect/relationship, and statistical significance, which entails detailed description of the nature of the uncertainty involved. Both an extensive literature and practice exist devoted to computing sufficient sample sizes for the uncovering of a precise size effect. Effective geographic sample size explicitly addresses this magnitude of difference between a posited null and its affiliated alternative hypothesis, as well.

Although these few dimensions of experimental design are not comprehensive, they demonstrate the relevance and importance of acknowledging, and even accounting for, the presence of non-zero SA when engaging in RS. Each is outside the purview of the CLT. However, each is capable of having a profound influence upon the execution of RS, highlighting the importance of this paper’s focus.

4.2. Some Reasons Why SA Encourages Model-Based Inference

In model-based inference, each real-world y_i is a random, rather than a fixed (as in design-based inference), quantity (see Appendix A). Now the random component comes from stochastic processes affiliated with RV Y in a superpopulation, in lieu of SRS. This model-based conceptualization presents the following two different inference problems pertaining to: (1) the realization mean, $\overline{\mathrm{y}}$, which varies from realization to realization in a way analogous to how this calculation varies across all possible SRS samples of size n; and, (2) the superpopulation mean counterpart to $\overline{\mathrm{y}}$, namely μ. The simplest descriptive model specification (i.e., no covariates) posits Y = μ1 + ε, where Y, 1, and ε are n-by-1 vectors, with all of the elements of 1 being one, and the elements of ε being drawings from a designated probability model (e.g., normal) with a zero mean—because scalar μ already is in the postulated specification—and finite nonzero variance; this is the case treated by Griffith [17]. It spawns a $\overline{\mathrm{y}}$ estimate with an attendant superpopulation variance estimator that simplifies to the one for SRS applied to an infinite population (i.e., no correction factor; hence the approximation variety for finite populations having n ≤ 0.05N) [52] (p. 43).

The presence of non-zero SA for the covariate-free specification alters OLS to GLS estimation for model-based calculations. The preceding linear model specification remains the same, whereas the variance estimation changes from

(Y − μ1)^TI(Y − μ1)/(1^TI1) to (Y − μ1)^TV⁻¹(Y − μ1)/(1^TV⁻¹1),

where, respectively, n-by-n matrix I denotes the identity matrix and V denotes the SA structure operator instilling geographic covariation. This conversion signals the importance of whether or not matrix V ≠ I matters when implementing SRS. Both expert opinion and content in Table 3 and Table 4 imply that it does.

4.3. A Monte Carlo Simulation Experiment Investigating Design- vs. Model-Based Inference

Brus [1] (p. 689) claims that Griffith [17] and Plant, per [18], perhaps among others, brand the classical SRS variance formula for $\hat{\mathsf{\mu }}$ as underestimating the true σ² in the presence of SA (see §2). His contention compels an exploration of the meaning of underestimation in terms of the way he uses the word, which, in part, becomes conditional upon the extent or scale of the geographic landscape in question. Table 4 already illustrates that variance estimation is insensitive to a change in sampling design from SRS to stratified RS when an attribute variable exhibits a purely random mixture geographic distribution Moreover, if strata are ineffective (e.g., they capture the presence of zero SA) in a stratified design, the estimated variance is expected to be the same as that for SRS. However, if these strata are effective (i.e., they capture prevailing non-zero SA, grouping within each stratum units that had roughly similar y-values), then the stratified variance estimator would capture the improved precision of the estimated mean achieved by this stratified design. Although design-based inference does not assume that all populations are random with no structure, the design-based variance estimators properly take into account features of strata and/or clusters. This is not the outcome when positive SA prevails because similar values cluster on its map, recurrently materializing as a conspicuous two-dimensional pattern, catapulting the notion of variance inflation—the only SRS variance estimation declaration made in Griffith [17]—to the forefront of SA distortion concerns (see Table 4).

For generalizability purposes, the fifth simulation experiment employed a moderate, rather than pronounced, degree of positive SA, and only the fairly universally agreed upon minimum sample size of 30. Its output is sufficient to exemplify that applying SRS to geospatial data containing SA for only a subregion of a larger landscape can cause underestimation of the variance, even though this same estimator furnishes an accurate variance estimate when applied to the entire parent geographic landscape under study (see

Table 5. SRS variance estimates for landscape-centered quadrant-of-the-plane subregions of a larger complete geographic landscape; 10,000 replications.

n	Data Type	Standard Deviation					Levene Test Probability
		Landscape-Wide	Q1	Q2	Q3	Q4	$\overline{probability}$	% < 0.10
population	---	5	5	5	5	5	1	---
realization (superpopulation; n = 40,000)	iid	5	5.01	4.98	5.03	4.97	0.64	---
	SA	5	4.09	4.09	4.06	4.11	0.69	---
30	iid	4.95	4.99	4.95	4.99	4.94	0.49	10.5
	SA	4.96	4.06	4.05	4.02	4.08	0.49	10.2

NOTE: Q_j denotes the j^th customary quadrant of the plane, in a counterclockwise direction; for iid data, MC = 0.00 and GR = 1.00; and for SA data, MC = 0.50 and GR = 0.50.

), whose boundaries almost always are unknown. In this context, both sets of variances conform to regular mathematical statistical theory, such as correct Type I error probabilities (see Table 5). A clustering of similar values when SA prevails reduces geographic variation within a subregion—paralleling the preceding stratified RS, with a region in this circumstance mirroring an individual stratum in that instance—while increasing contrasts among the given subregions (i.e., SA reduces within region, while increasing between regions, geographic variance); these discrepancies account for the missing components empowering SA to decrease the regional variation reported in Table 5. Trying to align a study area with its true but indeterminate larger scale landscape is all but impossible, explaining why variance underestimation, such as that critiqued in Brus’s [1] comments, may well occur. In effect, an analysis unknowingly is of a subdomain: estimated variances tend to vary over the different subdomains, with these subdomain variances not matching the variance estimated for samples from the full study region. A strategy for correcting this situation is becoming aware of the existence of such subdomains, after which design-based methodology certainly exists for properly handling them.

In summary, latent nonzero SA means that geotagged attribute values exhibit a two-dimensional organization deviating from the unpredictability depicting a fully random mixture of values. This data trait, in turn, can result in an incorrect identification of a target population, resulting in SRS producing an underestimation of the attribute’s variance. The elusiveness of almost always invisible geographic landscape boundaries argues for taking SA into account when sampling and analyzing geospatial data, and consulting model-based methodology for a reminder about helpful tools, such as effective geographic sample size, to which stratified SA also alludes.

5. The Role of iid in Sampling Designs

Preceding discussion tackles observational independence issues, the first letter in iid, with this initial i signifying that multiplication with either individual sample or population marginal probabilities is well-founded; this section mostly concentrates on the remaining id part of iid. Brus [1] (p. 289) states that “… in statistics [iid] is not a characteristic of populations, so the concept of iid populations does not make sense.” At best, this announcement seems intransigent, mainly given that mainstream mathematical statistical theory deriving the CLT that supports SRS statistical inference considers iid to be a pillar of SRS theory, whereas techniques such as Monte Carlo simulation and MCMC can couch superpopulations within the same framework category. Invoking this property allows the statistical/sampling distribution of the arithmetic mean, $\overline{\mathrm{y}}$, to have asymptotic convergence to a normal distribution with increasing sample size, n. In addition, iid enables an analytical computation of the rate of convergence across different RVs, a valuable input for deciding upon a SRS design value for n. Hoeffding [53] posits a moment matching theorem establishing the convergence in probability of density functions, which pertains here: if skewness asymptotically goes to zero, and kurtosis asymptotically goes to three (i.e., excess kurtosis asymptotically goes to zero), then the sampling distribution under study closely mimics a normal RV probability density function (PDF), one described by the CLT.

SRS from an infinite normal RV population is the most straightforward illustrative case. This RV’s moment generating function (MGF) is M_Y(t) = ${\mathrm{e}}^{\mathsf{\mu }\mathrm{t}+{\mathsf{\sigma }}^2{\mathrm{t}}^2}$. Its accompanying arithmetic mean MGF is ${\mathrm{M}}_{\overline{\mathrm{Y}}}(\mathrm{t})={\left[{\mathrm{e}}^{\mathsf{\mu }\mathrm{t}/\mathrm{n}+{\sigma }^2{\left(\frac{\mathrm{t}}{\mathrm{n}}\right)}^2}\right]}^{\mathrm{n}}=\left[{\mathrm{e}}^{\mathsf{\mu }\mathrm{t}+\left({\sigma }^2/\mathrm{n}\right)(\mathrm{t}{)}^2}\right]$, with the population iid property authorizing the product of the n individual observation MGFs as a power function. The resulting general sample MGF is that for a normal RV with a mean of μ and a variance of σ²/n, exact CLT outcomes. In other words, an n = 1 iid normal RV population sampling distribution achieves instant convergence, as the law of large numbers also confirms for samples of size n = 1. The question applied researchers find themselves asking, then, is how to detect the underlying RV nature of their data. Answering this question diverts them to an inspection of a histogram portrayal of their sample of attribute values, and hence often a goodness-of-fit test for the theoretical RV they hypothesize. Recognizing that determining an appropriate sample size for meaningful evaluation of normality is a difficult task (all goodness-of-fit diagnostics suffer from the following dual weaknesses: small sample sizes allow identification of only the most aberrant, whereas very large sample sizes invariably magnify trivial departures from normality, often delivering either statistically nonsignificant but substantively important, or statistically significant but substantively unimportant, inferential conclusions; accordingly, normality diagnostic statistics require a minimum sample size before they become informative; tests of normality have notoriously low power to detect non-normality in small samples). Graphs appearing in Razali and Yap [54] corroborate this contention; only normal approximations, the recipients of such assessments, exist in the real world, as conventional statistical wisdom purports that n needs to be between 30 and 100 for a sound statistical inference about a RV name. Razali and Yap [54] also furnish some contemporary wisdom based upon evidence from Shapiro–Wilk normality diagnostic statistical power simulation experiments: the minimum sample size for deciding upon an underlying RV appears to be about 250 (e.g., the chi-squared, gamma, and uniform RVs), and maybe more (e.g., the t-distribution RV) in order to maximize statistical power.

Table 6. CLT outcomes and analytical convergence rates for specimen RVs: Mathematica 12.3 output.

Feature	Normal	Exponential	Uniform	Sinusoidal	Mixture †
μ	1	1	1	1	1
σ	1/n	1/n	1/n	1/n	1/n
CLT skewness	0	0	0	0	0
CLT kurtosis	3	3	3	3	3
CLT skewness convergence rate	instant	−1/n3/2	instant	instant	−1/(8n)3/2
CLT kurtosis convergence rate	instant	−6/n2	6/(5n2)	3/(2n2)	−33/(40n2)

NOTE: the uniform RV interval is [1 − √3, 1 + √3]; sinusoidal = 2√2 B+(1 − √2), B~beta(½, ½); 25% of the examined mixture population units come from each specimen RV. ^† simulation experiment verification of findings using sample sampling distributions approximated with 300 samples of various sizes, and 1000 replications.

tabulates specimen results for a small array of RVs that span the complete spectrum of PDF forms, all with μ = 1 and σ = 1 by construction: bell-shaped, right-skewed, uniform, symmetric sinusoidal (i.e., U-shaped beta), and mixed (a blend of these previous four RVs). The first four of these table entries involve iid RV populations, with their analytics being expressions similar to the preceding normal RV power function. In other words, the sampling distribution MGF is ${\left[{\mathrm{M}}_{\mathrm{Y}}\left(\mathrm{t}/\mathrm{n}\right)\right]}^{\mathrm{n}}$ rather than ${\displaystyle \prod }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{M}}_{{\mathrm{Y}}_{\mathrm{i}}}\left(\mathrm{t}/\mathrm{n}\right)$—the more traditional mathematical expression that may be rewritten as a convex combination of separate orthodox PDFs (e.g., see Table 6)—representing sampled independent but non-id observations.

The nature of an iid population RV impacts the CLT convergence to normality with increasing n, in turn possibly establishing different appropriate minimum sample sizes for the SRS design-based sampling distribution of $\overline{\mathrm{y}}$ to adequately conform to a bell-shaped curve. This data analysis aspect is important for making proper design-based statistical inferences (e.g., the construction of arithmetic mean confidence intervals). Because population RV symmetry impacts the sampling distribution skewness rate of convergence, the focus here is on the kurtosis rate of convergence, which Table 6 documents as potentially fluctuating across RVs, justifying the need for RV-specific SRS minimum sample sizes. Some of these RVs have the increasing-n trajectory converging from above (e.g., exponential), whereas others have it converging from below (e.g., uniform and sinusoidal).

Research about non-iid RVs also has a long history, stretching back to its most cited early mixture publication by Pearson [10]. Zheng and Frey [55] ascertain that sample size, convex combination mixing weights, and degree of separation between component RVs impacts RS outcomes for a mixture RV. Sampling variance decreases with increasing sample size (that tendency from the CLT appears to apply; see Table 6), increasing separation between component RVs improves stability of RS results as well as increasing parameter independence. 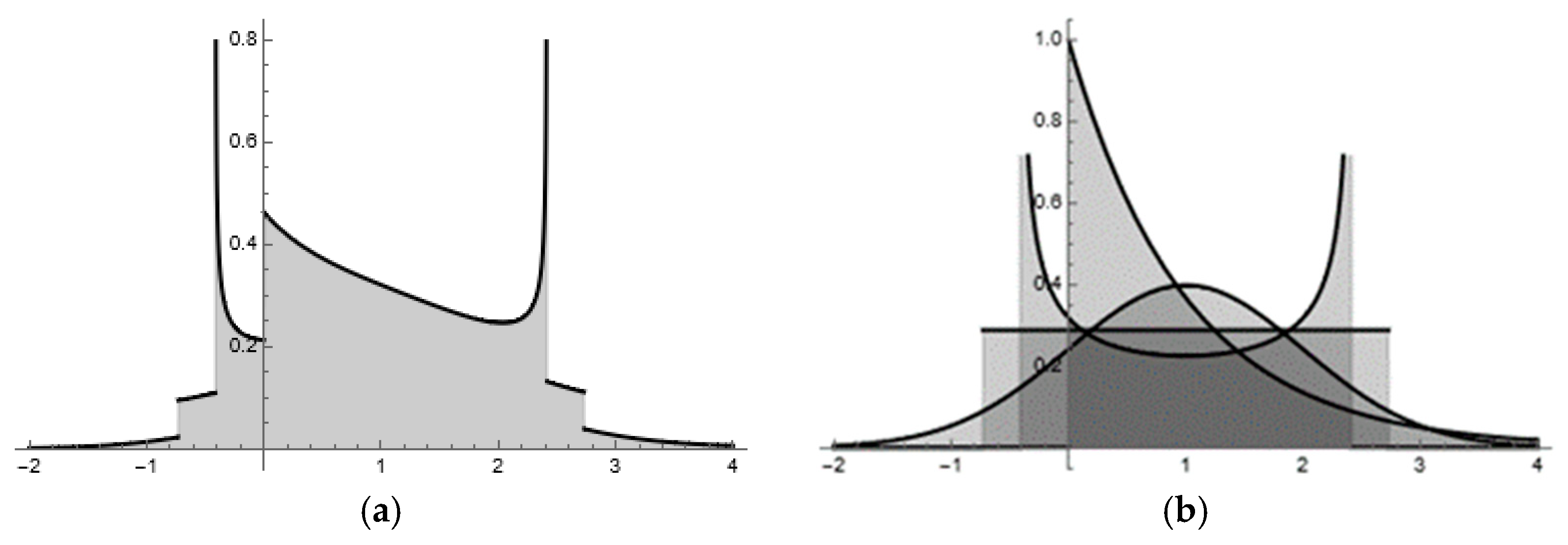Table 6 reports results for a mixture [56,57,58,59] of different RVs [here the respective population weights attached to RVs are the same, namely ¼, in the mixture PDF convex combination (Figure 1a), from which SRS drawings are made], partly illustrating that a principal consequence of non-iid population RVs (i.e., population heterogeneity)—here they vary by only their respective natures, not their means or variances (Figure 1b)—is induced by a correlation between pairs of sample means and variances [60], and a conceivable breakdown of part of the SRS-based CLT theory attributable to ‘a “bulge” in the confidence interval in the region of cumulative probability representing the inflection point between [RV] components’ [55] (p. 568) that is capable of shrinking or inflating a confidence interval. Thus, maintaining inferential integrity requires remedial action that aims to stabilize variability and uncertainty estimates for larger sample sizes, such as resorting to bootstrapping techniques [55]. For example, given the four familiar specimen RVs in Table 6 (see Figure 1b for a portrayal of their overlaid supports), their respective asymptotic sample size trajectories enter the considerably narrow kurtosis interval of 3 ± 0.049 with concomitant sample sizes of 1, 123, 25, and 31, which essentially is in keeping with conventional wisdom.

Meanwhile, the designated specimen mixture RV has a theoretical mean and variance of one, skewness of 0.5, and excess kurtosis of 0.825, naively designating it as a leptokurtic RV; however, Figure 1a pictures otherwise. This concocted mixture has virtually no separation of components (Figure 1b). It encounters a serious drawback vis-à-vis minimum sample size because mixture RVs: (1) have convergence rates that are a linear combination of those for their separate component RVs—after appropriate mixing weight substitutions, Table 6 entries become simplifications of expression −3(5p_N + 25p_E + p_U − 5)/(10n²), where p_N, p_E, and p_U, respectively, denote the mixing weights attached to the normal, exponential, and uniform RV components [i.e., p_S = (1 − p_N − p_E − p_U) for the sinusoidal RV]; (2) almost always encompass unidentified component RVs; and, (3) usually entail unknown mixing weights. These first two points jointly mean that the largest component RV minimum sample size defines n for ensuring that the CLT begins to regulate a sampling distribution; hence, n often tends to be near the end, rather than the beginning, of the routine n = 30–100 range. Meanwhile, the set of mixing weights, p_j, follows a multinomial distribution, impacting the minimum sample size when one goal of a sampling design is to draw a sample composition closely proportional to the prevailing set of mixing weights (i.e., representativeness—avoiding the 14 medleys other than at least one observation from each RV—unattainable with stratified RS because of ignorance about mixture properties). Accordingly, the smallest p_j harmonizes with one of the escorting RV convergence rates to delineate a suitable minimum sample size; e.g., invoking the 6σ principle, if the minimum p_j is 0.05, then, for example, 0.05 − √[(0.05)(0.95)/n] = 0.04 ⇒ n = 2850 ⇒ N ≥ 57,000 (magnitudes more akin to those for the law of large numbers). In other words, suppressing the id part of the iid assumption tends to increase the necessary minimum sample size, exemplifying the notorious inclination for mixture RVs to present statisticians with serious technical challenges.

In general, CLT convergence still occurs if either a single dominant RV subsample size, n_j, or the cumulative component n_js (i.e., these subset sizes sum to n) across RVs, goes to infinity. Unfortunately, when mixture distribution inflection points occur at component RV means, CLT-based confidence intervals can become distorted, which is one of the prominent examples of technical challenges arising when dealing with this category of RV [55]. Furthermore, without iid, the critical RV assumptions revert to a finite mean and a finite variance; without id, distinctiveness of component RVs may become critical, and SRS sampling variance can deteriorate. Nonetheless, among its inventory of well-known properties, the classical CLT still fails to preside over a mixture containing a Cauchy RV.

6. Discussion, Implications, and Concluding Comments

Contrary to assertions by Brus [1], SA in sample data does inflate the sample variance, whether inference is design- or model-based. Table 1 demonstrates this feature by displaying some simple simulation experiment results. Brus defines the sample variance to be that given by the classical formula for SRS RVs no matter what the degree of autocorrelation, and according to this definition, the sample variance is cast as being independent of autocorrelation; but this is not a particularly useful definition. Because, as the spatial statistics literature repeatedly emphasizes, each sample in a spatially autocorrelated dataset provides some information about the attribute values of its neighbors, a sample from such a dataset provides less information than would an equal sized sample of independent observations. Consequently, numerous distinguished statisticians offer methods for estimating an effective sample size, which provides a measure of the effect of SA on the precision of a chosen sample. This paper furnishes additional evidence corroborating this expert opinion. Additionally, knowledge of this quantity can provide useful information in the devising of future georeferenced sampling ventures. In the meantime, merging the design- and model-based perspectives, we proposed the following more comprehensive definition of effective geographic sample size: the number of equivalent iid or SRS geotagged observations that account for variance inflation attributable to SA uncovered by, respectively, the redundant information made explicit in spatial model specifications, or the tessellation stratified RS design effect made explicit in this geographic sampling plan [61].

A classical statistics problem paralleling this SA complication occurs when a sample collection takes place at the same location but at different dates following either a before and after controlled intervention, or a repeated measurements, protocol. A sample collected at n locations according to one of these two protocols has a size n, even though it contains 2n observations, the very essence of effective sample size.

According to Brus [1], the concept of iid RVs applies only to samples, and not to populations. Again, this is a case of developing a definition to suit one’s own purposes. By definition, any sample is a subset of a population, and if every sample drawn from a given population is iid, then one can consider iid to be a property of that population. A cursory inspection of the mathematical statistics literature reveals that this characterization is a pilar of the CLT. In addition, the spatial structure of a population is important when deciding about which sampling scheme to adopt. SRS is only one of many different forms of spatial sampling, examples of which are replete in the literature, as well as mentioned in a forgoing section of this paper. SRS frequently performs rather poorly in terms of individually selected samples drawn in realistic situations when compared with competing designs, a comparison well known and consistently true about both the design- and model-based approaches, because of certain SA effects; simulation results reported in this paper corroborate this claim.

The presence of SA in a dataset often motivates a model-based approach to analysis, for both practical and theoretical reasons. Webster and Oliver [20] show that the most efficient sampling pattern is that conducted using a regular hexagonal grid (i.e., tessellation stratified RS following the US EPA EMAP design), which geographically spaces nearer sample points to the greatest extent possible. A square grid is almost as efficient. Analyzing such a grid sample, if its locations in the sampled domain are random, may use a design-based procedure, but the organization of spatially autocorrelated data favors a model-based analysis. In particular, SRS from even mildly autocorrelated data can lead to both an inefficient estimate of a regional arithmetic mean, as well as an underestimation of the accompanying regional geographic variance. Simulation experiments summarized in this paper also verify these contentions.

Further simulation experiments demonstrate that the presence of SA does not alter a SRS sampling distribution. Nevertheless, ignoring SA risks failing to recognize the latent variance inflation that it induces. Accordingly, both theoretical and practical considerations frequently weigh against the use of SRS in the collection of data known or suspected of possessing a high degree of SA, and in the context of the frequently asserted dichotomy between model- and design-based analysis, this preference implies the use of a model-based analysis. Moreover, as noted in a preceding paragraph, numerical experiments demonstrate that applying SRS to a subregion of a larger geographic landscape can, if the data are spatially autocorrelated, result in an underestimation of the variance, even though this same estimator furnishes an accurate variance estimate when applied to the entire parent geographic landscape under study. Clearly, a need exists for a better appreciation and demystification of differences between design- and model-based inference. With regard to the controversy addressed in this paper, Brus [1] appears to complain more about fundamental design- rather than model-based approaches to spatial sampling, a crucial distinction he himself also previously recognized [14].

A final theme warranting commentary here is the phrase “model assisted estimators” that Brus [1] (especially pp. 37–38) uses, which seems very much akin to, for example, Griffith’s [17] (especially pp. 753–755) “model-informed, design-based” conception. Griffith’s contention [17] maintains that SA plays an important role if a researcher wants to pre-determine sample size with statistical power in mind. This viewpoint reflects Brus’s [1] model-assisted assertion that combines probability sampling and estimators built upon superpopulation models in order to realize a potential increase in the accuracy of design-based estimates. He discloses that the model-assisted approach relates to variance estimators exploiting auxiliary information correlated with the target variable of estimation (e.g., Y), such as SA, which Stehman and Overton [62] link to geographic tessellation stratified RS to secure more representative spatial sample outcomes (i.e., an estimator of a mean with a smaller standard error) in the presence of SA (e.g., how to incorporate unequal inclusion probabilities when hexagonal strata vary in size). Considerable consistency seems to exist here between what were labeled model-informed and model-assisted constructions.

In summary, the planning of a sampling campaign must, if it is to make optimal use of expended resources, employ all available information in designing its sampling scheme. The widespread undertaking of pre-sampling sample size determination exercises confirms that failure to incorporate informative calculations, whose practical usefulness was demonstrated in innumerable previous studies, simply because these calculations fail to satisfy an artificially constructed theoretical standard, can only detract from the effectiveness of these plans. More generally, acknowledging the broader contextualization of this problem, this paper bolsters the defense of spatial statistics/econometrics. More specifically, it rebukes debatable contentions posited by Brus [1], among others, furnishing further clarification about them.