1. Introduction
Observational studies are important for evaluating causal effects, especially when randomization of treatments is unethical or expensive. Valid inferences about causal effects from observational studies can only be drawn by controlling for all confounders, that is, pre-treatment variables that are related to both treatment allocation and the outcome, because the treated subjects generally differ systematically from the control subjects. For example, sicker HIV patients are more likely to take antiretroviral treatments to control the virus when their CD4 cell counts drop too low. The CD4 cell count, a measure of how well the immune system functions, is one clinical measure of the effectiveness of an antiretroviral treatment. Direct comparison of the CD4 counts between the treated and the control would lead to the false conclusion that antiretroviral treatments result in lower CD4 counts. Thus, to assess the effects of using antiretroviral treatments on the CD4 counts from an observational study, such as the Multicenter AIDS Cohort study (MACS) [
1], appropriate statistical methods are needed to remove confounding by patient characteristics.
To deal with confounding by patient characteristics, the propensity score, the conditional probability of assignment to a treatment given the observed covariates, is commonly used. Rosenbaum and Rubin (1983) [
2] showed that controlling for the propensity score is sufficient to remove bias due to differences in the observed covariates between treatment groups. The propensity score summarizes the observed covariates into a single measure and serves as a dimension reduction technique. Due to the balancing property of the propensity score, the treated and control subjects with similar propensity scores can be directly compared [
2]. For example, in our application, because sicker patients were more likely to be treated, we can adjust for that by controlling for the patient’s probability of receiving treatment given all observed histories prior to treatment. After controlling for the propensity score, the distribution of the observed covariates, in this case, the proportion of sicker patients, will be similar between the treated and the control subjects, so the CD4 counts between the treated and the control subjects with similar propensity scores can be compared.
More generally, propensity-score-based methods first estimate the probability of treatment assignment given potential confounding variables, and then use the estimated treatment probability in weighting, or as a predictor in regression models for the outcome under alternative treatment assignments. Inverse-probability of treatment weighting (IPTW) controls for confounding by weighting subjects by the inverse of the estimated probability of receiving the observed treatment. The weights in effect create a pseudo-population that is free of treatment confounders. The IPTW estimator is consistent if the propensity score model is correct. Like IPTW, augmented IPTW estimation (AIPTW) uses the estimated propensity score as a weight but incorporates predictions from a regression model for the outcome. The AIPTW estimator consistently estimates causal effects if the propensity score model is correctly, or the outcome model is correctly specified. Both IPTW and AIPTW estimators are based on the Rubin (1974) [
3] causal model framework. As such, the estimators are consistent under the causal model assumptions that there is no interference across units (stable unit treatment value assumption, SUTVA), that each unit has a non-zero probability of being assigned to either treatment group (positivity) and there are no unmeasured confounders (ignorability) [
3]. Here, we mean robustness to mis-specification of the covariates in regression models, rather than robustness to outliers in the residuals. That might be achieved by replacing the assumption of normality in the distribution of errors by a longer-tailed distribution, such as Student’s t [
4].
Another recently developed method, Penalized Spline of Propensity Methods for Treatment Comparison (PENCOMP), imputes missing potential outcomes using regression models that include splines on the logit of the estimated probability to be assigned that treatment, as well as other covariates that are predictive of the outcome. The idea is based on the potential outcome framework of the Rubin causal model [
3]. In the Rubin causal model, potential outcomes are defined as potentially observable outcomes under different treatments or exposure groups. Individual causal effects are defined as comparisons of the potential outcomes for that subject. Only the potential outcome corresponding to the treatment assigned is observed for any subject. Thus, causal inferences are based on comparisons of the imputed and the observed outcomes. Under the Rubin causal model assumptions, PENCOMP has a double robustness property for estimating treatment effects [
5]. Specifically, under these standard causal inference assumptions, PENCOMP consistently estimates the causal effects if the propensity score model is correctly specified and the relationship between the outcome and the logit of the propensity score is modeled correctly, or if the relationship between the outcome and other covariates is modeled correctly.
In this paper, we study important, unresolved questions concerning how to generate robust causal inferences from observational studies. As mentioned above, common approaches to robust causal inference involve fitting two models: (a) a propensity score model, where the outcome is the indicator for which treatment is assigned and the predictors are potential confounding variables; (b) the outcome model, which relates the outcome to the treatment, and includes the propensity score as a predictor variable or as a weight, usually the inverse of the estimated propensity to be selected. Our paper concerns practical strategies for how these regression models are specified.
For valid inferences, all true confounders should be included in the propensity score model. Ideally, we would know the set of true confounders, but in observational studies this information is rarely if ever known. Given this fact, the question of how to select variables to be included in the propensity score model is important and controversial. Some researchers have argued that all pre-treatment potential confounders should be included in the propensity model prior to seeing the outcome data, to avoid “data snooping” and mimic, as closely as possible, a randomized trial, where randomization occurs prior to observing the outcomes [
6].
On the other hand, this strategy may lead to inclusion of variables that are associated with treatment selection but are not associated with the outcome and, hence, are not true confounders; including them in the propensity score model can lead to highly inefficient and non-robust inferences. The reason is the including these variables shrinks the overlap region of the propensity score distributions for the treatments, leading to weighted estimators that have extreme weights, or regression estimators that are vulnerable to model mis-specification—for example, mis-specifying a nonlinear relationship as linear. Limiting this problem argues that variable selection should consider the relationship between the variable and the outcome, provided it is not done in a way that prejudices the estimated treatment effect [
7,
8,
9,
10].
Another consideration is that including variables in the outcome model that are not associated with treatment allocation—and, hence, are not true confounders—but are related to the outcome can improve the efficiency of the causal estimate [
11].
Our paper examines these aspects in detail with both simulation studies and an application, and, offers a broad discussion with a lot of important takeaways for both researchers who believe all pre-treatment confounders should be included and those who believe variable selection is always necessary. Specifically, we examine the performance of alternative confounder selection methods in PENCOMP, IPTW, and AIPTW, with and without considering the relationships between the covariates and the outcome. We also address issues of model selection and model uncertainty. For PENCOMP, we propose a new variant based on bootstrap smoothing, also called bagging. For AIPTW and IPTW, we consider an alternative approach for estimating standard errors and confidence intervals that accounts for model uncertainty.
In
Section 2, we describe estimands and causal inference assumptions. In
Section 3, we describe two versions of PENCOMP for estimating causal effects: one based on multiple imputation, and the other based on bootstrap smoothing, and two estimation procedures for AIPTW and IPTW. In
Section 4, we describe model selection for the propensity score model and the outcome model. In
Section 5, we examine using simulation studies how specification of propensity score model affects the performance of PENCOMP, AIPTW, and IPTW. In
Section 6, we illustrate our methods using the Multicenter AIDS Cohort study (MACS) to estimate the effect of antiretroviral treatment on CD4 counts in HIV-infected patients. We conclude with a discussion of the results and some possible future work.
2. Materials and Methods
2.1. Estimands and Assumptions
Let
denote the vector of baseline covariates, and
denote a binary treatment with
for treatment and
for control, for subject
, respectively. Under Rubin’s potential outcome framework [
3], causal effects at subject level are defined as the difference between the potential outcome for a subject under treatment and the potential outcome under control. Only one of the potential outcomes is observed for each subject. Let
be the potential outcome under treatment
. Here, we focus on inference about the average treatment effect (ATE),
, obtained by averaging subject-level causal effects across the entire population of interest.
We make the following assumptions in order to estimate causal effects.
- (1)
The stable unit-treatment value assumption (SUTVA) states that (a) the potential outcome under a subject’s observed treatment is precisely the subject’s observed outcome. In other words, there are no different versions of potential outcomes under a given treatment for each subject, and (b) the potential outcomes for a subject are not influenced by the treatment assignments of other subjects [
12,
13].
- (2)
Positivity states that each subject has a positive probability of being assigned to either treatment of interest: , where denotes the probability of being assigned to the treatment , given the observed covariates .
- (3)
The ignorable treatment assumption states that ; that is, treatment assignment is as if randomized conditional on the set of covariates .
2.2. PENCOMP and Multiple Imputation
Because each subject only receives one treatment, we observe the potential outcome under the observed treatment but not the potential outcome under the alternative treatment. PENCOMP imputes the missing potential outcomes using regression models that include splines on the logit of the estimated probability to be assigned that treatment, as well as other covariates that are predictive of the outcome. We then draw inferences based on comparisons of the imputed and observed outcomes. PENCOMP, which builds on the Penalized Spline of Propensity Prediction method (PSPP) for missing data problems [
14,
15], relies on the balancing property of propensity score, in combination with the outcome model. Under the assumptions stated above, PENCOMP has a double robustness property for causal effects. Specifically, if either (1) the model for the propensity score and the relationship between the outcome and the propensity score are correctly specified through penalized spline, or (2) the outcome model is correct, the causal effect of the treatment will be consistently estimated [
5].
Here, we briefly describe the estimation procedures for PENCOMP based on multiple imputation with Rubin’s combining rules [
16].
- (a)
For , ⋯, D, generate a bootstrap sample from the original data S by sampling units with replacement, stratified based on treatment group. Then, carry out steps (b)–(d) for each sample :
- (b)
Select and estimate the propensity score model for the distribution of Z given X, with regression parameters . The estimated probability to be assigned treatment is denoted as , where is the ML estimate of . Define log.
In practice, it is often unknown how treatments are assigned to subjects. There are several approaches that can be used to select the covariates to be included in the propensity score model. One approach is to include all the potential confounders from a large collection of pretreatment variables. Variables might also be selected based on how well they predict the treatment assignment. Lastly, variables can be selected based on how well they are predictive of the outcome, whether they are related to the treatment. For a binary treatment, a logistic regression is often used to model the treatment assignment.
- (c)
For each
, use the cases assigned to treatment group
z to estimate a normal linear regression of
on
X, with mean
denotes a penalized spline with fixed knots [
17,
18,
19], indexed by parameters
, and
represents a parametric function of covariates predictive of the outcome, indexed by parameters
. The spline model can be formulated and estimated as a linear mixed model [
19].
- (d)
Impute the missing potential outcomes for subjects in treatment group in the original dataset S with draws from the predictive distribution of given X from the regression in (c), with ML estimates substituted for the parameters , respectively. Repeat the above procedures to produce D complete datasets.
- (e)
Let
and
denote the difference in treatment means and associated pooled variance estimate, based on the observed and imputed values of
Y in each treatment group. The MI estimate of
is then
, and the MI estimate of the variance of
where
. The estimate
is t distributed with degree of freedom
v,
, where
.
2.3. PENCOMP and Bagging
As an alternative to multiple imputation combining rules, we can draw inference about the ATE using the bagging estimator, a form of model averaging that accounts for model uncertainty. Let denote the original dataset consisting of N subjects. A nonparametric bootstrap sample with replacement is denoted as . The procedures for PENCOMP are similar as described above, except in step (e). In step (e), the imputations are carried out on each bootstrap sample , instead of the original data S.
- (a)
For , ⋯, D, generate a bootstrap sample . Repeat steps (b)–(d) for each bootstrap sample to produce D complete datasets.
- (b)
Select and estimate the propensity score model as described in
Section 2.2 (b).
- (c)
Estimate the outcome model on X and a penalized spline on the logit of the propensity to the treatment z using the cases assigned to treatment z.
- (d)
Impute the missing potential outcomes for subjects in treatment group in the bootstrap sample with draws from the predictive distribution estimated in (c).
- (e)
Let
and
denote the estimate and standard error of the causal effect, respectively. The causal estimate
, where
is the mean difference in the potential outcomes obtained from bootstrap sample
. The standard error
is calculated as follows.
where
and
is the number of times that observation
j of the original data
S was selected into the
dth bootstrap sample
[
20].
estimates the bootstrap covariance between
and
. To estimate the standard error of the smoothed bootstrap causal estimate, a brute force approach would be to use a second level of bootstrapping that requires an enormous number of computations. The formula provides an approximation to such an estimate of the standard error.
Inference is made using the bootstrap smoothed estimator and confidence interval , instead of the Rubin’s multiple imputation combining rules.
2.4. Inverse Probability Treatment Weighted Estimator IPTW
Unlike PENCOMP, IPTW does not impute potential outcomes but uses only the observed outcomes. IPTW controls for confounding by weighting subjects based on their probabilities of receiving their observed treatments. Let
denote the estimated probability of being assigned to treatment
given the set of observed covariates
, obtained from the propensity score model for the distribution of
given
, with regression parameters
. The treated subjects are assigned weights
, and the control subjects are assigned weights
. Thus, the subjects who are under-represented in a given treatment arm are given higher weights. The weights in effect create a pseudo-population where treatment groups are balanced with respective to covariate distributions. The IPTW estimator is consistent if the propensity score model is correct under the assumptions stated in
Section 2.1.
The IPTW estimator is defined as
Let
denote the causal estimate on the original data
S. Here, we consider bootstrap methods for computing its standard errors and confidence intervals. The procedures are as follows.
- (a)
For , ⋯, D, generate a bootstrap sample . Then, repeat steps (b)–(d) for each sample :
- (b)
Select and estimate the propensity score model as described in
Section 2.2 (b).
- (c)
Compute for each bootstrap sample .
- (d)
Estimate the standard error
for
based on
D bootstrap samples as
where
. The standard
confidence intervals
. Alternatively, the bagging estimate of the causal effect is
and the 95% smoothed confidence interval is
, where the smoothed standard error
is computed based on Equation (
2) [
20].
2.5. Augmented Inverse Probability Treatment Weighted Estimator (AIPTW)
An alternative to IPTW is augmented IPTW estimation (AIPTW). AIPTW uses the estimated propensity score as a weight like IPTW but also incorporates predictions from a regression model for the outcome. Incorporating covariates predictive of the outcome in the outcome model can improve efficacy and reduce variability, especially when the weights are variable. The AIPTW estimator consistently estimates causal effects if the propensity score model or the outcome model is correctly specified under the assumptions stated in
Section 2.1.
Each subject
i is weighted by the balancing weight
. The AIPTW estimate is calculated on the original dataset
S [
21]:
where
and
. Similar procedures as in IPTW can be used to obtain point estimates and standard
confidence intervals. Alternatively, the bagging estimate of the causal effect is
and the 95% smoothed confidence interval
, can be obtained using the smoothed standard error
from Equation (
2) [
20].
3. Model Selection
We consider scenarios where there are some pre-treatment variables that are predictors of the outcome, some that are predictors of the treatment, some that are predictors of both the treatment and the outcome, and some that are spurious, in the sense that they affect neither the treatment or the outcome. We consider two strategies for building the propensity score model: (1) without seeing the outcome [
6], and (2) taking into account the relationships between the covariates and the outcome.
For strategy 1, one simple approach is to use the stepwise variable selection algorithm with the Bayesian Information Criterion (BIC) to select the variables that are predictive of the treatment, regardless of how well they predict the outcome. Separately, we use the same stepwise algorithm to select the outcome model for PENCOMP and AIPTW. The algorithm, abbreviated as SW, does not use outcome data and, hence, satisfies Rubin’s recommendation of separating analysis from design.
In strategy 2, we use the outcome adaptive lasso approach proposed by Shortreed and Ertefaie (2017) [
9]. By penalizing each covariate according to the strength of the relationship between the covariate and the outcome, the outcome adaptive lasso tends to select covariates that are predictive of the outcome and excludes covariates that are associated only with the treatment. The outcome adaptive lasso estimates for the propensity score model are:
where
such that
and minimizes the mean weighted standardized difference between the treated and control.
is the coefficient estimate for covariate
from ordinary least square or ridge regression by regressing the outcome
Y on the covariates and the treatment. Similarly, the outcome model can be selected via adaptive lasso. The adaptive lasso estimates are given as follows [
22].
where
and
.
This method is subject to Rubin’s criticism. Excluding the treatment variable in the regressions during variable selection might reduce the potential for biasing results.
4. Simulation
We simulate each dataset as described in Zigler and Dominici (2014) and Shortreed and Ertefaie (2017) [
9,
23]. Each simulated dataset contains
N subjects and
p covariates
X. The treatment
is Bernoulli distributed with logit of
. The outcome of interest
Y is normally distributed with a mean of
and a variance of 1. The treatment effect
is equal to 2, without loss of generality. We set all the coefficients 0, except the first 6 covariates
.
and
are true confounders.
and
are predictors of the outcome only.
and
are predictors of the treatment only. All the other
covariates are spurious. We vary the strength of the relationships among the covariates, the outcome and the treatment. In the first scenario,
and
are set as:
, and
. In the second scenario, confounders
and
have a weaker relationship with the treatment:
and
. In the third scenario, confounders
and
have a weaker relationship with the outcome:
and
. We also vary the sample sizes: N = 200 and N = 1000.
We consider four different specifications of the propensity score model: (1) True includes the true propensity score model used to generate the data; (2) trueConf includes only the true confounders; (3) outcomePred includes both the confounders and the predictors of the outcome; (4) allPoten includes all 20 variables. For these four specifications, the outcome models for PENCOMP and AIPTW are correctly specified. In addition, we consider the following variable selection techniques for the propensity score model and the outcome model.
- (a)
SW: stepwise variable selection algorithm with the Bayesian Information Criterion (BIC) separately for the propensity score mode and the outcome model.
- (b)
OAL: outcome adaptive lasso [
9] for the propensity score model, and adaptive lasso for the outcome model [
22].
- (c)
Step-ALT: outcome adaptive lasso for the propensity score model at the first stage and then adaptive lasso for the outcome model at the second stage using only the variables that are selected at the first stage.
- (d)
Step-ALY: adaptive lasso for the outcome model at the first stage and then logistic regression model with all the variables selected at the first stage for the propensity score model.
We evaluate the performance of the methods based on root mean squared error (RMSE), empirical non-coverage rate of the 95% confidence interval, empirical bias, and average length of 95% confidence intervals over 500 simulated datasets. For each dataset, the standard errors and confidence intervals are estimated using 1000 bootstrap samples. Within PENCOMP, we compare the multiple imputation approach and the bagging approach. Within AIPTW and IPTW, we compare the standard approach with the bagging approach.
5. Results
Table 1 shows the results on RMSEs for sample size of 200. By comparing the four propensity score models that were fixed within each bootstrap sample: true, trueConf, outcomePred, and allPotent, we can see that excluding spurious variables or variables that were associated only with the treatment reduced the RMSEs, and including variables associated only with the outcome reduced the RMSEs. Incorporating the outcome model as in PENCOMP and AIPTW attenuated the negative effect of including nonfounding variables on RMSEs. For example, using the standard approach in scenario 1, IPTW had RMSEs of 0.19, 0.22, 0.36, and 0.41 under outcomePred, trueConf, true, and allPotent, respectively. AIPTW had RMSEs of 0.16, 0.16, 0.22, and 0.28, respectively. Using the Rubin’s approach, PENCOMP had RMSEs of 0.16, 0.16, 0.21, and 0.21, respectively. Similar patterns were observed in scenario 2 and 3.
Bagging reduced the RMSEs for IPTW and AIPTW, especially when irrelevant covariates were included in the propensity score model, as in true and allPotent. The standard approach and the bagging approach yielded similar RMSEs under outcomePred and trueConf but different RMSEs under true and allPotent. For example, in scenario 1 under allPotent, IPTW had an RMSE of 0.34 when the bagging approach was used, but an RMSE of 0.41 when the standard approach was used. AIPTW had an RMSE of 0.25 when the bagging approach was used, but an RMSE of 0.28 when the standard approach was used. PENCOMP had an RMSE of 0.22 when the bagging approach was used, but an RMSE of 0.21 when Rubin’s combining rule was used. For PENCOMP, the bagging approach had slightly higher RMSEs than Rubin’s multiple imputation combining rule when many irrelevant variables were included as in allPotent. Similar patterns were observed in scenario 2 and 3.
The results in the variable selection cases were similar to the results without variable selection. The outcome adaptive selection procedure, such as OAL, resulted in smaller RMSEs than the variable selection procedure, such as SW, that selected variables solely based on how well they predicted the treatment.
Figure A1 in the
Appendix A presents the results on variable selection. For example, in scenario 1 with sample size of 200, all the variable selection procedures selected the confounders
and
about 99% of the time. OAL, Step-ALT, and Step-ALY selected the non-confounders
and
about 99% of the time, while SW selected them about 40% of the time. OAL selected
and
about 30% of the time; Step-ALT and Step-ALY about 8% of the time; and SW about 99% of the time. SW, OAL, Step-ALT, and Step-ALY selected spurious variables about 40%, 34%, 8%, and 8% of the times, respectively.
An outcome adaptive selection procedure can fail to select confounders that are weakly associated with the outcome, as seen in scenario 3 in
Figure A1 in the
Appendix A. Similarly, the stepwise variable selection algorithm can fail to select confounders that are weakly associated with the treatment, as seen in scenario 2. Excluding weak confounders increased the bias, as seen in
Table A1 in the
Appendix A. However, the reduction in variance by excluding irrelevant variables when using outcome adaptive selection procedure could offset the bias and the RMSEs could still be smaller, as seen in
Table 1. For example, in scenario 3, the empirical bias for IPTW was 0.146 (7%) under Step-ALT and 0.033 (2%) under SW. The RMSE for IPTW was 0.24 under Step-ALT and 0.33 under SW.
If the chosen selection procedure selects many irrelevant variables, especially the ones that are strong predictors of the treatment only, the bagging approach could reduce the RMSEs for IPTW and AIPTW. For example, in scenario 3, IPTW had an RMSE of 0.33 under SW when the standard approach was used, and an RMSE of 0.28 when the bagging approach was used. AIPTW had an RMSE of 0.25 under SW when the standard approach was used, and an RMSE of 0.23 when the bagging approach was used. PENCOMP had an RMSE of 0.21 under SW when the Rubin’s combining rule was used, and an RMSE of 0.22 when the bagging approach was used. In addition, performing variable selection within each bootstrap sample could increase the chance that weak confounders were selected in some bootstrap samples. Thus, in scenario 3, the bagging IPTW and AIPTW estimators had smaller empirical biases. For example, the empirical bias for IPTW under Step-ALT was 0.146 (7%) when the standard approach was used, but 0.083 (4%) when the bagging approach was used.
Table 2 shows the results on coverage probability for sample size of 200. The bagging approach tended to have coverage rates closer to the nominal coverage than the multiple imputation approach (PENCOMP) and the standard approach (AIPTW, IPTW) for small samples. The smoothed standard errors (SE) were closer the empirical SEs so the coverage rates were closer the nominal 95% coverage, and confidence interval widths were smaller. When there were many spurious variables in the propensity score model and/or when the different models could be selected across bootstrap samples, the distribution of the bootstrap estimates could become “jumpy and erratic”. Consequently, the bagging approach provided tighter confidence intervals.
As the sample size increased to 1000, the gain of using bootstrap smoothing attenuated, as seen in
Table 3 and
Table 4. Using the standard approach of calculating the confidence intervals in the case of IPTW and AIPTW, or using multiple imputation combining rules in the case of PENCOMP, performed better than using the bagging approach. In large sample sizes, each covariate had less impact on the estimates and the selected models across the bootstrap samples were similar, so there was little variability in the bootstrap estimates. In such scenario, bagging led to greater confidence interval widths and overcoverage. In summary, bagging was advantageous when the sample size was small and the data were noisy.
Overall, both PENCOMP and AIPTW had smaller RMSEs than IPTW. PENCOMP had smaller RMSEs than AIPTW, when the propensity score model included many irrelevant covariates. Even when there was no model selection, but the sample size was small, and the propensity score model included many irrelevant variables, especially variables that were strong predictors of the treatment only, the bagging approach could stabilize the IPTW and AIPTW estimators.
6. Application
The Multicenter AIDS Cohort study (MACS) was started in 1984 [
1]. A total of 4954 gay and bisexual men were enrolled in the study and followed up semi-annually. At each visit, data from physical examination, questionnaires about medical and behavioral history, and blood test results were collected. The primary outcome of interest was the CD4 count, a continuous measure of how well the immune system functions. We used this dataset to analyze the short term effects of using antiretroviral treatment. We restricted our analyses to visit 12. Treatment was coded as 1 if the patient reported taking any of antiretroviral treatment (ART) or enrolling in clinical trials of such drugs. We estimated the short-term (6-month) effects of using any antiretroviral treatment for HIV+ subjects. We excluded subjects with missing values on any of the covariates included in the models. We log-transformed the blood counts in this analysis.
We treated each visit as a single time point treatment. Let denote the time when the treatment was administered, and the time 6-month later when the outcome was measured. In addition, let denote 1, 2, and 3 visits before the current visit , respectively. Let denote the blood count histories prior to treatment assignment. Let Z be the binary treatment indicator. Let be the CD4 count 6 months after the treatment. For the outcome model, we considered blood counts-CD4, CD8, white blood cell (WBC), red blood cell (RBC), and platelets and treatment histories from the last 4 visits. For the propensity score model, we considered the same covariates as those in the outcome model, as well as demographic variables-college education, age, and race. The treatment Z was modeled using a logistic regression. We estimated the mean CD4 count difference between the treated and the control, denoted as . For PENCOMP, we replaced the simulated/imputed transformed CD4 values that were with 0 (i.e., below detection level). A total of 15 equally spaced knots and B spline were used.
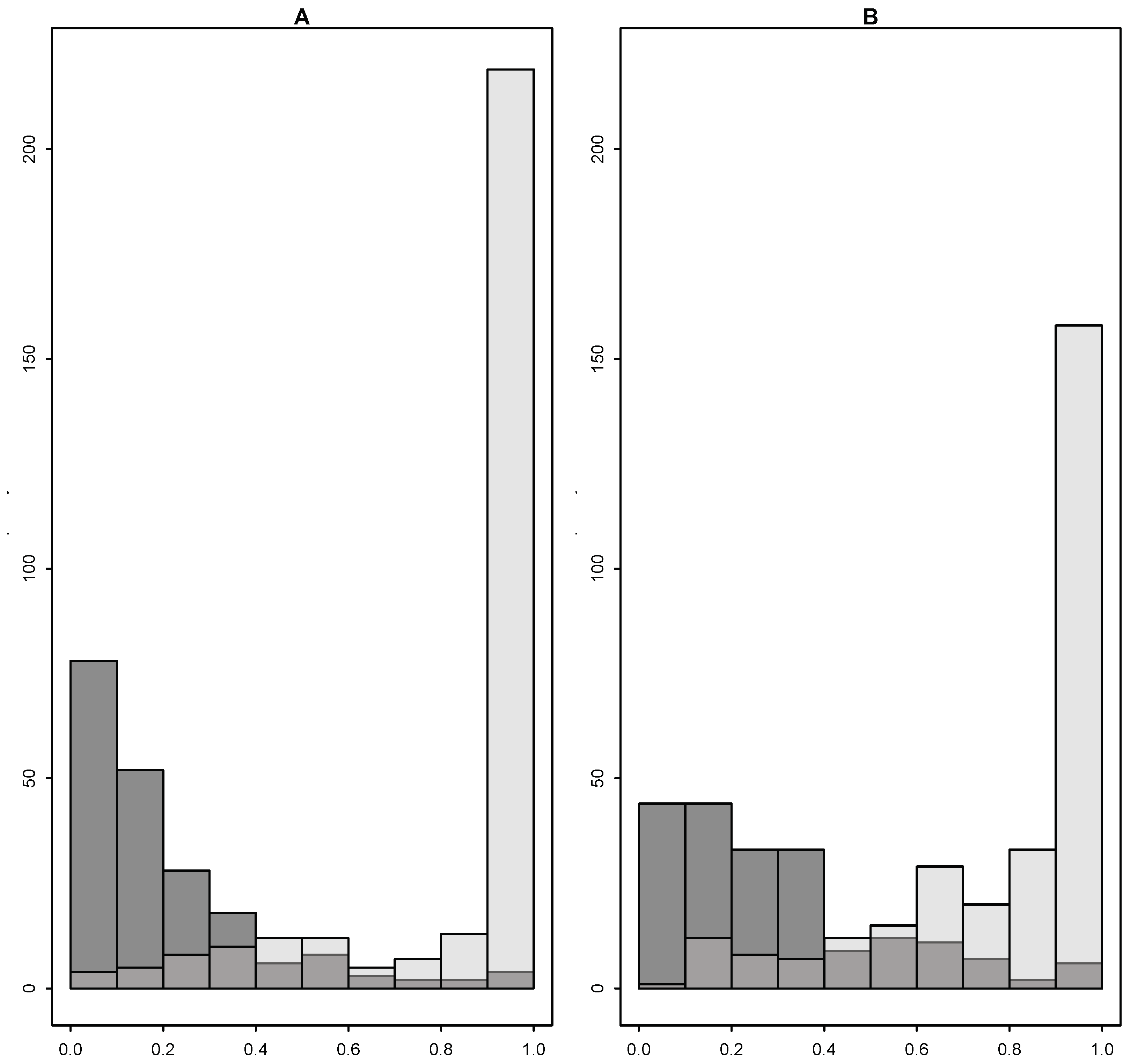
Figure 1 shows that the propensity score distributions were skewed, as the treated had propensity of treatment close 1 and the control close to 0. Here, we considered the variable selection methods in the simulation studies to select the relevant variables for the propensity score model. To quantify the amount of overlap, we measured the proportion of subjects in the control group whose propensity scores were between the 95th and 5th quantiles of the propensity score distribution of the treated group, denoted as
, where
F is the cumulative distribution. Similarly,
denotes the proportion of the treated subjects whose propensity scores were between the 95th and 5th quantiles of the propensity score distribution of the control group. Including only the covariates that were selected more than 20% of times by Step_ALT among 1000 bootstrap samples improved the overlap, as shown in
Figure 1.
Table A5 in the
Appendix B shows the proportion that each variable was selected across 1000 bootstrap samples. Because subjects who were treated during the recent visits were more likely to get treated again, prior treatments were highly predictive of future treatment. However, prior CD4 counts were more predictive of future CD4 count because those earlier antiretrovial treatments were not as effective. Thus, when we accounted for the outcome-covariate relationship when selecting propensity score model, prior treatment variables were selected less than 10% of the times, compared to close to 100% of the time in SW, and 58% of the time in OAL.
We estimated the short term effect of antiretroviral treatment on CD4 count using PENCOMP, AIPTW, and IPTW, shown in
Table 5. The standard errors were obtained using 1000 bootstrap samples. For PENCOMP, 1000 complete datasets were created. Overall, the IPTW estimates had the biggest confidence interval widths. Incorporating the outcome models as in AIPTW and PENCOMP decreased the standard errors and interval widths significantly. PENCOMP tended to have slightly smaller interval widths than AIPTW. The IPTW bootstrap estimates were much more variable, compared to the PENCOMP or AIPTW bootstrap estimates. As seen in the simulation studies, the bagging approach helped stabilize the IPTW and AIPTW estimators when the weights were variable. For PENCOMP, the multiple imputation approach and the bagging approach yielded similar results. Excluding irrelevant covariates from the propensity score model, as seen in Step-ALT and Step-ALY, improved the performance of IPTW significantly, in terms of the standard errors and confidence interval widths. Incorporating the outcome models in the AIPTW and PENCOMP attenuated some of the effect of including many irrelevant covariates.
7. Discussion
We propose a new version of PENCOMP via bagging that could improve confidence interval width and coverage, compared to PENCOMP with Rubin’s multiple imputation combining rules, when the sample size is small, and the data are noisy. However, when the sample size is large and there is little variability in the bootstrap estimates, the bagging approach seems to overcover. The bagging approach and the multiple imputation approach in PENCOMP have similar RMSEs because both incorporate model selection and smooth over the estimates. Similarly, bagging improves the performance of IPTW and AIPTW in terms of RMSE, coverage and confidence interval width, especially when the sample size is small, and the data are noisy. In practice, the propensity score model is often selected, and inferences based on the selected model. This simple approach ignores model uncertainty. Compared to the standard approach for AIPTW and IPTW, the bagging approach could perform better because it incorporates model selection effects.
Our simulation studies show that excluding strong predictors of the treatment but not of the outcome, or spurious variables, helps improve the performance of the propensity score methods, especially for the weighted estimators. However, PENCOMP is less affected by inclusion of many non-confounding variables in the propensity score model than the weighted estimators because a propensity score model with many irrelevant non-confounding variables could lead to extreme propensity scores and extreme weights.
An outcome adaptive approach could help exclude strong predictors of the treatment only. However, one shortcoming of using the outcome adaptive approach is that it can miss many weak confounders. While the outcome adaptive approach can decrease the standard errors of the estimates, by excluding spurious variables and strong predictors of the treatment only, it can potentially increase bias by excluding variables that are weakly associated with the outcome, especially in small samples. This is also a shortcoming in variable selection procedures that blind the outcome, such as stepwise variable selection algorithm, because it can fail to select confounders that are weakly associated with the treatment.
Whether using an outcome adaptive approach can be beneficial depends on specific studies. When there are many weak confounders in the data, the reduction in variance from using an outcome adaptive approach might not offset the increase in bias. For example, when studying a new disease, researchers might decide to include all pretreatment variables. When there are many potential confounding variables, including those that are strongly associated with the treatment only, in the propensity score model and the weights are highly variable, PENCOMP provides a valuable approach for estimating causal effects. When variable selection is involved, smoothing over bootstrap samples can reduce the chance of excluding important confounders, which results in bias.
In high dimensional settings, including all the observed variables in the propensity score model can lead to highly unstable or even infeasible estimation. One criticism of focusing on confounders rather than just predictors of treatment assignment (i.e., balancing covariates between the treatment arms) is that incorporating the outcome in the estimation procedure, whether via prognostic score [
24] or as we have done here, violates the principle that causal inference methods using observational data should mimic, as closely as possible, randomized trial designs, where outcomes are not considered until the final estimation step. Following such a rule avoids both overt and inadvertent attempts to bias model building toward preferred outcomes (“the garden of forking paths” [
25], per Gelman and Loken, 2013). One approach to reducing this potential for bias is to select variables into the propensity model based a regression on the outcome that excludes variables indicating the treatments. However, with the advent of advanced “automatic” penalized regression methods, such as adaptive lasso, the risk of such “model shopping” may be sufficiently reduced, though not eliminated, so that analysts that follow the approach outlined here should endeavor to pre-specify the procedures before the analysis begins.