Analysis of High-Temperature Superconducting Current Leads: Multiple Solutions, Thermal Runaway, and Protection
Abstract
1. Introduction
2. Analysis
2.1. Material Properties
2.2. The Electro-Thermal Problem in Dimensionless Form
2.3. Stability
3. Results and Discussion
4. Conclusions
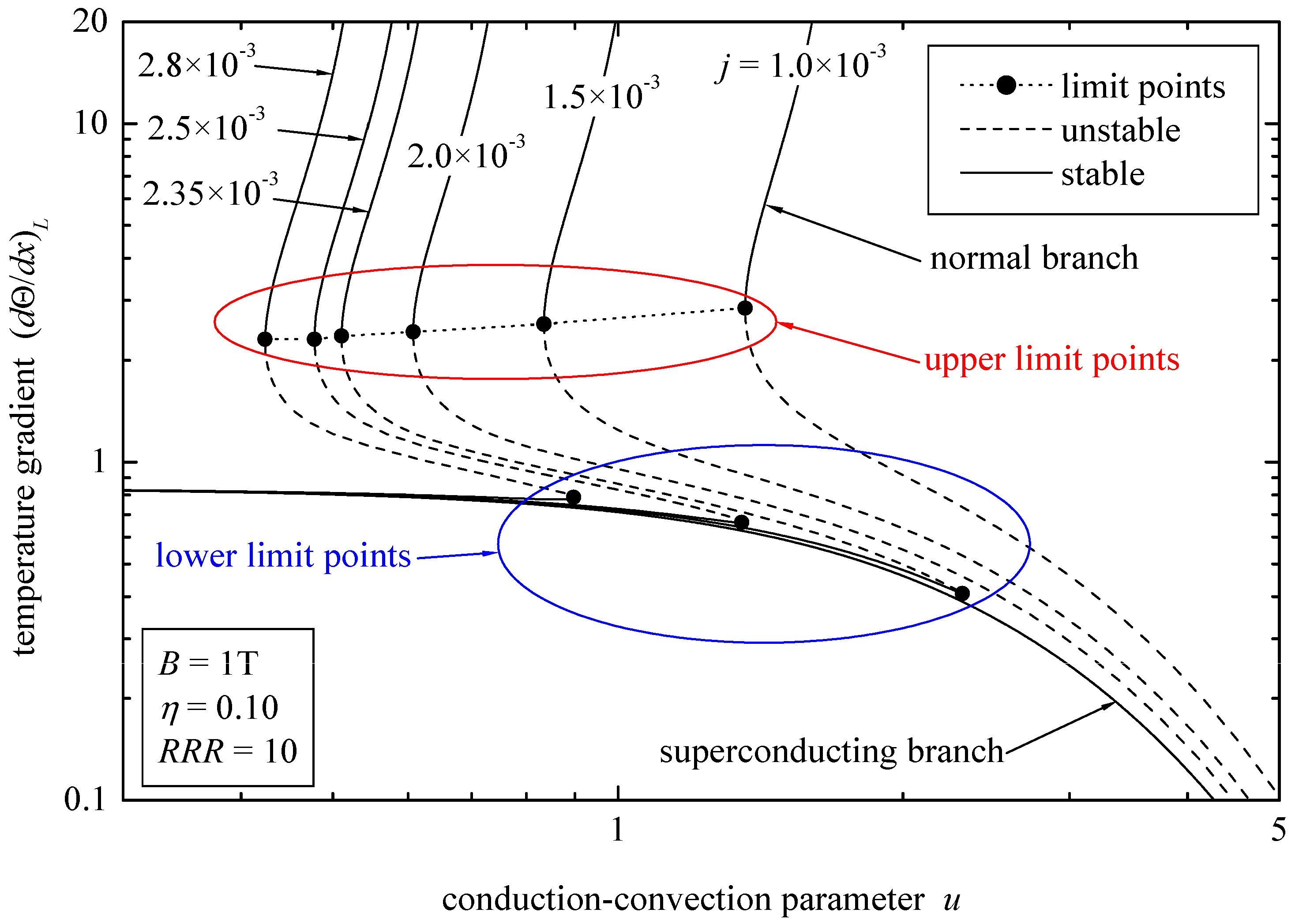
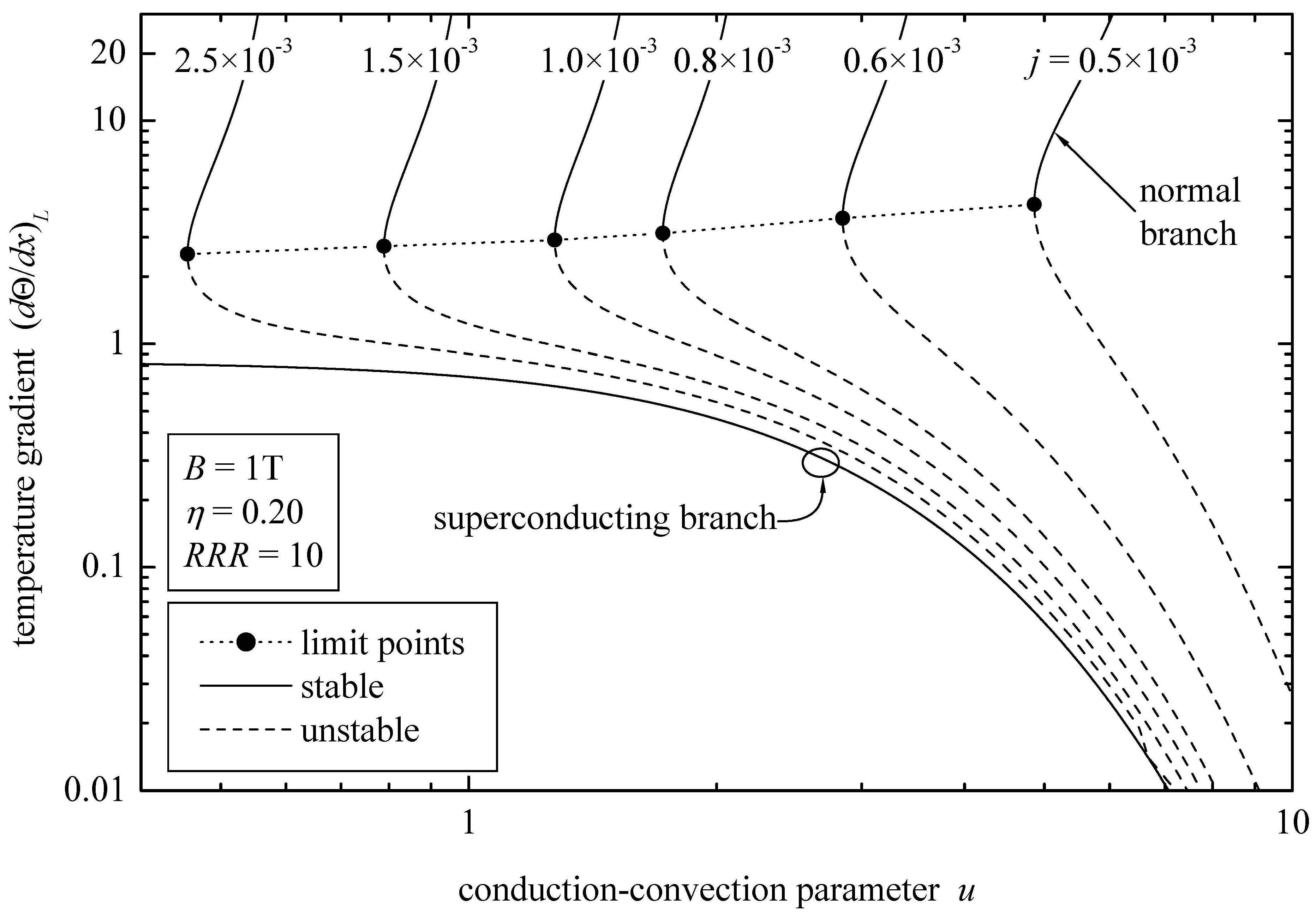
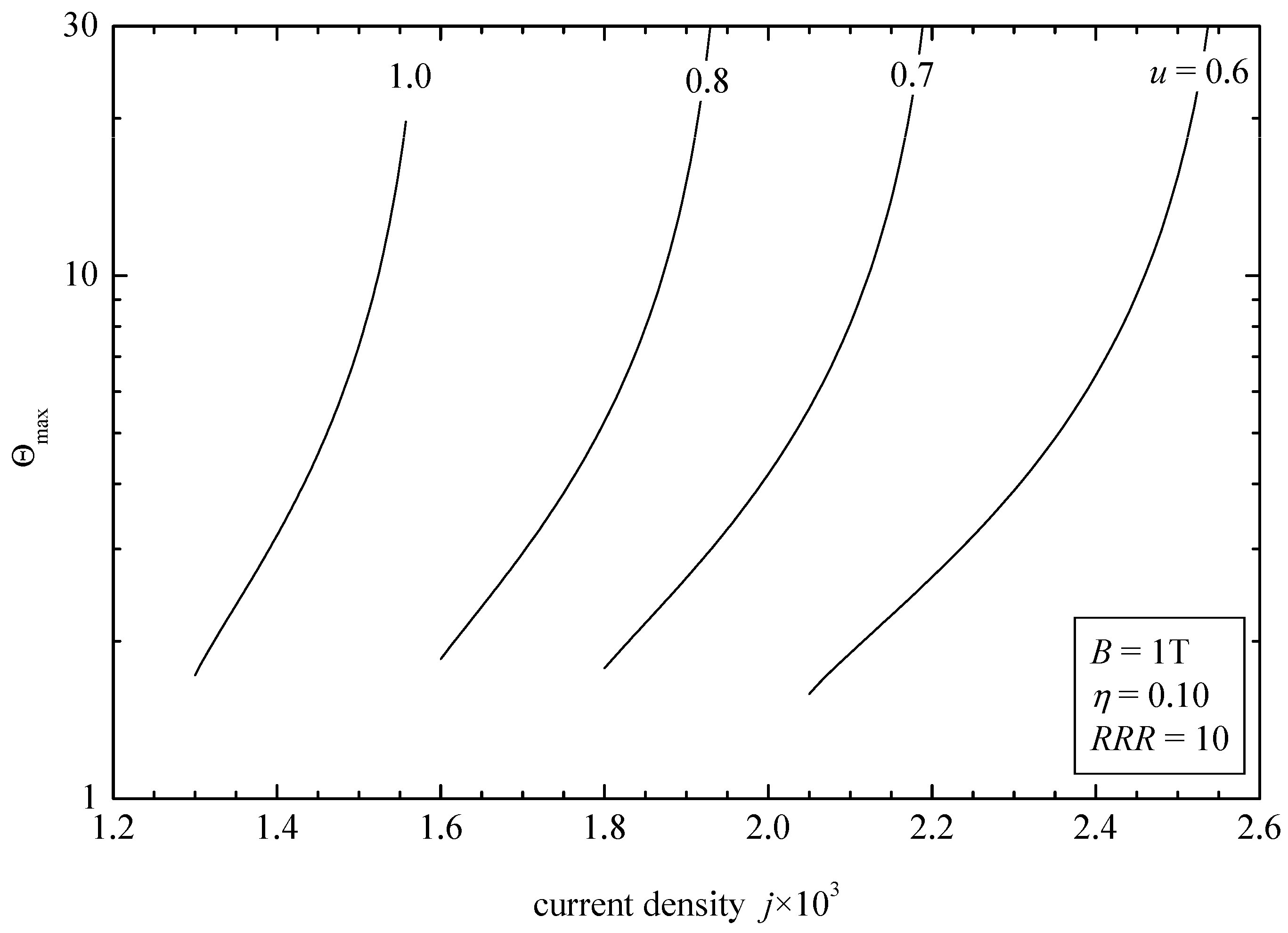
- For a specified current density and low filling ratios , no solution exists when u exceeds the lower limit point, i.e., (Figure 2).
- The upper limit point where the multiplicity region begins is a function of the applied current (Figure 2).
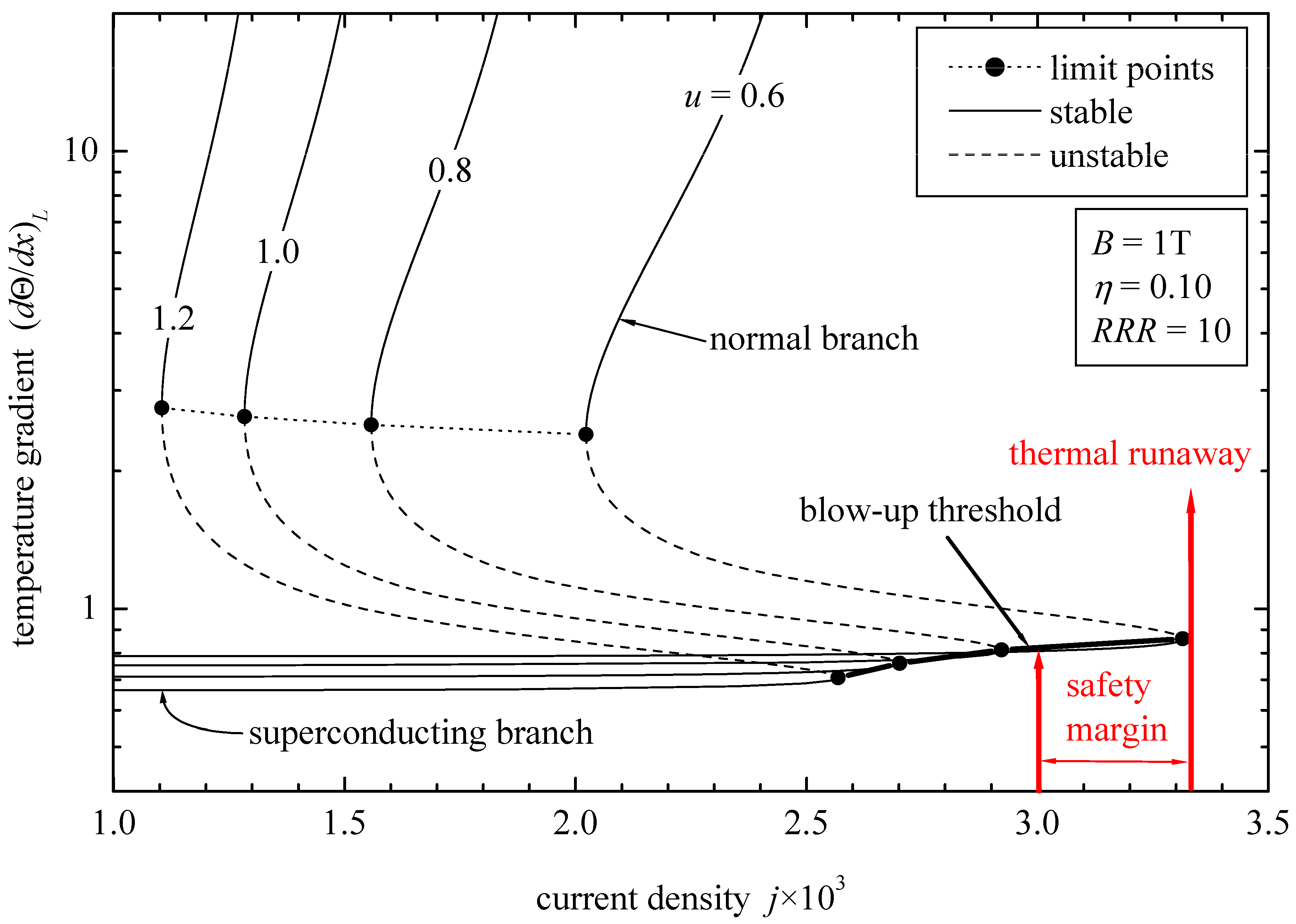
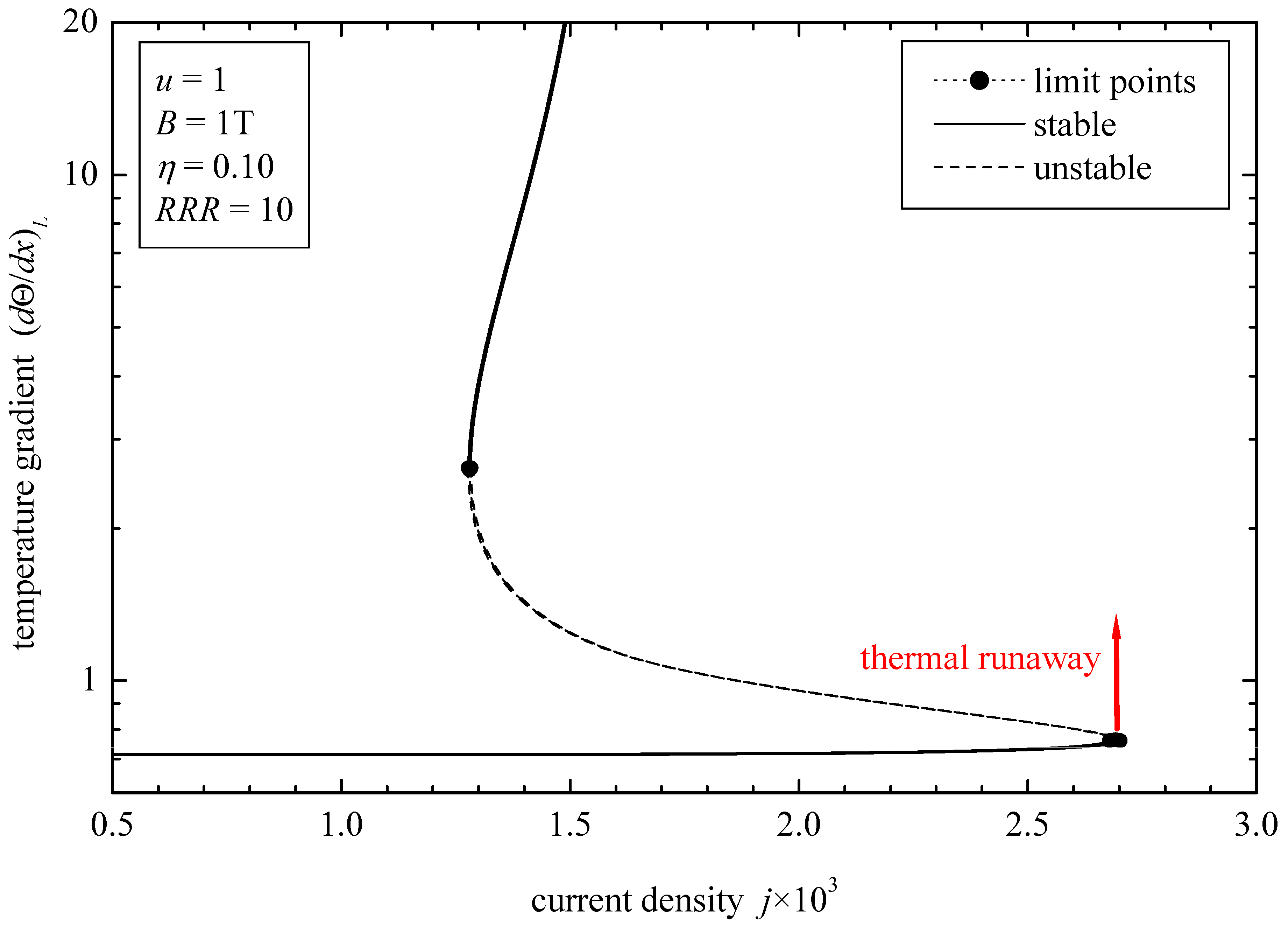
- Similar to the case of the metallic current leads, a temperature blow-up threshold exists defined by the lower limit points, which depend on the applied current and the conduction–convection parameter, beyond which thermal runaway is encountered (Figure 8).
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | conductor cross-sectional area | [m2] |
| B | magnetic field | [T] |
| c | reduced specific heat capacity | [–] |
| C | volumetric heat capacity | [J/(m3 K)] |
| E | electric field intensity | [V/m] |
| voltage criterion in Equation (5) | [V/m] | |
| F | flow number, Equation (13) | [–] |
| G | generation number, Equation (12) | [–] |
| h | reduced heat transfer coefficient | [–] |
| H | heat transfer coefficient | [W/(m2 K)] |
| J | current density | [A/m2] |
| k | reduced thermal conductivity | [–] |
| K | thermal conductivity | [W/(mK)] |
| L | conductor length | [m] |
| coolant mass flow rate | [kg/s] | |
| n | power-law exponent (n-value) | [–] |
| P | wetted perimeter | [m] |
| RRR | residual resistivity ratio | [–] |
| t | time | [sec] |
| T | temperature | [K] |
| u | conduction–convection parameter (CCP), Equation (14) | [–] |
| x | dimensionless distance along conductor | [–] |
| X | distance along conductor | [m] |
| Greek Symbols | ||
| α | thermal diffusivity | [m2/s] |
| δ | time scaling factor | [–] |
| η | filling ratio | [–] |
| Θ | dimensionless temperature | [–] |
| λ | eigenvalue | [–] |
| ρ | reduced electric resistivity | [–] |
| electric resistivity | [Ωm] | |
| τ | dimensionless time | [–] |
| Subscripts | ||
| c | critical property | |
| g | gas stream | |
| H | warm end | |
| L | cold end | |
| LP | reference to limit points | |
| m | matrix | |
| ref | reference value | |
| s | superconductor | |
| ss | reference to steady state | |
| Superscripts | ||
| derivative with respect to x | ||
| Abbreviations | ||
| CCP | conduction–convection parameter | |
| HTS | high-temperature superconductor | |
| LHC | Large Hadron Collider | |
| LOFA | loss of flow accident | |
References
- Bendorz, J.G.; Müller, K.A. Possible high-Tc superconductivity in the Ba-La-Cu-O system. Z. Physic Condens. Matter 1986, B64, 189–193. [Google Scholar]
- Wesche, R.; Heller, R.; Bruzzone, P.; Fietz, W.H.; Lietzow, R.; Vostner, A. Design of high temperature superconductor current leads for ITER. Fusion Eng. Des. 2007, 82, 1385–1390. [Google Scholar] [CrossRef]
- Ding, K.; Zhou, T.; Liu, C.; Du, Q.; Fernandez, A.V.; Zhu, S.; Devred, A.; Bauer, P.; Feng, H.; Fernandez-Hernando, L.; et al. Results of the testing of ITER CC HTS current leads prototypes. IEEE Trans. Appl. Supercond. 2016, 26, 4803404. [Google Scholar] [CrossRef]
- Ballarino, A. Operation of 1074 HTS current leads at the LHC: Overview of three years of powering the accelerator. IEEE Trans. Appl. Supercond. 2013, 23, 4801904. [Google Scholar] [CrossRef]
- Marshall, W.S.; Bai, H.; Bird, M.D.; Dixon, I.R.; Gavrilin, A.V.; Laureijs, G.A.; Lu, J.; Ouden, A.D.; Wijnen, F.J.P.; Wulffers, C.A.; et al. Fabrication and Testing of the 20 kA Binary Current Leads for the NHMFL Series-Connected Hybrid Magnet. IEEE Trans. Appl. Supercond. 2016, 26, 1–4. [Google Scholar] [CrossRef]
- Raach, H.; Schroeder, C.H.; Floch, E.; Bleile, A.; Schnizer, P.; Andersen, T.P. 14 kA HTS Current Leads with one 4.8 K Helium Stream for the Prototype Test Facility at GSI. Phys. Procedia 2015, 67, 1098–1101. [Google Scholar] [CrossRef]
- Drotziger, S.; Buscher, K.-P.; Fietz, W.H.; Heiduk, M.; Heller, R.; Hollik, M.; Lange, C.; Lietzow, R.; Moennich, T.; Richter, T.; et al. Overview of results from Wendelstein7-X HTS current lead testing. Fusion Eng. Des. 2013, 88, 1585–1588. [Google Scholar] [CrossRef]
- Isono, T.; Hamada, K.; Okuno, K. Design optimization of a HTS current lead with large current capacity for fusion application. Cryogenics 2006, 46, 683–687. [Google Scholar] [CrossRef]
- Kovalev, I.; Surin, M.; Naumov, A.; Novikov, M.; Novikov, S.; Ilin, A.; Polyakov, A.; Scherbakov, V.; Shutova, D. Test results of 12/18 kA ReBCO coated conductor current leads. Cryogenics 2017, 85, 71–77. [Google Scholar] [CrossRef]
- Diev, D.N.; Galimov, A.R.; Ilin, A.A.; Khodzhibagiyan, H.G.; Kovalev, I.A.; Makarenko, M.N.; Naumov, A.V.; Novikov, M.S.; Novikov, S.I.; Polyakov, A.V.; et al. HTS current leads for the NICA accelerator project. Cryogenics 2018, 94, 45–55. [Google Scholar] [CrossRef]
- Heller, R.; Fietz, W.H.; Kienzler, A. High power high temperature superconductor current leads at KIT. Fusion Eng. Des. 2017, 125, 294–298. [Google Scholar] [CrossRef]
- Wilson, M.N. Superconducting Magnets; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- Iwasa, Y. Case Studies in Superconducting Magnets. Design and Operational Issues, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Dresner, L. Stability of Superconductors; Springer+Bussiness Media: New York, NY, USA, 1995. [Google Scholar]
- Romanovskii, V.R. Basic Macroscopic Principles of Applied Superconductivity; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Paul, W.; Chen, M.; Lakner, M.; Rhyner, J.; Braun, D.; Lanz, W. Fault current limiter based on high temperature superconductors—Different concepts, test results, simulations, applications. Phys. C 2001, 354, 27–33. [Google Scholar] [CrossRef]
- Lee, H.G.; Kim, H.M.; Lee, B.W.; Oh, I.S.; Hyun, O.B.; Sim, J.; Chang, H.M.; Bascunan, J.; Iwasa, Y. Conduction-Cooled Brass Current Leads for a Resistive Superconducting Fault Current Limiter (SFCL) System. IEEE Trans. Appl. Supercond. 2007, 17, 2248–2251. [Google Scholar] [CrossRef]
- Noe, M.; Hobl, A.; Tixador, P.; Martini, L.; Dutoit, B. Conceptual Design of a 24 kV, 1 kA Resistive Superconducting Fault Current Limiter. IEEE Trans. Appl. Supercond. 2011, 22, 5600304. [Google Scholar] [CrossRef]
- Sarkar, D.; Roy, D.; Choudhury, A.; Yamada, S. Performance analysis of saturated iron core superconducting fault current limiter using Jiles–Atherton hysteresis model. J. Magn. Magn. Mater. 2015, 390, 100–106. [Google Scholar] [CrossRef]
- Farokhiyan, M.; Hosseini, M.; Kavousi-Fard, A. Current density distribution in resistive fault current limiters and its effect on device stability. Phys. C 2020, 580, 1353786. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, S.; Ma, T.; Li, Y.; He, D. Current limiting characteristics of a resistance-inductance type superconducting fault current limiter. Phys. C 2022, 601, 1354105. [Google Scholar] [CrossRef]
- Sotelo, G.G.; dos Santos, G.; Sass, F.; França, B.W.; Dias, D.H.N.; Fortes, M.Z.; Polasek, A.; de Andrade, R., Jr. A review of superconducting fault current limiters compared with other proven technologies. Superconductivity 2022, 3, 100018. [Google Scholar] [CrossRef]
- Jones, M.; Yeroshenko, V.; Starostin, A.; Yaskin, L. Transient behaviour of helium-cooled current leads for superconducting power transmission. Cryogenics 1978, 18, 337–343. [Google Scholar] [CrossRef]
- Aharonian, G.; Hyman, L.; Roberts, L. Behaviour of power leads for superconducting magnets. Cryogenics 1981, 21, 145–151. [Google Scholar] [CrossRef]
- Buchs, K.; Hyman, L.G. Investigation of multiple solutions for gas cooled current leads and results of survey information on current leads. Cryogenics 1983, 23, 362–366. [Google Scholar] [CrossRef]
- Krikkis, R.N. Multiplicities and thermal runaway of current leads for superconducting magnets. Cryogenics 2017, 83, 8–16. [Google Scholar] [CrossRef]
- Mumford, F.J. Superconducting current-leads made from high Tc superconductor and normal metal conductor. Cryogenics 1989, 29, 206–207. [Google Scholar] [CrossRef]
- Hull, J.R. High temperature superconducting leads for cryogenic apparatus. Cryogenics 1989, 29, 1116–1123. [Google Scholar] [CrossRef]
- Dresner, L. Superconductor stability 90: A review. Cryogenics 1991, 31, 489–498. [Google Scholar] [CrossRef]
- Wesche, R.; Fuchs, A. Design of superconducting current leads. Cryogenics 1994, 34, 145–154. [Google Scholar] [CrossRef]
- Lee, H.; Kim, H.M.; Iwasa, Y.; Kim, K.; Arakawa, P.; Laughon, G. Development of vapor-cooled HTS-copper 6-kA current lead incorporating operation in the current-sharing mode. Cryogenics 2004, 44, 7–14. [Google Scholar] [CrossRef]
- Jang, J.Y.; Lee, W.S.; Kang, J.S.; Jo, H.C.; Hwang, Y.J.; Na, J.B.; Sim, K.; Kim, H.M.; Yoon, Y.S.; Do Chung, Y.; et al. Experimental study of the new type of hts elements for current leads to be applied to the nuclear fusion devices. IEEE Trans. Appl. Supercond. 2012, 22, 4801204. [Google Scholar] [CrossRef]
- Drotziger, S.; Fietz, W.H.; Heiduk, M.; Heller, R.; Lange, C.; Lietzow, R.; Mohring, T. Investigation of HTS Current Leads Under Pulsed Operation for JT-60SA. IEEE Trans. Appl. Supercond. 2011, 22, 4801704. [Google Scholar] [CrossRef]
- Heller, R.; Bauer, P.; Savoldi, L.; Zanino, R.; Zappatore, A. Predictive 1-D thermal-hydraulic analysis of the prototype HTS current leads for the ITER correction coils. Cryogenics 2016, 80, 325–332. [Google Scholar] [CrossRef]
- Han, Q.; Ding, K.; Lu, K.; Liu, C.; Liu, C.; Huang, X.; Zhou, T.; Song, Y. Safety analysis of the 100 kA current lead for CFETR. Fusion Eng. Des. 2020, 153, 111481. [Google Scholar] [CrossRef]
- Dong, Y.; Ran, Q.; Lu, K.; Zheng, J.; Liu, C.; Liu, H.; Ding, K. Structure, design and test of 13 kA HTS current lead. Cryogenics 2023, 132, 103620. [Google Scholar] [CrossRef]
- Chang, H.-M.; Kim, N.H.; Oh, S. Thermodynamic optimization of 10–30 kA gas-cooled current leads with REBCO tapes for superconducting magnets at 20 K. Cryogenics 2023, 131, 1036667. [Google Scholar] [CrossRef]
- Bottura, L. Critical Surface for BSCCO-2212 Superconductor; Note CRYO/02/027; CryoSoft Library CERN: Thoiry, France, 2002. [Google Scholar]
- van der Laan, D.C.; van Eck, H.J.N.; Haken, B.T.; Schwartz, J.; ten Kate, H.H.J. Temperature and Magnetic Field Dependence of the Critical Current of BSCCO Tape Conductors. IEEE Trans. Appl. Supercond. 2001, 11, 3345–3348. [Google Scholar] [CrossRef]
- Wesche, R. Temperature dependence of critical currents in superconducting Bi-2212/Ag wires. Phys. C 1995, 246, 186–194. [Google Scholar] [CrossRef]
- Romanovskii, V.; Watanabe, K. Multi-stable static states of Bi-based superconducting composites and current instabilities at various operating temperatures. Phys. C 2005, 420, 99–110. [Google Scholar] [CrossRef]
- Dresner, L. Stability and protection of Ag/BSCCO magnets operated in the 20–40 K range. Cryogenics 1993, 33, 900–909. [Google Scholar] [CrossRef]
- Lim, H.; Iwasa, Y. Two-dimensional normal zone propagation in BSCCO-2223 pancake coils. Cryogenics 1997, 37, 789–799. [Google Scholar] [CrossRef]
- Krikkis, R.N.; Sotirchos, S.V.; Razelos, P. Analysis of multiplicity phenomena in longitudinal fins under multi-boiling conditions. ASME J. Heat Transf. 2004, 126, 1–7. [Google Scholar] [CrossRef]
- Krikkis, R.N. On the multiple solutions of boiling fins with heat generation. Int. J. Heat Mass Transf. 2015, 80, 236–242. [Google Scholar] [CrossRef]
- Krikkis, R.N. Laminar conjugate forced convection over a flat plate. Multiplicities and stability. Int. J. Therm. Sci. 2017, 111, 204–214. [Google Scholar] [CrossRef]
- Krikkis, R.N. On the Thermal Dynamics of Metallic and Superconducting Wires. Bifurcations, Quench, the Destruction of Bistability and Temperature Blowup. J 2021, 4, 803–823. [Google Scholar] [CrossRef]
- Pfotenhauer, J.; Lawrence, J. Characterizing thermal runaway in HTS current leads. IEEE Trans. Appl. Supercond. 1999, 9, 424–427. [Google Scholar] [CrossRef]
- Vysotsky, V.; Sytnikov, V.; Rakhmanov, A.; Ilyin, Y. Analysis of stability and quench in HTS devices—New approaches. Fusion Eng. Des. 2006, 81, 2417–2424. [Google Scholar] [CrossRef]
- Romanovskii, V.R.; Watanabe, K. Operating modes of high Tc composite superconductors and thermal runaway conditions under current charging. Supercond. Sci. Technol. 2006, 19, 541–550. [Google Scholar] [CrossRef]
- Werweij, A.P. Thermal Runaway of the 13kA busbar joints in the LHC. IEEE Trans. Appl. Supercond. 2010, 20, 2155–2159. [Google Scholar] [CrossRef]
- Willering, G.P.; Bottura, L.; Fessia, P.; Scheuerlein, C.; Verweij, A.P. Thermal Runaways in LHC Interconnections: Experiments. IEEE Trans. Appl. Supercond. 2011, 21, 1781–1785. [Google Scholar] [CrossRef]
- Maeda, H.; Yanagisawa, Y. Recent developments in high temperature superconducting magnet technology (review). IEEE Trans. Appl. Supercond. 2014, 24, 4602412. [Google Scholar] [CrossRef]




| 1.0 | [T] | |
| 465.5 | [T] | |
| 5.9 × 108 | [A/m2] | |
| 87.1 | [K] | |
| α | 10.33 | [–] |
| β | 6.76 | [–] |
| γ | 1.73 | [–] |
| χ | 0.27 | [–] |
| i | Stable (sc) | Unstable (ss) | Stable (n) | Stable (sc) | Unstable (ss) | stable (n) |
|---|---|---|---|---|---|---|
| 1 | −2.0966 | +5.1103 | −2.5046 | −13.1606 | +6.3686 | −2.6312 |
| 2 | −5.3865 | −3.4348 | −3.4076 | −49.6442 | −43.5204 | −38.2332 |
| 3 | −10.8696 | −9.5216 | −8.7940 | −110.4559 | −95.2391 | −98.6322 |
| 4 | −18.5460 | −16.1453 | −16.4449 | −195.6032 | −185.5839 | −184.0936 |
| 5 | −28.4155 | −26.6921 | −26.3705 | −305.0951 | −291.8693 | −294.5584 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krikkis, R.N. Analysis of High-Temperature Superconducting Current Leads: Multiple Solutions, Thermal Runaway, and Protection. J 2023, 6, 302-317. https://doi.org/10.3390/j6020022
Krikkis RN. Analysis of High-Temperature Superconducting Current Leads: Multiple Solutions, Thermal Runaway, and Protection. J. 2023; 6(2):302-317. https://doi.org/10.3390/j6020022
Chicago/Turabian StyleKrikkis, Rizos N. 2023. "Analysis of High-Temperature Superconducting Current Leads: Multiple Solutions, Thermal Runaway, and Protection" J 6, no. 2: 302-317. https://doi.org/10.3390/j6020022
APA StyleKrikkis, R. N. (2023). Analysis of High-Temperature Superconducting Current Leads: Multiple Solutions, Thermal Runaway, and Protection. J, 6(2), 302-317. https://doi.org/10.3390/j6020022





