Approximate Solutions for Undamped Nonlinear Oscillations Using He’s Formulation
Abstract
1. Introduction
2. The Duffing Equation
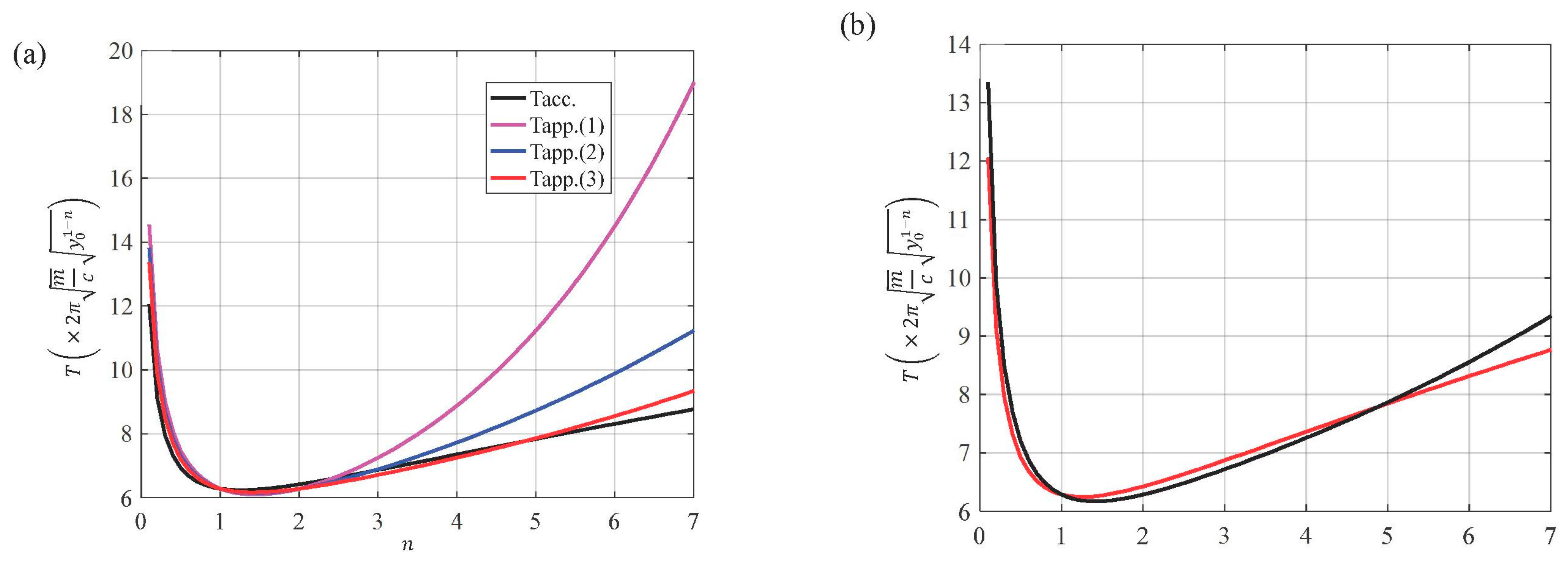
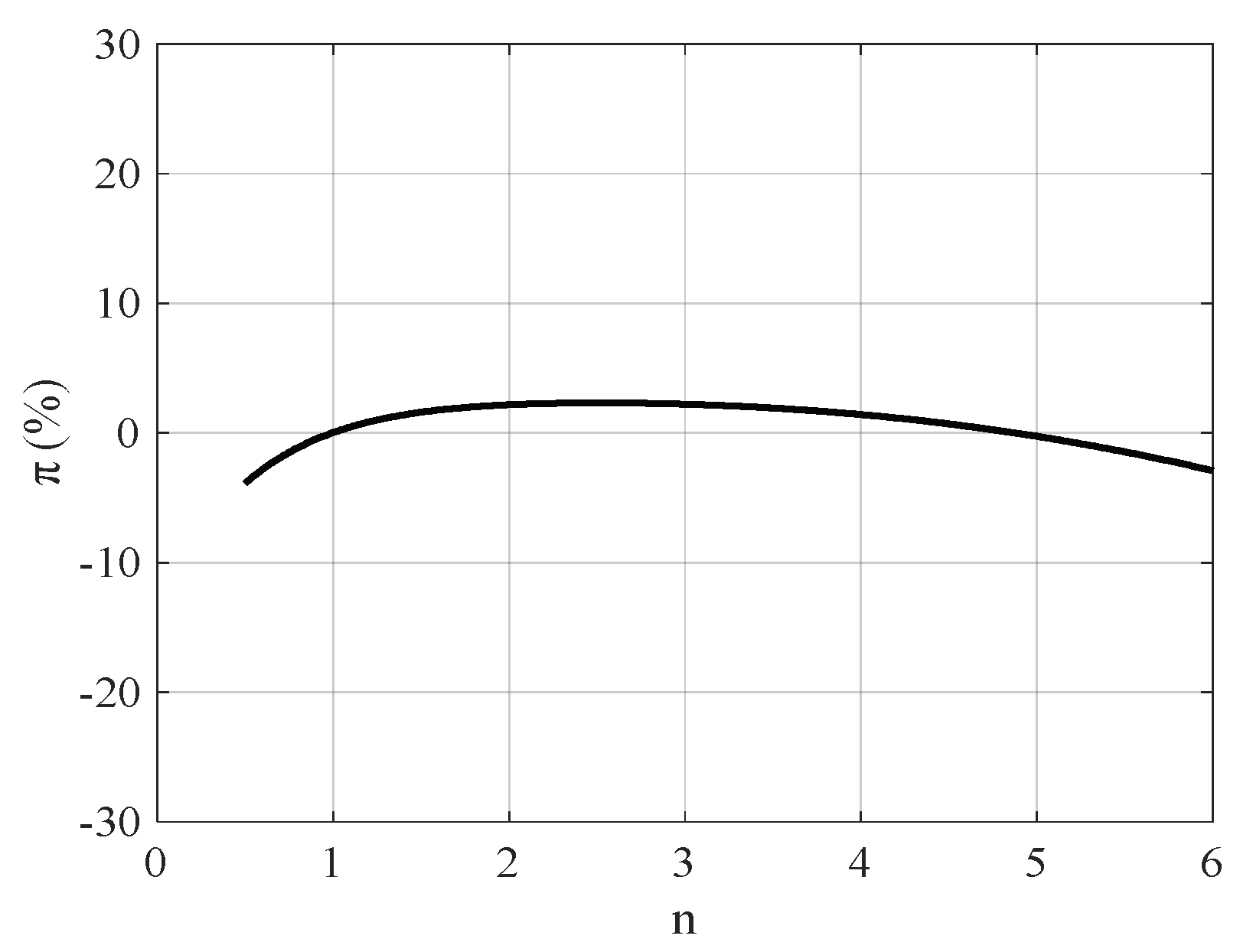
3. The Helmholtz Nonlinear Oscillator
4. The Simple Pendulum
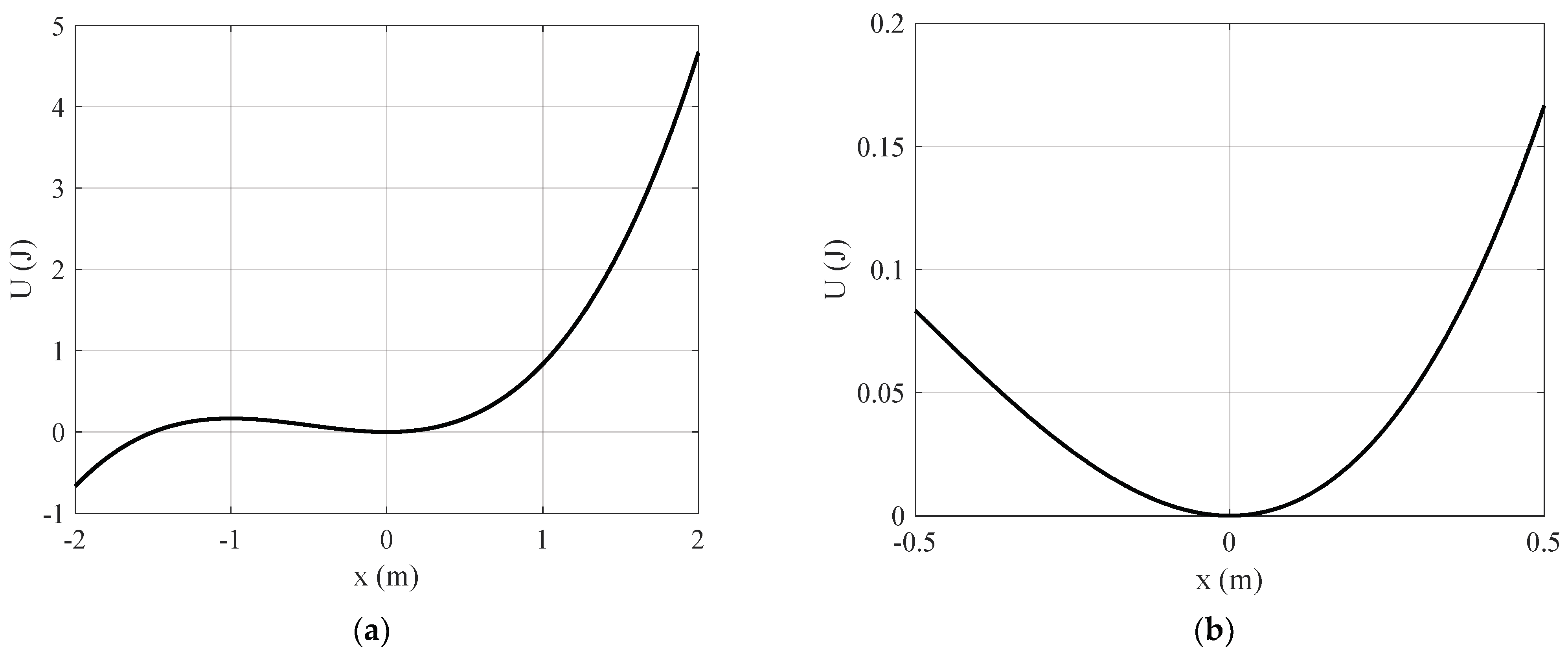
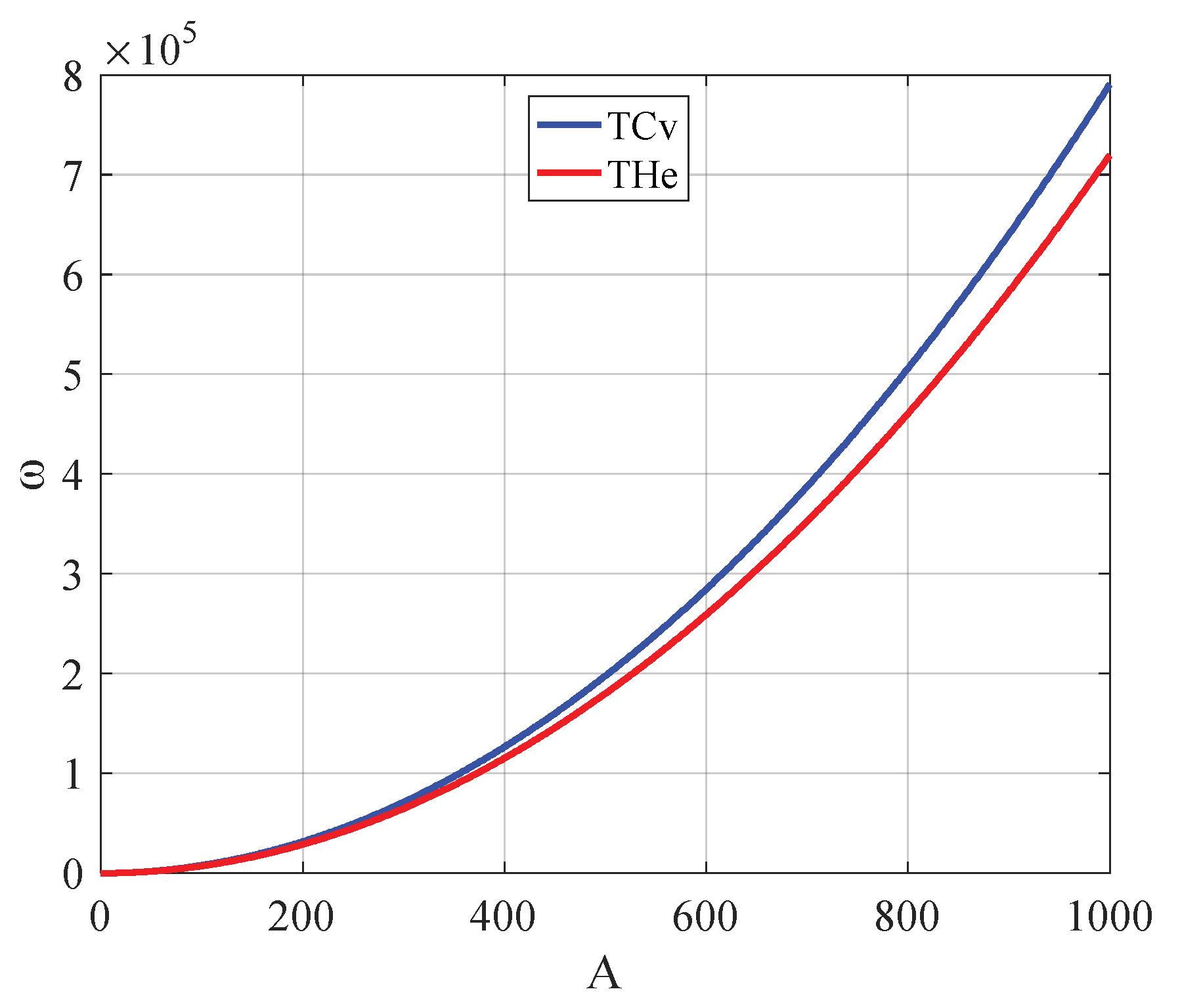
5. Vertical Oscillations under the Influence of Nonlinear Elastic Forces
6. Discussion
7. Conclusions
8. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Hagedorn, P. Non-Linear Oscillations; Clarendon: Oxford, UK, 1988. [Google Scholar]
- Cveticanin, L.; Kozmidis Luburic, U.; Mester, G. Periodic Motion in an excited and damped cubic nonlinear oscillator. Math. Probl. Eng. 2018, 2018, 3841926. [Google Scholar] [CrossRef]
- Big-Alabo, A. Approximate periodic solution and qualitative analysis of nonnatural oscillators based on the restoring force. Eng. Res. Express 2020, 2, 015029. [Google Scholar] [CrossRef]
- Big-Alabo, A. Approximate periodic solution for the large-amplitude oscillations of a simple pendulum. Int. J. Mech. Eng. Educ. 2019, 8, 335–350. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Malamou, A. Exploring the non-linear oscillation of a rigid sphere on an elastic half-space. Eur. J. Phys. 2021, 42, 025011. [Google Scholar] [CrossRef]
- Koruk, H. Modelling small and large displacements of a sphere on an elastic half-space exposed to a dynamic force. Eur. J. Phys. 2021, 42, 055006. [Google Scholar] [CrossRef]
- Stenflo, L.; Brodin, G. Temperature effects on large amplitude electron plasma oscillations. Phys. Plasmas 2016, 23, 074501. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Perturbation Methods; Wiley: New York, NY, USA, 1973. [Google Scholar]
- He, J.H. Homotopy perturbation method with two expanding parameters. Indian J. Phys. 2014, 88, 193–196. [Google Scholar] [CrossRef]
- Chowdhury, M.S.H.; Hosen, M.A.; Ahmad, K.; Ali, M.Y.; Ismail, A.F. High-order approximate solutions of strongly nonlinear cubic-quintic Duffing oscillator based on the harmonic balance method. Results Phys. 2017, 7, 3962–3967. [Google Scholar] [CrossRef]
- Akbarzade, M.; Farshidianfar, A. Nonlinear transversely vibrating beams by the improved energy balance method and the global residue harmonic balance method. Appl. Math. Model. 2017, 45, 393–404. [Google Scholar] [CrossRef]
- He, J.H. The simplest approach to nonlinear oscillators. Results Phys. 2019, 15, 102546. [Google Scholar] [CrossRef]
- Almendral, J.A.; Sanjuán, M.A.F. Integrability and Symmetries of the Helmholtz oscillator with Friction. J. Phys. Math. Gen. 2003, 36, 695–710. [Google Scholar] [CrossRef]
- Almendral, J.A.; Seoane, J.; Sanjuán, M.A.F. The Nonlinear Dynamics of the Helmholtz Oscillator. Recent Res. Dev. Sound Vib. 2004, 2, 115–150. [Google Scholar]
- Kovacic, I.; Gatti, G. Helmholtz, Duffing and Helmholtz-Duffing Oscillators: Exact Steady-State Solutions. In IUTAM Symposium on Exploiting Nonlinear Dynamics for Engineering Systems; Kovacic, I., Lenci, S., Eds.; ENOLIDES 2018; IUTAM Bookseries; Springer: Cham, Switzerland, 2020; Volume 37. [Google Scholar]
- Kontomaris, S.V.; Malamou, A. Exploring oscillations with a nonlinear restoring force. Eur. J. Phys. 2022, 43, 015006. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Malamou, A. Nonlinear oscillations in a constant gravitational field. Phys. Scr. 2022, 97, 015202. [Google Scholar] [CrossRef]
- Lai, S.K.; Lim, C.W.; Wu, B.S.; Wang, C.; Zeng, Q.C.; He, X.F. Newton-harmonic balancing approach for accurate solutions to nonlinear cubic-quintic Duffing oscillators. Appl. Math. Model. 2008, 33, 852–866. [Google Scholar] [CrossRef]
- Guo, Z.; Leung, A.Y.T.; Yang, H.X. Iterative homotopy harmonic balancing approach for conservative oscillator with strong odd-nonlinearity. Appl. Math. Model. 2011, 35, 1717–1728. [Google Scholar] [CrossRef]
- Khan, Y.; Akbarzadeb, M.; Kargar, A. Coupling of homotopy and the variational approach for a conservative oscillator with strong odd-nonlinearity. Sci. Iran A 2012, 19, 417–422. [Google Scholar] [CrossRef]
- Ganji, D.D.; Gorji, M.; Soleimani, S.; Esmaeilpour, M. Solution of nonlinear cubicquintic duffing oscillators using He’s Energy Balance Method. J. Zhejiang Univ. Sci. A 2009, 10, 1263–1268. [Google Scholar] [CrossRef]
- Ganji, S.S.; Barari, A.; Karimpour, S.; Domairry, G. Motion of a rigid rod rocking back and forth and cubic-quintic duffing oscillators. J. Theor. Appl. Mech. 2012, 50, 215–229. [Google Scholar]
- Pirbodaghi, T.; Hoseini, S.H.; Ahmadian, M.T.; Farrahi, G.H. Duffing equations with cubic and quintic nonlinearities. Comput. Math. Appl. 2009, 57, 500–506. [Google Scholar] [CrossRef]
- Razzak, M.A. An analytical approximate technique for solving cubic–quintic Duffing oscillator. Alex. Eng. J. 2016, 55, 2959–2965. [Google Scholar] [CrossRef]
- Zuniga, A.E. Exact solution of the cubic–quintic Duffing oscillator. Appl. Math. Model. 2013, 37, 2574–2579. [Google Scholar] [CrossRef]
- Zakeri, G.A.; Yomba, E. Exact solutions of a generalized autonomous Duffing-type equation. Appl. Math. Model. 2015, 39, 4607–4616. [Google Scholar] [CrossRef]
- Beléndez, A.; Beléndez, T.; Martínez, F.J.; Pascual, C.; Alvarez, M.L.; Arribas, E. Exact solution for the unforced Duffing oscillator with cubic and quintic nonlinearities. Nonlinear. Dyn. 2016, 86, 1687–1700. [Google Scholar] [CrossRef]
- Beléndez, A.; Arribas, E.; Beléndez, T.; Pascual, C.; Gimeno, E.; Álvarez, M.L. Closed form exact solutions for the unforced quintic nonlinear oscillator. Adv. Math. Phys. 2017, 14, 7396063. [Google Scholar] [CrossRef]
- Cveticanin, L.; Ismail, G.M. Higher-order approximate periodic solution for the oscillator with strong nonlinearity of polynomial type. Eur. Phys. J. Plus 2019, 134, 266. [Google Scholar] [CrossRef]
- Hamdan, M.N.; Shabaneh, H.J. On the large amplitude free vibrations of a restrained uniform beam carrying an intermediate lumped mass. J. Sound Vib. 1997, 199, 711–736. [Google Scholar] [CrossRef]
- El-Dib, Y.O. Insightful and comprehensive formularization of frequency–amplitude formula for strong or singular nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control. 2023, 42, 89–109. [Google Scholar] [CrossRef]
- Cveticanin, L. Analytic solution of the system of two coupled differential equations with the fifth-order non-linearity. Phys. A Stat. Mech. Its Appl. 2003, 317, 83–94. [Google Scholar] [CrossRef]
| A (m) | T(s) (Using Equation (7)) | T (s) (Using Equation (9)) | Error (%) |
|---|---|---|---|
| 0.1 | 6.2598 | 6.2597 | 1.5975 |
| 0.3 | 6.0818 | 6.0813 | 8.2213 |
| 0.5 | 5.7689 | 5.7658 | 5.3736 |
| 1 | 4.7680 | 4.7496 | 3.8591 |
| 2 | 3.1797 | 3.1416 | 1.1982 |
| 5 | 1.4419 | 1.4138 | 1.9488 |
| 10 | 0.7362 | 0.72073 | 2.1013 |
| 100 | 0.07416 | 0.07254 | 2.1845 |
| 1000 | 0.007416 | 0.007255 | 2.1710 |
| A (m) | T(s) (Using Equation (13)) | T (s) (Using Equation (14)) | Error (%) |
|---|---|---|---|
| 0.05 | 6.1540 | 6.1318 | 0.3607 |
| 0.10 | 6.0326 | 5.9908 | 0.6929 |
| 0.15 | 5.9183 | 5.8591 | 1.0003 |
| 0.20 | 5.8102 | 5.7357 | 1.2822 |
| 0.25 | 5.7080 | 5.6199 | 1.5434 |
| 0.30 | 5.6111 | 5.5107 | 1.7893 |
| 0.35 | 5.5189 | 5.4077 | 2.0149 |
| 0.40 | 5.4312 | 5.3103 | 2.2260 |
| 0.45 | 5.3476 | 5.2179 | 2.4254 |
| 0.50 | 5.2678 | 5.1302 | 2.6121 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kontomaris, S.V.; Chliveros, G.; Malamou, A. Approximate Solutions for Undamped Nonlinear Oscillations Using He’s Formulation. J 2023, 6, 140-151. https://doi.org/10.3390/j6010010
Kontomaris SV, Chliveros G, Malamou A. Approximate Solutions for Undamped Nonlinear Oscillations Using He’s Formulation. J. 2023; 6(1):140-151. https://doi.org/10.3390/j6010010
Chicago/Turabian StyleKontomaris, Stylianos Vasileios, Georgios Chliveros, and Anna Malamou. 2023. "Approximate Solutions for Undamped Nonlinear Oscillations Using He’s Formulation" J 6, no. 1: 140-151. https://doi.org/10.3390/j6010010
APA StyleKontomaris, S. V., Chliveros, G., & Malamou, A. (2023). Approximate Solutions for Undamped Nonlinear Oscillations Using He’s Formulation. J, 6(1), 140-151. https://doi.org/10.3390/j6010010









