A Novel True Random Number Generator in Near Field Communication as Memristive Wireless Power Transmission
Abstract
:1. Introduction
2. Wireless Power Transfer and Memristor
- It generates less heat than transistors or switches.
- It is capable of storing charge and remember its last state.
- It is possible to develop chaotic behaviour.
Typical Functionality
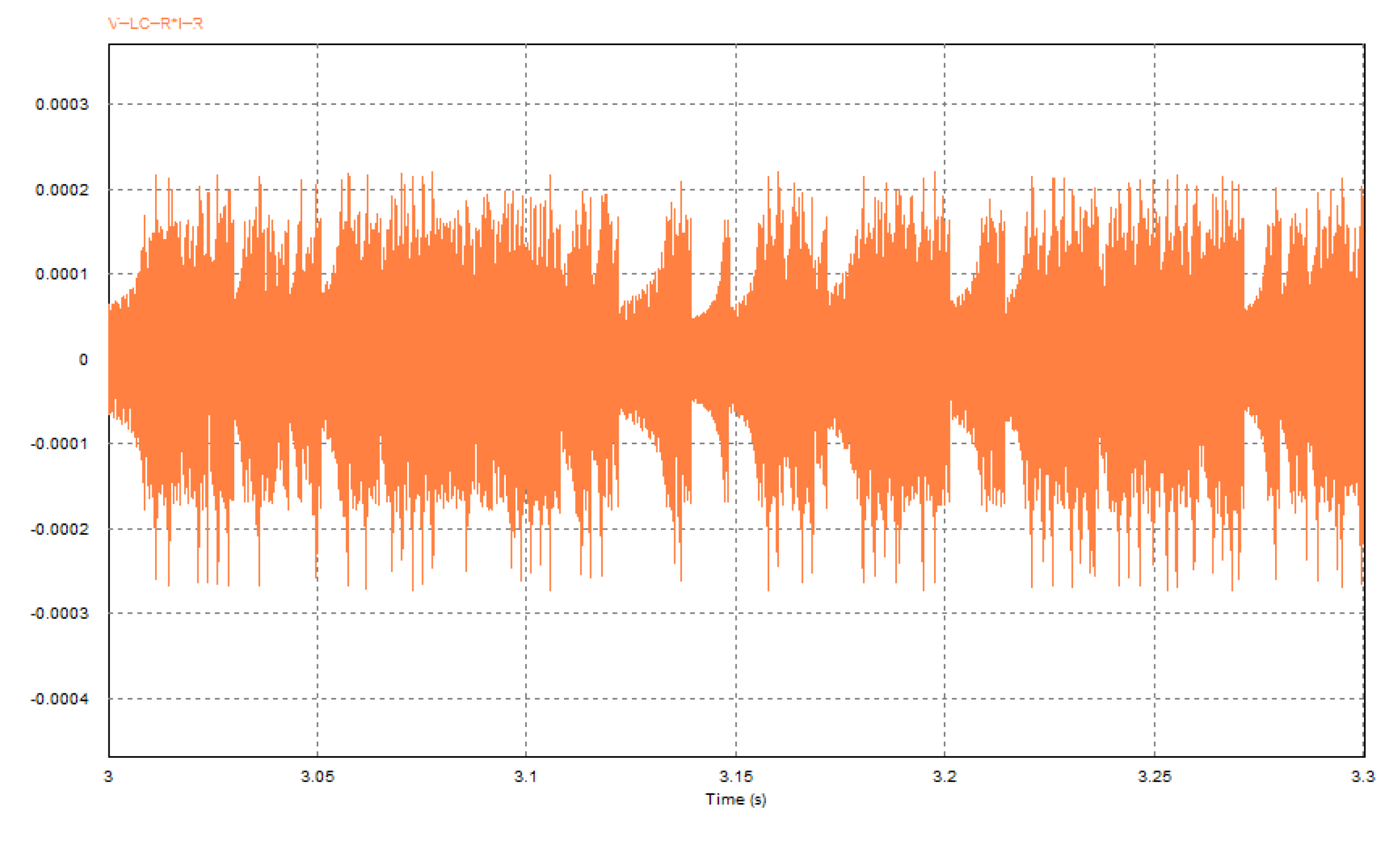
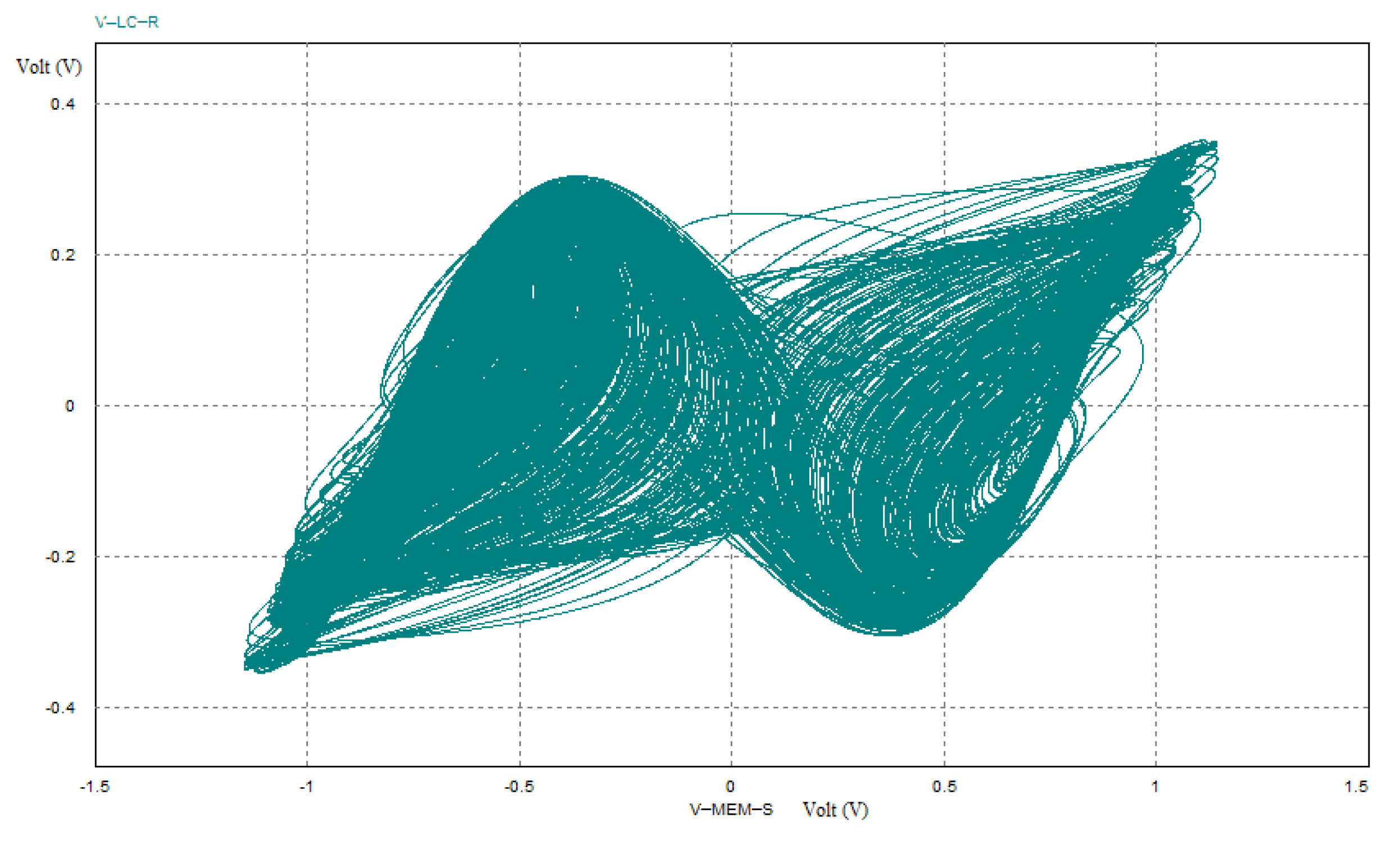
3. Stability and Chaotic Behaviour
3.1. Memristor State Variables
3.2. Theoretical Analysis
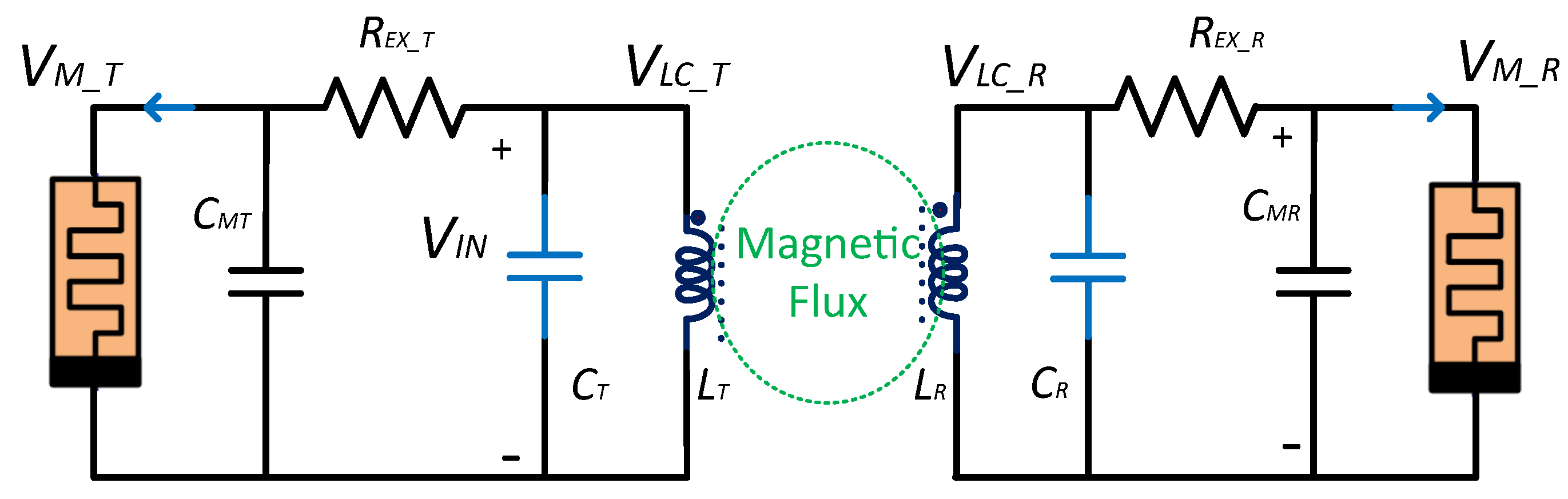
3.3. Wireless Power Transmission
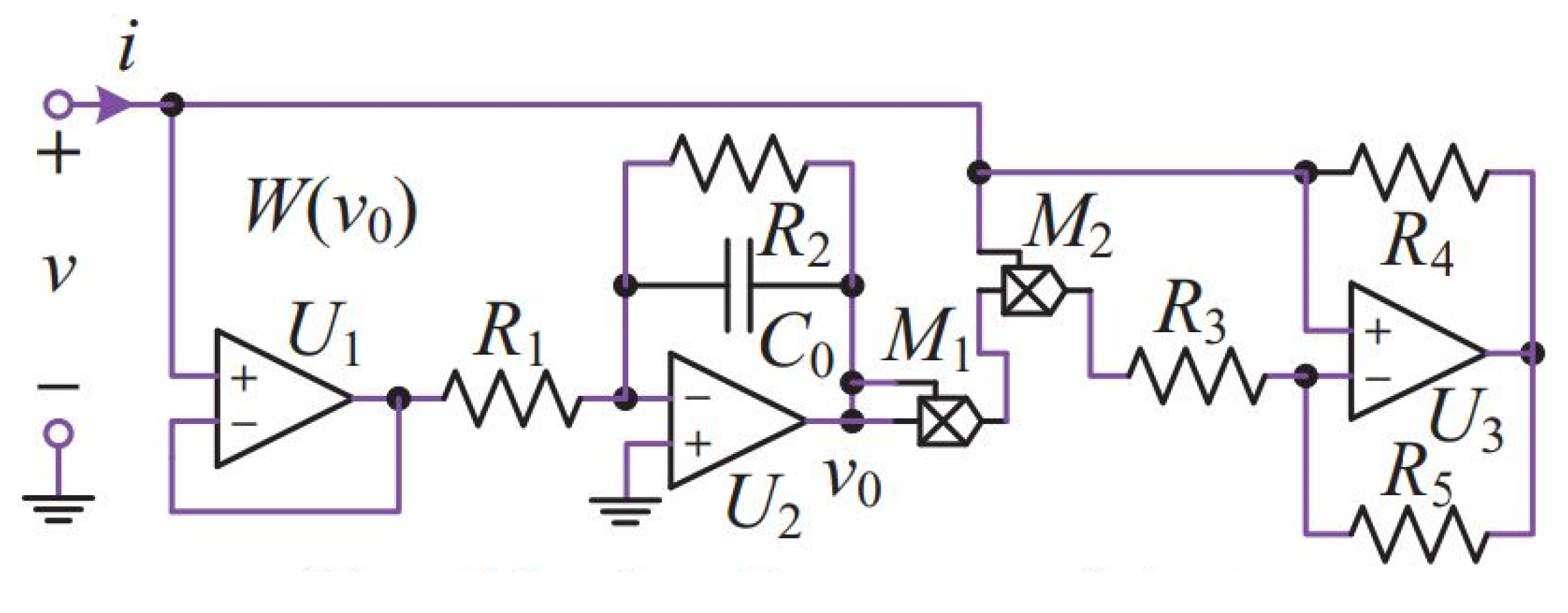
4. The Proposed Circuit and Algorithm
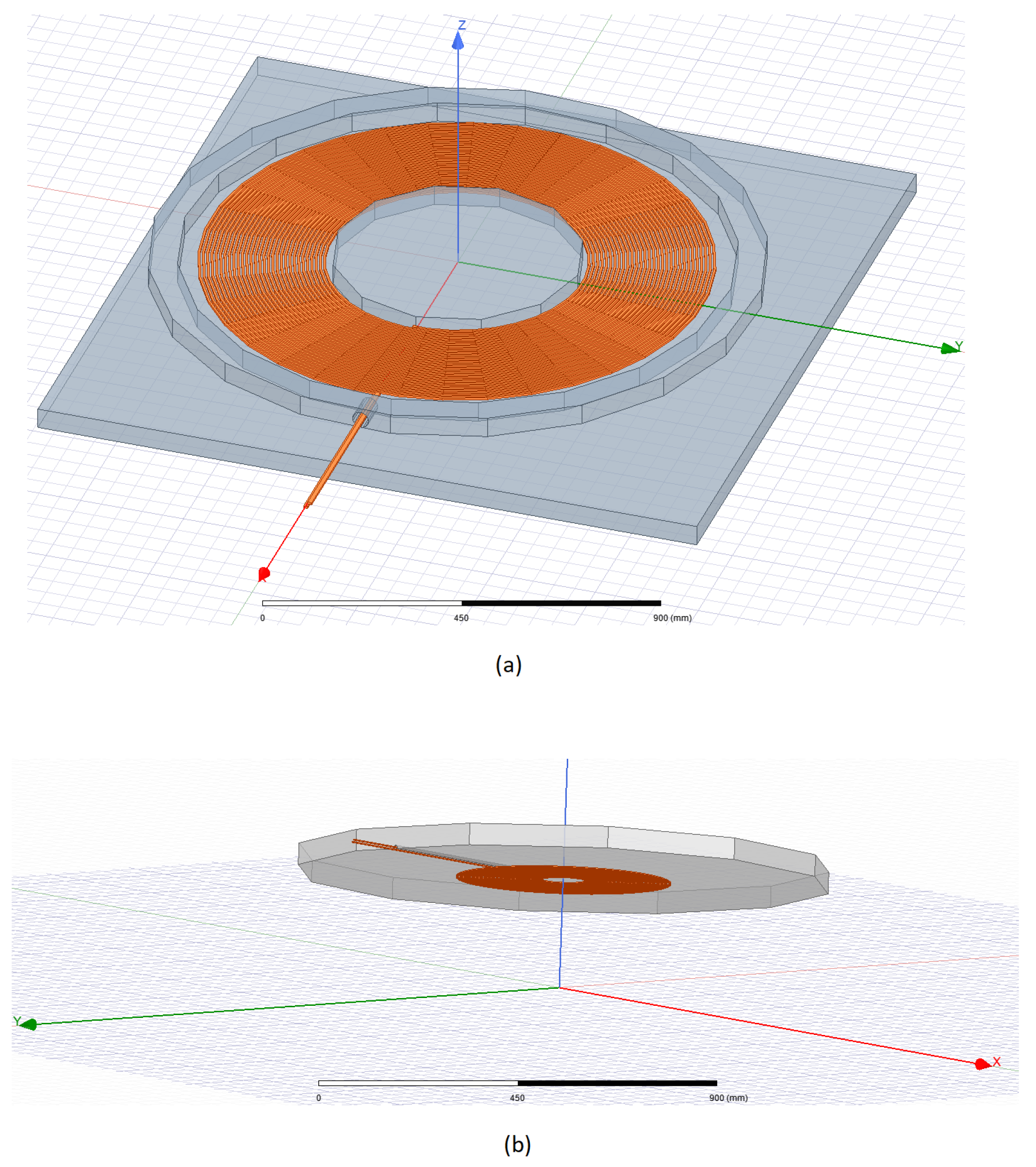
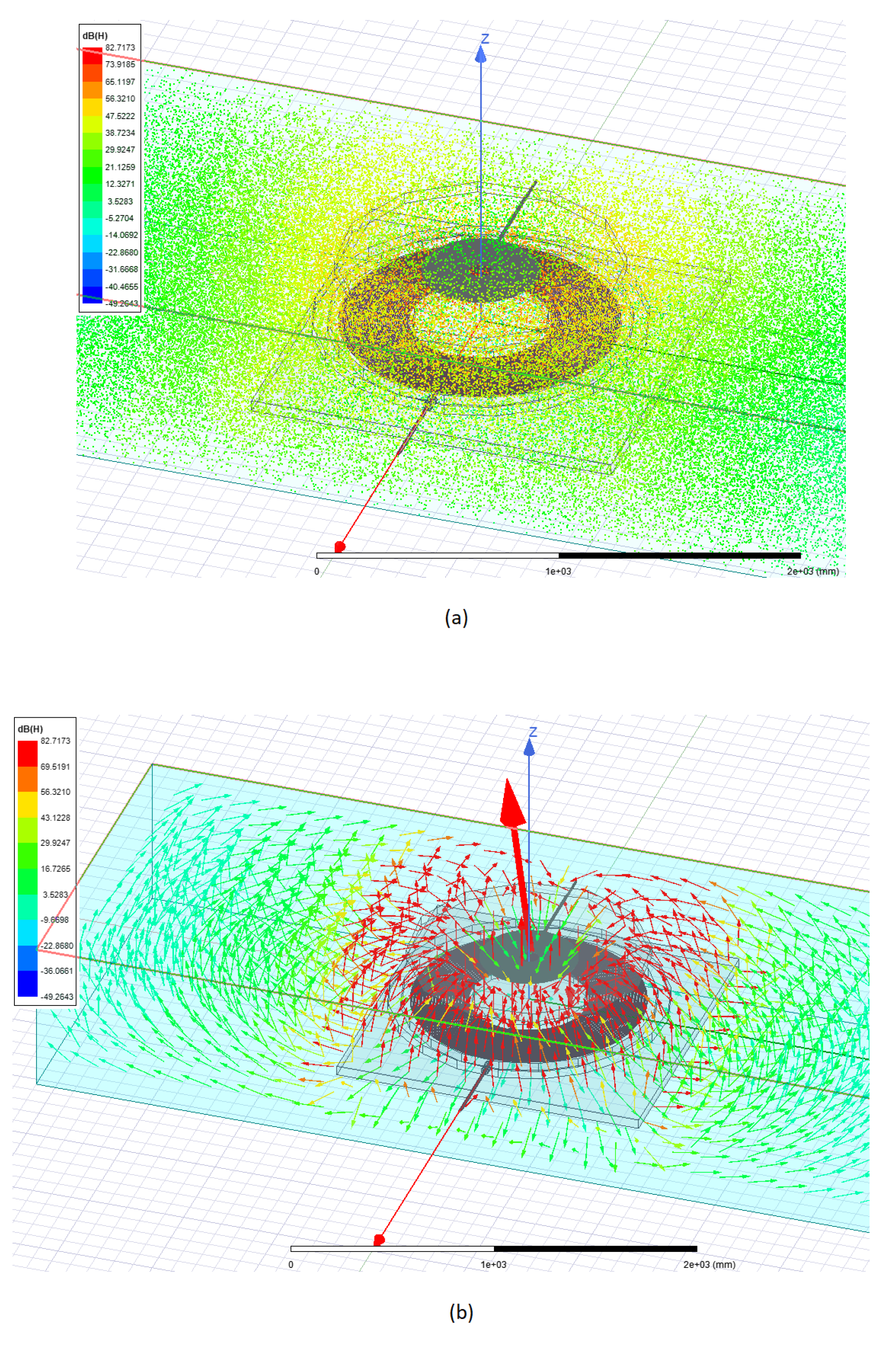
4.1. Magnetic Field
4.2. Circuit Simulation
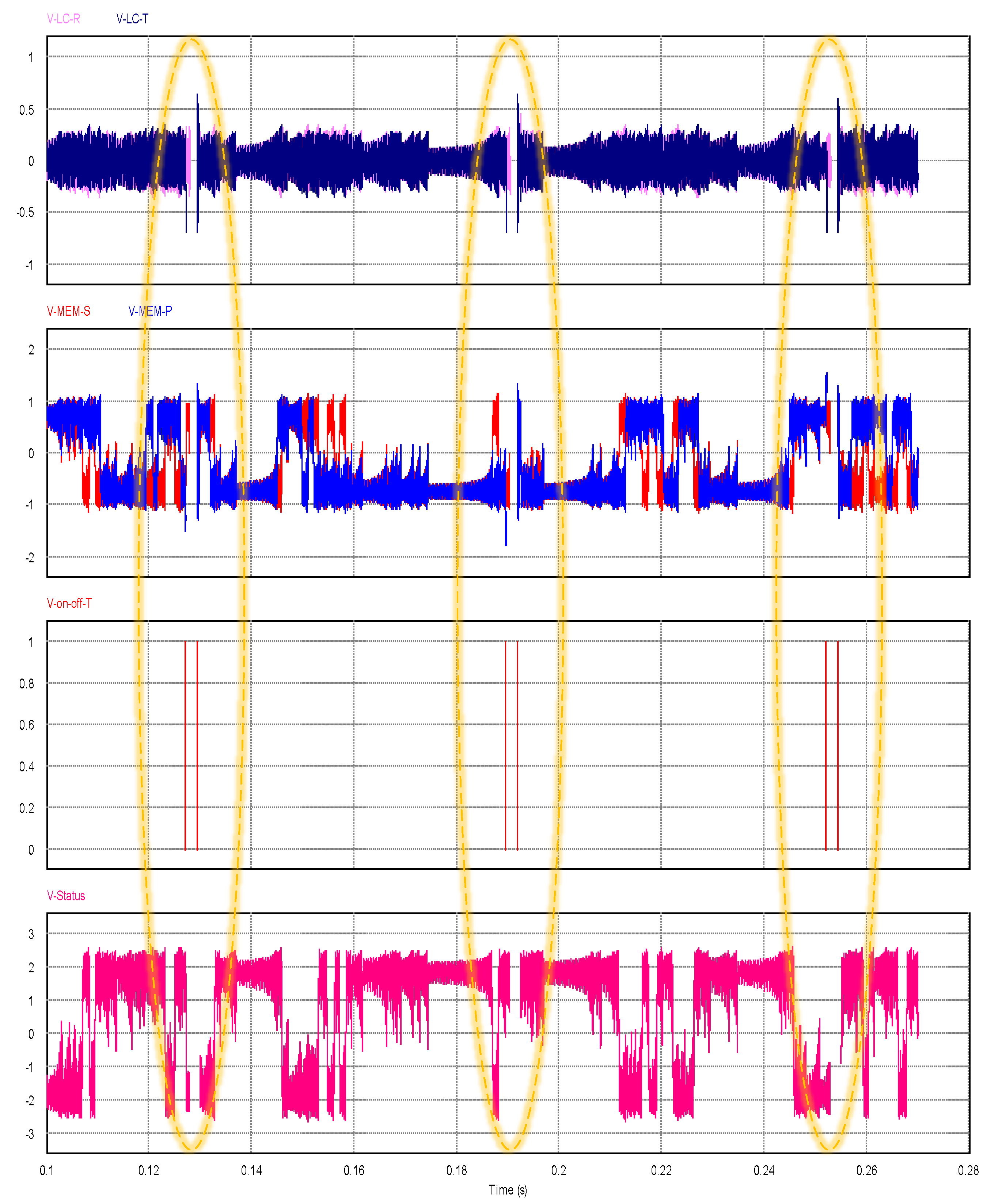
4.3. Experiment
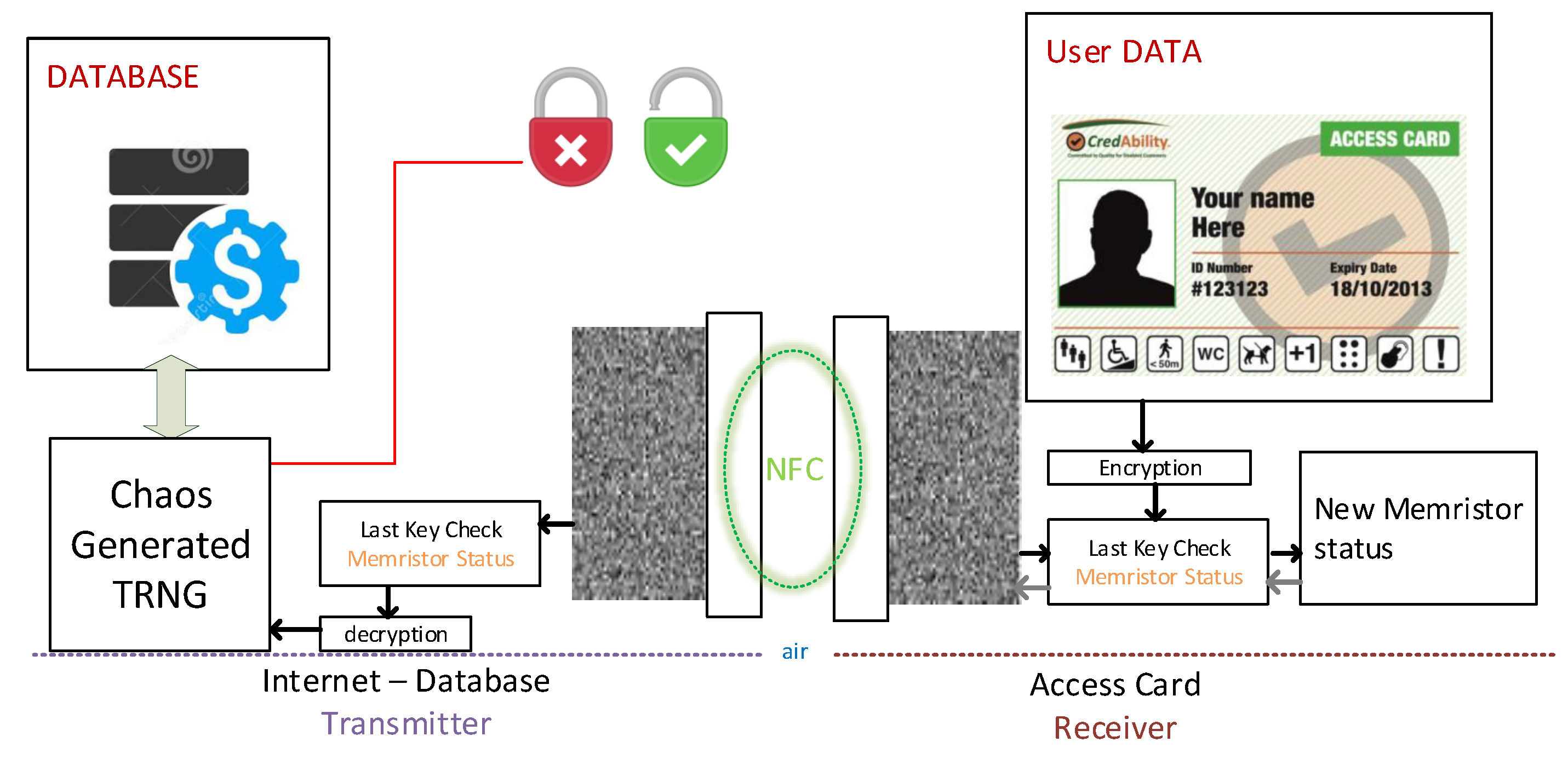
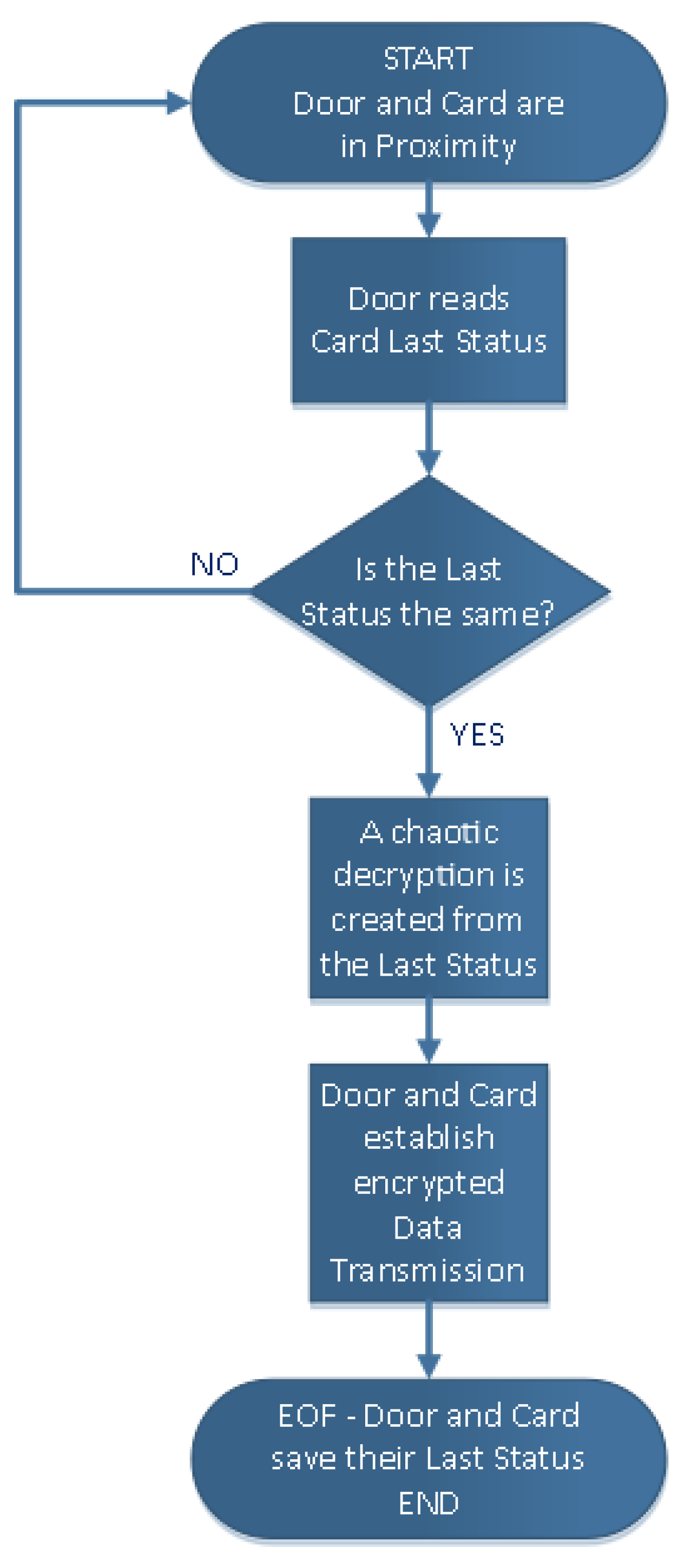
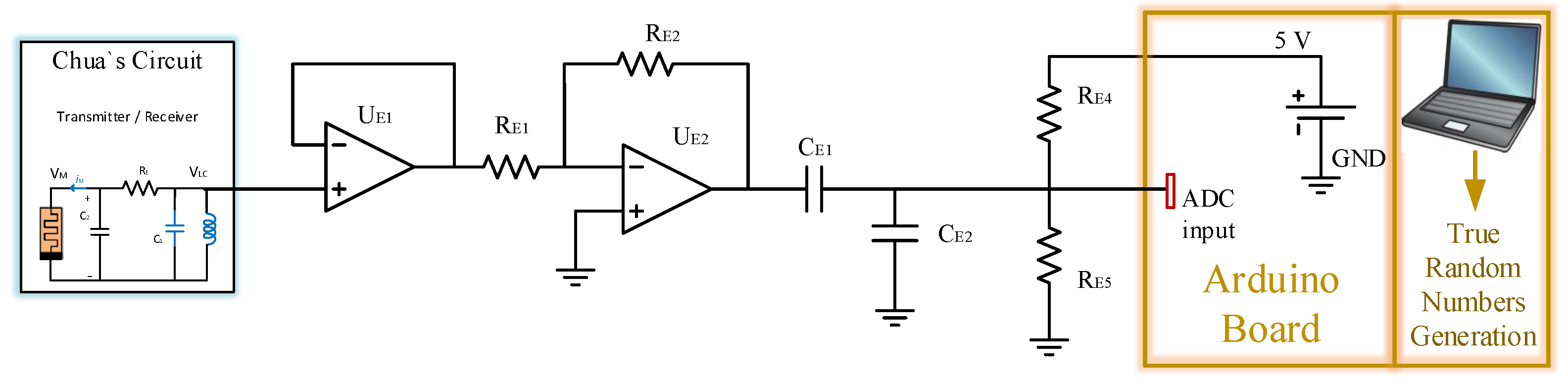
4.4. Arduino True Number Generation
4.5. Statistical Tests
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wei, X.; Wang, Z.; Dai, H. A critical review of wireless power transfer via strongly coupled magnetic resonances. Energies 2014, 7, 4316–4341. [Google Scholar] [CrossRef] [Green Version]
- Abou Houran, M.; Yang, X.; Chen, W. Magnetically coupled resonance WPT: Review of compensation topologies, resonator structures with misalignment, and EMI diagnostics. Electronics 2018, 7, 296. [Google Scholar] [CrossRef] [Green Version]
- Kuka, S.; Ni, K.; Alkahtani, M. A Review of Methods and Challenges for Improvement in Efficiency and Distance for Wireless Power Transfer Applications. Power Electron. Drives 2019, 5, 1–25. [Google Scholar] [CrossRef]
- Hou, J.; Chen, Q.; Wong, S.C.; Chi, K.T.; Ruan, X. Analysis and control of series/series-parallel compensated resonant converter for contactless power transfer. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 3, 124–136. [Google Scholar]
- Miller, J.M.; Onar, O.C.; Chinthavali, M. Primary-side power flow control of wireless power transfer for electric vehicle charging. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 3, 147–162. [Google Scholar] [CrossRef]
- Diekhans, T.; De Doncker, R.W. A dual-side controlled inductive power transfer system optimized for large coupling factor variations and partial load. IEEE Trans. Power Electron. 2015, 30, 6320–6328. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, C.; Lin, Z.; Du, J.; Hu, Y.; He, X. Wireless Power and Data Transfer via a Common Inductive Link Using Frequency Division Multiplexing. IEEE Trans. Ind. Electron. 2015, 62, 7810–7820. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Chau, K.; Liu, C.; Qiu, C.; Lin, F. An efficient wireless power transfer system with security considerations for electric vehicle applications. J. Appl. Phys. 2014, 115, 17A328. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Lu, T.; Zhao, Z.; He, F.; Chen, K.; Yuan, L. Selective Wireless Power Transfer to Multiple Loads Using Receivers of Different Resonant Frequencies. IEEE Trans. Power Electron. 2015, 30, 6001–6005. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Stanley Williams, R. How we found the missing memristor. In Chaos, CNN, Memristors and Beyond: A Festschrift for Leon Chua with DVD-ROM, Composed by Eleonora Bilotta; World Scientific: Singapore, 2013; pp. 483–489. [Google Scholar]
- Vaidyanathan, S.; Volos, C. Advances in Memristors, Memristive Devices and Systems; Springer: Berlin/Heidelberg, Germany, 2017; Volume 701. [Google Scholar]
- Bao, B.; Jiang, T.; Xu, Q.; Chen, M.; Wu, H.; Hu, Y. Coexisting infinitely many attractors in active band-pass filter-based memristive circuit. Nonlinear Dyn. 2016, 86, 1711–1723. [Google Scholar] [CrossRef]
- Iu, H.H.C.; Yu, D.S.; Fitch, A.L.; Sreeram, V.; Chen, H. Controlling Chaos in a Memristor Based Circuit Using a Twin-T Notch Filter. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 1337–1344. [Google Scholar] [CrossRef]
- Xu, Q.; Lin, Y.; Bao, B.; Chen, M. Multiple attractors in a non-ideal active voltage-controlled memristor based Chua’s circuit. Chaos, Solitons Fractals 2016, 83, 186–200. [Google Scholar] [CrossRef]
- Bao, H.; Wang, N.; Wu, H.; Song, Z.; Bao, B. Bi-stability in an improved memristor-based third-order Wien-bridge oscillator. IETE Tech. Rev. 2019, 36, 109–116. [Google Scholar] [CrossRef]
- Bao, B.; Bao, H.; Wang, N.; Chen, M.; Xu, Q. Hidden extreme multistability in memristive hyperchaotic system. Chaos Solitons Fractals 2017, 94, 102–111. [Google Scholar] [CrossRef]
- Bao, H.; Wang, N.; Bao, B.; Chen, M.; Jin, P.; Wang, G. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria. Commun. Nonlinear Sci. Numer. Simul. 2018, 57, 264–275. [Google Scholar] [CrossRef]
- Chen, M.; Yu, J.; Bao, B. Finding hidden attractors in improved memristor-based Chua’s circuit. Electron. Lett. 2015, 51, 462–464. [Google Scholar] [CrossRef]
- Hameed, S.; Hameed, B.; Hussain, S.A.; Khalid, W. Lightweight Security Middleware to Detect Malicious Content in NFC Tags or Smart Posters. In Proceedings of the 2014 IEEE 13th International Conference on Trust, Security and Privacy in Computing and Communications, Beijing, China, 24–26 September 2014; pp. 900–905. [Google Scholar] [CrossRef]
- Zhuang, Z.; Zhang, J.; Geng, W. Analysis and Optimization to an NFC Security Authentication Algorithm Based on Hash Functions. In Proceedings of the 2014 International Conference on Wireless Communication and Sensor Network, Wuhan, China, 13–14 December 2014; pp. 240–245. [Google Scholar] [CrossRef]
- Chattha, N.A. NFC—Vulnerabilities and defense. In Proceedings of the 2014 Conference on Information Assurance and Cyber Security (CIACS), Rawalpindi, Pakistan, 12–13 June 2014; pp. 35–38. [Google Scholar] [CrossRef]
- Aliexpress. NFC Door Lock. Available online: http://aliexpress.com (accessed on 30 June 2021).
- Li, W.; Yang, X. A Parallel and Reconfigurable United Architecture for Fibonacci and Galois LFSR. In Proceedings of the 2015 7th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 22–23 August 2015; Volume 1, pp. 203–206. [Google Scholar] [CrossRef]
- Essaid, M.; Akharraz, I.; Saaidi, A.; Mouhib, A. A New Image Encryption Scheme Based on Confusion-Diffusion Using an Enhanced Skew Tent Map. Procedia Comput. Sci. 2018, 127, 539–548. [Google Scholar] [CrossRef]
- Bagini, V.; Bucci, M. A Design of Reliable True Random Number Generator for Cryptographic Applications. In Cryptographic Hardware and Embedded Systems; Koç, Ç.K., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 204–218. [Google Scholar]
- Chen, W.; Che, W.; Yan, N.; Tan, X.; Min, H. Ultra-low power truly random number generator for RFID tag. Wirel. Pers. Commun. 2011, 59, 85–94. [Google Scholar] [CrossRef]
- Abunahla, H.; Shehada, D.; Yeun, C.Y.; OKelly, C.J.; Jaoude, M.A.; Mohammad, B. Novel microscale memristor with uniqueness property for securing communications. In Proceedings of the 2016 IEEE 59th International Midwest Symposium on Circuits and Systems (MWSCAS), Abu Dhabi, United Arab Emirates, 16–19 October 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, F.; Mou, J.; Sun, K.; Cao, Y.; Jin, J. Color Image Compression-Encryption Algorithm Based on Fractional-Order Memristor Chaotic Circuit. IEEE Access 2019, 7, 58751–58763. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Publication, F.I.P.S. Security Requirements for Cryptographic Modules. Available online: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.140-2.pdf (accessed on 30 June 2021).
- Hamming, R.W. Coding and Information Theory; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1986; pp. 104–108. [Google Scholar]
- Howes, L.; Thomas, D. Chapter 37. Efficient Random Number Generation and Application Using CUDA. Available online: https://developer.nvidia.com/gpugems/gpugems3/part-vi-gpu-computing/chapter-37-efficient-random-number-generation-and-application (accessed on 30 June 2021).
- Walker, J. Chi-Square Calculator. Available online: http://www.fourmilab.ch/rpkp/experiments/analysis/chiCalc.html (accessed on 30 June 2021).
- Knuth, D.E. Art of Computer Programming, Volume 2: Seminumerical Algorithms; Addison-Wesley Professional: Reading, MA, USA, 2014; pp. 35–65. [Google Scholar]











| WTP (NFC) | M-WPT | |
|---|---|---|
| Power | Transmitted (Harvested) | Harvested |
| Data | Oscillation | Chaos |
| Distance | Over 30 cm (10 cm) | 10 cm |
| Operating Frequency | Up to 13.5 MHz | Up to 7 KHz |
| Control | Timing, Switches and Data Algorithm | Data |
| Receivers | Many | Only one |
| Memristor Equivalent | |||
|---|---|---|---|
| Parameter | Value | Parameter | Value |
| 4 k | 2 k | ||
| 10 k | 1 nF | ||
| 1.4 k | 1 | ||
| 2 k | 0.1 | ||
| Chua’s Parameter | Transmitter | Receiver | Value |
|---|---|---|---|
| 6.8 nF | |||
| 68 nF | |||
| 2.18 k | |||
| L | 8 mH | ||
| M | 3.8 mH |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuka, C.S.; Hu, Y.; Xu, Q.; Chandler, J.; Alkahtani, M. A Novel True Random Number Generator in Near Field Communication as Memristive Wireless Power Transmission. J 2021, 4, 764-783. https://doi.org/10.3390/j4040052
Kuka CS, Hu Y, Xu Q, Chandler J, Alkahtani M. A Novel True Random Number Generator in Near Field Communication as Memristive Wireless Power Transmission. J. 2021; 4(4):764-783. https://doi.org/10.3390/j4040052
Chicago/Turabian StyleKuka, Colin Sokol, Yihua Hu, Quan Xu, James Chandler, and Mohammed Alkahtani. 2021. "A Novel True Random Number Generator in Near Field Communication as Memristive Wireless Power Transmission" J 4, no. 4: 764-783. https://doi.org/10.3390/j4040052
APA StyleKuka, C. S., Hu, Y., Xu, Q., Chandler, J., & Alkahtani, M. (2021). A Novel True Random Number Generator in Near Field Communication as Memristive Wireless Power Transmission. J, 4(4), 764-783. https://doi.org/10.3390/j4040052










