Energetics of Urban Canopies: A Meteorological Perspective
Abstract
:1. Introduction
- Surface impermeability (Section 3);
- Construction materials (Section 3);
- Building-street aspect ratio (Section 4);
- Presence of vegetation (Section 5.1);
- Presence of water bodies (Section 5.2).
2. Methods of Studying the Meteorology in Urban Areas
2.1. Field Experiments
2.2. Numeric Modeling
2.3. Lab Experiments
2.4. Remote Sensing
3. The Urban Heat Island
- In land cover materials—by changing the natural land cover (e.g., grass or bare ground) and the thermal and radiometric properties of the surface surfer modifications. The thermal properties of typical natural and construction materials can be found in the literature, such as [44]. The high thermal conductivity of these materials causes urban areas to have temperature variations more quickly than rural areas, while the high thermal capacity provides large energy storage in the urban canopy. The albedo also changes.
- By creating impervious spots—most civil construction materials make the ground surface impervious. This absolutely changes the surface hydraulic regime: rain water cannot percolate into the soil and runs off to other areas. Moreover, the soil moisture evaporation is halted. Since the water vapor heat capacity is high (2.5 MJ/kg), a substantial change in the surface energy partition between sensible and latent heat fluxes takes place, promoting a rise in the surface temperature during the daytime.
- By reducing vegetation cover—surface vegetation transpiration promotes the fall in ground surface temperature. The grass texture, for example, can also intercept a greater portion of incoming solar radiation which reduces the surface heating.
- by producing anthropogenic heat—human activity is marked by the energy consumption which eventually turns into useless heat that makes urban temperatures higher than rural temperatures.
- Changing the landscape geometry—the geometry of urban landscape is absolutely connected to how the energy coming in and goes out the urban canopy. These geometric features have mainly been parameterized by the aspect ratio, which we will discuss in detail in the next section.
4. Aspect Ratio
4.1. Influence on Energetics
- Trapping of longwave radiation (+)—the loss of radiant energy in an urban canopy occurs only after the light beam find the open skies. An infrared beam emitted from a surface, such as a street or wall, suffers multiple reflections before eventually leaving the canopy. Since each reflection is not perfectly elastic, a fraction of energy of the beam is left behind and absorbed by the street surface or wall. The higher the aspect ratio, the more reflection and energy are absorbed by the canopy. This process happens throughout the day, but is more relevant at night.
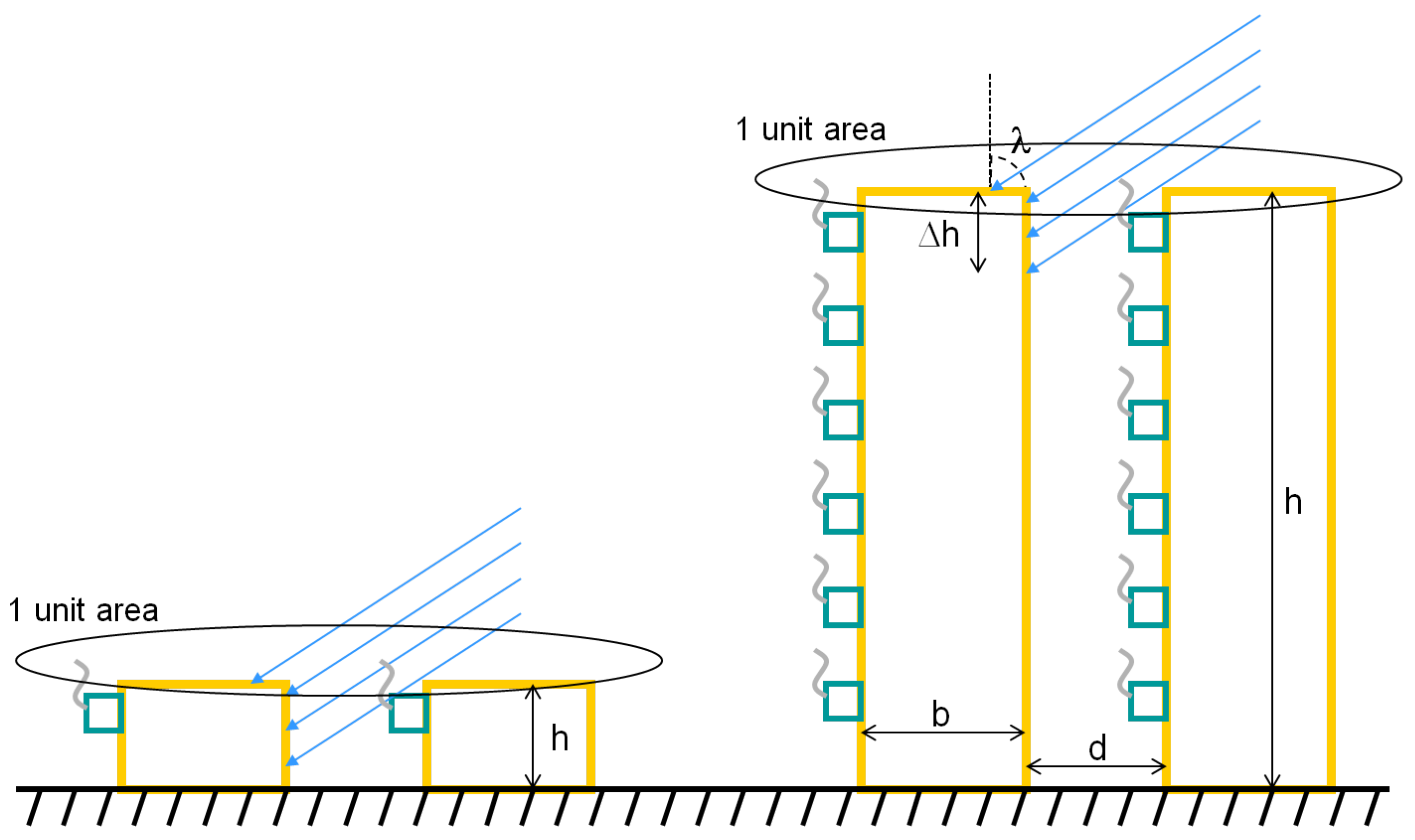
- Production of anthropogenic heat (+)—this is an indirect consequence of the aspect ratio. In this case, it is more intuitive to think of this in terms of a constant distance among buildings and a varying height (Figure 1). The volume of human activity is clearly proportional to the number of floors in building. As the figure suggests, in a multiple-floor building, the number of air conditioners, boilers, ovens, appliances, light bulbs, etc., is multiplied by the number of floors. The use of central system does not affect at all the reasoning, since the system capacity is likely to be equivalent, with only some energy savings perhaps. Moreover, in regions with more high-rise buildings, such as downtown, the traffic is much heavier. That means that there is more fuel burning per square area.
- Shading area (−)—in the opposite direction of the longwave trapping, in urban areas with high aspect ratios, there are larger portions of canopy under shade. These portions can be horizontal (streets, sidewalks, etc.) or vertical (walls). Regardless of the orientation, they are closer to the ground surface or the pedestrian level. Often there are areas that never receive direct solar radiation. In such cases, the surfaces heat up at the cost of diffuse solar radiation. As a consequence, the temperatures in these places are much lower.
- Canopy mass (−)—the two main temperatures forcesover building walls and its interior are the direct solar radiation and the synoptic conditions. Both contribute to an increase in conductive fluxes into the buildings walls, roofs and the interior. A variation in any of these conditions is increasingly damped down and delayed inasmuch as the canopy’s effective heat capacity is larger. Regardless of the construction materials employed, the canopy mass is a measure of its effective heat capacity. A high-rise building can be subjected to the same synoptic forces as low-rise buildings, but the direct solar radiation must be partitioned with a larger mass in the first case. The radiation reaches the urban canopy only in certain portions and heats the air and solid portions locally; this energy is diffused to all canopies.
- Wind speed inside the urban canopy (+)—this is an indirect effect. Wind speed in urban areas is influenced by urban obstacles and their orientation. This means that the temperature advection is reduced when aspect ratios are higher. Furthermore, the turbulence produced by the wind shear also reduces, making the vertical sensible heat fluxes less. This is a dynamical effect of the aspect ratio on urban energetics. It is worthwhile to mention that the overwhelming majority of urban paramerizations uses bulk formulas such as easily found in textbooks (e.g., [58]) to compute the sensible heat flux of the urban canopy and, therefore, its cooling rate. It is clear from that that the urban canopy in numeric models is rather sensitive to the wind speed, and consequently to the aspect ratio.
4.2. Influence on the Airflow and UBL Dynamics
4.2.1. Boundary Layer Growth
4.2.2. Aspect Ratio Impact on Boundary Layer Growth
4.3. Air Quality
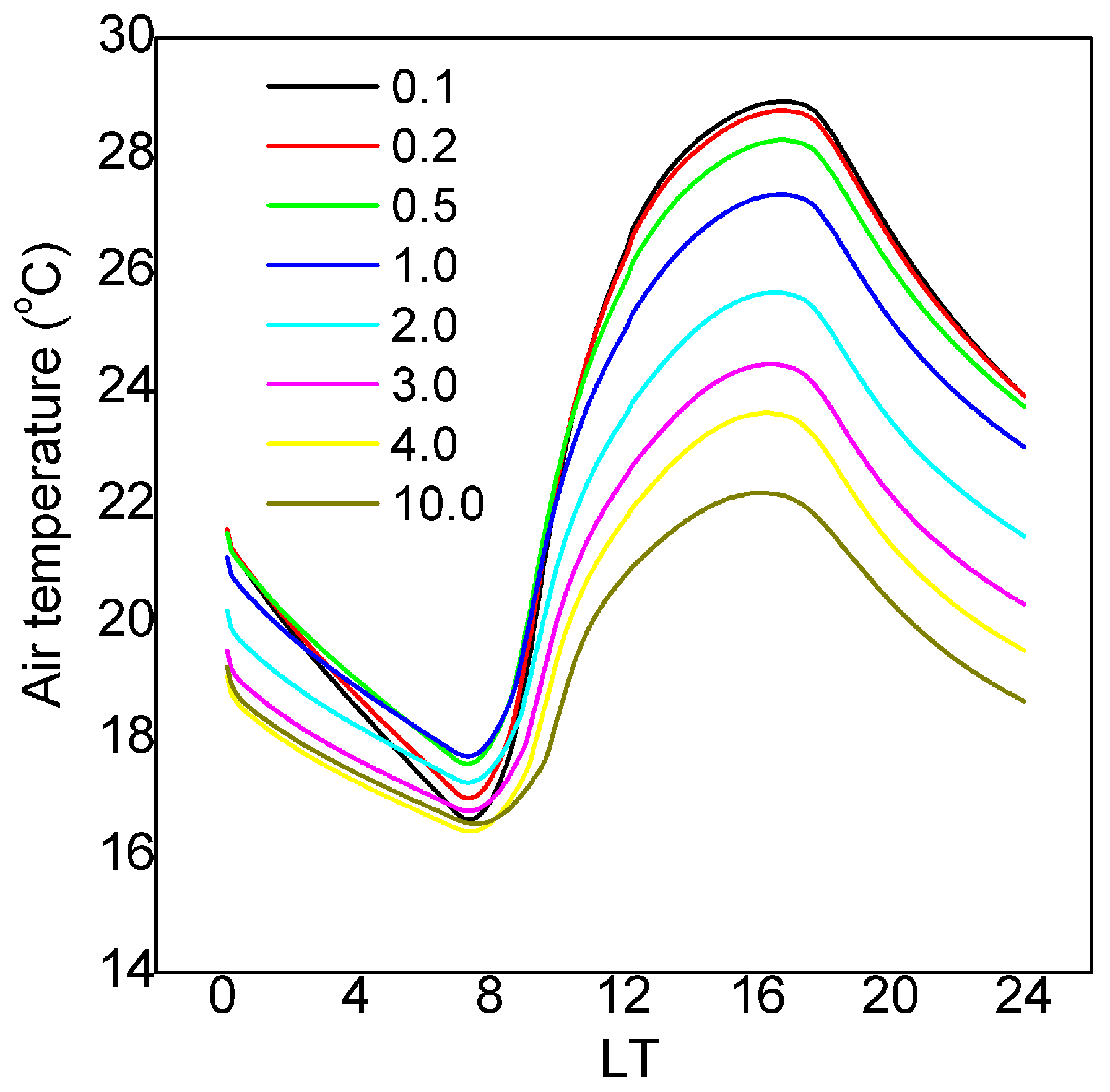
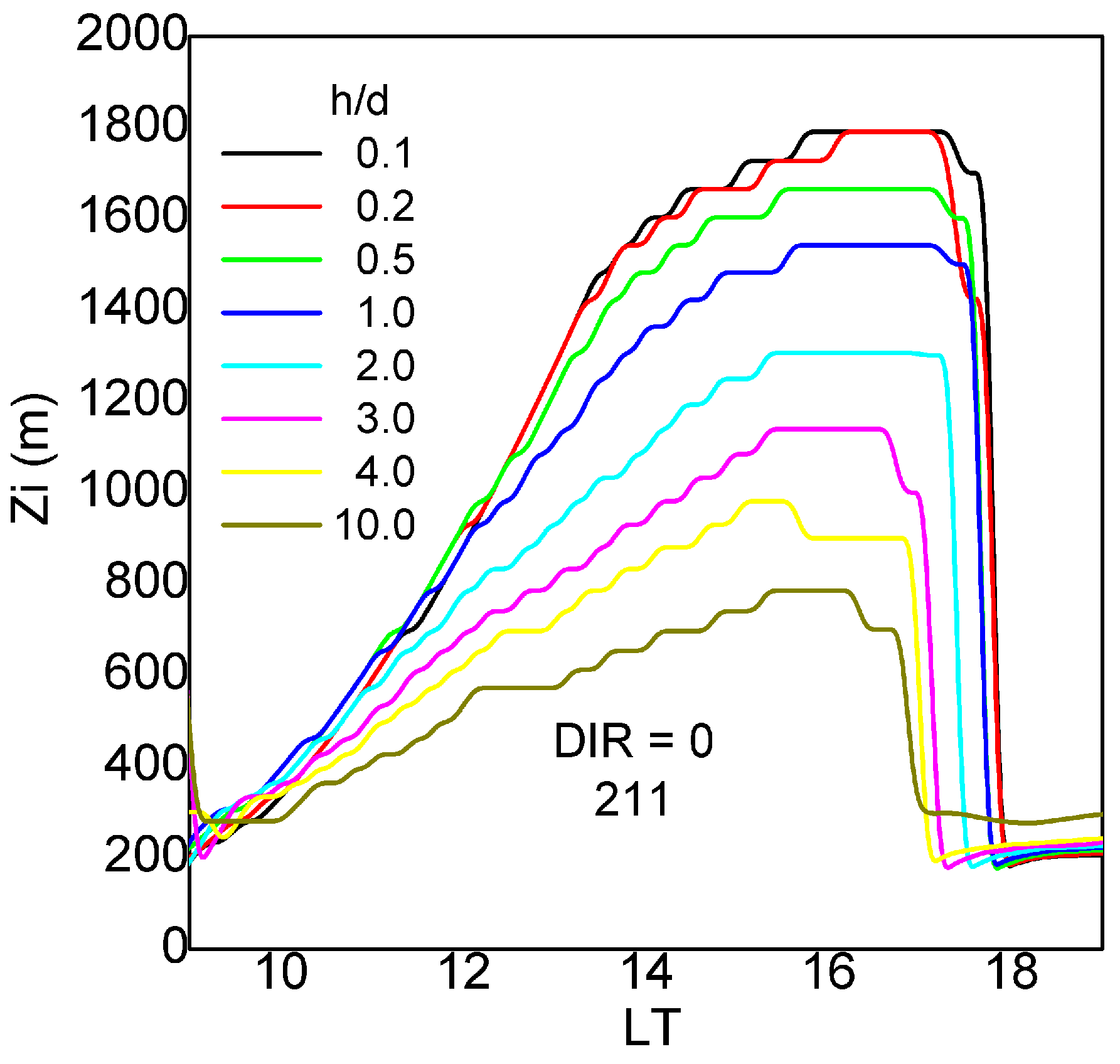
4.4. Sensible Heat Flux and Temperature an Tendency towards Downtown: The JU2003 Case
5. Other Effects: Presence of Vegetation and Water Bodies in Urban Canopies
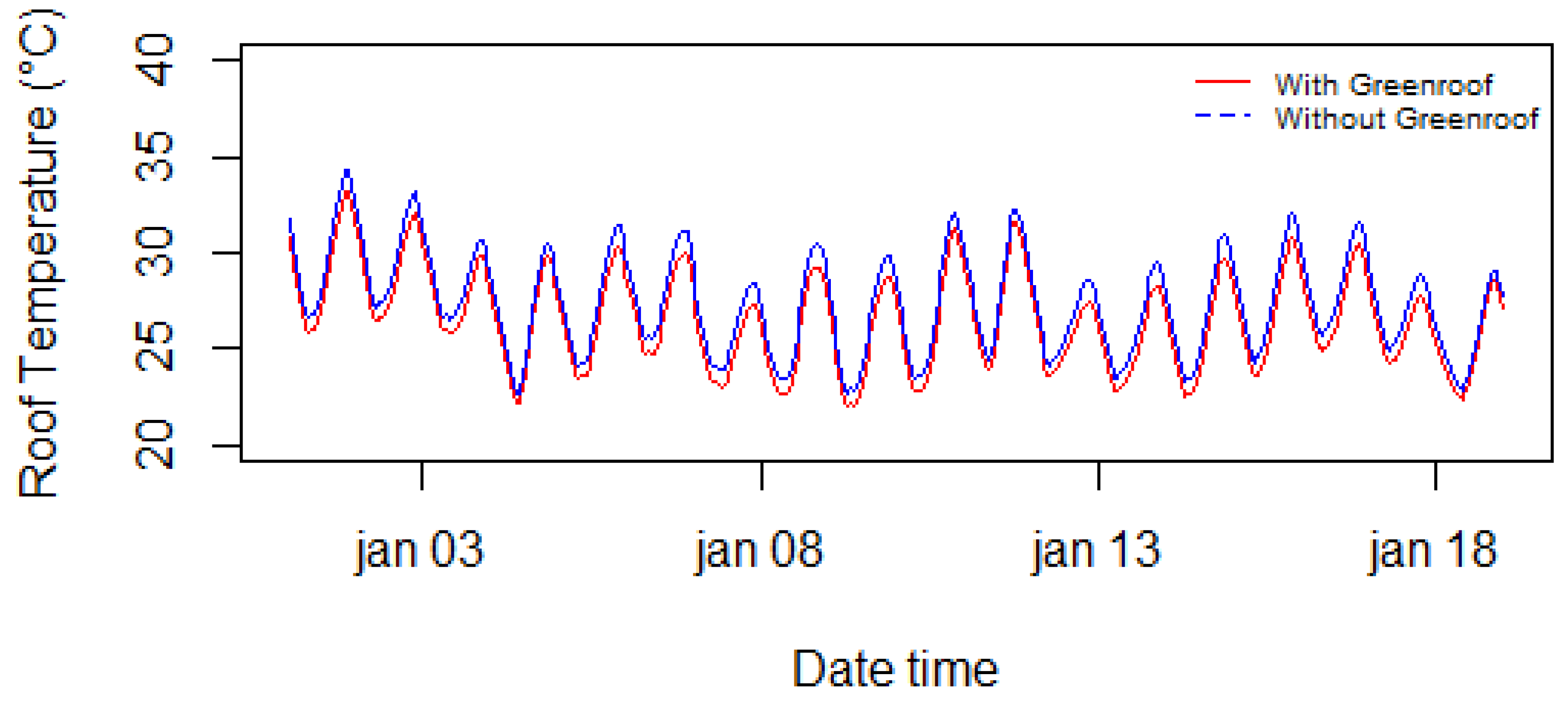
5.1. Effect of Vegetation
5.2. Effect of Water Bodies
6. Final Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oke, T.R. The urban energy balance. Prog. Phys. Geogr. 2001, 12, 471–508. [Google Scholar] [CrossRef]
- Rotach, M.W.; Vogt, R.; Bernhofer, C.; Batchvarova, E.; Christen, A.; Clappier, A.; Feddersen, B.; Gryning, S.-E.; Martucci, G.; Mayer, H.; et al. BUBBLE—An urban boundary layer meteorology project. Theor. Appl. Climatol. 2005, 81, 231–261. [Google Scholar] [CrossRef] [Green Version]
- Wood, C.R.; Arnold, S.J.; Balogun, A.A.; Barlow, J.F.; Belcher, S.E.; Britter, R.E.; White, I.R. Dispersion experiments in central London: The 2007 DAPPLE project. Bull. Am. Meteorol. Soc. 2009, 90, 955–970. [Google Scholar] [CrossRef]
- Mestayer, P.G.; Durand, P.; Augustin, P. The urban boundary-layer field campaign in marseille (ubl/clu-escompte): Set-up and first results. Bound. Lay. Meteorol. 2005, 114, 315–365. [Google Scholar] [CrossRef]
- Allwine, K.J.; Leach, M.J.; Stockham, L.W.; Shinn, J.S.; Hosker, R.P.; Bowers, J.F.; Pace, J.C. 2004: Overview of Joint Urban 2003—An atmospheric dispersion study in Oklahoma City. In Proceedings of the 84th AMS Annual Meeting, Seattle, WA, USA, 11–15 January 2004. [Google Scholar]
- Eliasson, I.; Offerle, B.; Grimmond, C.S.B.; Lindqvist, S. Wind fields and turbulence statistics in an urban street canyon. Atmos. Environ. 2006, 40, 1–16. [Google Scholar] [CrossRef]
- Kanda, M.; Kasamatsu, F.; Moriwaki, R. Spatial variability of turbulent fluxes and temperature profile in an urban roughness layer. Bound. Lay. Meteorol. 2006, 121, 339–350. [Google Scholar] [CrossRef]
- Doran, J.C.; Barnard, J.C.; Arnott, W.P.; Cary, R.; Coulter, R.; Fast, J.D.; Kassianov, E.I.; Kleinman, L.; Laulainen, N.S.; Martin, T.; et al. The T1-T2 Study: Evolution of Aerosol Properties Downwind of Mexico City. Atmos. Chem. Phys. 2007, 7, 1585–1598. [Google Scholar] [CrossRef] [Green Version]
- Hanna, S.; White, J.; Zhou, Y. Observed winds, turbulence, and dispersion in built-up downtown areas of Oklahoma City and Manhattan. Bound. Lay. Meteorol. 2007, 125, 441–468. [Google Scholar] [CrossRef]
- Pearlmutter, D.; Berliner, P.; Shaviv, E. Evaluation of urban surface energy fluxes using an open-air scale model. J. Appl. Meteor 2005, 44, 532–545. [Google Scholar] [CrossRef]
- Kanda, M.; Kawai, T.; Kanega, M.; Moriwaki, R.; Narita, K.; Hagishima, A. Simple energy balance model for regular building arrays. Bound. Lay. Meteorol. 2005, 116, 423–443. [Google Scholar] [CrossRef]
- Biltoft, C. 2001: Customer Report for Mock Urban Setting test (MUST). Rep. No. WDTC-FR-01-121, US Army Dugway Proving Ground. Available online: https://my.mech.utah.edu/~pardyjak/documents/MUSTCustReport.pdf (accessed on 21 August 2021).
- Kastner-Klein, P.; Fedorovich, E.; Rotach, M.W. A wind tunnel study of organized and turbulent air motions in urban street canyons. J. Wind Eng. Ind. Aerodyn. 2001, 89, 849–861. [Google Scholar] [CrossRef]
- Plate, E.J. Methods of investigating urban wind fields—Physical models. Atmos. Environ. 1999, 33, 3981–3989. [Google Scholar] [CrossRef]
- Robins, A.; Castro, I.; Hayden, P.; Steggel, N.; Contini, D.; Heist, D.; Taylor, T.J. A wind tunnel study of dense gas dispersion in a stable boundary layer over rough surface. Atmos. Environ. 2001, 35, 2253–2563. [Google Scholar] [CrossRef]
- Allwine, J.; Shinn, J.H.; Streit, G.E.; Clawson, K.L.; Brown, B. Overview of URBAN 2000: A multi-scale field study of dispersion through an urban environment. Bull. Am. Meteorol. Soc. 2002, 83, 521–536. [Google Scholar] [CrossRef] [Green Version]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows–Their Structure and Measurement; Oxford University Press: Oxford, UK, 1994; p. 289. [Google Scholar]
- Aubinet, M.; Vesala, T.; Papale, D. (Eds.) Eddy Covariance—A Practical Guide to Measurement and Data Analysis; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Oke, T.R. Initial Guidance to Obtain Representative Meteorological Observations at Urban Sites, WMO/TD-No. 1250. 2006. Available online: http://blogs.ubc.ca/toke/files/2015/12/IOM-81-UrbanMetObs.pdf (accessed on 21 August 2021).
- Pearlmutter, D.; Berliner, P.; Shaviv, E. Physical modeling of pedestrian energy exchange within the urban canopy. Build. Environ. 2006, 41, 783–795. [Google Scholar] [CrossRef]
- Martilli, A. Numerical Study of Urban Impact on Boundary Layer Structure: Sensitivity to Wind Speed, Urban Morphology, and Rural Soil Moisture. J. Appl. Meteorol. 2002, 41, 1247–1266. [Google Scholar] [CrossRef]
- Hamdi, R.; Schayes, G. Sensitivity study of the urban heat island intensity to urban characteristics. Int. J. Climatol. 2008, 28, 973–982. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Aerodynamic properties of urban area derived from analysis of surface form. J. Appl. Meteor. 1999, 38, 1261–1292. [Google Scholar] [CrossRef]
- Britter, R.E.; Hanna, S.R. Flow and dispersion in urban areas. Annu. Rev. Fluid Mech. 2003, 35, 469–496. [Google Scholar] [CrossRef]
- Antonia, R.; Luxton, R. The response of a turbulent boundary layer to a step change in surface roughness Part 1. Smooth to rough. J. Fluid Mech. 1971, 48, 721–761. [Google Scholar] [CrossRef]
- Antonia, R.; Luxton, R. The response of a turbulent boundary layer to a step change in surface roughness. Part 2. Rough-to-smooth. J. Fluid Mech. 1972, 53, 737–757. [Google Scholar] [CrossRef]
- Raupach, M.R.; Thom, A.S.; Edwards, I. A wind-tunnel study of turbulent flow close to regularly arrayed rough surfaces. Bound. Lay. Meteorol. 1980, 18, 373–397. [Google Scholar] [CrossRef]
- Barlow, J.B.; Rae, W.H., Jr.; Pope, A. Low-Speed WindTunnel Testing, 3rd ed.; John Wiley and Sons: New York, NY, USA, 1999. [Google Scholar]
- Counihan, J. An improved method of simulating an atmospheric boundary layer in a wind tunnel. Atmos. Environ. 1969, 3, 197–200. [Google Scholar] [CrossRef]
- Mehta, R.D.; Bradshaw, P. Design rules for small low speed wind tunnels. Aeronaut. J. 1979, 83, 443–449. [Google Scholar]
- Baik, J.J.; Park, R.E.; Chun, H.Y.; Kim, J.J. A laboratory model of urban street-canyon flows. J. Appl. Meteor. 2000, 39, 1592–1600. [Google Scholar] [CrossRef]
- Uehara, K.; Murakami, S.; Oikawa, S.; Wakamatsu, S. Wind tunnel experiments on how thermal stratification affects flow in and above urban street canyons. Atmos. Environ. 2000, 34, 1553–1562. [Google Scholar] [CrossRef]
- Allegrini, J.; Dorer, V.; Carmeliet, J. Wind tunnel measurements of buoyant flows in street canyons. Build. Environ. 2013, 59, 315–326. [Google Scholar] [CrossRef]
- Cui, P.-Y.; Li, Z.; Tao, W.-Q. Buoyancy flows and pollutant dispersion through different scale urban areas: CFD simulations and wind-tunnel measurements. Build. Environ. 2016, 104, 76–91. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Chew, L.W.; Kubilay, A.; Carmeliet, J. Isothermal and non-isothermal flow in street canyons: A review from theoretical, experimental and numerical perspectives. Build. Environ. 2020, 184, 107163. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, H.; Kubilay, A.; Carmeliet, J. Buoyancy effects on the flows around flat and steep street canyons in simplified urban settings subject to a neutral approaching boundary layer: Wind tunnel PIV measurements. Sci. Total. Environ. 2021, 797, 149067. [Google Scholar] [CrossRef]
- Park, S.-J.; Kim, J.-J.; Choi, W.; Kim, E.-R.; Song, C.-K.; Pardyjak, E.R. Flow Characteristics Around Step-Up Street Canyons with Various Building Aspect Ratios. Bound.-Layer Meteorol. 2020, 174, 411–431. [Google Scholar] [CrossRef] [Green Version]
- Jin, M.; Shepherd, J.M. Inclusion of Urban Landscape in a Climate Model. Bull. Amer. Meteor. Soc. 2005, 86, 681–689. [Google Scholar] [CrossRef] [Green Version]
- Menut, L.; Flamant, C.; Pelon, J.; Flamant, P.H. Urban boundary-layer height determination from lidar measurements over the Paris area. Appl. Opt. 1999, 38, 945–954. [Google Scholar] [CrossRef]
- Eichinger, W.E.; Cooper, D.I. Using lidar remote sensing for spatially resolved measurements of evaporation and other meteorological parameters. Agron. J. 2007, 99, 255–271. [Google Scholar] [CrossRef]
- Marciotto, E.R.; Nakaema, W.N.; Landulfo, E. Evolution of the atmospheric boundary layer: LIDAR observations and modeling. In Proceedings of the 26th International Laser Radar Conference (ILRC26), Porto Heli, Greece, 25–29 June 2012; Volume II. [Google Scholar] [CrossRef]
- Mahrt, L. Surface Heterogeneity and Vertical Structure of the Boundary Layer. Bound.-Layer Meteorol. 2000, 96, 33–62. [Google Scholar] [CrossRef]
- Redway, J.W. Urban versus suburban temperatures. Mon. Weather Rev. 1919, 47, 28–29. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Routledge: Methuen, MA, USA, 1987; ISBN 9780203407219. [Google Scholar]
- Marciotto, E.R. Estudo da Influência de um Dossel Urbano sobre o Balanço de Energia na Superfície e Implicações na Estrutura Vertical da Camada Limite Atmosférica. Ph.D. Thesis, Universidade de São Paulo, São Paulo, Brazil, 2008. [Google Scholar]
- Marciotto, E.R. Impact of city verticalization on urban surface energy budget: A modeling study. In Proceedings of the Seventh International Conference on Urban Climate, Yokohama, Japan, 29 June–3 July 2009. [Google Scholar]
- Marciotto, E.R.; Oliveira, A.P.; Hanna, S.R. Modeling study of the aspect ratio influence on urban canopy energy fluxes with a modified wall-canyon energy budget scheme. Build. Environ. 2010, 45, 2497–2505. [Google Scholar] [CrossRef]
- Tso, C.P.; Chan, B.K.; Hashim, M.A. An Improvement to the Basic Energy Balance Model for Urban Thermal Environment Analysis. Ener. Build 1990, 14, 143–152. [Google Scholar] [CrossRef]
- Martins, T.; Adolphe, L.; Bonhomme, M.; Faraut, S.; Ginestet, S.; Michel, C.; Guyard, W. Impact of Urban Cool Island measures on outdoor climate and pedestrian comfort: Solutions for a new district of Toulouse, France. Sustain. Cities Soc. 2016, 26, 2–26. [Google Scholar] [CrossRef]
- Theeuwes, N.E.; Steeneveld, G.J.; Ronda, R.J.; Heusinkveld, B.G.; Van Hove, L.W.A.; Holtslag, A.A.M. Seasonal dependence of the urban heat island on the street canyon aspect ratio. Q. J. R. Meteorol. Soc. 2014, 140, 2197–2210. [Google Scholar] [CrossRef]
- Herrmann, J.; Matzarakis, A. Mean radiant temperature in idealised urban canyons-examples from Freiburg, Germany. Int. J. Biometeorol. 2012, 56, 199–203. [Google Scholar] [CrossRef] [PubMed]
- Emmanuel, R.; Fernando, H. Urban heat islands in humid and arid climates: Role of urban form and thermal properties in Colombo, Sri Lanka and Phoenix, USA. Clim. Res. 2007, 34, 241–251. [Google Scholar] [CrossRef] [Green Version]
- Kong, J.; Zhao, Y.; Carmeliet, J.; Lei, C. Urban Heat Island and Its Interaction with Heatwaves: A Review of Studies on Mesoscale. Sustainability 2021, 13, 10923. [Google Scholar] [CrossRef]
- De Morais, M.V.B.; Marciotto, E.R.; Urbina Guerrero, V.V.; de Freitas, E.D. Effective albedo estimates for the Metropolitan Area of São Paulo using empirical sky-view factors. Urban Clim. 2017, 21, 183–194. [Google Scholar] [CrossRef]
- Johnson, G.T.; Watson, I.D. The Determination of View-Factors in Urban Canyons. J. Clim. Appl. Meteorol. 1984, 23, 329–335. [Google Scholar] [CrossRef]
- Chapman, L.; Thornes, J.E.; Bradly, A.V. Rapid Determination of Canyon Geometry Parameters for Use Surface Radiation Budgets. Theor. Appl. Climatol. 2001, 69, 81–89. [Google Scholar] [CrossRef]
- Lee, D.I.; Woo, J.W.; Lee, S.H. An analytically based numerical method for computing view factors in real urban environments. Theor. Appl. Climatol. 2018, 131, 445–453. [Google Scholar] [CrossRef]
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1994; ISBN 0-521-38052-9. [Google Scholar]
- Ali-Toudert, F.; Mayer, H. Numerical study on the effects of aspect ratio and orientation of an urban street canyon on outdoor thermal comfort in hot and dry climate. Build. Environ. 2006, 41, 94–108. [Google Scholar] [CrossRef]
- Höppe, P.R. The physiological equivalent temperature—A universal index for the bioclimatological assessment of the thermal environment. Int. J. Biometeorol. 1999, 4, 71–75. [Google Scholar]
- Marciotto, E.R.; Fisch, G. Wind tunnel study of turbulent flow past an urban canyon model. Environ. Fluid Mech. 2013, 13, 403–416. [Google Scholar] [CrossRef]
- Morais, M.V.B.; Freitas, E.D.; Marciotto, E.R.; Urbina Guerrero, V.V.; Martins, L.D.; Martins, J.A. Implementation of Observed Sky-View Factor in a Mesoscale Model for Sensitivity Studies of the Urban Meteorology. Sustainability 2018, 10, 2183. [Google Scholar] [CrossRef] [Green Version]
- Nair, K.N.; Freitas, E.D.; Sanchez-Ccoyllo, O.R.; Dias, M.S.; Silva Dias, P.L.; Andrade, M.F.; Massambani, O. Dynamics of urban boundary layer over São Paulo associated with mesoscale processes. Meteorol. Atmos. Phys. 2004, 86, 87–98. [Google Scholar] [CrossRef]
- Cheng, H.; Castro, I.P. Near Wall Flow over Urban-like Roughness. Bound. Lay Meteorol. 2002, 104, 229–259. [Google Scholar] [CrossRef]
- Vogt, R.; Christen, A.; Rotach, M.W.; Roth, M.; Satyanarayana, A.N.V. Temporal dynamics of CO2 fluxes and profiles over a Central European city. Theor. Appl. Climatol. 2006, 84, 117–126. [Google Scholar] [CrossRef]
- Marciotto, E.R. Variability of energy fluxes in relation to the net-radiation of urban and suburban areas: A case study. Meteorol. Atmos. Phys. 2013, 121, 17–28. [Google Scholar] [CrossRef]
- Hanna, S.; Marciotto, E.R.; Britter, R. Urban Energy Fluxes in Built-Up Downtown Areas and Variations across the Urban Area, for Use in Dispersion Models. J. Appl. Meteorol. Climatol. 2011, 50, 1341–1353. [Google Scholar] [CrossRef]
- De Morais, M.V.B.; de Freitas, E.D.; Urbina Guerrero, V.V.; Martins, L.D. A modeling analysis of urban canopy parameterization representing the vegetation effects in the megacity of São Paulo. Urban Clim. 2016, 17, 102–115. [Google Scholar] [CrossRef]
- De Morais, M.V.B.; Urbina Guerrero, V.V.; De Freitas, E.D.; Marciotto, E.R.; Valdés, H.; Correa, C.; Agredano, R.; Vera-Puerto, I. Sensitivity of Radiative and Thermal Properties of Building Material in the Urban Atmosphere. Sustainability 2019, 11, 6865. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Conry, P.; Fernando, H.J.S.; Hamlet, A.F.; Hellmann, J.J.; Chen, F. Green and cool roofs to mitigate urban heat island effects in the Chicago metropolitan area: Evaluation with a regional climate model. Environ. Res. Lett. 2016, 11, 064004. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R. Local climate zones for urban temperature studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Martilli, A.; Krayenhoff, E.S.; Nazarian, N. Is the Urban Heat Island intensity relevant for heat mitigation studies? Urban Clim. 2020, 31, 100541. [Google Scholar] [CrossRef]
- Masson, V.; Lemonsu, A.; Hidalgo, J.; Voogt, J. Urban climates and climate change. Annu. Rev. Environ. Resour. 2020, 45, 411–444. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, J.T.; Lee, M.G. Mitigation of urban heat island effect and greenroofs. Indoor Built Environ. 2014, 23, 62–69. [Google Scholar] [CrossRef]
- Kibert, C.J. Sustainable Construction: Green Building Design and Delivery; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016; ISBN 9781119055174. [Google Scholar]
- Santamouris, M. Cooling the cities—A review of reflective and green roof mitigation technologies to fight heat island and improve comfort in urban environments. Sol. Energy 2014, 103, 682–703. [Google Scholar] [CrossRef]
- Masson, V.; Marchadier, C.; Adolphe, L.; Aguejdad, R.; Avner, P.; Bonhomme, M.; Bretagne, G.; Briottet, X.; Bueno, B.; de Munck, C.; et al. Adapting cities to climate change: A systemic modelling approach. Urban Clim. 2014, 10, 407–429. [Google Scholar] [CrossRef]
- Vera, S.; Pinto, C.; Tabares-Velasco, P.C.; Bustamante, W. A critical review of heat and mass transfer in vegetative roof models used in building energy and urban enviroment simulation tools. Appl. Energy 2018, 232, 752–764. [Google Scholar] [CrossRef]
- Maiolo, M.; Pirouz, B.; Bruno, R.; Palermo, S.A.; Arcuri, N.; Piro, P. The role of the extensive green roofs on decreasing building energy consumption in the Mediterranean climate. Sustainability 2020, 12, 359. [Google Scholar] [CrossRef] [Green Version]
- Brackney, L.; Parker, A.; Macumber, D.; Benne, K. Building Energy Modeling with OpenStudio: A Practical Guide for Students and Professionals; Springer: Cham, Switzerland, 2018; ISBN 9783319778082. [Google Scholar]
- Niu, H.; Clark, C.; Zhou, J.; Adriaens, P. Scaling of economic benefits from green roof implementation in Washington, DC. Environ. Sci. Technol. 2010, 44, 4302–4308. [Google Scholar] [CrossRef]
- Duarte, D.H.S. Vegetation and climate-sensitive public places. In Urban Climate Challenges in the Tropics: Rethinking Planning and Design Opportunities; Emmanuel, R., Ed.; Imperial College Press: London, UK, 2016; pp. 111–162. [Google Scholar]
- Wong, N.H.; Kardinal Jusuf, S.; Aung La Win, A.; Kyaw Thu, H.; Syatia Negara, T.; Xuchao, W. Environmental study of the impact of greenery in an institutional campus in the tropics. Build. Environ. 2007, 42, 2949–2970. [Google Scholar] [CrossRef]
- Jauregui, E. Influence of a Large Urban Park on Temperature and Convective Precipitation in a Tropical City. Energy Build. 1990, 15–16, 457–463. [Google Scholar] [CrossRef]
- Wong, N.H.; Chen, Y. Tropical Urban Heat Islands: Climate, Building and Greenery; Taylor & Francis: New York, NY, USA, 2009; ISBN 0203931297. [Google Scholar]
- Duarte, D.H.S.; Shinzato, P.; dos Santos Gusson, C.; Alves, C.A. The impact of vegetation on urban microclimate to counterbalance built density in a subtropical changing climate. Urban Clim. 2015, 14, 224–239. [Google Scholar] [CrossRef]
- Redon, E.; Lemonsu, A.; Masson, V.; Morille, B.; Musy, M. Implementation of street trees in solar radiative exchange parameterization of TEB in SURFEX v8.0. Geosci. Model Dev. Discuss. 2016, 1–46. [Google Scholar] [CrossRef] [Green Version]
- Fernando, H.J.S. Fluid dynamics of urban atmospheres in complex terrain. Annu. Rev. Fluid Mech. 2010, 42, 365–389. [Google Scholar] [CrossRef]
- Dupont, S.; Otte, T.L.; Ching, J.K.S. Simulation of meteorological fields within and above urban and rural canopies with a mesoscale model (MM5). Bound.-Layer Meteorol. 2004, 113, 111–158. [Google Scholar] [CrossRef]
- Smith, A.B.; Jackson, D.W.T.; Cooper, J.A.G.; Hernández-Calvento, L. Quantifying the role of urbanization on airflow perturbations and dunefield evolution. Earth’s Futur. 2017, 5, 520–539. [Google Scholar] [CrossRef]
- Imran, H.M.; Kala, J.; Ng, A.W.M.; Muthukumaran, S. Effectiveness of green and cool roofs in mitigating urban heat island effects during a heatwave event in the city of Melbourne in southeast Australia. J. Clean. Prod. 2018, 197, 393–405. [Google Scholar] [CrossRef]
- Johansson, E.; Spangenberg, J.; Gouvêa, M.L.; Freitas, E.D. Scale-integrated atmospheric simulations to assess thermal comfort in different urban tissues in the warm humid summer of São Paulo, Brazil. Urban Clim. 2013, 6, 24–43. [Google Scholar] [CrossRef]
- Aboelata, A.; Sodoudi, S. Evaluating urban vegetation scenarios to mitigate urban heat island and reduce buildings’ energy in dense built-up areas in Cairo. Build. Environ. 2019, 166, 106407. [Google Scholar] [CrossRef]
- Badach, J.; Dymnicka, M.; Baranowski, A. Urban vegetation in air quality management: A review and policy framework. Sustainability 2020, 12, 1258. [Google Scholar] [CrossRef] [Green Version]
- Smolova, D.; Friedman, A. Potential Use of Indoor Living Walls in Canadian Dwellings. J 2021, 4, 116–130. [Google Scholar] [CrossRef]
- Akbari, H.; Pomerantz, M.; Taha, H. Cool surfaces and shade trees to reduce energy use and improve air quality in urban areas. Sol. Energy 2001, 70, 295–310. [Google Scholar] [CrossRef]
- Kumar, P.; Druckman, A.; Gallagher, J.; Gatersleben, B.; Allison, S.; Eisenman, T.S.; Hoang, U.; Hama, S.; Tiwari, A.; Sharma, A.; et al. The nexus between air pollution, green infrastructure and human health. Environ. Int. 2019, 133, 105181. [Google Scholar] [CrossRef] [PubMed]
- Eisenman, T.S.; Churkina, G.; Jariwala, S.P.; Kumar, P.; Lovasi, G.S.; Pataki, D.E.; Weinberger, K.R.; Whitlow, T.H. Urban trees, air quality, and asthma: An interdisciplinary review. Landsc. Urban Plan. 2019, 187, 47–59. [Google Scholar] [CrossRef]
- Urbina-Guerrero, V.V.; Morais, M.V.B.; De Freitas, E.D.; Martins, L.D. Numerical study of meteorological factors for tropospheric nocturnal ozone increase in the metropolitan area of São Paulo. Atmosphere 2021, 12, 287. [Google Scholar] [CrossRef]
- Churkina, G.; Kuik, F.; Bonn, B.; Lauer, A.; Grote, R.; Tomiak, K.; Butler, T.M. Effect of VOC Emissions from Vegetation on Air Quality in Berlin during a Heatwave. Environ. Sci. Technol. 2017, 51, 6120–6130. [Google Scholar] [CrossRef] [Green Version]
- Masi, F.; Rizzo, A.; Regelsberger, M. The role of constructed wetlands in a new circular economy, resource oriented, and ecosystem services paradigm. J. Environ. Manage. 2018, 216, 275–284. [Google Scholar] [CrossRef]
- Sun, R.; Chen, L. How can urban water bodies be designed for climate adaptation? Landsc. Urban Plan. 2012, 105, 27–33. [Google Scholar] [CrossRef]
- Deng, Y.; Jiang, W.; Tang, Z.; Li, J.; Lv, J.; Chen, Z.; Jia, K. Spatio-temporal change of lake water extent in Wuhan urban agglomeration based on Landsat images from 1987 to 2015. Remote Sens. 2017, 9, 270. [Google Scholar] [CrossRef] [Green Version]
- Solcerova, A.; van de Ven, F.; van de Giesen, N. Nighttime cooling of an urban pond. Front. Earth Sci. 2019, 7, 1–10. [Google Scholar] [CrossRef]
- Steeneveld, G.J.; Koopmans, S.; Heusinkveld, B.G.; Theeuwes, N.E. Refreshing the role of open water surfaces on mitigating the maximum urban heat island effect. Landsc. Urban Plan. 2014, 121, 92–96. [Google Scholar] [CrossRef]
- Imam Syafii, N.; Ichinose, M.; Kumakura, E.; Jusuf, S.K.; Chigusa, K.; Wong, N.H. Thermal environment assessment around bodies of water in urban canyons: A scale model study. Sustain. Cities Soc. 2017, 34, 79–89. [Google Scholar] [CrossRef]
- Syafii, N.I.; Ichinose, M.; Kumakura, E.; Jusuf, S.K.; Hien, W.N.; Chigusa, K.; Ashie, Y. Assessment of the Water Pond Cooling Effect on Urban Microclimate: A Parametric Study with Numerical Modeling. Int. J. Technol. 2021, 12, 461. [Google Scholar] [CrossRef]
- Tan, X.; Sun, X.; Huang, C.; Yuan, Y.; Hou, D. Comparison of cooling effect between green space and water body. Sustain. Cities Soc. 2021, 67, 102711. [Google Scholar] [CrossRef]
- Targino, A.C.; Coraiola, G.C.; Krecl, P. Green or blue spaces? Assessment of the effectiveness and costs to mitigate the urban heat island in a Latin American city. Theor. Appl. Climatol. 2019, 136, 971–984. [Google Scholar] [CrossRef]
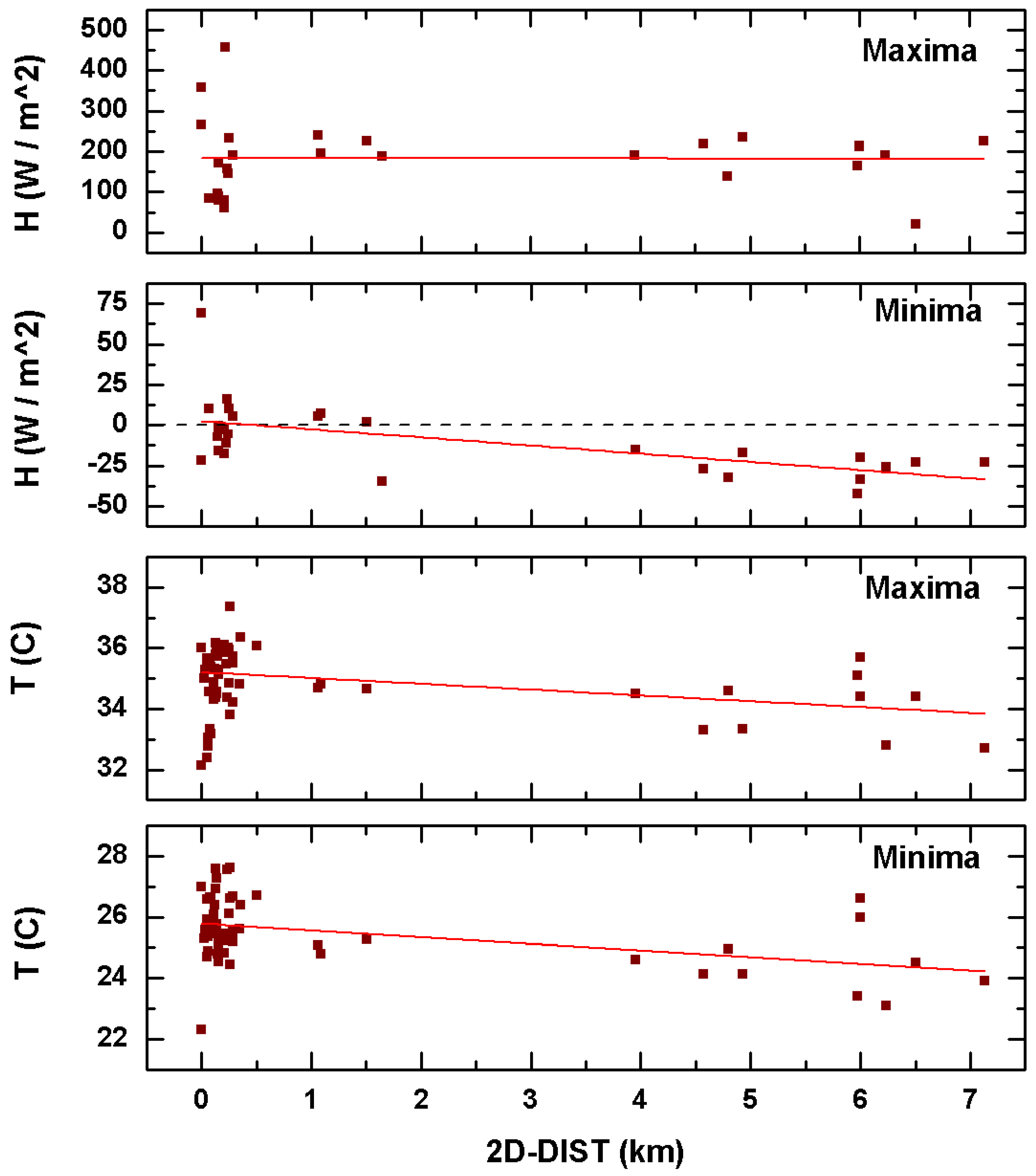
| Quantity | 2D-Distance | |
|---|---|---|
| Slope | Intercept | |
| −0.54 | 184 | |
| −5.06 | 2.51 | |
| −0.19 | 35.2 | |
| −0.22 | 25.8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marciotto, E.R.; de Morais, M.V.B. Energetics of Urban Canopies: A Meteorological Perspective. J 2021, 4, 645-663. https://doi.org/10.3390/j4040047
Marciotto ER, de Morais MVB. Energetics of Urban Canopies: A Meteorological Perspective. J. 2021; 4(4):645-663. https://doi.org/10.3390/j4040047
Chicago/Turabian StyleMarciotto, Edson R., and Marcos Vinicius Bueno de Morais. 2021. "Energetics of Urban Canopies: A Meteorological Perspective" J 4, no. 4: 645-663. https://doi.org/10.3390/j4040047
APA StyleMarciotto, E. R., & de Morais, M. V. B. (2021). Energetics of Urban Canopies: A Meteorological Perspective. J, 4(4), 645-663. https://doi.org/10.3390/j4040047






