Improved Rainfall Prediction Using Combined Pre-Processing Methods and Feed-Forward Neural Networks
Abstract
1. Introduction
2. Methodology
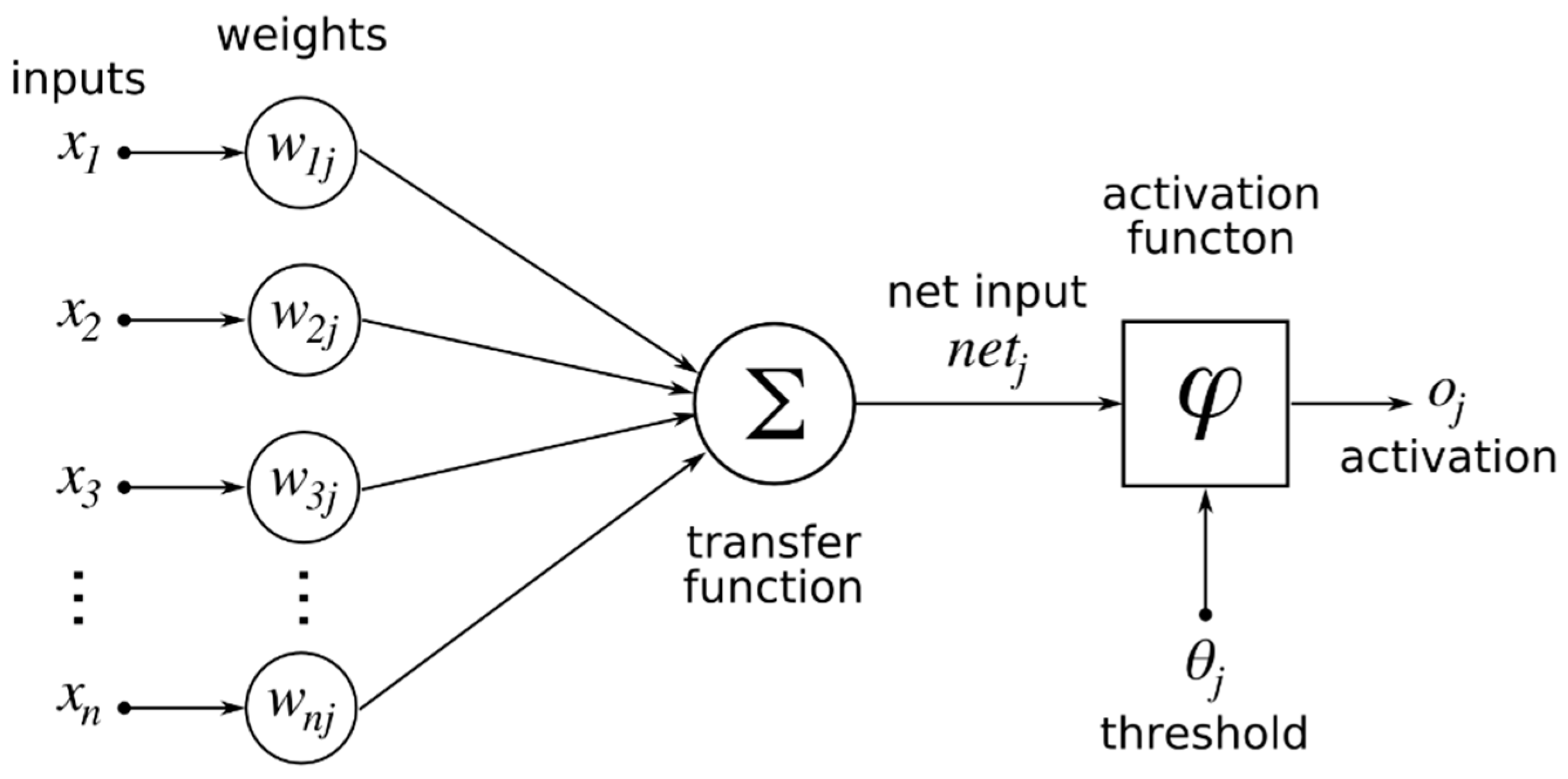
2.1. Artificial Neural Network (ANN)
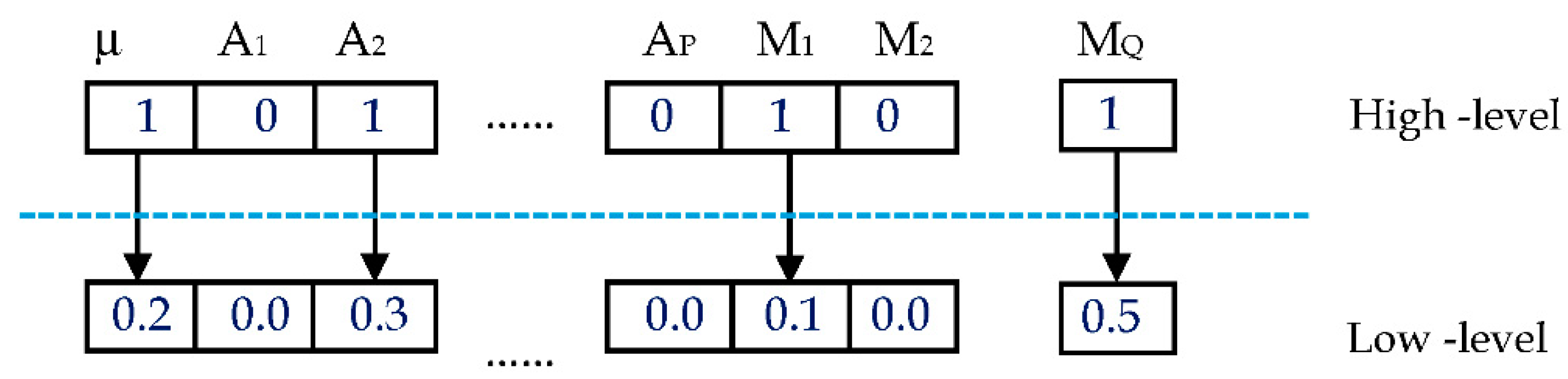
2.2. Seasonal Artificial Neural Network (SANN)
2.3. ARIMA and GA-SA Models
3. Data Analysis
3.1. Data Selection
3.2. Data Pre-Processing
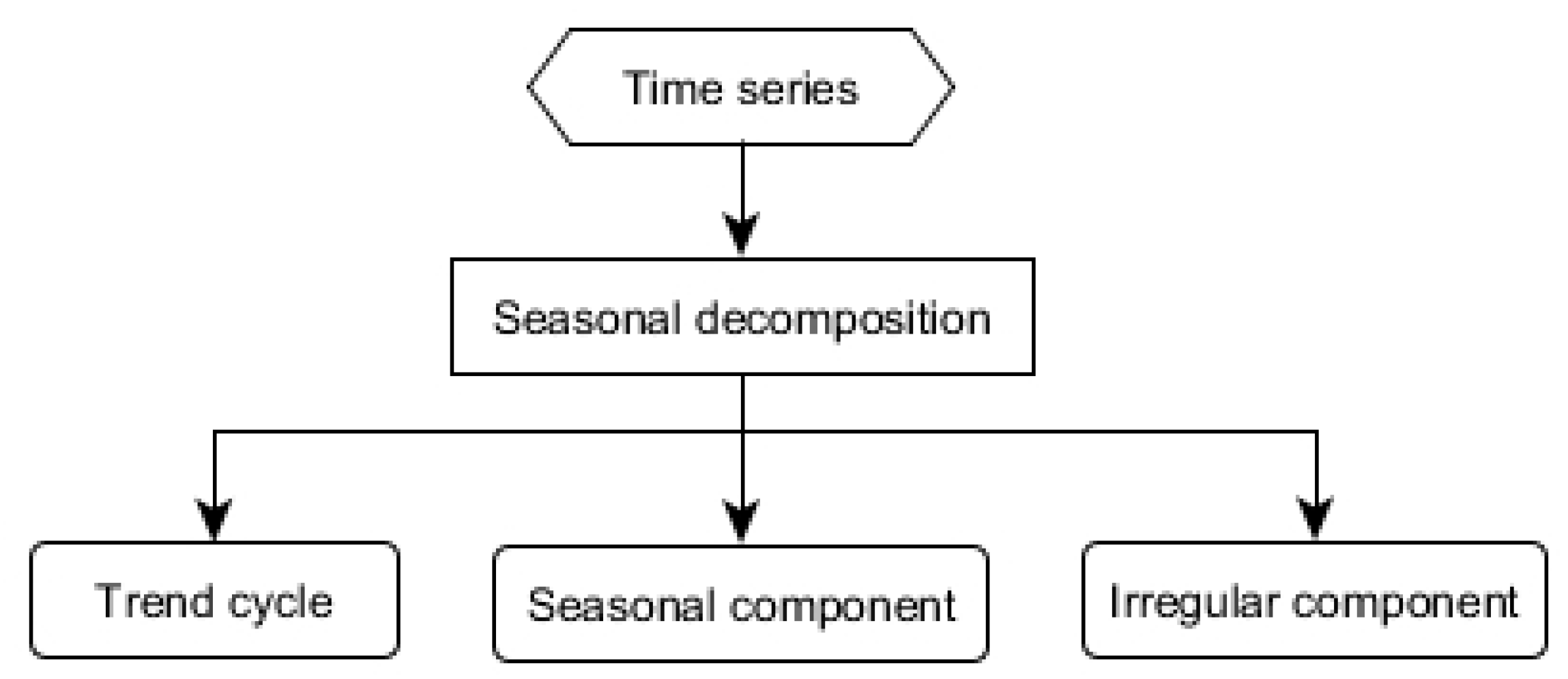
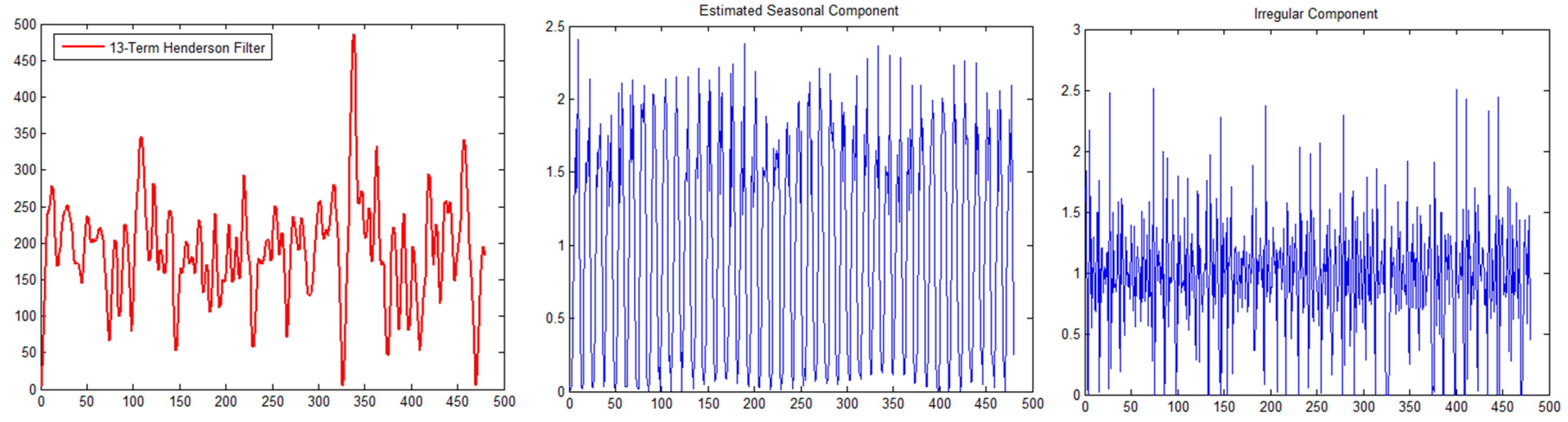
3.2.1. Seasonal Decomposition (SD)
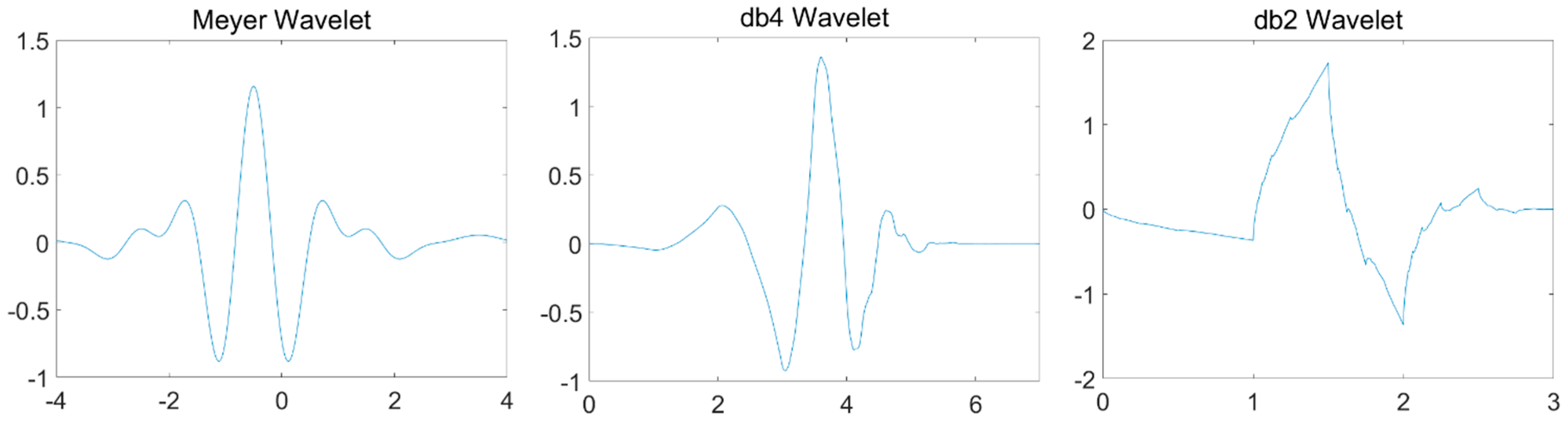
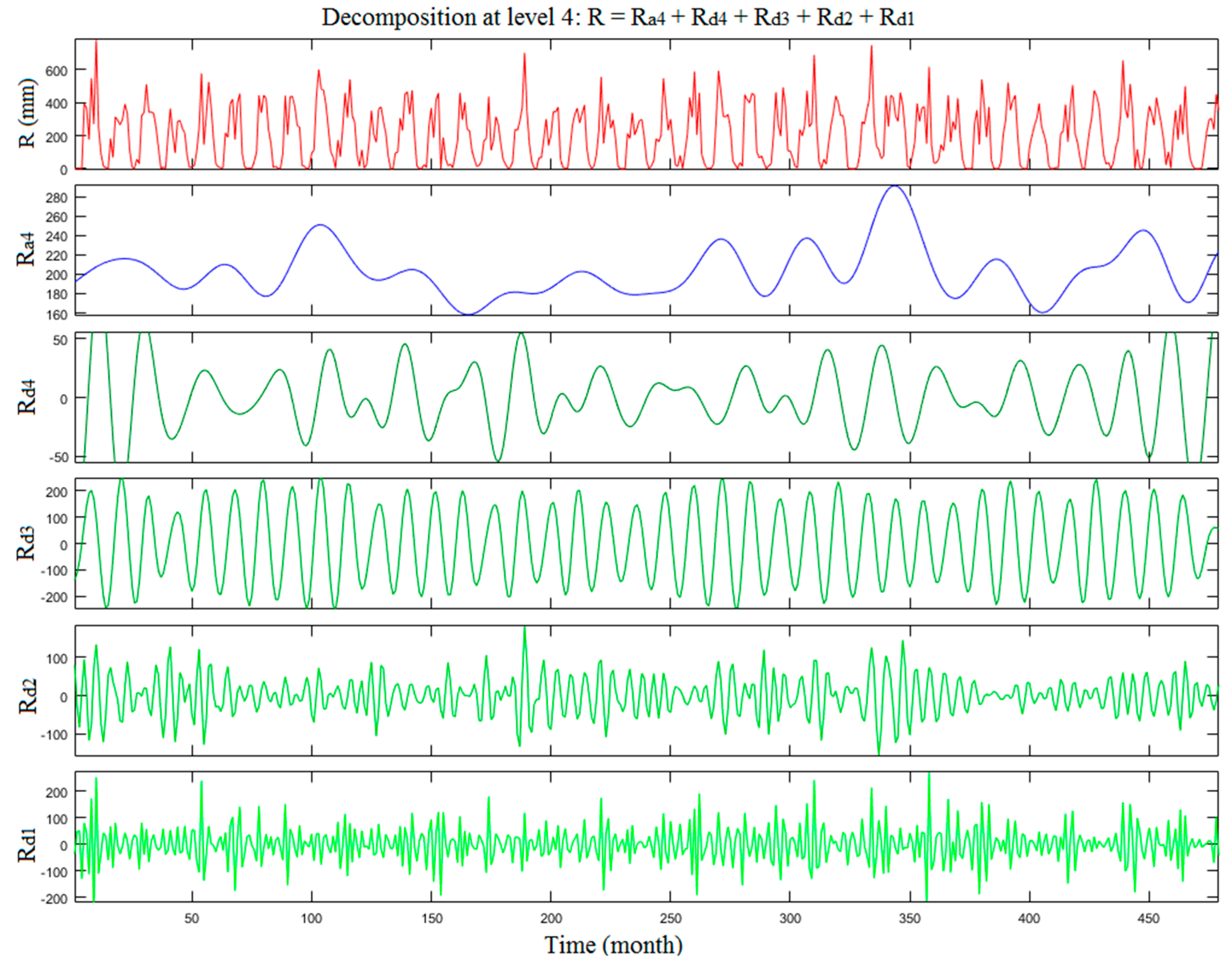
3.2.2. Wavelet Transform (WT)
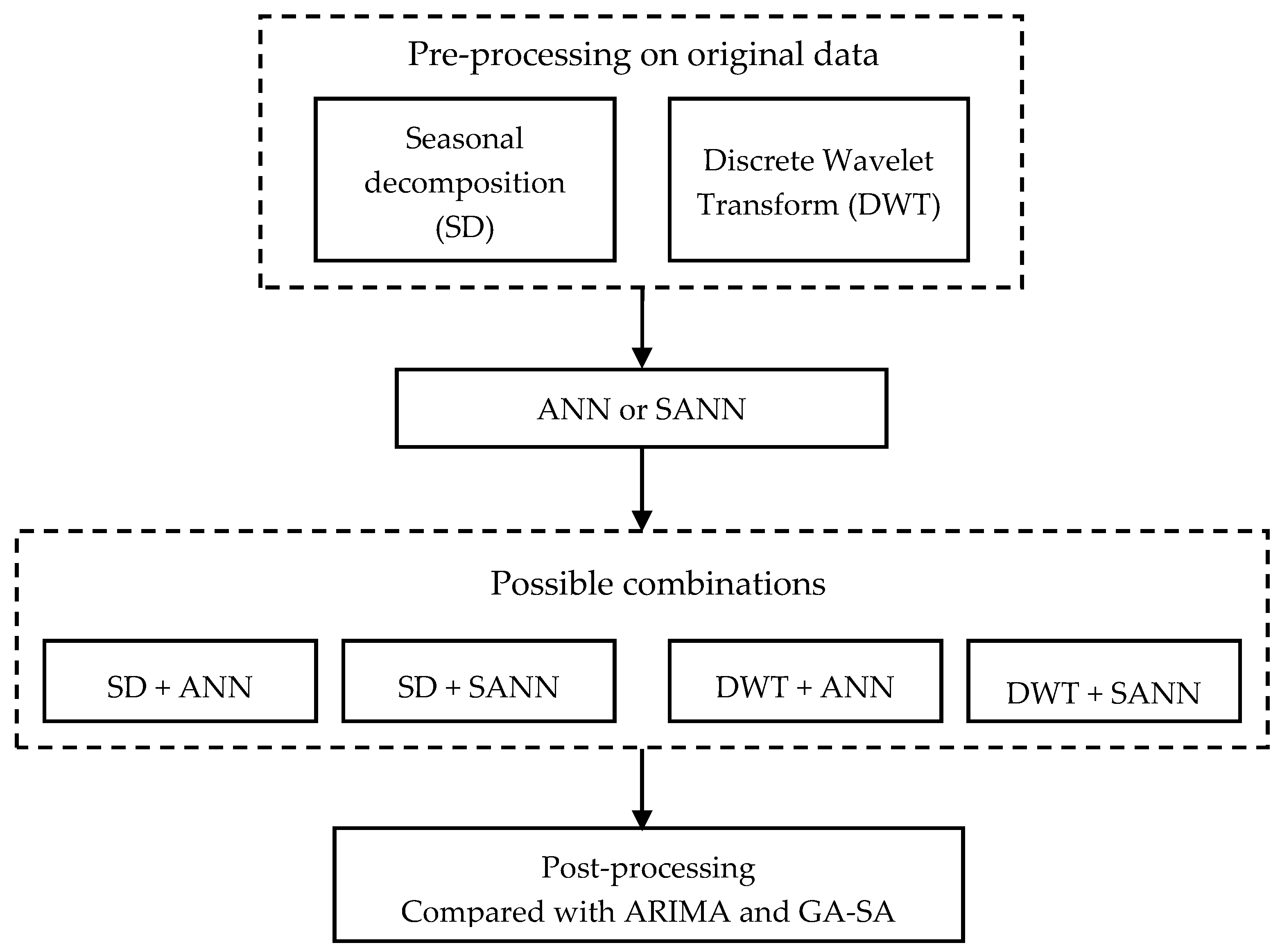
4. Model Application
4.1. Combination of Models
4.2. Model Evaluation
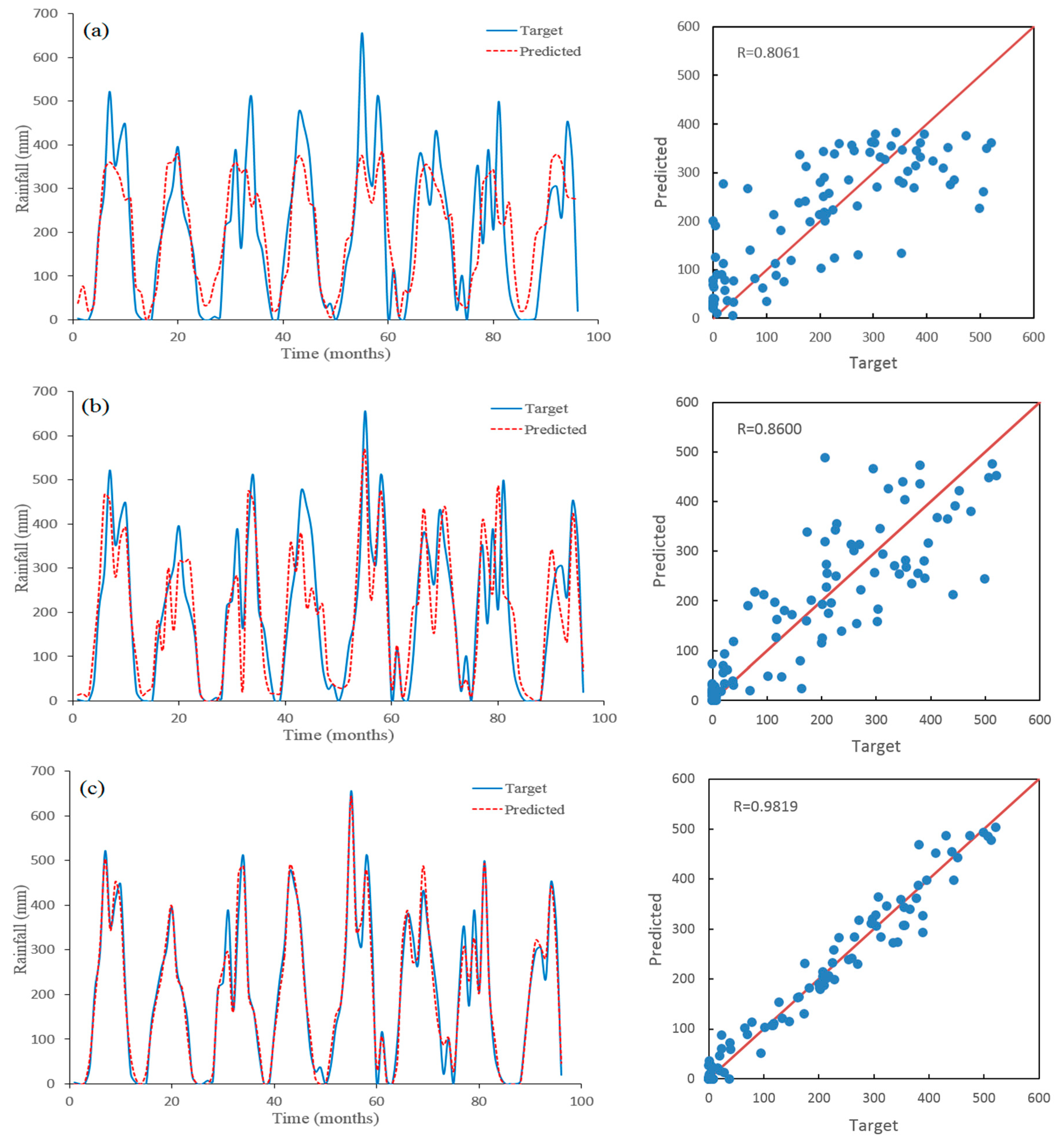
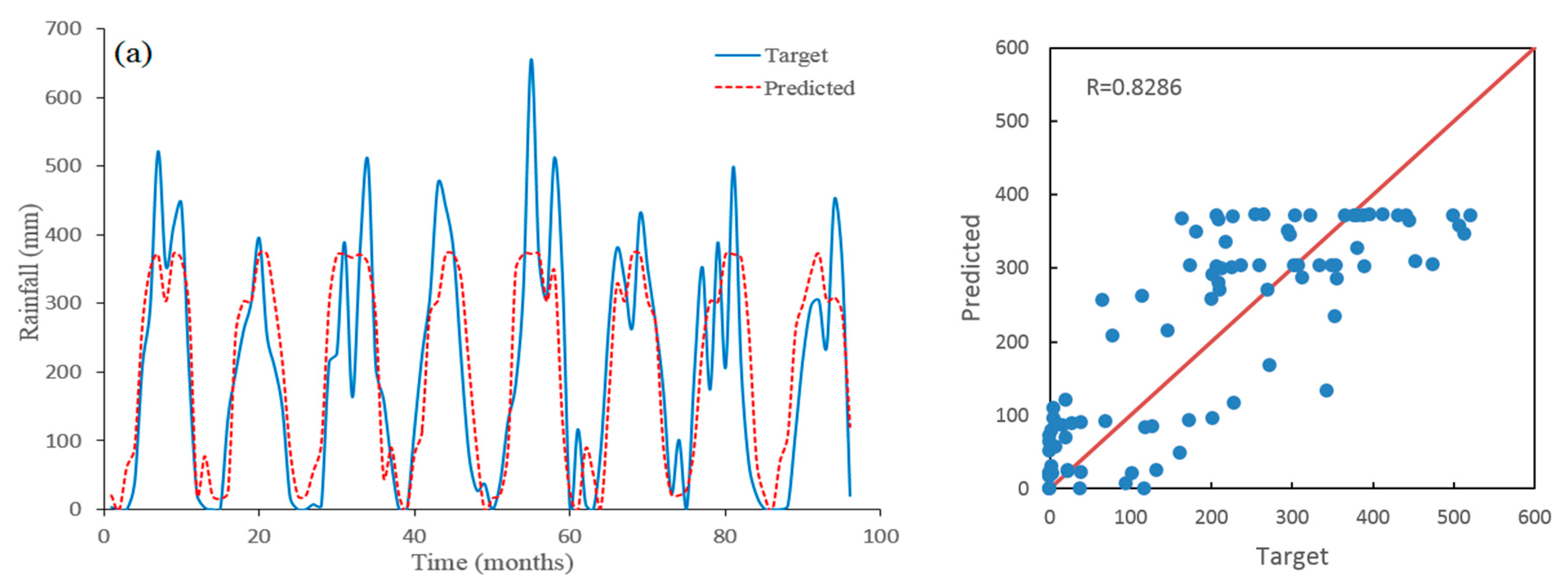
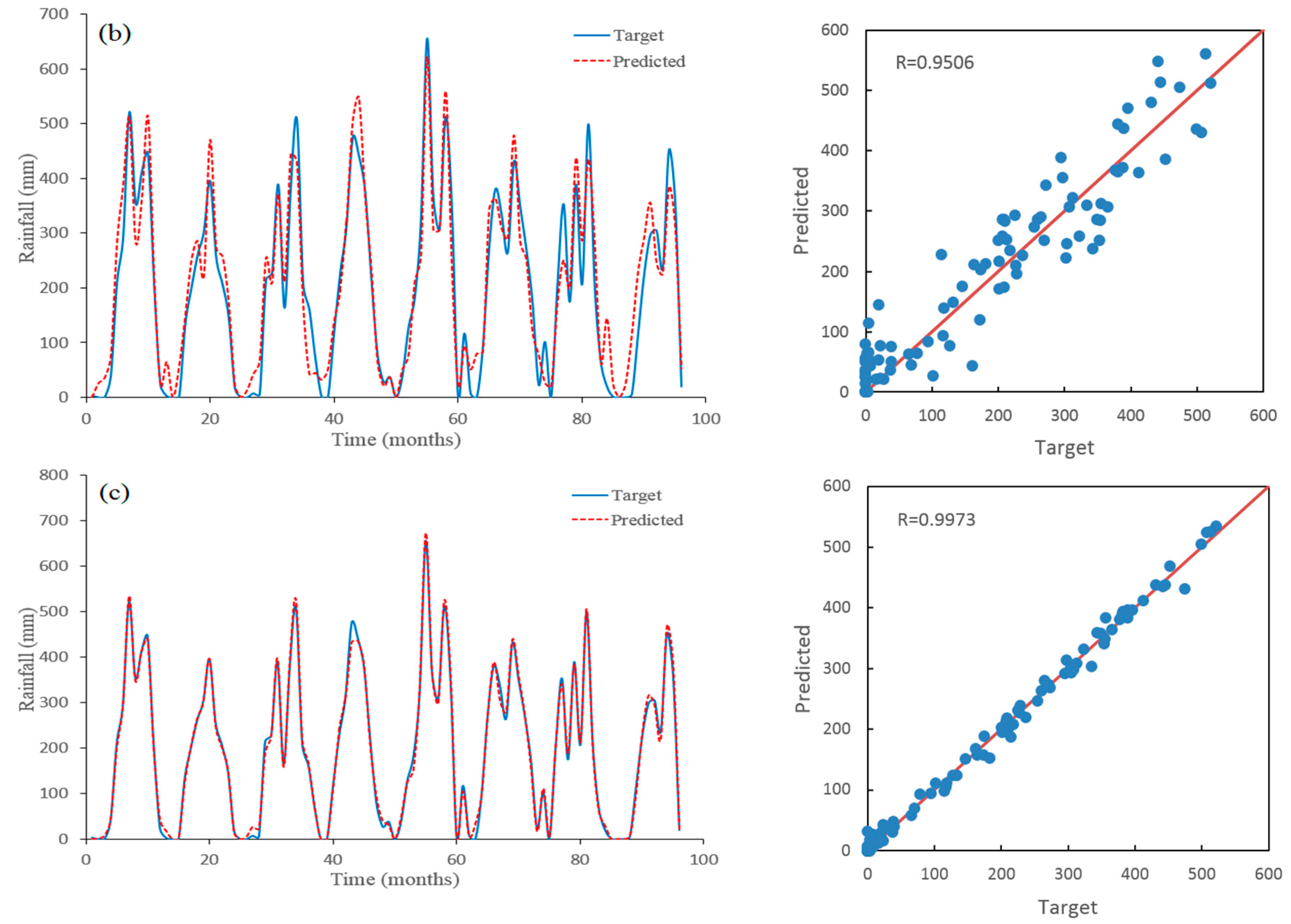
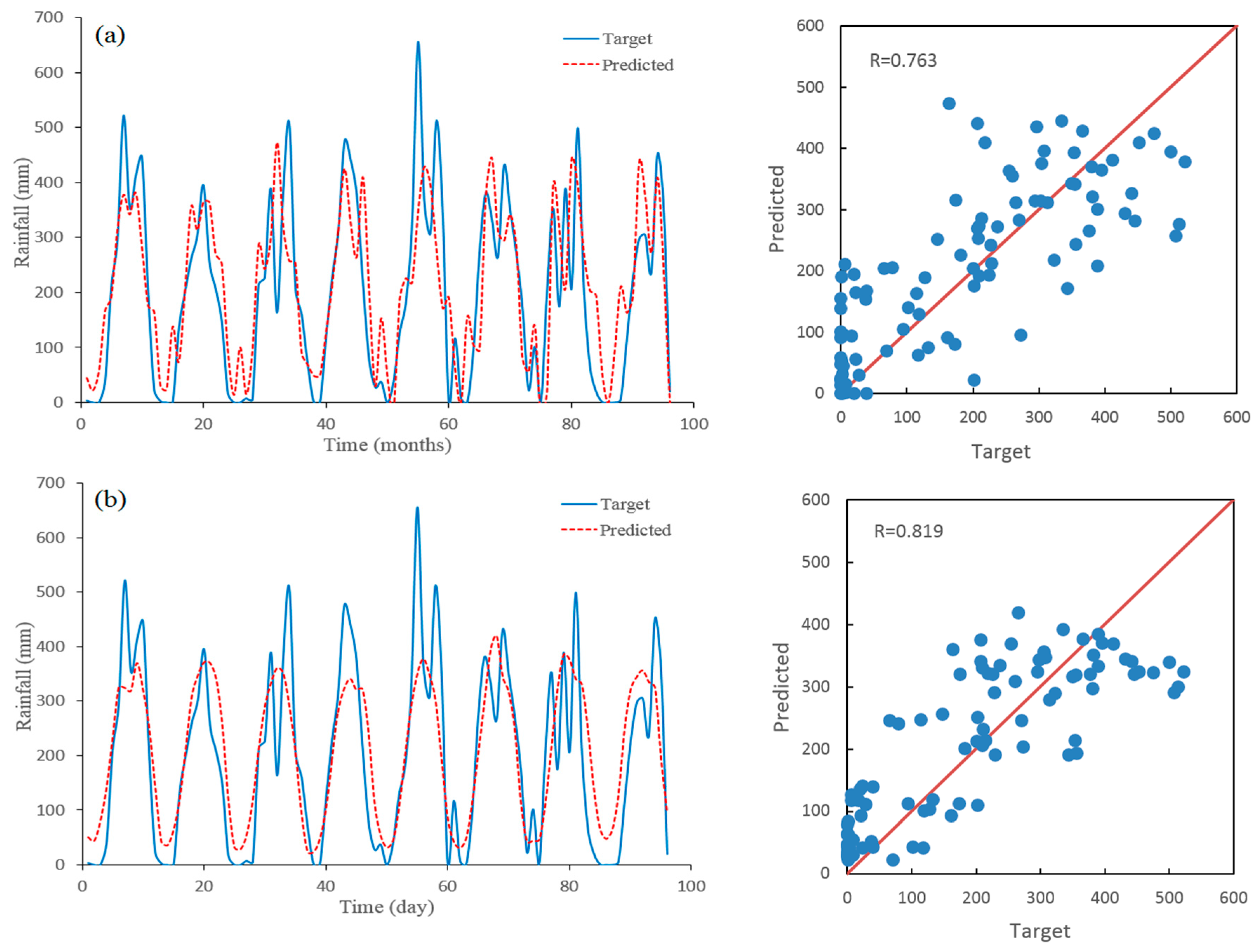
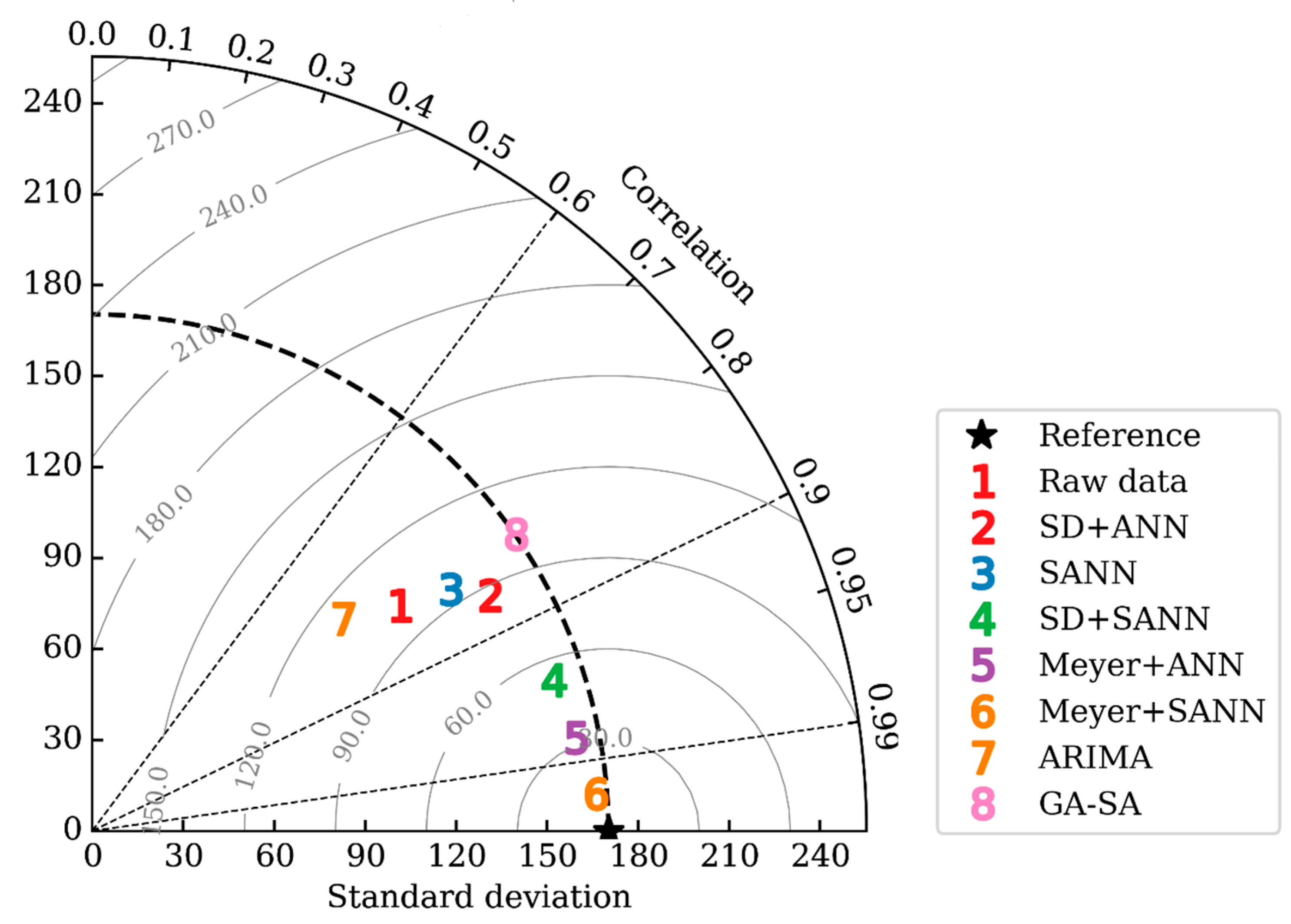
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- French, M.N.; Krajewski, W.F.; Cuykendall, R.R. Rainfall forecasting in space and time using neural network. J. Hydrol. 1992, 137, 1–31. [Google Scholar] [CrossRef]
- Trömel, S.; Schönwiese, C.D. A generalized method of time series decomposition into significant components including probability assessments of extreme events and application to observational German precipitation data. Meteorol. Z. 2005, 14, 417–427. [Google Scholar] [CrossRef]
- Davolio, S.; Miglietta, M.M.; Diomede, T.; Marsigli, C.; Morgillo, A.; Moscatello, A. A meteo-hydrological prediction system based on a multi-model approach for precipitation forecasting. Nat. Hazards Earth Syst. Sci. 2008, 8, 143–159. [Google Scholar] [CrossRef]
- Diomede, T.; Davolio, S.; Marsigli, C.; Miglietta, M.M.; Moscatello, A.; Papetti, P.; Paccagnella, T.; Buzzi, A.; Malguzzi, P. Discharge prediction based on multi-model precipitation forecasts. Meteorol. Atmos. Phys. 2008, 101, 245–265. [Google Scholar] [CrossRef]
- García-Mozo, H.; Yaezel, L.; Oteros, J.; Galán, C. Statistical approach to the analysis of olive long-term pollen season trends in southern Spain. Sci. Total Environ. 2014, 473, 103–109. [Google Scholar] [CrossRef] [PubMed]
- Mahsin, M. Modeling rainfall in Dhaka division of Bangladesh using time series analysis. J. Math. Model. Appl. 2011, 1, 67–73. [Google Scholar]
- Al-Ansari, N.A.; Shamali, B.; Shatnawi, A. Statistical analysis at three major meteorological stations in Jordan, Al Manara. J. Sci. Stud. Res. 2006, 12, 93–120. [Google Scholar]
- Al-Hajji, A.H. Study of Some Techniques for Processing Rainfall Time Series in the North Part of Iraq. Unpublished Master’s Thesis, Mosul University, Mosul, Iraq, 2004. [Google Scholar]
- Weesakul, U.; Lowanichchai, S. Rainfall Forecast for Agricultural Water Allocation Planning in Thailand. Thammasat Int. J. Sci. Tech. 2005, 10, 18–27. [Google Scholar]
- Chiew, G.H.S.; Stewardson, M.J.; Mcmahon, T.A. Comparison of six rainfall-runoff modeling approaches. J. Hydrol. 1993, 147, 1–36. [Google Scholar] [CrossRef]
- Langu, E.M. Detection of changes in rainfall and runoff patterns. J. Hydrol. 1983, 147, 153–167. [Google Scholar] [CrossRef]
- Brath, A.; Montanari, A.; Toth, E. Neural networks and non-parametric methods for improving real time flood forecasting through conceptual hydrological models. Hydrol. Earth Syst. Sci. 2002, 6, 627–640. [Google Scholar] [CrossRef]
- Tseng, F.M.; Yub, H.C.; Tzeng, G.H. Combining neural network model with seasonal time series ARIMA model. Technol. Forecast. Soc. Chang. 2002, 69, 71–87. [Google Scholar] [CrossRef]
- Toth, E.; Montanari, A.; Brath, A. Comparison of short-term rainfall prediction model for real-time flood forecasting. J. Hydrol. 2000, 239, 132–147. [Google Scholar] [CrossRef]
- Son, M.; Tuan, N.L.A.; Khoa, N.T.C.T.; Loc, L.Q.; Vinh, L.N. A new approach to time series forecasting using Simulated Annealing Algorithms. In Proceedings of the International Workshop on Advanced Computing and Applications, Las Vegas, NV, USA, 8–10 November 2010; pp. 190–199. [Google Scholar]
- Chiu, Y.C.; Chang, L.C.; Chang, F.J. Using a hybrid genetic algorithm–simulated annealing algorithm for fuzzy programming of reservoir operation. Hydrol. Process. Int. J. 2007, 21, 3162–3172. [Google Scholar] [CrossRef]
- Oliveira, R.; Loucks, D.P. Operating rules for multi-reservoir systems. Water Resour. Res. 1997, 33, 839–852. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E. Optimal selection of number and location of rainfall gauges for areal rainfall estimation using geostatistics and simulated annealing. J. Hydrol. 1998, 210, 206–220. [Google Scholar] [CrossRef]
- Wardlaw, R.; Sharif, M. Evaluation of genetic algorithms for optimal reservoir system operation. J. Water Resour. Plan. Manag. 1999, 125, 25–33. [Google Scholar] [CrossRef]
- Chang, F.J.; Chen, L.; Chang, L.C. Optimizing the reservoir operation rule curves by genetic algorithms. Hydrol. Process. 2005, 19, 2277–2289. [Google Scholar] [CrossRef]
- Cortez, P.; Rocha, M.; Neves, J. A Meta-Genetic Algorithms for Time Series Forecasting. In Proceedings of the Workshop on Artificial Intelligence Techniques for Financial Time Series Analysis (AIFTSA-01). In Proceedings of the 10th Portuguese Conference on Artificial Intelligence, Porto, Portugal, 17–20 December 2001. [Google Scholar]
- Maier, H.R.; Dandy, G.C. Application of neural networks to forecasting of surface water quality variables: Issues, applications and challenges. Environ. Model. Softw. 2000, 15, 348. [Google Scholar] [CrossRef]
- Maier, H.R. Application of natural computing methods to water resources and environmental modelling. Math. Comput. Model. 2006, 44, 413–414. [Google Scholar] [CrossRef]
- Hsu, K.; Gupta, H.V.; Sorooshian, S. Artificial neural network modeling of the rainfall-runoff process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Shamseldin, A.Y. Application of a neural network technique to rainfall-runoff modeling. J. Hydrol. 1997, 199, 272–294. [Google Scholar] [CrossRef]
- Zealand, C.M.; Burn, D.H.; Simonovic, S.P. Short term streamflow forecasting using artificial neural networks. J. Hydrol. 1999, 214, 32–48. [Google Scholar] [CrossRef]
- Abrahart, R.J.; See, L. Comparing neural network and autoregressive moving average techniques for the provision of continuous river flow forecast in two contrasting catchments. Hydrol. Proc. 2000, 14, 2157–2172. [Google Scholar] [CrossRef]
- Somvanshi, V.K.; Pandey, O.P.; Agrawal, P.K.; Kalanker, N.V.; Prakash, M.R.; Ramesh, C. Modelling and Prediction of Rainfall Using Artificial Neural Network and ARIMA Techniques. J. Ind. Geophys. Union 2006, 10, 141–151. [Google Scholar]
- Nelson, M.; Hill, T.; Remus, T.; O’Connor, M. Time series forecasting using neural networks. Should the data be deseasonalized first? J. Forecast. 1999, 18, 359–367. [Google Scholar] [CrossRef]
- Hill, T.; O’Connor, M.; Remus, W. Neural network models for time series forecasts. Manag. Sci. 1996, 42, 1082–1092. [Google Scholar] [CrossRef]
- Sivakumar, B.; Jayawardena, A.W.; Fernando, T.M.K.G. River flow forecasting: Use of phase-space reconstruction and artificial neural networks approaches. J. Hydrol. 2002, 265, 225–245. [Google Scholar] [CrossRef]
- Sharda, R.; Patil, R.B. Connectionist approach to time series prediction: An empirical test. J. Intell. Manuf. 1992, 3, 317–323. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W.; Fan, C. Prediction of rainfall time series using modular artificial neural networks coupled with data-preprocessing techniques. J. Hydrol. 2010, 389, 146–167. [Google Scholar] [CrossRef]
- Hamzaçebi, C. Improving artificial neural networks performance in seasonal time series forecasting. Inf. Sci. 2008, 178, 4550–4559. [Google Scholar] [CrossRef]
- Ahaneku, I.E.; Otache, Y.M. Stochastic characteristics and modelling of monthly rainfall time series of Ilorin, Nigeria. Open J. Modern Hydrol. 2014, 4, 67. [Google Scholar]
- Benkachcha, S.; Benhra, J.; El Hassani, H. Seasonal time series forecasting model based on Artificial Neural Network. Int. J. Comput. Appl. 2015, 116, 9–14. [Google Scholar]
- Wu, C.L.; Chau, K.W.; Li, Y.S. Methods to improve neural network performance in daily flows prediction. J. Hydrol. 2009, 372, 80–93. [Google Scholar] [CrossRef]
- Sang, Y.F. A review on the applications of wavelet transform in hydrology time series analysis. Atmos. Res. 2013, 122, 8–15. [Google Scholar] [CrossRef]
- McCann, D.W. A neural network short-term forecast of significant thunderstorms. Weather Forecast. 1992, 7, 525–534. [Google Scholar] [CrossRef]
- Kalogirou, S.; Neocleous, C.; Michaelides, S.; Schizas, C. A time series reconstruction of precipitation records using artificial neural networks. Proc. EUFIT 1997, 97, 2409–2413. [Google Scholar]
- Lee, S.; Cho, S.; Wong, P.M. Rainfall prediction using artificial neural networks. J. Geogr. Inf. Decis. Anal. 1998, 2, 233–242. [Google Scholar]
- Guhathakurta, P. Long-range monsoon rainfall prediction of 2005 for the districts and sub-division Kerala with artificial neural network. Curr. Sci. 2006, 90, 773–779. [Google Scholar]
- Paras, S.M.; Kumar, A.; Chandra, M. A feature based on weather prediction using ANN. World Acad. Sci. Eng. Technol. 2007, 34. [Google Scholar]
- Baboo, S.S.; Shereef, I.K. An efficient weather forecasting system using artificial neural network. Int. J. Environ. Sci. Dev. 2010, 1, 321. [Google Scholar] [CrossRef]
- Wong, K.W.; Wong, P.M.; Gedeon, T.D.; Fung, C.C. Rainfall prediction model using soft computing technique. Soft Comput. 2003, 7, 434–438. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, A.; Shi, C.; Wang, H. Filtering and multi-scale RBF prediction model of rainfall based on EMD method. In Proceedings of the 2009 1st International Conference on Information Science and Engineering (ICISE), Nanjing, China, 26–28 December 2009; pp. 3785–3788. [Google Scholar]
- Haykin, S. Neural Networks. A Comprehensive Foundation, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1999; p. 696. [Google Scholar]
- Bhattacharya, B.; Deibel, I.K.; Karstens, S.A.M.; Solomatine, D.P. Neural networks in sedimentation modelling for the approach channel of the port area of Rotterdam. In Proceedings in Marine Science; Elsevier: Amsterdam, The Netherlands, 2007; Volume 8, pp. 477–492. [Google Scholar]
- Bui, M.D.; Keivan, K.; Penz, P.; Rutschmann, P. Contraction scour estimation using data-driven methods. J. Appl. Water Eng. Res. 2015, 3, 143–156. [Google Scholar] [CrossRef]
- Shahin, M.A.; Maier, H.R.; Jaksa, M.B. Closure to “Predicting settlement of shallow foundations using neural networks” by Mohamed A. Shahin, Holger R. Maier, and Mark B. Jaksa. J. Geotech. Geoenviron. Eng. 2003, 129, 1175–1177. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting, and Control; Holden Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Kirpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimazation by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Dang, T.D.; Cochrane, T.A.; Arias, M.E.; Van, P.D.T. Future hydrological alterations in the Mekong Delta under the impact of water resources development, land subsidence and sea level rise. J. Hydrol. Reg. Stud. 2018, 15, 119–133. [Google Scholar] [CrossRef]
- Altun, H.; Bilgil, A.; Fidan, B.C. Treatment of multi-dimensional data to enhance neural network estimators in regression problems. Expert Syst. Appl. 2007, 32, 599–605. [Google Scholar] [CrossRef]
- Basak, A.; Mengshoel, O.J.; Kulkarni, C.; Schmidt, K.; Shastry, P.; Rapeta, R. Optimizing the decomposition of time series using evolutionary algorithms: Soil moisture analytics. In Proceedings of the Genetic and Evolutionary Computation Conference, Berlin, Germany, 15–19 July 2017; pp. 1073–1080. [Google Scholar]
- Findley, D.F.; Monsell, B.C.; Bell, W.R.; Otto, M.C.; Chen, B.C. New capabilities and methods of the X-12-ARIMA seasonal adjustment program. J. Bus. Econ. Stat. 1998, 16, 127–176. [Google Scholar]
- Shuai, Y.; Masek, J.G.; Gao, F.; Schaaf, C.B. An algorithm for the retrieval of 30-m snow-free albedo from Landsat surface reflectance and MODIS BRDF. Remote Sens. Environ. 2011, 115, 2204–2216. [Google Scholar] [CrossRef]
- Laniel, N. Design Criteria for the 13-Term Henderson End-Weights; Working Paper; Methodology Branch, Statistics Canada: Ottawa, ON, Canada, 1985. [Google Scholar]
- Sang, Y.F. A practical guide to discrete wavelet decomposition of hydrologic time series. Water Resour. Manag. 2012, 26, 3345–3365. [Google Scholar] [CrossRef]
- Goodwin, M.M. The STFT, sinusoidal models, and speech modification. In Handbook of Speech Processing; Benesty, J., Sondhi, M.M., Huang, Y., Eds.; Springer: Berlin, Germany, 2008; pp. 229–258. [Google Scholar]
- Rajaee, T. Wavelet and ANN combination model for prediction of daily suspended sediment load in rivers. Sci. Total Environ. 2011, 409, 2917–2928. [Google Scholar] [CrossRef] [PubMed]
- Labat, D.; Ababou, R.; Mangin, A. Rainfall–runoff relations for karstic springs. Part II: continuous wavelet and discrete orthogonal multiresolution analyses. J. Hydrol. 2000, 238, 149–178. [Google Scholar] [CrossRef]
- Gupta, K.K.; Gupta, R. Despeckle and geographical feature extraction in SAR images by wavelet transform. ISPRS J. Photogramm. Remote Sens. 2007, 62, 473–484. [Google Scholar] [CrossRef]
- Nourani, V.; Komasi, M.; Mano, A. A Multivariate ANN–Wavelet Approach for Rainfall-Runoff Modeling. J. Water Resour. Manag. 2009, 23, 2877–2894. [Google Scholar] [CrossRef]
- Liu, Y.; Sergey, F. Seismic data analysis using local time-frequency decomposition. J. Geophys. Prospect. 2013, 61, 516–525. [Google Scholar] [CrossRef]
- Marquez, M.; White, A.; Gill, R. A hybrid neural network, feature-based manufacturability analysis of mould reinforced plastic parts. Proc. Inst. Mech. Eng. Part B J. Manuf. Eng. 2001, 215, 1065–1079. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchocombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Dawson, C.W.; Wilby, R.L. Hydrological modeling using artificial neural networks. Prog. Phys. Geographys. 2001, 25, 80–108. [Google Scholar] [CrossRef]
- De Vos, N.J.; Rientjes, T.H.M. Constraints of artificial neural networks for rainfall-runoff modeling: Trade-offs in hydrological state representation and model evaluation. Hydrol. Earth Syst. Sci. 2005, 9, 111–126. [Google Scholar] [CrossRef]
- Schmitz, J.E.; Zemp, R.J.; Mendes, M.J. Artificial neural networks for the solution of the phase stability problem. Fluid Phase Equilibria 2006, 245, 83–87. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
| Algorithm 1: Simulation of Annealing | Algorithm 2: Genetic Frame-Work |
| Select an initial solution Select an initial temperature t = to > 0 Select number of phases maxphase Select a temperature reduction coefficient α While phase < maxphase While iteration_count < nrep /* s is a neighbor solution of s0 */ Randomly select s N(s0); /* compute the change in cost function */ δ = f(s) − f(s0) if δ < 0 then so = s else generate random x [0, 1] if x < exp(−δ/t) then so = s t = t * α | Initialize population with random candidate solutions Evaluate each candidate repeat repeat Select parents Recombine pairs of parents Mutate the resulting children until iteration_count = num_mate Evaluate children Select individuals for the next generation until Termination-Condition is satisfied |
| Statistical Parameters | Training Set | Validation Set | Testing Set | Whole Data |
|---|---|---|---|---|
| Min | 0 | 0 | 0 | 0 |
| Max | 782.1 | 748.7 | 656 | 782.1 |
| Mean | 198.29 | 223.798 | 196.655 | 202.43 |
| Sd | 170.266 | 176.683 | 166.183 | 170.53 |
| Cs | 0.568 | 0.559 | 0.437 | 0.543 |
| R1 | 0.568 | 0.480 | 0.629 | 0.565 |
| R2 | 0.297 | 0.239 | 0.339 | 0.298 |
| R3 | −0.003 | 0.057 | 0.049 | 0.023 |
| No. of Model | Pre-Processing Method | Model | Statistical Performance | Number of Neurons | ||||
|---|---|---|---|---|---|---|---|---|
| 3 | 5 | 8 | 10 | 15 | ||||
| 1 | - | ANN | R | 0.7948 | 0.8092 | 0.8061 | 0.7770 | 0.7248 |
| - | RMSE | 103.9385 | 101.4842 | 98.3109 | 104.9657 | 114.1420 | ||
| - | MAE | 84.3679 | 80.4982 | 74.0538 | 78.6600 | 82.7604 | ||
| 2 | - | R | 0.8432 | 0.8601 | 0.8408 | 0.8118 | 0.8300 | |
| SD | RMSE | 89.3413 | 85.5113 | 90.2806 | 101.5413 | 93.3553 | ||
| - | MAE | 66.1147 | 66.0452 | 69.2322 | 80.5990 | 70.6810 | ||
| 3 | DWT (Meyer) | R | 0.9802 | 0.9819 | 0.9723 | 0.9776 | 0.9612 | |
| RMSE | 33.0155 | 31.5850 | 38.7293 | 34.7847 | 45.9508 | |||
| MAE | 25.4845 | 24.6434 | 30.0314 | 27.5218 | 37.7463 | |||
| 4 | DWT (db2) | R | 0.9248 | 0.9237 | 0.9107 | 0.9299 | 0.8146 | |
| RMSE | 65.9907 | 64.0403 | 70.8502 | 62.1080 | 95.9548 | |||
| MAE | 52.6840 | 52.0136 | 54.0858 | 48.0775 | 71.8549 | |||
| 5 | DWT (db4) | R | 0.9625 | 0.9567 | 0.9617 | 0.9564 | 0.8889 | |
| RMSE | 45.1868 | 55.3045 | 46.7715 | 48.7092 | 76.6024 | |||
| MAE | 33.6868 | 44.3377 | 36.2730 | 38.0701 | 61.1264 | |||
| 6 | - | SANN | R | 0.8300 | 0.8287 | 0.8049 | 0.8171 | 0.8112 |
| RMSE | 94.8723 | 92.8862 | 99.5541 | 96.0473 | 97.0712 | |||
| MAE | 78.8377 | 74.2247 | 79.1828 | 78.0073 | 76.7192 | |||
| 7 | SD | R | 0.9507 | 0.9102 | 0.9284 | 0.9268 | 0.9211 | |
| RMSE | 52.1441 | 69.3786 | 61.9278 | 63.6088 | 65.1701 | |||
| MAE | 42.6135 | 54.1883 | 49.4063 | 49.5467 | 51.9533 | |||
| 8 | DWT (Meyer) | R | 0.9927 | 0.9973 | 0.9968 | 0.9955 | 0.9951 | |
| RMSE | 20.4926 | 12.1045 | 15.0972 | 16.0551 | 16.5294 | |||
| MAE | 15.5346 | 9.3213 | 11.7802 | 12.4678 | 11.8652 | |||
| 9 | DWT (db2) | R | 0.9624 | 0.9458 | 0.9479 | 0.9338 | 0.9352 | |
| RMSE | 45.8911 | 55.3706 | 53.3337 | 59.1869 | 58.8830 | |||
| MAE | 37.6343 | 43.2339 | 41.6543 | 47.8722 | 45.4037 | |||
| 10 | DWT (db4) | R | 0.9570 | 0.9487 | 0.9531 | 0.9612 | 0.9452 | |
| RMSE | 49.9123 | 52.6379 | 50.2059 | 46.1096 | 55.2336 | |||
| MAE | 38.7917 | 39.2650 | 37.7869 | 36.9486 | 44.3607 | |||
| No. of Model | Pre-Processing Method | Model | Statistical Performance | Number of Neurons | ||||
|---|---|---|---|---|---|---|---|---|
| 3 | 5 | 8 | 10 | 15 | ||||
| 1 | - | ANN | R | 0.7185 | 0.7389 | 0.7496 | 0.7323 | 0.7340 |
| - | RMSE | 119.3717 | 116.1545 | 112.7167 | 116.2497 | 115.5481 | ||
| - | MAE | 92.9199 | 90.6317 | 82.9759 | 85.3620 | 85.2603 | ||
| 2 | - | R | 0.8305 | 0.8569 | 0.8344 | 0.8627 | 0.8497 | |
| SD | RMSE | 94.8184 | 88.0335 | 94.2725 | 87.7624 | 91.2737 | ||
| - | MAE | 68.5089 | 60.6942 | 69.5760 | 62.6814 | 64.6820 | ||
| 3 | DWT (Meyer) | R | 0.9740 | 0.9804 | 0.9773 | 0.9791 | 0.9721 | |
| RMSE | 38.5218 | 33.5312 | 36.1287 | 34.6227 | 39.9093 | |||
| MAE | 30.5493 | 26.3544 | 27.7637 | 27.0257 | 30.1284 | |||
| 4 | DWT (db2) | R | 0.9174 | 0.9295 | 0.9290 | 0.9498 | 0.8475 | |
| RMSE | 69.0054 | 63.0776 | 64.3189 | 54.4427 | 90.2813 | |||
| MAE | 54.3111 | 48.8261 | 47.7219 | 39.6865 | 67.9992 | |||
| 5 | DWT (db4) | R | 0.9639 | 0.9596 | 0.9611 | 0.9597 | 0.9196 | |
| RMSE | 45.4499 | 53.0644 | 47.5084 | 47.8804 | 66.8622 | |||
| MAE | 34.4683 | 40.9454 | 36.4628 | 30.7056 | 47.5880 | |||
| 6 | - | SANN | R | 0.8010 | 0.8164 | 0.8070 | 0.8200 | 0.8213 |
| RMSE | 102.2606 | 97.1078 | 100.3804 | 96.7091 | 96.1686 | |||
| MAE | 79.9284 | 70.2974 | 73.5328 | 73.3155 | 71.8607 | |||
| 7 | SD | R | 0.9690 | 0.9393 | 0.9607 | 0.9521 | 0.9275 | |
| RMSE | 41.5860 | 57.7945 | 46.8358 | 52.4555 | 63.0528 | |||
| MAE | 31.3174 | 41.0834 | 31.3976 | 38.5993 | 47.0755 | |||
| 8 | DWT (Meyer) | R | 0.9919 | 0.9985 | 0.9965 | 0.9967 | 0.9972 | |
| RMSE | 22.0805 | 9.4251 | 15.4858 | 13.7718 | 12.5305 | |||
| MAE | 14.8010 | 6.6855 | 9.8296 | 10.0559 | 7.2495 | |||
| 9 | DWT (db2) | R | 0.9674 | 0.9593 | 0.9632 | 0.9615 | 0.9618 | |
| RMSE | 42.9408 | 47.5008 | 45.2887 | 46.2991 | 46.1271 | |||
| MAE | 31.6252 | 34.3351 | 32.4117 | 33.7197 | 32.1644 | |||
| 10 | DWT (db4) | R | 0.9747 | 0.9716 | 0.9744 | 0.9765 | 0.9639 | |
| RMSE | 37.9720 | 40.6086 | 37.8868 | 37.4568 | 44.8296 | |||
| MAE | 24.7977 | 29.0884 | 24.3499 | 26.9415 | 27.2420 | |||
| Methods | R | RMSE | MAE |
|---|---|---|---|
| ARIMA | 0.7628 | 108.070 | 83.235 |
| GA-SA | 0.8190 | 96.000 | 76.595 |
| Raw data + ANN | 0.8061 | 98.311 | 74.054 |
| Raw data + SANN | 0.8287 | 92.886 | 74.225 |
| SD + ANN | 0.8601 | 85.511 | 66.045 |
| SD + SANN | 0.9507 | 52.144 | 42.614 |
| Meyer Wavelet + ANN | 0.9819 | 31.585 | 24.643 |
| Meyer Wavelet + SANN | 0.9973 | 12.105 | 9.3213 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran Anh, D.; Duc Dang, T.; Pham Van, S. Improved Rainfall Prediction Using Combined Pre-Processing Methods and Feed-Forward Neural Networks. J 2019, 2, 65-83. https://doi.org/10.3390/j2010006
Tran Anh D, Duc Dang T, Pham Van S. Improved Rainfall Prediction Using Combined Pre-Processing Methods and Feed-Forward Neural Networks. J. 2019; 2(1):65-83. https://doi.org/10.3390/j2010006
Chicago/Turabian StyleTran Anh, Duong, Thanh Duc Dang, and Song Pham Van. 2019. "Improved Rainfall Prediction Using Combined Pre-Processing Methods and Feed-Forward Neural Networks" J 2, no. 1: 65-83. https://doi.org/10.3390/j2010006
APA StyleTran Anh, D., Duc Dang, T., & Pham Van, S. (2019). Improved Rainfall Prediction Using Combined Pre-Processing Methods and Feed-Forward Neural Networks. J, 2(1), 65-83. https://doi.org/10.3390/j2010006






