Abstract
Computer-based testing (CBT) is gaining importance for studies addressing the diagnosis of competencies, because it is possible to simulate authentic action situations and may reduce the effort of analyzing the data. This benefit is most important for the phase of item design. In this phase of assessment construction, the pattern of answers of a sample is used to draw conclusions on the functionality of the items. Currently, there are no standards for the encodement of items which consider the specifications of CBT-instruments. These specifications are, for example, the a posteriori non-variability of the coding, a lack of information when using conventional test scores and the need of standardization of different formats of items. Taking these specifications into consideration, this paper proposes and discusses a two-stage coding systematization for CBT-items. For this, a distinction between item-coding and answer-coding was done. The coding is discussed for single-section and multi-section formats as well as dichotomous and polytomous answer modes. Therefore, this paper is for users of CBT-instruments who want to achieve the optimal information value of their test results with efficient coding.
1. Introduction
In the educational sciences and enterprise training, Computer-Based Testing (CBT) is used more and more. CBT allows for a representation of authentic action situations with a higher amount of ecological validity compared to Paper-Based Testing. Therefore, it results in a higher degree of transferability of a test situation to reality [1,2,3,4].
Moreover, CBT enables an automation of large parts of data evaluation, which offers efficiency advantages especially for large samples. This increased efficiency is particularly relevant in the phase of item development, as test results can be transferred directly into statistics and evaluation software. Additionally, an IT-based analysis can, compared to manual analysis, contribute to a higher standardization of correction and thereby decrease the susceptibility to errors [5]. Thus, errors in coding, particularly those that are caused by inadvertence or differences in the coding of identical data sets, can be avoided.
The adequate coding of test data, which means the assignment of numerical values to different answer options of an item, is of central importance for test evaluation as it initially determines the reference frame of subsequent analyses. Kleinhans [6] demonstrated that the requirements in the context of CBT instruments go beyond those of paper-based tests: especially in the phase of test development, it is preferable to be able to adjust the encoding rules a posteriori, e.g., to optimize polytomous scaling. In contrast to paper-based procedures, in CBT the encoding rules have to be implemented prior to starting the test, as test results are typically calculated during the execution of the test. Further difficulties are added by the fact that classical CBT instruments often only provide one result field per task (e.g., point value), which is limited in its information value.
Additionally, in order to ensure efficient processing of test results and to reduce the likeability of errors in the evaluation, a standardized coding design for various item formats is of great importance. Usually, classical CBT instruments offer a variety of open and closed, single section and multi-part, as well as dichotomous and polytomous item formats, which can differ strongly in their structure. Here, the challenge of standardized coding systematization occurs especially. The proposed coding scheme is applicable on all platforms that allow editing of the encoding by the user.
Although the coding of CBTs requires additional demands compared to paper-based testing, so far, this issue has hardly been addressed in literature. Therefore, Kleinhans [6] proposed a two-stage coding scheme. However, this scheme is not detailed enough to address the requirements of test items with a high number of response options. For multi-part items, the lack of precession is increased.
This constitutes the starting point of this paper. The following research question will be discussed:
How does a coding scheme of computer-based items with a high number of answer options have to be designed to maximize the informational value of test scores generated with Computer Based Testing?
The development of the coding systematization to be displayed is based on the learning management system ILIAS (version 4.4). Nevertheless, the systematization claims to be applicable in the context of other typical CBT cases.
In Section 2, the basic terms will be defined and the requirements for the coding will be discussed. In Section 3, the basics of the coding systematization are described and in Section 4, the adapted and extended coding for items with a high number of response options is explained. The conclusion in Section 5 completes the contribution.
2. Basics of Coding
In this section, the term coding is defined and its requirements in context of CBT are explained.
2.1. Definition of Coding
Rost [7] defined coding as the numeric encryption of an item’s response options; the resulting numeric values represent the test-data. In extension of Rosts definition, for the following discussion, coding is understood as systematization of transformation of test data into a numeric relative. This systematization must be adequate to the requirements of analysis as well as to the interests of research. It has to be standardized for the test instrument, in design as well as in application, to ensure high replicability.
Scoring is the application of coding on a dataset. According to a dichotomous or polytomous response mode, a response variable is generated for every test person per item, representing the result of the test persons processing and indicating the test persons’ performance or attitude. This response variable is the basis for further analyses, for example, the calculation of frequencies of solutions or for complex procedures of scaling based on item-response-models.
Therefore, the coding is the basis for scoring and thereby the calculation of test scores. However, scientific literature mostly offers descriptions for coding for paper-based tests. This even applies to established surveys which are in parts also CBT-based, like PISA (Programme for International Student Assessment) [8,9,10] or PIACC (Programme for the International Assessment of Adult Competencies) [11]. The requirements and possibilities of a CBT-specific coding systematization have only been discussed lately by Kleinhans [6], who proposed a general approach, which is the basis for more specific coding systematization discussed in this paper.
2.2. Requirements for Coding
To discuss the abilities of the coding scheme, requirements have to be defined. Two basic functions have to be addressed by the scheme for adequate usability: firstly, information about the precisely chosen response options has to be provided. This allows the calculation of the frequency of the choices of particular options as well as the identification of frequently mentioned combinations of responses, which may for example be further processed in distractor analysis. Thereby, systematic errors of the test processing or relations between response alternatives may be identified. Reversely, a coding which only allows for a distinction between right and wrong answers, should be avoided because of its low degree of information. For the following discussion, this is function is specified as differentiating function of coding.
Secondly, there has to be the information, whether an item has been solved right or wrong and, if necessary, to which degree the solution is right (completely, partly). At the same time, coding should be flexible enough, so that it can be modified a posteriori in the phase of item development. This can be necessary in context of a pilot run and calibration of a test instrument to examine the consequences of different variations of dichotomous or polytomous scoring on the quality of a scale. For the following discussion, this function is termed as the rating function of coding.
These basic requirements are complemented by CBT-specific requirements. Since coding rules have to be implemented usually a priori in test software, the missing possibility of subsequent modification is a particular challenge. At the same time, a standardization of coding among different question types is essential, to gain a standardized data format for further evaluative steps. This is made difficult due to the basic focus of classical CBT-instruments: whether a distinct listing of all variables and their particular manifestations is needed for test construction, classical CBT instruments are primarily designed to automate the assessment process. This automation offers the possibility of immediate feedback for the participant regarding their results, for example in case of a formative usage. Thereby, for each item exactly one numeric value is created, which is usually the sum of the selected response options (e.g., two of three possible points when two of three attractors are chosen). Indeed, for item construction, this sum is insufficient, if the specific allocation of attractors and distractors cannot be deduced.
Thus, in the context of CBT the need to display information on the exact choice of response options using only one numeric value arises, as well as the claim of an a posteriori variability of coding and a high standardization.
3. General Coding scheme
This section describes the basic ideas of the coding scheme: the distinction of a two-tier coding and the use of decimal factors for item coding.
3.1. Two-Tier Coding
The coding of item formats with only one possible answer is the simplest case for coding, as only one response option has to be gathered. For this, the several options may be numbered consecutively (e.g., one to four in case of four response options). A partial credit scoring is not possible and an a posteriori modification of the coding not necessary. In case of the attribution of numeric tasks the coding is also simple, since only right and wrong solutions can be distinguished. This may be coded using the numbers 1 for the right and 0 for every wrong solution.
If several attractors and distractors must be distinguished per item, the identification of all selected response options becomes more complex. Furthermore, in the phase of item construction it is of high importance to be able to modify a posteriori the test scores which are needed to reach specific steps of a partial credit scoring. Because of this, a two-tier coding is presented in the following, which is differentiated between item coding (IC) and response coding (RC). In the process of test evaluation, the IC is done prior to RC, and RC is the basis for scoring.
The IC defines a priori the numeric values for each response option of an item, which is generated as test score if an option is selected. Therefore, the IC numerically presents the quantity of all possible combinations of responses. The second step, the RC, defines how each of the possible values of the IC is transformed into dichotomous or polytomous response variables for further analyses. Therefore, the values in RC are equal to the possible test scores of an item.
Two requirements have to be met to ensure the functionality of the coding: first, for each value of the IC, a value on the RC has to be defined, since otherwise, responses that cannot be considered in further evaluation could be generated. Second, there must not be several values in RC for one value in IC, otherwise a clear and distinct assignment of responses becomes impossible. In contrast, the assignment of several values of the IC to one value of the RC is valid and often necessary, representing the qualitative equality of different response combinations. An example of the application of Two-tier Coding is given in 3.2.
3.2. Decimal IC for Dichotomous and Polytomous Scoring
In most classical CBT-instruments—as well as in ILIAS—the score of an item is calculated as the sum of all scores of selected response options. In consequence, the value of each selected response option has to be chosen in a way that it still can be identified—even if the values of different selected options are summed up. To solve this every response option was assigned with a decimal power factor according to their initial sequence [6]. The simplest case is the number 1. Therefore, the first response option was coded with the value 1 (= 1 × 100), the second response option with the value 10 (= 1 × 101), the third response option with the value 100 (= 1 × 102) and so forth. If the test software sums all values of the response options selected by the test participant for test evaluation, the result will be a numerical sequence of 0 and 1. Every position of this response sum presents the selection or not-selection of the respective response option in a binary code. On the basis of this response sum—e.g., 10110 as a result of a test person, selecting the second, third and sixth response option (response sum has to be read from last to the first digit) of a multiple-choice item with a total of six response options—it was possible to reconstruct each specific choice
Example 1 in Figure 1 visualizes the application of the Two-tier Coding process in combination with the binary coding scheme on an example.
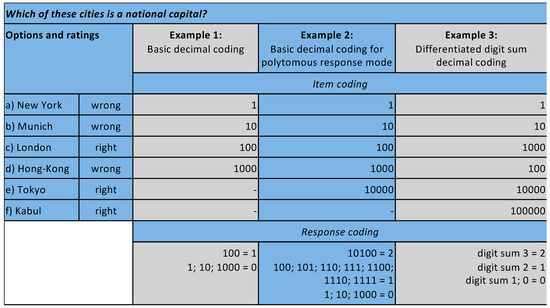
Figure 1.
Example of dichotomous and polytomous two-tier decimal coding.
Every city (= response option) was coded with a decimal power of 1, respectively, values from 1 to 1000. The right response option London was coded with the value 1 in the RC. All other values of the IC, which were the wrong options, were coded with 0 in the RC.
To apply a partial-credit scoring—as proposed by Masters [12]—the IC is the same, however, an adaption of the RC is necessary. This is explained in the second example of Figure 1. For good comprehensibility, the simplest polytomous model is used, which was based on three possible manifestations of the response variable: Completely correct solutions were coded with the value 2 and partly correct solutions were coded with the value 1. For polytomous models with more possible manifestations, the systematization was applicable by analogy. For the example, the optimal solution was the selection of the answers London and Tokyo, which, therefore, was coded with the value 2. Combinations of response options, which only display one right answer or a right and a wrong answer, were coded as partly correct with the value 1. All other possible combinations of response options were coded as wrong with the value 0. Furthermore, it was possible to change the scoring a posteriori by a modification of the requirements for the values 1 and 2 or by switching to a dichotomous response mode. Both was possible by a change in the RC.
4. Expanded Coding Scheme
The presented coding scheme comprised an application problem for great numbers of answer options. If a larger number of attractors and distractors was to be distinguished, the listing of all solution variants of an item could no longer be practical in the response coding process. To calculate the possible number of response combinations, the following formula of combinatorial analysis had to be used: n!/(n − k)! × k! with n equals the total number of response options and k equals the number of selected response options. This results in the quantity of IC values to be differentiated. Thus, in case of five response options with two possible choices there we already 15 possible combinations (5!/(5 − 2)! × 2! + 5!/(5 − 1)! × 1!).
As a solution to this problem, a digit sum was calculated via the response sum (which equals the value after application of the IC). Then, the RC was no longer based on the values of all possible response combinations, but on the digit sums of the IC. This is explained in detail in the following section. The further explanations are to be distinguished for two cases, depending on the epistemological interest: only the assignments of the different attractors can be distinguished, or the allocations of attractors as well as of distractors.
4.1. Digit Sum Coding
In the first case, a dichotomous coding of all attractors combined with the calculation of a digit sum was adequate. Thereby, all attractors were coded with a decimal power according to the systematization explained in Section 3.2. All distractors were coded with the value 0. Thereby, the selection of all attractors resulted in a maximal digit sum for an item and it could be displayed to which degree an item has been solved correctly. The response sum 11001 then allows, for example, the statement that the first and fourth and the fifth attractor have been selected, and the second and third attractors have not. At the same time, the digit sum with value 3 (= 1 + 0 + 0 + 1 + 1) directly contained the total number of all selected correct response alternatives, while a cross-section of five corresponded to the best possible score.
4.2. Differentiated Digit Sum Coding
If the exact selection of the attractors and distractors was to be distinguished, digit sum decimal coding had to be modified. It was necessary to separate different power ranges in the response sum. This results in a different response sums for attractors and distractors with different digit sums. Based on this, the RC must define how many selected attractors were needed for a specific test score, and moreover, how many selected distractors were tolerated, respectively. Thus, the combinations of both digit sum values were assigned.
A possible implementation was to display attractors by higher power ranges than distractors. If, for example, three attractors and five distractors were distinguished, the distractors can be multiplied by the factors 1 to 10,000 and the attractors by 100,000 to 10,000,000. An exemplary response sum of 10110010 (or 101.10010: attractors on the first three digits: 101, distractors on the digits four to eight: 10010) means that attractor 1 and 3, as well as distractor 2 and 5 were selected. Correspondingly, the calculation of the digit sum for the attractors only takes place over the first three digits and for the distractors over the last five digits. In the RC, it was now necessary to be determined how many attractors were needed for a particular test score and how many distractors were tolerated in each case by the assignment of the corresponding digit sums. It was important to standardize the ranges of values of the attractors and distractors between different tasks in a test in order to enable a uniform evaluation. Thus, the coding considers attractors as well as distractors. Additionally, it fulfilled the differentiation function of an encoding.
The functional principle is illustrated in the third example of Figure 1. Participants had to select those cities that are the capitals of a country out of a list of six cities. The attractors were coded with values from 1,000 to 100,000 in power-of-ten steps, and the distractors accordingly were coded with values from 1 to 100.
The optimal answer, the choice of capitals without the choice of a distractor, produced a response sum of 111000 (or 111.000) and a digit sum of 3 for the attractors and 0 for the distractors (ratio 3:0). The answer sum (or 101.010), on the other hand, displayed two correct and one wrong choice. For attractors, the digit sum resulted in the value 2 and for distractors in the value 1 (2:1). Only these totals were to be considered by the RC.
In case that attractors and distractors should be distinguished; however, an answer should be evaluated as wrong if only one of the attractors was selected, a simpler coding method was possible where different sections of attractor and distractor values are not needed. Here, the coding was according to Section 4.1, with the addition that distractors were coded with a value, which was above the digit sum for all attractors chosen at once. For example, if a response sum resulted in five digits, distractors should be coded with values of 6 and above. Then, each digit sum bigger than 5 was defined in the RC as wrong. A response sum of 11601 would display the selection of a distractor in the third place. Accordingly, the digit sum is 9, and therefore, in the quantity of wrong solutions. This method is also useful to impose sanctions on selected distractors, which are especially sensible.
4.3. IC for Dichotomous and Polytomous IC Scoring of Multi-Part Formats
The presented coding scheme is applicable for all common item types, including multiple-choice, ranking and free text items [6]. However, it is not suitable for multi-part Questions types like cloze items. Typically, multi-part questions types offer only one result field for all parts of an item. Therefore, all information concerning selected answer options has to be gathered in this one field. Therefore, Kleinhans [6] adopted the binary coding scheme to multi-part items at the example of cloze items. The basic adaptation of the systematization for multi-part items was done by using the particular digits (= decimal power) of the response sum for the display of partial tasks instead of the response options. In the simplest case (distractors were not considered yet) all attractors of a partial task were coded with the value 1 and the specific decimal power. This means that partial task one was coded with 1 (100), partial task two with 10 (= 101), partial task three with 100 (= 102) and so forth. This is shown in the first example of Figure 2. Again, digit sums were used to evaluate how many partial tasks were answered correctly by the participant.
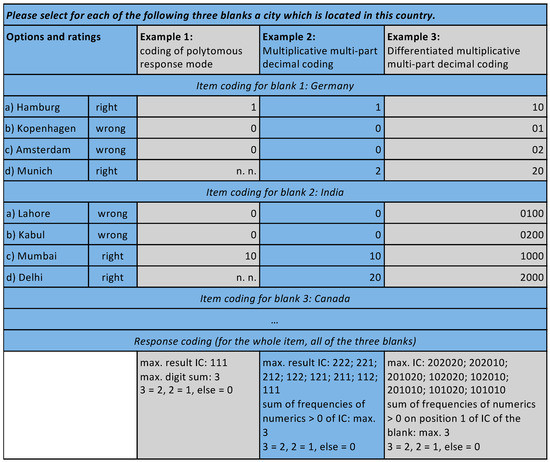
Figure 2.
Example of scoring for multi-part tasks.
Furthermore, a factor was introduced to divide between different attractors and distractors in each gap. This means that each response options got an increasing factor with individual values. Consequently, when, for example, three attractors were among the possible options of a gap, they could be coded with the factor 1 to 3 and multiplied with the specific decimal power of the gap. An example for this was shown in the second example of Figure 2. In the first gap the correct solutions Hamburg und Munich are coded increasingly with the values 1 (= 1 × 100) and 2 (= 2 × 100). In a possible second gap, for example asking for cities in India, the cities of Mumbai and Delhi would be analogous coded with the values 10 and 20 (= 1 × 101 and 2 × 101). A possible third gap for Canada would be coded with values 100, 200 and so forth. The response sum 012 displays, in this example, that in the first gap the second correct answer (= Munich) was chosen, in the second gap the first correct answer (= Mumbai) was chosen and in the third gap a distractor was chosen.
The use of digit sums to display the frequency of selected attractors is more difficult for this method. It may be restored by a modification on information technological level: all values higher 0 must be counted with the value 1. The digit sum of the response sum 012 is, in the example, 3. However, the frequency of values higher than 0, being relevant for the RC, is 2 with a maximum of 3 for three correct answers.
4.4. Differentiated Multiplicative Multi-Part Coding
This approach is quite limited, because a maximum of nine answer options can be divided in a digit by the factors 1 to 9. Especially for cloze questions with free text answers this can be a great constraint, in case that the given free text answers should be matched with a predefined word list. For example, a task in a medical test could be to name an appropriate medicine for a disease and the choice of the test taker has to be identified from a long list of possible drugs. Apart from this, the presented coding scheme requires gathering attractors and distractors in one digit. However, this can lead to great confusion if the number of attractors and distractors differ between different items. For example, the number 4 can be in one case the choice of the fourth attractor or in the other case the first distractor (if only three attractors were used). For response coding a high effort is needed to divide between each item and standardization is very low for the whole test.
Therefore, further adoption to the coding scheme is necessary. It is again proposed to use separated positions in the value of the IC for attractors and distractors. For example, two sequenced decimal powers can be used to display one partial task. The first number represented a chosen attractor and the second number a chosen distractor. The results were pairs of two numbers for each partial item. For example, a response value of 3001 for two partial items (better shown as 30.01) displays the selection of the third correct response option in gap one and of the first incorrect response option in gap two. The digit sum in the RC must be calculated with the frequencies of all values higher 0. A separate digit sum calculation for attractors and distractors was necessary.
Example 3 of Figure 2 illustrates this. Each of the three gaps present two correct and two incorrect cities. The response sum reserves one digit for attractors and one digit for distractors for each gap. Accordingly, two decimal powers are reserved for each gap in the IC. An optimal solution will result, for example, in the response sum 10.20.10, displaying the selection of a correct city in each gap. A response sum of 02.10.10 displays a partly correct solution, with a right choice in the first to gaps and a wrong chosen city in the third gap.
In this case, the probability of errors in response coding clearly decreased. Furthermore, it was possible to use more than one digit for the attractors and distractors for one gap of a cloze question. For example, one digit could be used to identify one of a maximum of nine attractors, and afterwards, two digits for distractors to gather one of in maximum 99 distractors. If the digit number was standardized for a test, this coding reduced effort and the probability of errors in response coding considerably and offered the needed space for long lists of answer as well.
5. Summary
This paper presented a coding systematization for items with a high number of response options as extension for the scheme already offered by Kleinhans [6]. Furthermore, the extended scheme could be used to identify attractors and distractors reliably, even in multi-part items. Therefore, digit sums and different digits for attractors and distractors were introduced to the scheme.
All advantages of the coding scheme of Kleinhans [6] remain:
The scheme was specified for the use in context of CBT, especially in the phase of item construction. A two-tier coding allowed a priori complete information on the possible combinations of response options, which may be chosen by a participant. At the same time, the scoring could be modified a posteriori via the RC.
As long as merely one single field for results was available in a test instrument, it should be used according to the proposed two-part system for the IC. Consequently, a system internal evaluation of correct and incorrect answers was not possible. This disadvantage, as long as it was not absolutely necessary, e.g., for a self-test, was acceptable if one considers that otherwise, no further analysis (e.g., distractor analysis) or a posteriori changes of the scoring would be possible. Furthermore, the standardized response sums of the IC could be directly imported into statistical software and response variables can be generated or distractor analyses can be performed, respectively.
Author Contributions
Conceptualization, writing and visualization: T.J.K. and J.K.
Funding
This research received no external funding.
Acknowledgments
The authors acknowledge financial support by the Deutsche Forschungsgemeinschaft and the Technische Universität Dortmund/TU Dortmund University within the funding program Open Access Publishing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Seeber, S.; Ketschau, T.J.; Rüter, T. Struktur und Niveau beruflicher Fachkompetenz Medizinischer Fachangestellter. Unterrichtswissenschaft 2016, 44, 185–203. (In German) [Google Scholar]
- Nickolaus, R.; Abele, S.; Walker, F.; Schmidt, T.; Gschwendtner, T.; Geißel, B.; Nitzschke, A.; Gönnenwein, A. Computergestützte Erfassung berufsfachlicher Kompetenzen. Berufsbildung: Zeitschrift für Praxis und Theorie in Betrieb und Schule 2014, 68, 13–16. (In German) [Google Scholar]
- Achtenhagen, F.; Winther, E. Konstruktvalidität von Simulationsaufgaben: Computergestützte Messung berufsfachlicher Kompetenz—am Beispiel der Ausbildung von Industriekaufleuten. Abschlussbericht für das Bundesministerium für Bildung und Forschung. 2009. Available online: https://www.bmbf.de/files/Endbericht_BMBF09.pdf (accessed on 23 December 2016). (In German).
- Benett, R.E.; Goodman, M.; Hessinger, J.; Kahn, H.; Ligget, J.; Marshall, G.; Zack, J. Using multimedia in large-scale computer-based testing programs ☆. Comput. Hum. Behav. 1999, 15, 283–294. [Google Scholar] [CrossRef]
- Moosbrugger, H.; Kelava, A. Qualitätsanforderungen an einen psychologischen Test. In Testtheorie und Fragebogenkonstruktion, 2nd ed.; Moosbrugger, H., Kelava, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2012. (In German) [Google Scholar]
- Kleinhans, J. IT-gestützte Werkzeuge zur Kompetenzmessung; wbv Media: Bielefeld, Germany, 2018. (In German) [Google Scholar]
- Rost, J. Lehrbuch Testtheorie—Testkonstruktion, 2nd ed.; Huber: Mannheim, Germany, 2004. (In German) [Google Scholar]
- OECD. PISA 2012 Technical Report; OECD Publishing: Paris, France, 2014. [Google Scholar]
- OECD. PISA 2009 Technical Report; OECD Publishing: Paris, France, 2012. [Google Scholar]
- OECD. PISA 2006 Technical Report; OECD Publishing: Paris, France, 2009. [Google Scholar]
- OECD. Technical Report of the survey of Adult Skills (PIACC); OECD Publishing: Paris, France, 2013. [Google Scholar]
- Masters, G.N. A Rasch Model for Partial Credit Scoring. Psychometrika 1982, 47, 149–174. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).