Ionic Imbalances and Coupling in Synchronization of Responses in Neurons
Abstract
1. Introduction
2. Voltage-Gated Ion Channels
2.1. Ionic Imbalances
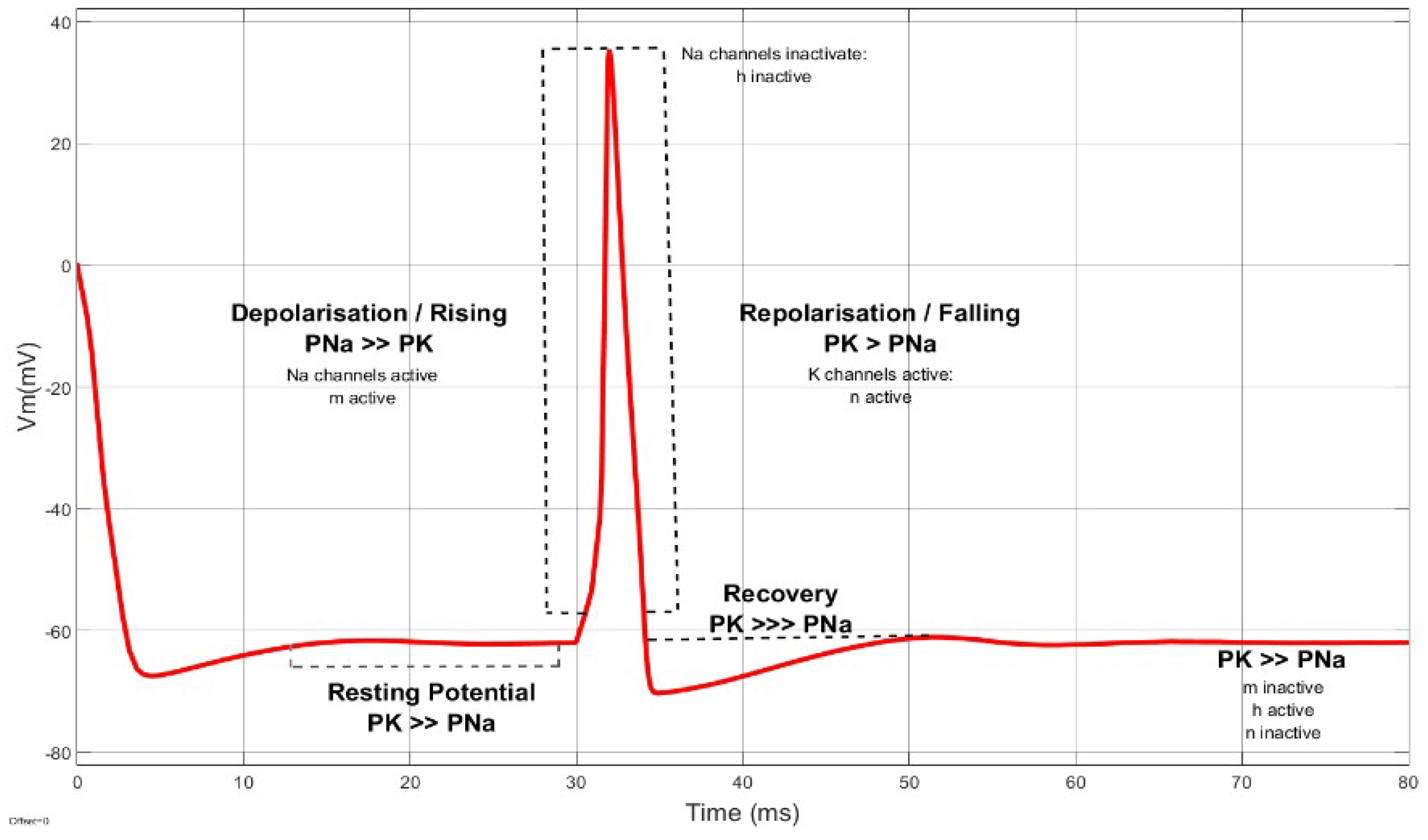
3. Membrane Potential Dynamics
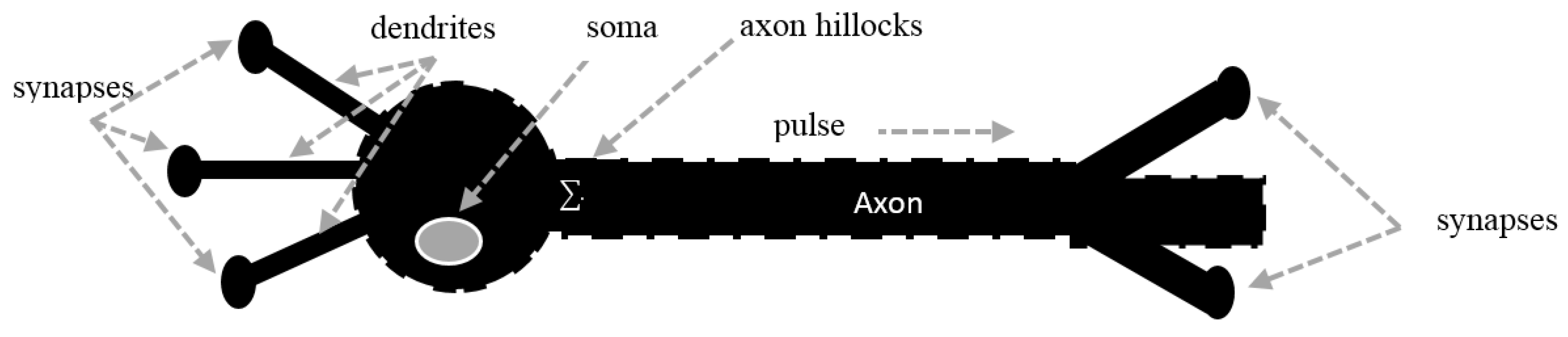
3.1. Generalized Form of Neurons
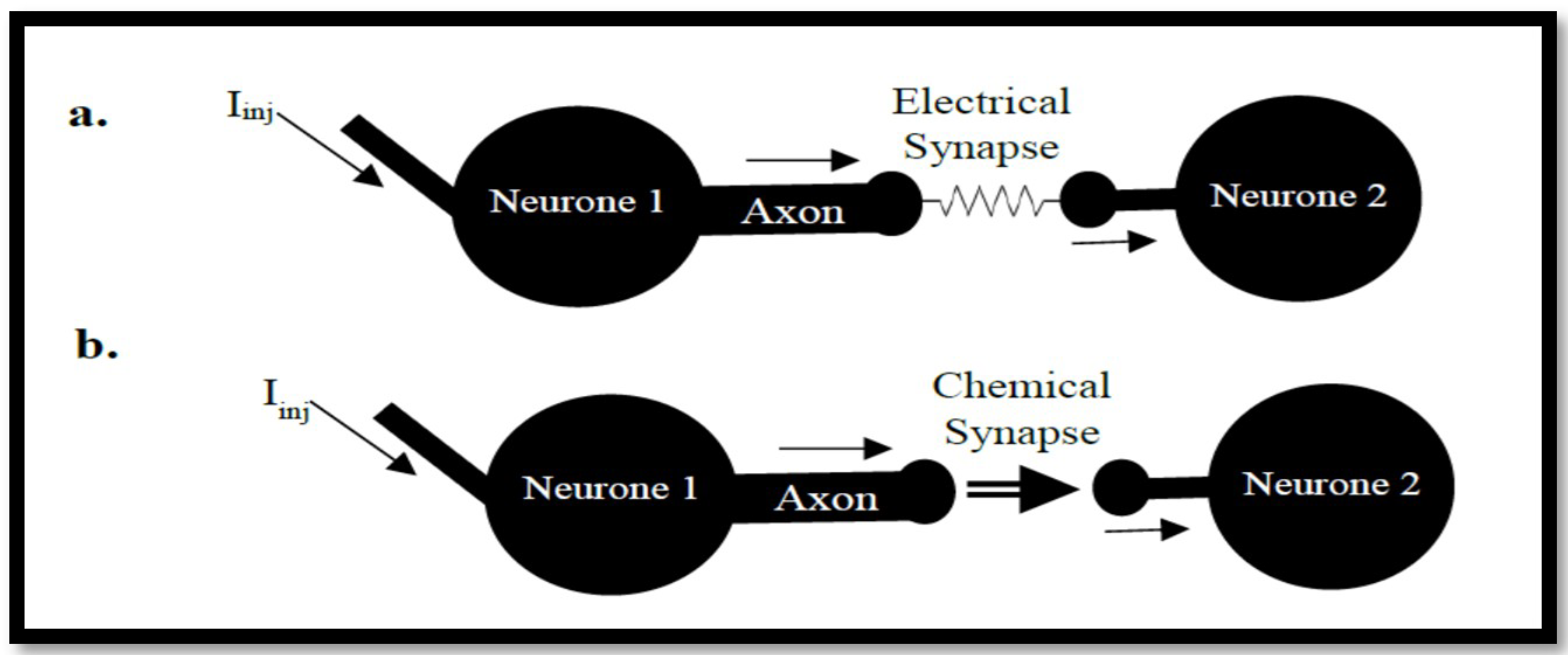
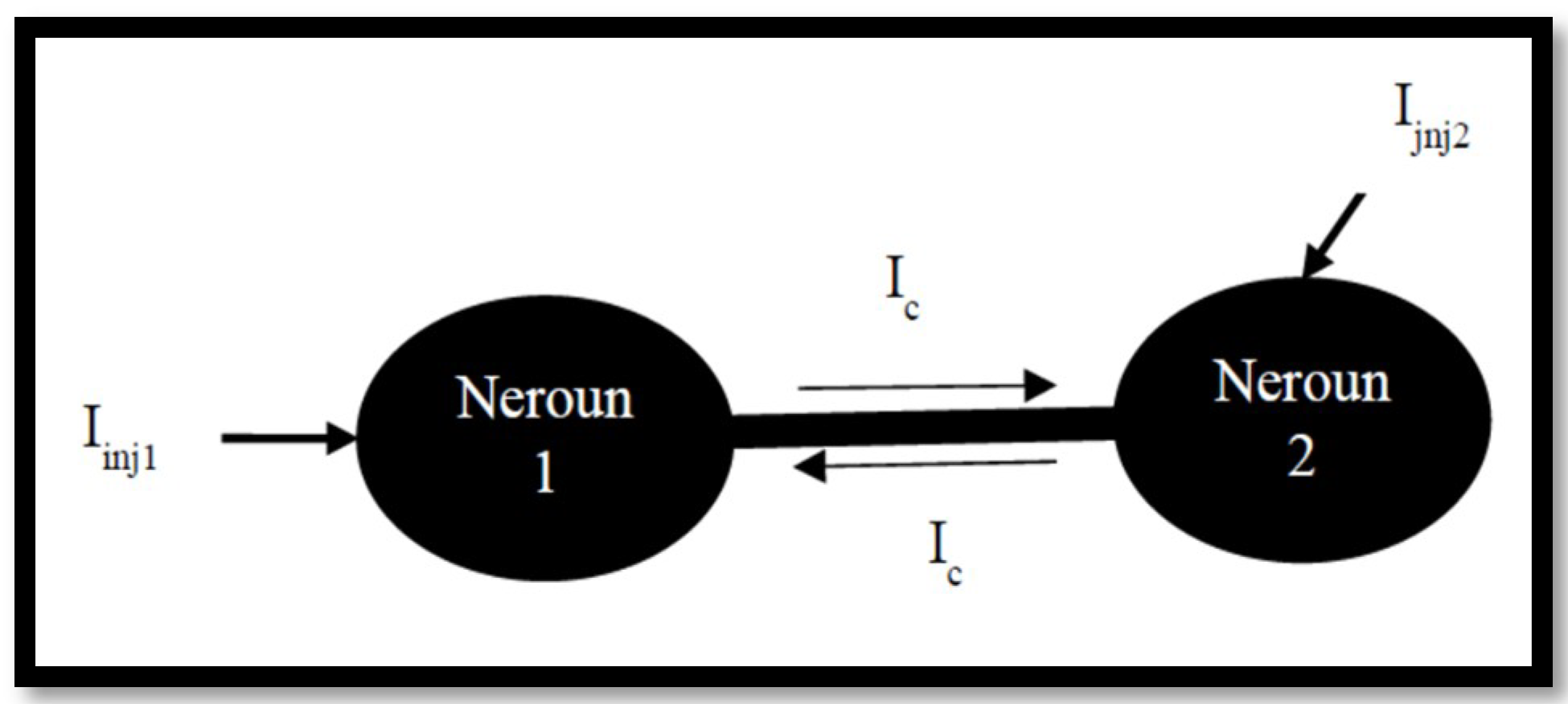
3.2. Coupled Type Equations
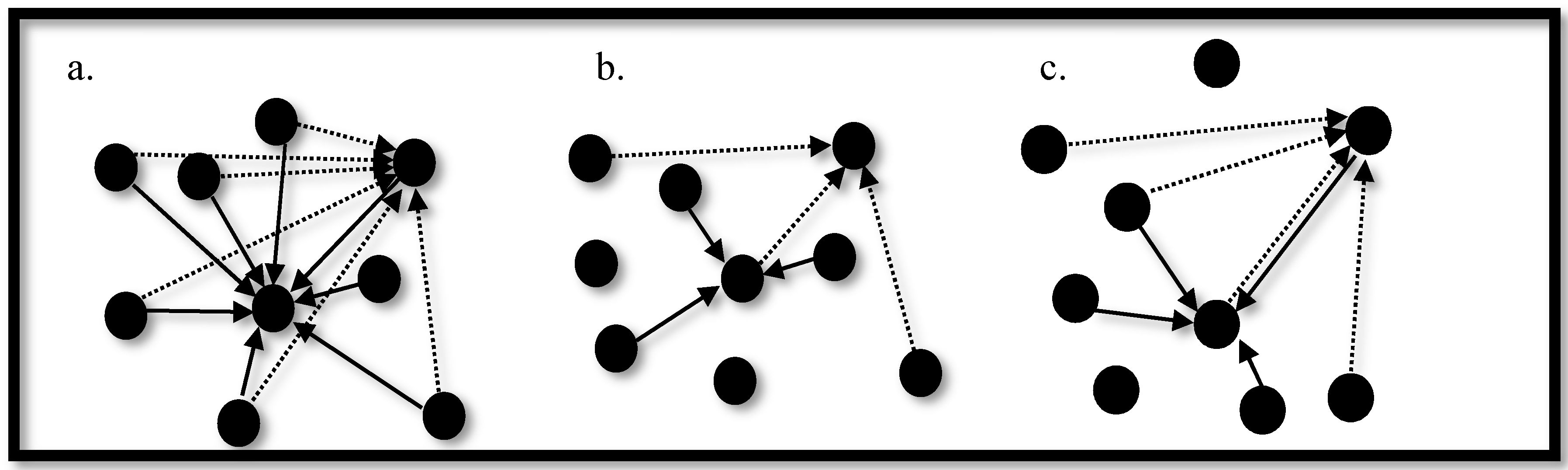
3.3. Synchronization in Coupled Neurons
3.4. The Region of Synchronicity
4. Simulation and Results
4.1. Ion Imbalances in Neural Networks
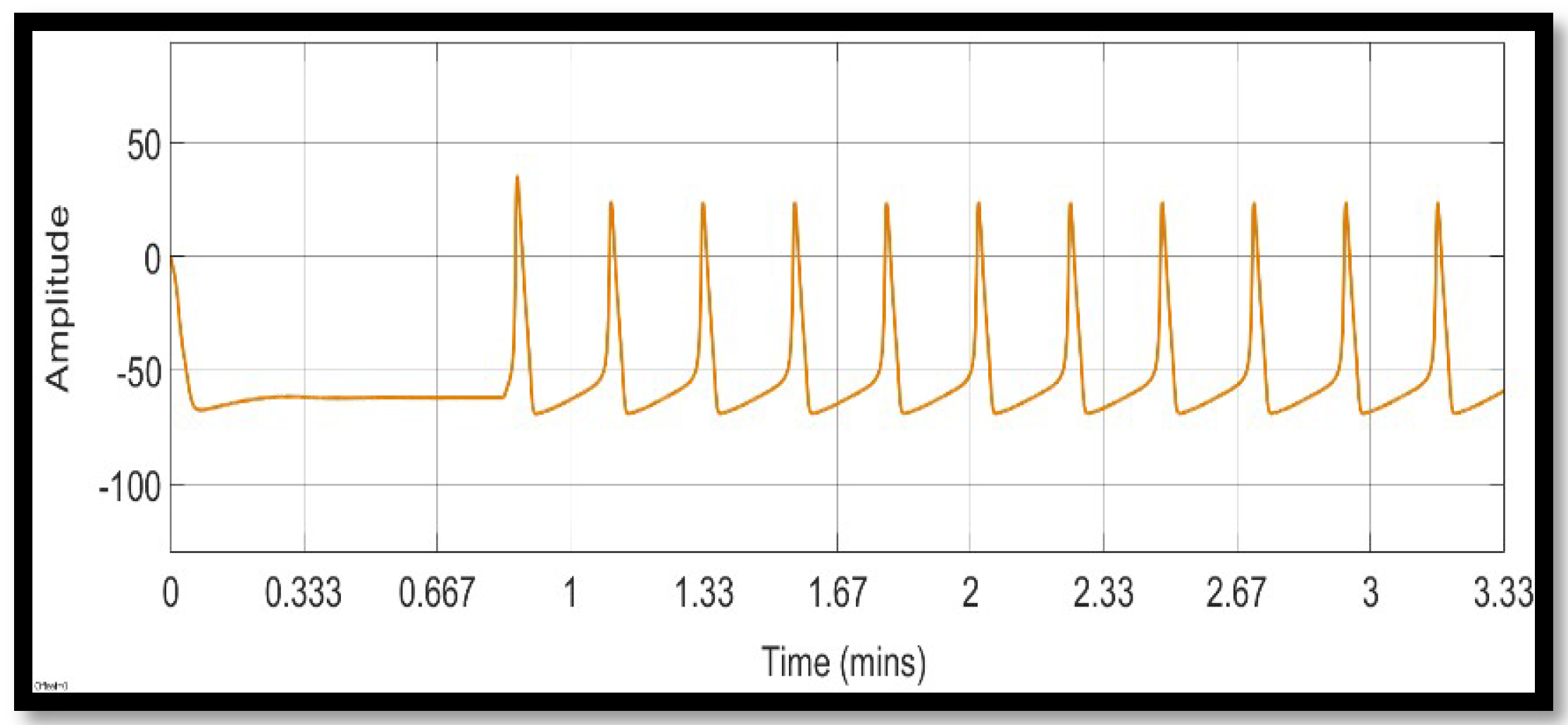
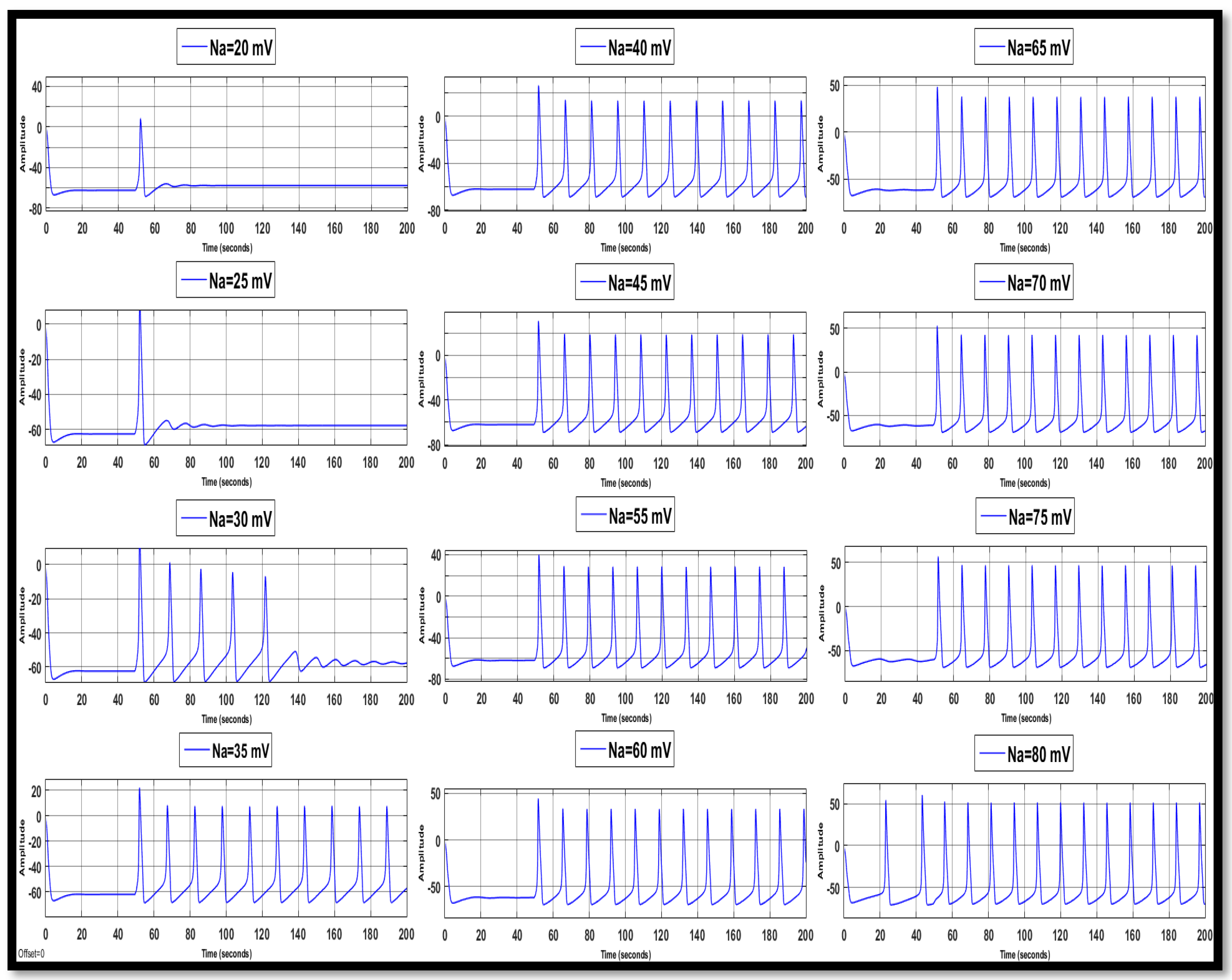
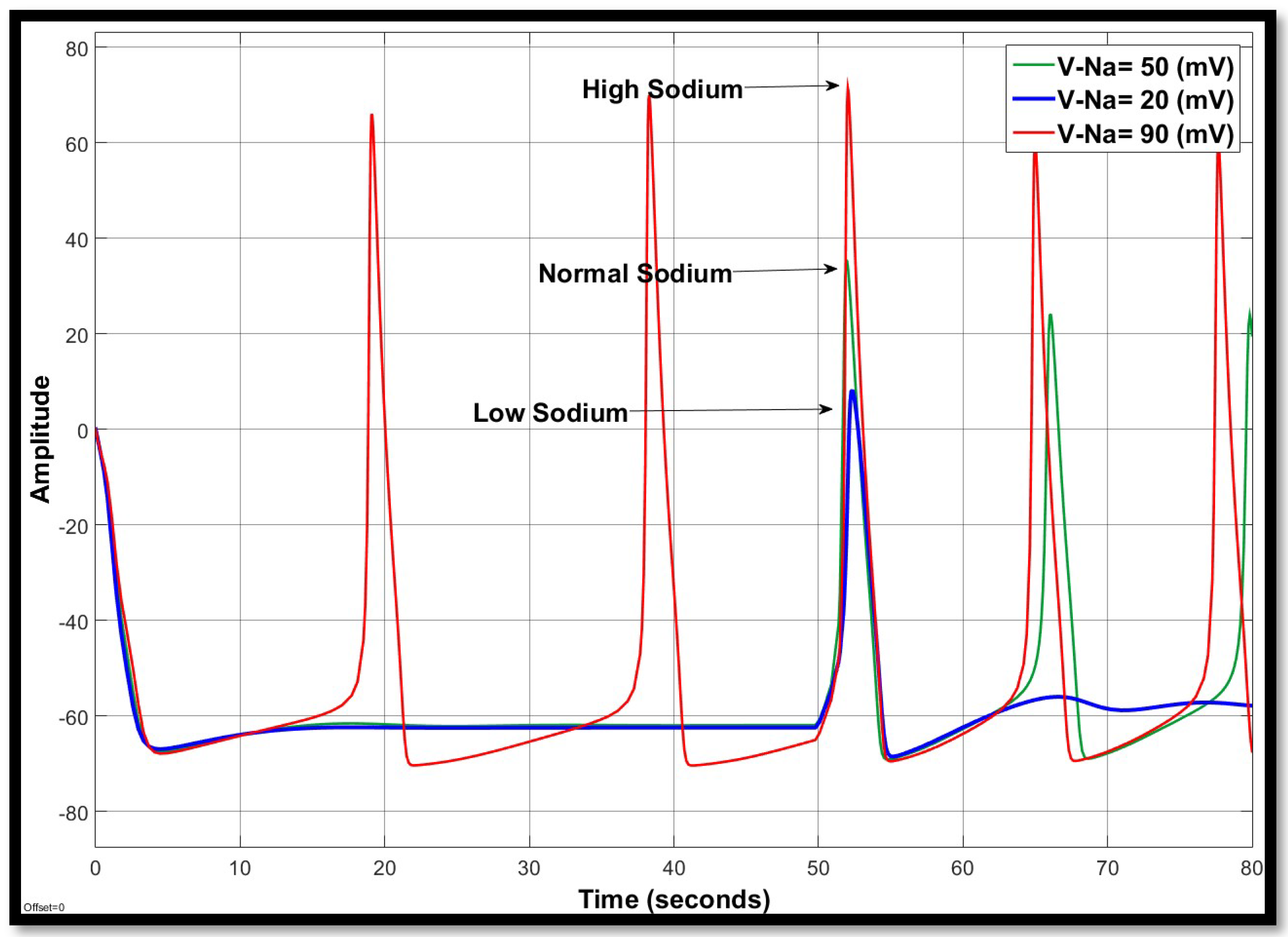
4.1.1. Sodium Ion Concentration Changes in a Single Neuron
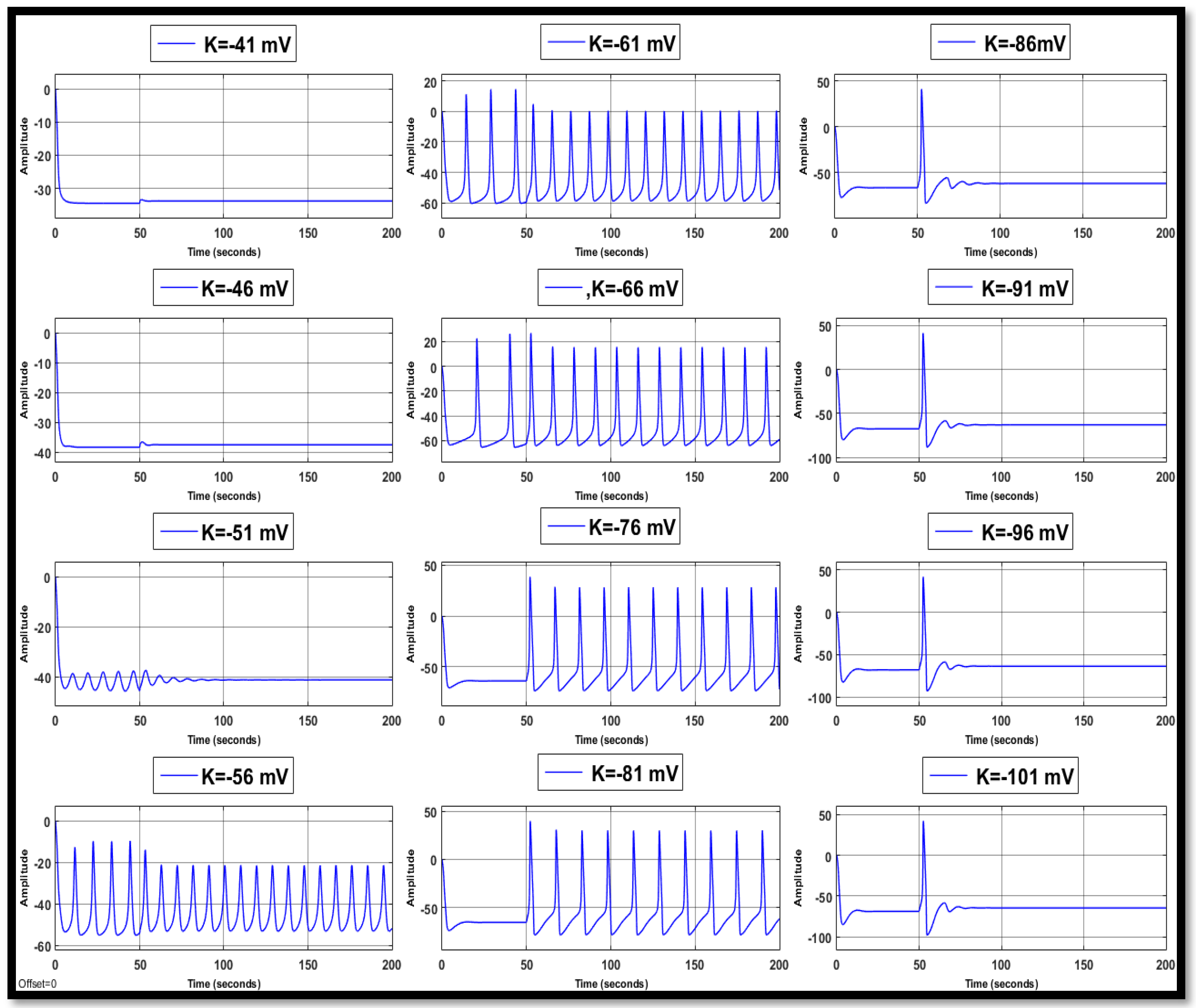
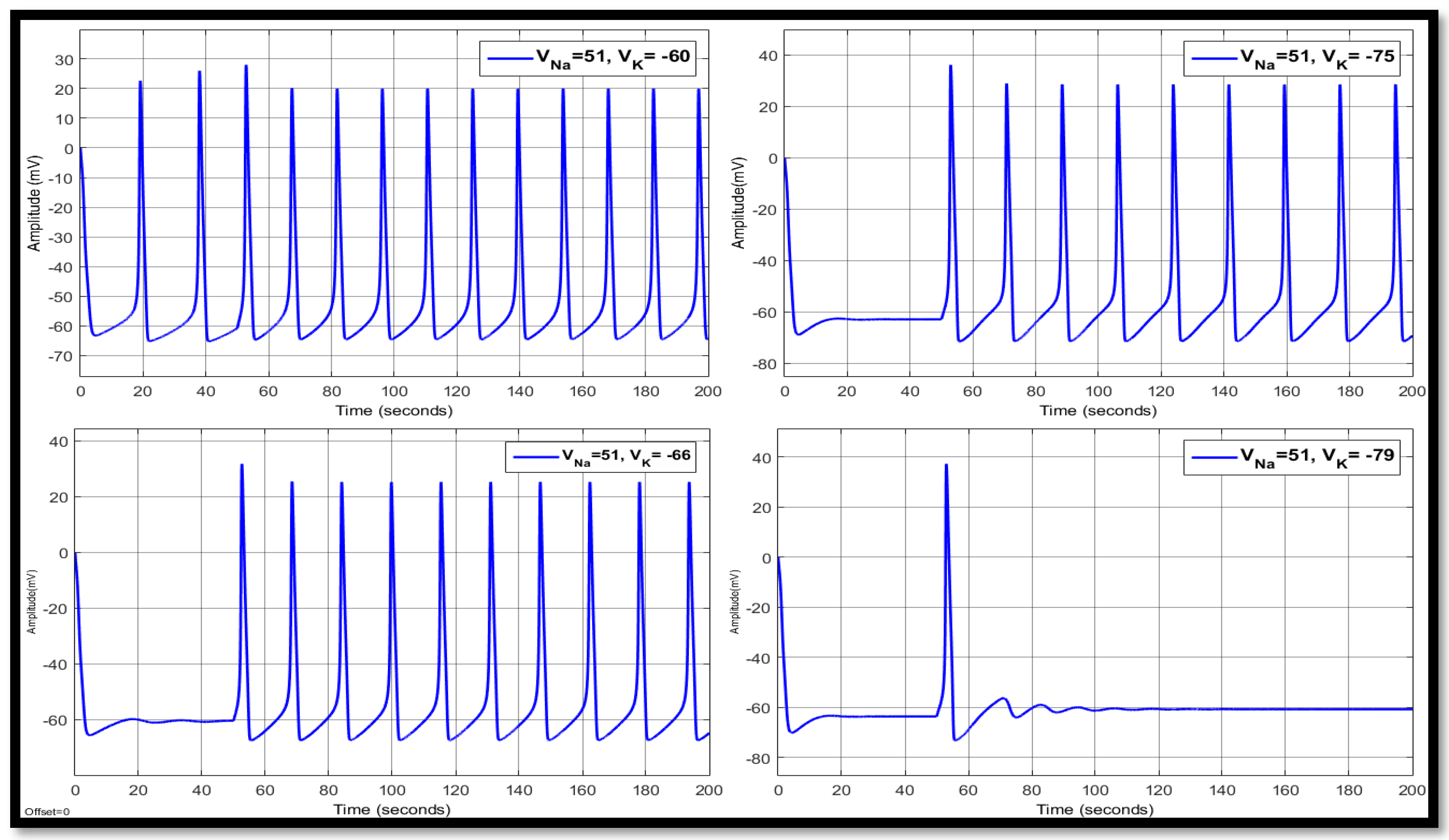
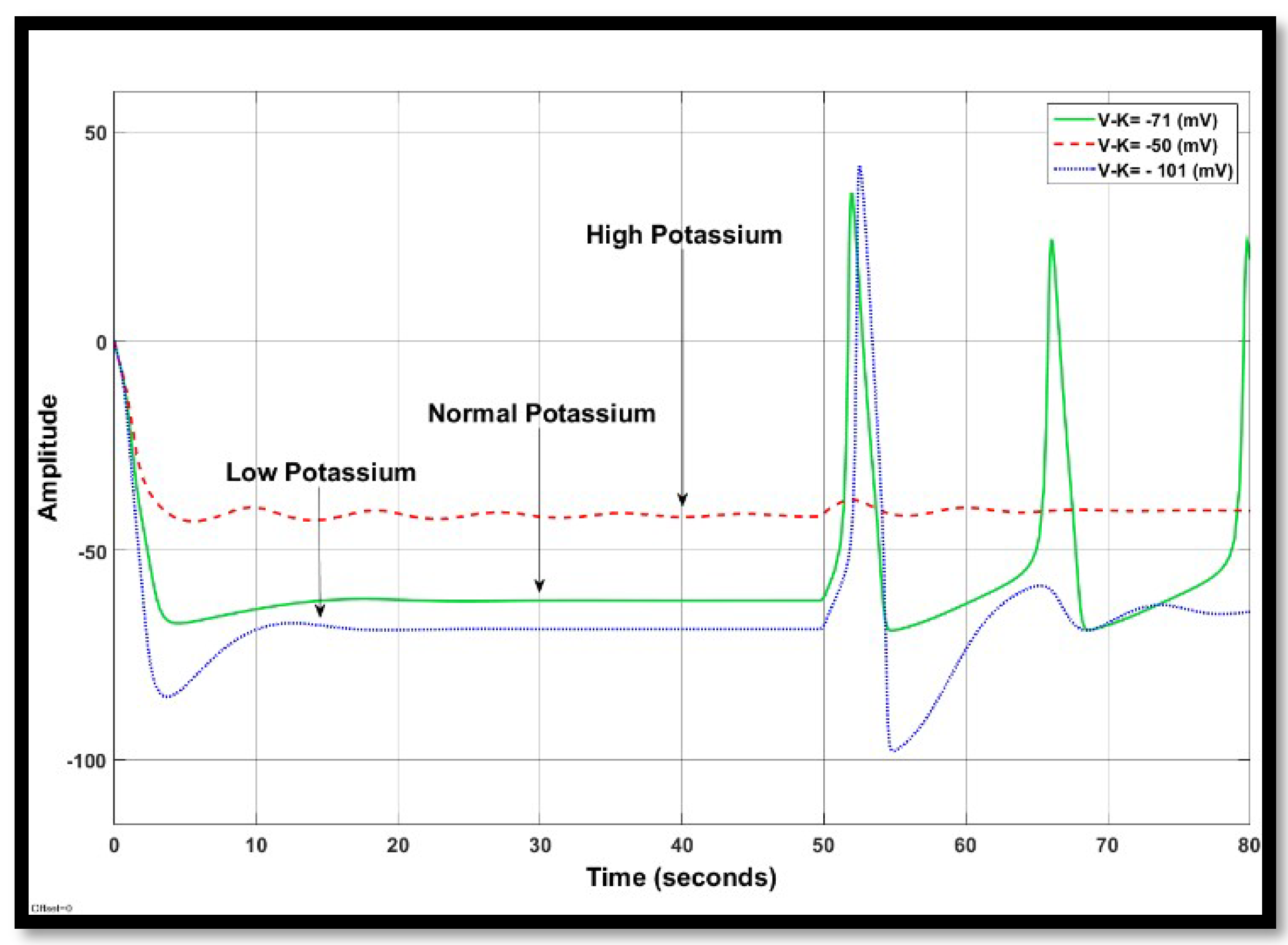
4.1.2. Changes in Potassium Concentration in a Single Neuron
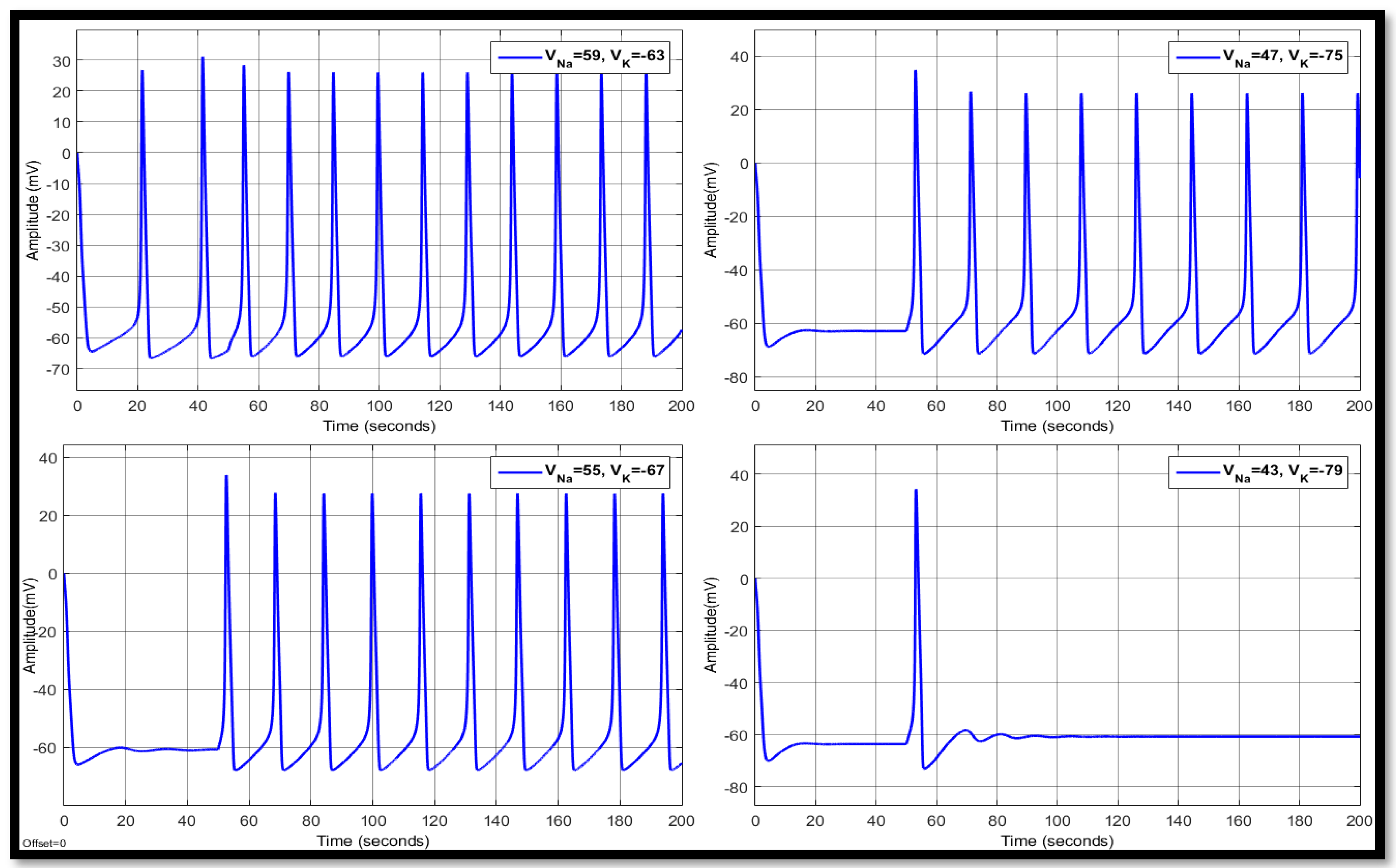
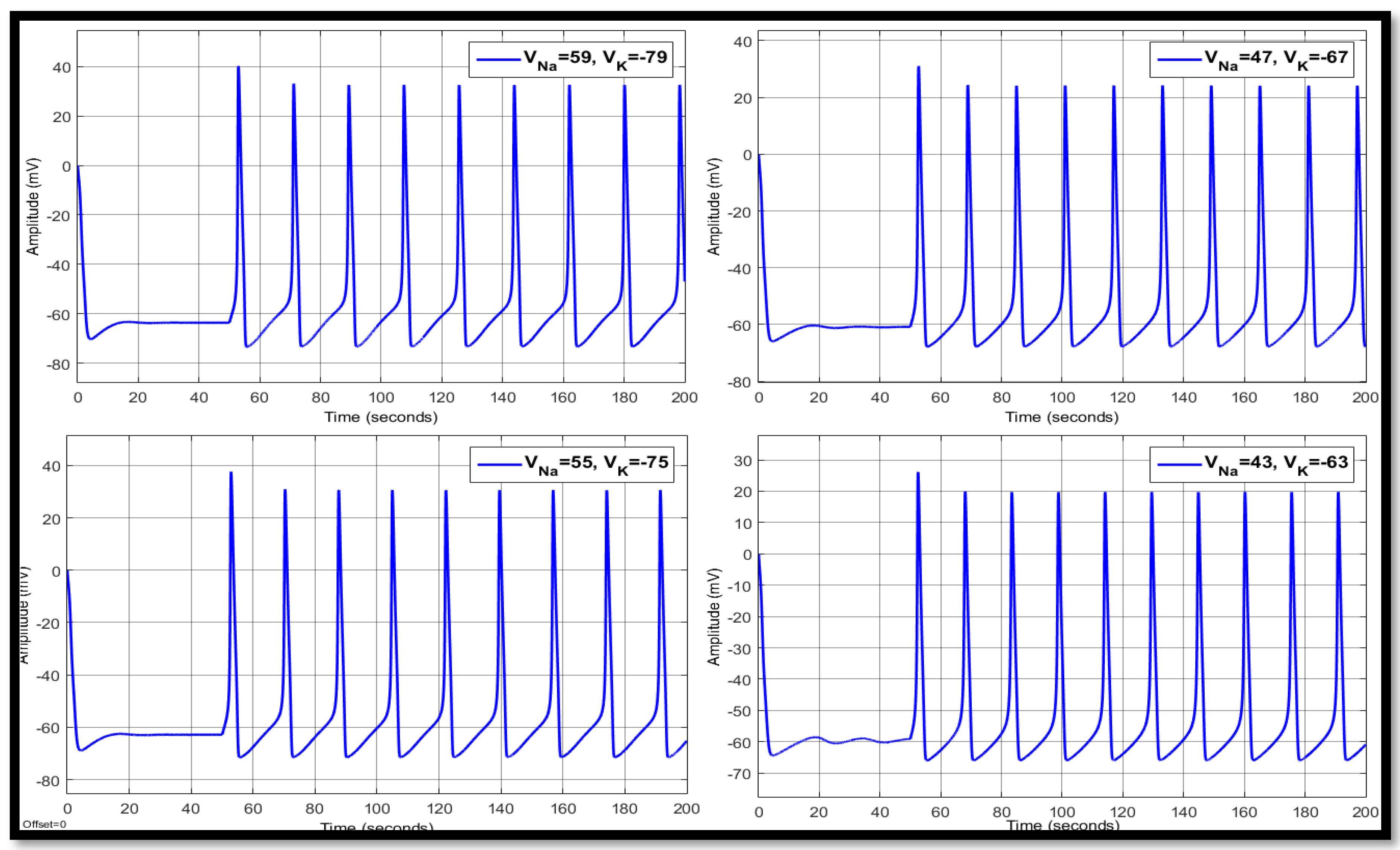
4.1.3. Combination of Changes in a Single Neuron
4.2. Ion Imbalances in Coupled Neurons
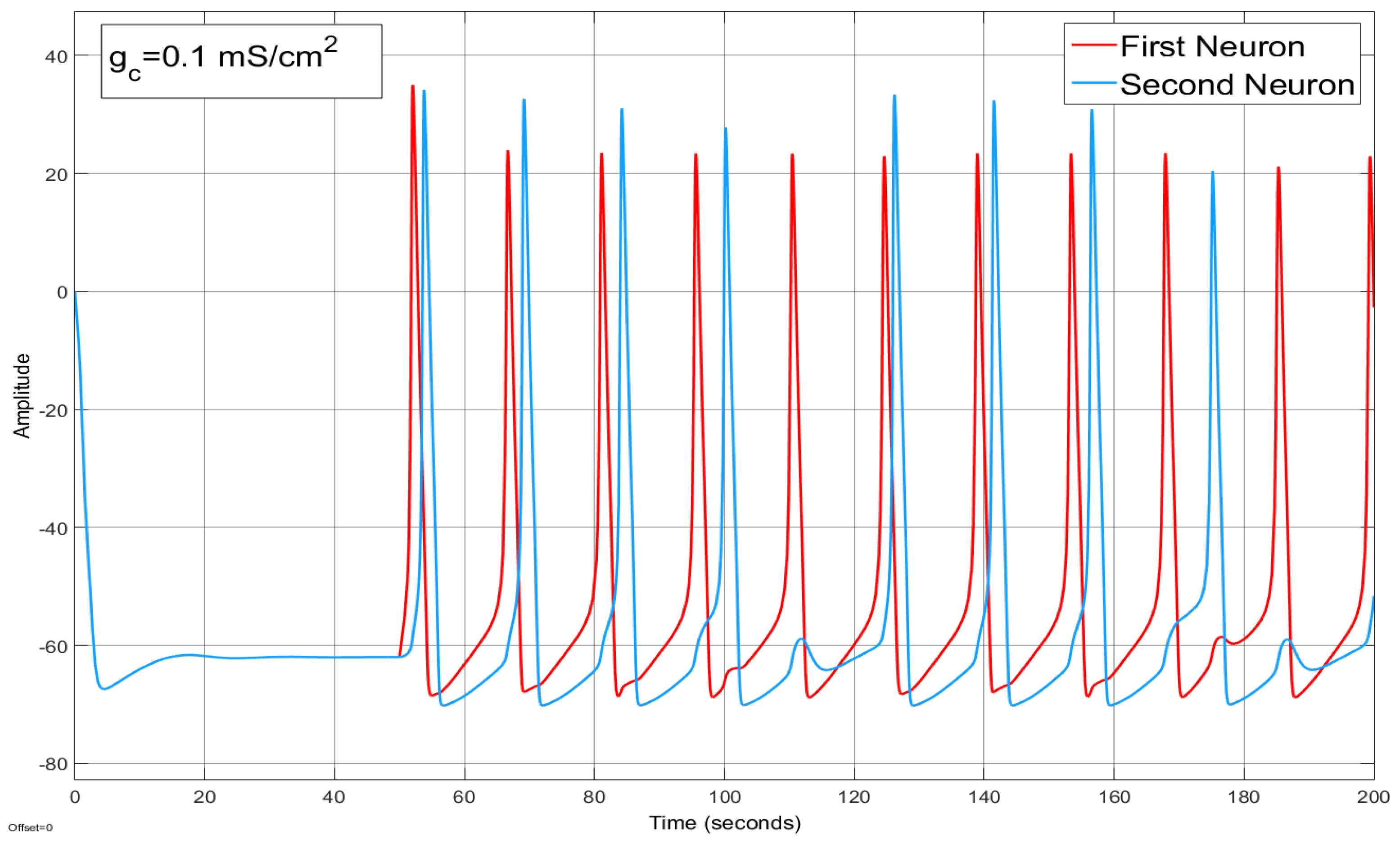
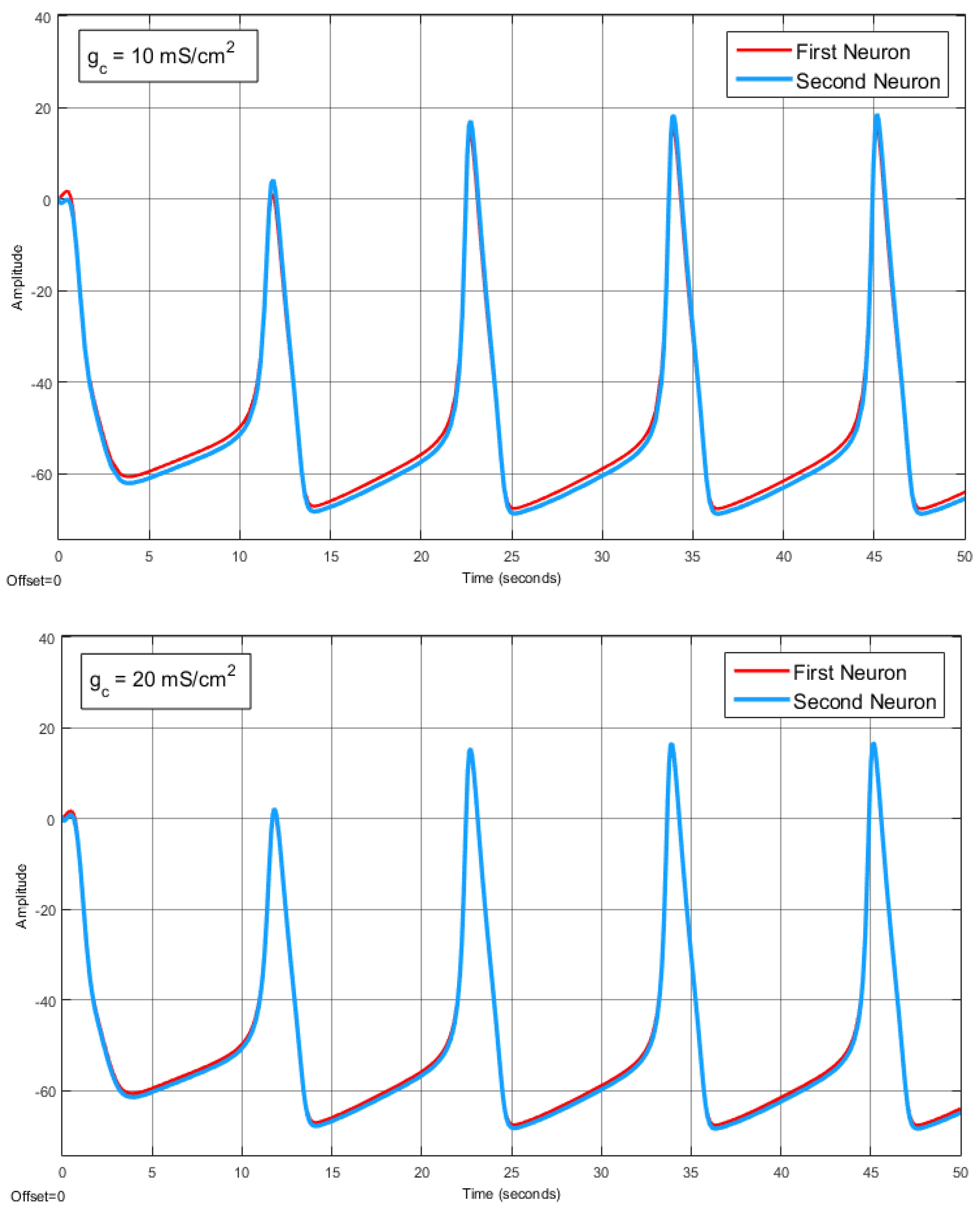
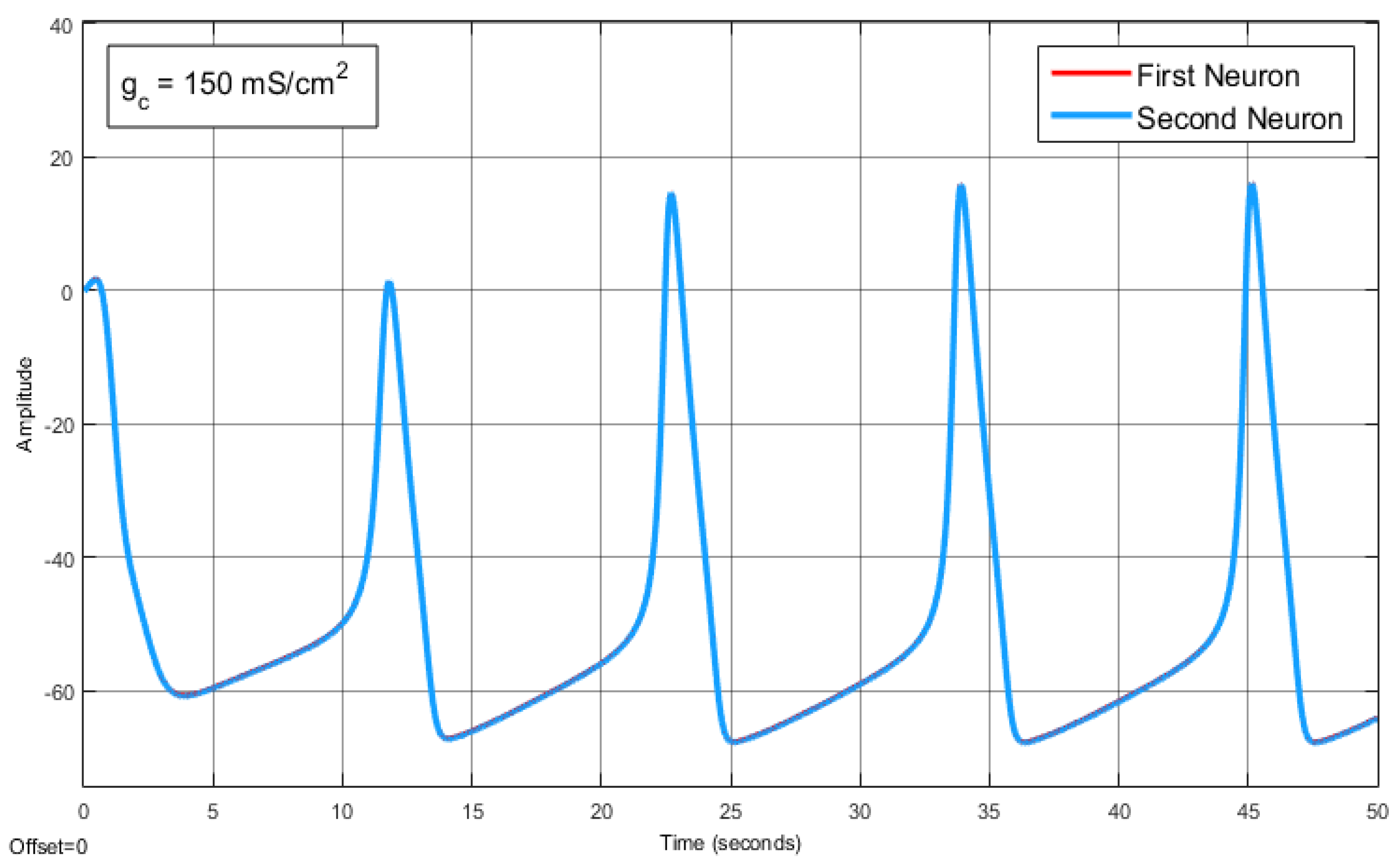
The Effect of Coupling Conductance on Synchronization
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sadegh Zadeh, S.-A.; Kambhampati, C. A Computational Investigation of the Role of Ion Gradients in Signal Generation in Neurons. In Proceedings of the Computing Conference, London, UK, 10–12 July 2018. [Google Scholar]
- Amthor, F.; Oyster, C.; Takahashi, E. Morphology of on-off direction-selective ganglion cells in the rabbit retina. Brain Res. 1984, 298, 187–190. [Google Scholar] [CrossRef]
- Ahmed, B.; Allison, J.D.; Douglas, R.J.; Martin, K. An intracellular study of the contrast-dependence of neuronal activity in cat visual cortex. Cereb. Cortex 1997, 7, 559–570. [Google Scholar] [CrossRef] [PubMed]
- Dodge, J. A Study of Ionic Permeability Changes Underlying Excitation in Myelinated Nerve Fibers of the Frog. Ph.D. Thesis, Rockefeller Institute, New York, NY, USA, 1967. [Google Scholar]
- Hodgkin, A.; Huxley, A. A quantitative description of membrane current and its application toconduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Matsuda, K.; Hoshi, T.; Kameyama, S. Electrophysiology of the heart. J. Exp. Med. 1958, 66. [Google Scholar]
- Raman, I.; Bean, B. Ionic Currents Underlying Spontaneous Action Potentials in Isolated Cerebellar Purkinje Neurons. J. Neurosci. 1999, 19, 1663–1674. [Google Scholar] [CrossRef]
- Sadegh Zadeh, S.-A.; Kambhampati, C. All-or-None Principle and Weakness of Hodgkin-Huxley Mathematical Model. In Proceedings of the 19th International Conference on Systems Biology and Bioengineering, Chicago, IL, USA, 26–27 October 2017. [Google Scholar]
- Cleeremans, A. Connecting Conscious and Unconscious Processing. Cogn. Sci. 2014, 38, 1286–1315. [Google Scholar] [CrossRef] [PubMed]
- Trenor, B.; Cardona, K.; Saiz, J.; Noble, D.; Giles, W. Cardiac action potential repolarization re-visited: Early repolarization shows all-or-none behaviour. J. Physiol. 2017, 595, 6599–6612. [Google Scholar] [CrossRef] [PubMed]
- Engel, J.; Pedley, T.; Aicardi, J. Epilepsy: A Comprehensive Textbook; Lippincott-Raven: Philadelphia, PA, USA, 2008. [Google Scholar]
- Singer, W. Neurobiology: Striving for coherence. Nature 1999, 397, 391–393. [Google Scholar] [CrossRef]
- Borgesa, R.; Borges, F.S.; Lameu, E.L.; Batista, A.M.; Iarosz, K.C.; Caldas, I.L.; Viana, R.L.; Sanjuán, M.A.F. Effects of the spike timing-dependent plasticity on the synchronisation in a random Hodgkin–Huxley neuronal network. Commun. Nonlinear Sci. Numer. Simul. 2016, 34, 12–22. [Google Scholar] [CrossRef]
- Prado Tde, L.; Lopes, S.R.; Batista, C.A.; Kurths, J.; Viana, R.L. Synchronization of bursting Hodgkin-Huxley-type neurons in clustered networks. Phys. Rev. E 2014, 90, 032818. [Google Scholar] [CrossRef] [PubMed]
- Hansel, D.; Mato, G.; Meunier, C. Synchrony in Excitatory Neural Networks. Neural Comput. 1995, 7, 307–337. [Google Scholar] [CrossRef]
- Belykh, V.N.; Osipov, G.V.; Petrov, V.S.; Suykens, J.A.K.; Vandewalle, J. Cluster synchronization in oscillatory networks. Chaos 2008, 18, 037106-1–037106-6. [Google Scholar] [CrossRef] [PubMed]
- Batistaa, C.; Lopesa, S.; Vianaa, R.; Batistab, A. Delayed feedback control of bursting synchronization in a scale-free neuronal network. Neural Netw. 2010, 23, 114–124. [Google Scholar] [CrossRef]
- Han, F.; Wiercigroch, M.; Fang, J.-A.; Wang, Z. Excitement and synchronization of small-world neuronal networks with short-term synaptic plasticity. Int. J. Neural Syst. 2011, 21, 415–425. [Google Scholar] [CrossRef] [PubMed]
- Gray, C.M.; Konig, P.; Engel, A.K.; Singer, W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature 1989, 338, 334–337. [Google Scholar] [CrossRef] [PubMed]
- Stopfe, M.; Bhagavan, S.; Smith, B.; Laurent, G. Impaired odour descrimination on desynchronization of odour-encoding neural assemblies. Nature 1997, 390, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Steinmetz, P.; Roy, A.; Fitzgerald, P.J.; Hsiao, S.S.; Johnson, K.O.; Niebur, E. Attention modulates synchronized neuronal firing in primate somatosensory cortex. Nature 2000, 404, 187–190. [Google Scholar] [CrossRef]
- Stern, E.; Jaeger, D.; Wilson, C.J. Membrane potential synchrony of simultaneously recorded striatal spiny neurons in vivo. Nature 1998, 394, 475–478. [Google Scholar] [CrossRef] [PubMed]
- Hodgkin, A.; Huxley, A. Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. J. Physiol. 1952, 116, 49–472. [Google Scholar] [CrossRef]
- Whelton, P. Hyponatremia in the general population. What does it mean? PubMed 2016, 26, 9–12. [Google Scholar] [CrossRef]
- Silva, A.; Belli, A.; Smith, M. Electrolyte and endocrine disturbances. In Oxford Textbook of Neurocritical Care; Kofke, A., Ed.; Oxford Medicine Online: Oxford, UK, 2016; pp. 375–386. [Google Scholar]
- Perez, C.; Ziburkus, J.; Ullah, G. Analyzing and Modeling the Dysfunction of Inhibitory Neurons in Alzheimer’s Disease. PLoS ONE 2016, 11, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Labouriau, I.S.; Ruas, M.A.S. Singularities of equations of Hodgkin–Huxley type. Dyn. Stabil. Syst. 1996, 11, 91–108. [Google Scholar] [CrossRef]
- Labouriau, I.; Rodrigues, H.M. Synchronization of Coupled Equations of Hodgkin-Huxley Type. Dyn. Contin. Discret. Impuls. Syst. Ser. A 2003, 10, 463–476. [Google Scholar]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization: A Universal Concept in Nonlinear, 1st ed.; Cambridge University: Cambridge, UK, 2003. [Google Scholar]
- Rossetto, M. A note on the falsification of the ionic theory of hair cell transduction. Commun. Integrat. Biol. 2016, 9, e1122144. [Google Scholar] [CrossRef]
- Kashyap, C.; Borkotoki, S.; Dutta, R.K. Study of Serum Sodium and Potassium Level in Patients with Alcoholic Liver Disease Attending Jorhat Medical College Hospital—A Hospital Based Study. Int. J. Health Sci. Res. 2016, 6, 113–116. [Google Scholar]
- Sadegh-Zadeh, S.-A.; Kambhampati, C. Computational Investigation of Amyloid Peptide Channels in Alzheimer’s Disease. J 2019, 2, 1–14. [Google Scholar] [CrossRef]
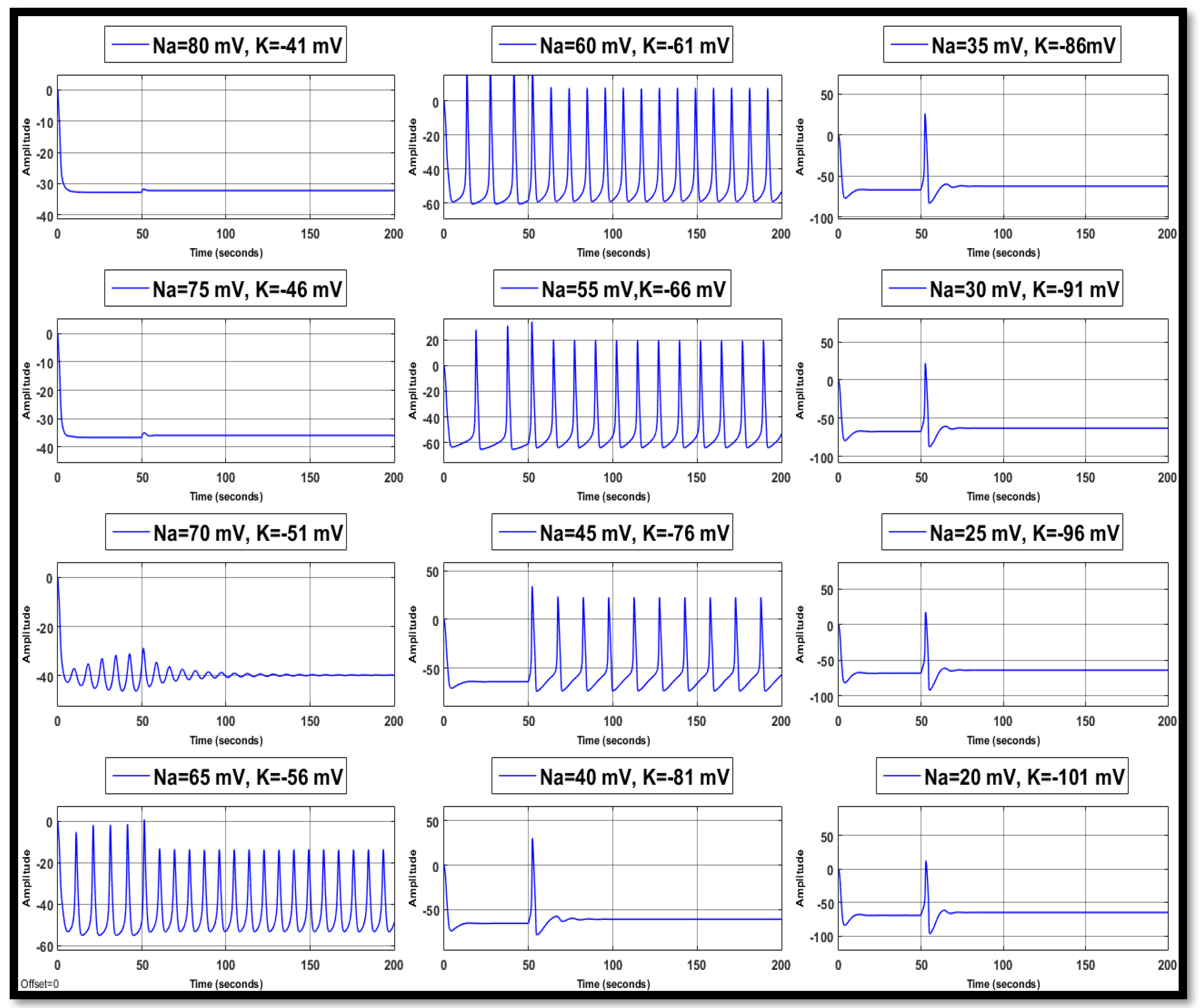
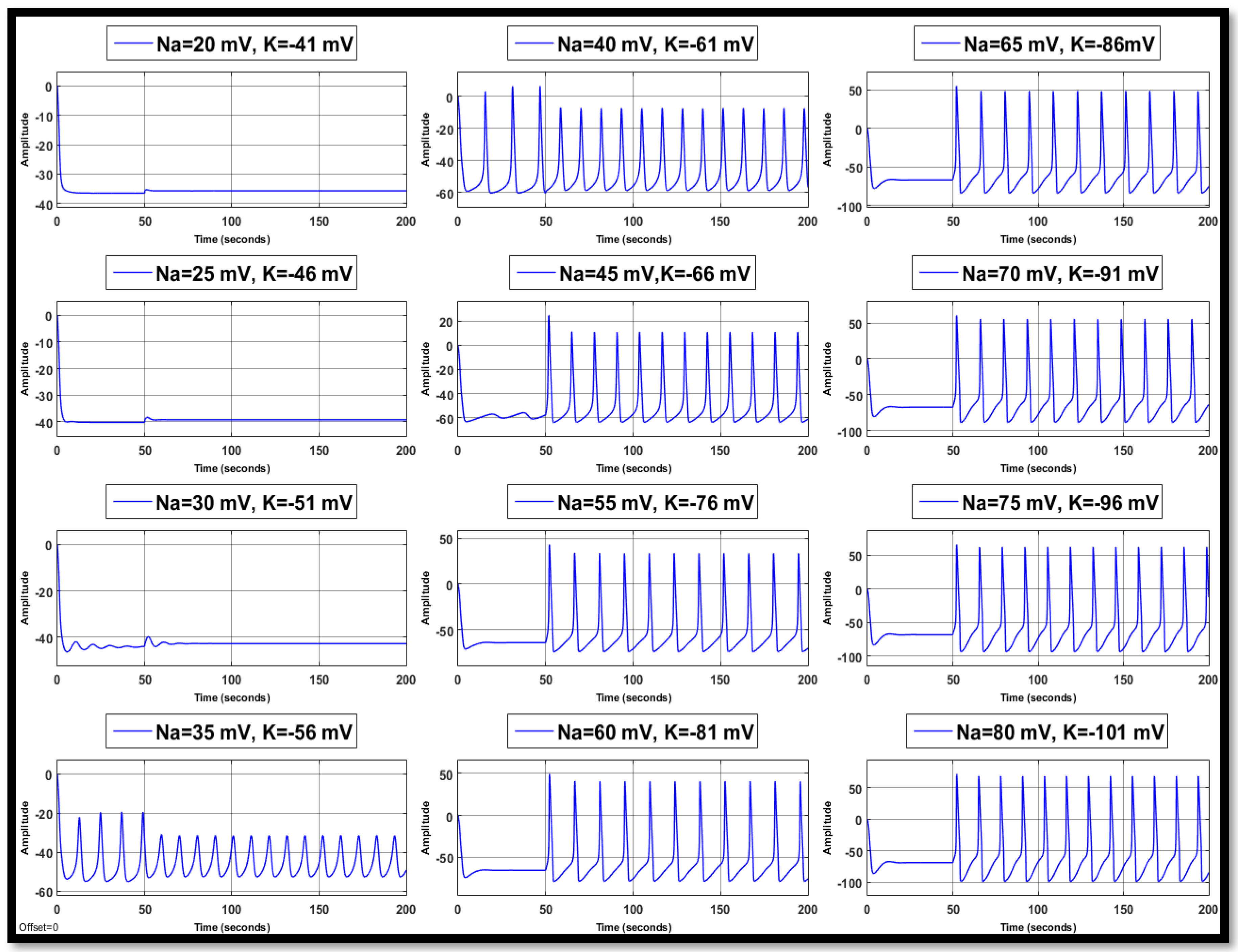
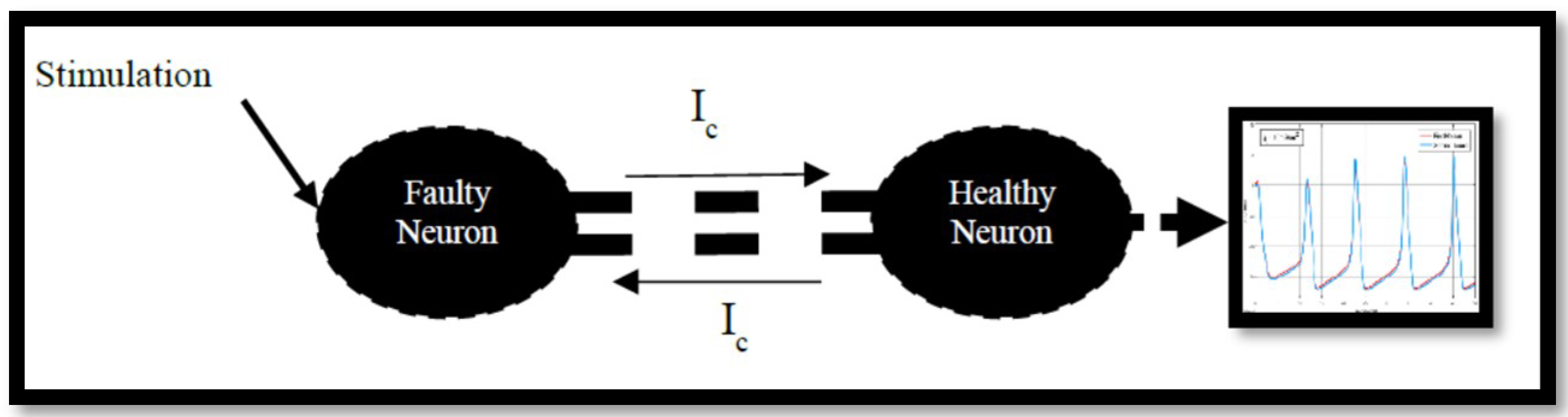
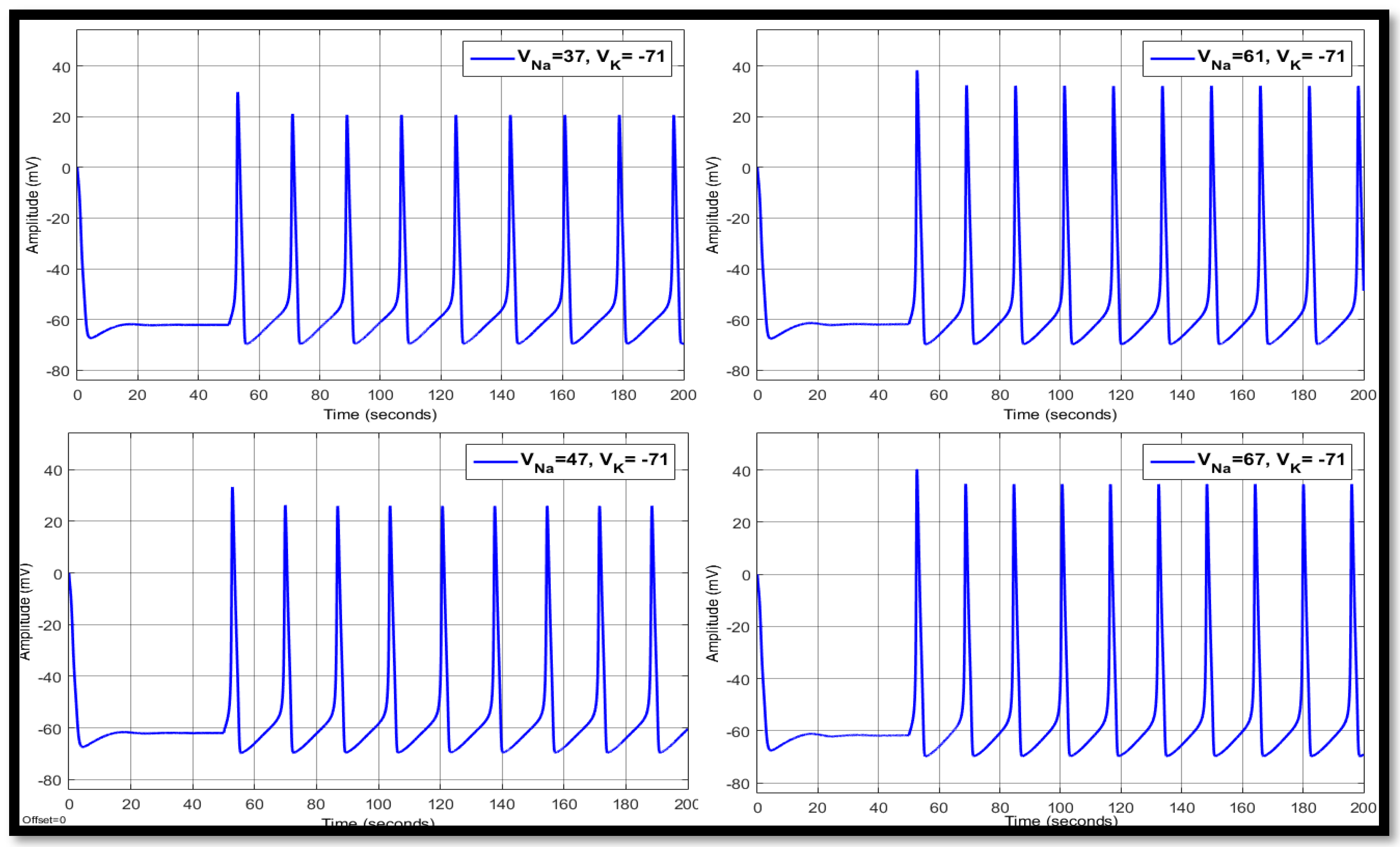
| Ions | Single Faulty Neuron | Faulty Neuron in the Chain | Output of the Coupled Neuron | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| VNa | VK | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential |
| 37 | −71 | 14.8758 | 10.5017 | −63.147 | 17.9775 | 19.8064 | −60.4662 | 17.9775 | 21.6552 | −60.4557 |
| 47 | −71 | 13.9576 | 21.0912 | −62.7366 | 16.9507 | 26.3103 | −59.9166 | 16.9468 | 26.7907 | −59.9224 |
| 50 | −71 | 13.7303 | 24.9737 | −62.5314 | 16.7455 | 28.1351 | −55.0608 | 16.7455 | 28.1554 | −55.0897 |
| 61 | −71 | 13.316 | 34.3568 | −61.8532 | 16.1699 | 34.5527 | −59.3163 | 16.1699 | 32.7097 | −59.3666 |
| 67 | −71 | 13.1332 | 39.8285 | −61.3425 | 15.9336 | 38.0282 | −59.0507 | 15.9336 | 35.1541 | −59.1272 |
| Ions | Single Faulty Neuron | Faulty Neuron in the Chain | Output of the Coupled Neuron | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| VNa | VK | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential |
| 51 | −60 | 10.7669 | −2.0199 | −50.6534 | 14.8411 | 21.2079 | −52.9945 | 14.8411 | 20.8429 | −53.3918 |
| 51 | −66 | 12.7091 | 16.7945 | −57.5069 | 15.7142 | 25.6603 | −58.0945 | 15.7142 | 25.4610 | −58.2092 |
| 50 | −71 | 13.7303 | 24.9737 | −62.5314 | 16.7455 | 28.1351 | −55.0608 | 16.7455 | 28.1554 | −55.0897 |
| 51 | −75 | 14.3446 | 28.8061 | −66.1146 | 17.8316 | 28.8506 | −61.0727 | 17.8316 | 28.9676 | −61.0148 |
| 51 | −79 | 14.8463 | 31.0643 | −69.3698 | 20.0183 | 31.2381 | −61.9963 | 20.0183 | 31.4256 | −61.9135 |
| Ions | Single Faulty Neuron | Faulty Neuron in the Chain | Output of the Coupled Neuron | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| VNa | VK | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential |
| 59 | −63 | 11.5193 | 15.0944 | −53.3364 | 15.1529 | 28.2043 | −53.3745 | 15.1529 | 26.7059 | −53.7817 |
| 55 | −67 | 12.7956 | 22.3954 | −58.2245 | 15.7045 | 29.0433 | −58.2096 | 15.7045 | 29.0433 | −58.2096 |
| 50 | −71 | 13.7303 | 24.9737 | −62.5314 | 16.7455 | 28.1351 | −55.0608 | 16.7455 | 28.1554 | −55.0897 |
| 47 | −75 | 14.655 | 24.6221 | −66.2517 | 18.2881 | 26.6333 | −61.1840 | 18.2881 | 27.1293 | −61.1367 |
| 43 | −79 | 17.1933 | 22.2911 | −69.5016 | - | 32.8146 | −62.5148 | - | 34.3358 | −62.4243 |
| Ions | Single Faulty Neuron | Faulty Neuron in the Chain | Output of the Coupled Neuron | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| VNa | VK | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential | Avg. Inter-Spike Intervals | Avg. Spike Amplitude | Avg. Resting Potential |
| 59 | −79 | 14.2584 | 39.5384 | −69.0874 | 18.1669 | 34.9578 | −61.8693 | 18.1669 | 33.5213 | −61.8110 |
| 55 | −75 | 14.109 | 32.8513 | −65.9258 | 17.3166 | 32.2044 | −60.6708 | 17.3166 | 31.4881 | −60.6250 |
| 50 | −71 | 13.7303 | 24.9737 | −62.5314 | 16.7455 | 28.1351 | −55.0608 | 16.7455 | 28.1554 | −55.0897 |
| 47 | −67 | 13.0706 | 15.0905 | −58.852 | 16.0560 | 24.5569 | −58.7456 | 16.0560 | 24.8891 | −58.8273 |
| 43 | −63 | 12.2359 | 2.2251 | −54.8835 | 15.3754 | 19.6940 | −57.1269 | 15.3791 | 20.3892 | −57.2454 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadegh-Zadeh, S.-A.; Kambhampati, C.; Davis, D.N. Ionic Imbalances and Coupling in Synchronization of Responses in Neurons. J 2019, 2, 17-40. https://doi.org/10.3390/j2010003
Sadegh-Zadeh S-A, Kambhampati C, Davis DN. Ionic Imbalances and Coupling in Synchronization of Responses in Neurons. J. 2019; 2(1):17-40. https://doi.org/10.3390/j2010003
Chicago/Turabian StyleSadegh-Zadeh, Seyed-Ali, Chandrasekhar Kambhampati, and Darryl N. Davis. 2019. "Ionic Imbalances and Coupling in Synchronization of Responses in Neurons" J 2, no. 1: 17-40. https://doi.org/10.3390/j2010003
APA StyleSadegh-Zadeh, S.-A., Kambhampati, C., & Davis, D. N. (2019). Ionic Imbalances and Coupling in Synchronization of Responses in Neurons. J, 2(1), 17-40. https://doi.org/10.3390/j2010003






