Computational Investigation of Amyloid Peptide Channels in Alzheimer’s Disease

Abstract

Aβ accumulation has been discovered to form large, relatively cation-permeable channels in the plasma membrane of a neuron. These channel formations in the membranes of a neuron could cause cell depolarisation, sodium and potassium dysregulation, depletion of neural energy stores and other types of cellular dysfunction. This study shows that the build-up of amyloid beta (Aβ) depositions during the onset of Alzheimer’s disease has profound effects on the activity of the local community of neurons in the central nervous system. These effects can include enhanced neural activity, spontaneous epileptiform activity and incidence of epileptic seizures. From the results in this area, it can be seen that the neurodegeneration observed in Alzheimer’s disease has been associated with the increase of toxicity of Aβ depositions. In this research paper, we examined this hypothesis in light of a computational model of a neuron.

1. Introduction

Neurodegenerative diseases are a kind of progressive disease in which the structure or function of the neurons is gradually destroyed and ultimately leads to their death. Neurons cannot be replaced by the biological body system if they become damaged or die. That is why such diseases are incurable [1]. Alzheimer’s disease is an example of a neurodegenerative disease that causes dementia with no known cure [2]. According to the Office for National Statistics, dementia, including Alzheimer’s disease, has overtaken heart disease as the leading cause of mortality in the United Kingdom [3]. This deadly neurodegenerative disease causes problems with mental functioning such as cognitive, memory and behavioural impairments. The most important Alzheimer’s disease symptoms can be intracellular neurofibrillary tangles and extracellular deposition of amyloid beta (Aβ) plaques [4,5]. Therefore, it can be said the driving force for Alzheimer’s disease pathogenesis outside the cell is the accumulation of Aβ oligomers or plaques and as a result the formation of Aβ channels [6]. This accumulation usually happens because of some imbalances between synthesis and clearance as a result of an abnormal processing of the amyloid precursor protein [7]. Extensive research shows that Aβ accumulation is an important factor in the development of early cognitive impairment and can be seen in the very early stages of Alzheimer’s disease [8]. It has been discovered that Aβ peptide forms large permeable channels under physiologic conditions [9]. However, the exact mechanism is not fully understood [10].

The channels made by Aβ are selective for cations over anions and can be inserted into the cell membrane from aqueous solution. These channels are voltage-independent, and they can be very large. These channels are heterogeneous and allow the flow of physiologically relevant ions such as Na⁺, K⁺, Ca²⁺, Cs⁺ and Li⁺ across the cell membrane [9]. The discovery of the Aβ channels hypothesis led to a wide range of research. The focus of most studies has been on the effects of these channels. Thus far, more than a dozen channels have been known to create these kinds of channels, and all have the same properties [11]. Investigation of Aβ channels has shown that almost all of the properties of these channels are preserved in all Aβ channel forms. These properties explain the cause of the toxicity of amyloid peptides, and this can distinguish these kinds of channels from the regular voltage-gated ion channels in excitable neurons. According to the Aβ channels hypothesis, these channels create an unregulated ionic leakage pathway in the cell membrane. They lead to cell depolarisation and an irregular flow of ions such as Na⁺ and K⁺. This damages the cellular processes, specifically inhibitory neurons, and causes vital energy stores to drop since the cellular pumps try to leak.

Various studies on the dysfunction of inhibitory neurons and Aβ channels have been published. Busche et al. [12] suggested that an impaired inhibitory neuron near amyloid plaques rather than the firing of an excitatory neuron underlies hyperactivity in the neuronal network. Verret et al. [13] evaluated inhibitory neurons and found that the disruption in the inhibitory neurons causes spontaneous epileptiform activity and hypersynchrony in human Alzheimer’s disease patients. In line with these studies, Hazra et al. [14] have recently shown the failure of inhibitory neurons leading to disruptions in hippocampal circuit activity to fire action potentials in the aged mouse model of Alzheimer’s disease. In their study, Perez et al. [10] applied the Hodgkin-Huxley model to use dynamic sodium conductance in the inhibitory neuron to find the pathways leading to impaired inhibitory neuronal activity in the hippocampus of the aged mouse model of Alzheimer’s disease. Their observations indicated that inhibitory neurons confronted with Aβ channels causing leakage of sodium cannot reliably fire action potentials and have higher resting membrane potentials. For this reason, they elevated the conductance of sodium leak channels to create conditions similar to Aβ channels in a single inhibitory neuron. As Aβ channels are permeable to all cations, in this study, we considered both sodium and potassium as two significant cations in the neuronal process in a single inhibitory neuron. Therefore, the conductance of potassium leak channels in addition to sodium leak channels is elevated. This paper is organized as follows. Section 2 describes the pathological background. Section 3 introduces the computational method. Section 4 presents the computational results, and finally, Section 5 discusses the results of this study.

2. Pathological Background

During their processes, in addition to releasing neurotransmitters in synapse space, neurons release very tiny peptides that are called Aβ. Neurotransmitters or chemical messengers are released in the synaptic space in order to enable communication between neurons. In the very early stage of Alzheimer’s disease, these spaces are targeted. These peptides typically clean and metabolize through microglia. For many decades, the action of microglia was completely unclear [1]. However, these days, it is known that microglia clear cellular debris from the nervous tissue. Although the molecular causes of Alzheimer’s disease are still controversial, the majority of scientists believe that the onset of Alzheimer’s disease is when the amyloid beta starts to accumulate [15]. After excessive exceeded accumulation of amyloid beta, a synaptic disorder occurs. In this condition, the amyloid peptide binds to itself, forming sticky aggregates that are called amyloid plaques. It usually takes about 15 to 20 years of amyloid plaque accumulation before it reaches a tipping point and produces a molecular cascade [15]. This step causes the clinical symptoms of the disease. In this stage, the microglia cells become hyper-activated and release chemicals that cause inflammations and neuronal damage. After the onset of the inflammation, an important protein called tau becomes hyper-phosphorylated and twists itself into tangles. These tangles choke off the neuron from the inside, and following the production of tangles, neuronal apoptosis begins. Therefore, in order to detect the disease at an early stage, the focus on Aβ peptide is very important.

Aβ peptide is a small fragment of a more abundant protein called amyloid precursor protein. Although researchers have not yet reveal the normal function of the amyloid precursor protein, they know how it appears to work [15]. The amyloid precursor protein through the passage of the membrane around the nerve cell spreads from the inner environment of the nerve cell to the outside. Then amyloid precursor protein is cut by other proteins into separate, smaller sections. It stays inside and outside the nerve cells. Under some circumstances, there are different ways for cutting the amyloid precursor protein. One of these produced cut-off pieces is called Aβ peptide.

Studies have shown that Aβ channels are permeable to cations including sodium and potassium, as far as these channels have been identified as cation channels [10,12]. The measuring direction of the flows is in the reversal potential of the ionic currents and the sequence permeability for cations is P_K > P_Na. Aβ oligomers increase the area per molecule of the membrane-forming lipids, accordingly thinning the membrane, and as a result, lowering the dielectric barrier and increases the conductance of the neuron [16]. In general, it can be said that Aβ can assume a conformation that enables the molecule to enter the lipid bilayer plasma membranes and form cation-selective channels.

Researchers have investigated sodium in the intracellular space; it can be considered a leak current because these currents are primarily driven by the potential difference across the membrane [10,15]. In their studies, Vitvitsky et al. [15] have shown that abnormal levels of ions like sodium and potassium in neurons cause the ionic imbalance that is linked to Alzheimer’s disease pathogenesis. To test their hypothesis, they analysed sodium and potassium in post-mortem brain samples of 12 normal and 16 Alzheimer’s disease individuals. They found remarkable ion imbalances in the cortical (sodium) and cerebellar (potassium) brain regions of people with Alzheimer’s disease. They suggested that the changes seen in the tissue samples reflect the changes in the intracellular pool. Using the mathematical modelling of experimental data from ion concentrations between normal and Alzheimer’s disease brain tissues they found that the intracellular sodium showed a two-fold increase and the intracellular potassium increased by 8–15% in the cortical and cerebellar brain regions, respectively, in Alzheimer’s disease.

3. Materials and Methods

As was evident from the Alzheimer’s pathology, amyloid accumulation in the synaptic space is a primary stage of Alzheimer’s development. Therefore, focusing on the model of Aβ can lead us to early diagnosis or even treatment of Alzheimer’s. In this section, we present a computational model of a single neuron in confrontation with Aβ plaques. For this purpose, a computational model of the neuron is applied to analyse amyloid channels in Alzheimer’s disease. The membrane potential, V, of a single neuron is modelled by:

$$V=\frac{1}{C_m}{\displaystyle \underset{0}{\overset{T}{{\displaystyle \int }}}{\displaystyle \sum }_j}{G}_j\left(V_j-V\right)+I_{inj}dt,$$

(1)

where, V_j is the reversal potential for current $j$ obtained from the Nernst equation. (V_j − V) is driving force for current j. I_inj is external current. For the original conductance-based model this equation is as follows:

$$V=\frac{1}{C_m}{\displaystyle \underset{0}{\overset{T}{{\displaystyle \int }}}}(I_{inj}+{\displaystyle {\displaystyle \sum }_j}{I}_j)dt,$$

(2)

where j = Na⁺, K, L, and ets and:

$$G_j={\overline{G}}_j{p}_j^x{q}_j^y,$$

(3)

where:

$$\frac{dp}{dt}={\alpha }_p\left(1-p\right)-{\beta }_{p}p\mathrm{and}\frac{dq}{dt}={\alpha }_q\left(1-q\right)-{\beta }_{q}q,$$

(4)

where p,q are gating variables and can rise to numbers x,y. for instance, m³h and n⁴ are gating variables for sodium and potassium. Therefore, for sodium and potassium, Equation (3) is $G_{Na}={\overline{G}}_{Na}{m}^{3}h$ and $G_K={\overline{G}}_K{n}^4$. In the following, we will show that amyloid aggregation will result in disruption of the sodium and potassium gating variables. The parameters α and β are opening and closing rates of the ion channel state transitions that are dependent on V. For sodium and potassium these parameters are as follows:

$${\alpha }_n\left(V\right)= \frac{0.01\left(V+55\right)}{1-\exp \left[-\left(V+55\right)/10\right]},$$

(5)

$${\beta }_n\left(V\right)=1.125\exp \left[-\frac{V+65}{80}\right],$$

(6)

$${\alpha }_m\left(V\right)=\frac{0.01\left(V+40\right)}{1-\exp \left[-\frac{V+40}{10}\right]},$$

(7)

$${\beta }_m\left(V\right)=4\exp \left[-\left(V+65\right)/18\right],$$

(8)

$${\alpha }_h\left(V\right)=0.07\exp \left[-\frac{V+65}{20}\right],$$

(9)

$${\beta }_h\left(V\right)=\frac{1}{1+\exp \left[-\frac{V+35}{10}\right]}.$$

(10)

For sodium, potassium, and leakage the currents are:

I_Na = G_Na(V − V_Na),

(11)

I_K = G_K(V − V_K),

(12)

I_L = G_L(V − V_L),

(13)

where G_Na, G_K and G_L are obtained from Equation (3) and the Nernst potential for sodium current (V_Na) is obtained using the Nernst equation as follows:

$$V_{Na}=26.6\ln \left(\frac{{[N{a}^{+}]}_{out}}{{[N{a}^{+}]}_{in}}\right),$$

(14)

where ${[N{a}^{+}]}_{out}$ represents extracellular sodium concentration and ${[N{a}^{+}]}_{in}$ represents intracellular sodium concentration. In the normal condition ${[N{a}^{+}]}_{out}$ >> ${[N{a}^{+}]}_{in}$. The Aβ channels, by producing extra channels that are permeable to cations, provide a condition in which the amount of intercellular Na⁺ increases. Following Equation (14), V_Na has a direct relation with $\ln \left(\frac{{[N{a}^{+}]}_{out}}{{[N{a}^{+}]}_{in}}\right)$. Therefore, by increasing the ${[N{a}^{+}]}_{in}$, the amount of V_Na decreases. Vitvitsky et al. [15] have proven that the amount of intracellular sodium in the post-mortem Alzheimer’s is doubled. Based on Equation (11), by decreasing $V_{Na}$, the current flow of $N{a}^{+}$ increases. The Nernst potential for potassium current is obtained as follows:

$$V_K=26.6\ln \left(\frac{{[K^{+}]}_{out}}{{[K^{+}]}_{in}}\right),$$

(15)

where ${[K^{+}]}_{out}$ represents extracellular potassium concentration and ${[K^{+}]}_{in}$ represents intracellular potassium concentration. Vitvitsky et al. [15] have also proven that the amount of intracellular potassium in the post-mortem Alzheimer’s brains are up to 15% higher than that of the normal brain. Following the above equation and by considering that ${[K^{+}]}_{out}$ << ${[K^{+}]}_{in}$, then, in the confrontation with Aβ channels, the amount of ${[K^{+}]}_{in}$ decreases. Therefore, unlike sodium, the value of $\ln \left(\frac{{[K^{+}]}_{out}}{{[K^{+}]}_{in}}\right)$ increases.

The Nernst potential for the chlorine ion is as follows:

$$V_{Cl}=26.6\ln \left(\frac{{[C{l}^{-}]}_{out}}{{[C{l}^{-}]}_{in}}\right),$$

(16)

Therefore, the Nernst potential for leakage current is:

$$V_L= 26.6\ln \left(\frac{0.085{\left[N{a}^{+}\right]}_{out}+{\left[K^{+}\right]}_{out}+0.1{\left[C{l}^{-}\right]}_{out}}{0.085{\left[N{a}^{+}\right]}_{in}+{\left[K^{+}\right]}_{in}+0.1{\left[C{l}^{-}\right]}_{in}}\right).$$

(17)

As can be seen, these equations are related to intercellular and extracellular ion concentrations. The Aβ peptides damage the membrane of neurons, which affects the total tissue sodium and potassium concentrations. The total tissue concentrations of sodium and potassium are described by the following equations:

$${\left[Na\right]}_{tot}=\frac{{\left[N{a}^{+}\right]}_{in}{\left[Vol\right]}_{in}+{\left[N{a}^{+}\right]}_{out}{\left[Vol\right]}_{out}}{{\left[Vol\right]}_{in}+{\left[Vol\right]}_{out}},$$

(18)

$${\left[K\right]}_{tot}=\frac{{\left[K^{+}\right]}_{in}{\left[Vol\right]}_{in}+{\left[K^{+}\right]}_{out}{\left[Vol\right]}_{out}}{{\left[Vol\right]}_{in}+{\left[Vol\right]}_{out}},$$

(19)

where ${[Na]}_{tot}$ and ${[K]}_{tot}$ are total sodium and potassium concentration in tissue. ${[N{a}^{+}]}_{in}$, ${[N{a}^{+}]}_{out}$, ${[K^{+}]}_{in}$ and ${[K^{+}]}_{out}$ are intracellular and extracellular sodium and potassium concentrations, respectively. ${[Vol]}_{in}$ and ${[Vol]}_{out}$ show intercellular and extracellular volume in the tissue. The volume is the total volume occupied by all neurons in the tissue sample. By considering the unit volume ${\left[Vol\right]}_{in}+{\left[Vol\right]}_{out}=1$, the equations transform to:

$${\left[Na\right]}_{tot}=\left({\left[N{a}^{+}\right]}_{in}{[Vol]}_{in}+{\left[N{a}^{+}\right]}_{out}\left(1-{\left[Vol\right]}_{in}\right)\right)={\left[N{a}^{+}\right]}_{out}+\left({\left[N{a}^{+}\right]}_{in}-{\left[N{a}^{+}\right]}_{out}\right){[Vol]}_{in},$$

(20)

$${\left[K\right]}_{tot}=\left({\left[K^{+}\right]}_{in}{\left[Vol\right]}_{in}+{\left[K^{+}\right]}_{out}\left(1-{\left[Vol\right]}_{in}\right)\right)={\left[K^{+}\right]}_{out}+\left({\left[K^{+}\right]}_{in}-{\left[K^{+}\right]}_{out}\right){\left[Vol\right]}_{in}.$$

(21)

These equations show that the total tissue concentrations of sodium and potassium are linear functions of the relative cell volume. It means that an increase in the cell volume leads to a decrease in total sodium concentration and an increase in total potassium concentration. These happen because:

$${[N{a}^{+}]}_{in}-{\left[N{a}^{+}\right]}_{out}<0,$$

(22)

$${[K^{+}]}_{in}-{\left[K^{+}\right]}_{out}>0.$$

(23)

Relations (22) and (23) in the healthy neuron are always established. However, with an increase in the Aβ channels, this relation changes to ${[N{a}^{+}]}_{in}-{\left[N{a}^{+}\right]}_{out}\to 0$ and ${[K^{+}]}_{in}-{\left[K^{+}\right]}_{out}\to 0$,then following the Nurnst equations in Equations (14) and (15) for sodium and potassium ions $V_{N{a}^{+}}\to 0$ and $V_{K^{+}}\to 0$ which cause neural deterioration.

The sodium and potassium ion concentrations inside and outside of the neuron can be obtained as follows:

$$\frac{d{\left[K^{+}\right]}_{out}}{dt}= \frac{1}{\tau } \left(\gamma \beta I_K-2\beta I_{pump}-I_{glia}-I_{diff}\right),$$

(24)

$$\frac{d{\left[N{a}^{+}\right]}_{in}}{dt}= \frac{1}{\tau } \left(-\gamma I_{Na}-3\gamma I_{pump}\right),$$

(25)

where concentrations are calculated in millimolar (mM). $I_{pump}$ is the current of the neuronal Na⁺/K⁺ pump. I_glia is the current associated with the glial buffering. $I_{diff}$ is the K⁺ diffusion current. γ = 4.45 × 10⁻² is a unit conversion factor. This factor converts the membrane currents into mM/s. β = 7 is the ratio of the interacellular to extracellular volume. τ = 10³ is the molar currents (mM/s) and balances the time units. The pump, glia, and diffusion molar currents are as follows:

$$I_{pump}= \rho {\left(1+\exp \left(\frac{25-{\left[N{a}^{+}\right]}_{in}}{3}\right)\right)}^{-1}\left(\frac{1}{1+\exp \left(5.5-{\left[K^{+}\right]}_{out}\right)}\right),$$

(26)

$$I_{glia}= G{\left(1+\exp \left(\frac{18-{\left[K^{+}\right]}_{out}}{2.5}\right)\right)}^{-1},$$

(27)

$$I_{diff}=\epsilon ({[K^{+}]}_{out}-K^{+}{}_{bath}),$$

(28)

where ρ = 1.25 mM/s, G = 66.666 mM/s, and ε = 1.333 Hz. K_bath is the potassium concentration in the reservoir and is K_bath = 4 mM for normal physiological conditions. To simplify the model and reduce complexity, we decided to neglect the pump, glia and diffusion currents in our experiment. The intracellular potassium and extracellular sodium concentrations are as follows:

$${[K^{+}]}_{in}=140+\left(18-{\left[N{a}^{+}\right]}_{in}\right),$$

(29)

$${\left[N{a}^{+}\right]}_{out}=144-\beta \left({\left[N{a}^{+}\right]}_{in}-18\right).$$

(30)

An ion channel transmits ions with a given conductance or in other words, resistance. By understanding the physical properties of Aβ channels, we can estimate the exact function of these channels and their deleterious effects on the neuron. This can be approached by obtaining the ion flux across the membrane. Following Arispe’s study [17], the ion flux $\phi$ inside the membrane can be obtained using the following equation:

$${\phi }_i=\left({\rho }_i{I}_i\right)/F,$$

(31)

where ${\phi }_i$ is the ion flux, ${\rho }_i$ is the fractional open time, $I_i$ is the ion current through the open Aβ channel, and F is the Faraday constant which is equal to 96.480 C/mole. Therefore, if a single 4 nS channel became active in a neuron of 25 μm diameter, the sodium influx could be calculated as 0.6 fmol/s, and the intracellular sodium concentration change would be 10 μM/s. By Equation (31), we can say Alzheimer’s is associated with abnormal cation ions fluxes inside the nervous cells. The reason we are addressing this is due to the following computational reasons:

Following Equation (3), the conductance of sodium (G_Na) can be represented as:

$$G_{Na}={\overline{G}}_{Na}{m}^{3}h.$$

(32)

As shown in Equations (3),(4),(7)–(10), the conductance of sodium depends on the other variables i.e. m, n, V, so it can be rewritten as:

$$G_{Na}={\overline{G}}_{Na}f\left(m,n,V\right).$$

(33)

On the other hand, the current of sodium in Equation (11) following Equation (14) depends on $N{a}_{in},N{a}_{out},\mathrm{and}V$. Therefore, Equation (11) can be written as:

$$I_{Na}={\overline{G}}_{Na}f\left(m,n,V\right)\cdot \overline{\phi }\left(N{a}_{in},N{a}_{out},V\right),$$

(34)

where $\overline{\phi }$ is a function that represents (V − V_Na) using the Nernst equation in Equation (14). Following these changes, the sodium flux across the membrane, obtained from Equation (31), is converted to:

$${\phi }_{Na}={\rho }_{Na}\left({\overline{G}}_{Na}f\left(m,n,V\right)\cdot \overline{\phi }\left(N{a}_{in},N{a}_{out},V\right)\right)/F.$$

(35)

If Na_in increases and Na_out remains stable (like the condition that occurred in accumulation of Aβ deposition), one or more variables, such as ρ_Na, m and h, are changed. ${\rho }_{Na}$ is the fractional open time and represents the fraction of the time that the channel is open. It is modulated by the Na_in concentration. Its function is somewhat like the functions of m and h in the activation and deactivation of sodium channels. The ρ_Na causes severe interruptions in the exact configuration of m and h, and these gates lose their real performance to some degree. With this description and from the above computational relations, it can be concluded that secretion of Aβ in Alzheimer’s disease causes a disease-like channels dysfunction in the nervous system. The same condition can be defined for the potassium influx into the neuron.

Therefore, in order to computationally simulate amyloid peptide channels at the plasma membrane in the Alzheimer’s disease condition, we need to somehow increase the amount of cations inside the cell. As noted above and shown in Equation (35) for a given ion, in this case sodium, the maximum conductance has a direct relation with the ion flux inside the membrane. Therefore, for any changes of intercellular ions, the maximum conductance should be changed. In support of this, we refer to the work of Perez, et al. [10]. In their work on intercellular ion changes, which are increased by created Aβ channels, Perez et al. [10] changed the maximum conductance of related ion. In order to find out how much change in the concentration of sodium and potassium is needed, we used the model introduced by Vitvitsky et al. [15]. For this reason, the intracellular sodium increased two-fold and the intracellular potassium increased by 8–15%. The nominal channel conductivity for sodium is 120 ms/cm²; for potassium it is 36 ms/cm². The equilibrium potential applied for sodium is 50 mV; for potassium it is −71 mV and for leakage it is −51 mV. The injected current is 10 nano-Amps. These equations are solved using the Ode45 method, which is based on an explicit Runge-Kutta method, with a time step of 0.01 ms. Codes reproducing key results are available upon request from the authors. For more details about the model refer to the work of Sadegh-Zadeh and Kambhampati [18].

4. Computational Results

In the following, we will investigate the behaviour of a neuron with Aβ channels in the model as compared to a standard neuron. Given the observed behaviour in Aβ channels, a faulty neuron would lead to two observations: an increase in the amplitude of membrane potential and an increased number of spikes. Four sets of experiments were carried out. The first experiment was performed for the standard condition where all conductances have nominal values. Based on the findings of Vitvitsky et al. [15], the second and third experiments were performed with a two-fold intracellular sodium change and 15% intracellular potassium change, respectively. The final experiment was performed with two-fold intracellular sodium and 15% intracellular potassium changes, simultaneously. All the experiments were carried out at a simulation time of 150.0 ss. The injected current varies from 0 nA, between 0.0 to 50.0 s, to 10 nA, between 51.0 to 1000.0 s. The reason for considering two different injection currents was to observe the behaviour of the system under both stimulation and non-stimulation conditions.

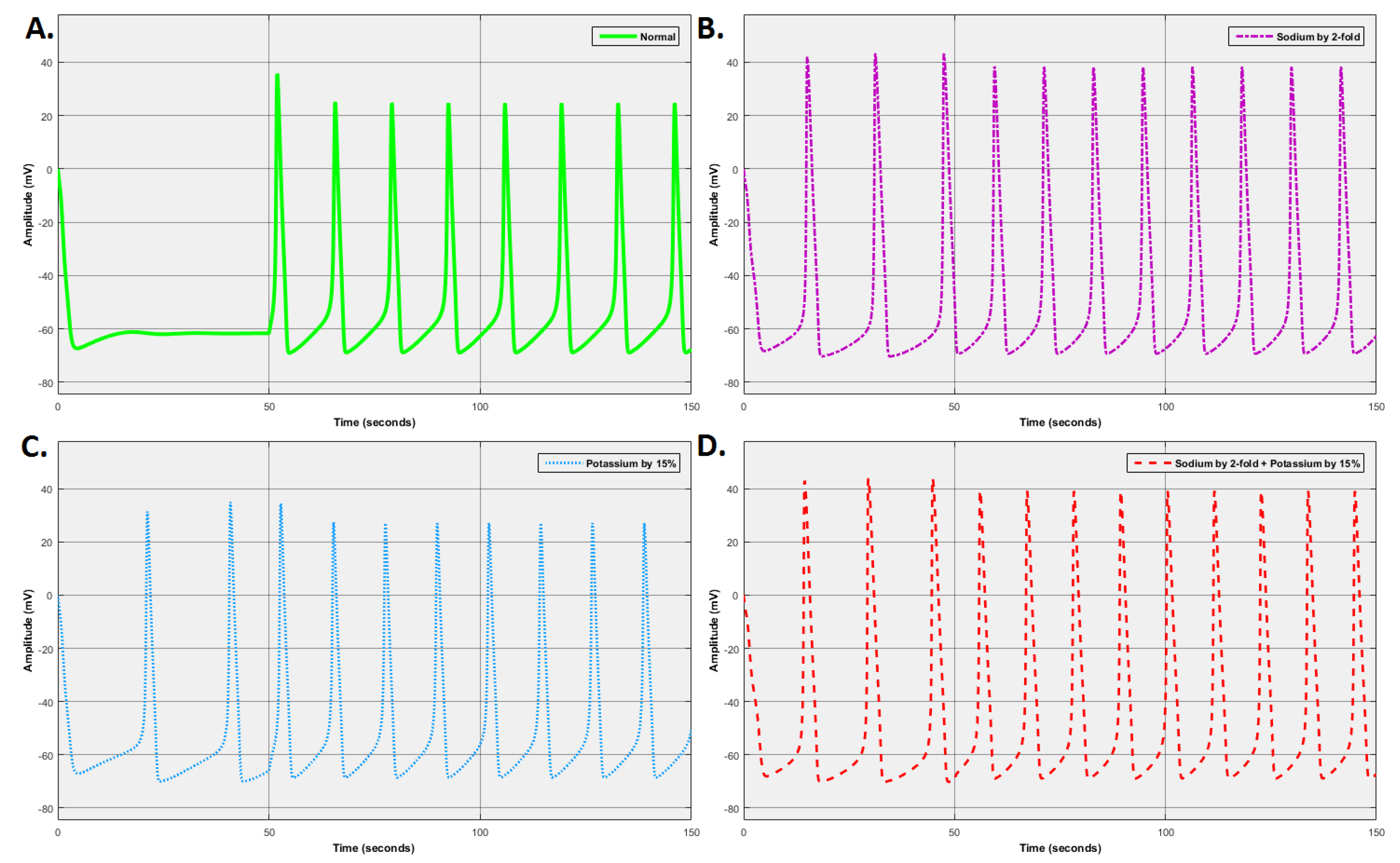
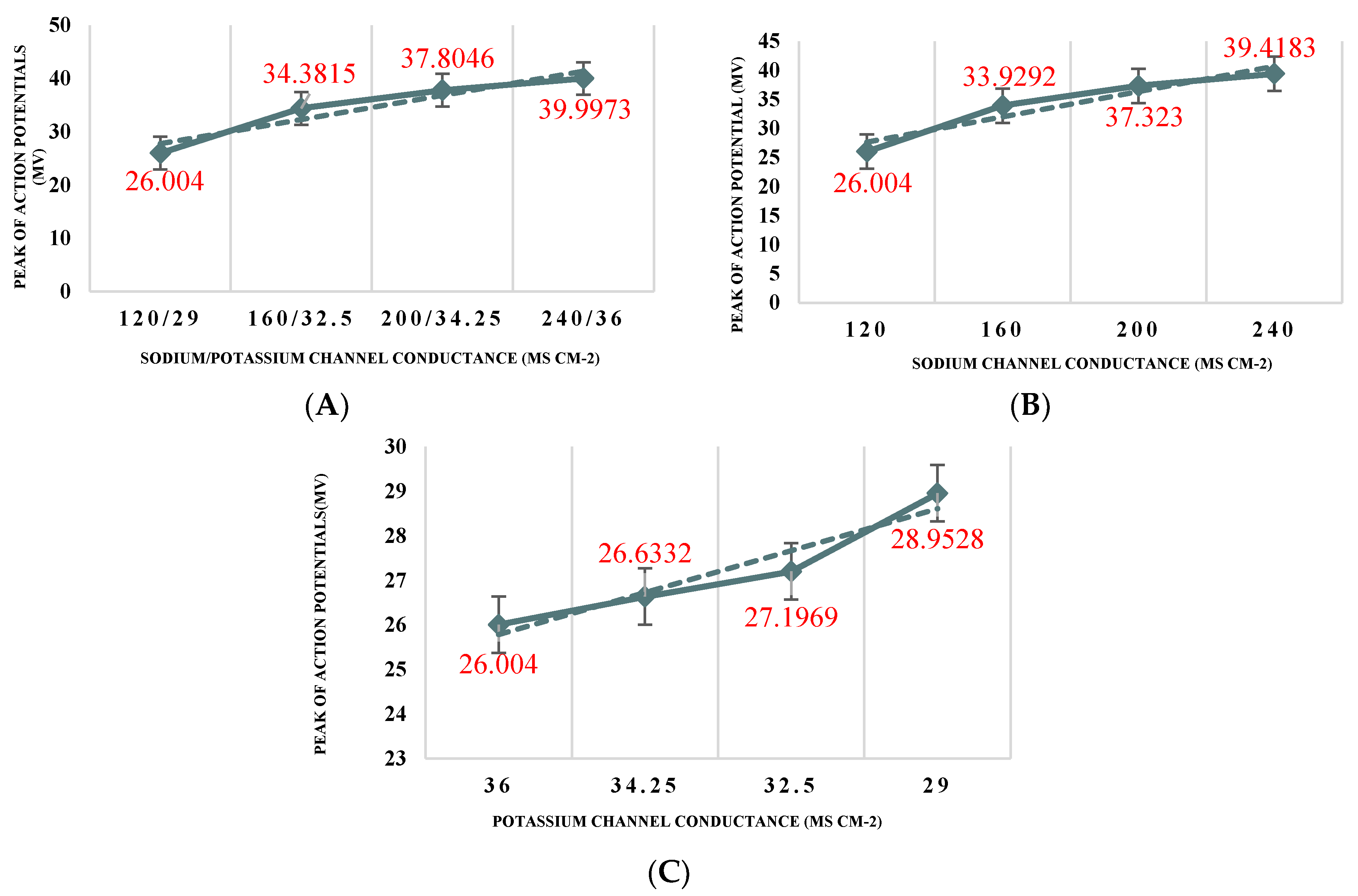
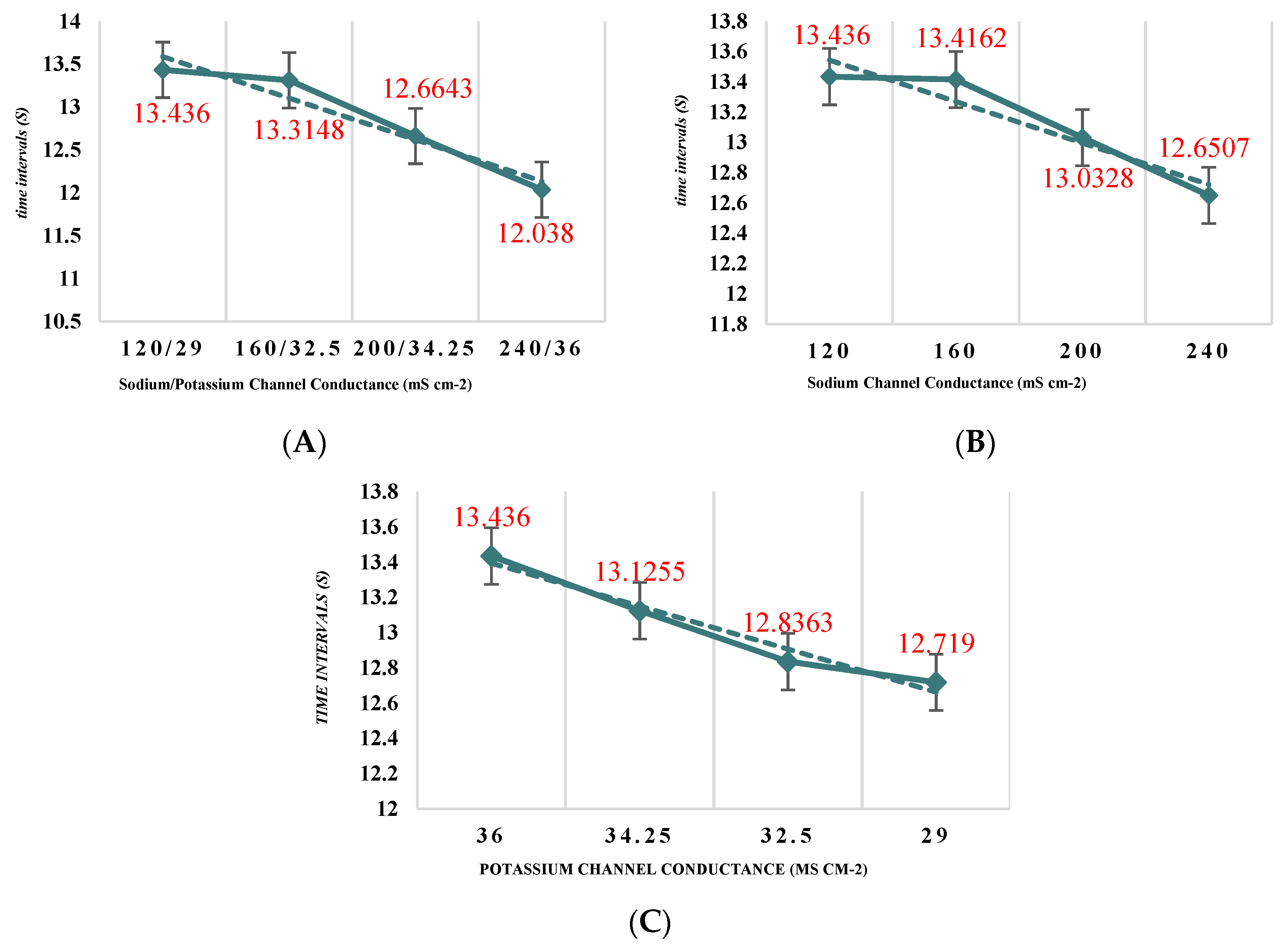
Figure 1A shows the responses of the neuron for the nominal set of values. As shown, the reactions are a series of spikes. These spikes have two main characteristics. The first characteristic is the magnitude of the spike and the second is the inter-spike interval. The analyses of these two characteristics for all changes are shown in Figure 2 and Figure 3. This spike is taken to be the ideal response, and all comparisons are made to this response. Figure 1B presents the reaction of the neuron to a 2-fold increase in sodium ion conductance. It can be seen that as the sodium ion conductance is increased from its nominal value, the spike magnitudes and the inter-spike interval are both increased. In other words, the neuron responds with more massive spikes at a more rapid rate.

In the same way, results were obtained for the conductance of potassium ion. The reaction is shown in Figure 1C. In this experiment, the effect of potassium conductance is more pronounced. It can be seen that as the potassium ion conductance increased by 15% from its nominal value, the time of inter-spike intervals decreased (see Figure 3). As the outcome indicates, the nerve cell is more sensitive to any potassium changes inside the cell than to sodium ion changes. The next experiment changed the combinations of sodium and potassium in a single neuron, simultaneously. This result is shown in Figure 1D. From the results, it is evident that changes in both sodium and potassium conductance at the same time affected both elements of the output, i.e., the inter-spike interval and the magnitude of the spikes. The results from this figure can be compared with the results in Figure 1B showing that when combined conductance changes occur in the cell, the effects are more severe than (but are consistent with) those reported for individual sodium or potassium conductance changes. Increasing $G_{Na}$ leads to an increase in the amplitude of the action potential of the neuron (see Figure 2B). On the other hand, increasing $G_K$ as compared to the value applied for the normal neuron increased the amplitude of spikes (see Figure 2C). As shown in Figure 2A combining both changes in a single neuron leads to increasing the amplitude of action potentials even more than the two previous separate changes. However, for $G_K$, a much higher change was required to reproduce the behaviour observed when increasing $G_{Na}$. In line with the observations, as can be seen, depolarization increased linearly. However, in comparison with increasing only $G_{Na}$, increasing both $G_K$ and $G_{Na}$ together did not change the slope significantly.

As shown in Figure 3B by increasing G_Na, the time interval of the response of a neuron to stimulation decreased. The same behaviour can be seen in Figure 3C for increasing G_K. The response of a neuron to the combined changes is shown in Figure 3A. The changes showed a decrease in the time interval of action potentials but the slope of changes was not significantly different from single changes of G_Na and G_K.

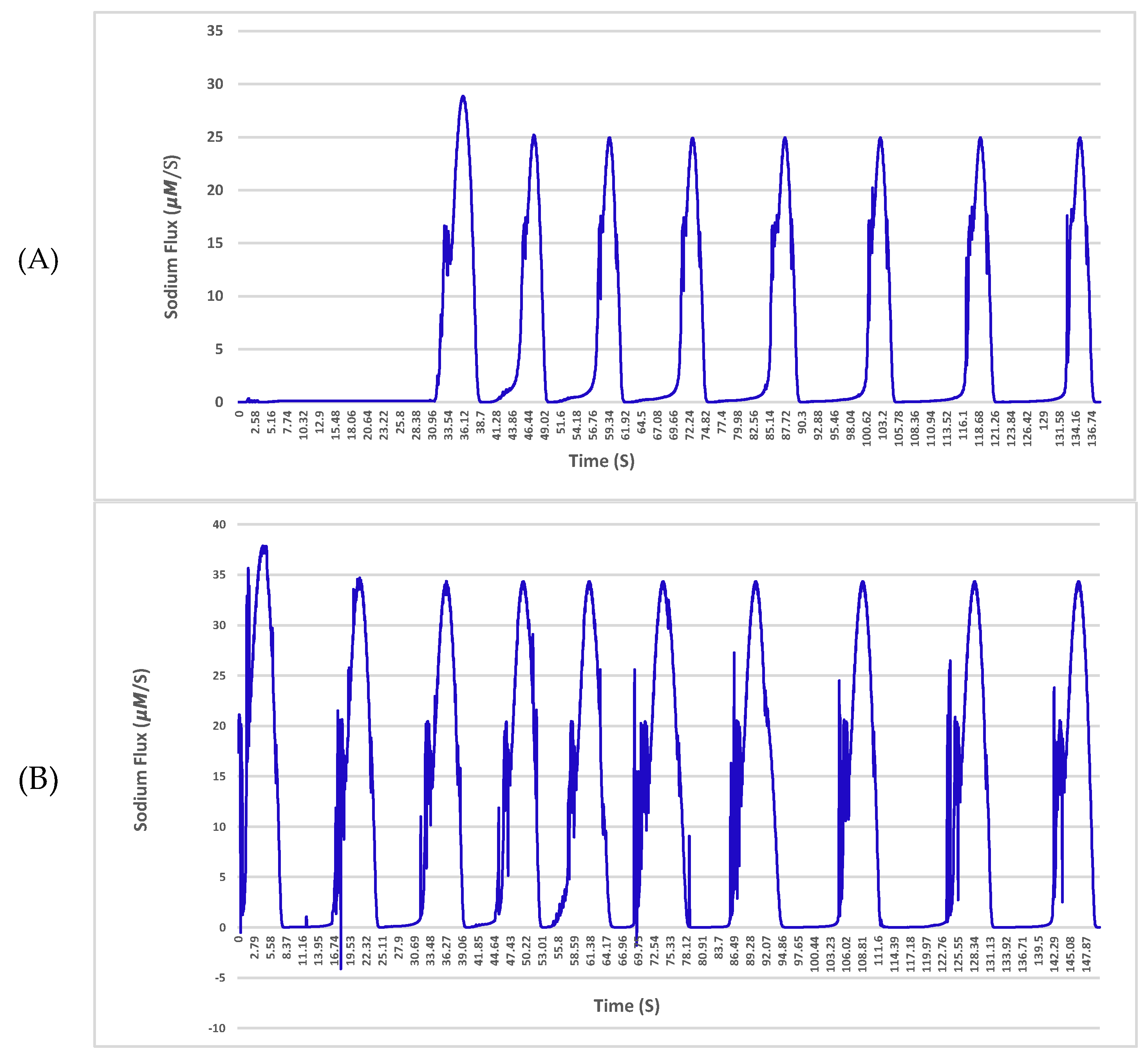
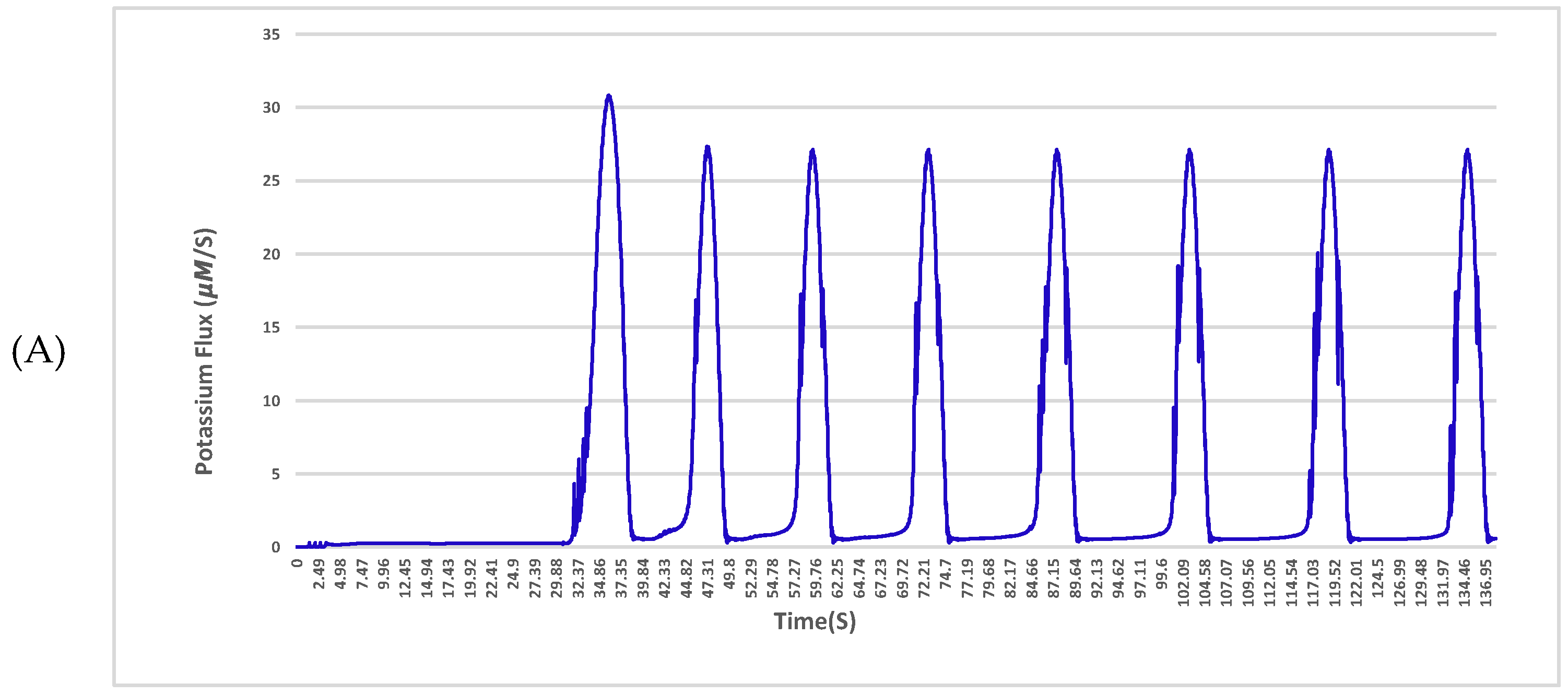
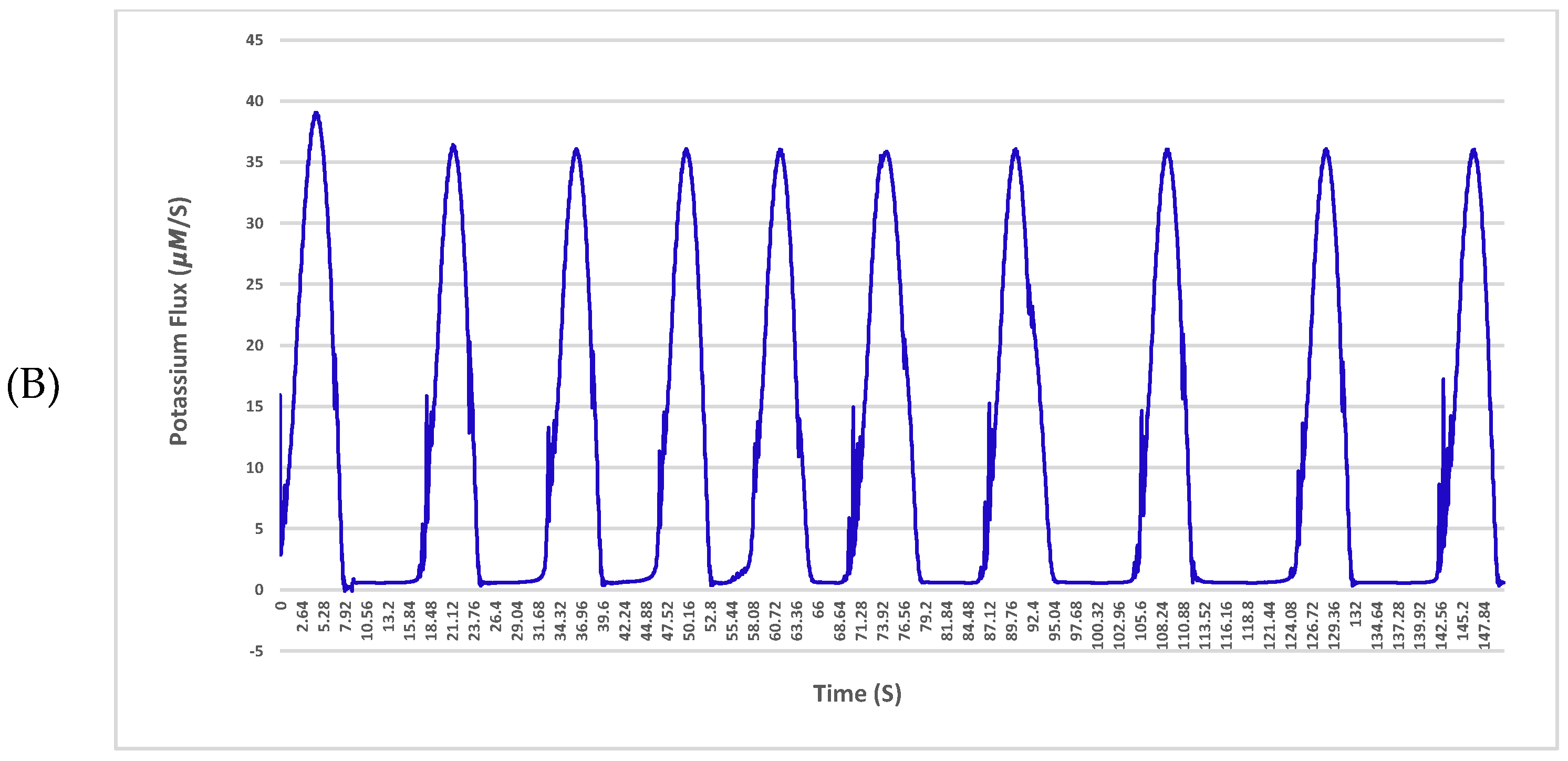
The sodium and potassium fluxes across the membrane for a given neuron with a single 4 nS channel and 25 μm diameter in the normal condition and affected by amyloid-β are shown in Figure 4 and Figure 5, respectively.

The results indicate a deterioration in the exchange of ions in the vicinity of the plasma membrane with the Aβ protein. As shown in Figure 5 in the hyperpolarization step, the neuron experiences huge fluctuations in sodium exchange. This delay or even fault in the turnover of ions across the neuronal membrane may result in crucial impairments of cellular performance and will lead to a potential threat to nerve cell longevity. The fluctuations are driven solely by Aβ pores, which are permeable to sodium and potassium. The pores cause damage to membranes of nerve cells and transform their specific functions such as ion homeostasis and also action potentials as shown in the results.

5. Discussion

Many efforts have been devoted to establishing a relationship between neurodegenerative disorders and the loss of functionality of a critical protein created by channelopathies. Growing evidence indicates that neurodegenerative disorders involve a substantial impact of dysfunctioning in ion channels. Many neurodegenerative disorders, such as Alzheimer’s disease, Parkinson’s disease and age-related disorders, are caused due to the transformation of functionality in ion channels [19]. Ion channels are a vital part of the neurons and are responsible for triggering signals and synaptic transmission. These channels play an essential role in the maintenance of cell homeostasis through an abundant transmembrane protein. The importance of these channels is enormous because they determine the membrane potential and have a crucial role in secretion of the nerve transmitters. These proteins make a passage for different ions like sodium and potassium to move across the impermeable lipid bilayer. Research has shown that the cause of dysfunctioning in ionic channels in neurodegenerative disorders like Alzheimer’s disease is related to the Aβ hypothesis [19]. Aβ peptide is a significant part of senile plaques. Although many studies have been conducted on beta-amyloid, several important questions about how this protein causes Alzheimer’s neuropathology remain unanswered. One of the main questions is: How is Aβ toxic to neurons? While plaques are additional deposits of neurons and with this assumption, it is difficult to imagine a toxic structure for them.

The preliminary results showed that the Aβ channels created on the membrane of neurones caused hyperactivity in the function of the neuron. The range of observations summarised in Figure 1B,C illustrates the complexity and the response of these channels to separate sodium and potassium ions. In comparison to Figure 1C, the hyperactivity is exacerbated in Figure 1B. It can be seen that the ion change lowers the dielectric barrier, and at the same time increases the conductance of the neuron. Since the output of change in sodium (see Figure 1B) and the output of combined changes in sodium and potassium (see Figure 1D) are very similar, it can be suggested that Aβ disrupts sodium homeostasis in a neuron more and it increases intracellular sodium. It seems that Aβ peptides might function similarly to sodium channels. In their studies, Vitvitsky et al. [15] have shown that abnormal levels of ions like sodium and potassium in neurons cause the ionic imbalance that is linked to Alzheimer’s disease pathogenesis. They found remarkable ion imbalances in the cortical (sodium) and cerebellar (potassium) of the brain in Alzheimer’s disease. According to other research [20,21,22,23], which was conducted on the early- and late-onset stages of Alzheimer’s disease, in the early stages of Alzheimer’s the cortical areas are most involved. After considering these studies and taking into account the results of our experiments, it may be concluded that changes of sodium ions in the intracellular neurons of the cortical regions can be considered as a hallmark of the early detection of Alzheimer’s disease.

These results can explain and answer the question of what the mechanisms underlying neuronal hyperactivity in neurodegenerative disorders like Alzheimer’s disease are. However, this raises another question of how, despite the increased excitability in hyperactive neurons, the neurodegeneration seen in Alzheimer’s disease can be associated with a reduction in the overall activity in neurons. This question was answered by another study done by Busche et al. [12] with regards to the role of inhibitory neurons in the general structure of the nervous system. Busche et al. mapped the distribution of types of neurons. In their studies, they showed that there are three types of neurons about the nearest three-dimensionally Aβ accumulations. These three types are hyperactive, silent and normal neurons. Hyperactive neurons are found only in very close proximity (usually less than 60 μm) to the borders of Aβ plaques. After this border and at increasing distances, the proportion of silent neurons significantly increases. Thus, a possible explanation for the two types of hyperactivity and silent neurons may be an impairment of inhibitory neurons. As it turns out from the results and studies done by Perez et al. [10] and Busche et al. [12], the hyperactivity caused by Aβ channels exacerbates the activity of inhibitory neurons. For this reason, one can assume that the activity of the neurons surrounding the hyperactive neurons can be viewed as silent, and in general, we see the lowering of neuronal activity in the central nervous system.

The results on the function of an individual neuron in the direct vicinity of Aβ plaques show the epileptiform activity in Figure 1B–D. As shown, the neuron experiences several action potentials even when there are no stimuli for the neuron. These results confirm the studies done by [12,14,24,25,26]. They revealed that, in addition to the increased neuronal activity in the direct vicinity of Aβ plaques, the risk of epileptic seizures is high in Alzheimer’s disease. In answer to our key question, we should point to this novel idea that Aβ is toxic to cortical and cerebral neurons, as this kind of protein forms aberrant ion channels in the plasma membrane of the neuron. As a result, it disrupts neuronal homeostasis, either partially or completely. Aβ interacts with different types of membranes, which leads to the formation of Aβ ionic channels; this could support the idea that Aβ is cytotoxic, largely due to the action of Aβ channels in the plasma membrane of the neuron. As more Aβ is deposited, the channels for sodium exchange increase, and therefore, we see that $N{a}_{in}$ increases and eventually, the relation (22) leads to [Na⁺]_in − [Na⁺]_out → 0, that is, a deterioration in the neuron. It is clear that there is deterioration in the signals. The rate at which this change occurs is important from the point of view of detecting the problem at an early stage.

Aβ accumulation has been discovered to form large, relatively cation-permeable channels under physiologic conditions. This channel formation in membranes of a neuron could cause cell depolarisation, sodium and potassium dysregulation, depletion of neural energy stores and other types of cellular dysfunction. As shown in Figure 4 and Figure 5, the build-up of Aβ depositions during the onset of Alzheimer’s disease has profound effects on the activity of the local community of neurons in the central nervous system. For instance, in the hyperpolarization step of the action potential, the neuron experiences huge fluctuations in sodium exchange. These effects can include enhanced neural activity [12], spontaneous epileptiform activity [24,25] and incidence of epileptic seizures [26,27]. According to the results of the experiments, it can be well understood that the neurodegeneration observed in Alzheimer’s disease is associated with the increase of toxicity of Aβ depositions. This study reveals that accumulation of Aβ during Alzheimer’s disease causes neuronal hyperexcitability in inhibitory neurons and also, makes neural networks susceptible to epileptiform activity.