Abstract
The EU’s energy targets are to achieve at least 32% renewables in the energy mix by 2030. Part of the solution is strengthening consumer rights by empowering individuals to generate their own electricity. The aim of this study was to identify the most suitable energy system for electricity generation of up to 50 kW in the EU residential sector. Multi-Criteria Decision Analysis was used to compare four systems: proton exchange membrane fuel cell with photovoltaic panels, photovoltaic panels, biomass-powered Stirling engine, and solar-powered Stirling engine. Based on the results, the most beneficial system for household electricity generation is the biomass-fueled Stirling engine system due to its affordability, reliability, and low environmental impact. Governments and businesses can use these findings to improve information for the residential sector and enable the transition to renewable energy.
1. Introduction
The European Union’s (EU) energy targets for 2030 are to reach at least 32% renewables in the EU’s energy mix and to reduce greenhouse gas (GHG) emissions by 40% in the energy sector [1]. One of the ways to achieve these goals is to strengthen consumer rights, giving individuals more power to generate their own electricity and store it or sell it back to the grid. The buildings sector is estimated to account for 40% of energy consumption and 36% of GHG emissions in the EU, thus being the largest energy consumer [1]. Currently, this consumption mainly consists of heating, cooling, ventilation, and hot water. However, in the upcoming years, various new needs, such as installing charging stations for electric vehicles in buildings, will significantly increase energy demand in this sector [2].
The motivation for individuals to produce their own energy is diverse. They are driven by economic benefits, environmental awareness, a sense of community, and reduced dependence on energy suppliers, and they are even willing to pay extra to become more resilient [2]. Overall, small-scale household solutions could help the energy sector transition faster to renewable energy [3]. A common method of decentralized electricity production is using electricity generators powered by fossil fuels, particularly diesel [4]. However, photovoltaic (PV) panels have recently gained popularity due to price reductions [2]. Therefore, the topic of self-sufficient and renewable energy systems has become relevant.
Several studies have looked at particular small-scale systems [2,5,6] or compared how different approaches could be adapted to them [7,8]. M. A. Khan and H. G. Darabkhani conducted a study comparing four micro-cogeneration systems for households [9]. The microturbine, gas engine, Stirling engine, and fuel cell systems were evaluated and compared using political, economic, social, technological, legal, and environmental risk analyses and Multi-Criteria Decision Analysis (MCDA). The results showed that fuel cells are the most environmentally friendly and, although they are expensive and have a long start-up time, they are one of the best technological options. However, Stirling engines are most suitable for households as they are a cheaper option. These types of evaluations are based on time-varying indicators, so results can change over time. A study by D. Streimikienė and T. Balžents supports this [10]. It is a 2013 study comparing the same technologies as the study discussed above using MCDA and similar criteria. However, the results are the opposite: microturbines scored best while reciprocating engines were the second-best technology.
Based on the findings of the reviewed study [9], this study focuses on two key technologies—fuel cells and Stirling engines. Fuel cells are an energy conversion technology that directly transform chemical energy from various fuels into electrical power with higher efficiency than traditional sources of power generation [11]. Fuel cells have several benefits, including their small size, quiet operation, and low environmental impact. Additionally, this technology can be utilized in a vast range of applications, with capacity ranging from a few watts to several gigawatts. The main drawbacks of fuel cells are their use of platinum as the catalyst layer, which increases production costs, and their requirement for high-purity hydrogen, which is currently primarily sourced from non-renewable resources [11].
A Stirling engine is an external combustion engine that is well suited for residential energy generation. It offers several advantages, including low emissions in the operating stage, minimal maintenance, reduced noise and vibration, high theoretical efficiency, and the ability to utilize different fuel sources [12]. M. A. Khan et al. summarized that the disadvantages of Stirling engines are high costs, issues with reliability, and low electrical efficiency [9]. The engine converts external heat energy into mechanical energy. Stirling engines can be used for heating, cooling, power generation, and mechanical propulsion, such as in electric vehicles and marine engines [13].
The reviewed study [9] compared systems that mainly use fossil fuels. Hence, the aim of this study is to compare renewable energy systems that could be used to generate energy in EU households. Systems that include technologies such as the fuel cell and the Stirling engine will be selected. The MCDA method will be used to compare the systems. The study’s novelty is the summarized data about the systems and the results obtained from MCDA and sensitivity analysis.
2. Methods
This study used two methods: literature review and MCDA. The literature review was based on scientific literature. MCDA was chosen because the reviewed study [9] showed that it is a suitable method for comparing energy systems according to different criteria, covering not only technical but also environmental aspects. The MCDA results give a ranking of the studied alternatives. To achieve the desired outcome, the following six steps were performed, shown in Figure 1. These steps are explained in the following sections.
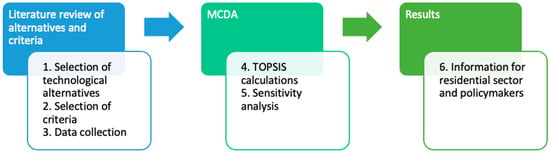
Figure 1.
Steps of the methodology.
2.1. Literature Review
Initially, decisions were made on which renewable electricity generation systems ought to be compared. Four systems were selected: proton exchange membrane fuel cell with photovoltaic panels (PEMFC/PV), photovoltaic panels (PV), biomass-fueled Stirling engine (SE/BM), and solar dish Stirling engine (SE/SD). As previously mentioned, the main objective was to compare fuel cell and Stirling engine technologies. The whole systems with these technologies, rather than just stand-alone technologies, were chosen to be able to analyze specific data rather than intervals of data. MCDA also included the PV system as it is the most widely used form of renewable energy in households [14]. It acts as a baseline scenario to assess the other systems better.
There are several fuel cell types: proton exchange membrane fuel cells (PEMFC), alkaline fuel cells, phosphoric acid fuel cells, molten carbonate fuel cells, and solid oxide fuel cells [11]. PEMFC was chosen because it is suitable for small-scale power generation, has a relatively high efficiency, and can produce electricity using renewable energy. These fuel cells are state-of-the-art and commercially accessible [2]. PEMFCs operate at 60–160 °C and have an electrical efficiency of around 50%. These cells operate on pure hydrogen [9]. The origin of the hydrogen determines whether the electricity generated by the system is renewable. Hydrogen can be produced from fossil fuels or by electrolysis. Hydrogen from natural gas is the most common, accounting for more than 48% of the total hydrogen produced, followed by oil reforming (30%), coal gasification (18%), and just 4% of hydrogen is produced by other technologies [15]. Hydrogen can be produced by electrolysis from renewable resources such as sun, wind, or water. The system considered in this study uses solar energy as it is the most suitable at the household level.
Stirling engines are generally fossil fuel-powered [7]. However, Stirling engines have the potential to use renewable energy sources with high efficiency. Over the years, hundreds of Stirling engine designs have been developed applying the basic principles of thermodynamics. They can be classified according to cylinder arrangement, operation mode, or piston coupling [13]. Stirling engines are most commonly classified by cylinder arrangement: alpha, beta, and gamma. A. Abuelyamen and R. Ben-Mansour [16] compared the energy efficiency of all three types at the same conditions and found that the alpha Stirling engine had the lowest output (0.9 W) and the lowest thermal efficiency (1.8%). The beta Stirling engine followed with output power and thermal efficiency of 8.7 W and 7.5%, respectively. The gamma Stirling engine had the highest output power and thermal efficiency—9.22 W and 9.8%. No specific Stirling engine type was defined for the systems considered in this study. Based on the reviewed research [7], two Stirling engine systems were selected for the MCDA: a biomass-fueled system and a solar dish system. All selected systems are shown in Figure 2.
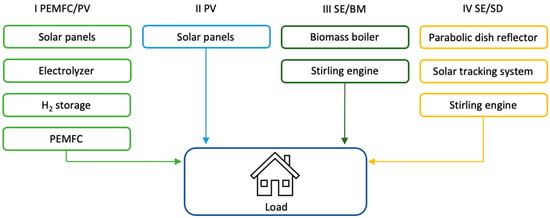
Figure 2.
Schemes of the systems covered in the present study.
After choosing the alternatives to compare, the next step was to select the criteria. The criteria were determined based on their relevance to the study’s objective and available data. Five criteria were identified from environmental, technical, and economic standpoints to evaluate energy generation systems. Table 1 shows the selected criteria. Ideal values (required further for MCDA) are indicated by “+” or “−”, with a plus symbol for maximal and a minus symbol for minimal values.

Table 1.
Criteria for Multi-Criteria Decision Analysis.
Levelized cost of energy (LCOE) is a comparative indicator used to evaluate policy decisions related to renewable electricity generation [17]. The LCOE indicator provides an estimate of the energy unit cost over the system’s entire lifetime, including capital, operating, and financing costs. More specifically, it usually consists of initial investment, installation costs, operation and maintenance costs, feed-in rates, discount rates, technical lifetime, and depreciation [7]. In this study, it reflects the economic aspect of the system and includes several economic indicators in one. The LCOE values will be taken from the literature, where it has been calculated using Equation (1) [8].
where is installation cost, is operation and maintenance cost, is total annual energy output, is discount rate, and is system lifetime.
Two technical parameters were selected—electrical efficiency and full-load operating hours. The system’s electrical efficiency indicates which system is more efficient in producing the required electricity. Operating hours indicate the system’s reliability—how well it will meet demand and whether backup power will be needed.
When comparing renewable energy systems, it is essential to include environmental indicators, as they have different environmental impacts during their life cycle. Of all the parameters analyzed in the life cycle analysis (LCA), global warming potential (GWP) was chosen for MCDA as it is one of the critical indicators and policy drivers for reducing net greenhouse gas emissions in the EU [15]. The second indicator, technical lifetime, reflects how long it takes until the new equipment is no longer useful. If a system has a shorter lifetime, new equipment will have to be produced more frequently, and the existing one will become waste. Additionally, if household convenience is considered, the owner will need to put in more effort to maintain the system.
2.2. Multi-Criteria Decision Analysis
MCDA is a method for comparing different alternatives based on relevant criteria. There are several MCDA methods, which have their own limitations and give different outcomes [18]. The method chosen for this study was the technique of order preference similarity to the ideal solution (TOPSIS). In this method, the final result is the proximity of the alternative to the ideal solution. This means that the closer the result is to 1, the closer this alternative is to the ideal solution. The calculation steps were taken from Zlaugotne B. et al.’s study [18]. Using the TOPSIS, energy generation systems will be compared with the five criteria identified in the literature review. All criteria were assumed to have the same importance, so equal weights were applied. MS Excel was used for all calculations.
The TOPSIS method has five calculation steps [18]. Initially, the decision matrix needs to be normalized. This is done according to Equation (2):
where R is the normalized matrix value, and X is the criterion value.
where V is the weighted value, and w is the weight of the criterion. As already mentioned, in this study, the weights of the criteria are equal, so w is one divided by the number of criteria, giving a weight of 0.20.
The next step is to identify ideal and anti-ideal values. If the ideal value is the maximum value, then is the highest of the weighted values, and is the lowest value. If the criterion conditions are reversed, and the ideal value is the minimum value, then is the smallest value of the weighted values, and is the highest.
The closeness to the ideal and anti-ideal value is then calculated. This can be done using Equations (4) and (5).
where is closeness to the ideal value and is the ideal value.
where is closeness to the anti-ideal value and is the anti-ideal value.
The end result is a relative closeness to the ideal solution. It is calculated according to Equation (6).
where is the relative proximity to the ideal solution. This value is obtained for each alternative and can be used to rank them.
Additional sensitivity analysis was carried out after the TOPSIS calculations. Sensitivity analysis can be performed to test the influence of the criteria on the alternatives. Sensitivity analysis has three steps. The calculation steps were taken from E. Teirumnieka et al.’s study [19].
In this method, the weights of the criteria are initially assumed to be equal. Equal weights are calculated according to Formula (7).
where is initial weight of criteria and n is the number of criteria.
The weight of one criterion is then adjusted according to the unitary variation ratio. This variable weight is the weight of the criterion being analyzed at that moment. Equation (8) is used to calculate this.
where is the weight of the criterion being changed and is unitary variation ratio. Sensitivity analysis was performed with five unitary variation ratios (0.01; 0.5; 1.5; 2; 2.5).
The weights of the remaining criteria are equal and can be calculated according to Equation (9).
where is the weight of the criterion, which is not subject to change.
Once the weights required for the sensitivity analysis have been calculated, they are used to calculate the relative proximity to the ideal solution for each criterion with every unitary variation ratio. For this purpose, the TOPSIS calculation steps are used.
3. Results
3.1. Data Summary
Quantitative data were available for each criterion and alternative. These are listed in Table 2. The aim was to find data compatible with the chosen system, data covering an EU region, and a small system of less than 50 kW. In some cases, it was possible to meet all these requirements, but data availability made this impossible in other cases, so the most appropriate data were selected. The sources of the values in the table are given in the table and described in more detail in the following subsections.

Table 2.
Multi-Criteria Decision Analysis decision matrix.
3.1.1. Levelized Cost of Energy
A number of studies have been carried out on the levelized cost of energy of fuel cells. Several of them deal with systems operating on non-renewable energy sources such as natural gas and diesel [3,5,27]. Other studies did not apply to this study as they dealt with high-capacity systems [28,29,30] or different applications, such as telecommunication stations [31] and greenhouses [21]. The LCOE from these studies ranged from 0.06 to 0.66 €/kWh. C. Ceylan and Y. Devrim [21] summarized various studies on PEMFC solar hybrid systems and found that the levelized cost of energy can reach 1.46 €/kWh. A study on a PV/PEMFC system capable of meeting the average daily consumption of a Turkish household (8 kW) was selected for the input data [8]. The study does not meet all input data requirements as it considers the weather conditions in Turkey, which affect the PV energy output and, consequently, the costs. The resulting levelized cost of energy was 0.54 $/kWh or 0.5 €/kWh for the system using methanol electrolysis.
In the case of PV, the LCOE considered PV systems installed on residential and commercial rooftops [20]. The installed capacity of these systems is less than 1 MW, which is higher than the defined capacity threshold. Between 2008 and 2018, the levelized cost of energy of PV panels decreased by almost 80%. This is due to a rapid drop in capital expenditure. In 2018, the LCOE for rooftop PV in the EU-27 ranged from 70 to 188 €/MWh [20]. The input value was the average of the two values, 0.13 €/kWh.
There have also been several studies on the levelized cost of energy of the Stirling engine system. The studies cover different Stirling engine systems with LCOEs ranging from 0.01 to 0.40 €/kWh. The levelized cost of energy was 0.08 €/kWh for a methane-fueled gas turbine with a Stirling engine [32]. In this case, the costs were reduced by 10% when a Stirling engine was added to the system. In the case of Morocco, the levelized cost of energy for a solar dish Stirling engine can range from 0.10 to 0.07 €/kWh [33]. LCOE depends on the production volume and the level of localization. For the system with a concentrated parabolic dish Stirling engine and horizontal axis wind turbines, the levelized cost of energy was between 0.12 and 0.14 €/kWh [34]. K. Pawananont et al. compared three technologies—the internal combustion engine, the organic Rankine cycle, and the Stirling engine—that could be used to generate electricity from landfill gas [35]. The resulting LCOEs were 0.11, 0.28, and 0.40 €/kWh, respectively. The input data for the Stirling engine systems were based on a study comparing the performance of a Stirling engine for two types of renewable energy sources—solar and biomass (pellets) [7]. The resulting LCOE for a 10 kW solar dish Stirling system was 0.17 €/kWh, and for a 25 kW biomass boiler with a Stirling engine, 0.11 €/kWh.
3.1.2. Efficiency and Reliability
The electrical efficiency of different types of fuel cells ranges from 20 to 70%. However, when looking at the efficiency of the systems in which they operate, it can be seen that they are typically in the range of 10 to 60% [11]. PEMFC has an electrical efficiency of between 50 and 60%, while the system in which it operates has an efficiency of between 30 and 50%. For the greenhouse system modeled [21], the PEMFC had an electrical efficiency of 48%, which falls within the limits defined above and was therefore used for the analysis.
In an LCA study on the solar PEMFC system, it was estimated that a typical fuel cell has an operating time of 1691 h/year [23], which was used as input data in this study. For this system, the reference point was China, so this number would differ in EU countries as it depends on the solar radiation. Also, it is unknown if these are full-load working hours.
The efficiency of PV panels has improved in recent years. The average efficiency in 2006 was 13% for multi-crystalline PV panels and 15% for mono-crystalline PV panels, while in 2018, it was 17% and 18%, respectively [22]. This upward trend is projected to continue until 2030. The efficiency of mono-crystalline PV panels was used as input data.
The capacity factor was used to calculate the full-load operating hours of the PV panels. The capacity factor represents the ratio between a power plant’s actual and maximum possible electricity generation. It is obtained by dividing the full-load running time by the number of hours per year. The average capacity factor of rooftop PV panels in the EU-27 is 15% [20]. The capacity factor is very country specific. Greece and Portugal have the highest rates at 17–20%, while Germany and France have 12–16%. In the Nordic countries, such as Poland and the Netherlands, capacity factors are below 12%. Multiplying the average capacity factor by the number of hours per year gives an average of 1314 h per year of operation at full capacity.
For Stirling engine systems, efficiency and operating hours were taken from the levelized cost of energy study used previously [7]. The biomass-fueled Stirling engine generated 88% more power than solar. It produced 4.3 kW with a total efficiency of 46.7%, while the solar-powered system generated 2.3 kW with 31.3% efficiency. The results of this study illustrate the importance of the energy source as it has a considerable impact on the performance of the Stirling engine. The authors chose a solar-powered system operating time of 2400 h, based on the number of hours of sunshine in Portugal. For the biomass system, 7000 h were obtained from a literature review.
3.1.3. Global Warming Potential and Lifetime
Comparing different fuel cells, PEMFC has a relatively high global warming potential—GWP for PEMFC (2 kW) is 0.75 kgCO2eq/kWh, for solid oxide fuel cells (125 kW) is 0.52 kgCO2eq/kWh, and for molten carbonate fuel cells (500 kW) is 0.55 kgCO2eq/kWh [11]. In this case, it is because hydrogen is produced from fossil fuels. Hydrogen production significantly affects the environmental impact of the fuel cell system [11]. R. Stropnik et al. conducted a cradle-to-gate LCA study of a 1 kW PEMFC system [15]. Different hydrogen production options were compared—EU-28 hydro, EU-28 wind, solar, and natural gas. PEMFC degradation in static and dynamic systems (automotive applications) was also considered. The results show a global warming potential of 0.71 kgCO2eq/kWh for a static natural gas system, 0.03 kgCO2eq/kWh for a static hydro system, 0.04 kgCO2eq/kWh for a static wind system, and 0.24 kgCO2eq/kWh for a static solar system. For the solar fuel cell system, only 4% was for the manufacturing and technology replacement stages. The remaining 96% was for the operation phase, which takes hydrogen production into account. PEMFC technology has a lifetime of about five years [26].
The study on the environmental impact assessment of PV rooftop panels in Europe was used to determine the global warming potential of PV panels [24]. Typical 4 kW PV systems in different European countries were considered. A total of 79 sites were covered in 26 countries. GWP ranged from 0.02 to 1.19 kgCO2eq/kWh. The lowest impacts were found in countries such as Iceland and Norway, while the highest were in Poland and Greece. The average GWP in the countries considered was 0.60 kgCO2eq/kWh. The lifetime of rooftop solar PV systems is 25 years [20].
In addition to cost, the environmental impact of Stirling engine systems depends on the fuel type. For the solar-powered system, a study on a grid-connected dish Stirling solar concentrator (33 kW) located on the Palermo University campus in Italy was chosen [25]. The resulting global warming potential is 30.15 kgCO2eq/MWh with system boundaries from cradle to gate. The key emission contributors were the electronic components (16%) and the steel used in the construction (37%). For the biomass-fueled Stirling engine system, an LCA study of four micro-scale (100 kW) cogeneration plants fueled by softwood forest residues was chosen [6]. This system had a capacity higher than the limit set in this study, but no suitable studies on this type of system were found. The system consisted of direct biomass combustion and a Stirling engine. The resulting GWP was 0.12 kgCO2eq/kWh. The distribution of heat and electricity had the most significant impact on the total life cycle emissions. Both systems used a Stirling engine, which has a lifetime estimate of 20 years [7].
3.2. TOPSIS
After the data were compiled, TOPSIS calculations were performed. The results are shown graphically in Figure 3. The analysis revealed that biomass-fueled Stirling engine has the highest relative closeness to the ideal solution, which makes it the best alternative. The rest of the systems showed significantly less satisfactory outcomes. The fuel cell solar system showed the poorest performance. The sequence between the best and worst systems can be predicted if the input data are examined. As can be seen in Table 2, the biomass-fueled Stirling engine system has the highest number of ideal values and no anti-ideals.
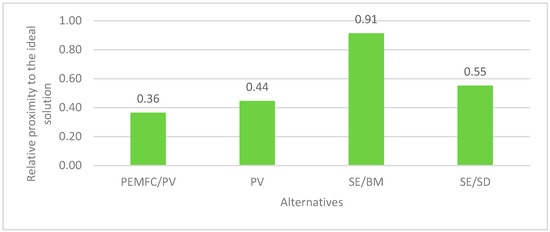
Figure 3.
Results from technique of order preference similarity to the ideal solution analysis.
3.3. Sensitivity Analysis
The sensitivity analysis shows that the biomass-fueled Stirling engine score remains relatively stable even when altering the criteria weights, except for the lifetime criterion, which shows a slight drop in score. See Figure 4 for details. Nonetheless, this system still appears as the best alternative. The analysis indicates that the biomass-fueled Stirling engine system is not sensitive to weight changes and would still be the best alternative if the criteria weights were not equal.
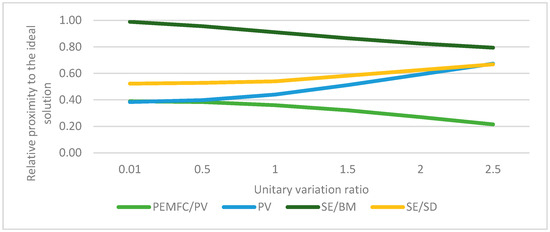
Figure 4.
Results of sensitivity analysis of lifetime criteria.
Other alternatives are more sensitive to weight changes. The relative proximity to the ideal solution and the distribution of the rankings changes noticeably as the criteria weights change. Reliability is the only criterion that maintains a constant order as the weight of the criterion changes, as shown in Figure 5.
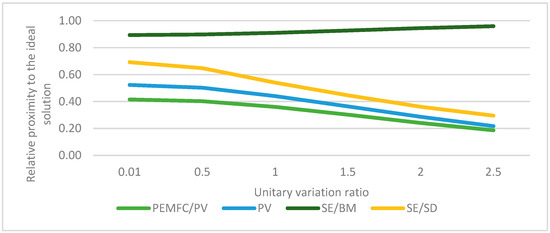
Figure 5.
Results of sensitivity analysis of reliability criteria.
In all cases where the criterion has a reduced impact, meaning a unitary variation ratio of 0.01, the solar-powered Stirling engine remains the second-best alternative. In such a case, PV and fuel cell systems swap places in the LCOE and lifetime criteria analysis, i.e., PV drops to last, and PEMFC/PV moves to third place. The results of the LCOE criterion analysis are shown in Figure 6.
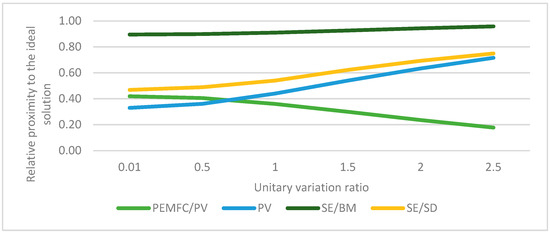
Figure 6.
Results of sensitivity analysis of levelized costs of energy criteria.
When the criterion is given a high impact (unitary variation ratio of 2.5), all alternatives except the biomass-fueled Stirling engine have a changing rank. The PEMFC/PV alternative improves from fourth to second place in the sensitivity analyses for the efficiency and GWP criteria. PV is ranked fourth for the same criteria. At a unitary variation ratio of 2.5, the solar powered Stirling engine comes in third place for the three analyzed criteria—efficiency, GWP, and lifetime.
4. Discussion
In the literature review, data for each energy system was summarized. Five criteria were selected for TOPSIS, considering environmental, economic, and technical aspects. It should be noted that in some cases, it was not possible to find MCDA matrix values that fully met the conditions of this study. However, these values were used to allow the criteria to be assessed quantitatively rather than qualitatively, which increases the reliability of the analysis results. The results show that the biomass-fueled Stirling engine system is the most favorable for household electricity generation (0.91). This is mainly because it is the cheapest, most reliable, and has a low environmental impact. The sensitivity analysis revealed that this system is not affected by weight changes and would remain the best alternative if the criteria weights were not the same.
TOPSIS was used in this study, although other MCDA methods were also applicable. Each method gives different results, and the ranking of alternatives may also differ [18]. The TOPSIS method was chosen because it has no consistency limitations, MS Excel can be used for calculations, and the input data can be both qualitative and quantitative [18]. An additional advantage is that the results range from 0 to 1, and the best alternative has the highest score so that the findings can be easily illustrated and understood. The results obtained by TOPSIS depend mainly on the criteria selected, the availability of data, and the chosen weight of the criteria. The reliability of the results is increased if the criteria are chosen appropriately and do not overlap, if the data collected are as precise as possible, and if the chosen weights of the criteria are validated and adjusted according to the aim of the analysis.
The reviewed research [9] suggests that the fuel cell is the best technological solution for small-scale heat and power generation, while the Stirling engine is more suitable for households because it is cheaper. Their study concludes that the fuel cell has the lowest environmental impact, but it takes into account direct emissions instead of whole life cycle environmental impact. The present study confirms that the Stirling engine is the best alternative for households. However, the fuel cell is the least favorable since it is the most expensive, has a short lifetime, and does not have the lowest environmental impact regarding life-cycle emissions.
When comparing the methodology of the reviewed study [9] with the present one, it is observed that in the present study, systems were selected for the MCDA instead of technologies. This decision allows the use of specific data rather than general descriptions or ranges of data, which in turn provides more accurate results for a specific system as opposed to a general technology assessment.
In this study, the number of criteria used was lower, but they were more comprehensive. For example, the reviewed study [9] looked at the direct emissions of the technology, but our analysis included a life-cycle assessment of environmental impacts. The same applies to costs: the reviewed study includes installation costs, while our study considers the unit cost of energy over the lifetime of the system.
In summary, the M. A. Khan et al. study [9] was used as a background for this study to obtain more detailed results on renewable electricity generation technologies from the perspective of an independent small system. These results can be used to improve existing information provided by governments and enterprises for the residential sector. It can also help policymakers to make decisions in the country’s transition to green energy. However, more in-depth research on the Stirling engine coupled with a biomass boiler is necessary before the study results can be used in practice, as this study uses data from different countries and for various system capacities. The data summarized in the study for each system, the results of the MCDA, and the sensitivity analysis are valuable for further research as they were previously not present in the scientific literature.
5. Conclusions
Transition to renewable energy in the EU will include small-scale household energy production solutions. Therefore, this study compared four renewable energy systems using MCDA: proton exchange membrane fuel cell with photovoltaic panels, photovoltaic panels, biomass-fueled Stirling engine, and solar-powered Stirling engine. The aim was to identify the most suitable energy system for household electricity generation in the EU, with production up to 50 kW.
A comparison of the systems using the TOPSIS method showed that the Stirling engine system powered by biomass is the best choice for household electricity generation. It is cost-effective, reliable, and environmentally friendly. These findings could be useful for governments and businesses to inform the private housing sector and promote the transition to renewable energy.
Author Contributions
Conceptualization, J.K., V.K. and D.B.; software, M.V.; validation, J.K., G.K., V.K. and D.B.; formal analysis, J.K. and M.V.; investigation, J.K. and M.V.; data curation, J.K. and M.V.; writing—original draft preparation, J.K., M.V. and G.K.; writing—review and editing, J.K., M.V. and G.K.; visualization, M.V.; supervision, J.K., V.K. and D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Latvian Council of Science project entitled “Alternative biomass knowledge for transition towards energy independence and climate targets (bioenergy Observatory)”, project No. lzp-2022/1-0414.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Abbreviations | Meaning |
| EU | European Union |
| GHG | greenhouse gas |
| GWP | global warming potential |
| LCA | life cycle analysis |
| LCOE | levelized cost of energy |
| MCDA | Multi-Criteria Decision Analysis |
| PEMFC | proton exchange membrane fuel cells |
| PEMFC/PV | proton exchange membrane fuel cell with photovoltaic panels |
| PV | photovoltaic panels |
| SE/BM | biomass-fueled Stirling engine |
| SE/SD | solar dish Stirling engine |
| TOPSIS | technique of order preference similarity to the ideal solution |
References
- Clean Energy for All Europeans. 2019. Available online: https://data.europa.eu/doi/10.2833/9937 (accessed on 16 October 2023).
- Knosala, K.; Kotzur, L.; Röben, F.T.C.; Stenzel, P.; Blum, L.; Robinius, M.; Stolten, D. Hybrid Hydrogen Home Storage for Decentralized Energy Autonomy. Int. J. Hydrogen Energy 2021, 46, 21748–21763. [Google Scholar] [CrossRef]
- Marocco, P.; Ferrero, D.; Lanzini, A.; Santarelli, M. The Role of Hydrogen in the Optimal Design of Off-Grid Hybrid Renewable Energy Systems. J. Energy Storage 2022, 46, 103893. [Google Scholar] [CrossRef]
- López-Castrillón, W.; Sepúlveda, H.H.; Mattar, C. Off-Grid Hybrid Electrical Generation Systems in Remote Communities: Trends and Characteristics in Sustainability Solutions. Sustainability 2021, 13, 5856. [Google Scholar] [CrossRef]
- Nižetić, S.; Tolj, I.; Papadopoulos, A.M. Hybrid Energy Fuel Cell Based System for Household Applications in a Mediterranean Climate. Energy Convers. Manag. 2015, 105, 1037–1045. [Google Scholar] [CrossRef]
- Ahmadi, L.; Kannangara, M.; Bensebaa, F. Cost-Effectiveness of Small Scale Biomass Supply Chain and Bioenergy Production Systems in Carbon Credit Markets: A Life Cycle Perspective. Sustain. Energy Technol. Assess. 2020, 37, 100627. [Google Scholar] [CrossRef]
- Ferreira, A.C.; Silva, J.; Teixeira, S.; Teixeira, J.C.; Nebra, S.A. Assessment of the Stirling Engine Performance Comparing Two Renewable Energy Sources: Solar Energy and Biomass. Renew. Energy 2020, 154, 581–597. [Google Scholar] [CrossRef]
- Budak, Y.; Devrim, Y. Comparative Study of PV/PEM Fuel Cell Hybrid Energy System Based on Methanol and Water Electrolysis. Energy Convers. Manag. 2019, 179, 46–57. [Google Scholar] [CrossRef]
- Khan, M.A.; Gohari Darabkhani, H. Technoeconomic Analysis and Risk Assessment of Deploying Micro-Combined Heat and Power (M-Chp) Systems for Domestic Applications. SSRN J. 2022. [Google Scholar] [CrossRef]
- Streimikiene, D.; Baležentis, T. Multi-Criteria Assessment of Small Scale CHP Technologies in Buildings. Renew. Sustain. Energy Rev. 2013, 26, 183–189. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.; Elsaid, K.; Wilberforce, T.; Kamil, M.; Sayed, E.T.; Olabi, A. Environmental Aspects of Fuel Cells: A Review. Sci. Total Environ. 2021, 752, 141803. [Google Scholar] [CrossRef]
- Zhu, S.; Yu, G.; Liang, K.; Dai, W.; Luo, E. A Review of Stirling-Engine-Based Combined Heat and Power Technology. Appl. Energy 2021, 294, 116965. [Google Scholar] [CrossRef]
- Salih, S.A.; Aljashaami, B.A.; Alwan, N.T.; Shcheklein, S.E.; Velkin, V.I.; Ali, O. Factors Affecting the Thermodynamic Performance of the Stirling Engines: A Review Study. IREME 2022, 16, 529–539. [Google Scholar] [CrossRef]
- Khezri, R.; Mahmoudi, A.; Aki, H. Optimal Planning of Solar Photovoltaic and Battery Storage Systems for Grid-Connected Residential Sector: Review, Challenges and New Perspectives. Renew. Sustain. Energy Rev. 2022, 153, 111763. [Google Scholar] [CrossRef]
- Stropnik, R.; Mlakar, N.; Lotrič, A.; Sekavčnik, M.; Mori, M. The Influence of Degradation Effects in Proton Exchange Membrane Fuel Cells on Life Cycle Assessment Modelling and Environmental Impact Indicators. Int. J. Hydrogen Energy 2022, 47, 24223–24241. [Google Scholar] [CrossRef]
- Abuelyamen, A.; Ben-Mansour, R. Energy Efficiency Comparison of Stirling Engine Types (α, β, and γ) Using Detailed CFD Modeling. Int. J. Therm. Sci. 2018, 132, 411–442. [Google Scholar] [CrossRef]
- Aldersey-Williams, J.; Rubert, T. Levelised Cost of Energy—A Theoretical Justification and Critical Assessment. Energy Policy 2019, 124, 169–179. [Google Scholar] [CrossRef]
- Zlaugotne, B.; Zihare, L.; Balode, L.; Kalnbalkite, A.; Khabdullin, A.; Blumberga, D. Multi-Criteria Decision Analysis Methods Comparison. Environ. Clim. Technol. 2020, 24, 454–471. [Google Scholar] [CrossRef]
- Teirumnieka, E.; Patel, N.; Laktuka, K.; Dolge, K.; Veidenbergs, I.; Blumberga, D. Sustainability dilemma of hemp utilization for energy production. Energy Nexus 2023, 11, 100213. [Google Scholar] [CrossRef]
- Final Report Cost of Energy (LCOE): Energy Costs, Taxes and the Impact of Government Interventions on Investments. 2020. Available online: https://energy.ec.europa.eu/system/files/2020-10/final_report_levelised_costs_0.pdf (accessed on 16 October 2023).
- Ceylan, C.; Devrim, Y. Design and Simulation of the PV/PEM Fuel Cell Based Hybrid Energy System Using MATLAB/Simulink for Greenhouse Application. Int. J. Hydrogen Energy 2021, 46, 22092–22106. [Google Scholar] [CrossRef]
- Future of Solar Photovoltaic: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects. 2019. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2019/Nov/IRENA_Future_of_Solar_PV_2019.pdf (accessed on 16 October 2023).
- Zhang, J.; Ling, B.; He, Y.; Zhu, Y.; Wang, Z. Life Cycle Assessment of Three Types of Hydrogen Production Methods Using Solar Energy. Int. J. Hydrogen Energy 2022, 47, 14158–14168. [Google Scholar] [CrossRef]
- Martinopoulos, G. Are Rooftop Photovoltaic Systems a Sustainable Solution for Europe? A Life Cycle Impact Assessment and Cost Analysis. Appl. Energy 2020, 257, 114035. [Google Scholar] [CrossRef]
- Backes, J.G.; D’Amico, A.; Pauliks, N.; Guarino, S.; Traverso, M.; Lo Brano, V. Life Cycle Sustainability Assessment of a Dish-Stirling Concentrating Solar Power Plant in the Mediterranean Area. Sustain. Energy Technol. Assess. 2021, 47, 101444. [Google Scholar] [CrossRef]
- Nagapurkar, P.; Smith, J.D. Techno-Economic Optimization and Environmental Life Cycle Assessment (LCA) of Microgrids Located in the US Using Genetic Algorithm. Energy Convers. Manag. 2019, 181, 272–291. [Google Scholar] [CrossRef]
- Ghenai, C.; Bettayeb, M. Optimized Design and Control of an off Grid Solar PV/Hydrogen Fuel Cell Power System for Green Buildings. IOP Conf. Ser. Earth Environ. Sci. 2017, 93, 012073. [Google Scholar] [CrossRef]
- Di Micco, S.; Romano, F.; Jannelli, E.; Perna, A.; Minutillo, M. Techno-Economic Analysis of a Multi-Energy System for the Co-Production of Green Hydrogen, Renewable Electricity and Heat. Int. J. Hydrogen Energy 2023, 48, 31457–31467. [Google Scholar] [CrossRef]
- Okundamiya, M.S. Integration of Photovoltaic and Hydrogen Fuel Cell System for Sustainable Energy Harvesting of a University ICT Infrastructure with an Irregular Electric Grid. Energy Convers. Manag. 2021, 250, 114928. [Google Scholar] [CrossRef]
- Praveenkumar, S.; Agyekum, E.B.; Ampah, J.D.; Afrane, S.; Velkin, V.I.; Mehmood, U.; Awosusi, A.A. Techno-Economic Optimization of PV System for Hydrogen Production and Electric Vehicle Charging Stations under Five Different Climatic Conditions in India. Int. J. Hydrogen Energy 2022, 47, 38087–38105. [Google Scholar] [CrossRef]
- Bartolucci, L.; Cordiner, S.; Mulone, V.; Pasquale, S. Fuel Cell Based Hybrid Renewable Energy Systems for Off-Grid Telecom Stations: Data Analysis and System Optimization. Appl. Energy 2019, 252, 113386. [Google Scholar] [CrossRef]
- Entezari, A.; Manizadeh, A.; Ahmadi, R. Energetical, Exergetical and Economical Optimization Analysis of Combined Power Generation System of Gas Turbine and Stirling Engine. Energy Convers. Manag. 2018, 159, 189–203. [Google Scholar] [CrossRef]
- Larchet, K.; Guédez, R.; Topel, M.; Gustavsson, L.; Machirant, A.; Hedlund, M.-L.; Laumert, B. Enhancing Economic Competiveness of Dish Stirling Technology through Production Volume and Localization: Case Study for Morocco. AIP Conf. Proc. 2017, 1850, 050002. [Google Scholar] [CrossRef]
- Shboul, B.; AL-Arfi, I.; Michailos, S.; Ingham, D.; AL-Zoubi, O.H.; Ma, L.; Hughes, K.; Pourkashanian, M. Design and Techno-Economic Assessment of a New Hybrid System of a Solar Dish Stirling Engine Instegrated with a Horizontal Axis Wind Turbine for Microgrid Power Generation. Energy Convers. Manag. 2021, 245, 114587. [Google Scholar] [CrossRef]
- Pawananont, K.; Leephakpreeda, T. Feasibility Analysis of Power Generation from Landfill Gas by Using Internal Combustion Engine, Organic Rankine Cycle and Stirling Engine of Pilot Experiments in Thailand. Energy Procedia 2017, 138, 575–579. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).