An Innovative Multi-Objective Rescheduling System for Mitigating Pandemic Spread in Aviation Networks
Abstract
1. Introduction
- (1)
- What is the risk of disease transmission on each flight?
- (2)
- How can the risk of infection be economically and effectively managed through flight adjustments?
2. Materials and Methods
2.1. Assumptions
- Irregular flights: Irregular flights refer to situations where aircraft experience failures or emergency changes, rendering the original flight plan temporarily infeasible.
- Flight adjustment actions: Depending on the duration of the irregularity, flights may be delayed or canceled. Short time intervals result in flight delays, while excessively long intervals lead to cancellations.
- Recovery: Flights return to their originally scheduled flight plan at the end of the recovery time interval.
- Rescheduling methods: Flight rescheduling can be achieved through aircraft exchange, flight delay, or flight cancellation. However, aircraft exchange is exceedingly rare in actual operations and is therefore excluded from the model.
- Aircraft types: Different aircraft types have varying seat capacities, affecting the execution of flight schedules.
- External factors: Changes in the original plan due to external factors, such as alterations in aircraft maintenance plans, are not considered during the recovery process.
- Crew conditions: It is assumed that the aircraft crew adheres to legal duty time regulations without fatigue or flight overruns, thereby not affecting flight operations.
- Infection dynamics: The number of infectious individuals at a study airport is proportionate to the cumulative reported cases at the airport over the preceding 14 days, and the proportion of flight movements between airports mirrors the movements of infectious persons between study areas.
- Time intervals: Determining the flight time interval in the space–time network is critical. Adequate time intervals aid in controlling airport crowding. Typically, domestic passengers are required to arrive at the airport one hour before departure, allowing for the setting of a one-hour flight time interval to disperse crowds.
- Flight execution: Each flight may only be executed once or canceled at most.
- Departure time: The actual departure time for each adjusted flight must not precede the originally planned departure time.
- Delay limit: Flight delay should not exceed the maximum allowable delay limit (not exceeding 4 h).
- Transit time: Due to the pandemic, the transit time between aircraft should be equal to or greater than one hour.
- Airport curfew: Compliance with airport curfew regulations is mandatory.
- Last flight destination: The last flight’s destination airport should remain consistent with the original plan.
2.2. Methodology
2.2.1. Variable Definition
2.2.2. Modeling
- The potential pandemic transmission cost
- 2.
- The flight delay cost
- 3.
- The flight cancellation cost
- 4.
- Passenger Transfer Perceived Value
- 5.
- Carbon emissions costs
2.2.3. Data Collection
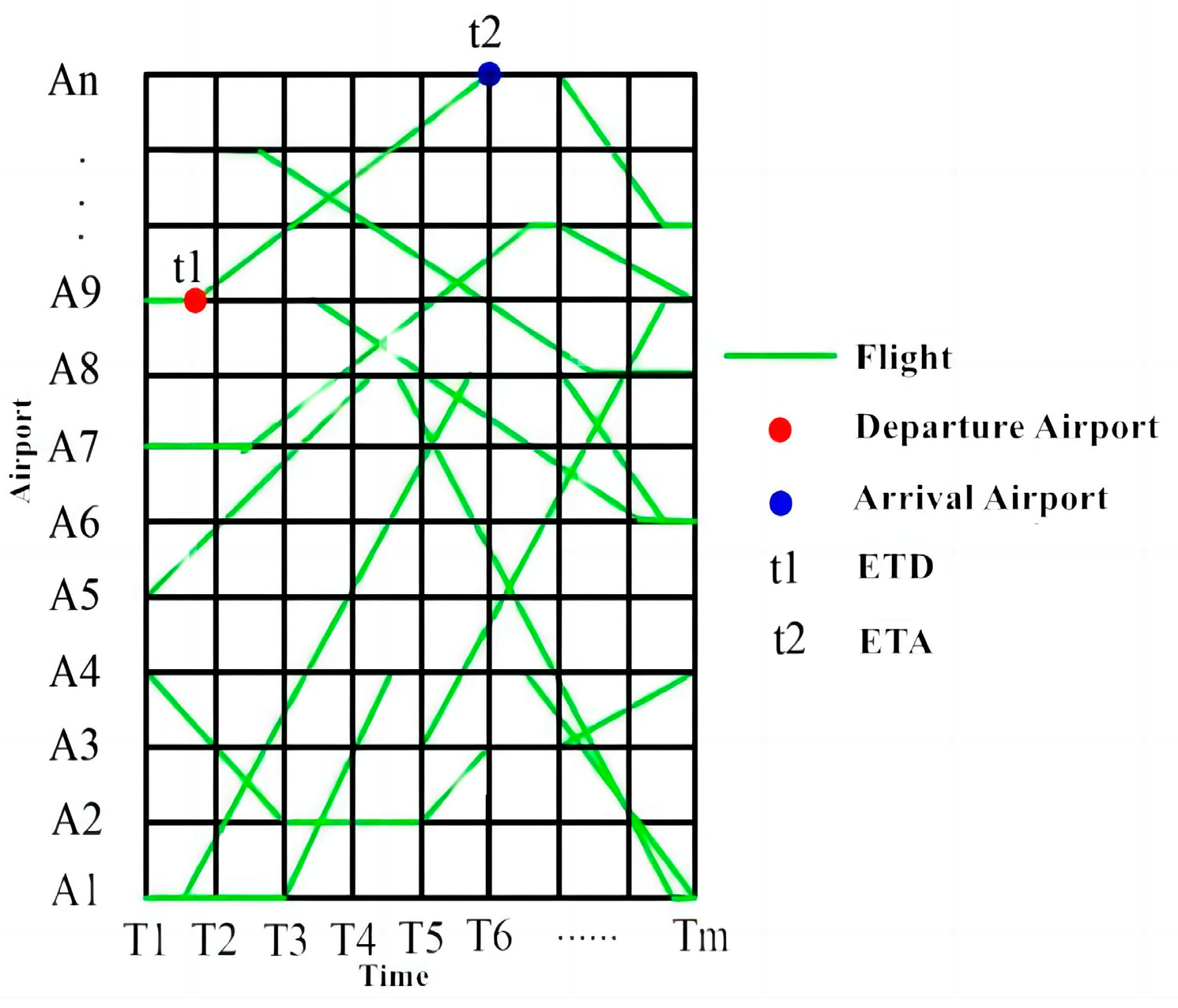
3. Space–Time Network Construction
4. Case Study
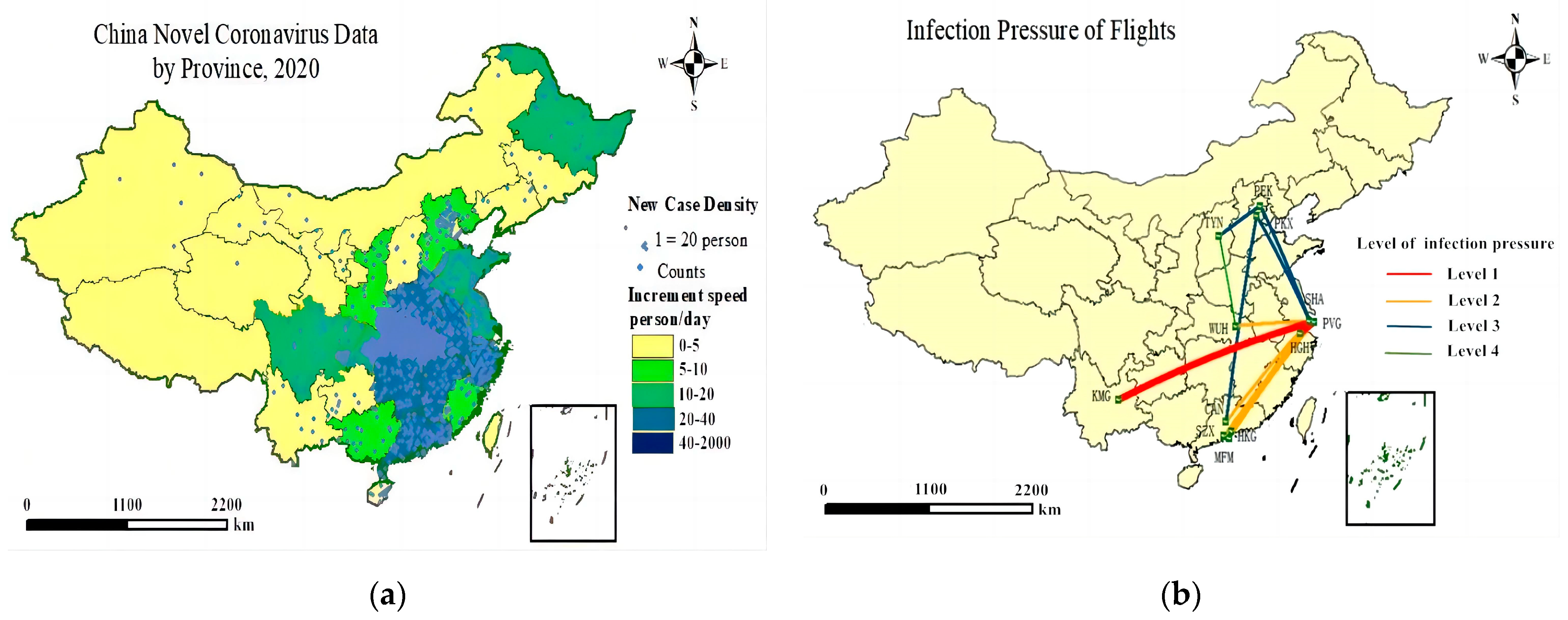
4.1. Infection Pressure
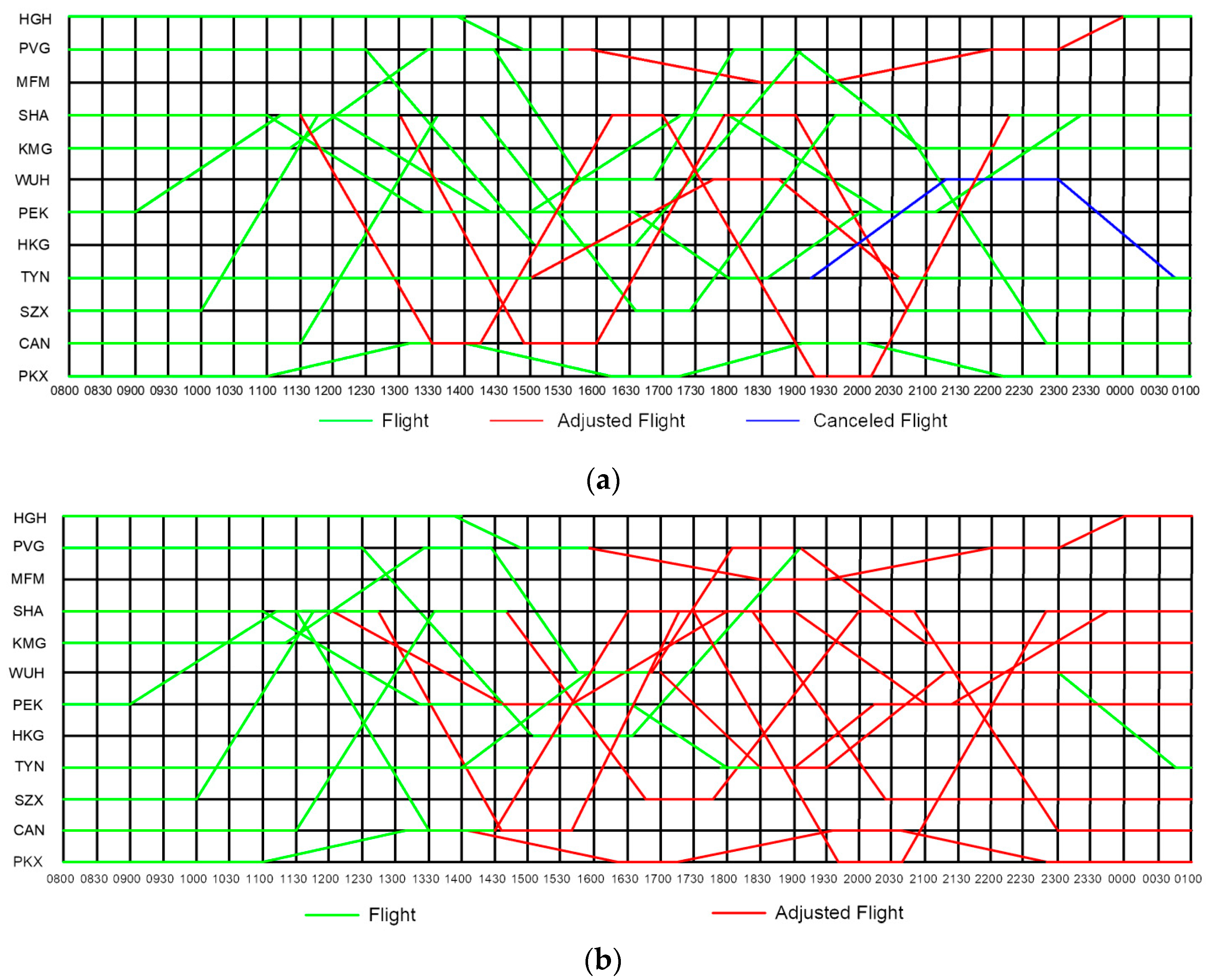
4.2. Results
4.3. Discussion
5. Conclusions
- This paper developed a mathematical model with the objectives of minimizing costs and reducing pandemic transmission. It leveraged real-time flight information to construct a discrete space–time network for managing irregular flights. An algorithm was devised to optimize the rescheduling of these irregular flights by utilizing the network. The algorithm effectively generated a set of viable flight recovery paths. Empirical testing confirmed the practicality and effectiveness of the model and algorithm.
- The case study shows that if stringent preventive and control measures are diligently implemented and prioritized in regions severely affected by a pandemic, the transmission pressure exerted by air travel within these areas may not exceed, and in some cases may even be lower than, that observed in less severely affected regions.
- Furthermore, when flights are scheduled with safe time intervals during a pandemic, it is more cost-effective to adjust flight delay times to prevent temporary airport closures than to cancel flights. This approach results in greater cost savings, even if it involves adjusting a larger number of flights compared to the alternative of canceling them.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
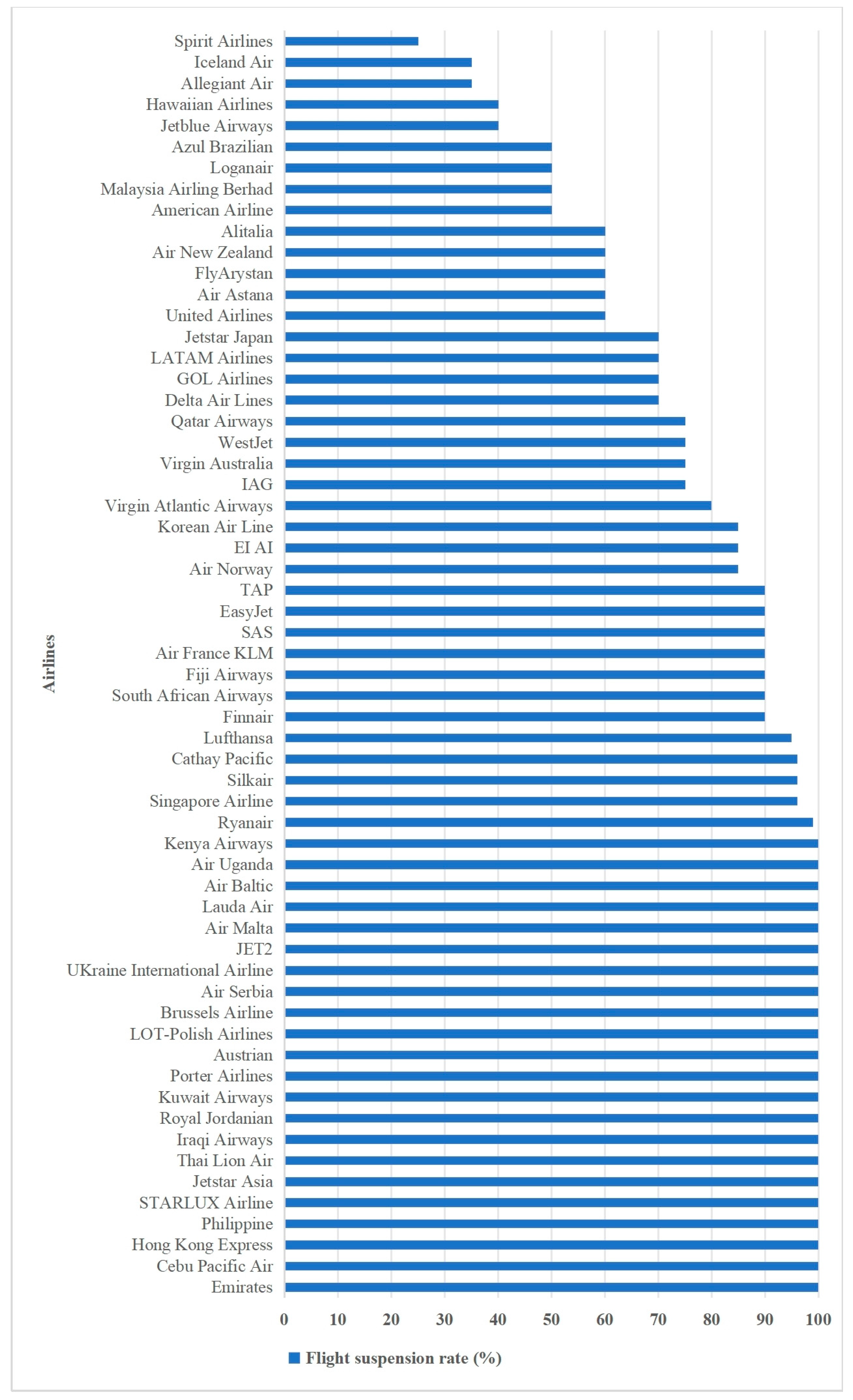
Appendix B
| Airport No. | Airport ID | Flight No. | Flight ID | Depart. | ETD | Arrival | ETA | Ticket/RMB | Passenger No. |
|---|---|---|---|---|---|---|---|---|---|
| 2153 | 1 | F828 | f11 | HGH | 1350 | PVG | 1450 | 709 | 241 |
| 2153 | 1 | F807 | f12 | PVG | 1540 | MFM | 1820 | 1081 | 241 |
| 2153 | 1 | F808 | f13 | MFM | 1910 | PVG | 2140 | 1013 | 241 |
| 2153 | 1 | F819 | f14 | PVG | 2240 | HGH | 2340 | 8269 | 241 |
| 2167 | 2 | F9182 | f21 | KMG | 1120 | PVG | 1325 | 683 | 127 |
| 2167 | 2 | F829 | f22 | PVG | 1425 | WUH | 1545 | 437 | 127 |
| 2167 | 2 | F830 | f23 | WUH | 1640 | PVG | 1810 | 492 | 127 |
| 2167 | 2 | F9449 | f24 | PVG | 1900 | KMG | 2050 | 711 | 127 |
| 2500 | 3 | F845 | f31 | PVG | 1230 | HKG | 1510 | 916 | 226 |
| 2500 | 3 | F846 | f32 | HKG | 1635 | PVG | 1910 | 888 | 226 |
| 2580 | 4 | F5107 | f41 | SHA | 1100 | PEK | 1320 | 1122 | 241 |
| 2580 | 4 | F5294 | f42 | PEK | 1635 | TYN | 1800 | 584 | 226 |
| 2580 | 4 | F5299 | f43 | TYN | 1835 | PEK | 2000 | 584 | 226 |
| 2580 | 4 | F5128 | f44 | PEK | 2105 | SHA | 2320 | 1100 | 241 |
| 2587 | 5 | F5166 | f51 | PEK | 900 | SHA | 1115 | 1122 | 241 |
| 2587 | 5 | F5109 | f52 | SHA | 1200 | PEK | 1425 | 1055 | 241 |
| 2587 | 5 | F5104 | f53 | PEK | 1500 | SHA | 1720 | 1493 | 241 |
| 2587 | 5 | F5128 | f54 | SHA | 1800 | PEK | 2025 | 1124 | 241 |
| 2588 | 6 | F2437 | f61 | TYN | 1400 | WUH | 1555 | 1047 | 127 |
| 2588 | 6 | F5400 | f62 | WUH | 1615 | TYN | 1750 | 656 | 127 |
| 2588 | 6 | F4112 | f63 | TYN | 1924 | WUH | 2120 | 518 | 127 |
| 2588 | 6 | F2438 | f64 | WUH | 2300 | TYN | 2440 | 1047 | 127 |
| 2145 | 7 | F2324 | f71 | SZX | 1000 | SHA | 1145 | 468 | 127 |
| 2145 | 7 | F2567 | f72 | SHA | 1235 | CAN | 1425 | 1049 | 127 |
| 2145 | 7 | F7788 | f73 | CAN | 1515 | SHA | 1705 | 794 | 127 |
| 2145 | 7 | F1324 | f74 | SHA | 1805 | SZX | 1950 | 468 | 127 |
| 2137 | 8 | F2476 | f81 | CAN | 1130 | SHA | 1335 | 434 | 241 |
| 2137 | 8 | F2019 | f82 | SHA | 1425 | SZX | 1635 | 352 | 241 |
| 2137 | 8 | F2020 | f83 | SZX | 1725 | SHA | 1935 | 352 | 241 |
| 2137 | 8 | F1284 | f84 | SHA | 2035 | CAN | 2240 | 434 | 241 |
| 2141 | 9 | F1105 | f91 | PKX | 1100 | CAN | 1310 | 359 | 226 |
| 2141 | 9 | F1385 | f92 | CAN | 1400 | PKX | 1615 | 536 | 226 |
| 2141 | 9 | F1107 | f93 | PKX | 1705 | CAN | 1915 | 492 | 226 |
| 2141 | 9 | F3231 | f94 | CAN | 2005 | PKX | 2215 | 462 | 226 |
| 2189 | 10 | F3234 | f101 | SHA | 1130 | CAN | 1330 | 476 | 241 |
| 2189 | 10 | F3432 | f102 | CAN | 1420 | SHA | 1625 | 625 | 241 |
| 2189 | 10 | F5432 | f103 | SHA | 1715 | PKX | 1920 | 497 | 241 |
| 2189 | 10 | F4321 | f104 | PKX | 2010 | SHA | 2225 | 417 | 241 |
References
- Duarte, C.C.; Cortiços, N.D. The Energy Efficiency Post-COVID-19 in China’s Office Buildings. Clean Technol. 2022, 4, 174–233. [Google Scholar] [CrossRef]
- Mack, E.A.; Agrawal, S.; Wang, S. The impacts of the COVID-19 pandemic on transportation employment: A comparative analysis. Transp. Res. Interdiscip. Perspect. 2021, 12, 100470. [Google Scholar] [CrossRef]
- Lai, C.S.; Jia, Y.; Dong, Z.; Wang, D.; Tao, Y.; Lai, Q.H.; Wong, R.T.K.; Zobaa, A.F.; Wu, R.; Lai, L.L. A Review of Technical Standards for Smart Cities. Clean Technol. 2020, 2, 290–310. [Google Scholar] [CrossRef]
- IATA. COVID-19 Updated Impact Assessment. 2020. Available online: https://www.iata.org/en/iata-repository/publications/economic-reports/third-impact-assessment/ (accessed on 28 December 2023).
- Du, W.B.; Zhang, M.Y.; Zhang, Y.; Cao, X.B.; Zhang, J. Delay causality network in air transport systems. Transp. Res. Part E Logist. Transp. Rev. 2018, 118, 466–476. [Google Scholar] [CrossRef]
- Wei, G.; Yu, G.; Song, M. Optimization model and algorithm for crew management during airline irregular operations. J. Comb. Optim. 1997, 1, 305–321. [Google Scholar] [CrossRef]
- Zellweger, A.G.; Donohue, G.L. Effects of Schedule Disruptions on the Economics of Airline Operations. In Air Transportation Systems Engineering; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2015. [Google Scholar]
- Kohl, N.; Larsen, A.; Larsen, J.; Ross, A.; Tiourine, S. Airline disruption management—Perspectives, experiences and outlook—ScienceDirect. J. Air Transp. Manag. 2007, 13, 149–162. [Google Scholar] [CrossRef]
- Abdelghany, K.F.; Abdelghany, A.F.; Ekollu, G. An integrated decision support tool for airlines schedule recovery during irregular operations. Eur. J. Oper. Res. 2008, 185, 825–848. [Google Scholar] [CrossRef]
- Abdi, M.R.; Sharma, S. Information system for flight disruption management. Int. J. Inf. Manag. 2008, 28, 136–144. [Google Scholar] [CrossRef]
- Li, X.; Le, M. Multi objective aircraft and passenger recovery stage by stage heuristic algorithm. Comput. Appl. Res. 2014, 31, 2270–2274. [Google Scholar]
- Le, M.; Li, X. Integrated recovery model of aircraft and passenger flow. Ind. Eng. 2013, 16, 113–119. [Google Scholar]
- Wang, Q.; Yany, X.-S. DEA Model for Analysis of Domestic Three Major Airport Groups Efficiency. Aeronaut. Comput. Tech. 2017, 47, 45–49. [Google Scholar]
- Zhang, D.T.; Yang, K. Deterministic analysis of threshold value of control load. Command Inf. Syst. Technol. 2016, 7, 47–50. [Google Scholar]
- Zhou, H.; Zhang, S. Study on the Service Recovery Quality of Flight Delay by the Synthetic Fuzzy Evaluation. Sci. Technol. Manag. Res. 2010, 30, 66–70. [Google Scholar]
- Mou, D.; Zhao, W. An Irregular Flight Scheduling Model and Algorithm under the Uncertainty Theory. J. Appl. Math. 2013, 2013, 361926. [Google Scholar] [CrossRef]
- Holme, P.; Saramaki, J. Temporal networks. Phys. Rep. 2011, 519, 97–125. [Google Scholar] [CrossRef]
- Lambiotte, R.; Tabourier, L.; Delvenne, J.C. Burstiness and spreading on temporal networks. Phys. Condens. Matter 2013, 86, 320. [Google Scholar] [CrossRef]
- Perotti, J.I.; Jo, H.H.; Holme, P.; Saramäki, J. Temporal network sparsity and the slowing down of spreading. arXiv 2014, arXiv:1411.5553. [Google Scholar]
- Casteigts, A.; Flocchini, P.; Quattrociocchi, W.; Santoro, N. Time-varying graphs and dynamic networks. Int. J. Parallel Emergent Distrib. Syst. 2010, 27, 346–359. [Google Scholar]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Grassly, N.C.; Fraser, C. Mathematical models of infectious disease transmission. Nat. Rev. Microbiol. 2008, 6, 477–487. [Google Scholar] [CrossRef]
- Viboud, C.; Bjørnstad, O.N.; Smith, D.L.; Simonsen, L.; Miller, M.A.; Grenfell, B.T. Synchrony, Waves, and Spatial Hierarchies in the Spread of Influenza. Science 2006, 312, 447–451. [Google Scholar] [CrossRef]
- Eggo, R.M.; Cauchemez, S.; Ferguson, N.M. Spatial dynamics of the 1918 influenza pandemic in England, Wales and the United States. J. R. Soc. Interface 2011, 8, 233–243. [Google Scholar] [CrossRef] [PubMed]
- Grenfell, B.T.; Bjornstad, O.N.; Kappey, J. Travelling waves and spatial hierarchies in measles pandemics. Nature 2001, 414, 716–723. [Google Scholar] [CrossRef] [PubMed]
- Bharti, N.; Tatem, A.J.; Ferrari, M.J.; Grais, R.F.; Djibo, A.; Grenfell, B.T. Explaining Seasonal Fluctuations of Measles in Niger Using Nighttime Lights Imagery. Science 2011, 334, 1424. [Google Scholar] [CrossRef]
- Crepey, P.; Barthelemy, M. Detecting robust patterns in the spread of pandemics: A case study of influenza in the United States and France. Am. J. Epidemiol. 2007, 166, 1244–1251. [Google Scholar] [CrossRef]
- Spoof-Tuomi, K.; Niemi, S. Environmental and Economic Evaluation of Fuel Choices for Short Sea Shipping. Clean Technol. 2020, 2, 34–52. [Google Scholar] [CrossRef]
- Bengtsson, L.; Gaudart, J.; Lu, X.; Moore, S.; Wetter, E.; Sallah, K.; Rebaudet, S.; Piarroux, R. Using mobile phone data to predict the spatial spread of cholera. Sci. Rep. 2014, 5, 8923. [Google Scholar] [CrossRef]
- Dou, F.; Jia, L.; Jie, X.U.; Kang, Y. Research on Train Dispatching Model Based on the Passenger Flow during Holidays. In Proceedings of the International Symposium on Innovation and Sustainability of Modern Railway, School of Traffic and Transportation, Beijing, China, 20 September 2012; Beijing Jiaotong University: Beijing, China; State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University: Beijing, China, 2012. [Google Scholar]
- ICAO. ICAO Carbon Emissions Calculator Methodology Version 11; ICAO: Montreal, QC, Canada, 2018. [Google Scholar]
- ICAO. Annex 16 to the Convention on International Civil Aviation—Environmental Protection—Volume II: Aircraft Engine Emissions; ICAO: Montreal, QC, Canada, 2008. [Google Scholar]

| Variable | Definition |
|---|---|
| A set of flights in a normal flight schedule | |
| The flight, | |
| A set of aircraft, | |
| All airports involved in the interrupt recovery decision | |
| The airport, | |
| A set of feasible paths | |
| One feasible path, | |
| The number of aircraft required to stay at the airport during normal operation period | |
| Actual time of departure | |
| Estimated time of departure | |
| , otherwise | |
| flight schedule terminated at airport S, otherwise | |
| The delaying costs of airplane at airport | |
| The churn rate of passengers caused by the flight’s delay | |
| The churn rate of passengers caused by the flight’s cancellation | |
| The ticket price of passenger on flight at time ; represents the passengers of first class, business class, and economic class separately | |
| The average daily proportion of flight volume relocating from study area to , | |
| The infectious pressure sustained by each airport during the period from 14 days () after the disease onset of the first case | |
| The number of reported cases in airport at time | |
| The operating expense of flight , including gas cost and flight-related expenses | |
| The carbon emissions during the LTO phase (kg); = 1, 2, 3, 4 corresponds to the four operational phases of takeoff, climb, approach, and taxi | |
| The flight duration of flight during phase (s) | |
| The fuel flow rate during phase i for flight (kg/s) | |
| The number of engines | |
| The carbon emission factor for aviation kerosene, generally established at 3.157 kg CO2/kg | |
| The carbon emissions of the aircraft during the CCD phase (kg) | |
| The duration of the aircraft’s operation during the CCD phase (s) | |
| The fuel flow rate of the aircraft during the CCD phase (kg/s) | |
| The extra waiting time of passengers at the airport | |
| The actual arrival time at the airport | |
| The actual check-in time when passengers transfer at airport | |
| The maximum waiting time that passengers can accept at airport | |
| The actual waiting time of passengers at airport | |
| The number of passengers transferred to the airport | |
| The risk preference. The values range between 0 and 1, which are determined by the sensitivity to the waiting time of transit passengers | |
| The aversion coefficients. The values range between 0 and 1, which are determined by the sensitivity to the waiting time of transit passengers | |
| The sensitive coefficient to the cost loss caused by passenger transit waiting | |
| flight has been canceled, otherwise | |
| flight is operating normally, otherwise | |
| delay cost, delay time , otherwise , where | |
| passenger perceived value, , otherwise | |
| the carbon emissions of the aircraft during one complete takeoff and landing cycle (kg), , otherwise | |
| infectious pressure, flight has potential infectious pressure, otherwise |
| Data Type | Symbol | Definition |
|---|---|---|
| Airport data | Airport_name | Airport name |
| Curfew_time | Airport curfew time | |
| Close_starttime, Close_endtime | Airport closing time. Due to the pandemic situation, weather, or air traffic control, the time that the airport temporarily closed | |
| Pandemic_no. | The number of outbreaks in the city where the airport is located | |
| Flight data | Flight_no | Flight number |
| Depart_airport | Departure airport | |
| Depart_time | Planned departure time | |
| Arrive_airport | Arrival airport | |
| Arrive_time | Planned arrival time | |
| Passenger_no. | Number of passengers | |
| Ticket_price | Airfare | |
| Other data | Delay_cost | Flight delay cost |
| Cancel_cost | Flight cancellation cost | |
| Retention_cost | Passenger detention cost | |
| Recovery_starttime, Recovery_endtime | Recovery interval | |
| MCT | Minimum connection time |
| Algorithm: Network transformation pseudo-code |
|---|
| input: T = original flight schedule, II = reschedule discretization plan |
| output: N = space-time network, A = ordered list of space-time node |
| 1: for each airport do |
| 2: for each time segment in reschedule period do |
| Place space-time mode i at beginning of time segment |
| i = n |
| 3: end for |
| 4: end for |
| 5: let A = { } |
| 6: for each space-time mode i do |
| If mark (i) < n then place mode in A |
| 7: end for |
| 8: end for |
| Airport Name | City | Infection Pressure |
|---|---|---|
| HGH | Hangzhou | 1316.32 |
| PVG | Shanghai | 2650.05 |
| MFM | Macau | 597.5 |
| KMG | Kunming | 910.72 |
| WUH | Wuhan | 31.57 |
| HKG | Hong Kong | 84.24 |
| SHA | Shanghai | 1459.77 |
| PEK | Beijing | 272.75 |
| TYN | Taiyuan | 1379.47 |
| SZX | Shenzhen | 1300.57 |
| CAN | Guangzhou | 1518.41 |
| PKX | Beijing | 70.96 |
| Measures | Traditional Method | Proposed Method |
|---|---|---|
| No. of delayed flights | 12 | 24 |
| Total delay (min) | 439 | 495 |
| No. of canceled flights | 2 | 0 |
| Total delay cost (RMB) | 13,170 | 14,850 |
| Total flight cancellation cost (RMB) | 198,755 | 0 |
| Total reduced infection pressure (after adjusting the flight) (RMB) | 26,139.02 | 56,131.55 |
| Total cost (RMB) | 238,064.02 | 70,981.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Wang, Y.; Jiang, X.; Lai, C.S. An Innovative Multi-Objective Rescheduling System for Mitigating Pandemic Spread in Aviation Networks. Clean Technol. 2024, 6, 77-92. https://doi.org/10.3390/cleantechnol6010006
Yuan Y, Wang Y, Jiang X, Lai CS. An Innovative Multi-Objective Rescheduling System for Mitigating Pandemic Spread in Aviation Networks. Clean Technologies. 2024; 6(1):77-92. https://doi.org/10.3390/cleantechnol6010006
Chicago/Turabian StyleYuan, Yujie, Yantao Wang, Xiushan Jiang, and Chun Sing Lai. 2024. "An Innovative Multi-Objective Rescheduling System for Mitigating Pandemic Spread in Aviation Networks" Clean Technologies 6, no. 1: 77-92. https://doi.org/10.3390/cleantechnol6010006
APA StyleYuan, Y., Wang, Y., Jiang, X., & Lai, C. S. (2024). An Innovative Multi-Objective Rescheduling System for Mitigating Pandemic Spread in Aviation Networks. Clean Technologies, 6(1), 77-92. https://doi.org/10.3390/cleantechnol6010006








