Improvement of Onsite Wastewater Systems Performance: Experimental and Numerical Investigation
Abstract
:1. Introduction
2. Materials and Methods
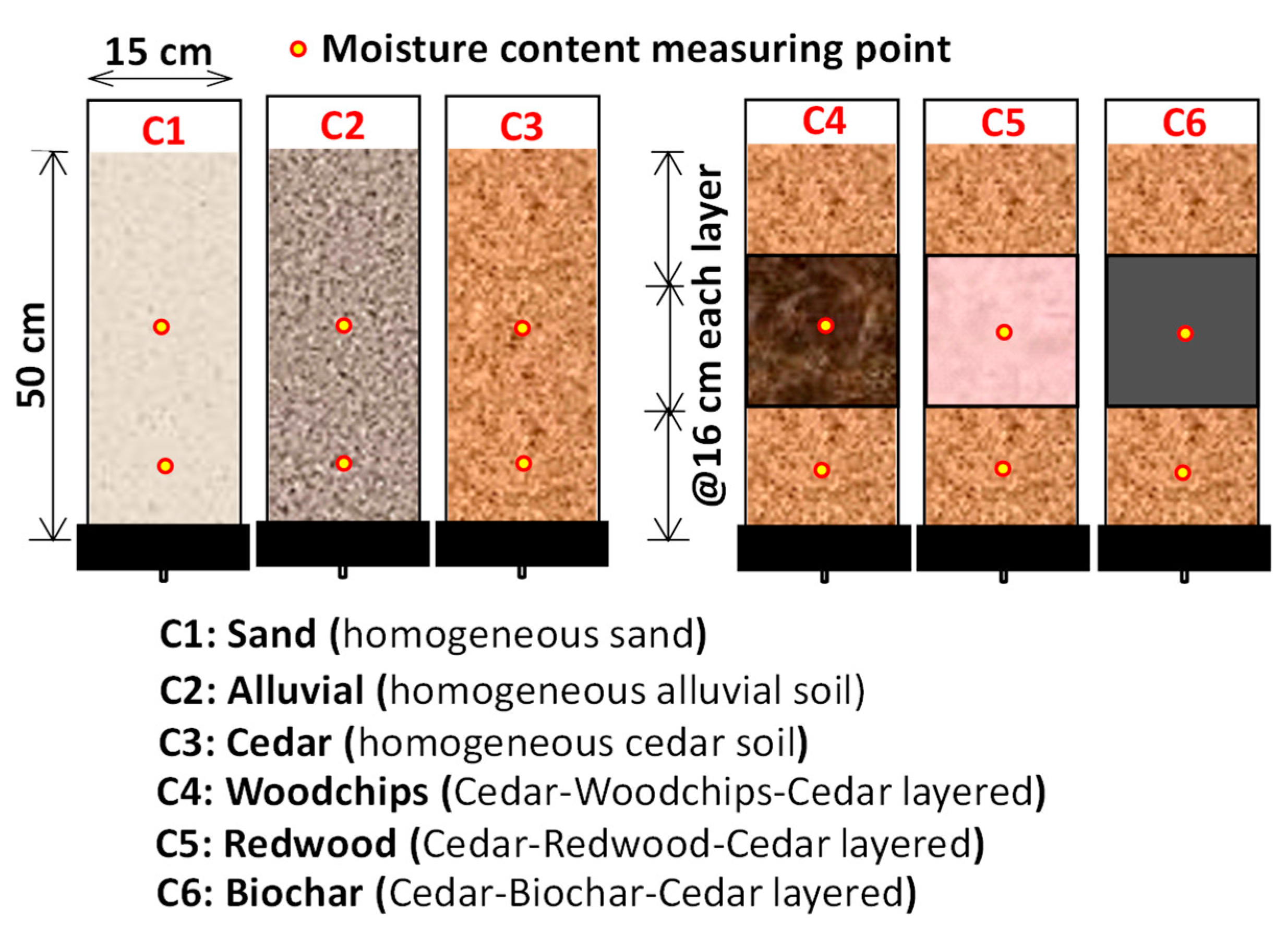
2.1. Experimental Setup
2.2. Numerical Modeling
2.2.1. Subsubsection
2.2.2. Governing Equations for Solute Transport
2.2.3. Model Setup
2.2.4. Parameter Sensitivity Analysis
2.3. Scenario Analysis
3. Results and Discussion
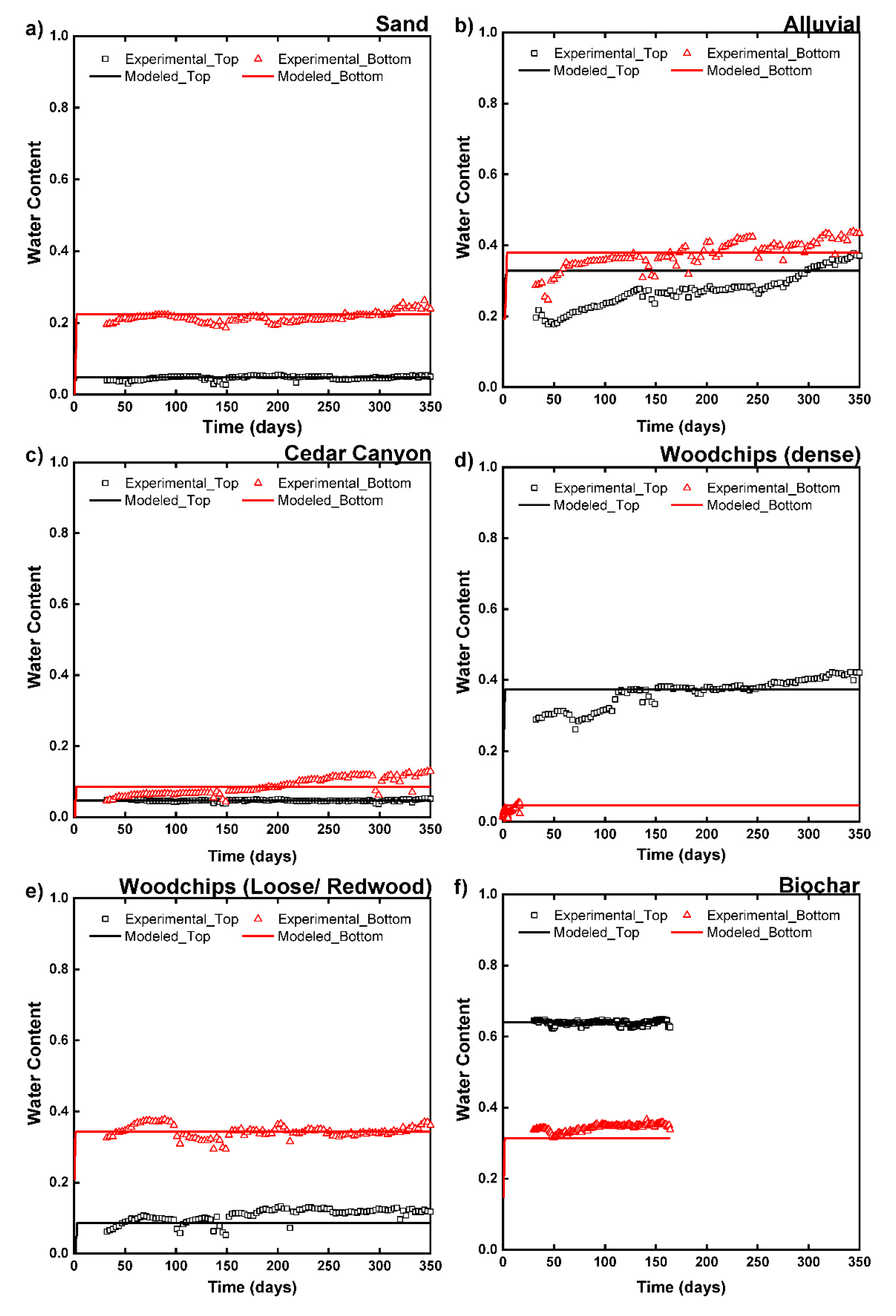
3.1. Parameterization of Hydraulic Parameters
3.2. Nitrate Parameter Calibration Using Observed Nitrate Concentration
3.3. Sensitivity Analysis
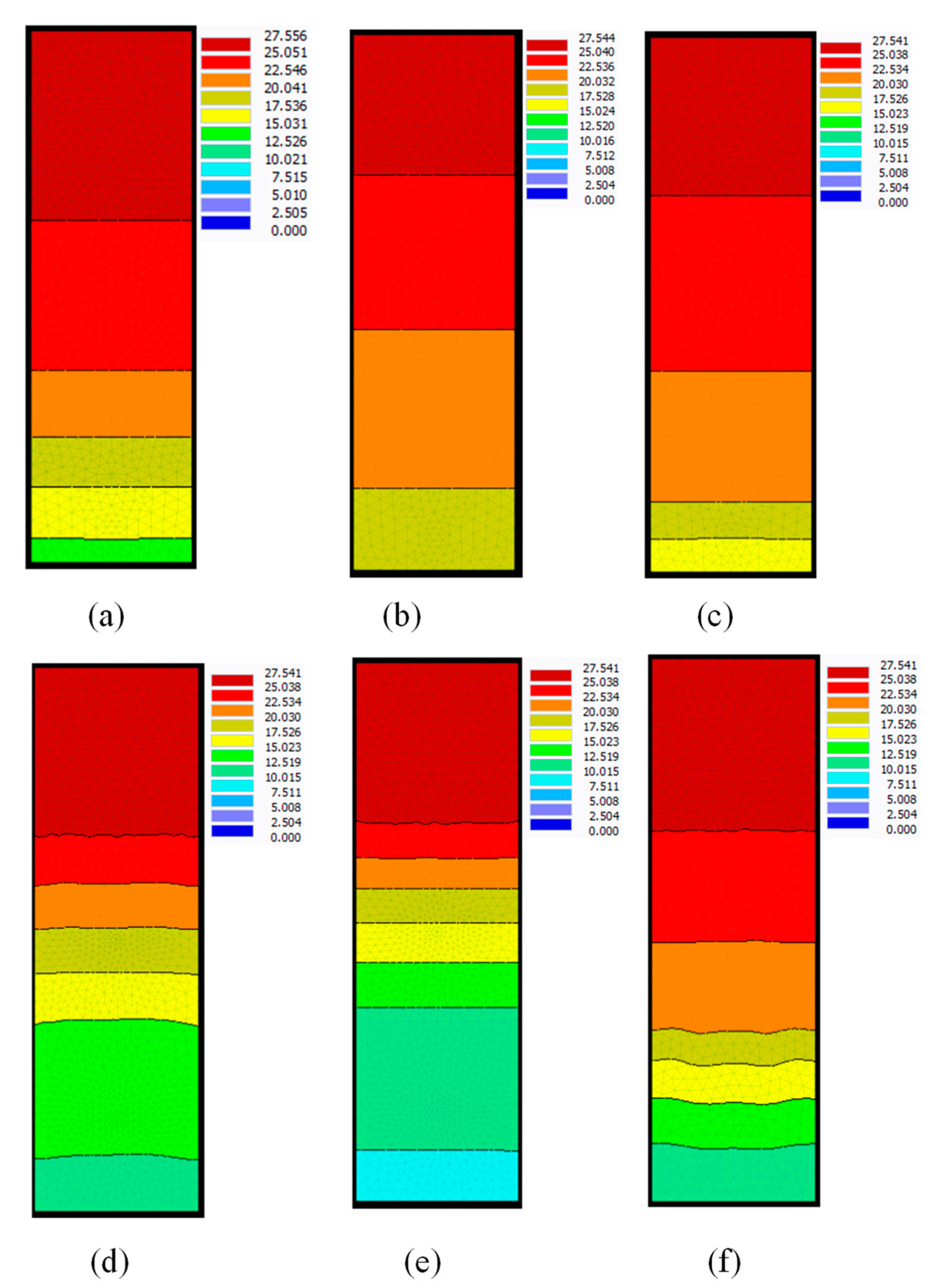
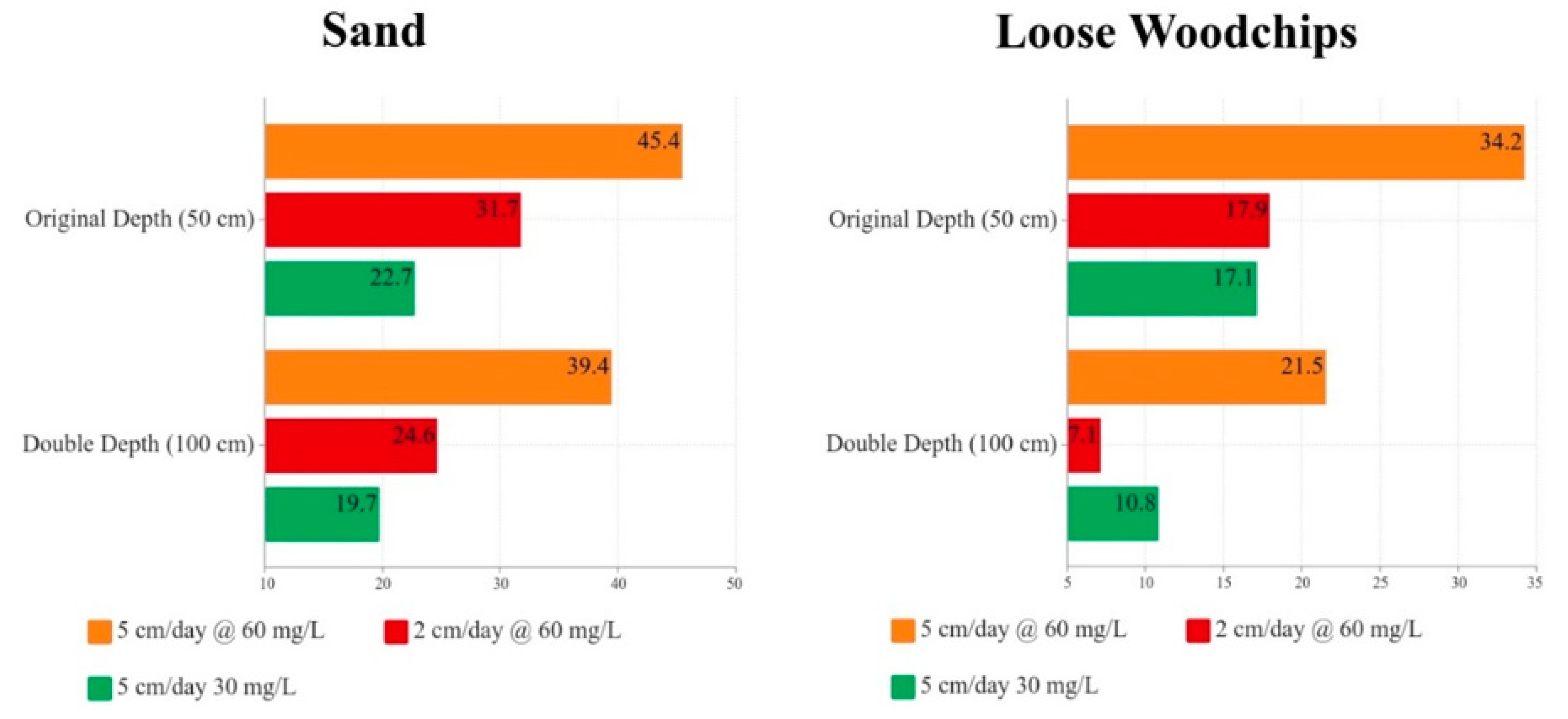
3.4. Scenario Analysis Modeling
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bdour, A. Perspectives on sustainable wastewater treatment technologies and reuse options in the urban areas of the Mediterranean region. In Proceedings of the World Environmental and Water Resources Congress 2007: Restoring Our Natural Habitat, Tampa, FL, USA, 15–19 May 2007; pp. 1–15. [Google Scholar]
- Geza, M.; McCray, J.E. Modeling the effect of population growth on stream nutrient concentration in turkey creek watershed using the WARMF model. In Proceedings of the Eleventh Individual and Small Community Sewage Systems Conference, Warwick, RI, USA, 20–24 October 2007; p. 9. [Google Scholar]
- Hojjati-Najafabadi, A.; Mansoorianfar, M.; Liang, T.; Shahin, K.; Karimi-Maleh, H. A review on magnetic sensors for monitoring of hazardous pollutants in water resources. Sci. Total Environ. 2022, 824, 153844. [Google Scholar] [CrossRef] [PubMed]
- Siegrist, R.L. Advancing the science and engineering of onsite wastewater systems. In Proceedings of the On-Site Wastewater Treatment, Armidale, Australia, 25–27 September 2001; p. 1. [Google Scholar]
- Van Cuyk, S.; Siegrist, R.; Logan, A.; Masson, S.; Fischer, E.; Figueroa, L. Hydraulic and purification behaviors and their interactions during wastewater treatment in soil infiltration systems. Water Res. 2001, 35, 953–964. [Google Scholar] [CrossRef]
- Tchobanoglous, G.; Burton, F.L.; Stensel, H. Solution Manual for Use With Wastewater Engineering: Treatment and Reuse; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Robbins, D.M.; Ligon, G.C. How to Design Wastewater Systems for Local Conditions in Developing Countries; IWA Publishing: London, UK, 2014. [Google Scholar]
- Akter, A. Groundwater Recharge. In Rainwater Harvesting—Building a Water Smart City; Springer: Berlin/Heidelberg, Germany, 2022; pp. 191–214. [Google Scholar]
- Beach, D.N.; McCray, J.E.; Lowe, K.S.; Siegrist, R.L. Temporal changes in hydraulic conductivity of sand porous media biofilters during wastewater infiltration due to biomat formation. J. Hydrol. 2005, 311, 230–243. [Google Scholar] [CrossRef]
- Geza, M.; Lowe, K.S.; Huntzinger, D.N.; McCray, J.E. New conceptual model for soil treatment units: Formation of multiple hydraulic zones during unsaturated wastewater infiltration. J. Environ. Qual. 2013, 42, 1196–1204. [Google Scholar] [CrossRef] [PubMed]
- Bradshaw, J.K.; Radcliffe, D.E.; Šimůnek, J.; Wunsch, A.; McCray, J.E. Nitrogen fate and transport in a conventional onsite wastewater treatment system installed in a clay soil: A nitrogen chain model. Vadose Zone J. 2013, 12, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Radcliffe, D.; Amador, J.; Atoyan, J.; Boving, T.; Kalen, D.; Loomis, G. State of the Science: Review of Quantitative Tools to Determine Wastewater Soil Treatment Unit Performance; The Water Research Foundation: Denver, CO, USA, 2009. [Google Scholar]
- Hasan, M.S.; Vasquez, R.; Geza, M. Application of Biochar in Stormwater Treatment: Experimental and Modeling Investigation. Processes 2021, 9, 860. [Google Scholar] [CrossRef]
- Hasan, M.S.; Geza, M.; Vasquez, R.; Chilkoor, G.; Gadhamshetty, V. Enhanced Heavy Metal Removal from Synthetic Stormwater Using Nanoscale Zerovalent Iron–Modified Biochar. Water Air Soil Pollut. 2020, 231, 220. [Google Scholar] [CrossRef]
- Kabir, T.; Hasan, M.S.; Das, P. Applicability of Activated Carbon Filtration in Surface Water Treatment. Asian J. Innov. Res. Sci. Eng. Technol. 2018, 1. Available online: http://engineeringjournal.info/index.php/AJIRSET/article/view/28 (accessed on 9 May 2022).
- Akber, M.; Islam, M.; Dutta, M.; Billah, S.M. Nitrate contamination of water in dug wells and associated health risks of rural communities in southwest Bangladesh. Environ. Monit. Assess. 2020, 192, 163. [Google Scholar] [CrossRef]
- Ramalingam, G.; Nagapandiselvi, P.; Priya, A.; Rajendran, S. A review of graphene-based semiconductors for photocatalytic degradation of pollutants in wastewater. Chemosphere 2022, 300, 134391. [Google Scholar] [CrossRef]
- Geza, M.; Lowe, K.S.; McCray, J.E. STUMOD—A tool for predicting fate and transport of nitrogen in soil treatment units. Environ. Model. Assess. 2014, 19, 243–256. [Google Scholar] [CrossRef]
- Kabuba, J.; Lephallo, J.; Rutto, H. Comparison of various technologies used to eliminate nitrogen from wastewater: A review. J. Water Process Eng. 2022, 48, 102885. [Google Scholar] [CrossRef]
- McCray, J.E.; Christopherson, S.H. On-site wastewater systems and interactions with the environment. J. Hydrol. Eng. 2008, 13, 653–654. [Google Scholar] [CrossRef]
- Heinrich, C.J. Modeling Watershed-Scale Impacts of On-Site Wastewater Systems on Nitrogen Loadings in the Black Hills. Master’s Thesis, South Dakota School of Mines and Technology, Rapid City, SD, USA, 2021. [Google Scholar]
- Trapp, J. Experimental and Numerical Investigation and Improvement of Performance of Onsite Wastewater Systems. Master’s Thesis, South Dakota School of Mines and Technology, Rapid City, SD, USA, 2021. [Google Scholar]
- Waller, R.M. Ground Water and the Rural Homeowner; US Department of the Interior, US Geological Survey, U.S. Government Printing Office: Washington, DC, USA, 1994.
- Rahn, P.H. Sickness Caused by Septic Disposal Systems in the Black Hills. In Proceedings of the South Dakota Academy of Science, Rapid City, SD, USA, 24 July 2011. [Google Scholar]
- Long, A.J.; Sawyer, J.F.; Putnam, L.D. Environmental tracers as indicators of karst conduits in groundwater in South Dakota, USA. Hydrogeol. J. 2008, 16, 263–280. [Google Scholar] [CrossRef]
- Boulding, J.R.; Ginn, J.S. Practical Handbook of Soil, Vadose Zone, and Ground-Water Contamination: Assessment, Prevention, and Remediation; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Šimůnek, J.; van Genuchten, M.; Sejna, M. HYDRUS Technical Manual: The HYDRUS Software Package for Simulating the Two- and Three-Dimensional Movement of Water, Heat and Multiple Solutes in Variably-Saturated Porous Media; Technical Manual Version; PC Progress: Prague, Czech Republic, 2012; p. 2. [Google Scholar]
- Hasan, M.S.; Geza, M.; Petersen, J.B.; Gadhamshetty, V. Graphene oxide transport and retention in biochar media. Chemosphere 2021, 264, 128397. [Google Scholar] [CrossRef] [PubMed]
- Geza, M.; Deb, S.K.; Leinauer, B.; Stanek, S.; Sevostianova, E.; Serena, M. Modeling NO3–N leaching during establishment of turfgrasses irrigated with tailored reclaimed water. Vadose Zone J. 2021, 20, e20112. [Google Scholar] [CrossRef]
- Hasan, M.S.; Dong, J.; Gadhamshetty, V.; Geza, M. Modeling graphene oxide transport and retention in biochar. J. Contam. Hydrol. 2022, 248, 104014. [Google Scholar] [CrossRef]
- Rudaz, A.O.; Davidson, E.A.; Firestone, M.K. Sources of nitrous oxide production following wetting of dry soil. FEMS Microbiol. Lett. 1991, 85, 117–124. [Google Scholar] [CrossRef] [Green Version]
- Peters, R.W.; Walker, T.J.; Ku, Y.; Berdanier, B.; Chang, T.-K.; Freund, D. Physical and chemical methods. J. Water Pollut. Control Fed. 1983, 55, 599–612. [Google Scholar]
- Simunek, J.; Van Genuchten, M.T. Using the HYDRUS-1D and HYDRUS-2D codes for estimating unsaturated soil hydraulic and solute transport parameters. In Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media; U.S. Salinity Laboratory, Agricultural Research Service, U.S. Department of Agriculture: Riverside, CA, USA, 1999; Volume 1, pp. 1523–1538. [Google Scholar]
- Ghane, E.; Feyereisen, G.W.; Rosen, C.J. Non-linear hydraulic properties of woodchips necessary to design denitrification beds. J. Hydrol. 2016, 542, 463–473. [Google Scholar] [CrossRef]
- Heath, R.C. Basic Ground-Water Hydrology; US Department of the Interior, US Geological Survey: Reston, VA, USA, 1998; Volume 2220.
- Kouanda, A.; Hua, G. Determination of nitrate removal kinetics model parameters in woodchip bioreactors. Water Res. 2021, 195, 116974. [Google Scholar] [CrossRef] [PubMed]
- Hoover, N.L.; Bhandari, A.; Soupir, M.L.; Moorman, T.B. Woodchip denitrification bioreactors: Impact of temperature and hydraulic retention time on nitrate removal. J. Environ. Qual. 2016, 45, 803–812. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maxwell, B.M.; Birgand, F.; Schipper, L.A.; Christianson, L.E.; Tian, S.; Helmers, M.J.; Williams, D.J.; Chescheir, G.M.; Youssef, M.A. Drying–rewetting cycles affect nitrate removal rates in woodchip bioreactors. J. Environ. Qual. 2019, 48, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Gao, B.; Yao, Y.; Xue, Y.; Inyang, M. Synthesis of porous MgO-biochar nanocomposites for removal of phosphate and nitrate from aqueous solutions. Chem. Eng. J. 2012, 210, 26–32. [Google Scholar] [CrossRef]
- Alagha, O.; Manzar, M.S.; Zubair, M.; Anil, I.; Mu’azu, N.D.; Qureshi, A. Comparative adsorptive removal of phosphate and nitrate from wastewater using biochar-MgAl LDH nanocomposites: Coexisting anions effect and mechanistic studies. Nanomaterials 2020, 10, 336. [Google Scholar] [CrossRef] [Green Version]
- Sui, M.; Li, Y.; Jiang, Y.; Wang, L.; Zhang, W.; Sathishkumar, K.; Zakaria, H. Sediment-based biochar facilitates highly efficient nitrate removal: Physicochemical properties, biological responses and potential mechanism. Chem. Eng. J. 2021, 405, 126645. [Google Scholar] [CrossRef]
- Li, R.; Wang, B.; Niu, A.; Cheng, N.; Chen, M.; Zhang, X.; Yu, Z.; Wang, S. Application of biochar immobilized microorganisms for pollutants removal from wastewater: A review. Sci. Total Environ. 2022, 837, 155563. [Google Scholar] [CrossRef]



| Parameter | Sand | Alluvial | Cedar Canyon | Dense Woodchips | Loose Woodchips | Biochar | Mixed |
|---|---|---|---|---|---|---|---|
(cm3/cm3) | Study by Hasan et al. [13] | Inverse modeling | Inverse Modeling | Study by Ghane et al. [34] | Study by Ghane et al. [34] | Study by Hasan et al. [30] | Homogenous Cedar Canyon |
(cm3/cm3) | Inverse Modeling | Study by R.C. Heath [35] | Saturated Water Content Test | Saturated Water Content Test | Homogenous Cedar Canyon | ||
(1/cm) | Soil Moisture Characteristic Curve | Inverse Modeling | Inverse Modeling | Inverse Modeling | Inverse Modeling | ||
| Soil Moisture Characteristic Curve | Inverse Modeling | Inverse Modeling | Inverse Modeling | Inverse Modeling | |||
(cm/day) | Inverse Modeling | Study by R.C. Heath [35] | Inverse Modeling | Inverse Modeling | Inverse Modeling |
| Parameters | C1 | C2 | C3 | C4 | C5 | C6 | |
|---|---|---|---|---|---|---|---|
| Sand | Alluvial | Cedar Canyon | Dense Woodchips | Loose Woodchips | Biochar | Mix | |
(cm3/cm3) | 0.002 | 0.02 | 0.001 | 0.21 | 0.21 | 0.001 | 0.001 |
(cm3/cm3) | 0.24 | 0.47 | 0.34 | 0.44 | 0.66 | 0.64 | 0.34 |
(cm−1) | 0.070 | 0.17 | 0.16 | 0.046 | 0.121 | 0.00001 | 0.11 |
| 4.45 | 1.34 | 5.97 | 4.33 | 4.47 | 3.07 | 1.35 | |
(cm/day) | 720 | 750 | 689 | 746 | 114 | 554 | 25 |
| R2 | 0.98 | 0.57 | 0.57 | 0.97 | 0.98 | 0.99 | |
| Parameters | C1 | C2 | C3 | C4 | C5 | C6 | |
|---|---|---|---|---|---|---|---|
| Sand | Alluvial | Cedar Canyon | Dense Woodchips | Loose Woodchips | Biochar | Mix | |
| Observed/Modeled Concentration (mg/L) | 14.22/ 14.25 | 18.71/ 18.69 | 15.54/ 15.55 | 10.14/ 10.14 | 8.28/ 8.26 | 10.25/ 10.26 | |
| First Order Reaction Constant (1/day) | 0.26 | 0.045 | 0.28 | 0.17 | 0.24 | 0.032 | 0.28 |
| Media | Initial Concentration | Nitrate Removal Efficiency | Reference |
|---|---|---|---|
| (mg/L) | (%) | ||
| Woodchips | 10 | 98.7 | [36] |
| 30 | 39 ± 9 | [37] | |
| 10 | 79 ± 14 | [37] | |
| 50 | 29 ± 12 | [37] | |
| 41.2 | 35 to 43 | [38] | |
| 28 | 70.46 | Our Study | |
| Biochar | 20 | 15 to 20 | [39] |
| 10 | 20 to 40 | [40] | |
| 10 | 57.1 ± 2.1 | [41] | |
| 100 | 20.63 | [42] | |
| 28 | 63.39 | Our Study |
| Scenario | Flux Rate (cm/Day) | Influx Concentration (mg/L) | Flow Depth (cm) |
|---|---|---|---|
| Scenario 1 | 2 | 60 | 50 |
| Scenario 2 | 5 | 60 | 50 |
| Scenario 3 | 5 | 30 | 50 |
| Scenario 4 | 2 | 60 | 100 |
| Scenario 5 | 5 | 60 | 100 |
| Scenario 6 | 5 | 30 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, M.S.; Trapp, J.; Geza, M. Improvement of Onsite Wastewater Systems Performance: Experimental and Numerical Investigation. Clean Technol. 2022, 4, 824-840. https://doi.org/10.3390/cleantechnol4030051
Hasan MS, Trapp J, Geza M. Improvement of Onsite Wastewater Systems Performance: Experimental and Numerical Investigation. Clean Technologies. 2022; 4(3):824-840. https://doi.org/10.3390/cleantechnol4030051
Chicago/Turabian StyleHasan, Md Sazadul, Joshua Trapp, and Mengistu Geza. 2022. "Improvement of Onsite Wastewater Systems Performance: Experimental and Numerical Investigation" Clean Technologies 4, no. 3: 824-840. https://doi.org/10.3390/cleantechnol4030051
APA StyleHasan, M. S., Trapp, J., & Geza, M. (2022). Improvement of Onsite Wastewater Systems Performance: Experimental and Numerical Investigation. Clean Technologies, 4(3), 824-840. https://doi.org/10.3390/cleantechnol4030051






