Changes in Water Infiltration after Simulated Wetting and Drying Periods in two Biochar Amendments
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Analysis
2.2. Statistical Analysis
2.3. Modelling of Infiltration
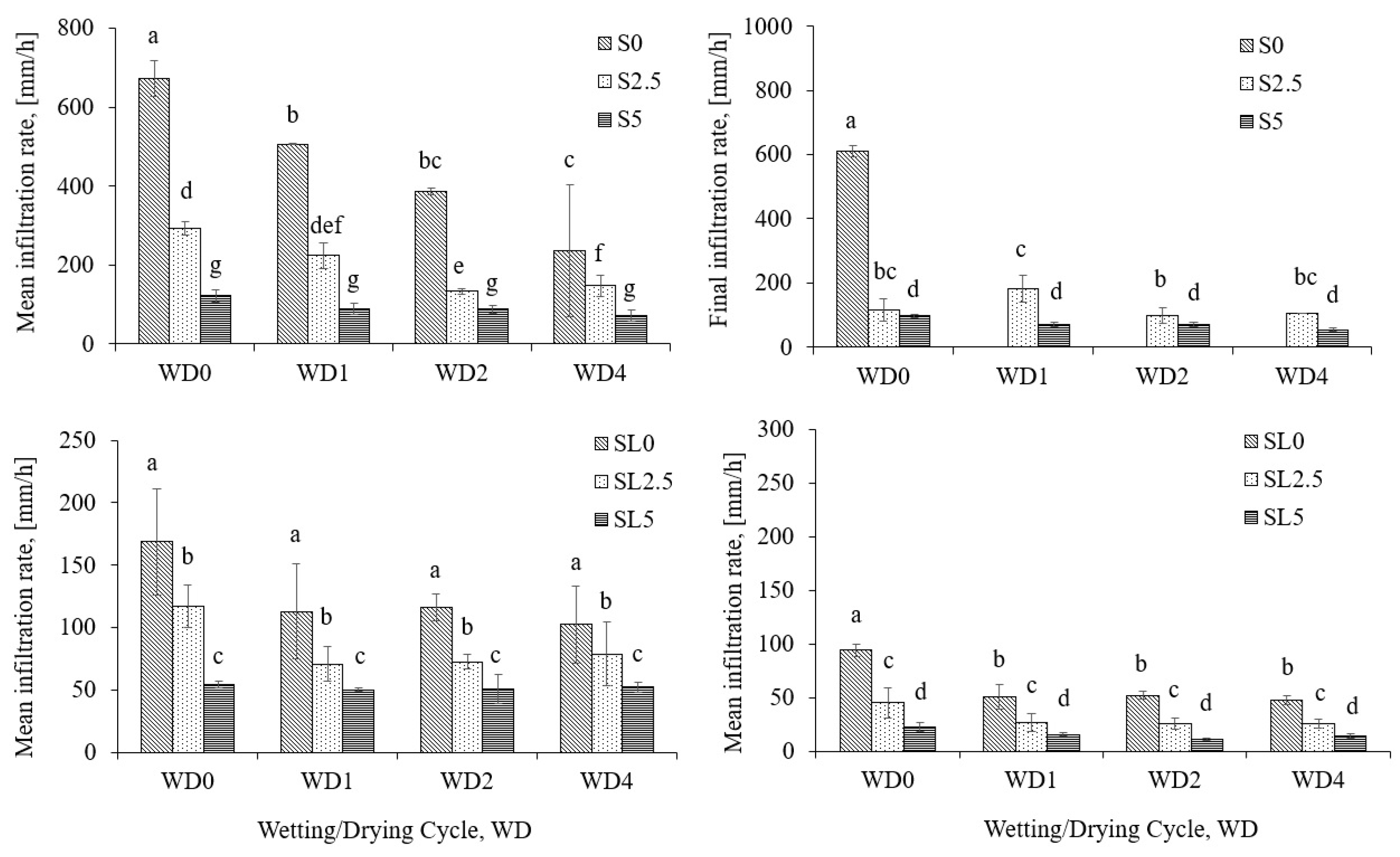
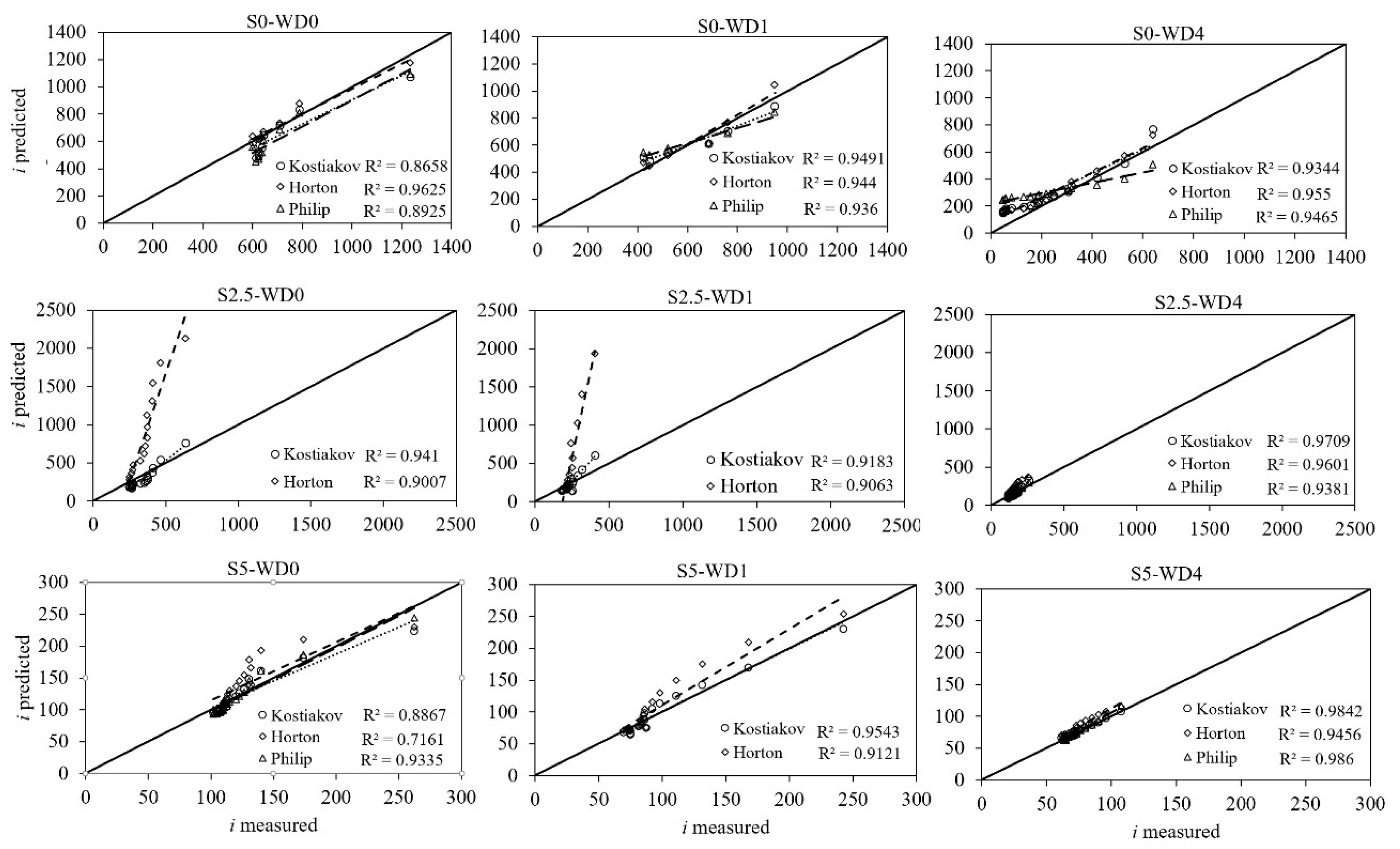
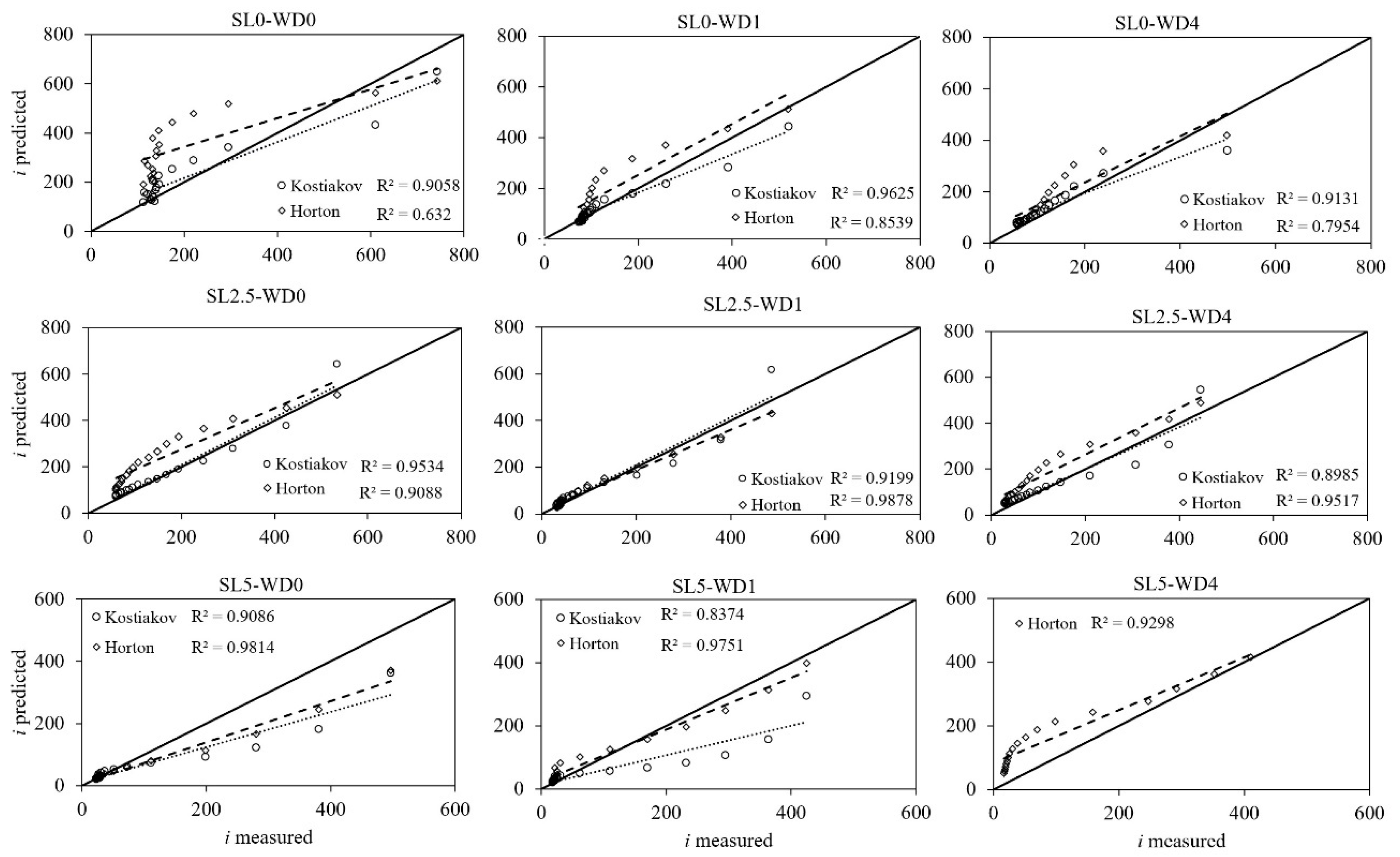
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Core Writing Team]; Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar] [CrossRef]
- FAO; ITPS. Status of the World’s Soil Resources (SWSR); Main Report; Food and Agriculture Organization of the United Nations and Intergovermental Technical Panel on Soils: Rome, Italy, 2015; ISBN 978-92-5-109004-6. [Google Scholar]
- Eastman, C.M. Soil Physical Characteristics of an Aeric Ochraqualf Amended with Biochar. Master’s Thesis, Ohio State University, Columbus, OH, USA, 2011. [Google Scholar]
- Bayabil, H.K.; Lehman, J.C.; Yitaferu, B.; Stoof, C.R.; Steenhuis, T.S. Hydraulic properties of clay soils as affected by biochar and charcoal amendments. In Rainwater Management for Resilient Livelihoods in Ethiopia, Proceedings of the Nile Basin Development Challenge Science Meeting, Addis Ababa, Ethiopia, 9–10 July 2013; NBDC Technical Report 5; Mekuria, W., Ed.; International Livestock Research Institute: Nairobi, Kenya, 2013. [Google Scholar]
- Barnes, R.T.; Gallagher, M.E.; Masiello, C.A.; Liu, Z.; Dugan, B. Biochar-Induced Changes in Soil Hydraulic Conductivity and Dissolved Nutrient Fluxes Constrained by Laboratory Experiments. PLoS ONE 2014, 9, e108340. [Google Scholar] [CrossRef] [PubMed]
- Githinji, L. Effect of Biochar Application Rate on Soil Physical and Hydraulic Properties of a Sandy Loam. Arch. Agron. Soil Sci. 2014, 60, 457–470. [Google Scholar] [CrossRef]
- Ouyang, L.; Wang, F.; Tang, J.; Yu, L.; Zhang, R. Effects of Biochar Amendment on Soil Aggregates and Hydraulic Properties. J. Soil Sci. Plant Nutr. 2013, 13, 991–1002. [Google Scholar] [CrossRef]
- Hardie, M.; Clothier, B.; Bound, S.; Oliver, G.; Close, D. Does Biochar Influence Soil Physical Properties and Soil Water Availability? Plant Soil 2014, 376, 347–361. [Google Scholar] [CrossRef]
- Lopez, V.D. Biochar as a Soil Amendment: Impact on Hydraulic and Physical Properties of an Arable Loamy Sand Soil. Master’s Thesis, University of California, Merced, CA, USA, 2014. [Google Scholar]
- Ajayi, A.E.; Holthusen, D.; Horn, R. Changes in Microstructural Behaviour and Hydraulic Functions of Biochar Amended Soils. Soil Tillage Res. 2016, 155, 166–175. [Google Scholar] [CrossRef]
- Lim, T.J.; Spokas, K.A.; Feyereisen, G.; Novak, J.M. Predicting the Impact of Biochar Additions on Soil Hydraulic Properties. Chemosphere 2016, 142, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Obia, A.; Mulder, J.; Martinsen, V.; Cornelissen, G.; Børresen, T. In Situ Effects of Biochar on Aggregation, Water Retention and Porosity in Light-Textured Tropical Soils. Soil Tillage Res. 2016, 155, 35–44. [Google Scholar] [CrossRef]
- Sohi, S.; Lopez-Capel, E.; Krull, E.; Bol, R. Biochar’s Roles in Soil and Climate Change: A Review of Research Needs; CSIRO Land and Water Science Report 05/09; CSIRO: Canberra, Australia, 2009; p. 64. [Google Scholar]
- Novak, J.M.; Busscher, W.J.; Watts, D.W.; Amonette, J.E.; Ippolito, J.A.; Lima, I.M.; Gaskin, J.; Das, K.C.; Steiner, C.; Ahmedna, M.; et al. Biochars Impact on Soil-Moisture Storage in an Ultisol and two Aridisols. Soil Sci. 2012, 177, 310–320. [Google Scholar] [CrossRef]
- Burrell, L.D.; Zehetner, F.; Rampazzo, N.; Wimmer, B.; Soja, G. Long-Term Effects of Biochar on Soil Physical Properties. Geoderma 2016, 282, 96–102. [Google Scholar] [CrossRef]
- Ajayi, A.E.; Horn, R. Comparing the Potentials of Clay and Biochar in Improving Water Retention and Mechanical Resilience of Sandy Soil. Int. Agrophys. 2016, 30, 391–399. [Google Scholar] [CrossRef]
- Römkens, M.J.M.; Prasad, S.N. Rain Infiltration into Swelling/Shrinking/Cracking Soils. Agric. Water Manag. 2006, 86, 196–205. [Google Scholar] [CrossRef]
- Chartier, M.P.; Rostagno, C.M.; Pazos, G.E. Effects of Soil Degradation on Infiltration Rates in Grazed Semiarid Rangelands of Northeastern Patagonia, Argentina. J. Arid Environ. 2011, 75, 656–661. [Google Scholar] [CrossRef]
- Hardie, M.A. Effect of Antecedent Soil Moisture on Infiltration and Preferential Flow in Texture Contrast Soils. Ph.D. Thesis, University of Tasmania, Hobart, Australia, 2011. [Google Scholar]
- De Almeida, W.S.; Panachuki, E.; de Oliveira, P.T.S.; da Silva Menezes, R.; Sobrinho, T.A.; de Carvalho, D.F. Effect of soil tillage and vegetal cover on soil water infiltration. Soil Tillage Res. 2018, 175, 130–138. [Google Scholar] [CrossRef]
- Gopal, P.; Bordoloi, S.; Ratnam, R.; Lin, P.; Cai, W.; Buragohain, P.; Garg, A.; Sreedeep, S. Investigation of Infiltration Rate for Soil-Biochar Composites of Water Hyacinth. Acta Geophys. 2019, 67, 231–246. [Google Scholar] [CrossRef]
- Novak, J.; Sigua, G.; Watts, D.; Cantrell, K.; Shumaker, P.; Szogi, A.; Johnson, M.G.; Spokas, K. Biochars Impact on Water Infiltration and Water Quality through a Compacted Subsoil Layer. Chemosphere 2016, 142, 160–167. [Google Scholar] [CrossRef] [PubMed]
- Villagra-Mendoza, K.; Ortiz-Malavassi, E.; Otterpohl, R. Role of Charcoal Addition on Infiltration Processes and Soil water Content Characteristics of a Sandy Loam Soil. Agric. Eng. Int. CIGR J. 2017, 19, 9–15. [Google Scholar]
- Itsukushima, R.; Ideta, K.; Iwanaga, Y.; Sato, T.; Shimatani, Y. Evaluation of Infiltration Capacity and Water Retention Potential of Amended Soil Using Bamboo Charcoal and Humus for Urban Flood Prevention. In Proceedings of the 11th International Symposium on Ecohydraulics, Melbourne, Australia, 7–12 February 2016. [Google Scholar]
- Hamidreza Sadeghi, S.; Hazbavi, Z.; Kiani Harchegani, M. Controllability of Runoff and Soil Loss from Small Plots Treated by Vinasse-Produced Biochar. Sci. Total Environ. 2016, 541, 483–490. [Google Scholar] [CrossRef] [PubMed]
- Hardie, M.A.; Cotching, W.E.; Doyle, R.B.; Holz, G.; Lisson, S.; Mattern, K. Effect of Antecedent Soil Moisture on Preferential Flow in a Texture-Contrast Soil. J. Hydrol. 2011, 398, 191–201. [Google Scholar] [CrossRef]
- Doerr, S.H.; Thomas, A.D. The Role of Soil Moisture in Controlling Water Repellency: New Evidence from Forest Soils in Portugal. J. Hydrol. 2000, 231–232, 134–147. [Google Scholar] [CrossRef]
- Liang, C.; Zhu, X.; Fu, S.; Méndez, A.; Gascó, G.; Paz-Ferreiro, J. Biochar Alters the Resistance and Resilience to Drought in a Tropical Soil. Environ. Res. Lett. 2014, 9, 1–6. [Google Scholar] [CrossRef]
- Chau, H.W.; Goh, Y.K.; Vujanovic, V.; Si, B.C. Wetting Properties of Fungi Mycelium Alter Soil Infiltration and Soil Water Repellency in a γ-Sterilized Wettable and Repellent Soil. Fungal Biol. 2012, 116, 1212–1218. [Google Scholar] [CrossRef] [PubMed]
- Zhi-Guo, L.; Chi-Ming, G.; Run-Hua, Z.; Mohamed, I.; Guo-Shi, Z.; Li, W.; Runqin, Z.; Fang, C.; Yi, L. The Benefic Effect Induced by Biochar on Soil Erosion and Nutrient Loss of Slopping Land under Natural Rainfall Conditions in Central China. Agric. Water Manag. 2017, 185, 145–150. [Google Scholar]
- Abrol, V.; Ben-Hur, M.; Verheijen, F.G.A.; Keizer, J.J.; Martins, M.A.S.; Tenaw, H.; Tchehansky, L.; Graber, E.R. Biochar Effects on Soil Water Infiltration and Erosion under Seal Formation Conditions: Rainfall Simulation Experiment. J. Soils Sediments 2016, 16, 2709–2719. [Google Scholar] [CrossRef]
- Van De Genachte, G.; Mallants, D.; Ramos, J.; Deckers, J.A.; Feyen, J. Estimating Infiltration Parameters from Basic Soil Properties. Hydrol. Process. 1996, 10, 687–701. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Feng, J. Green–Ampt Model for Layered Soils with Nonuniform Initial Water Content Under Unsteady Infiltration. Soil Sci. Soc. Am. J. 2008, 72, 1041. [Google Scholar] [CrossRef]
- Jačka, L.; Pavlásek, J.; Pech, P.; Kuráž, V. Assessment of Evaluation Methods Using Infiltration Data Measured in Heterogeneous Mountain Soils. Geoderma 2016, 276, 74–83. [Google Scholar] [CrossRef]
- Igbadunh, E.; Othman, M.K.; Ajayi, A.S. Performance of Selected Water Infiltration Models in Sandy Clay Loam Soil in Samaru Zaria. Glob. J. Res. Eng. 2016, 16, 8–14. [Google Scholar]
- Xue, J.; Gavin, K. Effect of Rainfall Intensity on Infiltration into Partly Saturated Slopes. Geotech. Geol. Eng. 2008, 26, 199–209. [Google Scholar] [CrossRef]
- Ghosh, B.; Pekkat, S. A Critical Evaluation of Measurement Induced Variability in Infiltration Characteristics for a River Sub-Catchment. Meas. J. Int. Meas. Confed. 2019, 132, 47–59. [Google Scholar] [CrossRef]
- Adindu, R.U.; Igbokwe Kelechi, K.; Chigbu Timothy, O.; Ike-Amadi, C.A. Application of Kostiakov’s Infiltration Model on the Soils of Umudike, Abia State—Nigeria. Am. J. Environ. Eng. 2014, 4, 1–6. [Google Scholar] [CrossRef]
- Uloma, A.R.; Samuel, A.C.; Kingsley, I.K. Estimation of Kostiakov’s Infiltration Model Parameters of Some Sandy Loam Soils of Ikwuano–Umuahia, Nigeria. Open Trans. Geosci. 2014, 1, 34–38. [Google Scholar] [CrossRef]
- Barrera, D.; Masuelli, S. An Extension of the Green-Ampt Model to Decreasing Flooding Depth Conditions, with Efficient Dimensionless Parametric Solution. Hydrol. Sci. J. 2011, 56, 824–833. [Google Scholar] [CrossRef]
- Angelaki, A.; Sakellariou-Makrantonaki, M.; Tzimopoulos, C. Theoretical and Experimental Research of Cumulative Infiltration. Transp. Porous Media 2013, 100, 247–257. [Google Scholar] [CrossRef]
- Elrick, D.E.; Reynolds, W.D. Infiltration from constant-head well permeameters and infiltrometers. In Advances in Measurement of Soil Physical Properties: Bringing Theory into Practice; Topp, G.C., Reynolds, D., Green, R.E., Eds.; SSSA Spec. Publ. 30; Soil Science Society of America: Madison, WI, USA, 1992. [Google Scholar] [CrossRef]
- Clothier, B.; Scotter, D. Unsaturated water transmission parameters obtained from infiltration. In Methods of Soil Analysis, Part 4: Physical Methods; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 879–898. [Google Scholar]
- Dohnal, M.; Dušek, J.; Vogel, T.; Císlerová, M.; Lichner, L.; Štekauerová, V. Ponded Infiltration into Soil with Biopores—Field Experiment and Modeling. Biologia 2009, 64, 580–584. [Google Scholar] [CrossRef]
- Zhao, Y.; De Maio, M.; Vidotto, F.; Sacco, D. Influence of Wet-Dry Cycles on the Temporal Infiltration Dynamic in Temperate Rice Paddies. Soil Tillage Res. 2015, 154, 14–21. [Google Scholar] [CrossRef]
- Peng, X.; Horn, R.; Smucker, A. Pore Shrinkage Dependency of Inorganic and Organic Soils on Wetting and Drying Cycles. Soil Sci. Soc. Am. J. 2007, 71, 1095–1104. [Google Scholar] [CrossRef]
- Villagra-Mendoza, K.; Horn, R. Effect of Biochar Addition on Hydraulic Functions of Two Textural Soils. Geoderma 2018, 326, 88–95. [Google Scholar] [CrossRef]
- Boden, A.G. Bodenkundliche Kartieranleitung, 5th ed.; Schweizerbart’sche Verlagsbuchhandlung: Stuttgart, Germany, 2005. [Google Scholar]
- Burbaum, B.; Filipinski, M. Die Böden Schleswig-Holsteins—Entstehung, Verbreitung, Nutzung, Eigenschaften und Gefährdung; Landesamt für Landwirtschaft, Umwelt und ländliche Räume Schleswig-Holstein: Flintbek, Germany, 2012; Volume 4. [Google Scholar]
- Hallett, P.D. An introduction to soil water repellency. In Proceedings of the 8th International Symposium on Adjuvants for Agrochemicals (ISAA2007), Columbus, OH, USA, 6–9 August 2007. [Google Scholar]
- Tillman, R.W.; Scotter, D.R.; Wallis, M.G.; Clothier, B.E. Water-Repellency and Its Measurement by Using Intrinsic Sorptivity. Aust. J. Soil Res. 1989, 27, 637–644. [Google Scholar] [CrossRef]
- White, I.; Sully, M.J. Macroscopic and Microscopic Capillary Length and Time Scales from Field Infiltration. Water Resour. Res. 1987, 23, 1514–1522. [Google Scholar] [CrossRef]
- Lal, R.; Shukla, M.K. Principles of Soil Physics; Taylor & Francis: New York, NY, USA, 2005. [Google Scholar]
- Baver, L.D.; Gardner, W.H.; Gardner, W.R. Soil Physics, 4th ed.; Sons, J.W., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 1972. [Google Scholar]
- Kostiakov, A.N. The Dynamics of the Coefficient of Water Percolation in Soils and the Necessity for Studying It from a Dynamic Point of View for Purpose of Amelioration. Soc. Soil Sci. 1932, 14, 17–21. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quatification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Sun, F.; Lu, S. Biochars Improve Aggregate Stability, Water Retention, and Pore-Space Properties of Clayey Soil. J. Plant Nutr. Soil Sci. 2014, 177, 26–33. [Google Scholar] [CrossRef]
- Bodner, G.; Scholl, P.; Kaul, H.P. Field Quantification of Wetting-Drying Cycles to Predict Temporal Changes of Soil Pore Size Distribution. Soil Tillage Res. 2013, 133, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Villagra-Mendoza, K.; Horn, R. Effect of Biochar on the Unsaturated Hydraulic Conductivity of Two Amended Soils. Int. Agrophys. 2018, 32, 373–378. [Google Scholar] [CrossRef]
- EUROPA; Verheijen, F.; Jeffery, S.; Bastos, A.C.; van der Velde, M.; Diasfas, I. Biochar Application to Soils: A Critical Scientific Review of Effects on Soil Properties, Processes and Functions; EUROPA: Luxembourg, 2010. [Google Scholar] [CrossRef]
- Li, Y.; Ren, X.; Hill, R.; Malone, R.; Zhao, Y. Characteristics of Water Infiltration in Layered Water-Repellent Soils. Pedosphere 2017, 28, 775–792. [Google Scholar] [CrossRef]
- Doerr, S.H.; Shakesby, R.A.; Walsh, R.P.D. Soil Water Repellency: Its Causes, Characteristics and Hydro-Geomorphological Significance. Earth Sci. Rev. 2000, 51, 33–65. [Google Scholar] [CrossRef]
- Herath, H.M.S.K.; Camps-Arbestain, M.; Hedley, M. Effect of Biochar on Soil Physical Properties in Two Contrasting Soils: An Alfisol and an Andisol. Geoderma 2013, 209–210, 188–197. [Google Scholar] [CrossRef]
- Canarache, A.; Motoc, E.; Dumitriu, R. Infiltration Rate as Related to Hydraulic Conductivity, Moisture Deficit and Other Soil Properties. Soil Sci. 1968, 392–401. [Google Scholar]
- Hasan, M.; Chowdhury, T.; Drabo, M.; Kassu, A.; Glenn, C. Modeling of Infiltration Characteristics by Modified Kostiakov Method. J. Water Resour. Prot. 2015, 7, 1309–1317. [Google Scholar] [CrossRef]
- Bayabil, H.K.; Dile, Y.T.; Tebebu, T.Y.; Engda, T.A.; Steenhuis, T.S. Evaluating Infiltration Models and Pedotransfer Functions: Implications for Hydrologic Modeling. Geoderma 2019, 338, 159–169. [Google Scholar] [CrossRef]
- Haghiabi, A.H.; Abedi-Koupai, J.; Heidarpour, M.; Mohammadzadeh-Habili, J. A New Method for Estimating the Parameters of Kostiakov and Modified Kostiakov Infiltration Equations. World Appl. Sci. J. 2011, 1515, 129–135. [Google Scholar]
- Ayodele, A.; Oguntunde, P.; Joseph, A.; De Souza Dias Junior, M. Numerical Analysis of the Impact of Charcoal Production on Soil Hydrological Behavior, Runoff Response and Erosion Susceptibility. Revista Brasileira de Ciência do Solo 2009, 33, 137–145. [Google Scholar] [CrossRef]
- Carrick, S.; Buchan, G.; Almond, P.; Smith, N. Atypical Early-Time Infiltration into a Structured Soil near Field Capacity: The Dynamic Interplay between Sorptivity, Hydrophobicity, and Air Encapsulation. Geoderma 2011, 160, 579–589. [Google Scholar] [CrossRef]

| Cycle | Description of the Sequence of the Cycle | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| WD0 | Sampling preparation | Inf | ||||||||
| WD1 | Dry | Inf | ||||||||
| WD2 | Dry | Inf | ||||||||
| WD4 | Dry | Inf | Dry | Inf | ||||||
| Treatment | pH | TC | Sand | Silt | Clay |
|---|---|---|---|---|---|
| % | % | ||||
| S0 | 7.54 | 0.16 ± 0.01 a | 99 | 0.4 | 0.6 |
| S2.5 | 7.47 | 1.83 ± 0.02 b | 99 | 0.7 | 0.3 |
| S5 | 7.50 | 3.56 ± 0.03 c | 99 | 0.0 | 1.0 |
| SL0 | 6.83 | 1.35 ± 0.01 d | 54.1 | 32.5 | 13.4 |
| SL2.5 | 6.98 | 3.27 ± 0.03 e | 54.0 | 32.9 | 13.1 |
| SL5 | 7.08 | 4.85 ± 0.04 f | 53.7 | 33.9 | 12.4 |
| Biochar | 7.12 | 78.36 | |||
| Wetting and Drying Cycles (WD) | ||||||||
|---|---|---|---|---|---|---|---|---|
| WD0 | WD1 | WD2 | WD4 | |||||
| S0 | 1.55 | 1.3 ± 0.54 | 1.54 ± 0.03 | 1.1 ± 0.45 | 1.61 ± 0.07 | 1.2 ± 0.46 | 1.71 | 1.0 |
| S2.5 | 1.52 ± 0.03 | 2.0 ± 1.32 | 1.49 ± 0.03 | 1.7 ± 1.14 | 1.47 ± 0.03 | 1.1 ± 0.31 | 1.48 | 0.7 |
| S5 | 1.48 ± 0.01 | 1.7 ± 0.31 | 1.46 ± 0.02 | 1.1 ± 0.28 | 1.46 ± 0.02 | 1.1 ± 0.21 | 1.43 | 0.8 |
| SL0 | 1.38 ± 0.02 | 4.6 ± 0.72 | 1.36 ± 0.02 | 1.8 ± 0.10 | 1.37 ± 0.01 | 2.1 ± 0.17 | 1.38 | 1.9 |
| SL2.5 | 1.40 ± 0.05 | 5.5 ± 0.86 | 1.39 ± 0.06 | 1.9 ± 0.04 | 1.38 ± 0.05 | 2.4 ± 0.12 | 1.35 | 1.6 |
| SL5 | 1.40 ± 0.04 | 5.2 ± 0.79 | 1.36 ± 0.05 | 1.9 ± 0.11 | 1.35 ± 0.02 | 2.3 ± 0.11 | 1.37 | 1.9 |
| Treatment | WD1 | WD2 | WD4 |
|---|---|---|---|
| S0 | 0.6 | 2.27 | 0.38 |
| S2.5 | 0.94 | 0.69 | 0.78 |
| S5 | 0.48 | 0.99 | 1.10 |
| SL0 | 1.76 | 2.28 | 1.52 |
| SL2.5 | 1.99 | 3.14 | 2.51 |
| SL5 | 1.89 | 1.64 | 2.33 |
| Model/WD | Parameter | S0 | S2.5 | S5 | SL0 | SL2.5 | SL5 |
|---|---|---|---|---|---|---|---|
| Kostiakov | |||||||
| WD0 | A | 355.1 | 164.8 | 92.1 | 111.7 | 65.3 | 18.7 |
| B | −0.369 | −0.510 | −0.295 | −0.588 | −0.762 | −0.989 | |
| NSE | 0.75 | 0.42 | 0.88 | 0.86 | 0.95 | 0.72 | |
| RMSE | 94.10 | 72.98 | 12.50 | 63.45 | 30.92 | 72.96 | |
| 201.56 | 98.58 | 98.58 | 176.97 | 136.17 | 141.42 | ||
| WD1 | A | 319.8 | 128.7 | 61.6 | 65.3 | 35.7 | 18.7 |
| B | −0.340 | −0.520 | −0.440 | −0.641 | −0.951 | −0.921 | |
| NSE | 0.89 | −0.63 | 0.95 | 0.92 | 0.90 | 0.57 | |
| RMSE | 62.16 | 70.04 | 9.01 | 34.43 | 40.16 | 85.67 | |
| 204.22 | 56.66 | 56.66 | 123.44 | 133.93 | 133.88 | ||
| WD4 | A | 142.2 | 93.6 | 60.9 | 70.1 | 44.8 | N.D |
| B | −0.563 | −0.417 | −0.244 | −0.714 | −0.834 | N.D | |
| NSE | 0.78 | 0.60 | 0.98 | 0.84 | 0.90 | -- | |
| RMSE | 79.88 | 23.20 | 2.01 | 41.04 | 40.07 | -- | |
| 175.44 | 37.86 | 37.86 | 106.80 | 127.44 | 129.10 | ||
| Horton | |||||||
| WD0 | Io | 1829.2 | 2503.2 | 252.4 | 666.5 | 568.5 | 565.2 |
| Ib | 610.5 | 91.8 | 84.6 | 97.9 | 36.9 | 22.6 | |
| 15.3 | 3.4 | 2.9 | 2.0 | 2.4 | 8.9 | ||
| NSE | 0.96 | −44.94 | 0.55 | −0.03 | 0.55 | 0.84 | |
| RMSE | 38.78 | 649.35 | 24.50 | 174.73 | 88.88 | 55.62 | |
| 201.56 | 98.58 | 98.58 | 176.97 | 136.17 | 141.42 | ||
| WD1 | Io | 1540.4 | 2682.0 | 313.0 | 609.0 | 564.0 | 507.6 |
| Ib | 407.5 | 121.6 | 68.4 | 50.5 | 26.8 | 15.6 | |
| 11.5 | 6.9 | 5.5 | 3.7 | 5.7 | 5.0 | ||
| NSE | 0.92 | −92.92 | 0.76 | 0.64 | 0.97 | 0.95 | |
| RMSE | 53.18 | 531.69 | 20.49 | 72.34 | 21.81 | 29.52 | |
| 204.22 | 56.66 | 56.66 | 123.44 | 133.93 | 133.88 | ||
| WD4 | Io | 936.3 | 386.8 | 128.8 | 585.3 | 572.0 | 474.5 |
| Ib | 157.1 | 64.4 | 52.4 | 47.4 | 25.6 | 14.1 | |
| 6.3 | 1.7 | 2.1 | 3.7 | 3.3 | 2.8 | ||
| NSE | 0.81 | −3.30 | 0.49 | 0.62 | 0.70 | 0.65 | |
| RMSE | 74.48 | 76.27 | 9.05 | 64.21 | 67.99 | 73.74 | |
| 175.44 | 37.86 | 37.86 | 106.80 | 127.44 | 129.10 | ||
| Philip | |||||||
| WD0 | A | 125.8 | N.D | 46.5 | −86.4 | −66.2 | −137.2 |
| S | 431.1 | N.D | 88.4 | 363.9 | 271.2 | 293.0 | |
| NSE | 0.66 | -- | 0.92 | -- | -- | -- | |
| RMSE | 110.20 | -- | 10.18 | -- | -- | -- | |
| 201.56 | 98.58 | 98.58 | 176.97 | 136.17 | 141.42 | ||
| WD1 | A | 305.1 | N.D | N.D | −57.1 | −143.2 | −115.4 |
| S | 241.1 | N.D | N.D | 230.7 | 312.4 | 241.7 | |
| NSE | 0.79 | -- | -- | -- | -- | -- | |
| RMSE | 86.17 | -- | -- | -- | -- | -- | |
| 204.22 | 56.66 | 56.66 | 123.44 | 133.93 | 133.88 | ||
| WD4 | A | 161.9 | 56.6 | 34.4 | −87.5 | −65.2 | −68.9 |
| S | 154.2 | 106.2 | 51.9 | 309.2 | 246.0 | 234.8 | |
| NSE | 0.33 | 0.88 | 0.94 | -- | -- | -- | |
| RMSE | 139.81 | 12.49 | 3.06 | -- | -- | -- | |
| 175.44 | 37.86 | 37.86 | 106.80 | 127.44 | 129.10 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villagra-Mendoza, K.; Horn, R. Changes in Water Infiltration after Simulated Wetting and Drying Periods in two Biochar Amendments. Soil Syst. 2019, 3, 63. https://doi.org/10.3390/soilsystems3040063
Villagra-Mendoza K, Horn R. Changes in Water Infiltration after Simulated Wetting and Drying Periods in two Biochar Amendments. Soil Systems. 2019; 3(4):63. https://doi.org/10.3390/soilsystems3040063
Chicago/Turabian StyleVillagra-Mendoza, Karolina, and Rainer Horn. 2019. "Changes in Water Infiltration after Simulated Wetting and Drying Periods in two Biochar Amendments" Soil Systems 3, no. 4: 63. https://doi.org/10.3390/soilsystems3040063
APA StyleVillagra-Mendoza, K., & Horn, R. (2019). Changes in Water Infiltration after Simulated Wetting and Drying Periods in two Biochar Amendments. Soil Systems, 3(4), 63. https://doi.org/10.3390/soilsystems3040063





