Abstract
Reliable predictions of (anti)neutrino spectra and luminosities are essential for assessing the feasibility of detecting pre-supernova neutrinos. Using the stellar evolution code MESA, we calculate the (anti)neutrino spectra and luminosities under realistic conditions of temperature, density, and electron fraction. Our study includes (anti)neutrinos produced by both thermal processes and nuclear weak-interaction reactions. By comparing the results of the thermal quasiparticle random-phase approximation with the standard technique based on the effective Q-value method, we investigate how thermal effects influence the spectra and luminosities of emitted (anti)neutrinos. Our findings show that a thermodynamically consistent treatment of Gamow–Teller transitions in hot nuclei enhances both the energy luminosity and the average energies of the emitted (anti)neutrinos.
1. Introduction
It is now widely recognized that in stellar interiors characterized by high temperatures and densities, the emission of neutrinos and antineutrinos plays a significant role in energy loss, entropy removal from the stellar core, and the acceleration of stellar evolution [1,2,3]. The detection of neutrino bursts from SN 1987A [4,5,6] significantly advanced our understanding of supernova mechanisms and stimulated the research in neutrino astrophysics. With substantial advancements in neutrino detection technologies, the potential for observing neutrino signals from new astrophysical sources has been extensively explored in recent decades. It is anticipated that neutrinos and antineutrinos emitted by stars in the pre-supernova phase, located within a distance of less than a few kpc, can soon be observed by Earth-based neutrino observatories [7,8,9]. Consequently, recent efforts have focused on calculating precise neutrino spectra and luminosities from pre-supernova stellar cores.
In stellar matter, neutrino emission arises from various thermal processes and nuclear weak-interaction reactions. Thermal (anti)neutrinos from pre-supernova cores are primarily produced via electron–positron pair annihilation (PA), with their spectra fully determined by the matter temperature (T), density (), and electron fraction () [10].
During the final stages preceding collapse, as the star undergoes silicon burning into iron, weak-interaction reactions involving atomic nuclei become the dominant source of (anti)neutrino production [9,11,12]. The expected pre-supernova neutrino spectra and the corresponding detector signals were derived in [11,12]. Notably, the authors applied the methodology described in [13] to compute the nuclear contribution to the spectra. This approach approximates each nucleus at given temperature-density conditions as undergoing a single transition from a parent to a daughter state using an effective Q-value () method. This Q-value is adjusted to reproduce the average neutrino energy predicted by shell-model calculations for nuclear weak processes in stellar environments [14]. As first noted in [15], the method may fail to reproduce key spectral features, particularly when thermally excited nuclear states dominate the weak transitions.
At typical pre-supernova temperatures ( K or higher), too many nuclear excited states become thermally populated making a state-by-state analysis of individual contributions to stellar weak-interaction processes computationally infeasible. Shell-model calculations address this challenge by employing the Brink hypothesis and the ‘back-resonances’ method [16]. In our recent publications [17,18,19], we demonstrated that the contributions of thermally excited states to (anti)neutrino production can be accurately evaluated using the thermal quasiparticle random-phase approximation (TQRPA). This framework provides a thermodynamically consistent treatment of both excitation and de-excitation processes in hot nuclei. Unlike alternative approaches, the TQRPA does not rely on the Brink hypothesis and inherently satisfies the detailed balance condition. Additionally, the method enables the treatment of neutral-current nuclear de-excitation where a hot nucleus emits neutrino-antineutrino pairs. The potential significance of this process for generating high-energy pre-supernova (anti)neutrinos was first highlighted in [12,15] and later confirmed by TQRPA calculations [17,18,19].
The present work extends our previous studies, and here we apply the TQRPA to compute the temporal evolution of luminosities and spectra for a specific pre-supernova model and compare the TQRPA results with those predicted by the effective Q-value method.
2. Neutrino Spectra Within the TQRPA Framework and Pre-Supernova Model
In stellar matter, every nucleus at a given temperature-density () condition can emit neutrinos and antineutrinos through various weak-interaction processes. These include continuum electron/positron capture (EC/PC), -decay, and nuclear de-excitation (ND) accompanied by the emission of a -pair. It is important to note that EC (PC) and ()-decay produce electron (anti)neutrinos only, whereas nuclear de-excitation generates -pairs of all three neutrino flavors. In this regard, the ND process resembles thermal processes. However, unlike thermal processes, the ND mechanism produces identical spectra for all (anti)neutrino flavors [17].
Under stellar conditions, the aforementioned reactions are predominantly governed by Gamow–Teller (GT) transitions: charge-exchange () transitions drive electron (positron) capture and ()-decay, while charge-neutral transitions mediate the ND process. In a thermally excited nucleus, both positive and negative energy GT transitions are possible: electron and positron captures can proceed through both positive and negative energy transitions, while only negative energy transitions contribute to -decay and -pair emission. The explicit formulations for the neutrino spectra expressed in terms of GT strength functions are detailed in [17,18]. These calculations involve integrating the corresponding phase-space factors over the transition energy. For charge-exchange processes, the phase-space factors additionally depend on the electron and positron distributions. The latter are given by the Fermi distributions with temperature T and chemical potentials that depend on the temperature, matter density, and electron fraction. Since no charged leptons are involved in nuclear de-excitation, this process is independent of matter density.
We compute the strength functions using the TQRPA framework, a technique that extends the quasiparticle random-phase approximation to finite temperature through the superoperator formalism in Liouville space [20]. Within the TQRPA framework, the Gamow–Teller (GT) strength function is expressed in terms of transition matrix elements from the thermal vacuum to eigenstates (thermal phonons) of the thermal Hamiltonian:
Here, is the transition strength to the i-th thermal phonon state of a hot nucleus and is the respective transition energy; for charge-neutral transitions, while for charge-exchange transitions , where is the difference between neutron and proton chemical potentials in the nucleus, and MeV is the neutron–proton mass splitting. Note that eigenvalues of the thermal Hamiltonian, , can be either positive or negative. Consequently, the strength functions (1) for upward () and downward satisfy the detailed balance principle:
This property ensures the thermodynamic consistency of the TQRPA framework. Following [17,18,19], our current TQRPA calculations are self-consistent employing the SkM* parameterization of the Skyrme effective nucleon–nucleon interaction.
As in [19], we utilize the stellar evolutionary web interface [21] from the MESA project [22,23,24,25,26] to simulate the evolution of a progenitor star with an initial mass of . The remaining input parameters for our pre-supernova model are provided in [19]. For each evolutionary time step, MESA outputs temperature, density, electron fraction and isotopic composition as a function of the mass coordinate m. These quantities are subsequently used to derive (anti)neutrino spectra and luminosities from both nuclear weak reactions and pair annihilation.
Figure 1 shows the evolution of the central temperature and density during the final day before core collapse (). The plot reveals that both temperature and density increase nearly monotonically, except during the period between h and h when 28Si burning (primarily into 54Fe) occurs in the layer surrounding the iron core. Throughout this entire time interval, 56Fe remains the dominant isotope in the core’s hottest region, which extends up to approximately (see Figure 2 in [19]). In addition to 56Fe, the following isotopes were included into calculations of the (anti)neutrino spectra and luminosities: 52,54Fe, 56Ni, 32S and 28Si. Among them, only 52Fe and 56Ni are unstable in their ground state and produce through -decay.
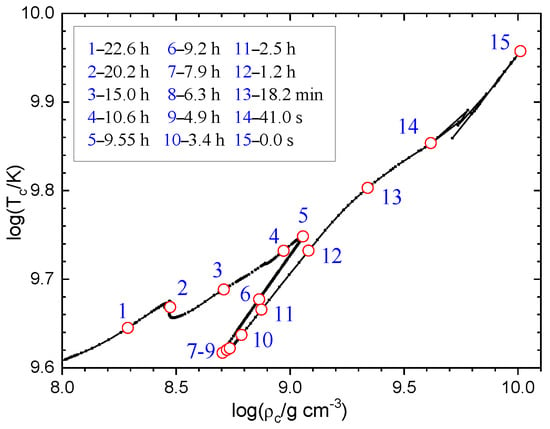
Figure 1.
The trajectory in the plane central temperature and central density . The open circles correspond to the points at which the (anti)neutrino luminosities were calculated. For each point we indicate the time t to collapse.
3. Results
3.1. Luminosities and Spectra of Pre-Supernova Neutrinos
Let us first examine the time evolution of the considered pre-supernova model in terms of the (anti)neutrino energy luminosity. Initially, we focus on the luminosities of and species from nuclear processes without including flavor oscillations. In Figure 2, we compare the luminosities calculated using the TQRPA and method. First of all, we note that both methods predict a luminosity peak at h followed by a minimum and a subsequent rapid increase. These variations clearly reflect changes in temperature and density along the stellar evolution trajectory (see Figure 1).
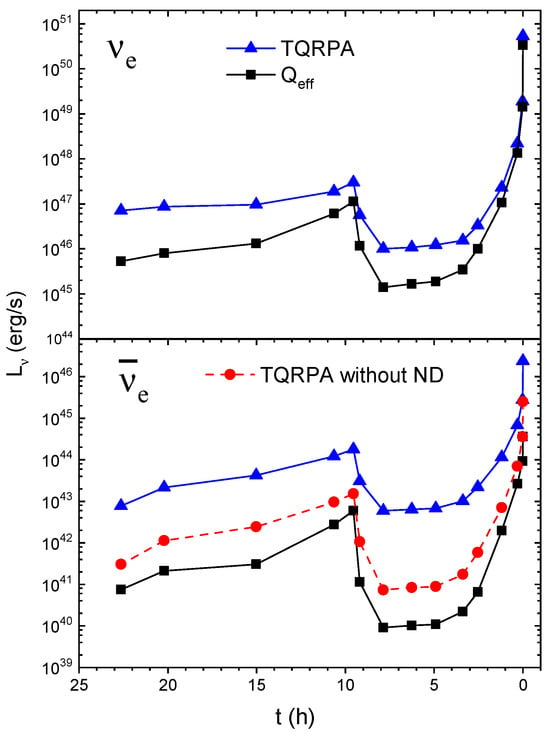
Figure 2.
Time evolution of the nuclear contributions to and luminosities computed employing the TQRPA and approaches. For we also show the luminosity without the ND contribution.
Although the temporal evolution of luminosities appears similar between the approaches, the method consistently predicts lower luminosity values than the TQRPA approach. For electron neutrinos, this discrepancy diminishes with increasing temperature and density, becoming negligible at the core collapse onset (). This convergence can be understood by considering that electron capture is the main source of [17,18,19]. At , under high-temperature and high-density conditions the electron chemical potential is large enough ( MeV) and EC on iron-group nuclei occurs primarily through resonance excitation. As both approaches result in roughly equal energies and transition strengths to the resonance state, the luminosity calculations naturally converge at the point of core collapse.
At lower temperatures and densities, the available electron energy is insufficient to excite the resonance. Under these conditions, electron capture occurs primarily through downward (negative energy) transitions from thermally excited states. The significance of downward transitions was demonstrated in [19] through comparative analysis of luminosities from hot versus cold nuclei. Namely, it was shown that during the final day before core collapse downward transitions may amplify the luminosity by over an order of magnitude. As discussed in the Introduction, the method employs average neutrino energies derived from prior shell-model calculations. In Ref. [18], through a direct comparison of TQRPA and shell-model results, we demonstrated that the thermodynamically consistent treatment of negative energy transitions in the TQRPA framework produces not only higher electron capture rates but also greater neutrino energies. This fundamental difference explains why the method systematically predicts lower luminosities in the pre-collapse phase compared to the TQRPA.
Regarding electron antineutrino emission in nuclear processes, the dominant mechanism is charge-neutral nuclear de-excitation. As shown in the lower panel of Figure 2, the ND process enhances the luminosity by approximately an order of magnitude. Since charge-neutral de-excitation is not taken into account in shell-model calculations, the method significantly underestimates these luminosities. It should be mentioned that for nuclear processes, emission of heavy-lepton flavor (anti)neutrinos occurs exclusively through the ND process, and the corresponding luminosities and spectra coincide with that of electron (anti)neutrinos.
Let us now examine how the inclusion of thermal processes influences luminosity predictions in both approaches. Recall that the dominant thermal process is pair annihilation. As demonstrated in [18,19], the PA process contributes to emission significantly less than electron capture. Consequently, luminosities remain virtually unchanged when including thermal processes and both approaches yield results consistent with the upper panel of Figure 2.
The situation is different for other (anti)neutrino species, and , (). As shown in Figure 3, their emission primarily arises from pair annihilation. For the PA contribution is more significant because production via pair annihilation occurs through both neutral and charged currents [27]. Consequently, the total luminosities are in close agreement between both approaches throughout the entire time period. The luminosities also show consistent agreement between both approaches with discrepancies emerging only at peak temperatures when the ND and PA luminosities become comparable. Thus, at h the TQRPA predicts slightly greater luminosities than the method.
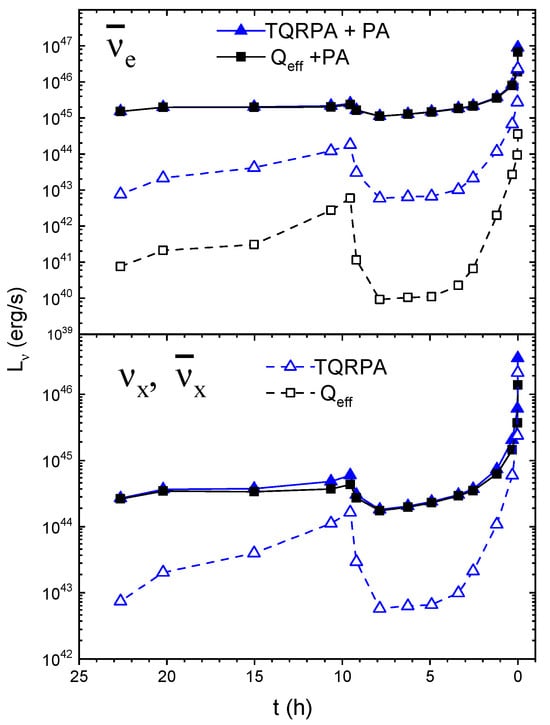
Figure 3.
Time evolution of the total and , luminosities computed employing the TQRPA and approaches. For comparison we also show (empty symbols) the luminosities from nuclear processes. Note that within the method , can be produced only in thermal processes.
Figure 4 shows the energy luminosity spectra at selected times and h with contributions from nuclear and thermal processes displayed separately. Both approaches predict a low-energy peak in the spectra originating from electron capture via resonance excitation. The TQRPA spectra additionally exhibit a distinct high-energy peak (absent in results) caused by negative energy transitions from thermally excited states. Thus, including negative energy transitions not only increases luminosity but also hardens the spectrum.
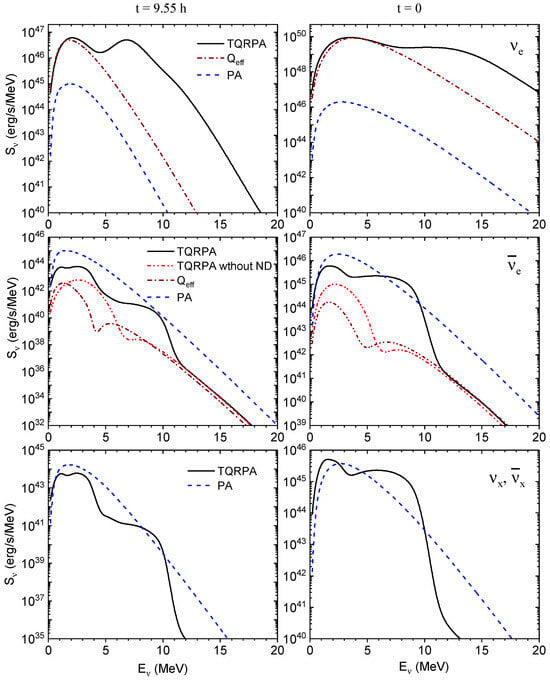
Figure 4.
Comparison of (anti)neutrino spectra from nuclear and thermal process at h (left panels) and (right panels). For and we also compare the TQRPA and spectra from nuclear processes.
As shown in the middle panel of Figure 4, without the ND component the TQRPA and spectra of display a double-peaked structure originating from positron capture and -decay. Both approaches indicate that without nuclear de-excitation, pre-supernova spectra is dominated by pair annihilation. However, the TQRPA reveals that including ND processes significantly enhances the impact of nuclear reactions on production. Notably, in the MeV energy range, the high-energy ND component becomes comparable to or even surpasses the PA contribution. As discussed in [17,18], this high-energy component stems from the de-excitation of the resonance. The relative contribution of the ND process is even more significant for heavy-lepton flavor (anti)neutrinos (see the lower panel of Figure 4), as their PA contributions are intrinsically smaller.
3.2. Neutrino Oscillations
Thus far, we have examined (anti)neutrino emission processes in the pre-supernova phase without considering neutrino oscillations. However, the flavor composition of the pre-supernova neutrino flux at Earth differs from that at production due to flavor oscillations. In this analysis, we focus specifically on electron (anti)neutrinos, as these are most relevant for detection. When accounting for both vacuum oscillations and the Mikheyev–Smirnov–Wolfenstein effect, the flux at Earth can be expressed as [10]:
Here F represents either the spectral or luminosity flux, and the superscript 0 denotes the unoscillated flux (For brevity, in (3) we omit the geometric factor due to the distance to the star). An analogous expression holds for with the replacement and . The energy independent quantities p and are the survival probabilities. They are connected with the neutrino mixing angles as , for the normal hierarchy (NH) of neutrino masses and , for the inverted hierarchy (IH) (see e.g., Ref. [28]).
In Figure 5, we compare the time evolution of unoscillated total and luminosities (computed using both the TQRPA and approaches) with the corresponding luminosities after accounting for normal (NH) and inverted (IH) hierarchy oscillations. The figure clearly demonstrates that luminosity experiences strong suppression under the NH, while the suppression is less pronounced for the IH. Conversely, NH oscillations only marginally reduce the original luminosity, whereas IH leads to substantially greater suppression. These effects can be directly understood from Equation (3). Specifically, the survival probability for the NH, and since , this results in a dramatic suppression of . A similar mechanism explains the stronger reduction of luminosity under IH oscillations.
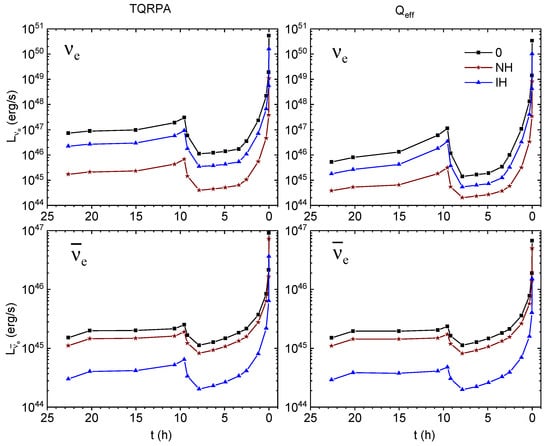
Figure 5.
Time evolution of the total (upper panels) and (lower panels) luminosities. On each plot, the luminosities obtained with the normal (NH) and inverted (IH) hierarchy are compared with the original unoscillated luminosity (0). The left and right plots show the results obtained employing the TQRPA and approaches.
As discussed in [19], inverted hierarchy oscillations effectively replace nearly the entire original flux with , while no equivalent substitution occurs for . This preservation amplifies the impact of nuclear temperature effects on oscillated luminosities. The thermal effects on oscillated luminosities become particularly apparent when comparing the TQRPA and results. Following from our earlier examination of Figure 2, the substantial discrepancy between unoscillated values stems from the fact that the method fails to capture downward transitions from thermally excited states. For the same reason, oscillated luminosities obtained by using the method are generally suppressed with respect to the TQRPA results. In contrast, luminosity after oscillations remains predominantly driven by pair annihilation. Here, thermal enhancement of nuclear processes produces only marginal increase in oscillated TQRPA luminosity compared to predictions, except during high-temperature phases at h where nuclear de-excitation contributions become significant.
Figure 6 illustrates the combined effects of flavor oscillations and nuclear thermal excitations on electron (anti)neutrino spectra calculated using both the TQRPA and approaches at two time points h and . For spectra, oscillations primarily reduce the overall flux magnitude while leaving the spectral shape largely unaffected. Both approaches yield nearly identical low-energy peaks, the TQRPA showing an additional high-energy peak from electron capture on thermally excited nuclear states. The average energy remains stable due to incomplete conversion.
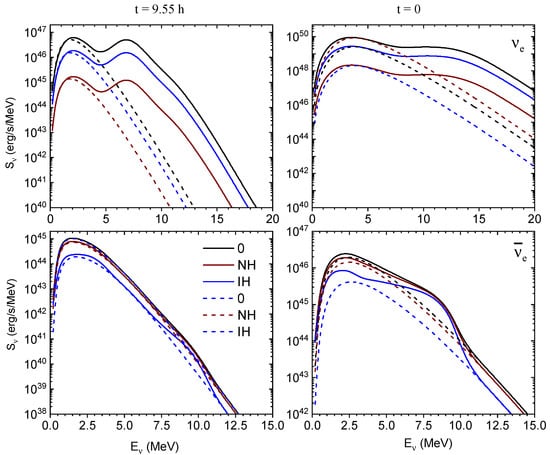
Figure 6.
The total spectra for (upper panels) and (lower panels) obtained with the normal (NH) and inverted (IH) hierarchy at h and are compared with the original unoscillated spectra (0). On each plot we compare the spectra obtained with the TQRPA (solid lines) and method (dashed lines).
For , oscillations enhance the thermal modifications of the TQRPA spectrum. This is particularly evident in the inverted hierarchy (IH) scenario where the original flux is largely replaced by , leading to a strong suppression across most of the spectrum except for the energy range MeV, where the ND contribution dominates. Since the ND spectrum is identical for all flavors, it remains unchanged by oscillations. As a result, the interplay between the ND process and IH oscillations boosts the fraction of high-energy in the spectrum, with this effect being more pronounced at higher temperatures (i.e., at ). Regarding the spectrum computed within the method, the absence of the ND process prevents any increase in the average neutrino energy. For the same reason, in the inverted hierarchy scenario the spectrum experiences significantly stronger suppression compared to the TQRPA approach.
4. Conclusions
In this work, we have investigated how nuclear temperature influences pre-supernova (anti)neutrino emission by comparing luminosities and spectra derived from two methods: the recently developed Thermal Quasiparticle Random-Phase Approximation (TQRPA) and the conventional effective Q approach. Based on our earlier studies [17,18,19], we demonstrated that the thermodynamically consistent treatment of Gamow–Teller (GT) transitions in hot nuclei within the TRQPA approach enhance the nuclear contribution to (anti)neutrino emission in comparison with the method results. For , downward transitions from thermally excited states not only increase the high-energy luminosity but also produce a harder spectrum compared to the method. While flavor oscillations suppress the luminosity in both approaches, they leave the spectral shape unchanged. In the case of emission at high temperatures, TQRPA calculations reveal that the neutral-current de-excitation process plays a more prominent role when oscillations are accounted for, significantly enhancing the fraction of high-energy in the spectrum. Unlike the TQRPA approach, no such enhancement is observed in the method. These results have critical implications for detecting pre-supernova (anti)neutrinos in terrestrial experiments. In [18], we demonstrated that the ND process can significantly enhance the detection rate of pre-supernova via inverse beta-decay. However, as illustrated in Figure 6, during the pre-supernova phase the flux exceeds the flux by orders of magnitude. This suggests that detection channels sensitive to electron neutrinos may play a crucial role in observing the final hours of stellar evolution. In future work, we plan to investigate how thermal effects—particularly the hardening of the spectrum predicted by the TQRPA framework—influence the detectability of pre-supernova through alternative interaction channels, including elastic scattering on electrons, charged- and neutral-current interactions with nuclei, and coherent elastic neutrino–nucleus scattering.
Author Contributions
Conceptualization: A.A.D. and A.V.Y.; formal analysis: A.A.D., A.V.Y., N.V.D.-B. and A.I.V.; software: A.A.D., A.V.Y. and N.V.D.-B.; writing—original draft preparation: A.A.D.; writing—review and editing: A.A.D., A.I.V., A.V.Y. and N.V.D.-B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Woosley, S.E.; Heger, A.; Weaver, T.A. The evolution and explosion of massive stars. Rev. Mod. Phys. 2002, 74, 1015–1071. [Google Scholar] [CrossRef]
- Janka, H.T.; Langanke, K.; Marek, A.; Martínez-Pinedo, G.; Müller, B. Theory of core-collapse supernovae. Phys. Rep. 2007, 442, 38–74. [Google Scholar] [CrossRef]
- Balasi, K.; Langanke, K.; Martínez-Pinedo, G. Neutrino–nucleus reactions and their role for supernova dynamics and nucleosynthesis. Prog. Part. Nucl. Phys. 2015, 85, 33–81. [Google Scholar] [CrossRef]
- Hirata, K.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; et al. Observation of a neutrino burst from the supernova SN1987A. Phys. Rev. Lett. 1987, 58, 1490–1493. [Google Scholar] [CrossRef]
- Bionta, R.M.; Blewitt, G.; Bratton, C.B.; Casper, D.; Ciocio, A.; Claus, R.; Cortez, B.; Crouch, M.; Dye, S.T.; Errede, S.; et al. Observation of a neutrino burst in coincidence with supernova 1987A in the Large Magellanic Cloud. Phys. Rev. Lett. 1987, 58, 1494–1496. [Google Scholar] [CrossRef]
- Alekseev, E.N.; Alekseeva, L.N.; Volchenko, V.I.; Krivosheina, I.V. Possible detection of a neutrino signal on 23 February 1987 at the Baksan underground scintillation telescope of the Institute of Nuclear Research. Sov. J. Exp. Theor. Phys. Lett. 1987, 45, 589. [Google Scholar]
- Odrzywolek, A.; Misiaszek, M.; Kutschera, M. Detection possibility of the pair-annihilation neutrinos from the neutrino-cooled pre-supernova star. Astropart. Phys. 2004, 21, 303–313. [Google Scholar] [CrossRef]
- Odrzywolek, A.; Misiaszek, M.; Kutschera, M. Neutrinos from Pre-Supernova Star. Acta Phys. Pol. B 2004, 35, 1981. [Google Scholar] [CrossRef]
- Asakura, K.; Gando, A.; Gando, Y.; Hachiya, T.; Hayashida, S.; Ikeda, H.; Inoue, K.; Ishidoshiro, K.; Ishikawa, T.; Ishio, S.; et al. KamLAND sensitivity to neutrinos from pre-supernova stars. Astrophys. J. 2016, 818, 91. [Google Scholar] [CrossRef]
- Kato, C.; Delfan Azari, M.; Yamada, S.; Takahashi, K.; Umeda, H.; Yoshida, T.; Ishidoshiro, K. Pre-supernova Neutrino Emissions from ONe Cores in the Progenitors of Core-collapse Supernovae: Are They Distinguishable from Those of Fe Cores? Astrophys. J. 2015, 808, 168. [Google Scholar] [CrossRef]
- Patton, K.M.; Lunardini, C.; Farmer, R.J. Presupernova Neutrinos: Realistic Emissivities from Stellar Evolution. Astrophys. J. 2017, 840, 2. [Google Scholar] [CrossRef]
- Patton, K.M.; Lunardini, C.; Farmer, R.J.; Timmes, F.X. Neutrinos from Beta Processes in a Presupernova: Probing the Isotopic Evolution of a Massive Star. Astrophys. J. 2017, 851, 6. [Google Scholar] [CrossRef]
- Langanke, K.; Martínez-Pinedo, G.; Sampaio, J.M. Neutrino spectra from stellar electron capture. Phys. Rev. C 2001, 64, 055801. [Google Scholar] [CrossRef]
- Langanke, K.; Martínez-pinedo, G. Rate tables for the weak processes of pf-shell nuclei in stellar environments. At. Data Nucl. Data Tables 2001, 79, 1–46. [Google Scholar] [CrossRef]
- Misch, G.W.; Fuller, G.M. Nuclear neutrino energy spectra in high temperature astrophysical environments. Phys. Rev. C 2016, 94, 055808. [Google Scholar] [CrossRef]
- Langanke, K.; Martínez-Pinedo, G. Shell-model calculations of stellar weak interaction rates: II. Weak rates for nuclei in the mass range /A=45-65 in supernovae environments. Nucl. Phys. A 2000, 673, 481–508. [Google Scholar] [CrossRef]
- Dzhioev, A.A.; Yudin, A.V.; Dunina-Barkovskaya, N.V.; Vdovin, A.I. Neutrino Spectrum and Energy Loss Rates Due to Weak Processes on Hot 56Fe in Pre-Supernova Environment. Particles 2023, 6, 682–692. [Google Scholar] [CrossRef]
- Dzhioev, A.A.; Yudin, A.V.; Dunina-Barkovskaya, N.V.; Vdovin, A.I. Neutrinos from pre-supernova in the framework of TQRPA method. Mon. Not. R. Astron. Soc. 2024, 527, 7701–7712. [Google Scholar] [CrossRef]
- Dzhioev, A.A.; Yudin, A.V.; Dunina-Barkovskaya, N.V.; Vdovin, A.I. Neutrinos from pre-supernova: Effects of nuclear temperature on luminosities and spectra. Int. J. Mod. Phys. E 2024, 33, 2441014. [Google Scholar] [CrossRef]
- Dzhioev, A.A.; Vdovin, A.I. Superoperator Approach to the Theory of Hot Nuclei and Astrophysical Applications: I – Spectral Properties of Hot Nuclei. Phys. Part. Nucl. 2022, 53, 885–938. [Google Scholar] [CrossRef]
- Available online: http://user.astro.wisc.edu/~townsend/static.php?ref=mesa-web (accessed on 18 May 2024).
- Paxton, B.; Bildsten, L.; Dotter, A.; Herwig, F.; Lesaffre, P.; Timmes, F. Modules for Experiments in Stellar Astrophysics (MESA). Astrophys. J. Suppl. Ser. 2011, 192, 3. [Google Scholar] [CrossRef]
- Paxton, B.; Cantiello, M.; Arras, P.; Bildsten, L.; Brown, E.F.; Dotter, A.; Mankovich, C.; Montgomery, M.H.; Stello, D.; Timmes, F.X.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Planets, Oscillations, Rotation, and Massive Stars. Astrophys. J. Suppl. Ser. 2013, 208, 4. [Google Scholar] [CrossRef]
- Paxton, B.; Marchant, P.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Cantiello, M.; Dessart, L.; Farmer, R.; Hu, H.; Langer, N.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Binaries, Pulsations, and Explosions. Astrophys. J. Suppl. Ser. 2015, 220, 15. [Google Scholar] [CrossRef]
- Paxton, B.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Blinnikov, S.; Duffell, P.; Farmer, R.; Goldberg, J.A.; Marchant, P.; Sorokina, E.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Convective Boundaries, Element Diffusion, and Massive Star Explosions. Astrophys. J. Suppl. Ser. 2018, 234, 34. [Google Scholar] [CrossRef]
- Paxton, B.; Smolec, R.; Schwab, J.; Gautschy, A.; Bildsten, L.; Cantiello, M.; Dotter, A.; Farmer, R.; Goldberg, J.A.; Jermyn, A.S.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Pulsating Variable Stars, Rotation, Convective Boundaries, and Energy Conservation. Astrophys. J. Suppl. Ser. 2019, 243, 10. [Google Scholar] [CrossRef]
- Misiaszek, M.; Odrzywołek, A.; Kutschera, M. Neutrino spectrum from the pair-annihilation process in the hot stellar plasma. Phys. Rev. D 2006, 74, 043006. [Google Scholar] [CrossRef]
- Kolupaeva, L.; Gonchar, M.; Ol’shevskii, A.; Samoylov, O. Neutrino oscillations: Status and prospects for the determination of neutrino mass ordering and the leptonic CP-violation phase. Phys. Usp. 2023, 66, 753. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).