Effect of the Coulomb Interaction on Nuclear Deformation and Drip Lines
Abstract
1. Introduction
1.1. Basic Properties of Nuclei
1.2. Energy Density Functional Method
1.3. Electromagnetic Interaction in Nuclei
1.4. Scope of the Present Paper
2. Hartree–Fock–Bogoliubov Theory
3. Results
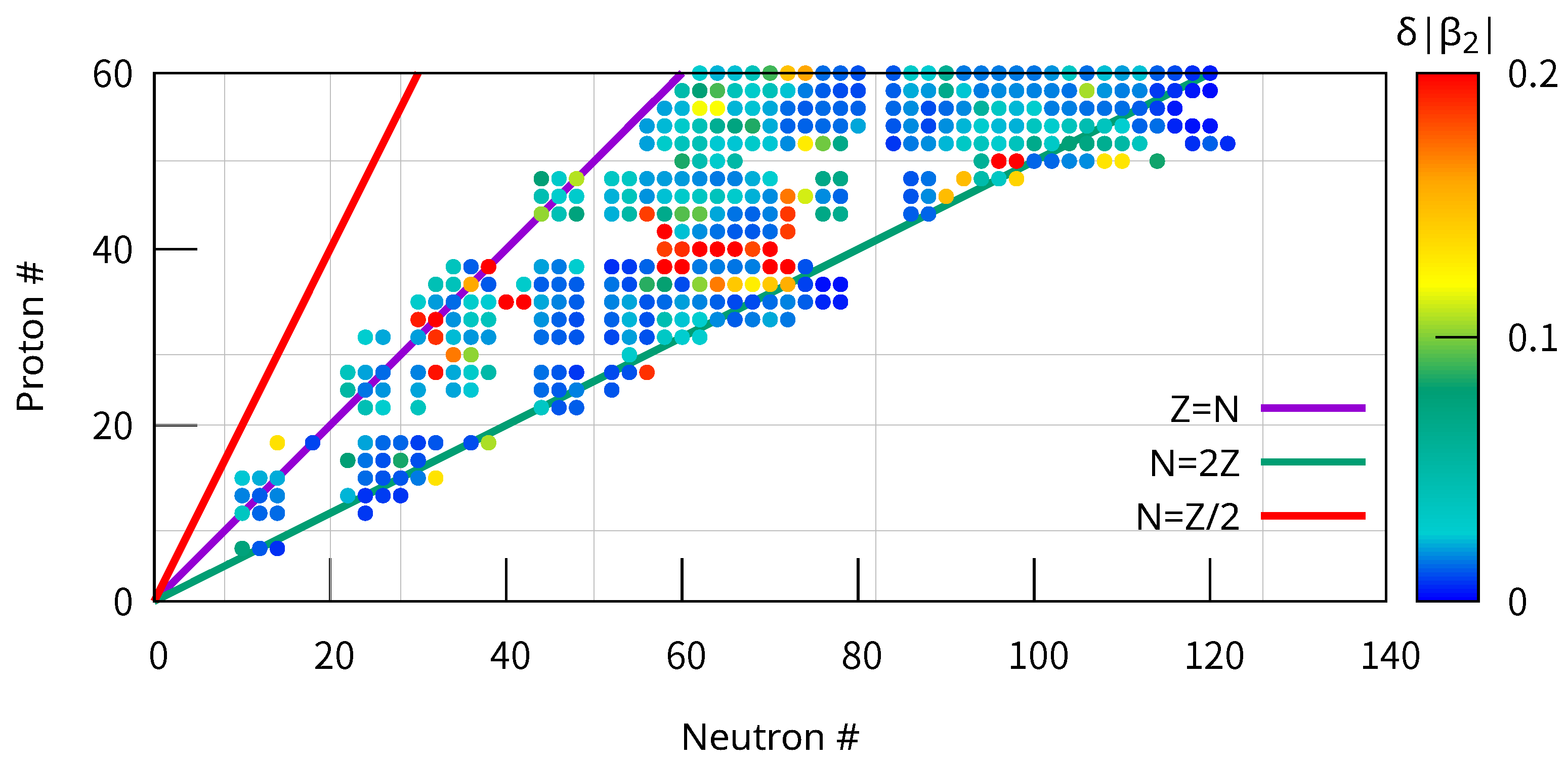
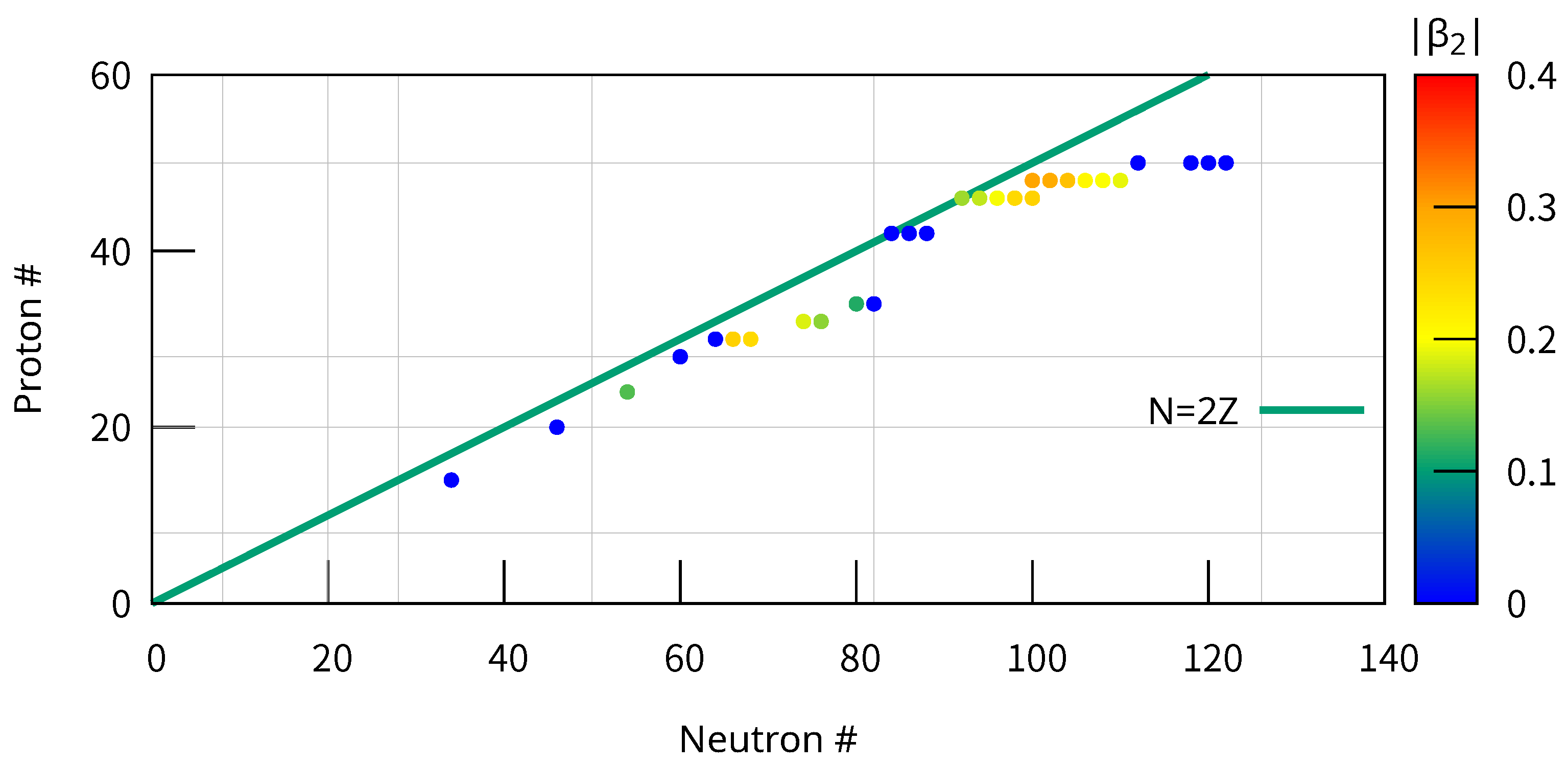
3.1. Quadrupole Deformation
3.2. Neutron Drip Line
3.3. Canonical Single-Particle Energy of Neutrons
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bohr, A.; Mottelson, B.R. Nuclear Structure; W. A. Benjamin: New York, NY, USA, 1969; Volume I. [Google Scholar]
- Bohr, A.; Mottelson, B.R. Nuclear Structure; W. A. Benjamin: New York, NY, USA, 1975; Volume II. [Google Scholar]
- Li, J.J.; Margueron, J.; Long, W.H.; Van Giai, N. Magicity of neutron-rich nuclei within relativistic self-consistent approaches. Phys. Lett. B 2016, 753, 97–102. [Google Scholar] [CrossRef]
- Åberg, S.; Flocard, H.; Nazarewicz, W. Nuclear Shapes in Mean Field Theory. Annu. Rev. Nucl. Part. Sci. 1990, 40, 439–528. [Google Scholar] [CrossRef]
- Heyde, K.; Wood, J.L. Shape Coexistence in Atomic Nuclei. Rev. Mod. Phys. 2011, 83, 1467–1521. [Google Scholar] [CrossRef]
- Gade, A.; Liddick, S.N. Shape Coexistence in Neutron-Rich Nuclei. J. Phys. G: Nucl. Part. Phys. 2016, 43, 024001. [Google Scholar] [CrossRef]
- Leoni, S.; Fornal, B.; Bracco, A.; Tsunoda, Y.; Otsuka, T. Multifaceted character of shape coexistence phenomena in atomic nuclei. Prog. Part. Nucl. Phys. 2024, 139, 104119. [Google Scholar] [CrossRef]
- Aprahamian, A.; Lee, K.; Lesher, S.R.; Bijker, R. The nature of 0+ excitations in deformed nuclei. Prog. Part. Nucl. Phys. 2025, 143, 104173. [Google Scholar] [CrossRef]
- Alder, K.; Bohr, A.; Huus, T.; Mottelson, B.; Winther, A. Study of Nuclear Structure by Electromagnetic Excitation with Accelerated Ions. Rev. Mod. Phys. 1956, 28, 432–542. [Google Scholar] [CrossRef]
- Nakatsukasa, T.; Matsuyanagi, K.; Matsuzaki, M.; Shimizu, Y.R. Quantal rotation and its coupling to intrinsic motion in nuclei. Phys. Scr. 2016, 91, 073008. [Google Scholar] [CrossRef]
- Nakatsukasa, T.; Matsuyanagi, K.; Matsuo, M.; Yabana, K. Time-dependent density-functional description of nuclear dynamics. Rev. Mod. Phys. 2016, 88, 045004. [Google Scholar] [CrossRef]
- Carlson, J.; Gandolfi, S.; Pederiva, F.; Pieper, S.C.; Schiavilla, R.; Schmidt, K.E.; Wiringa, R.B. Quantum Monte Carlo methods for nuclear physics. Rev. Mod. Phys. 2015, 87, 1067–1118. [Google Scholar] [CrossRef]
- Gandolfi, S.; Lonardoni, D.; Lovato, A.; Piarulli, M. Atomic Nuclei From Quantum Monte Carlo Calculations With Chiral EFT Interactions. Front. Phys. 2020, 8, 117. [Google Scholar] [CrossRef]
- Hagen, G.; Papenbrock, T.; Hjorth-Jensen, M.; Dean, D.J. Coupled-cluster computations of atomic nuclei. Rep. Prog. Phys. 2014, 77, 096302. [Google Scholar] [CrossRef] [PubMed]
- Somà, V. Self-Consistent Green’s Function Theory for Atomic Nuclei. Front. Phys. 2020, 8, 340. [Google Scholar] [CrossRef]
- Hergert, H. A Guided Tour of ab initio Nuclear Many-Body Theory. Front. Phys. 2020, 8, 379. [Google Scholar] [CrossRef]
- Miyagi, T. Nuclear radii from first principles. Front. Phys. 2025, 13, 1581854. [Google Scholar] [CrossRef]
- Epelbaum, E.; Hammer, H.W.; Meißner, U.G. Modern theory of nuclear forces. Rev. Mod. Phys. 2009, 81, 1773–1825. [Google Scholar] [CrossRef]
- Machleidt, R.; Entem, D. Chiral effective field theory and nuclear forces. Phys. Rep. 2011, 503, 1–75. [Google Scholar] [CrossRef]
- Epelbaum, E.; Krebs, H.; Reinert, P. High-Precision Nuclear Forces From Chiral EFT: State-of-the-Art, Challenges, and Outlook. Front. Phys. 2020, 8, 98. [Google Scholar] [CrossRef]
- Machleidt, R.; Sammarruca, F. Recent advances in chiral EFT based nuclear forces and their applications. Prog. Part. Nucl. Phys. 2024, 137, 104117. [Google Scholar] [CrossRef]
- Vautherin, D.; Brink, D.M. Hartree-Fock Calculations with Skyrme’s Interaction. I. Spherical Nuclei. Phys. Rev. C 1972, 5, 626–647. [Google Scholar] [CrossRef]
- Bender, M.; Heenen, P.H.; Reinhard, P.G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 2003, 75, 121–180. [Google Scholar] [CrossRef]
- Negele, J.W. The mean-field theory of nuclear structure and dynamics. Rev. Mod. Phys. 1982, 54, 913–1015. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Negele, J.W.; Vautherin, D. Density-Matrix Expansion for an Effective Nuclear Hamiltonian. Phys. Rev. C 1972, 5, 1472–1493. [Google Scholar] [CrossRef]
- Gamow, G. Zur Quantentheorie des Atomkernes. Z. Phys. 1928, 51, 204–212. [Google Scholar] [CrossRef]
- Bohr, N.; Wheeler, J.A. The Mechanism of Nuclear Fission. Phys. Rev. 1939, 56, 426–450. [Google Scholar] [CrossRef]
- Ragnarsson, I.; Nilsson, S.G. Nuclear fission and the liquid-drop model. In Shapes and Shells in Nuclear Structure; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Brack, M.; Damgaard, J.; Jensen, A.S.; Pauli, H.C.; Strutinsky, V.M.; Wong, C.Y. Funny Hills: The Shell-Correction Approach to Nuclear Shell Effects and Its Applications to the Fission Process. Rev. Mod. Phys. 1972, 44, 320–405. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problems; Texts and Monographs in Physics; Springer: New York, NY, USA, 1980. [Google Scholar]
- Roeckl, E. Decay Studies of N~Z Nuclei. Lect. Notes Phys. 2004, 651, 223–261. [Google Scholar] [CrossRef]
- Perez, R.N.; Schunck, N.; Lasseri, R.D.; Zhang, C.; Sarich, J. Axially deformed solution of the Skyrme–Hartree–Fock–Bogolyubov equations using the transformed harmonic oscillator basis (III) hfbtho (v3.00): A new version of the program. Comput. Phys. Commun. 2017, 220, 363–375. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Nucl. Phys. A 1997, 627, 710–746. [Google Scholar] [CrossRef]
- Robledo, L.M.; Rodríguez, T.R.; Rodríguez-Guzmán, R.R. Mean field and beyond description of nuclear structure with the Gogny force: A review. J. Phys. G: Nucl. Part. Phys. 2018, 46, 013001. [Google Scholar] [CrossRef]
- Hirata, D.; Sumiyoshi, K.; Tanihata, I.; Sugahara, Y.; Tachibana, T.; Toki, H. A systematic study of even–even nuclei up to the drip lines within the relativistic mean field framework. Nucl. Phys. A 1997, 616, 438–445. [Google Scholar] [CrossRef]
- Stoitsov, M.V.; Dobaczewski, J.; Nazarewicz, W.; Pittel, S.; Dean, D.J. Systematic study of deformed nuclei at the drip lines and beyond. Phys. Rev. C 2003, 68, 054312. [Google Scholar] [CrossRef]
- Ebata, S.; Nakatsukasa, T. Octupole deformation in the nuclear chart based on the 3D Skyrme Hartree–Fock plus BCS model. Phys. Scr. 2017, 92, 064005. [Google Scholar] [CrossRef]
- Delion, D.S.; Liotta, R.J.; Wyss, R. Systematics of Proton Emission. Phys. Rev. Lett. 2006, 96, 072501. [Google Scholar] [CrossRef]
- Santhosh, K.P.; Biju, R.K.; Sahadevan, S. Spontaneous fission versus alpha radioactivity in heavy and super heavy nuclei. Proc. Int. Symp. Nucl. Phys. 2009, 54, 216–217. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hagihara, K.; Nakatsukasa, T.; Hinohara, N. Effect of the Coulomb Interaction on Nuclear Deformation and Drip Lines. Particles 2025, 8, 72. https://doi.org/10.3390/particles8030072
Hagihara K, Nakatsukasa T, Hinohara N. Effect of the Coulomb Interaction on Nuclear Deformation and Drip Lines. Particles. 2025; 8(3):72. https://doi.org/10.3390/particles8030072
Chicago/Turabian StyleHagihara, Kenta, Takashi Nakatsukasa, and Nobuo Hinohara. 2025. "Effect of the Coulomb Interaction on Nuclear Deformation and Drip Lines" Particles 8, no. 3: 72. https://doi.org/10.3390/particles8030072
APA StyleHagihara, K., Nakatsukasa, T., & Hinohara, N. (2025). Effect of the Coulomb Interaction on Nuclear Deformation and Drip Lines. Particles, 8(3), 72. https://doi.org/10.3390/particles8030072





