Differentiable Deep Learning Surrogate Models Applied to the Optimization of the IFMIF-DONES Facility
Abstract
1. Introduction
2. Materials and Methods
2.1. General Methodology
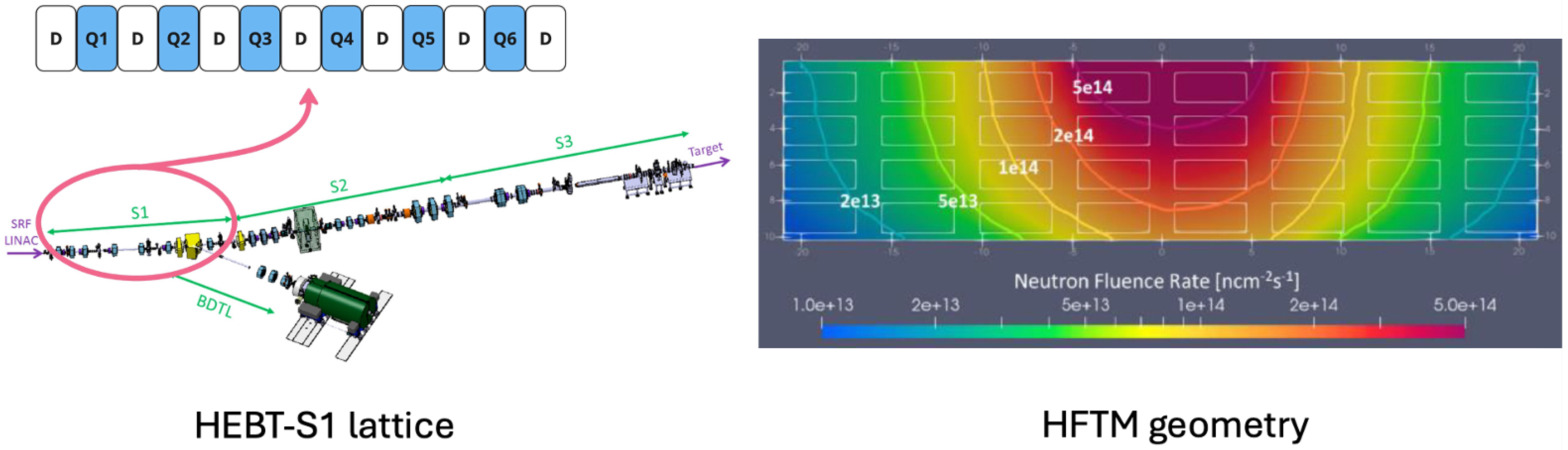
2.2. Optimizing the HEBT-S1 Lattice
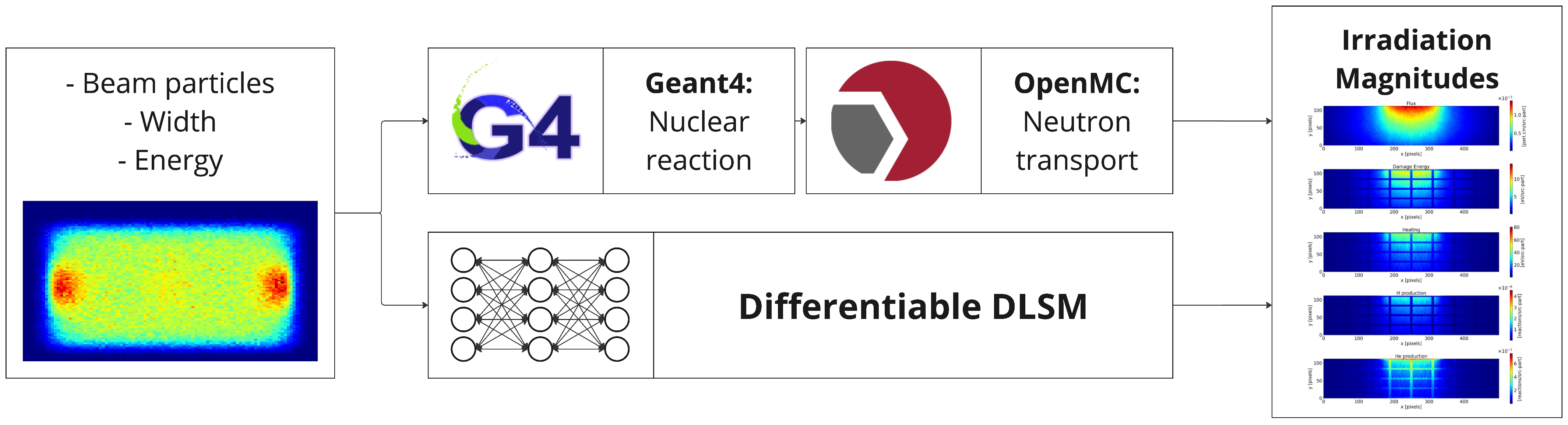
2.3. Surrogates for Materials Irradiation Variables in HFTM
3. Results
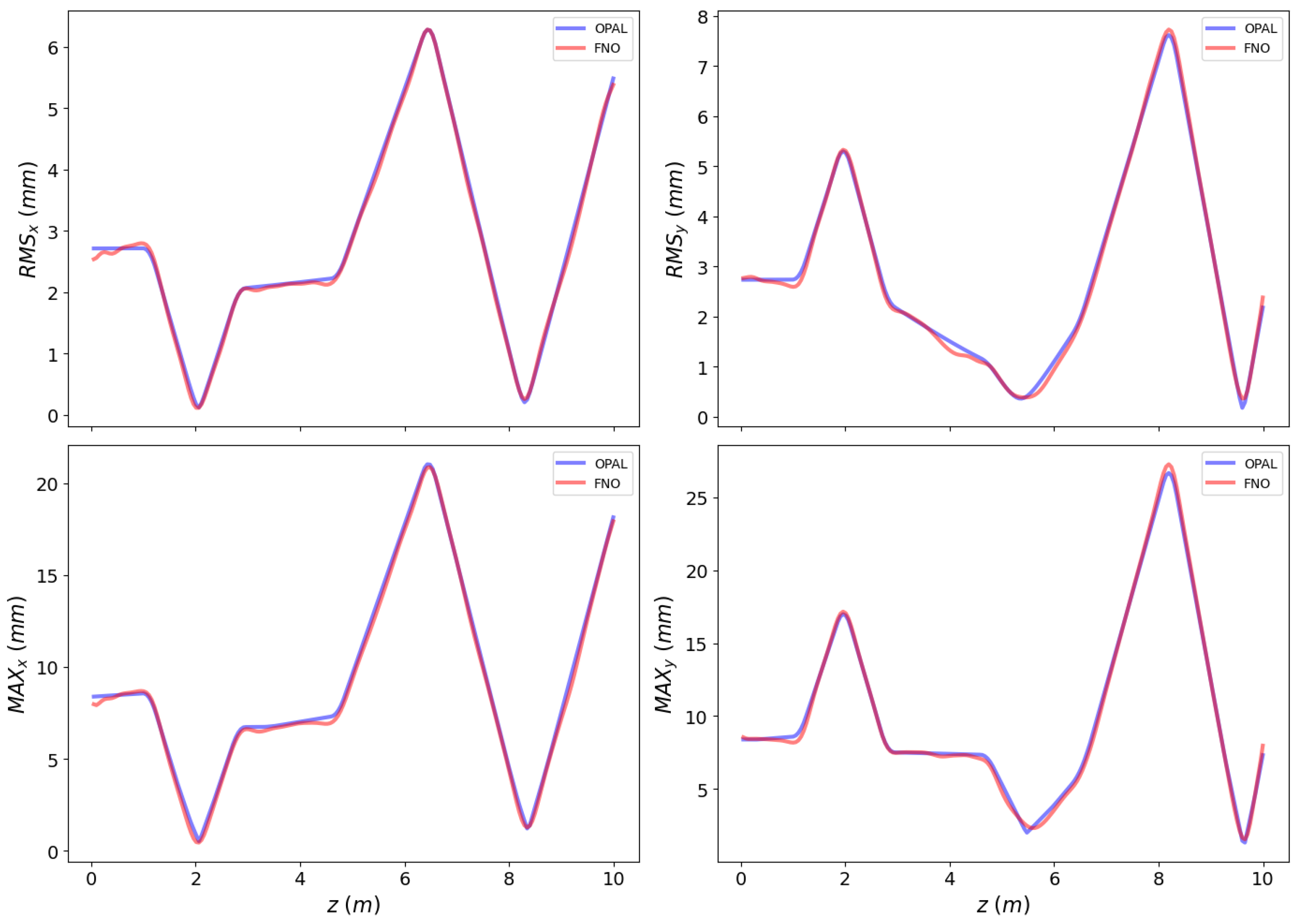
3.1. Quadrupoles Optimization in the HEBT-S1 Lattice
3.2. Neutronic Irradiation Models for HFTM
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DLSM | Deep Learning Surrogate Model |
| DeepONet | Deep Operator Network |
| DRL | Deep Reinforcement Learning |
| FFT | Fast Fourier Transform |
| FNO | Fourier Neural Operator |
| GD | Gradient Descent |
| HEBT-S1 | 1st section of the High Energy Beam Transport line |
| HFTM | High Flux Test Module |
| IFMIF-DONES | International Fusion Materials Irradiation Facility-Demo Oriented Neutron Source |
| MAE | Mean Absolute Error |
| MAPE | Mean Average Percentage Error |
| MC | Monte Carlo |
| MSE | Mean Square Error |
| NMAE | Normalized Mean Average Error |
| NO | Neural Operator |
| PDE | Partial differential equations |
| RMS | Root Mean Square |
| sMAPE | Symmetric Mean Average Percentage Error |
Appendix A. Physical Parameters for the Simulations
| Variable | Value | Description |
|---|---|---|
| Particle | Deuteron | Type of particle used for simulation. |
| Number of particles | 100,000 | Number of particles in the simulation. |
| Energy | 40 MeV | Energy of the particles in the simulation. |
| Injection type | Gauss | Type of distribution used for the injection |
| 28 mm | Standard deviations for the spatial distribution in x, y, and z. | |
| 0.023 | Standard deviations for the momentum distribution in x and y. | |
| 0.039 | Standard deviation for the momentum distribution in z. | |
| MAXSTEPS | 10,000 | Maximum number of simulation steps. |
| DT | 1.65 | Time step for the simulation. |
| ZSTOP | 10 | Stop condition for the z-coordinate during the simulation. |
| METHOD | PARALLEL-T | The OPAL mode. |
| FIELDSOLVER | FFT | Field solver method used in the simulation. |
| 16 | Number of grid points in the x, y, and t directions. | |
| PARFFTX,Y,T | true | Whether the FFT solver is parallelized for x, y, and t. |
| BCFFTX,Y,T | open | Boundary conditions used for the FFT solver in x, y, and t. |
| BBOXINCR | 1 | Increment for the bounding box size. |
| GREENSF | STANDARD | Green’s function type used in the simulation. |
| Variable | Value | Description |
|---|---|---|
| OpenMC | ||
| Run mode | Fixed source | Simulation mode with a constant neutron source. |
| Cross-section library | FENDL 3.2 | Cross-section library used in the simulation. |
| Boundary type | Vacuum | Boundary condition to simulate no reflection at the walls. |
| Material package | neutronics_material_maker | Python library to import materials such as Eurofer 97. |
| Geant4 | ||
| PhysicsList | QGSP_BIC_AllHP | Physics list for accurate modeling of Li(d,xn) stripping reactions. |
| Variable | Description |
|---|---|
| Tally Scores | |
| Flux | Tracks the total particle flux. |
| Heating (MT = 301) | Nuclear heating associated with the reaction rates. |
| Damage-energy (MT = 444) | Calculates the damage energy produced by the reactions. |
| H Production (n, p) | Tally for hydrogen (H) production via (n, p) reactions. |
| He Production (n, a) | Tally for helium (He) production through (n, ) reactions. |
| Filters | |
| MeshFilter | Covers the entire volume of the HFTM geometry. |
| Element | Length (m) | Edge (m) | Element Type |
|---|---|---|---|
| DR1 | 1.00 | 0.00 | Drift |
| Q1 | 0.25 | 1.00 | Quadrupole |
| DR2 | 0.60 | 1.25 | Drift |
| Q2 | 0.25 | 1.85 | Quadrupole |
| DR3 | 0.60 | 2.10 | Drift |
| Q3 | 0.25 | 2.70 | Quadrupole |
| DR4 | 1.65 | 2.95 | Drift |
| Q4F | 0.25 | 4.60 | Quadrupole |
| DR5 | 1.50 | 4.85 | Drift |
| Q5 | 0.25 | 6.35 | Quadrupole |
| DR6 | 1.50 | 6.60 | Drift |
| Q6 | 0.25 | 8.10 | Quadrupole |
| DR7 | 1.65 | 8.35 | Drift |
Appendix B. System Specifications
| Category | Specification |
|---|---|
| System Specifications | |
| GPU Model | NVIDIA GeForce RTX 3060 |
| CUDA Version | 12.2 |
| CPU Model | Intel(R) Core(TM) i9-10900K @ 3.70 GHz |
| CPUs | 12 |
| Software Specifications | |
| OS | Ubuntu 22.04.4 LTS (Docker) |
| nvidia-modulus.sym | 1.5.0 |
| OPAL | 2022.1.0 |
| openmpi | 4.1.4 |
| Torch | 2.3.0 |
| Geant4 | 11.2.1 |
| OpenMC | 0.14.0 |
| DeepXDE | 1.12.0 |
Appendix C. Hyperparameters
| Hyperparameter | Value |
|---|---|
| scheduler | tf_exponential_lr |
| optimizer | adam |
| loss | sum |
| decoder.nr_layers | 1 |
| decoder.layer_size | 256–512 |
| fno.dimension | 1–2 |
| fno.nr_fno_layers | 4 |
| fno.fno_modes | 12 |
| scheduler.decay_rate | 0.95 |
| scheduler.decay_steps | 1000 |
| training.max_steps | 10,000 |
| batch_size.grid | 32–8 |
| batch_size.validation | 32–8 |
| Hyperparameter | Value |
|---|---|
| scheduler | exponential_lr |
| optimizer | adam |
| loss | custom distance |
| scheduler.gamma | 0.999 |
| max_steps | 100,000 |
| early_stop_loss | 0.005 |
| learning_rate | 1 |
| Hyperparameter | Value |
|---|---|
| # trainable parameters | |
| Input layers (Trunk) | 2 neurons |
| Input layers (Branch) | 3 neurons |
| Hidden layers (Trunk) | 6 layers of 100 neurons |
| Hidden layers (Branch) | 5 layers of 50 neurons + 1 of 100 neurons |
| Output layer | 1 neuron |
| Training epochs | |
| Batch size | 1 full image ( points) |
| Learning rate and decay rate | and |
| Optimizer | Adam |
| Loss | MSE |
| Regularization | L2 regularization with L2 parameter |
Appendix D. Optimization Results
| Target (mm) | Achieved (mm) | (Tm−1) | t (min) | n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSx | RMSy | MAXx | MAXy | RMSx | RMSy | MAXx | MAXy | k1 | k2 | k3 | k4 | k5 | k6 | ||
| 5.4 | 2.4 | 18.0 | 8.0 | 5.4 | 2.4 | 17.9 | 8.0 | 5.9 | −7.1 | 6.9 | −5.2 | 5.0 | −6.3 | 10.42 | 1.00 |
| 4.7 | 2.6 | 16.0 | 7.0 | 4.7 | 2.6 | 15.6 | 6.9 | 5.1 | −5.7 | 7.6 | −6.4 | 5.1 | −6.0 | 3.42 | 0.99 |
| 2.5 | 3.4 | 9.0 | 12.0 | 2.6 | 3.1 | 8.9 | 12.0 | 5.0 | −8.0 | 7.4 | −7.7 | 5.0 | −6.9 | 10.44 | 1.00 |
| 3.0 | 3.0 | 11.0 | 10.0 | 3.0 | 3.0 | 10.5 | 9.8 | 5.3 | −6.7 | 7.9 | −8.0 | 5.0 | −6.0 | 1.52 | 0.99 |
| 6.4 | 8.5 | 22.0 | 30.0 | 6.3 | 8.5 | 21.5 | 27.0 | 5.4 | −6.2 | 7.9 | −6.3 | 5.4 | −7.2 | 3.34 | 0.99 |
| 11.8 | 10.4 | 38.9 | 33.0 | 11.7 | 10.3 | 39.0 | 32.5 | 5.0 | −6.3 | 7.9 | −6.6 | 5.9 | −7.5 | 10.45 | 0.99 |
| 16.5 | 1.0 | 50.0 | 3.4 | 16.5 | 1.0 | 49.8 | 3.3 | 6.5 | −7.5 | 7.1 | −5.6 | 6.5 | −5.8 | 2.30 | 0.99 |
| 9.8 | 10.2 | 33.4 | 37.3 | 9.8 | 10.2 | 32.5 | 31.3 | 5.0 | −6.0 | 7.6 | −6.3 | 5.6 | −7.4 | 3.7 | 0.99 |
| 7.0 | 6.6 | 23.5 | 19.5 | 7.0 | 6.0 | 23.2 | 19.5 | 6.4 | −7.8 | 6.2 | −5.0 | 5.0 | −7.8 | 10.43 | 0.99 |
| 13.3 | 4.3 | 48.6 | 14.2 | 13.3 | 4.3 | 45.7 | 13.6 | 5.5 | −6.5 | 7.7 | −6.5 | 6.2 | −6.4 | 1.48 | 0.99 |
| 7.7 | 11.6 | 25.9 | 29.9 | 7.7 | 11.6 | 25.9 | 29.4 | 6.0 | −5.0 | 5.1 | −6.0 | 5.0 | −7.3 | 4.31 | 0.98 |
| 4.2 | 13.1 | 14.5 | 37.5 | 4.1 | 13.1 | 14.5 | 36.7 | 5.0 | −5.5 | 5.0 | −6.9 | 5.0 | −7.6 | 10.47 | 0.99 |
Appendix E. Loss Function for the Optimization Algorithm
Appendix F. Errors
| FNO 1D Model Errors | ||
| Variable | MAPE (%) | MAE |
| RMSx | 4.38 | 0.11 |
| RMSy | 5.63 | 0.16 |
| MAXx | 3.92 | 0.30 |
| MAXy | 3.76 | 0.39 |
| 0.92 | 0.01 | |
| FNO 2D Model Errors | ||
| Variable | MAPE (%) | MAE |
| - | 4.7 | |
| - | 5.6 | |
| Variable | sMAPE (%) | NMAE | R2 |
|---|---|---|---|
| Flux | 2.3 | 0.031 | 0.996 |
| Damage E. | 9.2 | 0.120 | 0.968 |
| Heating | 8.9 | 0.111 | 0.972 |
| H prod. | 16.8 | 0.139 | 0.967 |
| He prod. | 8.3 | 0.095 | 0.977 |
Appendix G. More Test Examples
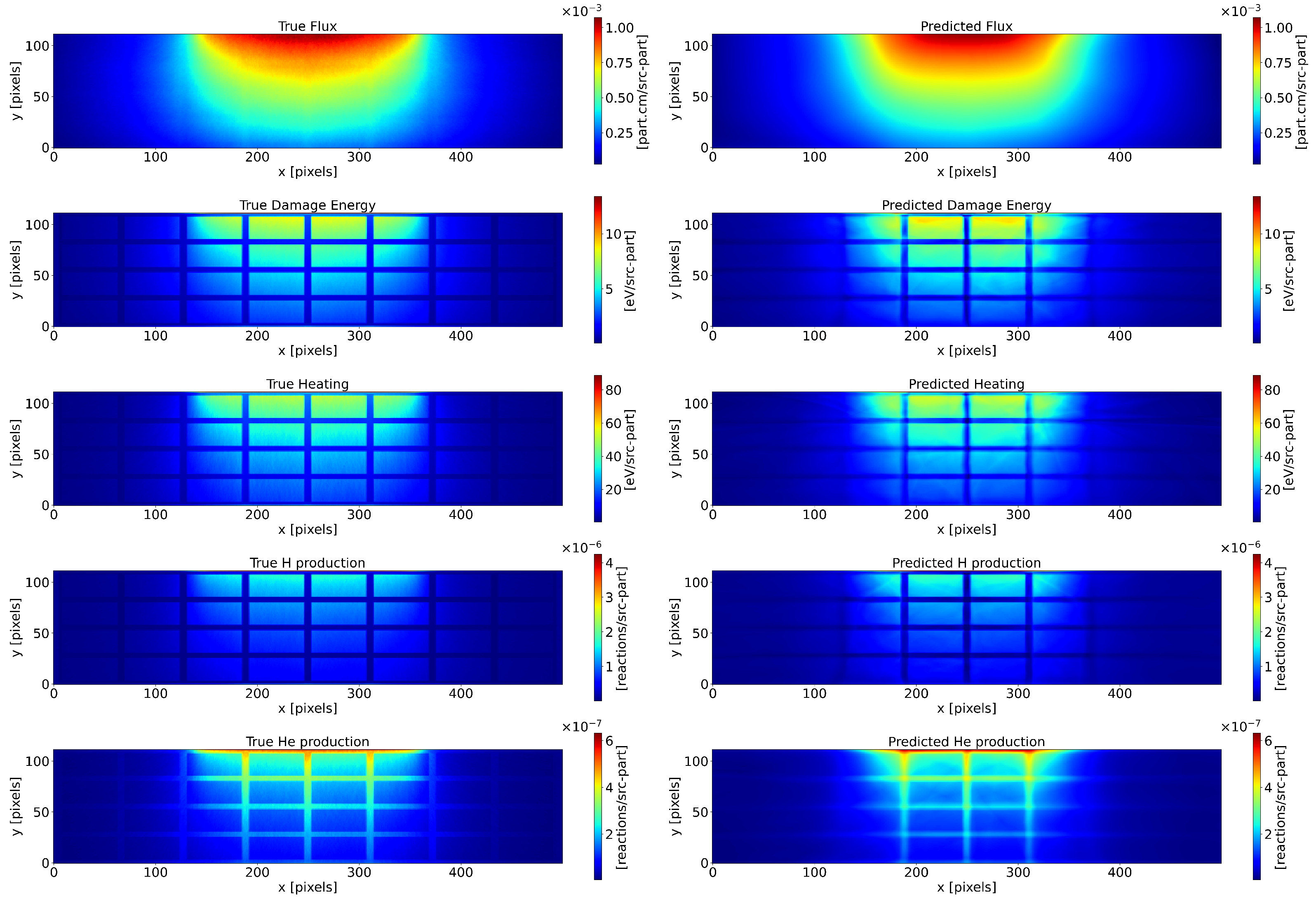
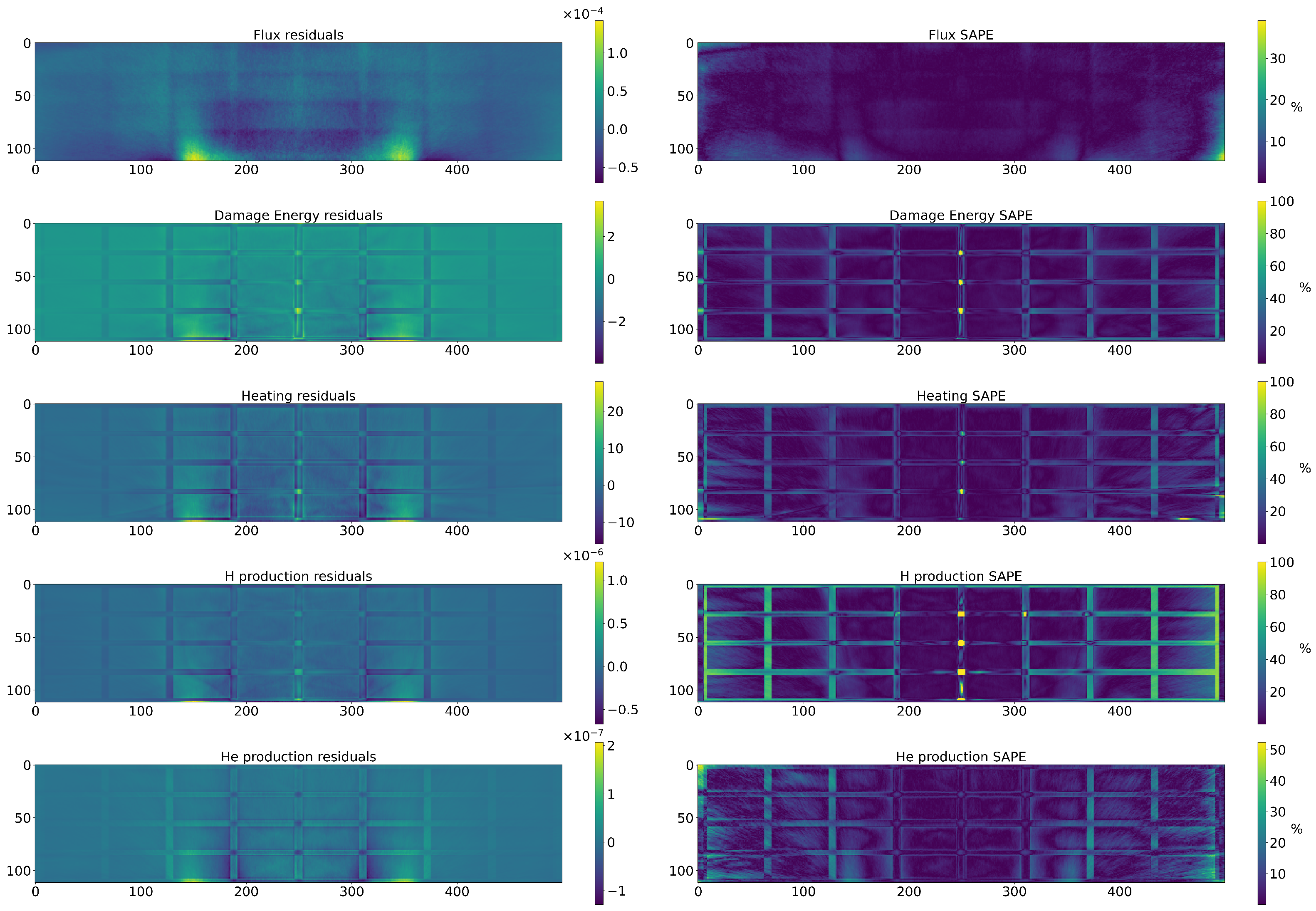
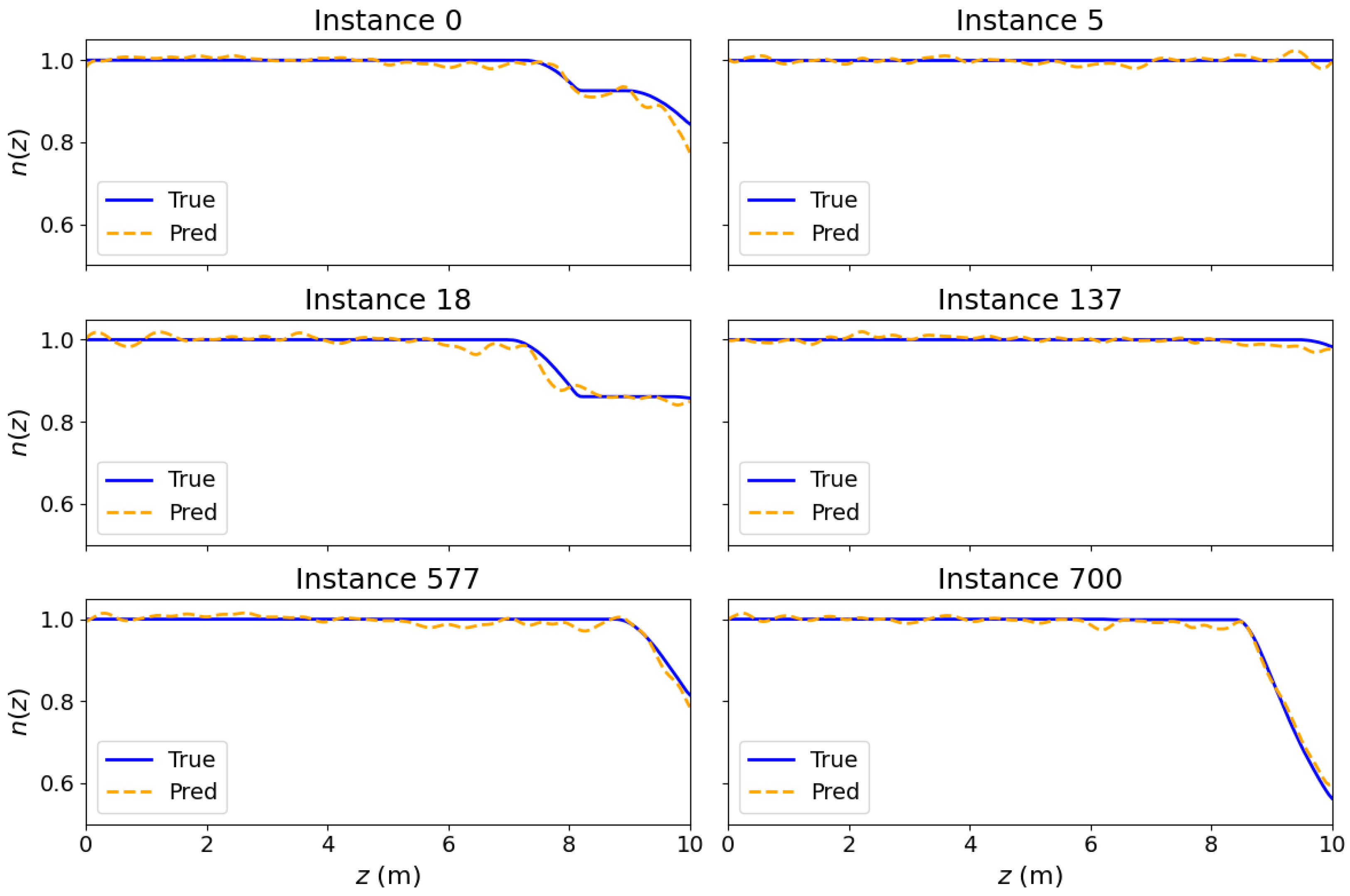
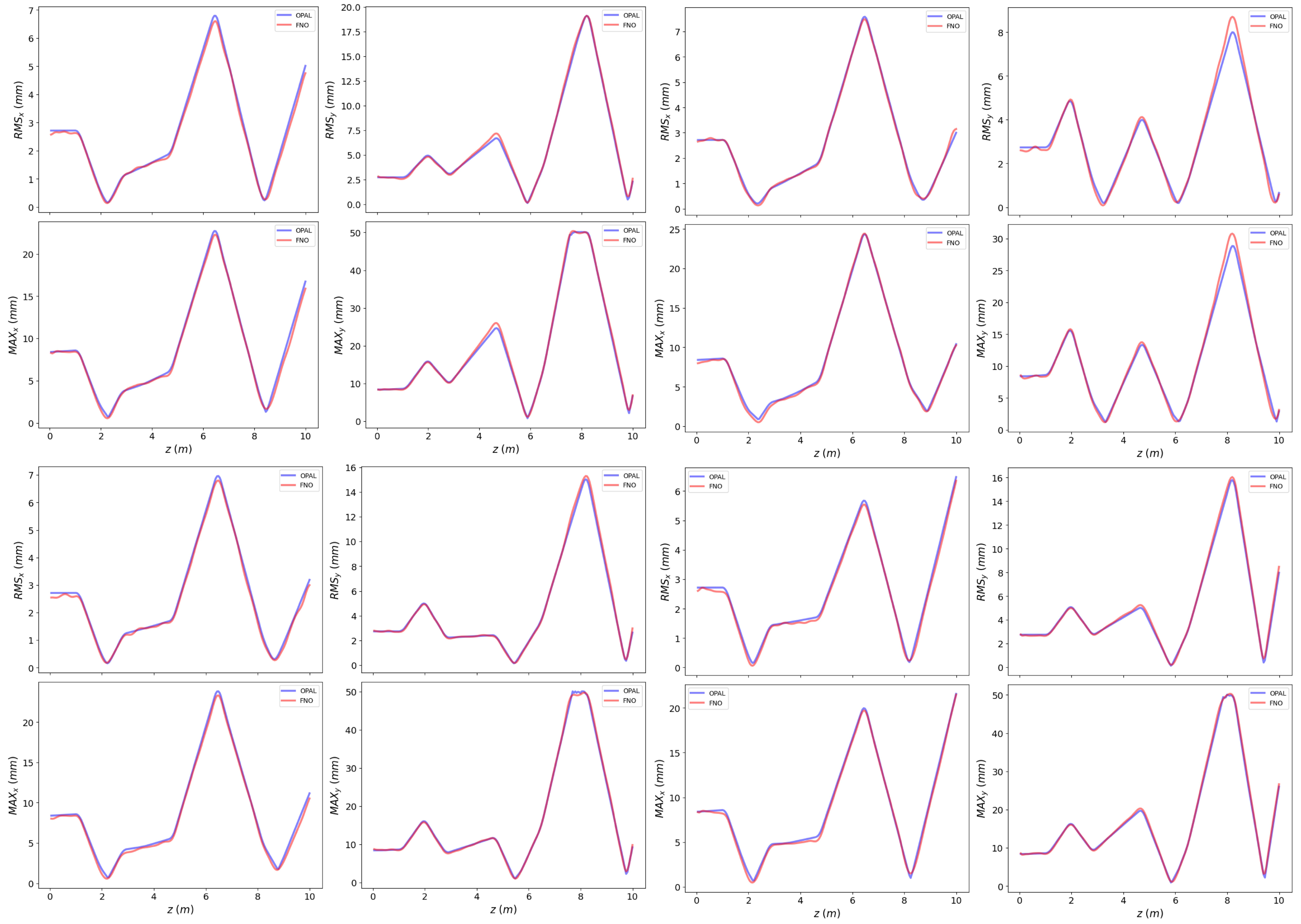

References
- Sadik-Zada, E.R.; Gatto, A.; Weißnicht, Y. Back to the Future: Revisiting the Perspectives on Nuclear Fusion and Juxtaposition to Existing Energy Sources. Energy 2024, 290, 129150. [Google Scholar] [CrossRef]
- Alba, R.; Iglesias, R.; Cerdeira, M.Á. Materials to Be Used in Future Magnetic Confinement Fusion Reactors: A Review. Materials 2022, 15, 6591. [Google Scholar] [CrossRef]
- Ibarra, A.; Arbeiter, F.; Bernardi, D.; Krolas, W.; Cappelli, M.; Fischer, U.; Heidinger, R.; Martin-Fuertes, F.; Micciché, G.; Muñoz, A.; et al. The European Approach to the Fusion-like Neutron Source: The IFMIF-DONES Project. Nucl. Fusion 2019, 59, 065002. [Google Scholar] [CrossRef]
- Qiu, Y.; Arbeiter, F.; Fischer, U.; Schwab, F. IFMIF-DONES HFTM Neutronics Modeling and Nuclear Response Analyses. Nucl. Mater. Energy 2018, 15, 185–189. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N.; Koutsourelakis, P.S.; Perdikaris, P. Physics-Constrained Deep Learning for High-Dimensional Surrogate Modeling and Uncertainty Quantification without Labeled Data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
- Ruder, S. An Overview of Gradient Descent Optimization Algorithms. arXiv 2017, arXiv:1609.04747. [Google Scholar]
- Li, Y. Deep Reinforcement Learning: An Overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Azizzadenesheli, K.; Kovachki, N.; Li, Z.; Liu-Schiaffini, M.; Kossaifi, J.; Anandkumar, A. Neural Operators for Accelerating Scientific Simulations and Design. Nat. Rev. Phys. 2024, 6, 320–328. [Google Scholar] [CrossRef]
- Kovachki, N.; Li, Z.; Liu, B.; Azizzadenesheli, K.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Neural Operator: Learning Maps between Function Spaces with Applications to PDEs. J. Mach. Learn. Res. 2024, 24, 4061–4157. [Google Scholar]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier Neural Operator for Parametric Partial Differential Equations. arXiv 2021, arXiv:2010.08895. [Google Scholar]
- Lu, L.; Jin, P.; Karniadakis, G.E. DeepONet: Learning Nonlinear Operators for Identifying Differential Equations Based on the Universal Approximation Theorem of Operators. Nat. Mach. Intell. 2021, 3, 218–229. [Google Scholar] [CrossRef]
- Pathak, J.; Subramanian, S.; Harrington, P.; Raja, S.; Chattopadhyay, A.; Mardani, M.; Kurth, T.; Hall, D.; Li, Z.; Azizzadenesheli, K.; et al. FourCastNet: A Global Data-driven High-resolution Weather Model Using Adaptive Fourier Neural Operators. arXiv 2022, arXiv:2202.11214. [Google Scholar]
- Kushwaha, S.; Park, J.; Koric, S.; He, J.; Jasiuk, I.; Abueidda, D. Advanced Deep Operator Networks to Predict Multiphysics Solution Fields in Materials Processing and Additive Manufacturing. arXiv 2024, arXiv:2403.14795. [Google Scholar] [CrossRef]
- Kobayashi, K.; Alam, S.B. Deep Neural Operator-Driven Real-Time Inference to Enable Digital Twin Solutions for Nuclear Energy Systems. Sci. Rep. 2024, 14, 2101. [Google Scholar] [CrossRef]
- Podadera, I.; Ibarra, A.; Jiménez-Rey, D.; Mollá, J.; Nomen, O.; Oliver, C.; Sánchez-Herranz, D.; Varela, R.; Villamayor, V. Beam Diagnostics for the Multi-MW High Energy Beam Transport Line of DONES. In Proceedings of the 8th International Beam Instrumentation Conference (IBIC’19), Malmö, Sweden, 8–12 September 2019; JACOW Publishing: Geneva, Switzerland, 2019; pp. 200–204. [Google Scholar] [CrossRef]
- Álvarez, I.; Anguiano, M.; Mota, F.; Hernández, R.; Qiu, Y. Neutronic Assessment of the IFMIF-DONES HFTM Specimen Stack Distribution. Fusion Eng. Des. 2024, 200, 114212. [Google Scholar] [CrossRef]
- Oliver, C.; Dzitko, H.; Ibarra, A.; Mollá, J.; Nomen, O.; Podadera, I.; Sánchez-Herranz, D.; Varela, R. Impact of the Magnet Alignment and Field Errors on the Output Uniform Beam at the DONES HEBT Line. In Proceedings of the 12th International Particle Accelerator Conference 2021, IPAC2021, Campinas, Brazil, 24–28 May 2021; pp. 3251–3253. [Google Scholar] [CrossRef]
- Adelmann, A.; Calvo, P.; Frey, M.; Gsell, A.; Locans, U.; Metzger-Kraus, C.; Neveu, N.; Rogers, C.; Russell, S.; Sheehy, S.; et al. OPAL a Versatile Tool for Charged Particle Accelerator Simulations. arXiv 2019, arXiv:1905.06654. [Google Scholar]
- Hennigh, O.; Narasimhan, S.; Nabian, M.A.; Subramaniam, A.; Tangsali, K.; Rietmann, M.; Ferrandis, J.d.A.; Byeon, W.; Fang, Z.; Choudhry, S. NVIDIA SimNetTM: An AI-accelerated Multi-Physics Simulation Framework. arXiv 2020, arXiv:2012.07938. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Simakov, S.P.; Fischer, U.; Kondo, K.; Pereslavtsev, P. Status of the McDeLicious Approach for the D-Li Neutron Source Term Modeling in IFMIF Neutronics Calculations. Fusion Sci. Technol. 2012, 62, 233–239. [Google Scholar] [CrossRef]
- Serikov, A.; FISCHER, U.; GROSSE, D. High Performance Parallel Monte Carlo Transport Computations for ITER Fusion Neutronics Applications. Prog. Nucl. Sci. Technol. 2011, 2, 294–300. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A Simulation Toolkit. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Romano, P.K.; Horelik, N.E.; Herman, B.R.; Nelson, A.G.; Forget, B.; Smith, K. OpenMC: A State-of-the-Art Monte Carlo Code for Research and Development. Ann. Nucl. Energy 2015, 82, 90–97. [Google Scholar] [CrossRef]
- Álvarez, I.; Anguiano, M.; Mota, F.; Hernández, R.; Moro, F.; Noce, S.; Qiu, Y.; Park, J.; Arbeiter, F.; Palermo, I.; et al. Comparative Analysis of Neutronic Features for Various Specimen Payload Configurations within the IFMIF-DONES HFTM. Fusion Eng. Des. 2025, 210, 114729. [Google Scholar] [CrossRef]
- Hu, Y.; Qiu, Y.; Fischer, U.; Lu, Y. Benchmarking and Verification of the OpenMC Code for Accelerator-Based Neutron Source Analyses. Fusion Eng. Des. 2021, 170, 112512. [Google Scholar] [CrossRef]
- Mendoza, E.; Cano-Ott, D.; Ibarra, A.; Mota, F.; Podadera, I.; Qiu, Y.; Simakov, S.P. Nuclear Data Libraries for IFMIF-DONES Neutronic Calculations. Nucl. Fusion 2022, 62, 106026. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A Deep Learning Library for Solving Differential Equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, H.; Kovachki, N.; Jin, D.; Chen, H.; Liu, B.; Azizzadenesheli, K.; Anandkumar, A. Physics-Informed Neural Operator for Learning Partial Differential Equations. arXiv 2023, arXiv:2111.03794. [Google Scholar] [CrossRef]
- Rodríguez-Llorente, G.; Romero, G.G.; Martín, R.G.E. Applications of Fourier Neural Operators in the Ifmif-Dones Accelerator. In Proceedings of the ICLR 2024 Workshop on AI4DifferentialEquations in Science, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Lindstrøm, C.A.; Thévenet, M. Emittance Preservation in Advanced Accelerators. J. Instrum. 2022, 17, P05016. [Google Scholar] [CrossRef]
- He, J.; Koric, S.; Abueidda, D.; Najafi, A.; Jasiuk, I. Geom-DeepONet: A Point-Cloud-Based Deep Operator Network for Field Predictions on 3D Parameterized Geometries. Comput. Methods Appl. Mech. Eng. 2024, 429, 117130. [Google Scholar] [CrossRef]

| Parameter | Ranges | Step |
|---|---|---|
| Energy () | 20–40 MeV | 5 MeV |
| Beam width (L) | 10–20 cm | 2 cm |
| Parameter | Values | |
| Number of deuterons (D) | , , , , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallardo Romero, G.; Rodríguez-Llorente, G.; Magariños Rodríguez, L.; Morant Navascués, R.; Khvatkin Petrovsky, N.; Lorenzo Ortega, R.; Gómez-Espinosa Martín, R. Differentiable Deep Learning Surrogate Models Applied to the Optimization of the IFMIF-DONES Facility. Particles 2025, 8, 21. https://doi.org/10.3390/particles8010021
Gallardo Romero G, Rodríguez-Llorente G, Magariños Rodríguez L, Morant Navascués R, Khvatkin Petrovsky N, Lorenzo Ortega R, Gómez-Espinosa Martín R. Differentiable Deep Learning Surrogate Models Applied to the Optimization of the IFMIF-DONES Facility. Particles. 2025; 8(1):21. https://doi.org/10.3390/particles8010021
Chicago/Turabian StyleGallardo Romero, Galo, Guillermo Rodríguez-Llorente, Lucas Magariños Rodríguez, Rodrigo Morant Navascués, Nikita Khvatkin Petrovsky, Rubén Lorenzo Ortega, and Roberto Gómez-Espinosa Martín. 2025. "Differentiable Deep Learning Surrogate Models Applied to the Optimization of the IFMIF-DONES Facility" Particles 8, no. 1: 21. https://doi.org/10.3390/particles8010021
APA StyleGallardo Romero, G., Rodríguez-Llorente, G., Magariños Rodríguez, L., Morant Navascués, R., Khvatkin Petrovsky, N., Lorenzo Ortega, R., & Gómez-Espinosa Martín, R. (2025). Differentiable Deep Learning Surrogate Models Applied to the Optimization of the IFMIF-DONES Facility. Particles, 8(1), 21. https://doi.org/10.3390/particles8010021







