Abstract
The deformed relativistic Hartree–Bogoliubov theory in continuum (DRHBc) has garnered significant attention for its ability to describe the properties of nuclei across the entire nuclear chart, from light to heavy nuclei, including both stable and exotic ones. As part of ongoing efforts to construct a mass table using the DRHBc theory, determining the ground states of nuclei is a crucial task in the systematic studies of deformed nuclei. In this work, a strategy for identifying the ground state in the superheavy nuclei region is proposed and evaluated, by taking and 135 isotopes as examples. First, we examine how the step size of the initial quadrupole deformation parameter, , affects the pattern of the potential energy curves (PECs) and the determination of the ground state. Our findings indicate that producing smooth and well-defined PECs while maintaining an acceptable numerical cost. Next, we explore the convergence of PECs with respect to the angular momentum cutoff, . Based on the results, we recommend using , especially for nuclei with competing oblate and prolate minima. Finally, we conclude that the accurate identification of the ground state can be achieved by performing unconstrained calculations around the minima of the PECs.
1. Introduction
The importance of nuclear mass cannot be overstated in the realm of nuclear physics [1,2]. It serves as a fundamental property that influences various phenomena, including nuclear stability, decay processes, and the structure of atomic nuclei. Accurate knowledge of nuclear masses is essential for understanding the underlying nucleon–nucleon interactions and for predicting the behavior of isotopes in astrophysical environments, such as nucleosynthesis in stars [3,4] and stellar neutrino emission [5].
The nuclear mass of superheavy nuclei [6] with is particularly interesting, in the sense that the exploration of charge and mass limits of atomic nuclei and the synthesis of long-lived or stable superheavy nuclei are at the frontier of modern nuclear physics [7,8,9]. Determining the ground states of superheavy nuclei is exceptionally challenging due to their short-lived nature and the complexities associated with their production. Nevertheless, advancements in experimental techniques, such as the use of gas-filled separators [10] and advanced detection systems [11,12], have enabled significant progress in identifying and characterizing these elusive nuclei. The insights gained from these studies are crucial for understanding the limits of nuclear stability and exploring the location of the island of stability [13,14]. Experimentally, the element Og with proton number is the highest Z element observed so far [15]. Although we have witnessed the prosperous development of new generations of radioactive ion beam facilities, most neutron-rich nuclei far from the stability valley will remain beyond experimental access in the foreseeable future.
A reliable theoretical nuclear mass table is highly desired to further understand the nuclear landscape. Lots of efforts towards precise descriptions of nuclear masses have been made with various macroscopic–microscopic models [16,17,18], nonrelativistic density functional theories (DFTs) with Skyrme [19,20] and Gogny [21] interactions, and relativistic DFTs [22,23,24,25,26,27,28,29,30,31]. Among them, the deformed relativistic Hartree–Bogoliubov theory in continuum (DRHBc) [32,33] with the PC-PK1 [34] density functional has shown its remarkable ability on the satisfactory description of the ground-state properties with powerful explorations [35], due to the self-consistent consideration of the nuclear superfluidity, deformation, and continuum effects. In particular, the DRHBc Mass Table Collaboration [36] represents a concerted effort not only to calculate masses for stable and unstable nuclei but also to provide a more complete picture of the nuclear landscape.
Systematic numerical convergence checks from light to heavy nuclei for the DRHBc calculations have been justified in refs. [33,37]. Following the strategy and techniques presented in those articles, the nuclear mass table calculated by the DRHBc theory with PC-PK1 has been constructed for even–even nuclei [28] and even-Z nuclei with [29]. Recently, this collaboration has extended its research scope to heavier nuclei.
In this work, we focus on the application of the DRHBc theory in the superheavy region with , especially the determination of the ground state. In the literature, those nuclei with are also called hyperheavy nuclei [38,39,40]. This paper is organized as follows: Section 2 provides a brief overview of the theoretical framework, while Section 3 presents the numerical details. The results and discussions are presented in Section 4, and a summary is given in Section 5.
2. Theoretical Framework
For the sake of completeness, we lay out some key elements of the DRHBc theory with point-coupling density functionals. For details on the theoretical framework, we refer the reader to refs. [32,33,37,41].
The relativistic Hartree–Bogoliubov (RHB) equation describing the motion of nucleons in nuclei reads
where is the Dirac Hamiltonian, is the pairing field, is the Fermi energy for neutron or proton , are the quasiparticle wave functions, and is the quasiparticle energy.
In a nuclear system with time-reversal symmetry, the Dirac Hamiltonian in the coordinate space is written as
Here, M is the nucleon mass, and are Dirac matrices, and and are the scalar and vector potentials. In the point-coupling framework [34], the scalar potential and vector potential are defined as follows
where is the electric potential, for neutron and proton. The coupling constants ’s, ’s, ’s, and ’s are adjustable parameters in the point-coupling Lagrangian and can be determined by fitting the binding energies and charge radii of a set of spherical nuclei as in ref. [34]. The local densities , and are calculated with the quasiparticle wave functions
Note that the no-sea approximation is adopted in Equation (4), i.e., the summations are performed only over the quasiparticle states in the Fermi sea.
The pairing field in the RHB Equation (1) is expressed as [32,33]
where the spin and isospin indexes are not shown for simplicity. The quantity is the pairing tensor and is the density-dependent zero-range pairing force
In Equation (6), is the pairing strength, is the saturation density of nuclear matter, is the projector for the spin-zero component in the pairing channel.
A deformed model is employed here because it enables us to determine the shape of nuclei, whether they are spherical or axially deformed, based on the total energies. This is definitely important because most studies on hyperheavy nuclei within DFTs [38,39,42,43] have been performed only for spherical shapes, while there is no guarantee that spherical minimum in potential energy surface exists for those nuclei. For an axially deformed nucleus with spatial reflection symmetry, the potentials in Equation (3) and densities in Equation (4) can be expanded in terms of the Legendre polynomials
with
In practical calculations, the deformed RHB Equation (1) is solved in a spherical Dirac Woods–Saxon basis, which is obtained by solving a Dirac equation with spherical scalar and vector potentials in Woods–Saxon forms [44]. Both the positive- and negative-energy states for the solution of Dirac equations are considered. In recent years, the completeness of the full Dirac space is crucial also for ab initio studies of nuclear structure [45] and nuclear matter [46,47]. The solution of the RHB equations provides us with the expansion coefficients of quasiparticle wave functions, from which new densities and potentials can be obtained. These quantities are iterated in the RHB equations until the convergence is achieved.
3. Numerical Details
The numerical details for constructing the DRHBc mass table have been examined thoroughly in refs. [33,37]. For nuclei with , according to ref. [37], the box size and the mesh size are fm and fm; the energy cutoff for the levels in the Fermi sea is MeV; the number of states in the Dirac sea is taken to be the same as that in the Fermi sea; The angular momentum cutoff is ; the Legendre expansion truncation in Equation (7) is chosen as for nuclei with , and , respectively. For the pairing channel, the pairing strength and the sharp pairing window of 100 MeV are used. A detailed examination of the numerical details for nuclei with is in progress. In this work, we will discuss the convergence of potential energy curves (PECs) with respect to the in the region of superheavy nuclei. Other numerical details are aligned with the suggestions in Refs. [33,37], including typically the Legendre expansion truncation and the box size fm.
The point-coupling density functional PC-PK1 is used in this work. Uncertainty quantification of DRHBc calculations from parameters can be obtained with thorough analysis of parameter fitting [48,49] and/or using machine learning techniques [50,51], which are beyond this scope and can be considered in future work. Regarding the extrapolation reliability of the theoretical framework and density functional adopted in this work, ref. [35] has shown that the DRHBc theory with PC-PK1 has an impressive performance.
In addition, for the following discussions, we temporarily adopt a systematic IUPAC name for nuclei with [52]. Specifically, nuclei with and are named by Utq and Utp, respectively.
4. Results and Discussion
Firstly, we investigate how the pattern of PECs changes as the step size of the initial quadrupole deformation parameter is varied. Here, has a standard meaning of deformations of the ellipsoid-like density distributions. One can easily expect that for too small the calculation costs cannot be ignored, while for too large the PECs are not smooth though to locate the local minimum. In Figure 1, we show the PECs of with three different initial deformation step sizes, i.e., 0.1, 0.05, and 0.01. For clarity, the values for and have been shifted by adding up 20 and 10 MeV. Obviously, constrained calculations with lead to an overly dense PEC, which is not necessary since there are 200 times calculations in the range of . On the other hand, provides a loose PEC which is dangerous for possible missing of local minimum. Choosing is a very appropriate compromise considering both the computational cost and smoothness, as can be seen in Figure 1. We also show the unconstrained results, which is consistent with the constrained calculations. In the discussions below, if there is no explicit statement, the PECs are obtained with an initial deformation step size .
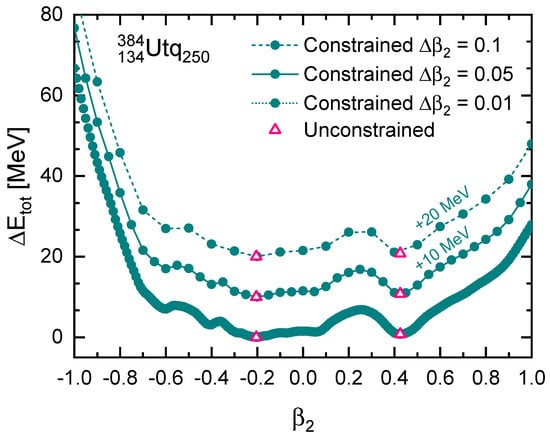
Figure 1.
Potential energy curves of in constrained DRHBc calculations with initial deformation step size (upper), 0.05 (middle), and 0.01 (lower). The unconstrained results are also shown with pink empty triangles. The energy for the ground state has been shifted to zero, while the values for and have been additionally shifted by adding up 20 and 10 MeV, respectively.
In Figure 1, one finds that the ground state results from the competition between two local minima. One has an oblate deformation with , the other one has a prolate deformation with , which is much larger than the deformation for most nuclei [53]. According to the conventional deformed shell model, a larger prolate deformation causes a greater downward shift in single-particle levels with high angular momentum. Besides, the PECs in Figure 1 do not show fission possibilities even for , which is unusual for such a superheavy nucleus. These two facts imply that the present cutoff of the angular momentum might not be enough to contain high-order orbits for the superheavy nuclei.
Figure 2 shows how the PECs evolve with the increasing . The nucleus is chosen as an example because, for the normal cutoff , the ground state is located at , which has a large prolate deformation that needs to be checked. As expected, with the increase in , the total energies with extreme deformations decrease and a fission pattern is found. For deformation in the range of , as highlighted with two pink vertical dashed lines, has already provided a large enough cutoff. In contrast, for a larger deformation with , is a better cutoff not only to obtain converged results but also to find the correct ground state. Notice that in these calculations, the pairing effects are neglected for simplicity as conducted in ref. [33]. Furthermore, increasing the Legendre expansion truncation from 10 to 12 does not alter the conclusion here.
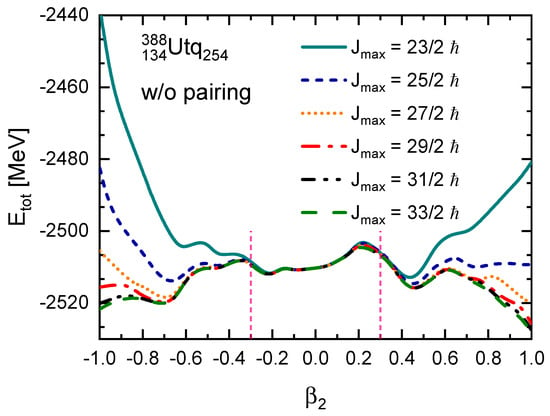
Figure 2.
Potential energy curves of with the angular momentum cutoff ranging from to . The pairing correlation is neglected. Two pink vertical dashed lines at are used to guide the eye.
The observations from the previous two figures inspire us the following three steps in the determination of the ground state:
- Choose the initial deformation step size with to obtain a smooth enough PEC with acceptable computational costs.
- Check the total energies for large deformation with by calculations with .
- Perform unconstrained calculations in the vicinity of local minima in PEC. The configuration with the lowest total energy is the ground state.
Following the above strategy, we study the total energies of as a function of deformation and present the results in Figure 3. In this case, we consider the pairing through the Bogoliubov theory, where the pairing strengths are fixed at for [33] and for . Both combinations can reproduce the experimental odd–even mass differences in Ca and Pb isotope chains as in ref. [33]. It should be mentioned that a weaker pairing strength is required for a higher angular momentum cutoff because the zero-range pairing force adopted in Equation (6) needs to be renormalized to the enlarged model space.
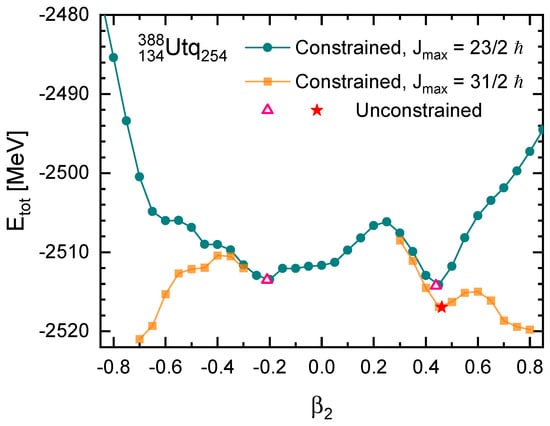
Figure 3.
Potential energy curves of in constrained DRHBc calculations with the angular momentum cutoff and initial deformation step size . The results for constrained calculations with higher for and unconstrained calculations are also shown.
From the PEC shown in Figure 3, the modification on total energy from to becomes more evident for larger deformation. Moreover, it is evident that there is competition between the two minima. This indicates that indeed provides a PEC with smoothness and clarity. Since the right minimum is around , it is necessary to perform examinations with a larger cutoff of angular momentum. By increasing to , the total energies around the prolate minimum decrease by 2–3 MeV, prohibiting a more advantageous stability in comparison with its competitor with oblate deformation. For the oblate side, we also perform calculations with , while no new minimum is found in addition to the one with . After the unconstrained calculations, we come to the conclusion that the ground-state energy of is MeV with deformation .
The strategy for determining the ground state is applied to three additional nuclei in the isotope chain with , 288, and 320. These three nuclei are chosen as representatives considering that the proton and neutron drip lines in this isotope chain are at and , respectively. As depicted in Figure 4, is a good choice to obtain smooth and clear PECs, for both and . For , the candidate for ground state at the oblate side has a deformation of , while the candidate at the other side is less deformed. By increasing the cutoff of angular momentum, the ground state is confirmed with an oblate deformation with a lower total energy. For , the situation is reversed and it is the prolate candidate that has large deformation and needs to be checked. Interestingly, calculations with find a more stable minimum with larger oblate deformation , which does not show up with . This indicates that the examination with a larger cutoff is of high necessity even for cases where the oblate and/or prolate deformation of ground-state candidates is not larger than . For shown in the lower panel in Figure 4, the PEC is rather simple with , showing a softness around the spherical configuration. However, with , an oblate minimum shows up, which is found to be the ground state.
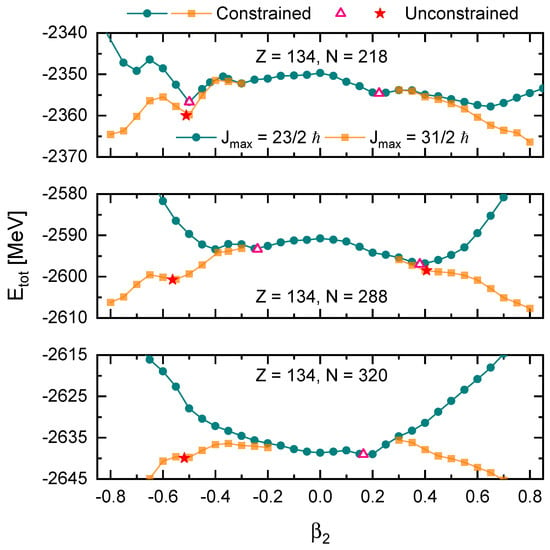
Figure 4.
Potential energy curves of nucleus with 218 (upper), 288 (middle), and 320 (lower) in constrained DRHBc calculations with initial deformation step size . Results with , as well as the ones with , for , 288, and 320 are shown. The unconstrained results are also shown with pink empty triangles and red stars.
All the aforementioned discussions are for even–even nuclei. The three steps are further applied to odd-A nuclei, where the time-reversal invariance is retained by blocking the quasiparticle configurations within the equal-filling approximation [37]. In Figure 5, the PECs of three nuclei in the isotope chain with N = 218, 288 and 320 are given. Despite the difficulties in a quite demanding computational procedure, a smooth and clear PEC can be obtained with initial deformation step size . Besides, by increasing from to , one can identify the correct ground state, no matter if it is oblate or prolate with a deformation parameter smaller or larger than .
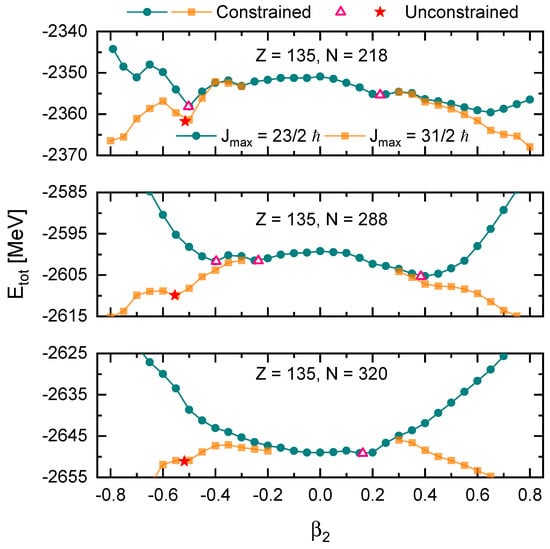
Figure 5.
Similar to Figure 4, but for nucleus .
5. Summary
Determining the ground states of superheavy nuclei is particularly challenging but important for both experimental and theoretical studies. Starting from the PC-PK1 point-coupling density functional, we studied the properties of superheavy nuclei with and 135 within the deformed relativistic Hartree–Bogoliubov theory in continuum (DRHBc). By investigating how the pattern of potential energy curves (PECs) varies with the changes in the step size for the initial quadrupole deformation parameter and its convergence with respect to the cutoff of angular momentum , we propose three steps for determining the ground state, in balancing the computational complexity and accuracy:
- Choose the initial deformation step size with to obtain a smooth enough PEC with acceptable computational costs.
- Check the total energies for large deformation with by calculations with .
- Perform unconstrained calculations in the vicinity of local minima in PEC. The configuration with the lowest total energy is the ground state.
These three steps are then applied to three representative nuclei in the isotope chain with , and 320. The ground states for the first two nuclei arise from the competition between oblate and prolate configurations which are already observed with , while the ground state for is obtained only after performing calculations with . The validation of the strategy is also confirmed for odd-A nuclei with and and 320. This work provides guidance for large-scale calculations of superheavy nuclei as a new extension of the DRHBc mass table.
Author Contributions
Conceptualization, S.W.; methodology, P.G. and C.P.; software, P.G. and C.P.; formal analysis, S.W.; writing—original draft preparation, S.W.; writing—review and editing, All authors; visualization, S.W.; project administration, S.W.; funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China (NSFC) under Grant No. 12205030, and the Project No. 2024CDJXY022 supported by the Fundamental Research Funds for the Central Universities. Part of this work was achieved by using the supercomputer OCTOPUS at the Cybermedia Center, Osaka University under the support of Research Center for Nuclear Physics of Osaka University.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
S.W. thanks Xin-Hui Wu for fruitful discussions. Helpful discussions with members of the DRHBc Mass Table Collaboration are highly appreciated.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lunney, D.; Pearson, J.M.; Thibault, C. Recent trends in the determination of nuclear masses. Rev. Mod. Phys. 2003, 75, 1021–1082. [Google Scholar] [CrossRef]
- Blaum, K. High-accuracy mass spectrometry with stored ions. Phys. Rep. 2006, 425, 1–78. [Google Scholar] [CrossRef]
- Mumpower, M.; Surman, R.; McLaughlin, G.; Aprahamian, A. The impact of individual nuclear properties on r-process nucleosynthesis. Prog. Part. Nucl. Phys. 2016, 86, 86–126. [Google Scholar] [CrossRef]
- Jiang, X.F.; Wu, X.H.; Zhao, P.W. Sensitivity Study of r-process Abundances to Nuclear Masses. Astrophys. J. 2021, 915, 29. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G.F.; Schulze, H.J.; Taranto, G. Nucleon effective masses within the Brueckner-Hartree-Fock theory: Impact on stellar neutrino emission. Phys. Rev. C 2014, 89, 048801. [Google Scholar] [CrossRef]
- Hofmann, S.; Münzenberg, G. The discovery of the heaviest elements. Rev. Mod. Phys. 2000, 72, 733–767. [Google Scholar] [CrossRef]
- Oganessian, Y.T.; Utyonkov, V.K. Super-heavy element research. Rep. Prog. Phys. 2015, 78, 036301. [Google Scholar] [CrossRef] [PubMed]
- Giuliani, S.A.; Matheson, Z.; Nazarewicz, W.; Olsen, E.; Reinhard, P.G.; Sadhukhan, J.; Schuetrumpf, B.; Schunck, N.; Schwerdtfeger, P. Colloquium: Superheavy elements: Oganesson and beyond. Rev. Mod. Phys. 2019, 91, 011001. [Google Scholar] [CrossRef]
- Smits, O.R.; Düllmann, C.E.; Indelicato, P.; Nazarewicz, W.; Schwerdtfeger, P. The quest for superheavy elements and the limit of the periodic table. Nat. Rev. Phys. 2024, 6, 86–98. [Google Scholar] [CrossRef]
- Gregorich, K. Simulation of recoil trajectories in gas-filled magnetic separators. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2013, 711, 47–59. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Gan, Z.G.; Yang, H.B.; Ma, L.; Huang, M.H.; Yang, C.L.; Zhang, M.M.; Tian, Y.L.; Wang, Y.S.; Sun, M.D.; et al. New Isotope 220Np: Probing the Robustness of the N = 126 Shell Closure in Neptunium. Phys. Rev. Lett. 2019, 122, 192503. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Zhang, Z.Y.; Gan, Z.G.; Zhou, X.H.; Yang, H.B.; Huang, M.H.; Yang, C.L.; Zhang, M.M.; Tian, Y.L.; Wang, Y.S.; et al. Short-Lived α-Emitting Isotope 222Np and the Stability of the N = 126 Magic Shell. Phys. Rev. Lett. 2020, 125, 032502. [Google Scholar] [CrossRef] [PubMed]
- Myers, W.D.; Swiatecki, W.J. Nuclear masses and deformations. Nucl. Phys. 1966, 81, 1–60. [Google Scholar] [CrossRef]
- Viola, V.; Seaborg, G. Nuclear systematics of the heavy elements—II Lifetimes for alpha, beta and spontaneous fission decay. J. Inorg. Nucl. Chem. 1966, 28, 741–761. [Google Scholar] [CrossRef]
- Oganessian, Y.T.; Abdullin, F.S.; Alexander, C.; Binder, J.; Boll, R.A.; Dmitriev, S.N.; Ezold, J.; Felker, K.; Gostic, J.M.; Grzywacz, R.K.; et al. Production and Decay of the Heaviest Nuclei 293,294117 and 294118. Phys. Rev. Lett. 2012, 109, 162501. [Google Scholar] [CrossRef]
- Aboussir, Y.; Pearson, J.; Dutta, A.; Tondeur, F. Nuclear mass formula via an approximation to the Hartree–Fock method. At. Data Nucl. Data Tables 1995, 61, 127–176. [Google Scholar] [CrossRef]
- Wang, N.; Liu, M.; Wu, X.; Meng, J. Surface diffuseness correction in global mass formula. Phys. Lett. B 2014, 734, 215–219. [Google Scholar] [CrossRef]
- Möller, P.; Sierk, A.; Ichikawa, T.; Sagawa, H. Nuclear ground-state masses and deformations: FRDM(2012). At. Data Nucl. Data Tables 2016, 109–110, 1–204. [Google Scholar] [CrossRef]
- Samyn, M.; Goriely, S.; Heenen, P.H.; Pearson, J.; Tondeur, F. A Hartree–Fock–Bogoliubov mass formula. Nucl. Phys. A 2002, 700, 142–156. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Skyrme-Hartree-Fock-Bogoliubov Nuclear Mass Formulas: Crossing the 0.6 MeV Accuracy Threshold with Microscopically Deduced Pairing. Phys. Rev. Lett. 2009, 102, 152503. [Google Scholar] [CrossRef] [PubMed]
- Goriely, S.; Hilaire, S.; Girod, M.; Péru, S. First Gogny-Hartree-Fock-Bogoliubov Nuclear Mass Model. Phys. Rev. Lett. 2009, 102, 242501. [Google Scholar] [CrossRef]
- Lalazissis, G.; Raman, S.; Ring, P. Ground-state properties of even–even nuclei in the relativistic mean-field theory. At. Data Nucl. Data Tables 1999, 71, 1–40. [Google Scholar] [CrossRef]
- Geng, L.; Toki, H.; Meng, J. Masses, Deformations and Charge Radii—Nuclear Ground-State Properties in the Relativistic Mean Field Model. Prog. Theor. Phys. 2005, 113, 785–800. [Google Scholar] [CrossRef]
- Afanasjev, A.; Agbemava, S.; Ray, D.; Ring, P. Nuclear landscape in covariant density functional theory. Phys. Lett. B 2013, 726, 680–684. [Google Scholar] [CrossRef]
- Agbemava, S.E.; Afanasjev, A.V.; Ray, D.; Ring, P. Global performance of covariant energy density functionals: Ground state observables of even–even nuclei and the estimate of theoretical uncertainties. Phys. Rev. C 2014, 89, 054320. [Google Scholar] [CrossRef]
- Afanasjev, A.V.; Agbemava, S.E.; Ray, D.; Ring, P. Neutron drip line: Single-particle degrees of freedom and pairing properties as sources of theoretical uncertainties. Phys. Rev. C 2015, 91, 014324. [Google Scholar] [CrossRef]
- Xia, X.; Lim, Y.; Zhao, P.; Liang, H.; Qu, X.; Chen, Y.; Liu, H.; Zhang, L.; Zhang, S.; Kim, Y.; et al. The limits of the nuclear landscape explored by the relativistic continuum Hartree–Bogoliubov theory. At. Data Nucl. Data Tables 2018, 121–122, 1–215. [Google Scholar] [CrossRef]
- Zhang, K.; Cheoun, M.K.; Choi, Y.B.; Chong, P.S.; Dong, J.; Dong, Z.; Du, X.; Geng, L.; Ha, E.; He, X.T.; et al. Nuclear mass table in deformed relativistic Hartree–Bogoliubov theory in continuum, I: Even–even nuclei. At. Data Nucl. Data Tables 2022, 144, 101488. [Google Scholar] [CrossRef]
- Guo, P.; Cao, X.; Chen, K.; Chen, Z.; Cheoun, M.K.; Choi, Y.B.; Lam, P.C.; Deng, W.; Dong, J.; Du, P.; et al. Nuclear mass table in deformed relativistic Hartree–Bogoliubov theory in continuum, II: Even-Z nuclei. At. Data Nucl. Data Tables 2024, 158, 101661. [Google Scholar] [CrossRef]
- Geng, J.; Long, W.H. Relativistic Hartree-Fock-Bogoliubov model for axially deformed nuclei. Phys. Rev. C 2022, 105, 034329. [Google Scholar] [CrossRef]
- Geng, J.; Zhao, P.W.; Niu, Y.F.; Long, W.H. A coherent microscopic picture for the exotic structure of 11Be. Phys. Lett. B 2024, 858, 139036. [Google Scholar] [CrossRef]
- Li, L.; Meng, J.; Ring, P.; Zhao, E.G.; Zhou, S.G. Deformed relativistic Hartree–Bogoliubov theory in continuum. Phys. Rev. C 2012, 85, 024312. [Google Scholar] [CrossRef]
- Zhang, K.; Cheoun, M.K.; Choi, Y.B.; Chong, P.S.; Dong, J.; Geng, L.; Ha, E.; He, X.; Heo, C.; Ho, M.C.; et al. Deformed relativistic Hartree–Bogoliubov theory in continuum with a point-coupling functional: Examples of even–even Nd isotopes. Phys. Rev. C 2020, 102, 024314. [Google Scholar] [CrossRef]
- Zhao, P.W.; Li, Z.P.; Yao, J.M.; Meng, J. New parametrization for the nuclear covariant energy density functional with a point-coupling interaction. Phys. Rev. C 2010, 82, 054319. [Google Scholar] [CrossRef]
- Zhang, K.; He, X.; Meng, J.; Pan, C.; Shen, C.; Wang, C.; Zhang, S. Predictive power for superheavy nuclear mass and possible stability beyond the neutron drip line in deformed relativistic Hartree–Bogoliubov theory in continuum. Phys. Rev. C 2021, 104, L021301. [Google Scholar] [CrossRef]
- DRHBc Mass Table Collaboration. Available online: http://drhbctable.jcnp.org (accessed on 20 December 2024).
- Pan, C.; Cheoun, M.K.; Choi, Y.B.; Dong, J.; Du, X.; Fan, X.H.; Gao, W.; Geng, L.; Ha, E.; He, X.T.; et al. Deformed relativistic Hartree–Bogoliubov theory in continuum with a point-coupling functional. II. Examples of odd Nd isotopes. Phys. Rev. C 2022, 106, 014316. [Google Scholar] [CrossRef]
- Dechargé, J.; Berger, J.F.; Dietrich, K.; Weiss, M. Superheavy and hyperheavy nuclei in the form of bubbles or semi-bubbles. Phys. Lett. B 1999, 451, 275–282. [Google Scholar] [CrossRef]
- Bender, M.; Nazarewicz, W.; Reinhard, P.G. Shell stabilization of super- and hyperheavy nuclei without magic gaps. Phys. Lett. B 2001, 515, 42–48. [Google Scholar] [CrossRef]
- Afanasjev, A.; Agbemava, S.; Gyawali, A. Hyperheavy nuclei: Existence and stability. Phys. Lett. B 2018, 782, 533–540. [Google Scholar] [CrossRef]
- Zhou, S.G.; Meng, J.; Ring, P.; Zhao, E.G. Neutron halo in deformed nuclei. Phys. Rev. C 2010, 82, 011301. [Google Scholar] [CrossRef]
- Zhang, W.; Meng, J.; Zhang, S.; Geng, L.; Toki, H. Magic numbers for superheavy nuclei in relativistic continuum Hartree–Bogoliubov theory. Nucl. Phys. A 2005, 753, 106–135. [Google Scholar] [CrossRef]
- Brodziński, W.; Skalski, J. Predictions for superheavy elements beyond Z = 126. Phys. Rev. C 2013, 88, 044307. [Google Scholar] [CrossRef]
- Zhou, S.G.; Meng, J.; Ring, P. Spherical relativistic Hartree theory in a Woods–Saxon basis. Phys. Rev. C 2003, 68, 034323. [Google Scholar] [CrossRef]
- Shen, S.; Liang, H.; Long, W.; Meng, J.; Ring, P. Towards an ab initio covariant density functional for nuclear structure. Prog. Part. Nucl. Phys. 2019, 109, 103713. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Q.; Ring, P.; Meng, J. Nuclear matter in relativistic Brueckner-Hartree-Fock theory with Bonn potential in the full Dirac space. Phys. Rev. C 2021, 103, 054319. [Google Scholar] [CrossRef]
- Wang, S.; Tong, H.; Wang, C.; Zhao, Q.; Ring, P.; Meng, J. Tensor-force effects on nuclear matter in relativistic ab initio theory. Sci. Bull. 2024, 69, 2166–2169. [Google Scholar] [CrossRef] [PubMed]
- Nikšić, T.; Paar, N.; Reinhard, P.G.; Vretenar, D. Optimizing relativistic energy density functionals: Covariance analysis. J. Phys. G Nucl. Part. Phys. 2015, 42, 034008. [Google Scholar] [CrossRef][Green Version]
- Agbemava, S.E.; Afanasjev, A.V.; Taninah, A. Propagation of statistical uncertainties in covariant density functional theory: Ground state observables and single-particle properties. Phys. Rev. C 2019, 99, 014318. [Google Scholar] [CrossRef]
- Wu, X.H.; Pan, C.; Zhang, K.Y.; Hu, J. Nuclear mass predictions of the relativistic continuum Hartree–Bogoliubov theory with the kernel ridge regression. Phys. Rev. C 2024, 109, 024310. [Google Scholar] [CrossRef]
- Guo, Y.Y.; Yu, T.; Wu, X.H.; Pan, C.; Zhang, K.Y. Nuclear mass predictions of the relativistic continuum Hartree–Bogoliubov theory with the kernel ridge regression. II. Odd-even effects. Phys. Rev. C 2024, 110, 064310. [Google Scholar] [CrossRef]
- Chat, J. Recommendations for the Naming of Elements of Atomic Numbers Greater than 100. Pure Appl. Chem. 1979, 51, 381–384. [Google Scholar] [CrossRef]
- Yang, Y.L.; Wang, Y.K.; Zhao, P.W.; Li, Z.P. Nuclear landscape in a mapped collective Hamiltonian from covariant density functional theory. Phys. Rev. C 2021, 104, 054312. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
