Abstract
Natural supersymmetry with light higgsinos is most favored to emerge from the string landscape, since the volume of a scan parameter space shrinks to tiny volumes for electroweak unnatural models. Rather general arguments favor a landscape selection of soft SUSY breaking terms tilted to large values, but they are tempered by the atomic principle that the derived value of the weak scale in each pocket universe lies not too far from its measured value in our universe. But, that leaves (at least) three different paradigms for gaugino masses in natural SUSY models: unified (as in nonuniversal Higgs models), anomaly mediation form (as in natural AMSB), and mirage mediation form (with comparable moduli- and anomaly-mediated contributions). We perform landscape scans for each of these, and we show that they populate different, but overlapping, positions in and space. The first of these may be directly measurable at high-lumi LHC via the soft opposite-sign dilepton plus jets plus signature arising from higgsino pair production, while the second of these could be extracted from direct wino pair production, leading to same-sign diboson production.
1. Introduction
Superstring compactification on a Calabi–Yau manifold leaves some remnant supersymmetry (SUSY) in the resulting theory [1], and the question then is as follows: at which scale (where is the reduced Planck mass) is SUSY broken? Phenomenologically, does SUSY play a role [2,3] in stabilizing the measured value of the weak scale GeV against blow-up to much higher mass scales due to quantum corrections to ? Recent LHC search results [4,5], which require gluino masses TeV and top-squark masses TeV (within the context of simplified models), suggest SUSY as a somewhat disfavored mechanism for extending the Standard Model [5], although this sentiment is based on theoretical prejudices arising from pre-21st century physics.
Expectations for weak-scale SUSY (WSS) changed in the 21st century with the advent of the string landscape [6,7]. In the landscape picture, it was found that there exists an enormous number (the number is an oft-quoted value [8], but much higher numbers are also entertained) of string flux compactification possibilities [9], each leading to different laws of physics (but still based on CY compactifications with their remnant SUSY in the theory). Each of these vacua possibilities can be realized in the eternally inflating multiverse leading to Weinberg’s anthropic solution to the cosmological constant problem [10]: if is much larger than its measured value, then each pocket universe would expand so quickly that large-scale structure (e.g., galaxy condensation and, hence, star formation) would not occur, and hence the needed complexity for observers would not ensue. Weinberg’s scheme relies on a landscape comprising SM-like models, where only scans in the multiverse.
Arkani-Hamed et al. present arguments for a so-called friendly landscape, wherein only super-renormalizable operators scan [11], and hence, only dimensionful quantities such as and scan on the landscape. In this case, gauge groups, gauge couplings, and Yukawa couplings are instead determined by dynamics instead of by anthropics, yielding a so-called predictive landscape. For models including WSS [12], where the weak scale arises as a consequence of soft SUSY breaking, we expect instead the overall SUSY breaking scale to scan in the multiverse. Since in string theory no scale is preferred over any other, the F-term fields should be distributed as complex numbers, while D-term breaking fields are distributed as real numbers over the decades of possibilities; this leads to an expected power-law draw to large soft terms [11,13,14]
within the string landscape. For the textbook case of SUSY breaking via a single F-term, there is already a linear draw to large soft terms.
The draw to large soft terms must be tempered by the anthropic requirement that electroweak symmetry breaking (EWSB) properly occurs—and with no charge or color breaking (CCB) minima [15]. Also, for complex nuclei to be formed, the magnitude of the pocket universe (PU) weak scale must lie within the so-called ABDS window of values [16]
where is the weak scale, as measured in our universe, while is the derived weak scale in each pocket universe within the greater multiverse:
The ABDS window provides a (statistical) upper bound on the soft SUSY breaking terms. By combining the draw to large soft terms with the ABDS window, and rescaling to its measured value in our universe, we can gain probability distributions for Higgs boson and sparticle masses from the landscape [17]. From a variety of well-motivated SUSY models (gravity-mediated [17], anomaly-mediated [18], and mirage-mediated [19] SUSY breaking), one finds probability distributions that peak around GeV, with sparticles somewhat or well-beyond LHC search limits. From this point of view, LHC experiments have only now begun to explore the expected SUSY model parameter space, and hence, it is no surprise that SUSY has yet to be revealed at the LHC [20].
2. Three Paradigms for Gaugino Masses
The different dependences of the various soft SUSY breaking terms on the hidden sector fields means that different soft terms should scan to large values independently of each other [21]. This leads to three broad expectations for sparticle mass spectra oriented according to the relative values of the different gaugino masses, which are referred to as the gaugino code in Ref. [22].
2.1. Gravity-Mediated SUSY Breaking
Under gravity mediation, scalar masses can be computed from the supergravity Kähler potential , where the label hidden sector fields are where SUSY breaking takes place. In realistic compactifications, K can be a complicated function of the , leading to nonuniversal scalar masses [23,24,25], which may be regarded as a prediction from the sort of SUGRA theories arising from string flux compactification (The original mSUGRA model [26] thought to arise from SUGRA models has an enforced ad hoc implementation of scalar mass universality, which violates this expectation. Thus, it is probably better to call that model a constrained MSSM, or CMSSM [27], in that the universality condition goes against the expectations from supergravity). The ad hoc scalar mass universality of the mSUGRA/CMSSM models was implemented in the earlier days of SUSY phenomenology to enforce the super-GIM mechanism to suppress flavor violation in SUSY models. Nowadays, universality forces the CMSSM into EW unnaturalness, whereas nonuniversal Higgs masses allow for radiatively driven naturalness [28,29], wherein large high-scale values of are driven to natural weak scale values. In addition, the pull of the string landscape on first/second generation scalar masses is to the 10–40 TeV level, but the flavor independent upper bounds that arise from 2-loop RGE terms [30]. This yields a landscape decoupling/quasi-degeneracy solution to the SUSY flavor and CP problems [31]. Figuratively, scalar masses arise from operators such as
where the hidden sector X fields develop a SUSY breaking F-term , yielding scalar masses , where the gravitino mass TeV for . Thus, we expect nonuniversal scalar masses of order in SUGRA theories [32]. But since the scalar fields of each generation fill out a complete 16-dimensional spinor rep of , we expect universality of the scalar masses within each generation such that are all independent (this follows from local grand unification [33] in string compactifications and follows one of Nilles’ golden rules of string phenomenology [34]). Therefore, with regard to soft SUSY-breaking scalar masses, which we expect most plausibly from string flux compactifications that
but with .
The gaugino masses in SUGRA arise from the holomorphic gauge kinetic function (GKF) , where A and B are gauge indices. For a simple GKF , then one gains universal gaugino masses, e.g.,
with gaugino mass .
2.2. Anomaly-Mediated SUSY Breaking (AMSB)
Notice in this case that since is holomorphic that if hidden sector fields leading to SUSY breaking have a surviving R-symmetry or other conserved quantum number, then the gaugino masses will be forbidden at the tree level, unlike scalar masses, and then their leading contribution will be from the loop-suppressed anomaly-mediated terms [35,36,37], where
where is the beta function of the associated gauge group. Then, we expect
where the loop suppression from is evident. Thus, in such models, one can expect heavier scalar masses of the order TeV, while gaugino masses may be at or below the TeV scale but of the AMSB form. This scenario has been termed PeV-scale SUSY by Wells [38], and split [39] and minisplit [40] (depending on the magnitude of scalar masses) and can be parametrized within the minimal AMSB model with parameters [41,42]:
where is an ad hoc bulk scalar mass introduced to avoid the problem of tachyonic slepton masses in the case of pure anomaly mediation [35]. Famously, mAMSB models feature a wino as the lightest SUSY particle (LSP). A wino LSP seems to be ruled out by direct and indirect WIMP search experiments [43,44,45]. Also, requiring GeV, in Ref. [46] it was found that the mAMSB was highly EW-fine-tuned over all remaining parameter space. By extending the bulk scalar mass contributions to include independent Higgs terms and , and by including bulk A terms , then the AMSB model could be generalized [47] such that GeV was allowed, along with EW naturalness, although in the EW-natural regions, the higgsinos were the lightest EWinos, while the wino was still the lightest of the gauginos. This natural generalized AMSB model [47] is thus parametrized by
where and have been traded for the more convenient weak scale parameters and .
2.3. Comparable Gravity and Anomaly Mediation (Mirage Mediation)
The mirage mediated form of soft SUSY breaking terms was originally derived [48] within the context of KKLT [49] flux compactifications of type IIB string theory on a Calabi–Yau orientifold. In KKLT, background gauge fields in the 6-d compact space are given quantized flux values that thread various cycles, leading to the stabilization of the dilaton and all complex structure moduli fields and gain masses of order the ultra-high Kaluza–Klein (KK) scale. The remaining Kähler moduli are assumed to be stabilized via nonperturbative effects such as gaugino condensation [50], and they gain much smaller masses. At this stage, the model has unbroken SUSY with an AdS vacuum. To obtain a broken SUSY theory with deSitter vacuum, KKLT assumed a SUSY breaking anti- brane at the tip of a Klebanov–Strassler [51] throat, which gave an uplift to a metastable dS vacuum. In this setup, it was pointed out by Choi et al. [48] that the construct allowed for weak scale SUSY as a solution to the GHP, but with a little hierarchy
where the proportionality factor between terms in Equation (13) was a factor . In such a case, the gravity/moduli-mediated soft terms were while the anomaly-mediated contributions were , which were suppressed by a loop factor but now comparable to the gravity-mediated contributions due to the hierarchy in Equation (13).
The original derivation of soft terms is given in Ref. [48], which combined gravity- and anomaly-mediated contributions in a scenario that assumed a single Kähler modulus, with visible fields on a D3 or D7 brane. This class of models is known as mirage mediation, since the gaugino masses start off at with nonuniversal values, but which evolve to a unified value at some intermediate scale [52]
where the RG evolution offsets the displacement of gaugino masses by the AMSB term, which includes the gauge group beta function. Here, parametrizes the relative AMSB vs. gravity-mediated contributions to gaugino masses. These models, with discrete values of gravity-mediated soft terms, were found to be highly unnatural under the conservative fine-tuning measure for GeV [46].
However, in Ref. [53] it was proposed that the soft terms could be generalized to a form which ought to hold under more realistic compactifications, where the Kähler moduli could number in the hundreds. This generalized mirage mediation model (GMM) has soft terms given by
where parametrizes the relative modulus/AMSB mixing in the gaugino masses, define the gauge -function coefficients for gauge group a, and the are the corresponding gauge couplings. Also, the parameters , etc., , , , , and are all now generalized to be continuously variable. Furthermore, where the are the superpotential Yukawa couplings, the is the quadratic Casimir for the ath gauge group corresponding to the representation to which the sfermion belongs, is the anomalous dimension, and . Expressions for the last two quantities involving anomalous dimensions can be found in the Appendices of Ref. [52].
The generalized MM parameter space is thus given by
where i = 1–3 runs over the generations. The independent values of and , which set the modulus-mediated contribution to the Higgs soft masses, can be traded for the more convenient weak scale values of and . Thus, the final parameter space is given by
where i is a generation index. For convenience, we will also take the first two generation , since these are pulled to large values TeV in the landscape, which leads to a mixed quasi-degeneracy/decoupling solution to the SUSY flavor problem [31].
2.4. The Gaugino Code in Natural SUSY
The three possibilities for natural SUSY spectra are displayed in Figure 1, which displays the gaugino code, as emphasized in Ref. [22]. For all three cases, we expect in the string landscape picture that first/second generation scalars will be drawn to the 10–40 TeV range (thus solving the SUSY flavor/CP problems), while light stops lie in the range 1–3 TeV, and heavier stops are at 3–8 TeV [17,18,19]. Also, we expect the (SUSY conserving) higgsino mass terms to lie in the natural range of 100–350 GeV. The distinguishing characteristic between the three models lies with the orientation of the gaugino masses, as is figuratively displayed in Figure 1. Supergravity models with a simple linear form of gauge kinetic function (GKF) or (where the singlet hidden sector field S is a dilaton and T is a Kähler modulus) give rise to unified gaugino masses at scale , while RG evolution leads to the ratios at , as is typical of the three extra parameter nonuniversal Higgs model (NUHM3) of Figure 1. If the SUSY breaking fields are charged, perhaps under an R-symmetry, then the linear form of the GKF is forbidden, and the dominant contribution to the gaugino masses comes from the loop-suppressed AMSB form with , as shown in the nAMSB column. Alternatively, if the gaugino masses obtain comparable gravity and AMSB- = contributions as in mirage mediation models, where , then we expect a more compressed form of gaugino masses, which unify at the mirage scale and would be intermediate between the weak and GUT scales. This pattern is shown in the GMM’ column. While each of the three cases leads to its own orientation for gaugino masses, we expect from naturalness that the lightest EWinos will be the triplet of higgsino states , , as denoted by the gray dashed lines. The question then becomes the following: can experiments at high-luminosity LHCs distinguish between these three cases, thus decoding the gaugino code?
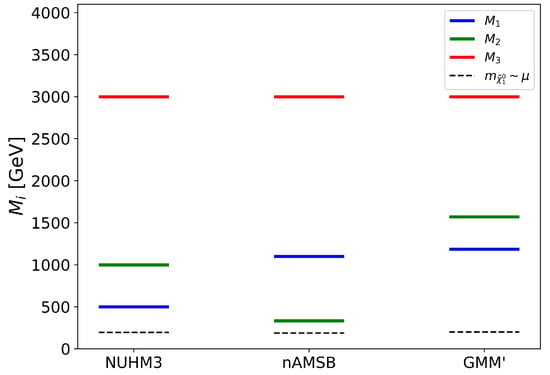
Figure 1.
Figurative plot of gaugino/higgsino masses in the three-paradigm natural SUSY models with TeV and GeV.
3. Revealing the Gaugino Code Naturally at High-Lumi LHCs
The LHC has two promising avenues toward decoding the natural gaugino code, namely, by observing 1. higgsino pair production and 2. wino pair production.
It turns out each of these channels is quite distinctive to the case of natural SUSY models, and signals should gradually emerge as the LHC accrues higher and higher integrated luminosity. From Run 2 data, both ATLAS and CMS seem to have small excesses in the higgsino pair production channel [54,55]. It is thus of great interest to see if these excesses build up or fade away with the Run 3 and HL-LHC data sets.
3.1. Higgsino Pair Production
Charged higgsino pair production followed by decay (where f stands for SM fermions) typically yields very soft visible decay products and , as well as a rather indistinct signature. Neutral higgsino pair production [56]
may also lead to very low visible energy, unless the scattering reaction recoils from a hard initial state quark/gluon radiation [57,58,59] (ISR). In this latter case, letting f be e or , we then expect soft opposite-sign dilepton plus jet plus production (OSDLJMET), where the opposite-sign (OS) dilepton pair has an invariant mass kinematically bounded by . Thus, in the signal distribution, we expect an excess beyond SM expectations for , while the data should agree with SM expectations for higher invariant dilepton masses [60]. Along with offering a distinctive signal channel for natural SUSY models at the HL-LHC, this channel also provides a direct measure of the neutral higgsino mass difference . A rough estimate of the superpotential parameter may also be gleaned from this channel based on the total rate, since and the total production rate mainly depends on the raw higgsino masses. In fact, the exclusion limits are typically plotted in the vs plane [61]. More refined cuts for extracting the OSDLJMET signal have recently been presented in Refs. [62,63].
3.2. Wino Pair Production
Another distinctive SUSY discovery channel, which is endemic to natural SUSY models, is the clean same-sign diboson signal (SSdB), which arises from wino pair production:
where the is the charged wino, and is the neutral wino in nAMSB, or is the neutral wino in GMM’ or NUHM3. Since the visible decay products of the daughter higgsinos are very soft, and upon leptonic decays of the final state W bosons, this reaction leads half the time to a hadronically clean (aside from the usual ISR) same-sign dilepton final state, which has very low SM backgrounds [64,65,66]. This is different from the older same-sign dilepton signals arising from gluino and squark pair production, which would be accompanied by multiple hard jets [67,68,69,70].
Due to the required two W-boson leptonic branching fractions, the rate for this channel for the current LHC Run 2 data set is typically expected around the one-event level, so at present, no search limits are available from this channel. However, as more integrated luminosity accrues, this channel will become more and more important due to the extremely low SM background levels. Since the production rate mainly depends on , and the wino branching fractions to W bosons are well-known and theoretically stable, the direct production rate can yield a measure of the gaugino mass [66]. In Ref. [66], it is estimated that with 3 ab−1 of integrated luminosity (corresponding to ∼ 10–100 events), the HL-LHC should be able to determine to around the 5–10% level based on the signal rate alone, including statistical errors.
3.3. Decoding the Gaugino Code at HL-LHC
Next, we performed string landscape scans of soft SUSY breaking parameters, assuming the textbook case of an power-law landscape draw to large soft terms. Each class of soft terms (gaugino mass, scalar mass, and A-terms) should scan independently on the landscape owing to the different functional dependences of the soft terms on the hidden sector fields for different string compactification possibilities [21]. Thus, we scanned the NUHM3 over the range (We used Isajet 7.91 [71] for sparticle and Higgs mass and generation):
- : 0.1–60 TeV,
- : 0.1–20 TeV,
- : 0.5–10 TeV,
- 50–0 TeV (negative only).
This was done at first for fixed GeV (since is not a soft term but arises from whatever solution to the SUSY problem is assumed) (Twenty solutions to the SUSY problem have been reviewed in Ref. [72]). For each parameter set, the expected value of the weak scale in each pocket universe was computed from and solutions, with being rejected as lying beyond the ABDS window. (An important technical point is that the scan range upper limits must be selected to be beyond the upper limits imposed by the anthropic ABDS window.) To gain probability distributions for Higgs and sparticle masses in our universe, then must be adjusted (but not fine-tuned!) as a final step to our value GeV.
For the nAMSB model, our landscape scan was over the following [18]:
- : 80–400 TeV,
- : 1–20 TeV,
- : 1–10 TeV,
- : 0–20 TeV (positive only).
For the GMM’, our scan followed Ref. [19] with fixed TeV:
- 3–25 (with draw),
- ,
- : 3–80,
- : 3–100.
For all cases, we scanned with a linear draw : 0.25–10 TeV and uniformly over 3–60.
The results of our scans are plotted in Figure 2 in the vs. plane. Green dots denote nAMSB points, blue dots denote NUHM3 points, and red dots denote GMM’ points. From Figure 2, we see the three models inhabit somewhat different locuses in the plane. The green nAMSB points extend to rather large values—as high as GeV—since in this case, the light winos can mix with the higgsinos, thus breaking the expected inter-higgsino mass degeneracy. Also, the range in for nAMSB points only extends as high as GeV. In contrast, the NUHM3 model with unified gaugino masses has a maximal GeV but can extend as high as GeV, where GeV. The GMM’ is intermediate between these models, since it has mixed gravity/AMSB mediation. At low , where is small, it looks more like AMSB spectra and has a slight overlap with the green points, while at high values, it looks more like gravity mediation and lies closer to the blue points, although the compressed GMM’ gaugino spectrum allows to extend much further, as high as TeV, where is as low as GeV. Notice in all cases the never reaches below the few GeV case, since for that to occur, the values would have to be so high that would become unnatural [73] and lie outside the ABDS window.
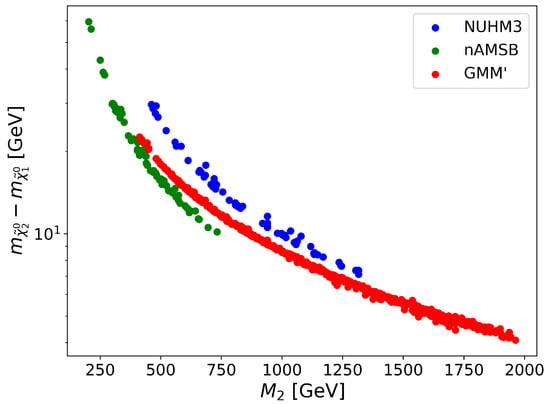
Figure 2.
Locus of landscape scan points from the NUHM3 model: the nAMSB model and GMM’ model in the vs. plane for fixed value GeV.
In Figure 3, we again plotted the locus of landscape scan points in the vs. plane, but this time including a uniform scan over : 100–350 GeV in case the parameter could not be well measured. In this case, the model scan points broadened out and have some substantial overlap in the intermediate mass region. Nonetheless, the landscape scan regions still maintain some degree of separation, as shown by the colored dots, so depending on where the ultimate measure values of and lie, the locus may or may not lie within a distinguishable region. Clearly, a more precise measured value of will help aid in this enterprise.
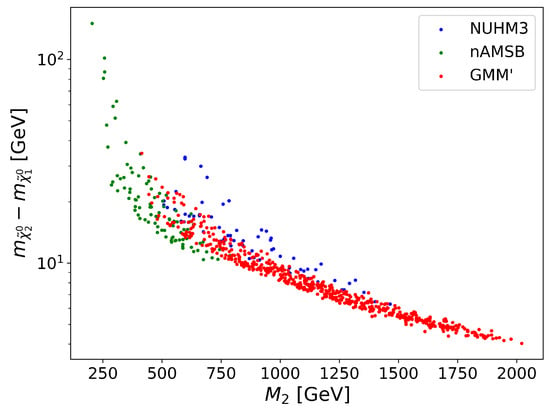
Figure 3.
Locus of landscape scan points from the NUHM3 model: the nAMSB model and GMM’ model in the vs. plane for a uniform scan over GeV.
4. Conclusions
String flux compactifications on a Calabi–Yau manifold with special holonomy preserve some remnant supersymmetry, which provides a ’t Hooft technical natural solution to the big hierarchy problem. The question then is the following: what is the scale of SUSY breaking, and does the subsequent SUSY spectrum avoid the little hierarchy problem based on practical naturalness? Rather general arguments from the string landscape favor a power-law draw to large soft terms tempered by the anthropic requirement that the derived value of the weak scale lies within the so-called ABDS window. In this case, EW natural SUSY models are most likely to emerge as opposed to fine-tuned SUSY models, since the latter viable parameter space shrinks to a relatively tiny volume compared to natural models (one must happen upon the fine-tuned parameters that lead to a weak scale that is not too far removed from its measured value in our universe). These natural models would be characterized by first/second generation scalars in the 10–40 TeV range, while top squarks inhabit the smaller TeV range, and higgsinos lie not to far from in the 100–350 GeV range. Within the context of natural models, three main paradigms are viable, which are distinguished by the orientation of the gaugino masses: unified gaugino masses—as in the NUHM3 model, AMSB gaugino masses—as in the nAMSB, and mirage mediated gaugino masses—as in the GMM’ model.
Can forthcoming data from the HL-LHC distinguish these cases, thus decoding the gaugino code? Two avenues to detection of natural SUSY models lie in the OSDLJMET signal from higgsino pair production and the SSdB signature arising from wino pair production. The first admits a precise measurement of via the expected edge in the distribution, while wino pair production may allow extraction of the wino mass from the total rate of SSdB production. By placing these measurements within the vs. plane, one may well be able to decode the gaugino code, since SUSY models that predict the different cases may inhabit distinctive regions of this parameter plane.
Author Contributions
Writing—original draft preparation, H.B.; writing—review and editing, V.B.; software, K.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
VB gratefully acknowledges support from the William F. Vilas estate. HB gratefully acknowledges support from the Avenir Foundation.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Candelas, P.; Horowitz, G.T.; Strominger, A.; Witten, E. Vacuum configurations for superstrings. Nucl. Phys. B 1985, 258, 46–74. [Google Scholar] [CrossRef]
- Witten, E. Dynamical Breaking of Supersymmetry. Nucl. Phys. B 1981, 188, 513. [Google Scholar] [CrossRef]
- Kaul, R.K. Gauge Hierarchy in a Supersymmetric Model. Phys. Lett. B 1982, 109, 19–24. [Google Scholar] [CrossRef]
- Canepa, A. Searches for Supersymmetry at the Large Hadron Collider. Rev. Phys. 2019, 4, 100033. [Google Scholar] [CrossRef]
- Aad, G.; Aakvaag, E.; Abbott, B.K.; Abeling, K.; Abicht, N.J.; Abidi, H.; Aboelela, M.; Aboulhorma, A.; Abramowicz, H.; Abreu, H.; et al. The quest to discover supersymmetry at the ATLAS experiment. arXiv 2024, arXiv:2403.02455. [Google Scholar]
- Bousso, R.; Polchinski, J. Quantization of four form fluxes and dynamical neutralization of the cosmological constant. J. High Energy Phys. 2000, 2000, 6. [Google Scholar] [CrossRef]
- Susskind, L. The Anthropic landscape of string theory. arXiv 2003, arXiv:hep-th/0302219. [Google Scholar]
- Ashok, S.; Douglas, M.R. Counting flux vacua. J. High Energy Phys. 2004, 2004, 060. [Google Scholar] [CrossRef]
- Douglas, M.R.; Kachru, S. Flux compactification. Rev. Mod. Phys. 2007, 79, 733–796. [Google Scholar] [CrossRef]
- Weinberg, S. Anthropic Bound on the Cosmological Constant. Phys. Rev. Lett. 1987, 59, 2607. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Kachru, S. Predictive landscapes and new physics at a TeV. arXiv 2005, arXiv:hep-th/0501082. [Google Scholar]
- Baer, H.; Tata, X. Weak Scale Supersymmetry: From Superfields to Scattering Events; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Douglas, M.R. Statistical analysis of the supersymmetry breaking scale. arXiv 2004, arXiv:hep-th/0405279. [Google Scholar]
- Susskind, L. Supersymmetry breaking in the anthropic landscape. In From Fields to Strings: Circumnavigating Theoretical Physics: A Conference in Tribute to Ian Kogan; World Scientific: Singapore, 2004; pp. 1745–1749. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Savoy, M.; Serce, H. The Higgs mass and natural supersymmetric spectrum from the landscape. Phys. Lett. B 2016, 758, 113–117. [Google Scholar] [CrossRef]
- Agrawal, V.; Barr, S.M.; Donoghue, J.F.; Seckel, D. Viable range of the mass scale of the standard model. Phys. Rev. D 1998, 57, 5480–5492. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Serce, H.; Sinha, K. Higgs and superparticle mass predictions from the landscape. J. High Energy Phys. 2018, 2018, 002. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Bolich, J.; Dutta, J.; Sengupta, D. Natural anomaly mediation from the landscape with implications for LHC SUSY searches. Phys. Rev. D 2024, 109, 035011. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Sengupta, D. Mirage mediation from the landscape. Phys. Rev. Res. 2020, 2, 013346. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Salam, S.; Sengupta, D.; Sinha, K. Status of weak scale supersymmetry after LHC Run 2 and ton-scale noble liquid WIMP searches. Eur. Phys. J. Spec. Top. 2020, 229, 3085–3141. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Salam, S.; Sengupta, D. String landscape guide to soft SUSY breaking terms. Phys. Rev. D 2020, 102, 075012. [Google Scholar] [CrossRef]
- Choi, K.; Nilles, H.P. The Gaugino code. J. High Energy Phys. 2007, 2007, 006. [Google Scholar] [CrossRef]
- Soni, S.K.; Weldon, H.A. Analysis of the Supersymmetry Breaking Induced by N = 1 Supergravity Theories. Phys. Lett. B 1983, 126, 215–219. [Google Scholar] [CrossRef]
- Kaplunovsky, V.S.; Louis, J. Model independent analysis of soft terms in effective supergravity and in string theory. Phys. Lett. B 1993, 306, 269–275. [Google Scholar] [CrossRef]
- Brignole, A.; Ibanez, L.E.; Munoz, C. Towards a theory of soft terms for the supersymmetric Standard Model. Nucl. Phys. B 1994, 422, 125–171, Erratum in Nucl. Phys. B 1995, 436, 747–748. [Google Scholar] [CrossRef]
- Arnowitt, R.L.; Nath, P. Supersymmetry and Supergravity: Phenomenology and Grand Unification. arXiv 1993, arXiv:hep-ph/9309277. [Google Scholar]
- Kane, G.L.; Kolda, C.F.; Roszkowski, L.; Wells, J.D. Study of constrained minimal supersymmetry. Phys. Rev. D 1994, 49, 6173–6210. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P.; Mustafayev, A.; Tata, X. Radiative natural SUSY with a 125 GeV Higgs boson. Phys. Rev. Lett. 2012, 109, 161802. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P.; Mickelson, D.; Mustafayev, A.; Tata, X. Radiative natural supersymmetry: Reconciling electroweak fine-tuning and the Higgs boson mass. Phys. Rev. D 2013, 87, 115028. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Murayama, H. Can the supersymmetric flavor problem decouple? Phys. Rev. D 1997, 56, R6733–R6737. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Sengupta, D. Landscape solution to the SUSY flavor and CP problems. Phys. Rev. Res. 2019, 1, 033179. [Google Scholar] [CrossRef]
- Cremmer, E.; Ferrara, S.; Girardello, L.; Proeyen, A.V. Yang-Mills Theories with Local Supersymmetry: Lagrangian, Transformation Laws and SuperHiggs Effect. Nucl. Phys. B 1983, 212, 413. [Google Scholar] [CrossRef]
- Buchmuller, W.; Hamaguchi, K.; Lebedev, O.; Ratz, M. Local grand unification. arXiv 2005, arXiv:hep-ph/0512326. [Google Scholar]
- Nilles, H.P.; Vaudrevange, P.K.S. Geography of Fields in Extra Dimensions: String Theory Lessons for Particle Physics. Mod. Phys. Lett. A 2015, 30, 1530008. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. Out of this world supersymmetry breaking. Nucl. Phys. B 1999, 557, 79–118. [Google Scholar] [CrossRef]
- Giudice, G.F.; Luty, M.A.; Murayama, H.; Rattazzi, R. Gaugino mass without singlets. J. High Energy Phys. 1999, 1998, 027. [Google Scholar] [CrossRef]
- Bagger, J.A.; Moroi, T.; Poppitz, E. Anomaly mediation in supergravity theories. J. High Energy Phys. 2000, 2000, 009. [Google Scholar] [CrossRef]
- Wells, J.D. PeV-scale supersymmetry. Phys. Rev. D 2005, 71, 015013. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Giudice, G.F.; Romanino, A. Aspects of split supersymmetry. Nucl. Phys. B 2005, 709, 3–46. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Craig, N.; Dimopoulos, S.; Villadoro, G. Mini-Split. J. High Energy Phys. 2013, 2013, 126. [Google Scholar] [CrossRef]
- Gherghetta, T.; Giudice, G.F.; Wells, J.D. Phenomenological consequences of supersymmetry with anomaly induced masses. Nucl. Phys. B 1999, 559, 27–47. [Google Scholar] [CrossRef]
- Feng, J.L.; Moroi, T. Supernatural supersymmetry: Phenomenological implications of anomaly mediated supersymmetry breaking. Phys. Rev. D 2000, 61, 095004. [Google Scholar] [CrossRef]
- Cohen, T.; Lisanti, M.; Pierce, A.; Slatyer, T.R. Wino Dark Matter Under Siege. J. Cosmol. Astropart. Phys. 2013, 2013, 061. [Google Scholar] [CrossRef]
- Fan, J.; Reece, M. In Wino Veritas? Indirect Searches Shed Light on Neutralino Dark Matter. J. High Energy Phys. 2013, 2013, 124. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Serce, H. SUSY under siege from direct and indirect WIMP detection experiments. Phys. Rev. D 2016, 94, 115019. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Mickelson, D.; Padeffke-Kirkland, M. SUSY models under siege: LHC constraints and electroweak fine-tuning. Phys. Rev. D 2014, 89, 115019. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Sengupta, D. Anomaly mediated SUSY breaking model retrofitted for naturalness. Phys. Rev. D 2018, 98, 015039. [Google Scholar] [CrossRef]
- Choi, K.; Falkowski, A.; Nilles, H.P.; Olechowski, M. Soft supersymmetry breaking in KKLT flux compactification. Nucl. Phys. B 2005, 718, 113–133. [Google Scholar] [CrossRef]
- Kachru, S.; Kallosh, R.; Linde, A.D.; Trivedi, S.P. De Sitter vacua in string theory. Phys. Rev. D 2003, 68, 046005. [Google Scholar] [CrossRef]
- Nilles, H.P. Gaugino Condensation and Supersymmetry Breakdown. Int. J. Mod. Phys. A 1990, 5, 4199–4224. [Google Scholar] [CrossRef]
- Klebanov, I.R.; Strassler, M.J. Supergravity and a confining gauge theory: Duality cascades and chi SB resolution of naked singularities. J. High Energy Phys. 2008, 2008, 052. [Google Scholar] [CrossRef]
- Falkowski, A.; Lebedev, O.; Mambrini, Y. SUSY phenomenology of KKLT flux compactifications. J. High Energy Phys. 2005, 2005, 034. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Serce, H.; Tata, X. Natural generalized mirage mediation. Phys. Rev. D 2016, 94, 115017. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abed Abud, A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; et al. Searches for electroweak production of supersymmetric particles with compressed mass spectra in = 13 TeV pp collisions with the ATLAS detector. Phys. Rev. D 2020, 101, 052005. [Google Scholar] [CrossRef]
- Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Dragicevic, M.; Escalante Del Valle, A.; Fruehwirth, R.; Jeitler, M.; Krammer, N.; et al. Search for supersymmetry in final states with two or three soft leptons and missing transverse momentum in proton-proton collisions at = 13 TeV. J. High Energy Phys. 2022, 2022, 091. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P. Hidden SUSY at the LHC: The light higgsino-world scenario and the role of a lepton collider. J. High Energy Phys. 2011, 2011, 31. [Google Scholar] [CrossRef]
- Han, Z.; Kribs, G.D.; Martin, A.; Menon, A. Hunting quasidegenerate Higgsinos. Phys. Rev. D 2014, 89, 075007. [Google Scholar] [CrossRef]
- Baer, H.; Mustafayev, A.; Tata, X. Monojet plus soft dilepton signal from light higgsino pair production at LHC14. Phys. Rev. D 2014, 90, 115007. [Google Scholar] [CrossRef]
- Han, C.; Kim, D.; Munir, S.; Park, M. Accessing the core of naturalness, nearly degenerate higgsinos, at the LHC. J. High Energy Phys. 2015, 2015, 132. [Google Scholar] [CrossRef]
- Kitano, R.; Nomura, Y. Supersymmetry, naturalness, and signatures at the LHC. Phys. Rev. D 2006, 73, 095004. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Salam, S.; Sengupta, D.; Tata, X. The LHC higgsino discovery plane for present and future SUSY searches. Phys. Lett. B 2020, 810, 135777. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Sengupta, D.; Tata, X. New angular and other cuts to improve the Higgsino signal at the LHC. Phys. Rev. D 2022, 105, 095017. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Sengupta, D.; Tata, X. Angular cuts to reduce the τj background to the higgsino signal at the LHC. arXiv 2022, arXiv:2203.03700. [Google Scholar]
- Baer, H.; Barger, V.; Huang, P.; Mickelson, D.; Mustafayev, A.; Sreethawong, W.; Tata, X. Same sign diboson signature from supersymmetry models with light higgsinos at the LHC. Phys. Rev. Lett. 2013, 110, 151801. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P.; Mickelson, D.; Mustafayev, A.; Sreethawong, W.; Tata, X. Radiatively-driven natural supersymmetry at the LHC. J. High Energy Phys. 2013, 2013, 013, Erratum in J. High Energy Phys. 2015, 6, 053. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Gainer, J.S.; Savoy, M.; Sengupta, D.; Tata, X. Aspects of the same-sign diboson signature from wino pair production with light higgsinos at the high luminosity LHC. Phys. Rev. D 2018, 97, 035012. [Google Scholar] [CrossRef]
- Baer, H.; Tata, X.; Woodside, J. Searching for 100-GeV–300-GeV gluinos at the tevatron and ssc. Phys. Rev. D 1990, 42, 1568–1576. [Google Scholar] [CrossRef]
- Barnett, R.M.; Gunion, J.F.; Haber, H.E. Like sign dileptons as a signal for gluino production. In Proceedings of the 1988 DPF Summer Study on High-energy Physics in the 1990s (Snowmass 88), Snowmass, CO, USA, 27 June–15 July 1988. [Google Scholar]
- Baer, H.; Tata, X.; Woodside, J. Gluino Cascade Decay Signatures at the Tevatron Collider. Phys. Rev. D 1990, 41, 906–915. [Google Scholar] [CrossRef]
- Barnett, R.M.; Gunion, J.F.; Haber, H.E. Discovering supersymmetry with like sign dileptons. Phys. Lett. B 1993, 315, 349–354. [Google Scholar] [CrossRef]
- Paige, F.E.; Protopopescu, S.D.; Baer, H.; Tata, X. ISAJET 7.69: A Monte Carlo event generator for pp, anti-p p, and e+e- reactions. arXiv 2003, arXiv:hep-ph/0312045. [Google Scholar]
- Bae, K.J.; Baer, H.; Barger, V.; Sengupta, D. Revisiting the SUSY μ problem and its solutions in the LHC era. Phys. Rev. D 2019, 99, 115027. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Savoy, M. Upper bounds on sparticle masses from naturalness or how to disprove weak scale supersymmetry. Phys. Rev. D 2016, 93, 035016. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).