Abstract
We propose a model for the QCD running coupling constant based on the analytical inverse QCD coupling constant concept with an additional regularization in the low momentum region. Analyticity in the -complex plane, where q is the four-momentum transfer, is imposed by methods of the Analytic Perturbation Theory. The model incorporates a peculiar low-momentum behavior for as a divergence at to retrieve color confinement, without spoiling its correct high-momentum behavior. This was achieved by means of a two-parameter regularization function, for which we considered three possible analytic expressions. In fact, within the framework of the Analytic Perturbation Theory, assumes a finite value for , at all perturbative orders (infrared stability), hence the infrared divergence cannot be implemented. For this reason, we found it more straightforward to work with its reciprocal, namely, , imposing its vanishing at the origin of the -complex plane via the multiplication of the aforementioned regularizing functions and the spectral density. Once the two free parameters of the regularization functions were settled by fitting to the experimental values of at the momenta where these data were available and reliable, the model could reproduce the QCD running coupling constant at any other momentum transferred.
1. Introduction
The goal of our model is to define and use the inverse QCD coupling constant (ICC)
As we see in more detail in the following, the advantages of using the ICC go beyond the simpler arithmetical inversion of in the formula [1]. The failure of perturbation theories at renormalization scales where the running coupling constant is approaching from below the edge of the convergence domain is a well-known limit of such theories. In the leading logarithmic approximation, the expression of the QCD running coupling constant is [2,3]
where depends on , the number of active quark flavors, i.e., those with masses below the energy . The parameter represents Landau’s pole or ghost pole at the spacelike momentum squared . Approximations above the leading order of perturbation theory present similar issues, namely, logarithmic divergences.
A procedure adopted to avoid the appearance of these singularities in the definition of the running coupling constant is the Analytic Perturbation Theory (APT) [2,3,4], which indeed aims to improve the results of the Perturbation Theory (PT) in Quantum Field Theories (QFTs), imposing the general principles of analyticity, hence causality, and unitarity. It assumes that propagators and coupling constants, as functions of , can be extended analytically in the whole -complex plane using the Källén–Lehmann’s Spectral Representation (KL), which formally is a dispersion relation. For the QCD running coupling, the KL is [2]
where is the spectral density and corresponds to the imaginary part of calculated on the lower edge of the physical cut, i.e.,
In this way, all the unphysical singularities produced as artifacts of the PT expansion at finite orders, such as ghost poles and unphysical cuts, are eliminated. We worked with the cut along the negative real semi-axis, taking as the opposite of the space-like four-momentum squared. From Equation (2), the expression of at the leading order becomes
where the argument has simply been changed in by omitting the negative sign. Of course, in this form, the Landau’s ghost pole occurs at .
By calculating the spectral density from Equation (4) using Equation (5) and then solving the integral of Equation (3), we obtain
which is regular at . The Landau’s pole has been subtracted, and hence is finite in the infrared (IR) region, namely, at ; in particular, its value at the origin is
Moreover, this result is independent of the order of the loop expansion [4], a property of the theory called infrared stability [2,3]. As a consequence, to have a coupling constant with an explosive IR behavior, divergent in the limit , i.e., a behavior which could produce the color confinement phenomenon of QCD, it needs to define a different spectral density.
The goal of our model is then to go beyond the APT result, which relies on the simple cancellation of Landau’s ghost pole either by subtraction or multiplication. Indeed, in our case, Landau’s pole problem is bypassed by defining a spectral function for the ICC defined in Equation (1), which is inferred by the leading-order expression of the QCD running coupling constant of Equation (5), and by analytically continuing it at each . The advantage of working with the ICC is consequently explained by the fact that confinement is translated into going to zero at . Also, this condition implies the vanishing of the imaginary part of the ICC, which corresponds to the spectral density of Equation (4), in the same limit .
Since the APT does not directly give a confining expression of the ICC, we introduce three different types of regularizing functions in the spectral density of the KL to incorporate color confinement.
The paper is organized as follows. In Section 2, we describe the main features of our model which brings together the methods of the APT and the regularizing function approach. We propose three parameterizations for the regularizing function, ensuring correct high- and low-momentum behaviors, and as a final result, we present analytical formulae for the momentum dependence of both ICC and within two-loop orders. Numerical predictions of ICC and the QCD running coupling constant at certain momentum points and their comparison with experimental data are obtained and discussed in Section 3. In particular, we compute the ICC at the Z-boson mass, i.e., at . Technical details of the calculations are collected in Appendix A.
2. Application of APT Formalism with Additional Regularizing Functions for the ICC
To apply the KL to the ICC of Equation (1), it is necessary to start from its PT expansion [5,6], from which we obtain the renormalization group equation for the ICC
which implies
The solution of Equation (6) truncated at the leading ultraviolet (UV) behavior of the 2-loop order is
where , with . For , it is and . The 1-loop term is , while is the 2-loop correction. Using the KL, we obtain the analytical expressions
where is the spacelike Mandelstam variable. The dispersion relation subtracted at is required, otherwise the integral would be divergent for any complex value of t. The expressions of the two spectral densities are obtained from
Similarly to , Equations (11) and (12) have the correct analytical behavior, although they do not show confinement. We then introduce a regularizing function in the spectral density to achieve
This means that the spectral density, which is the imaginary part of the ICC, also has to be zero in the same limit. Moreover, the regularizing function must also not spoil the correct perturbative UV limit. Therefore, this function can be chosen from the set of arbitrary continuous functions fulfilling the conditions
It follows that the KL representation becomes
where the regularized spectral densities are
The subtraction parameter is then fixed by requiring the vanishing at of the functions of Equation (14). The three parameterizations for the regularizing function , shown in Figure 1, ensuring the correct high- and low-momentum behaviors of Equation (13) are
where and . The constraints on p are demanded by Equation (13); in addition, the condition guarantees the convergence of some integrals appearing in the soft-gluon resummation theory [7]. In other words, we want to be divergent in the IR region but still integrable.
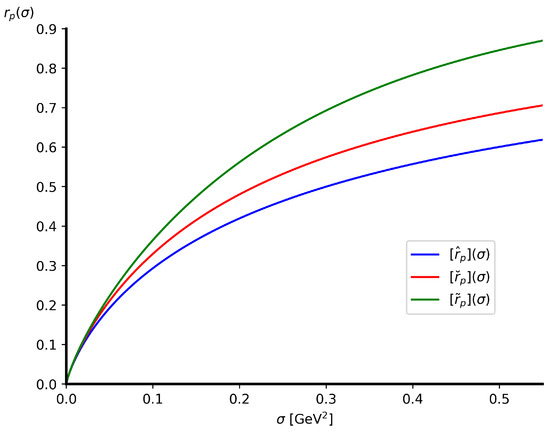
Figure 1.
The three regularizing functions, with and .
To simplify the reading, we present here the scheme to obtain only for the regularizing function in the form of Equation (17). In a similar way, can be obtained for the other two parameterizations. The corresponding calculations are reported in Appendix A.
Thus, following Equation (7), the zero-order ICC is written as
where the regularized spectral density is
Using the expression of Equation (17) for the spectral density, we find the following form
where
By means of the expansion for the regularizing function
with the convergence condition , we obtain
where is the Euler–Mascheroni constant and
is the exponential integral function [5].
We calculate an expression for the ICC at the zeroth order, which is given by a sum of the analytical unconfined ICC of Equation (11) and several confining corrections terms, whose definitions contain the function and the constant .
At the same time, the confined expression for ICC at the first order is obtained by repeating the same steps as in Equation (18). In this way, we obtain an expression which is written in the form of confining corrections to the analytical unconfined contribution of ICC at the first order, see Equation (12), but in this case, the confining corrections are written in an implicit integral form, i.e.,
with
These integrals are not solvable in a closed form because of the function , given in Equation (10). Some procedures for solving the integrals of Equation (20) are defined in Ref. [5].
The details regarding the calculations of the other two parameterizations are given in Appendix A, and additional details can be found in Refs. [5,6].
Our main analytical result can be summarized by the expression
where for the regularizing function with the exponential of Equation (17) are presented in Equations (18) and (19), and the remaining two parameterizations are presented in Appendix A.
3. Numerical Results
First, we illustrate the results obtained in the previous sections by considering the momentum spectra for both and .
In Figure 2 and Figure 3, we show the momentum distributions according to our model for three regularizing function parametrizations, where , , and .
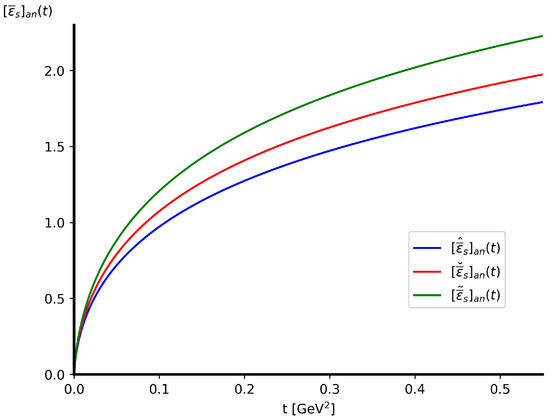
Figure 2.
The ICC , with , and .

Figure 3.
Four-momentum distribution for , for , and .
As a next step, we calculated at the Z-boson mass. Results for several values of p and are reported in Table 1, Table 2 and Table 3. In fact, our values are compatible with the world average value [8]
for all three regularizing function parameterizations. For all values of p and presented in Table 1, Table 2 and Table 3 the difference between the model prediction and the PDG value is less than for all three parameterizations.

Table 1.
Best values of the parameter at fixed values of the parameter p for the model .

Table 2.
Best values of the parameter at fixed values of the parameter p for the model .

Table 3.
Best values of the parameter at fixed values of the parameter p for the model .
By setting MeV, the values of the parameter p obtained by fitting to the data for , measured by the experiments JADE, LEPII, and CMS [9] and the corresponding ’s are
The theoretical curves are shown in Figure 4.
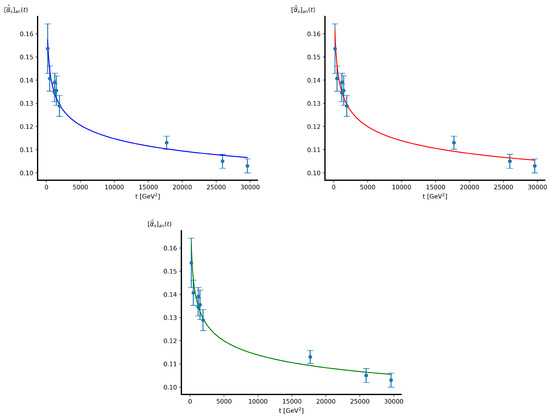
Figure 4.
The running coupling constant , with MeV and the optimal values of p.
In conclusion, it is worth mentioning that all results presented here can be produced using our code [10], both Mathematica [11] and Python versions are presented there. The numerical values produced by the codes differed by less than , and Table 1, Table 2 and Table 3 contain the values obtained from the Python code. It is to be noted that the “quad” method from the scientific library SciPy [12] was applied in the Python code, whereas the “GaussKronrodRule” method was chosen in Mathematica.
4. Conclusions
This study represented an attempt to define an analytic model for the QCD coupling constant, where for the first time, the function of interest was the ICC. The advantage of using the inverse of the coupling constant, which could be interpreted as the QCD vacuum permittivity, lies in the possibility of formally treating poles and hence singularities of the coupling constant, since they coincide with zeros of the ICC. It follows that, assuming quite naturally that the running coupling constant does not vanish at finite values, the analyticity domain of the ICC is larger than that of . In particular, the phenomenon of the QCD color confinement occurring at low momentum, i.e., at large distances, assumed to be a consequence of the divergence of the coupling constant as goes to zero, should correspond to a regular zero for the ICC in the same limit .
The procedure for defining an analytic expression of the ICC as a function of the four-momentum transferred squared, having the desired IR behavior, was achieved by exploiting the APT approach to introduce a parametric regularizing function which ensured the vanishing of the ICC as .
Three possible parameterizations were considered for such a regularizing function. All three expressions, given in Equations (15)–(17), depended on the same pair of parameters, namely, the adimensional power p, whose values were limited in the interval by the convergence condition of the dispersion relations’ integral and the momentum scale .
Concerning the meaning of these parameters, while can be naturally identified as the QCD momentum scale, the adimensional p instead does not have a clear physical interpretation. There are, however, studies (see, e.g., Ref. [7]) where a similar p-power law has been used to regularize soft-gluon resummation in the IR limit of QCD.
Finally, we presented the first attempts to fit the free parameters of the regularizing functions to the data on the QCD coupling constant. Preliminary results, shown in the three panels of Figure 4, which correspond to the three parameterizations of the regularizing functions given in Equations (15)–(17), were quite encouraging because the values which provided the best description of the data were in agreement with the physical expectations. In these cases, by setting the momentum scale to the value of 300 MeV, only single-parameter fits were performed. Such a limitation was due to the computing power required by the double-parameter fit procedure being too high.
A complete study is in progress where the effect of both parameters is taken into account, also considering other observables in which the -functional form of , especially in the IR region, plays a crucial role, such as the hadronic contributions [13,14] to the anomalous magnetic moment of the muon [15] and to the inclusive decay width of the lepton [16].
Author Contributions
Conceptualization, R.M., L.P., O.S. and S.P.; methodology, R.M., L.P., O.S. and S.P.; software, R.M., L.P., O.S. and S.P.; validation, R.M., L.P., O.S. and S.P.; formal analysis, R.M., L.P., O.S. and S.P.; investigation, R.M., L.P., O.S. and S.P.; resources, R.M., L.P., O.S. and S.P.; data curation, R.M., L.P., O.S. and S.P.; writing—original draft preparation, R.M., L.P., O.S. and S.P.; writing—review and editing, R.M., L.P., O.S. and S.P.; visualization, R.M., L.P., O.S. and S.P.; supervision, R.M., L.P., O.S. and S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
This appendix provides a brief guide for the calculation taking into account the regularizing functions of Equations (15) and (16).
Appendix A.1. Model (σ)
The parametrization consists in Equation (15). It has to be inserted in the integral of Equation (8) to obtain the contributions of both ICC contributions. The zero-order term of the regularized spectral density is
Inserting this expression in the integral of Equation (8), we obtain
In the case of , with n and m positive integers, the result is
where
with .
Using the spectral density
we calculate the two-loop ICC term
where and
with and .
Appendix A.2. Model (σ)
The parametrization proposed in Equation (16) gives to the spectral densities the forms [6]
The two contributions to the ICC are therefore calculated by inserting these expressions in Equation (8). We obtain
where is the Gaussian Hypergeometric Function, the analytic continuation of the Gaussian Hypergeometric series
the Pochhammer symbol here is used for the ascending factorial
The two-loop ICC term is not calculated in a closed form, but we arrive at a partial expression which contains a series instead of an integral, valid when
where A is a constant given in terms of an integral depending only on the parameter p, namely,
References
- Srivastava, Y.; Pacetti, S.; Pancheri, G.; Widom, A. Dispersive techniques for alpha(s), R(had) and instability of the perturbative vacuum. arXiv 2001, arXiv:hep-ph/0106005. [Google Scholar] [CrossRef]
- Solovtsov, I.L.; Shirkov, D.V. The analytic approach in quantum chromodynamics. Theor. Math. Phys. 1999, 120, 1220–1244. [Google Scholar] [CrossRef]
- Shirkov, D.V.; Solovtsov, I.L. Ten years of the analytic perturbation theory in QCD. Theor. Math. Phys. 2007, 150, 132–152. [Google Scholar] [CrossRef]
- Milton, K.A.; Solovtsov, I.L. Analytic perturbation theory in QCD and Schwinger’s connection between the β function and the spectral density. Phys. Rev. D 1997, 55, 5295–5298. [Google Scholar] [CrossRef]
- Pierini, L. A Confining Model for the Analytical QCD Running Coupling Constant. 2023. Available online: https://www.fe.infn.it/u/lpierini/perugia/tesi/Tesi_Magistrale_LP.pdf (accessed on 15 July 2024). (In Italian).
- Malaspina, R. Analytic Continuation of the Inverse QCD Coupling Constant. 2023. Available online: https://www.fe.infn.it/u/lpierini/perugia/tesi/Tesi_Magistrale_Malaspina.pdf (accessed on 15 July 2024). (In Italian).
- Grau, A.; Godbole, R.M.; Pancheri, G.; Srivastava, Y.N. Soft gluon kt-resummation and the Froissart bound. Phys. Lett. B 2009, 682, 55–60. [Google Scholar] [CrossRef]
- Huston, J.; Rabbertz, K.; Zanderighi, G. Quantum Chromodynamics. arXiv 2023, arXiv:2312.14015. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; Frühwirth, R.; et al. Measurement of the inclusive 3-jet production differential cross section in proton–proton collisions at 7 TeV and determination of the strong coupling constant in the TeV range. Eur. Phys. J. C 2015, 75, 186. [Google Scholar] [CrossRef] [PubMed]
- Pierini, L.; Malaspina, R. Mathematica and Python Codes to Produce Results in Section 3. 2024. Available online: https://github.com/lorenzo23pierini/alpha_s (accessed on 15 July 2024).
- Wolfram Research Inc. Mathematica, Version 14.0; Wolfram Research: Champaign, IL, USA, 2024. [Google Scholar]
- SciPy Library. 2024. Available online: https://www.scipy2024.scipy.org/ (accessed on 15 May 2024).
- Eidelman, S.; Jegerlehner, F. Hadronic contributions to (g-2) of the leptons and to the effective fine structure constant α(MZ2). Z. Phys. C Part. Fields 1995, 67, 585–601. [Google Scholar] [CrossRef]
- Actis, S.; Arbuzov, A.; Balossini, G.; Beltrame, P.; Bignamini, C.; Bonciani, R.; Carloni Calame, C.M.; Cherepanov, V.; Czakon, M.; Czyż, H. Quest for precision in hadronic cross sections at low energy: Monte Carlo tools vs. experimental data. Eur. Phys. J. C 2010, 66, 585–686. [Google Scholar] [CrossRef]
- Aguillard, D.P.; Albahri, T.; Allspach, D.; Anisenkov, A.; Badgley, K.; Baeßler, S.; Bailey, I.; Bailey, L.; Baranov, V.A.; Barlas-Yucel, E.; et al. Measurement of the Positive Muon Anomalous Magnetic Moment to 0.20 ppm. Phys. Rev. Lett. 2023, 131, 161802. [Google Scholar] [CrossRef] [PubMed]
- Pich, A. Precision tau physics. Prog. Part. Nucl. Phys. 2014, 75, 41–85. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).