Ultrafast Modulations in Stellar, Solar and Galactic Spectra: Dark Matter and Numerical Ghosts, Stellar Flares and SETI
Abstract
1. Introduction
2. Real and “Ghost” Frequencies Introduced by the Data Analysis
2.1. Which Frequency Could Be Better from Axion Physics
2.2. Further Results from Other Observations and Data Analysis
2.3. Frequency Drift and from Different Observations
2.4. Stability in Time of the Ultrafast Oscillations
3. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Properties of the Spectra of the Source Samples
Appendix B. Common Features of Spectral Classes and Spectral Lines
| Spectral | Temperature | Absorption | % Stars | % w/Signal |
|---|---|---|---|---|
| Class | K | Lines | 236 | |
| A | 7.5–10 | H(S), Ca II, Mg II, Fe II | 0.6% | 1.7% |
| F | 6–7.5 | H(w), Ca II | 3% | 61.9% |
| ionized M | ||||
| G | 5.2–6 | H(w), Ca II | 7.6% | 17.4% |
| ionized + neutral M | ||||
| K | 3.7–5.2 | H(W), Ca II (S) | 12.1% | 14.8% |
| neutral M (s) | ||||
| M5 | 2.4-3-7 | Neutral atoms (s), TiO | 76% | 0.4% |
References
- Tamburini, F.; Licata, I. Can the periodic spectral modulations observed in 236 Sloan Sky Survey stars be due to dark matter effects? Phys. Scr. 2017, 92, 095001. [Google Scholar] [CrossRef]
- Kolb, E.W.; Turner, M.S. The Early Universe; Addison-Wesley: New York, NY, USA, 1990. [Google Scholar]
- Li, M.; Li, X.D.; Wang, S.; Wang, Y. Dark energy: A brief review. Front. Phys. 2013, 8, 828–846. [Google Scholar] [CrossRef]
- Clarkson, C.; Ellis, G.; Larena, J.; Umeh, O. Does the growth of structure affect our dynamical models of the universe? The averaging, backreaction and fitting problems in cosmology. Rept. Prog. Phys. 2011, 74, 112901. [Google Scholar] [CrossRef]
- The Planck Collaboration. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Clowe, D.; Gonzalez, A.; Markevich, M. Weak lensing mass reconstruction of the interacting cluster 1E0657-558: Direct evidence for the existence of dark matter. Astrophys. J. 2003, 604, 596–603. [Google Scholar] [CrossRef]
- Markevitch, M.; Gonzalez, A.H.; Clowe, D.; Vikhlinin, A.; David, L.; Forman, W.; Jones, C.; Murray, S.; Tucker, W. Direct constraints on the dark matter self-interaction cross-section from the merging galaxy cluster 1E0657-56. Astrophys. J. 2003, 606, 819–824. [Google Scholar] [CrossRef]
- Zwicky, F. Astrophysics and Dark Matter Theory. Helv. Phys. Acta 1933, 6, 110. [Google Scholar]
- Bertone, G.; Hooper, D.; Silk, J. Particle Dark Matter: Evidence, Candidates and Constraints. Phys. Rep. 2005, 405, 279. [Google Scholar] [CrossRef]
- Frenk, C.S.; White, S.D.M. Dark matter and cosmic structure. Ann. Phys. 2012, 524, 507. [Google Scholar] [CrossRef]
- Fields, B.D.; Molaro, P.; Sarkar, S. Big-Bang Nucleosynthesis, in The Review of Particle Physics 2014 by the Particle Data Group. Chin. Phys. C 2014, 38, 339–344. [Google Scholar]
- Preskill, J.; Wise, M.B.; Wilczek, F. Cosmology of the Invisible Axion. Phys. Lett. B 1983, 120, 127–132. [Google Scholar] [CrossRef]
- Abbott, L.F.; Sikivie, P. A Cosmological Bound on the Invisible Axion. Phys. Lett. B 1983, 120, 133–136. [Google Scholar] [CrossRef]
- Dine, M.; Fischler, W. The Not So Harmless Axion. Phys. Lett. B 1983, 120, 137–141. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H. CP Conservation in the Presence of Pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Guenther, J.; Kampert, K.H.; Katz, S.D.; Kawanai, T.; Kovacs, T.G.; Mages, S.W.; Pasztor, A.; Pittler, F.; et al. Calculation of the axion mass based on high-temperature lattice quantum chromodynamics. Nature 2016, 539, 69–71. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Kampert, K.-H.; Katz, S.D.; Kawanai, T.; Kovacs, T.G.; Mages, S.W.; Pasztor, A.; Pittler, F.; Redondo, J.; et al. Lattice QCD for Cosmology, DESY 16-105. arXiv 2016, arXiv:1606.07494v2. [Google Scholar]
- Buschmann, M.; Foster, J.W.; Hook, A.; Peterson, A.; Willcox, D.E.; Zhang, W.; Safdi, B.R. Dark matter from axion strings with adaptive mesh refinement. Nat. Commun. 2022, 13, 1049. [Google Scholar] [CrossRef]
- Galanti, G.; Roncadelli, M.; Tavecchio, F. Explanation of the very-high-energy emission from GRB221009A. arXiv 2022, arXiv:2210.05659. [Google Scholar]
- Zhang, G.; Ma, B.Q. Axion-photon conversion of LHAASO multi-TeV and PeV photons. Chin. Phys. Lett. 2023, 40, 011401. [Google Scholar] [CrossRef]
- Nakagawa, S.; Takahashi, F.; Yamada, M.; Yin, W. Axion dark matter from first-order phase transition, and very high energy photons from GRB 221009A. Phys. Lett. B 2023, 839, 137824. [Google Scholar] [CrossRef]
- Anastassopoulos, V.; Aune, S.; Barth, K.; Belov, A.; Cantatore, G.; Carmona, J.M.; Castel, J.F.; Cetin, S.A.; Christensen, F.; Collar, J.I.; et al. New CAST limit on the axion-photon interaction. Nat. Phys. 2017, 13, 584–590. [Google Scholar]
- Duffy, L.D.; van Bibber, K. Axions as Dark Matter Particles. New J. Phys. 2009, 11, 105008. [Google Scholar] [CrossRef]
- Wilczek, F. Two applications of axion electrodynamics. Phys. Rev. Lett. 1987, 58, 1799. [Google Scholar] [CrossRef]
- Sikivie, P. Experimental Tests of the Invisible Axion. Phys. Rev. Lett. 1983, 51, 1415. [Google Scholar] [CrossRef]
- Olive, K.A.; Particle Data Group. Review of Particle Physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Bertone, G. The moment of truth for WIMP Dark Matter. Nature 2010, 468, 389. [Google Scholar] [CrossRef]
- Akerib, D.S.; Alsum, S.; Araújo, H.M.; Bai, X.; Bailey, A.J.; Balajthy, J.; Beltrame, P.; Bernard, E.P.; Bernstein, A.; Biesiadzinski, T.P.; et al. (LUX Collaboration), Results from a Search for Dark Matter in the Complete LUX Exposure. Phys. Rev. Lett. 2017, 118, 021303. [Google Scholar] [CrossRef]
- Tan, A.; Xiao, M.; Cui, X.; Chen, X.; Chen, Y.; Fang, D.; Fu, C.; Giboni, K.; Giuliani, F.; Gong, H.; et al. Dark Matter Results from First 98.7 Days of Data from the PandaX-II Experiment. Phys. Rev. Lett. 2016, 117, 121303. [Google Scholar] [CrossRef]
- Eröncel, C.; Servant, G. ALP dark matter mini-clusters from kinetic fragmentation. J. Cosmol. Astropart. Phys. 2023, 2023, 009. [Google Scholar] [CrossRef]
- Chatrchyan, A.; Eröncel, C.; Koschnitzke, M.; Servant, G. ALP dark matter with non-periodic potentials: Parametric resonance, halo formation and gravitational signatures. arXiv 2023, arXiv:2305.03756. [Google Scholar] [CrossRef]
- Davidson, S. Axions: Bose Einstein condensate or classical field? Astropart. Phys. 2015, 65, 101–107. [Google Scholar] [CrossRef]
- Barranco, J.; Carrillo Monteverde, A.; Delepine, D. Can the dark matter halo be a collisionless ensemble of axion stars? Phys. Rev. D 2013, 87, 103011. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Okawa, H. Accretion of dark matter by stars. Phys. Rev. Lett. 2015, 115, 111301. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Macedo, F.B.; Okawa, H.; Palenzuela, C. Interaction between bosonic dark matter and stars. Phys. Rev. D 2016, 93, 044045. [Google Scholar] [CrossRef]
- Borra, E.F.; Trottier, E. Discovery of peculiar periodic spectral modulations in a small fraction of solar type stars. Publ. Astron. Soc. Pac. 2016, 128, 969. [Google Scholar] [CrossRef]
- Borra, E.F. The Discovery of Periodic Modulations In The Optical Spectra of Galaxies, Possibly Due to Ultrarapid Light Bursts From Their Massive Central Black Holes. Astrophys. J. 2013, 774, 142. [Google Scholar] [CrossRef]
- Kurucz, R.L. New atlases for solar flux, irradiance, central intensity, and limb intensity. Mem. Della Soc. Astron. Ital. Suppl. 2005, 8, 189. [Google Scholar]
- Kurucz, R.L. Physical, numerical, and computational limits for Kurucz codes. Mem. Della Soc. Astron. Ital. Suppl. 2005, 8, 73. [Google Scholar]
- Hippke, M. Periodic Spectral Modulations Arise from Nonrandom Spacing of Spectral Absorption Lines. Publ. Astron. Soc. Pac. 2019, 131, 034502. [Google Scholar] [CrossRef]
- Isaacson, H.; Siemion, A.P.V.; Marcy, G.W.; Hickish, J.; Price, D.C.; Enriquez, J.E.; Gizani, N. The Breakthrough Listen Search for Intelligent Life: No Evidence of Claimed Periodic Spectral Modulations in High-resolution Optical Spectra of Nearby Stars. Publ. Astron. Soc. Pac. 2019, 131, 014201. [Google Scholar] [CrossRef]
- Ma, P.X.; Ng, C.; Rizk, L.; Croft, S.; Siemion, A.P.; Brzycki, B.; Czech, D.; Drew, J.; Gajjar, V.; Hoang, J.; et al. A deep-learning search for technosignatures from 820 nearby stars. Nat. Astron. 2023, 7, 492–502. [Google Scholar] [CrossRef]
- Aiello, L.; Richardson, J.W.; Vermeulen, S.M.; Grote, H.; Hogan, C.; Kwon, O.; Stoughton, C. Constraints on Scalar Field Dark Matter from Colocated Michelson Interferometers. Phys. Rev. Lett. 2022, 128, 121101. [Google Scholar] [CrossRef] [PubMed]
- Abi, B.; The Muon g-2 Collaboration. Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm. Phys. Rev. Lett. 2021, 126, 141801. [Google Scholar] [CrossRef] [PubMed]
- Janish, R.; Ramani, H. Muon g-2 and EDM experiments as muonic dark matter detectors. Phys. Rev. D 2020, 102, 115018. [Google Scholar] [CrossRef]
- Gurgone, A. On behalf of the McMule Team. Looking for an axion in a haystack of muons. J. Instrum. 2023, 18, C08006. [Google Scholar] [CrossRef]
- Buen-Abad, M.A.; Fan, J.; Reece, M.; Sun, C. Challenges for an axion explanation of the muon g-2 measurement. J. High Energy Phys. 2021, 2021, 101. [Google Scholar] [CrossRef]
- Brdar, V.; Jana, S.; Kubo, J.; Lindner, M. Semi-secretly interacting Axion-like particle as an explanation of Fermilab muon g-2 measurement. Phys. Lett. B 2021, 820, 136529. [Google Scholar] [CrossRef]
- Alexandrou, C.; Bacchio, S.; De Santis, A.; Dimopoulos, P.; Finkenrath, J.; Frezzotti, R.; Gagliardi, G.; Garofalo, M.; Hadjiyiannakou, K.; Kostrzewa, B.; et al. Probing the energy-smeared R-ratio using lattice QCD. Phys. Rev. Lett. 2023, 130, 241901. [Google Scholar] [CrossRef] [PubMed]
- Ruelle, D.; Takens, F. On the Nature of Turbulence. Commun. Math. Phys. 1971, 20, 167–192. [Google Scholar] [CrossRef]
- Valdez-Alvarado, S.; Palenzuela, C.; Alic, D.; Ureña-López, L.A. Dynamical evolution of fermion-boson stars. Phys. Rev. D 2013, 87, 084040. [Google Scholar] [CrossRef]
- Masaki, E.; Aoki, A.; Soda, J. Photon-Axion Conversion, Magnetic Field Configuration, and Polarization of Photons. Phys. Rev. D 2017, 96, 043519. [Google Scholar] [CrossRef]
- The Event Horizon Telescope—Multi-Wavelength Science Working Group; The Event Horizon Telescope Collaboration; The Fermi Large Area Telescope Collaboration; H.E.S.S. Collaboration; MAGIC Collaboration; VERITAS Collaboration; EAVN Collaboration. Broadband Multi-wavelength Properties of M87 during the 2018 EHT Campaign including a Very High Energy Flaring Episode. arXiv 2024, arXiv:2404.17623. [Google Scholar]
- Tamburini, F.; Thidé, B.; Della Valle, M. Measurement of the spin of the M87 black hole from its observed twisted light. Mon. Not. R. Astron. Soc. Lett. 2020, 492, L22–L27. [Google Scholar] [CrossRef]
- Murchikova, L. S0-2 Star, G1- and G2-objects, and Flaring Activity of the Milky Way’s Galactic Center Black Hole in 2019. Astrophys. J. Lett. 2021, 910, L1. [Google Scholar] [CrossRef]
- Clayton, D.D. Principles of Stellar Evolution and Nucleosynthesis; The University of Chicago Press: Chicago, IL, USA, 1983. [Google Scholar]
- Padmanabhan, T. Theorethical Astrophysics; Volume II: Stars and Stellar Systems; Cambrige University Press: New York, NY, USA, 2001. [Google Scholar]
- Iben, I., Jr. Stellar Evolution Physics; Cambrige University Press: London, UK, 2013. [Google Scholar]
- Kolb, E.W.; Tkachev, I.I. Axion Miniclusters and Bose Stars. Phys. Rev. Lett. 1993, 71, 3051–3054. [Google Scholar] [CrossRef] [PubMed]
- Visinelli, L.; Baum, S.; Redondo, J.; Freese, K.; Wilczek, F. Dilute and dense axion stars. Phys. Lett. B 2018, 777, 64–72. [Google Scholar] [CrossRef]
- Visinelli, L. Boson Stars and Oscillatons: A Review, accepted for publication on IJMPD. Int. J. Mod. Phys. D 2021, 30, 2130006. [Google Scholar] [CrossRef]
- Kumar, S.; Kulshreshtha, U.; Kulshreshtha, D.S. Charged Compact Boson Stars and Shells in the Presence of a Cosmological Constant. Phys. Rev. D 2016, 94, 125023. [Google Scholar] [CrossRef]
- Beck, C. Axion mass estimates from resonant Josephson junctions. Phys. Dark Univ. 2015, 7–8, 6–11. [Google Scholar] [CrossRef][Green Version]
- Yoon, Y.S.; Park, H.K.; Bhang, H.; Choi, J.H.; Choi, S.; Hahn, I.S.; Jeon, E.J.; Joo, H.W.; Kang, W.G.; Kim, B.H.; et al. Search for solar axions with CsI(Tl) crystal detectors. J. High Energ. Phys. 2016, 11, 1–10. [Google Scholar] [CrossRef]
- Ballesteros, G.; Redondo, J.; Ringwald, A.; Tamarit, C. Unifying inflation with the axion, dark matter, baryogenesis and the seesaw mechanism. Phys. Rev. Lett. 2017, 118, 071802. [Google Scholar] [CrossRef] [PubMed]
- Di Luzio, L.; Giannotti, M.; Nardi, E.; Visinelli, L. The landscape of QCD axion models. Phys. Rep. 2020, 870, 1–117. [Google Scholar]
- Tartini, G. Trattato di musica secondo la vera scienza dell’armonia; Stamperia del Seminario: Padova, Italy, 1754. [Google Scholar]
- Helmholtz, H.L. Die Lehre von den Tonempfindungen als Physiologische Grundlage für die Theorie der Musik (in German, 1863 1st ed.) on the Sensations of Tone as a Physiological Basis for the Theory of Music; Longmans, Green, and Co., Translated in English by Ellis, Alexander J.; Cambridge University Press: Cambridge, UK, 1877. [Google Scholar]
- Caselli, G.; Cecchi, G.; Malacarne, M.; Masetti, G. Analysis of violin combination tones and their contribution to Tartini’s third tone. Savart J. 2020. Available online: https://openportal.isti.cnr.it/data/2020/447372/2020_447372.published.pdf (accessed on 21 June 2024).
- Caselli, G.; Cecchi, G.; Masetti, G. Characteristics, mechanisms, and perceivability of combination tones in violins. J. Acoust. Soc. Am. 2022, 152, 2513–2523. [Google Scholar] [CrossRef]
- Curdt, W.; Brekke, P.; Feldman, U.; Wilhelm, K.; Dwivedi, B.N.; Schühle, U.; Lemaire, P. The SUMER spectral atlas of solar-disk features. Astron. Astrophys. 2001, 375, 591–613. [Google Scholar] [CrossRef]
- DDelbouille, L.; Neven, L.; Roland, G. Atlas photométrique du spectre solaire de λ3000 a λ10000; Institut d’Astrophysique, Université de Liège: Liège, Belgium, 1973. [Google Scholar]
- Delbouille, L.; Roland, G.; Brault, J.W.; Testerman, L. Photometric Atlas of the Solar Spectrum from 1850 to 10,000 cm−1; Kitt Peak National Observatory: Tucson, AR, USA, 1981. [Google Scholar]
- Krucker, S.; Giménez de Castro, C.G.; Hudson, H.S.; Kudaka, A.S.; Cabezas, D.P.; Cassiano, M.M.; Francile, C.; Fernandes, L.O.T.; Hidalgo Ramirez, R.F.; Luoni, M.; et al. Solar flares at submillimeter wavelengths. Astron. Astrophys. Rev. 2013, 21, 58. [Google Scholar] [CrossRef]
- Kaufmann, P.; White, S.M.; Marcon, R.; Kudaka, A.S.; Cabezas, D.P.; Cassiano, M.M.; Francile, C.; Fernandes, L.O.T.; Hidalgo Ramirez, R.F.; Luoni, M.; et al. Bright 30 THz impulsive solar bursts. Geophys. Res. Space Phys. 2015, 120, 4155–4163. [Google Scholar] [CrossRef]
- Kaufmann, P.; Giménez de Castro, C.G.; Correia, E.; Costa, J.E.; Raulin, J.P.; Valio, A.S. Rapid Pulsations in Sub-THz Solar Bursts. Astrophys. J. 2009, 697, 420–427. [Google Scholar] [CrossRef]
- Walker, C.K. Terahertz Astronomy; CRC Press; Taylor & Francis Group: Boca Raton, FL, USA, 2016. [Google Scholar]
- Lynn, D.; Matthews, L.D. Radio Stars: From kHz to THz. Publ. Astron. Soc. Pac. 2019, 131, 016001. [Google Scholar]
- Marshall, J.P.; Kirchschlager, F.; Ertel, S.; Augereau, J.C.; Kennedy, G.M.; Booth, M.; Wolf, S.; Montesinos, B.; Eiroa, C.; Matthews, B. Interpreting the extended emission around three nearby debris disc host stars. Astron. Astrophys. 2014, 570, A114. [Google Scholar] [CrossRef]
- Diemand, J.; Kuhlen, M.; Madau, P.; Zemp, M.; Moore, B.; Potter, D.; Stadel, J. Clumps and streams in the local dark matter distribution. Nature 2008, 454, 735–738. [Google Scholar] [CrossRef] [PubMed]
- Inoue, K.T.; Minezaki, T.; Matsushita, S.; Nakanishi, K. ALMA Measurement of 10 kpc Scale Lensing-power Spectra toward the Lensed Quasar MG J0414+0534. Astrophys. J. 2023, 954, 197. [Google Scholar] [CrossRef]
- Rogers, K.K.; Hlǒzek, R.; Lagüe, A.; Ivanov, M.M.; Philcox, O.H.; Cabass, G.; Akitsu, K.; Marsh, D.J. Ultra-light axions and the S8 tension: Joint constraints from the cosmic microwave background and galaxy clustering. J. Cosmol. Astropart. Phys. 2023, 2023, 023. [Google Scholar] [CrossRef]
- Raffelt, G.G. Stars as Laboratories for Fundamental Physics; The University of Chicago Press: Chicago, IL, USA; London, UK, 1996; ISBN 9780226702728. [Google Scholar]
- Friedland, A.; Giannotti, M.; Wise, M. Constraining the Axion-Photon Coupling with Massive Stars. Phys. Rev. Lett. 2013, 110, 061101. [Google Scholar] [CrossRef] [PubMed]
- Millar, A.J.; Baum, S.; Lawson, M.; Marsh, M.C.D. Axion-photon conversion in strongly magnetised plasmas. J. Cosmol. Astropart. Phys. 2021, 2021, 013. [Google Scholar] [CrossRef]
- Gnedin, Y.N. Searching for Massless and Low Mass Axions by Astronomical and Experimental Methods. Comments Astrophys. 1996, 18, 257. [Google Scholar]
- Dent, J.B.; Dutta, B.; Newstead, J.L.; Thompson, A. Inverse Primakoff Scattering as a Probe of Solar Axions at Liquid Xenon Direct Detection Experiments. Phys. Rev. Lett. 2020, 125, 131805. [Google Scholar] [CrossRef]
- Arnquist, I.J.; Avignone, F.T., III; Barabash, A.S.; Barton, C.J.; Bhimani, K.H.; Blalock, E.; Bos, B.; Busch, M.; Buuck, M.; Caldwell, T.S.; et al. Search for solar axions via axion-photon coupling with the Majorana Demonstrator. Phys. Rev. Lett. 2022, 129, 081803. [Google Scholar] [CrossRef]
- Liebling, S.L.; Palenzuela, C. Dynamical Boson Stars. Living Rev. Relativ. 2017, 20, 5. [Google Scholar] [CrossRef]
- Jofré, P.; Weiss, A. The age of the Milky Way halo stars from the Sloan Digital Sky Survey. Astron. Astrophys. 2011, 533, A59. [Google Scholar]
- Borra, E.F. Spectral signatures of ultra-rapidly varying objects in spectroscopic surveys. Astron. Astrophys. Lett. 2010, 511, L6. [Google Scholar] [CrossRef]
- Borra, E.F. Searching for Extraterrestrial Intelligence Signals In Astronomical Spectra, Including Existing Data. Astron. J. 2012, 144, 181. [Google Scholar] [CrossRef]
- Kitamura, J.R.; Martins, L.P.; Coelho, P. A study on missing lines in the synthetic solar spectrum near the Ca triplet. Astron. Astrophys. 2017, 600, A58. [Google Scholar] [CrossRef]
- Scott, P.; Grevesse, N.; Asplund, M.; Sauval, A.J.; Lind, K.; Takeda, Y.; Collet, R.; Trampedach, R.; Hayek, W. The elemental composition of the Sun I. The intermediate mass elements Na to Ca. Astron. Astrophys. 2015, 573, A25. [Google Scholar] [CrossRef]
- Kennicutt, R.C., Jr. The Integrated Spectra of Nearby Galaxies: General Properties and Emission-Line Spectra. Astrophys. J. 1992, 388, 310–327. [Google Scholar] [CrossRef]
- Giannotti, M.; Irastorza, I.; Redondo, J.; Ringwald, A. Cool WISPs for stellar cooling excesses. J. Cosmol. Astropart. Phys. 2016, 5, 057. [Google Scholar] [CrossRef]
- Fernie, J.D. The λ 4226 Line as a Spectrum–Luminosity Indicator in Late-Type Stars. Mon. Not. R. Astron. Soc. 1966, 132, 485–493. [Google Scholar] [CrossRef][Green Version]
- Skrutskie, M.F.; Cutri, R.; Stiening, R.; Weinberg, M.D.; Schneider, S.; Carpenter, J.M.; Beichman, C.; Capps, R.; Chester, T.; Elias, J.; et al. The Two Micron All Sky Survey (2MASS). Astron. J. 2006, 131, 1163. [Google Scholar] [CrossRef]
- West, A.A.; Hawley, S.L.; Walkowicz, L.M.; Covey, K.R.; Silvestri, N.M.; Raymond, S.N.; Harris, H.C.; Munn, J.A.; McGehee, P.M.; Ivezić, Ž.; et al. Spectroscopic Properties of Cool Stars In The Sloan Digital Sky Survey: N Analysis of Magnetic Activity and A Search for Subdwarfs. Astron. J. 2004, 12, 426–436. [Google Scholar] [CrossRef]
- Habets, G.M.H.J.; Heinze, J.R.W. Empirical bolometric corrections for the main-sequence. Astron. Astrophys. Suppl. Ser. 1981, 46, 193–237. [Google Scholar]
- Ledrew, G. The Real Starry Sky. J. R. Astron. Soc. Can. 2001, 95, 32. [Google Scholar]
- Silva, D.R.; Cornell, M.E. A New Library of Stellar Optical Spectra. Astrophys. J. Suppl. 1992, 81, 865–881. [Google Scholar] [CrossRef]
- Bjørgen, J.P.; Sukhorukov, A.V.; Leenaarts, J.; Carlsson, M.; de la Cruz Rodríguez, J.; Scharmer, G.B.; Hansteen, V.H. Three-dimensional modeling of the Ca II H and K lines in the solar atmosphere. Astron. Astrophys. 2018, 611, A62. [Google Scholar] [CrossRef]
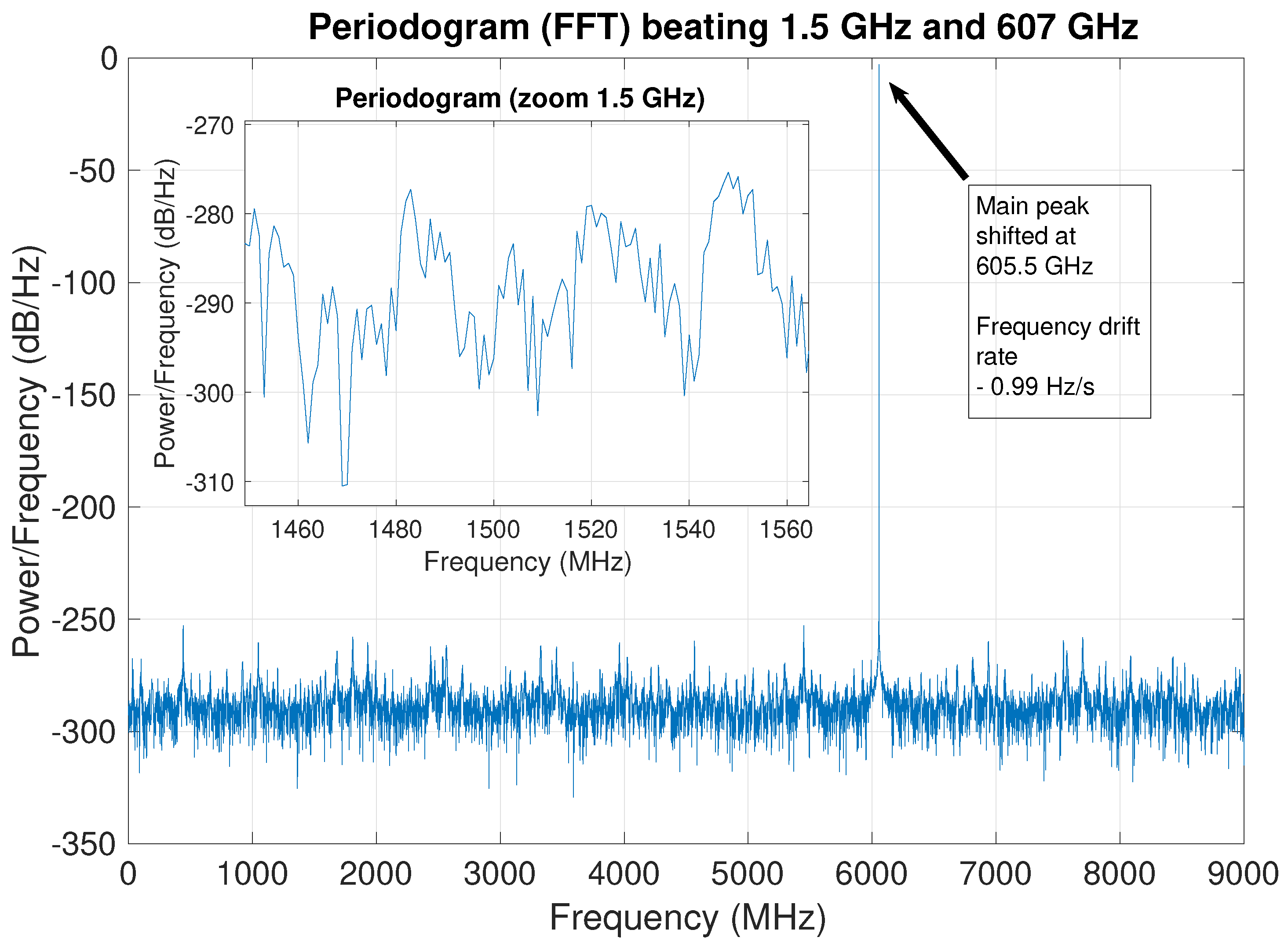
| Star | Drift Rate | Simulated | Frequency | SpT |
|---|---|---|---|---|
| HIP 62207 | Hz/s | MHz | G0 V | |
| ” | Hz/s | Hz/s | MHz | ” |
| HIP 54677 | Hz/s | MHz | K4V | |
| ” | Hz/s | Hz/s | MHz | ” |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamburini, F.; Licata, I. Ultrafast Modulations in Stellar, Solar and Galactic Spectra: Dark Matter and Numerical Ghosts, Stellar Flares and SETI. Particles 2024, 7, 576-594. https://doi.org/10.3390/particles7030032
Tamburini F, Licata I. Ultrafast Modulations in Stellar, Solar and Galactic Spectra: Dark Matter and Numerical Ghosts, Stellar Flares and SETI. Particles. 2024; 7(3):576-594. https://doi.org/10.3390/particles7030032
Chicago/Turabian StyleTamburini, Fabrizio, and Ignazio Licata. 2024. "Ultrafast Modulations in Stellar, Solar and Galactic Spectra: Dark Matter and Numerical Ghosts, Stellar Flares and SETI" Particles 7, no. 3: 576-594. https://doi.org/10.3390/particles7030032
APA StyleTamburini, F., & Licata, I. (2024). Ultrafast Modulations in Stellar, Solar and Galactic Spectra: Dark Matter and Numerical Ghosts, Stellar Flares and SETI. Particles, 7(3), 576-594. https://doi.org/10.3390/particles7030032






